热工过程自动调节,课后习题答案,1到6章
(完整版)热工基础课后题答案

(完整版)热⼯基础课后题答案⼆零⼀七年,秋第⼀章热⼒学第⼀定律1-1⽤⽔银压⼒计测量容器中的压⼒,在⽔银柱上加⼀段⽔,若⽔柱⾼1020mm ,⽔银柱⾼900mm ,当时⼤⽓压⼒计上的度数为b 755mmHg p =。
求容器中⽓体的压⼒。
解:查表可知:21mmH O=9.80665Pa 1mmHg=133.3224Pa 由题中条件可知2H O Hg b1020 mm 9.80665 Pa 900mm 133.3224Pa 755mm 133.3224Pa 230.651 KPa 0.231MPap p p p =++=?+?+?=≈容器即容器中⽓体的压⼒为0.231MPa 。
1-2容器中的真空度为600mmHg v p =,⽓压计上的⾼度是b 755mmHg p =,求容器中⽓体的绝对压⼒(⽤Pa 表⽰)。
如果容器中的绝对压⼒不变,⽽⽓压计上⾼度为b 770mmHg p =,求此时真空表的度数(以mmHg 表⽰).解:因为600mmHg=600mm 133.3224Pa=79993.4Pa v p =? b 755mmHg=755mm 133.3224Pa=100658.4Pa p =?容器中⽓体的绝对压⼒为b v 100658.479993.420665Pa p p p =-=-=若以mmHg 表⽰真空度,则2066520665Pa=mmHg 155mmHg 133.3224p ==则当⽓压计⾼度为b 770mmHg p =时,真空表的读数为770mmHg 155mmHg 615mmHg vb p p p '=-=-=1-3⽤斜管压⼒计测量锅炉烟道⽓的真空度,管⼦倾斜⾓30α=?,压⼒计使⽤密度30.8g/cm ρ=的煤油,斜管中液柱长200mm l =,当地⼤⽓压⼒b 745mmHg p =。
求烟⽓的真空度(mmHg )及绝对压⼒。
解:压⼒计斜管中煤油产⽣的压⼒为33sin 0.810kg /m 9.80.2m sin30=784Pa j p gl ρα==当地⼤⽓压为b 745mmHg=745mm 133.3224Pa/mm=99325.2Pa p =?则烟⽓的绝对压⼒为b j 99325.2Pa 784Pa 98541.2Pa p p p =-=-=若压⼒计斜管中煤油产⽣的压⼒⽤mmH 2O 表⽰,则烟⽓的真空度为22784=784Pa=mmH O=79.95mmH O 9.80665j p1-6⽓体初态为3110.3MPa, 0.2m p V ==,若在等压条件下缓慢可逆地膨胀到320.8m V =,求⽓体膨胀所做的功。
热工原理课后习题答案

提供的热量为:
•
Q m质(h2 h1)
(1)用平均定压质量比热容数据计算
查表并通过插值可得到:
cP
20 0
1.0044kJ
/(kg.K )
cP
270 0
1.0169kJ
/(kg.K )
cP
270 20
270 1.0169 270
20 1.0044 20
1.0179kJ
/(kg.K )
•
tw1
t f1
q h
20
24.66 4
13.840C
tw2
t f2
q h
10
24.66 6
5.890 C
8-6 解:传热系数 h
1 1
1
1
1 0.4
1
0.8696W /(m2 K )
h1 h2 4 0.5 10
热流通量为: q h t f1 t f2 0.8696 20+10=26.087W / m2
1.8105 Pa
前两种情况能使气球充到 2m3
W pb ΔV 0.9 105 2 1.8 105 J
情况三:
V气球+贮气罐=
p贮气罐V贮气罐 pb
0.15 2 0.09
3.333m3
所以气球只能被充到V气球=3.333-2=1.333m3 的大小,故气体对外作的功为:
W 0.9105 1.333 1.2105 J
6-6 解: (1)k=1.4
循环热效率为:
1
1 k1
1
1 7.51.41
55.33%
压缩过程为可逆绝热过程,所以有:
k 1
T2
T1
v1 v2
东北电力大学自动化学院热工基础课后习题答案

热工基础答案第一章1-1 解:kPa bar p b 100.61.00610133.37555==⨯⨯=-1. kPa p p p g b 6.137********.100=+=+=2. kPa bar p p p b g 4.149494.1006.15.2==-=-=3. kPa mmHg p p p v b 3315.755700755==-=-=4. kPa bar p p p b v 6.50506.05.0006.1==-==-1-2图1-8表示常用的斜管式微压计的工作原理。
由于有引风机的抽吸,锅炉设备的烟道中的压力将略低于大气压力。
如果微压机的斜管倾斜角︒=30α, 管内水 解:根据微压计原理,烟道中的压力应等于环境压力和水柱压力之差 mmHg Pa gh p 35.79805.0102008.91000sin 3==⨯⨯⨯⨯=-αρ=水柱mmHg p p p b 65.74835.7756=-=-=水柱1-3解:bar p p p a b 07.210.197.01=+=+= bar p p p b 32.075.107.212=-=-= bar p p p b C 65.032.097.02=-=-=1-4 解:kPa H p p p b 2g mm 15745760==-==汞柱真空室- kPa p p p a 36236021=+=+=真空室kPa p p p b 19217036212=-=-= kPa p p p b c 1902192=-=-=真空室kN A p p F b 8.150.45π41133.3745)(2=⨯⨯⨯⨯=-=真空室1-4 解:bar mmHg p p p p b 11.215828003.133/81.9300760=⨯+==++=+汞柱水柱1-5解:由于压缩过程是定压的,所以有KJ V V p pdV W V V 200)4.08.0(105.0)(62121=-⨯⨯=-==⎰1-6解:改过程系统对外作的功为⎰⎰=--===--0.50.33.013.023.1111.33.115.03.02585.)(0.3VW 1kJ V V V p dV V p pdV1-7 解:由于空气压力正比于气球的直径,所以可设cD p =,式中c 为常数,D 为气球的直径,由题中给定的初始条件,可以得到:5000003.015000011====D p D p c该过程空气对外所作的功为kJD D c dD D c D cDd pdV W D D D D V V 36.34)3.04.0(500000081)(8121)61(44414233212121=-⨯⨯=-====⎰⎰⎰ππππ1-8 解:(1)气体所作的功为:⎰⨯=⨯+=0.30.146101.76d 100.04)(0.24J V V W(2)摩擦力所消耗的功为:J L f W 10000.1)(0.32.01000Δ=-⨯==摩擦力所以减去摩擦力消耗的功后活塞所作的功为: J W W W 41066.1⨯-==摩擦力活塞1-9 解:由于假设气球的初始体积为零,则气球在充气过程中,内外压力始终保持相等,恒等于大气压力0.09MPa ,所以气体对外所作的功为:J V p W 56108.121009.0⨯=⨯⨯==∆1-11 解:确定为了将气球充到2m 3的体积,贮气罐内原有压力至少应为(此时贮气罐的压力等于气球中的压力,同时等于外界大气压b p )Pa V V p V V p p 551121121101.822)(2100.92)(2)(⨯=+⨯⨯=+=+=前两种情况能使气球充到2m 3J V p W b 55101.82100.9Δ⨯=⨯⨯==情况三:3333.309.0215.0m p V p V b=⨯=贮气罐贮气罐气球+贮气罐=所以气球只能被充到3333.12333.3m V =-=气球的大小,故气体对外作的功为:J W 55101.231.33100.9⨯=⨯⨯=第二章 习 题2-1 解:kJ U Q W 308050Δ-=-=-= ,所以是压缩过程 2-2 解:kJ Q W Q W 145012006502000放压吸膨=-+=-+= 2-3 解:h J Q U /107.23600102Δ63⨯=⨯⨯== 2-4解:状态b 和状态a 之间的内能之差为:kJ W Q U U U a b ab 6040100Δ=-=-=-=所以,a-d-b 过程中工质与外界交换的热量为:kJ W U Q ab b d a 802060Δ=+=+=--工质沿曲线从b 返回初态a 时,工质与外界交换的热量为:kJ W U W U U Q ab b a a b 903060Δ-=--=+-=+-=-根据题中给定的a 点内能值,可知b 点的内能值为60kJ ,所以有:kJ U U U d b ad 204060=-=-=∆由于d-b 过程为定容过程,系统不对外作功,所以d-b 过程与外界交换的热量为:kJ U U U Q db b d b d 20=∆=-=-所以a-d-b 过程系统对外作的功也就是a-d 过程系统对外作的功,故a-d 过程系统与外界交换的热量为:kJ W U W U U Q b d a ad d a a d d a 60)20(40=--=-∆=--=----2-52-5 解:由于汽化过程是定温、定压过程,系统焓的变化就等于系统从外界吸收的热量,即汽化潜热,所以有:kg kJ q h /2257Δ==内能的变化为:kgkJ v v p h pv h u /20881.674)(0.001101.012257)()(Δ212=-⨯⨯+=--∆=∆-∆=2-6 解:选取气缸中的空气作为研究的热力学系统,系统的初压为:Pa A G p p b 54511102.939101009.8195101.028⨯=⨯⨯+⨯=+=-当去掉一部分负载,系统重新达到平衡状态时,其终压为:Pa AG p p b 54522101.959101009.895101.028⨯=⨯⨯+⨯=+=-由于气体通过气缸壁可与外界充分换热,所以系统的初温和终温相等,都等于环境温度即:021T T T ==根据理想气体的状态方程可得到系统的终态体积,为:335245211210261.5101.959101010100102.939m p V p V ---⨯=⨯⨯⨯⨯⨯⨯==所以活塞上升的距离为: cm m AV V L 26.5260.0510100101010010261.5Δ46312==⨯⨯⨯-⨯=-=---由于理想气体的内能是温度的函数,而系统初温和终温相同,故此过程中系统的内能变化为零,同时此过程可看作定压膨胀过程,所以气体与外界交换的热量为:J L A p W Q 04.103260.0510100101.959Δ452=⨯⨯⨯⨯===-2-8 解:压缩过程中每千克空气所作的压缩功为:kg kJ u q w /196.5146.550Δ-=--=-=忽略气体进出口宏观动能和势能的变化,则有轴功等于技术功,所以生产每kg 压缩空气所需的轴功为:kg kJ h q w /252100.845)0.10.175(0.8146.550Δ3s -=⨯⨯-⨯---=-=所以带动此压气机所需的功率至少为:kW w P s 426010=⨯-=2-9 解:是否要用外加取暖设备,要看室内热源产生的热量是否大于通过墙壁和门窗传给外界的热量,室内热源每小时产生的热量为:kJ q 51098.13600)1005050000(⨯⨯⨯=+=热源小于通过墙壁和门窗传给外界的热量为3⨯105 kJ ,所以必须外加取暖设备,供热量为:h kJ Q /101.021098.1103555⨯=⨯-⨯=2-10 解:取容器内的气体作为研究的热力学系统,根据系统的状态方程可得到系统终态体积为:32.112.112112 1.78)5.01(1)(m p p V V =⨯==过程中系统对外所作的功为: ⎰⎰=--===--1.7811.7812.012.021.2111.21.2116.4540.2)(kJ V V Vp dV VV p pdV W所以过程中系统和外界交换的热量为:kJ W U Q 6.4506.45440Δ=+-=+=为吸热。
热工控制系统习题集及答案

第四章、自动控制系统的时域分析
4- 1、系统的特征方程如下,用劳斯判据判定每个系统的稳定性。
(a)
4
s
3
3s
2
3s
2s
2
0
(b) 0.02s3 0.3s2 s 10 0
(c)
s5 12s4 44 s3 48s2 s 1 0
(d)
0.1s4 1.25s3 2.6s2 26s 25 0
4- 2、图 4-1 表示采用比例积分调节器的调节系统,为使该系统稳定,调节器 的参数 Kp 和 Ti 之间应有什么关系?并在 Kp- Ti 坐标平面上表示这两个参 数的取值范围。
数H s W s。
3- 5、如图 3- 3 所示,分别为线性弹簧、阻尼器和机械平移系统,设输入信号 为作用力 f(t) ,输出为位移 x(t),写出它们的传递函数,并列出相似参量和
变量。
x(t) f (t) k (a)
x (t) f (t) (b)
x(t)
m
f(t)
(c)
图 3-3 习题 3- 5 图
什么?
第二章、控制系统的传递函数与基本环节
2- 1、某系统的微分方程为:
d3y t a 3 dt 3
d2y t a2 dt 2
dy t a1
dt
a0y t
dx t b1
dt
b0 x t
其中 y(t) 为系统的输出, x(t) 为系统的输入,写出其传递函数。 2- 2、图 2-1 所示的微分电路,试证明它的传递函数为
C
u1
R
u2
图 2- 1 微分电路
2- 3、图 2-2 为一滞后校正回路,图
G s U2 s U1 s
RCs RCs 1
大学-热工过程自动控制课后答案

陈绍炳于向军编著《热工自动控制原理》习题参考答案长沙理工大学能源与动力工程学院 自动化教研室 石阳春E-mail: shiyc_110@第2章 线性自动控制系统的数学描述2-1 系统框图如图2-44所示,求输入为给定函数时的输出响应。
图2-44 系统框图解:(a) 212111)()(+=⋅+=S SS S U S Y , 21)(SS U = 225.025.05.0)2(1)(22++−=+=S S S S S S Y , ∴ te t t y 225.025.05.0)(−+−= (b)221212)()(+=⋅+=S S S S U S Y , S S U 1)(=22)(+=S S Y , ∴ te t y 22)(−=(c) )41)(21(1414212)()(++=+⋅+=S S S S S U S Y , S S U 1)(=41162188)41)(21(1)(+−++=++=S S S S S S S Y ,∴421688)(tt e e t y −−−+=(d) 15225121512)()(+=⋅+++=S SS S U S Y , S S U 1)(=(a) 输入u(t) = t(b) 输入u(t) = 1(t)(c) 输入u(t) = 1(t)(d) 输入u(t) = 1(t)(e) 输入u(t) = 1(t)(f) 输入u(t) = 1(t)15252)1(52)(+−=+=S S S S S Y , ∴t e t y −−=5252)( (e) 01.0)1.0(01.01)110(1)101(11)101(1)()(2222++=++=+++=S S S S S U S Y , S S U 1)(=01.0)1.0(1.05.001.0)1.0()1.0(5.05.0]01.0)1.0[(01.0)(222++×−+++−=++=S S S S S S S Y ∴ 10sin 5.010cos 5.05.0)(1010te t et y t t −−−−=或 )2(5.0)02.02.0(02.05.0]01.0)1.0[(01.0)(2002222ωζωω++×=++×=++=S S S S S S S S S Y ∴ )4510sin(21(5.0)(10°+−=−tet y t(f))1(3)13(2131212)()(++=+⋅+=S S S S U S Y , S S U 1)(=13432)1(3)13(2)(++=++=S S S S S S Y , ∴t e t y −+=3432)(2-2 由电阻R 和电容C 组成如图2-45所示的电路:图2-45 系统电路图⑴建立传递函数)()()(12S U S U S G =的表达式,说明为何种环节;⑵当输入u 1为单位阶跃函数时,画出输出u 2(t)响应曲线,并标出特征参数。
第五章习题热工过程自动调节答案

第五章习题5-1 求输入信号为)30sin(︒+t 的单位反馈系统的稳态输出,已知系统的开环传递函数为:110)(+=s s G k 解:闭环系统的传递函数为:G(s)=10/(s+11) 频率特性G(jw)=10/(jw+11)由w=1,得 G(j1)=10/(j1+11)= o19.5905.0111122101-∠=∠*-tg故C (t )=0.905sin(t+oo19530⋅-)=0.905sin(t+o81.24)5-2 自动调节系统的传递函数为)1)(1()(21s T s T ks G ++=写出系统的幅频特性和相频特性的表达式。
解:1112()22221212()(1)(1)11j tg T tg T k kG j e j T j T T T ωωωωωωω---+==++++幅频特性222212()11kM TT ωωω=++相频特性1112()()tg T tg T θωωω--=-+5-3 已知各系统的开环传递函数,试用奈魁斯特判断各闭环系统的稳定性。
1) )1)(1()(21++=s T s T ks G k2) )1)(1)(1()(321+++=s T s T s T ks G k解:1) T 1、T 2为正 所以求出的开环特征根均落在S 平面的左半部,开环系统稳定。
观察图知没过(-1,j0)点,则系统稳定。
2) T 1、T 2、T 3均为正 所以求出的开环特征根均落在S 平面的左半部,开环系统稳定。
观察图知过(-1,j0)点,则系统不稳定,且有两个正实数根。
5-4 已知各系统的开环传递函数,试图用奈魁斯特判断各闭环系统的稳定性。
1)36)1(4)(+=s s G k2) )1(1)(6+=s s G k 2s e -解,1)三个开环特征根均为-1/6,所以开环系统稳定()1(36)33244()(16)136j tg k G j e j ωωωω--==→++令()324()1136M ωω==+得ω=36rad/s 此时得()θω= -π考虑到随ω值增加,开环系统频率特性的模单调减小,在模为1时,相角为-π,所以曲线过 (-1,j0)点,系统边界稳定。
热工过程自动调节,课后习题答案,1到6章
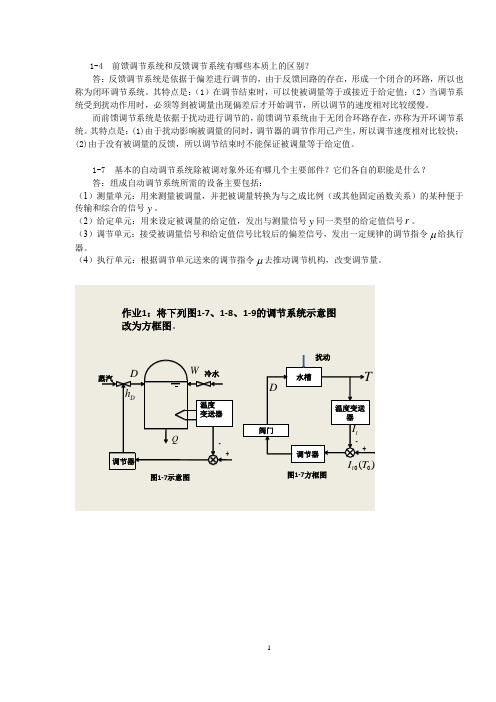
1-4 前馈调节系统和反馈调节系统有哪些本质上的区别?答:反馈调节系统是依据于偏差进行调节的,由于反馈回路的存在,形成一个闭合的环路,所以也称为闭环调节系统。
其特点是:(1)在调节结束时,可以使被调量等于或接近于给定值;(2)当调节系统受到扰动作用时,必须等到被调量出现偏差后才开始调节,所以调节的速度相对比较缓慢。
而前馈调节系统是依据于扰动进行调节的,前馈调节系统由于无闭合环路存在,亦称为开环调节系统。
其特点是:(1)由于扰动影响被调量的同时,调节器的调节作用已产生,所以调节速度相对比较快;(2)由于没有被调量的反馈,所以调节结束时不能保证被调量等于给定值。
1-7 基本的自动调节系统除被调对象外还有哪几个主要部件?它们各自的职能是什么?答:组成自动调节系统所需的设备主要包括:(1)测量单元:用来测量被调量,并把被调量转换为与之成比例(或其他固定函数关系)的某种便于传输和综合的信号y。
(2)给定单元:用来设定被调量的给定值,发出与测量信号y同一类型的给定值信号r。
(3)调节单元:接受被调量信号和给定值信号比较后的偏差信号,发出一定规律的调节指令μ给执行器。
(4)执行单元:根据调节单元送来的调节指令μ去推动调节机构,改变调节量。
or2—8 答案第三章3-1 什么是有自平衡能力对象和无自平衡能力对象?答案: 所谓有自平衡能力对象,就是指对象在阶跃扰动作用下,不需要经过外加调节作用,对象的输出量经过一段时间后能自己稳定在一个新的平衡状态。
所谓无自平衡能力对象,就是指对象在阶跃扰动作用下,若没有外加调节作用,对象的输出量经过一段时间后不能自己稳定在一个新的平衡状态。
3-2 试分析P、PI、PID规律对系统调节质量的影响?答案:P调节器,有一个相对较大的超调量,有较长的调节时间,存在静态误差。
PI调节器,综合了P调节器和I调节器两者的性质。
它的超调量及调节时间与P调节器差不多,但没有静态误差。
PID调节器兼有比例、积分和微分作用的特点,只要三个调节作用配合得当就可以得到比较好的调节效果,它具有比PD调节还要小的超调量,积分作用消除了静态误差,但由于积分作用的引入,调节时间比PD调节器要长。
热工课后题答案

热工课后题答案习题及部分解答第一篇工程热力学第一章基本概念 1. 指出下列各物理量中哪些是状态量,哪些是过程量:答:压力,温度,位能,热能,热量,功量,密度。
2. 指出下列物理量中哪些是强度量:答:体积,速度,比体积,位能,热能,热量,功量,密度。
3. 用水银差压计测量容器中气体的压力,为防止有毒的水银蒸汽产生,在水银柱上加一段水。
若水柱高200mm,水银柱高800mm,如图2-26所示。
已知大气压力为735mmHg,试求容器中气体的绝对压力为多少kPa?解:根据压力单位换算pH2O?200???103??800???105Pa??pb?(p H2O?pHg)??(?)? 4. 锅炉烟道中的烟气常用上部开口的斜管测量,如图2-27所示。
若已知斜管倾角??30?,压力计中使用??/cm3的煤油,斜管液体长度L?200mm,当地大气压力pb?,求烟气的绝对压力解:p?L?gsin??200??????10?6MPap?pb?pv???10?6? 5.一容器被刚性壁分成两部分,并在各部装有测压表计,如图2-28所示,其中C为压力表,读数为110kPa,B为真空表,读数为45kPa。
若当地大气压pb?97kPa,求压力表A的读数pgA?155kPa 6. 试述按下列三种方式去系统时,系统与外界见换的能量形式是什么。
.取水为系统;.取电阻丝、容器和水为系统;.取图中虚线内空间为系统。
答案略。
7.某电厂汽轮机进出处的蒸汽用压力表测量,起读数为;冷凝器内的蒸汽压力用真空表测量,其读数为706mmHg。
若大气压力为,试求汽轮机进出处和冷凝器内的蒸汽的绝对压力p1? 7P;ap2?测得容器的真空度pv?550mmHg,大气压力pb?,求容器??,求此时真空表上的读内的绝对压力。
若大气压变为pb?? 数为多少mmMPa?p?,pv9.如果气压计压力为83kPa,试完成以下计算:.绝对压力为时的表压力;.真空计上的读数为70kPa时气体的绝对压力;.绝对压力为50kPa时的相应真空度;.表压力为时的绝对压力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-4 前馈调节系统和反馈调节系统有哪些本质上的区别?答:反馈调节系统是依据于偏差进行调节的,由于反馈回路的存在,形成一个闭合的环路,所以也称为闭环调节系统。
其特点是:(1)在调节结束时,可以使被调量等于或接近于给定值;(2)当调节系统受到扰动作用时,必须等到被调量出现偏差后才开始调节,所以调节的速度相对比较缓慢。
而前馈调节系统是依据于扰动进行调节的,前馈调节系统由于无闭合环路存在,亦称为开环调节系统。
其特点是:(1)由于扰动影响被调量的同时,调节器的调节作用已产生,所以调节速度相对比较快;(2)由于没有被调量的反馈,所以调节结束时不能保证被调量等于给定值。
1-7 基本的自动调节系统除被调对象外还有哪几个主要部件?它们各自的职能是什么?答:组成自动调节系统所需的设备主要包括:(1)测量单元:用来测量被调量,并把被调量转换为与之成比例(或其他固定函数关系)的某种便于传输和综合的信号y。
(2)给定单元:用来设定被调量的给定值,发出与测量信号y同一类型的给定值信号r。
(3)调节单元:接受被调量信号和给定值信号比较后的偏差信号,发出一定规律的调节指令μ给执行器。
(4)执行单元:根据调节单元送来的调节指令μ去推动调节机构,改变调节量。
or2—8 答案第三章3-1 什么是有自平衡能力对象和无自平衡能力对象?答案: 所谓有自平衡能力对象,就是指对象在阶跃扰动作用下,不需要经过外加调节作用,对象的输出量经过一段时间后能自己稳定在一个新的平衡状态。
所谓无自平衡能力对象,就是指对象在阶跃扰动作用下,若没有外加调节作用,对象的输出量经过一段时间后不能自己稳定在一个新的平衡状态。
3-2 试分析P、PI、PID规律对系统调节质量的影响?答案:P调节器,有一个相对较大的超调量,有较长的调节时间,存在静态误差。
PI调节器,综合了P调节器和I调节器两者的性质。
它的超调量及调节时间与P调节器差不多,但没有静态误差。
PID调节器兼有比例、积分和微分作用的特点,只要三个调节作用配合得当就可以得到比较好的调节效果,它具有比PD调节还要小的超调量,积分作用消除了静态误差,但由于积分作用的引入,调节时间比PD调节器要长。
3-3 在相同衰减率的前提下,为什么采用PI规律的比例带δ要采用P规律时选择得大一些?答案:PI调节器兼有比例调节作用和积分调节作用的特点,由于积分调节作用是随时间而逐渐增强的,与比例调节作用相比较过于迟缓,在改善静态品质的同时却恶化了动态品质,使过渡过程的振荡加剧,甚至造成系统不稳定。
为保证相同衰减率,要通过增大比例带值来削弱振荡倾向。
3-4 怎样判别调节对象被控制的难易程度?答案:不论调节对象有无自平衡能力,都可统一用ε、ρ、τ三个特征参数来表示对象的动态特性。
调节对象惯性越大、迟延越大越难被控制 3-6 为何积分调节器称为无差调节器?答案:具有积分作用的调节器,只要对象的被调量不等于给定值,执行器就会不停地动作,只有当偏差等于零时,调节过程才结束;调节过程结束,则必然没有偏差,这是积分作用的特点。
因此,积分作用调节器也称为无差调节器。
第四章习题4-1 调节系统如图4-13所示,试分别求当K =10和K =20时,系统的阻尼比 ζ、无阻尼自然振荡频率ωn 、单位阶跃响应的超调量M p 、峰值时间t p 、衰减率ψ、调节时间t s 和稳态误差e (∞),并讨论K 的大小对过渡过程性能指标的影响。
解:系统的闭环传递函数为2()10()()1010C s KG s R s S S K==++二阶系统传递函数的通用形式为'222()2nn nK G s S S ωζωω=++二式比较,可得, K’=1n ω=ζ=K =10时,10n ω==0.5ζ==由此可以求得:阻尼振荡频率8.66(/)d nrad s ωω==== 峰值时间 0.363()8.66pd t s ππω===超调量0.57716.3%p M eeπζπ--===衰减率2 1.1541197.3%eeπζπψ--=-=-=调节时间采用2%的误差带 : 440.8()5sn t s ζω≈==采用5%的误差带 : 330.6()5sn t s ζω===稳态误差0'2220()1()1()lim 11[()]lim 1lim 21'0S S nS n n e c SC s S G s SK S S K ωζωω→→→∞=-∞=-=-⋅=-++=-=K =20时,n ω==ζ==阻尼振荡频率13.23(/)d nrad s ωω=== 峰值时间 0.237()13.23pd t s ππω=== 超调量/0.25839.3%p M eeπζπ--===衰减率20.5161180.4%eeπζπψ--=-=-=调节时间采用2%的误差带 : 440.8()5s n t s ζω≈==采用5%的误差带 : 330.6()5s n t s ζω===稳态误差()1'0e K ∞=-=4-2 调节系统如图4-14所示,试分别求出当系统的瞬态响应为ψ=0.75和ψ=0.9时的 δ 值。
解:由系统方框图可写出闭环特征方程式:11105(110)S S δ+=+整理得:21101050S S δ++= 考虑到二阶系统的标准形式为:0222=++nn S S ωξω可见:n ω=, 120nξω= 当取ψ=0.75时,阻尼比ξ=0.216,据此可求得: 22180.37350δζω=== 当取ψ=0.9时,阻尼比ξ=0.344,据此可求得:22180.94750δζω===4-3 试用劳斯判据和古尔维茨判据确定下列特征方程式的系统的稳定性。
如果不稳定,指出在S 右半平面根的个数。
(1)0516188234=++++S S S S (2)053232345=+++++S S S S S (3)025103234=++++S S SS (4)01681023=+++S S S答案: (1) 劳斯阵列:43210118581616513.55S S S S S第一列元素全为正,所以系统稳定。
(2) 劳斯阵列:54321013312512453.255S S S SS S --第一列元素符号改变两次,所以系统不稳定,有2个根在S 右半平面。
(3)劳斯阵列:4321035210147210153472S S S S S - 第一列元素符号改变两次,所以系统不稳定,有2个根在S 右半平面。
(4) 劳斯阵列:32101810166.416S S S S第一列元素全为正,所以系统稳定。
4-4 已知系统特征方程式如下,试求系统在S 右半平面的根数。
(1)0482*******345=+++++S S S S S (2)025********345=+++++S S S S S (3)0108744423456=+--+-+S S S S S S 答案: (1) 劳斯阵列:5 4 3 2 111232 32448 416 124800SSSSS由于出现全零行,故用2S行系数构成辅助多项式。
2f(s)=12S+48f'(s)=24S5 4 3 2 1 011232 32448 416 1248 24048SSSSSS第一列元素全为正,说明特征方程式没有正根,而由辅助方程式,212S+48=0S=j2和S=-j2这就是系统特征方程式的两对虚根,因此系统边界稳定。
(2) 劳斯阵列:5 4 3 2 111235 32025 1638030 52500SSSSS由于出现全零行,故用2S行系数构成辅助多项式2f(s)=5S+25f'(s)=10S5 4 3 2 1 011235 32025 1638030 52510025SSSSSS第一列元素全为正,说明特征方程式没有正根,而由辅助方程式25S+25=0S=jS=-j 这就是系统特征方程式的两对虚根,因此系统边界稳定。
4-5 调节系统如图所示,G1(s)=K,G2(s)=1/s(0.1s+1)(0.2s+1)习题4-5图(1) 确定系统稳定时的K 值范围;(2) 如果要求闭环系统的根全部位于1-=S 垂线之左,K 值范围应取多大? 答案: (1)系统特征方程 11()2()10(0.11)(0.21)KG s G s s s s +=+=++,即(10)(5)500s s s K +++= 321550500s s s K +++= 劳斯阵列:32115015501050350S KS KS S K-系统稳定,则需第一列元素全为正,10500,5003KK ->>所以015K <<。
(2) 用11-=s s 代入特征方程中,可得32111(1)15(1)50(1)500s s s K -+-+-+= 32111122334500s s s K ++-+=3121110112312503431050125034S K S K S S K ---要求闭环系统的根全部位于1-=S 垂线之左,则310500,5034012KK ->->,即0.68 6.2K <<。
4-6 已知单位负反馈系统的开环传递函数为 2(0.50.1)()(1)(0.51)K S G s S S S S +=+++试确定系统稳定时的K 值范围。
答案: (1)系统特征方程 2(0.50.1)1()1(1)(0.51)K S G s S S S S ++=++++=0 即;2(1)(0.51)S S S S ++++(0.51)K S +=0 4320.5 1.520.510s s s s Ks K +++++=43210.5211.510.5(2.50.25)11.5(10.5) 2.25(2.50.25)1S k S k S S k k S +-+--系统稳定,则需第一列元素全为正,2.50.25 1.5k- >0 (10.5) 2.25(2.50.25)k k +-->0即05<K <第五章习题5-1 求输入信号为)30sin(︒+t 的单位反馈系统的稳态输出,已知系统的开环传递函数为:110)(+=s s G k 解:闭环系统的传递函数为:G(s)=10/(s+11) 频率特性G(jw)=10/(jw+11)由w=1,G(j1)=10/(j1+11)=故C (t )=0.905sin(t+)=0.905sin(t+)5-2 自动调节系统的传递函数为)1)(1()(21s T s T ks G ++=写出系统的幅频特性和相频特性的表达式。
o19.5905.0111122101-∠=∠*-tg oo19530⋅-o81.24解:1112()12()(1)(1)j tg T tg T k k G j e j T j T ωωωωω---+==++幅频特性()kM ω=相频特性1112()()tg T tg T θωωω--=-+ 5-3 已知各系统的开环传递函数,试用奈魁斯特判断各闭环系统的稳定性。
