管理统计学第四章
统计学第四章课后习题答案

第四章一.思考题1、一组数据的分布特征可以从哪几个方面进行测度?答:可以从三个方面进行测度和描述:一是分布的集中趋势,反映各数据向其中心值靠拢或聚集的程度;二是分布的离散程度,反映各数据远离其中心值的趋势;三是分布的形状,反映数据分布的偏态和峰态。
2、怎样理解平均数在统计学中的地位?答:平均数在统计学中具有重要的地位,它是进行统计分析和统计推断的基础。
从统计学思想上看,平均数是一组数据的重心所在,是数据误差相互抵消后的必然结果。
3、简述四分位数的计算方法。
答:四分位数是一组数据排序后处于25%和75%位子上的值。
四分位数是通过3个点将全部数据等分成4分,其中每部分包含25%的数据。
中间的四分位数就是中位数,因此通常所说的四分位数是指处在25%位置上的数值和处在75%位置上的数值。
它是根据为分组数据计算四分位数时,首先对数据进行排序,然后确定四分位数所在的位置,该位置上的数据就是四分位数。
4、对于比率数据的平均数为什么采用几何平均?答:几何平均数是适用于特殊数据的一种平均数,主要适用于计算平均比率。
当所掌握的变量值本身是比率的形式时,采用几何平均法计算平均比率更为合理。
5、简述众数、中位数、平均数的特点和应用场合。
答:众数是数据中出现次数次数最多的变量值。
主要应用于分类数据。
中位数是一组数据排序后处于中间位置的变量值,其适用于顺序数据。
平均数也称均值,它是一组数据相加后除以数据个数的结果,是集中去世的主要测量值,它适用于数值型数据。
6、简述异众比率、四分位差、方差、标准差的使用场合。
答:异众比率主要适合测度分类数据的离散程度,对于顺序数据以及数值型数据也可以计算异众比率。
四分位差主要用于测度顺序数据的离散程度。
方差和标准差适用于测度数值型数据的离散程度。
7、标准分数有哪些用途?答:首先是比较不同单位和不同质数据的位置。
其次是和正态分布结合起来,求得概率和标准分值之间的对应关系。
还有就是在假设检验和估计中应用。
统计学-第四章 总量指标和相对指标

统计工作的第四个阶段——统计分析的基础
2020/1/10
引例
统计指标,无处不在。如≪中华人民共和国 2017年国民经济和社会发展统计公报≫中所说: “初步核算,全年国内生产总值827122亿元,比 上年增长6.9%。其中,第一产业增加值65468亿 元,增长3.9%;第二产业增加值334623亿元, 增长6.1%;第三产业增加值427032亿元,增长 8.0%。第一产业增加值占国内生产总值的比重为 7.9%,第二产业增加值比重为40.5%,第三产业 增加值比重为51.6%。如图4-1、图4-2所示。
50
第五年第3季至第四年第4季:52;
第五年第2季至第四年第3季:51;
第五年第1季至第四年第2季:50。
提前三个季度完成五年计划。
2(重点)
3.中长期计划任务的检查
累计法:计划任务数以累计数形式出现。可用于检查计 划执行情况。计算公式为:
计划完成相对指标
A.总产量520万元
B.净产值320万元
C.职工人数160万人
D.工人占职工人数的80%
5.2001年我国发行长期建设国债1500亿元;2001年末,居民个 人储蓄存款 余额突破75000亿元。这两个指标()
A.都是时期数 B.都是时点数 C.都是绝对数
D.前者是时点数,后者是时期数 E.前者是时期数,后者是 时点数
这些指标数据说明了2017年我国经济总量及增长速度、 价格情况、粮食产量、人口及就业等构成的发展状况。而这 些指标的涵义就是我们本章要学习的总量指标和相对指标所 涉及的内容。
2020/1/10
学习内容
1.总量指标 2.相对指标
学习重点
1.掌握绝对数和相对数的 特点及相应的计算方法
管理统计学第四章组距数列众数
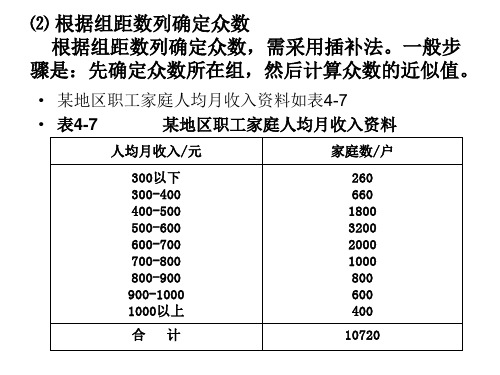
• 某地区职工家庭人均月收入资料如表4-7 • 表4-7 某地区职工家庭人均月收入资料
人均月收入/元 家庭数/户
300以下 300-400 400-500 500-600 600-700 700-800 800-900 900-1000 1000以上
2 i = U 1 2
M0
U
——众数; ——众数组的上限; ——众数组的下限;
L
1
——众数组次数与下一组次数之差;
——众数组次数与上一组次数之差; ——组距。
2
i
根据表4-7的资料,将有关数据代入公式,得到众数
的近似值:
下限公式:
3200 1800 1400 M 0 500 (600 500) 500 100 553.85 (元) (3200 1800) (3200 2000) 1400 1200
上限公式:
M 0 600
3200 2000 1200 (600 500) 600 100 553.85 (元) (3200 1800) (3200 2000) 1400 1200
例如:根据下表的资料计算200名工人的工资众数。 某厂某月职工工资资料 工资(元) 300~350 350~400 400~450 450~500 500~550 合计 职工人数(人) 20 70 37 43 30 200
表47某地区职工家庭人均月收入资料人均月收入元家庭数户300以下30040040050050060060070070080080090090010001000以上260660180032002000100080060040010720从表4ห้องสมุดไป่ตู้中可知家庭户数最多的是3200户它所对应的人均月收入500600元为众数所在组
管理统计学习题参考答案第四章

第四章1.解:时间序列是反映现象随着时间的变化而变化的数据系列,也称为时间数列或动态数列。
时期数和时点数的区别主要在于是否具有可加性。
产品产量、销售额、工资总额、利润总额等都是具有可加性的指标,称为时期数;而产品库存量、期末现金量、期末人口数等都不具有可加性,或者说相加无意义,则称为时点数。
2. 解:2012年至2015年各季度饮料销售量变化情况(1)报告期水平与基期水平之比称为发展速度。
(2)其中,当基期水平为上期水平时,就称为环比发展速度。
环比发展速度计算公式:X1 / X0, X2 / X1 , X3 / X2 , … , X n / X n-1。
(3)当基期水平为某个时期的固定发展水平(X0)时,就称为定基发展速度。
定基发展速度计算公式:X1 / X0 , X2 / X0 , X3 / X0, … , X n / X0。
(4)二者的关系:(X n / X0)=(X1 / X0)·(X2 / X1)·…(X n / X n-1)。
(5)发展速度减去1就等于增长速度或增长率,分别有环比增长率和定基增长率。
(6)为了消除季节引起的波动问题,需要计算同比发展(增长)速度指标。
同比指标是报告期水平与上年同期水平的对比结果。
例如,2014年第一季度销售量同比增长量就为210-150=60,同比增长率为60 / 150 = 40%。
3. 解:(1)序时平均数也称为动态平均数,它反映的是现象在一定时期内发展水平达到的一般水平。
(2)用X 表示饮料销售量(时期数),其中,X 0=1710、X 1 =2110、X 3=3310、X 4=4020。
2012年至2015年饮料销售量年平均为∑=n X X /=(1710+2110+3310+4020)/4=11150/4=2787.5(箱)用W 表示库存量(时点数),W 0=350、W 1=400、W 2=550、W 3=800、W 4=950,则有2012年至2015年饮料年平均库存量为:42243210W W W W W W ++++== 600429508005504002350=++++(箱) (3)用K 表示库存周转速度或次数(相对数),2012年至2015年饮料库存的平均周转速度为646.46005.2787422443210==++++==∑W W W W W XW X K (次) 4. 解:(1)平均发展速度反映的是现象在一定时期内发展速度的一般水平。
统计学第4章综合指标

直接观察数据中出现次数最多的数。
平均指标在统计分析中应用
描述统计
用平均指标描述数据的集中 趋势和一般水平,如用算术 平均数描述班级学生的平均 成绩。
比较分析
通过比较不同组数据的平均 指标,揭示它们之间的差异 和联系,如比较不同班级的 平均成绩以评估教学效果。
推断统计
在总体分布未知的情况下, 利用样本平均指标对总体进 行推断,如通过样本均值推 断总体均值。
总量指标的作用
作为计算相对指标和平均指标的基础
描述社会经济现象的总规模和总水平
总量指标种类与计算方法
总量指标的种类
01
时点指标:反映现象在某一时刻上的总量 ,如年末人口数、股票价格等。
03
02
时期指标:反映现象在一段时期内的总量, 如国内生产总值、人口数等。
04
总量指标的计算方法
直接计数法:对总体单位进行逐一计数, 然后汇总得到总量指标。
相对指标种类与计算方法
结构相对指标
部分与总体之比,反映总
总体中不同部分数量之比,反映各部分之间的 比例关系。
比较相对指标
同一现象在不同空间条件下的数量对比,反映现象在不同地区的差异程度。
相对指标种类与计算方法
强度相对指标
两个性质不同但有一定联系的总量指标之比,反映现象的强度、密度和普遍程度。
平均指标种类与计算方法
算术平均数
$bar{x} = frac{sum x}{n}$,其中$sum x$为所有数值之和,$n$为 数值个数。
几何平均数
$G = sqrt[n]{prod x_i}$,其中$prod x_i$为所有数值之积,$n$为 数值个数。
中位数
将数据从小到大排列,若数据量为奇数则取中间数,若数据量为偶数 则取中间两数的平均值。
统计学第四章课后题及答案解析

统计学第四章课后题及答案解析第四章⼀、单项选择题1.由反映总体单位某⼀数量特征的标志值汇总得到的指标是()A.总体单位总量B.质量指标C.总体标志总量D.相对指标2.各部分所占⽐重之和等于1或100%的相对数()A.⽐例相对数B.⽐较相对数C.结构相对数D.动态相对数3.某企业⼯⼈劳动⽣产率计划提⾼5%,实际提⾼了10%,则提⾼劳动⽣产率的计划完成程度为()A.104.76%B.95.45%C.200%D.4.76%4.某企业计划规定产品成本⽐上年度降低10%实际产品成本⽐上年降低了14.5%,则产品成本计划完成程度()A.14.5%B.95%C.5%D.114.5%5.在⼀个特定总体内,下列说法正确的是( )A.只存在⼀个单位总量,但可以同时存在多个标志总量B.可以存在多个单位总量,但必须只有⼀个标志总量C.只能存在⼀个单位总量和⼀个标志总量D.可以存在多个单位总量和多个标志总量6.计算平均指标的基本要求是所要计算的平均指标的总体单位应是()A.⼤量的B.同质的C.有差异的D.不同总体的7.⼏何平均数的计算适⽤于求()A.平均速度和平均⽐率B.平均增长⽔平C.平均发展⽔平D.序时平均数8.⼀组样本数据为3、3、1、5、13、12、11、9、7这组数据的中位数是()A.3B.13C.7.1D.79.某班学⽣的统计学平均成绩是70分,最⾼分是96分,最低分是62分,根据这些信息,可以计算的测度离散程度的统计量是()A.⽅差B.极差C.标准差D.变异系数10.⽤标准差⽐较分析两个同类总体平均指标的代表性⼤⼩时,其基本的前提条件是( )A.两个总体的标准差应相等B.两个总体的平均数应相等C.两个总体的单位数应相等D.两个总体的离差之和应相等11.已知4个⽔果商店苹果的单价和销售额,要求计算4个商店苹果的平均单价,应采⽤()A.简单算术平均数B.加权算术平均数C.加权调和平均数D.⼏何平均数12.算术平均数、众数和中位数之间的数量关系决定于总体次数的分布状况。
统计学第四章重点知识点

第四章 差异量教学目的:1.理解全距、四分位距、百分位距、平均差、方差、标准差和差异系数等概念;2.掌握各种差异量指标的计算方法。
数据的分布特征不仅有集中趋势,还有离中趋势。
以动态的眼光,从不同的角度看,数据是向中间变动的,也是向两端变动的。
两组数据可能平均水平相同,但两组数据的分布特征并不完全相同。
【如】:比较以下两组数据 A 组:88、82、73、76、81 B 组:92、86、70、72、80两组平均数,80==B A X X 但R A =88-73=15,R B=92-70=22。
即A 组较集中,B 组较分散。
因此,我们描述一组数据的分布特征,既要描述其集中趋势,也要描述其离中趋势。
差异量:表示一组数据的离中趋势或变异程度的量称为差异量。
常用的差异量指标有全距、四分位距、百分位距、平均差、方差、标准差和差异系数。
第一节全距、四分位距、百分位距一、全距全距:是一组数距中最大值与最小值之差。
优点:意义明确,计算方便。
缺点:反响不灵敏,易受极端值影响。
二、四分位距〔一〕四分位距的的概念四分位距:是指一组按大小顺序排列的数据中间部位50%个频数距离的一半。
QD :表示四分位距; Q 3:表示第三四分位数; Q 1:表示第一四分位数。
所以:四分位距的公式又为: 〔二〕四分位数的计算方法 1、原始数据计算法〔1〕将数据由小到大进行排列;〔2〕分别求出三位四分位数〔点〕;〔3〕代入公式计算。
【例如】:有以下16个数据25、22、29、12、40、15、14、39、37、31、33、19、17、20、35、30,其中四分位距的计算方法如下:〔1〕先将原始数据从小到大排列好;12、14、15、17、*19、20、22、25、*29、30、31、33、*35、37、39、40Q1=18 Md=27 Q3=34〔2〕求出Q1、Md、Q3;〔3〕将Q1、Md、Q3的得数代入公式〔4.1〕。
2、频数分布表计算法利用频数分布表计算公式为:关键是分别计算P75和P25,百分位数计算方法掌握了,这里的计算就不会有什么问题。
统计学(第4章)

连续变动结果的总量指标,时期指标是
一个流量。
时间维度上
时期指标的三个特点 具有可加性
时期指标可以累计
时期指标数值大小与时期长短有直接关系
时期指标的数值一般为连续登记
2019/6/15
第四章 描述统计
5
统计学
2、时点指标
时点指标又叫存量指标,是指反映社 会经济现象在某一时点上的总量指标,
四 季度
1 500
计划完成百分数=
1400+1420+1470+1500 5000
=115.8%
注:2010年第一季度前的四个季度的累计量已达5000,说明五年计 划提前三个季度完成。
2019/6/15
第四章 描述统计
33
统计学
(2)累计法
如何确定提前 完成时间?
计算公式:
计划完成相对指标 长期计划期间实际累计完成数 长期计划规定的累计数
时点指标是一个存量。
时间维度上
时点指标的三个特点
不具可加性
不同时点指标数值是不能累加
时点指标数值大小与时点间隔长短无直 接关系
时点指标一般为间断统计
2019/6/15
第四章 描述统计
6
统计学
三、总量指标的计量单位
1、实物量单位(包括度量衡单位) 2、价值量单位 3、劳动量单位(工时和工日)
5 000 1 250 1 340 1 280
102.4
52.4
4 000 1 000 1 030 1 215
121.5
56.1
2 000 500 600 400
80.0
50.0
11 000 2 750 2 970 2 895 105.33
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(二)调和平均数
调和平均数(Harmonic mean)是均值的另 一种重要表示形式,由于它是根据变量值 倒数计算的,也叫倒数平均数,一般用字 母表示 Hm。 根据所给资料情况的不同,调和平均数可 分为:简单调和平均数和加权调和平均数 两种。
(二)调和平均数
1.简单调和平均数
n 1 1 1 x1 x2 xn n
i
由此可以看出,当权重mi相等时,则加权调和平 均数则转换为简单调和平均数。 例
(二)调和平均数
3.调和平均数是算术平均数的变形 在一定的条件下,加权调和平均数和加权算术 平均数只是计算形式不同,在经济内容上没有 实质性的区别,调和平均数是算术平均数的变 形,是在缺少总体单位的资料时才被迫使用的 计算平均数的一种方法。即:
3.根据组距数列确定中位数 如果我们掌握的资料是分组后得到的组 距数列,则确定中位数的步骤为: (1)确定中位数的位置 。 (2)计算累计次数,据以找出中位数 所在的组。 (3)利用以下公式,确定中位数的近 似值 f 1
i
i
2
(一)中位数
fi
下限公式: M e L 2 s m 1 fm s m 1 i
集中趋势(General tendency)是指分布 的定位,它是指一组数据向某一中心值靠 拢的倾向,或是表明一组统计数据所具有 的一般水平。 对集中趋势进行测度也就是寻找数据一般 水平的代表值或中心值。 对集中趋势的度量有数值平均数和位置平 均数之分。
4.1 数据分布的集中趋势测度
数据的特征和度量
(一)中位数
1.根据未分组数据确定中位数 对于未分组的数据,确定其中位数的具体 步骤为: (1)将变量按变量值大小从小到大进行 排列。 (2)确定中位数的位置,即中点位置。 一般的,设一组数据的个数为,则中点的 位置为(n+1)/2 。 (3)确定中位数。
(一)中位数
如果观测值的数目n为奇数,则(n+1) /2为整数,该位置上所对应的变量即为所 求的中位数 如果观测值的数目n为偶数,则 (n+1) /2为非整数,则取位于中间位置的两个变 量值的算术平均数作为中位数。 例
(一)算术平均数
③加权算术平均数计算公式中频数的大小起着 重要作用,当变量值比较大的次数多时,平均 数就接近于变量值大的一方;当变量值比较小 的次数多时,平均数就接近于变量值小的一方。 可见,次数对变量值在平均数中的影响起着某 种权衡轻重的作用,因此被称为权数。 ④在加权算术平均数计算中当各组变量的权重 相等时,则权重的权衡轻重的作用也就消失了, 此时加权算术平均数转化为简单算术平均数的 计算形式。
x1 x 2 x3 x 4 x5 46 54 42 46 32 44 5 5
xi x n
(一)算术平均数
2.加权算术平均数 加权算术平均数计算的所依靠的数据是经 过一定整理的,即是根据一定规则分组的。 可分为 (1)由数列计算加权算术平均数 (2)根据组距计算加权算术平均数
xi f i xi f i n fi
(一)算术平均数
设某班级10名同学的年龄分别为:18, 19,17,18,17,18,19,18,18, 19。则根据简单平均数的公式,我们可 计算得到该班10名同学的平均年龄:
n 10
x i 18 19 17 18 17 18 19 18 18 19 x 18
集中趋势
算术平均数 调和平均数 几何平均数 中位数 众数 百分位数 四分位数
离中趋势
极差 四分位距 平均差 方差与标准差 标准分数 离散系数
分布形状
偏态测度 峰态测度
一、数值平均数
数值平均数又称均值(Mean),是根 据统计资料的数值计算而得到,在统计 学中具有重要的作用和地位,是度量集 中趋势的最主要的指标之一。 平均的对象可理解为变量 x ,平均数可 记为 x 。
(一)算术平均数
1.简单算术平均数 简单算术平均数是根据原始数据直接计算 均值。一般地,设一组数据为,其简单算 术平均数计算的一般公式可表达为 :
x1 x 2 x n x n
xi
n
(一)算术平均数
例如:为了研究目前大学中班级学生人 数的情况,从北京某大学抽样五个班级, 其学生人数分别为:46,54,42,46, x5 x2 分别表示 32。我们使用, x1… 该五个数据,计算其均值,可以写成:
fi
上限公式: M e U 2
fm 式中: L ——中位数所在组的下限; U ——中位数所在组的上限; S m 1 ——从低到高累计至中位数所在组前一组止的次数; S m 1 ——从高到低累计至中位数所在组后一组止的次数;
i
f m ——中位数所在组的次数; i ——中位数所在组的组距。
第4章 描述统计中的测度
数据的特征和度量
对于描述统计中的测度,主要可以分为三 个方面来描述: 一是数据的集中趋势,反映各数据向其中 心值靠拢或聚焦的程度; 二是分布的离散程度,反映各数据远离其 中心值的趋势; 三是数据分布的形状,即数据分布的偏态 和峰度。
4.1 数据分布的集中趋势测度
(三)几何平均数
1.简单几何平均数 假定有n个变量值x1,x2,……xn,则简单几 何平均数的基本计算公式为:
G n x1 x2 xn n
x
i 1
n
i
(三)几何平均数
2.加权几何平均数 当掌握的数据资料为分组资料,且各个变 量值出现的次数不相同时,应用加权方法 计算几何平均数。 加权几何平均数的公式为:
f m 1 ——从高到低累计至众数所在组后一组的次数;
i ——众数所在组的组距。
二、众数、中位数与均值的比较
(一)正态分布时三者的关系 正态分布是以算术平均数为对称轴,两边 频数相等。其中频数最大的标志值就是数 列居中位置的标志值,也就是权数最大、 最具有代表性的那个变量值。因此,正态 分布时,算术平均数、中位数和众位数(Median)是度量数据集中趋势的 另一重要测度,它是一组数据按数值的大 小从小到大排序后,处于中点位置上的变 量值。通常用表示Me。 定义表明,中位数就是将某变量的全部数 据均等地分为两半的那个变量值。其中, 一半数值小于中位数,另一半数值大于中 位数。 中位数是一个位置代表值,因此它不受极 端变量值影响。
Hm
1 xi
事实上简单调和平均数是权数均相等条件下的 加权调和平均数的特例。当权数相等时,就产 生了通常所说的加权调和平均数。例
(二)调和平均数
2.加权调和平均数 用公式表示为:
m1 m 2 m n Hm mn m1 m 2 x1 x2 xn
mi
mi mi x
(二)众数
1.未分组资料或单项数列资料众数 观察给定的数据,某个变量出现次数最 多,则该变量即为所求众数。这样的方 法确定比较容易,不需要计算。
(二)众数
2.根据组距变量数量确定众数,具体步骤为:
(1) 确定众数的位置。 将次数最多的组确定为众数组, 因为众数一定在次数最多的组里面。 (2)利用以下公式,确定众数的近似值: f m f m 1 下限公式: M o L i f m f m1 f m f m1 f m f m 1 上限公式: M e U i f m f m1 f m f m1 式中: L ——众数所在组的下限; U ——众数所在组的上限; f m ——众数所在组的次数; f m 1 ——从低到高累计至众数所在组前一组的次数;
(一)算术平均数
(1)由数列计算加权算术平均数 由单项变量数列计算加权算术平均数的基 础是要先将数据进行分组,即将n个数据 按变量值(xi)进行分组,并统计在各个 变量取值出现的次数,或称为频数( fi )。 其加权算术平均数的计算公式如下:
x1 f 1 x 2 f 2 x n f n x f1 f 2 f n
x Me Mo
二、众数、中位数与均值的比较
f
x Me Mo
图4.1单峰对称分布
x
f
f
x
Me
Mo
x
Mo
Me x
x
图4.2左偏分布平均数、中位数和众数的关系
图4.3右偏分布平均数、中位数和众数的关系
二、众数、中位数与均值的比较
(二)偏态分布时三者的关系 频数分布呈偏态时,算术平均数、中位数和 众数的计算结果不同。当右偏时,算术平均数 大于中位数,而中位数又大于众数,左偏时众 数大于中位数,中位数大于算术平均数。 在 偏态分布情况下,算术平均数、中位数和众数 的上述关系是容易理解的,由于算术平均数受 极端值影响,在发生右偏出现较大极端值时, 算术平均数将增加得更快,而中位数总是居于 中间位置,。 x Me Mo 左偏同样可作类似的解释,从而有
(一)算术平均数
年龄(岁)
17 18 19 合计
x
人数
2 6 2 10
f
人数比重
f
f
2/10 (0.2) 6/10 (0.6) 2/10 (0.2) 1
xi f i x 17 2 18 6 19 2 / 2 6 2 18 f
(一)算术平均数
(2)根据组距计算加权算术平均数 选择适当的组距来对数据进行分组,再求 加权平均数往往就简单、容易许多。根据 组距计算加权平均数的方法与上面所述的 数列加权平均数方法基本相同,只需以各 组的组中值来代替相应的x值即可
m1 m2 mn Hm mn m1 m2 x1 x2 xn
