数学实验完整
数学活动实验报告

一、实验目的本次数学活动实验旨在通过实践活动,培养学生的动手操作能力、观察分析能力和创新思维,提高学生对数学知识的理解和运用能力。
同时,通过实验活动,激发学生对数学的兴趣,培养学生的团队合作精神。
二、实验内容本次实验内容为“探究三角形的稳定性”。
三角形是数学中常见的几何图形,具有稳定性强的特点。
通过实验,让学生了解三角形稳定性的原因,并运用所学知识解决实际问题。
三、实验步骤1. 实验准备(1)实验器材:铁丝、剪刀、胶带、直尺、三角板、钩码、支架等。
(2)实验分组:将学生分成若干小组,每组4-6人。
2. 实验过程(1)观察三角形的稳定性:引导学生观察生活中常见的三角形结构,如桥梁、建筑等,感受三角形稳定性的重要性。
(2)制作三角形框架:每组学生根据所学知识,利用铁丝和剪刀制作一个三角形框架。
要求三角形框架的边长满足一定条件,如边长比例为1:1:√2。
(3)测试三角形稳定性:将三角形框架固定在支架上,逐渐增加钩码的重量,观察三角形框架的变形情况。
(4)分析实验结果:引导学生分析实验结果,总结三角形稳定性的原因。
3. 实验总结(1)各小组汇报实验结果,分享实验心得。
(2)教师点评各小组的实验过程和结果,总结三角形稳定性的原因。
四、实验结果与分析1. 实验结果在实验过程中,大部分小组制作的三角形框架在增加钩码重量时,能够保持较好的稳定性,只有少数小组的框架发生了较大变形。
2. 实验分析(1)三角形稳定性原因:三角形具有稳定性强的特点,主要原因是三角形的内角和为180°,当外力作用于三角形时,三个角能够均匀分担外力,使三角形保持稳定。
(2)影响三角形稳定性的因素:边长比例、材料强度、受力方式等。
五、实验结论通过本次实验,学生掌握了三角形稳定性的基本原理,了解了三角形在实际生活中的应用。
同时,培养了学生的动手操作能力、观察分析能力和创新思维,提高了学生对数学知识的理解和运用能力。
六、实验反思1. 实验过程中,部分学生动手能力较差,需要教师在实验过程中给予指导和帮助。
50个简单的数学小实验

50个简单的数学小实验1. 滚动骰子,记录每个点数的数量,进行统计分析。
2. 观察不同颜色的薯片在水中的沉浮情况,研究密度与沉浮关系。
3. 使用不同比例的液体混合,观察颜色的变化。
4. 抛掷硬币,记录正反面的次数,进行概率分析。
5. 用尺子测量不同物品的长度、宽度和高度,并计算体积。
6. 研究太阳光的折射现象,观察镜面反射和散射。
7. 测量水的密度,并探究不同温度下密度的变化。
8. 按照不同比例混合物质制作彩色火焰,观察颜色的变化。
9. 观察火柴棒在水中的漂浮情况,探究密度与沉浮关系。
10. 测量不同颜色纸张的吸光度,并研究颜色与吸光度的关系。
11. 投掷骰子,计算点数之和的概率分布。
12. 测量不同材质的物体上的摩擦系数,并计算摩擦力。
13. 研究声音的传播和反射,观察声波在不同介质中的特性。
14. 制作简易水银温度计,测量温度的变化。
15. 用万能表测量不同电器的电阻、电流和电压。
16. 研究气体的扩散速率,观察气体分子在不同温度下的运动状态。
17. 测量不同颜色光线的波长和频率,并探究颜色与波长频率的关系。
18. 使用不同硬度的铅笔在不同纸张上写字,观察痕迹的深浅和清晰度。
19. 用扫描电镜观察不同物质的微观结构,并比较不同物质之间的差异。
20. 研究磁场的强度和方向,探究电流与磁场的相互作用关系。
21. 设计和制作简易的电磁铁,测量其磁场强度和电阻。
22. 投掷飞镖,研究飞行轨迹和命中准确度。
23. 测量不同物体的密度,计算质量和体积的比值。
24. 制作水晶,观察不同溶液的晶体形态和颜色。
25. 研究不同材质之间的传热过程,探究热传导和热辐射的特性。
26. 测量不同物体的电荷量,研究电荷与电力的相互作用关系。
27. 观察不同金属的折射率和反射率,研究光的特性在金属中的表现。
28. 测量不同水平面上的液体压力和重力,探究液体压力和重力的关系。
29. 研究不同状态的气体压强,探究气体压强与体积的关系。
六年级上册数学好玩实验报告单

学校
班级
六年级
时间
实验名称
反弹高度
实验器材:篮球、乒乓球、米尺、足球、测量表
我的猜测:篮球的平均反弹高度是78.6cm厘米,乒乓球是19.6cm。篮球的反弹高度是起初高度的52.4%。而乒乓球的反弹高度大约是起初高度的13.1%。
步骤:周强德量出长度,杨洋拉直尺子,李丰名负责扔球。周强德观看落点,妥小悦记录。
观察到的现象:球体弹起的高度与材料,重量,大小,力度,高度,接触面有关。
结论:我认为在相同高度自由落下篮球和乒乓球后,谁反弹高些?经过我们小组实验,篮球的反弹高度高些。篮球一般在70厘米到80厘米左右,而乒乓球却在ຫໍສະໝຸດ 0厘米到20厘米左右。指导老师
评定等级
A
小学数学趣味实验报告(3篇)

第1篇实验名称:探究“奇数和偶数的奇妙之旅”实验目的:通过趣味实验,让学生了解奇数和偶数的概念,感受数学的乐趣,培养动手操作能力和观察能力。
实验时间:2023年4月15日实验地点:小学一年级教室实验器材:数字卡片、彩笔、白纸、剪刀、胶水、透明胶带实验参与人员:一年级全体学生实验过程:一、导入1. 教师展示数字卡片,引导学生说出奇数和偶数的概念。
2. 学生分享自己对奇数和偶数的理解。
二、实验操作1. 学生每人准备一张白纸,用彩笔在纸上画出若干个数字,要求每个数字之间留有足够的空间。
2. 学生用剪刀将画出的数字剪下来,形成数字卡片。
3. 学生将奇数卡片用红色标记,偶数卡片用蓝色标记。
4. 学生将奇数卡片和偶数卡片分别用透明胶带粘贴在黑板上。
5. 教师提问:奇数卡片和偶数卡片在黑板上排列后,有什么规律?6. 学生观察、讨论,得出结论:奇数卡片之间相差2,偶数卡片之间相差2,且奇数卡片和偶数卡片交替排列。
三、实验验证1. 教师提问:如果我们把黑板上奇数卡片和偶数卡片的顺序打乱,还会出现这样的规律吗?2. 学生分组进行实验,验证打乱顺序后,奇数卡片和偶数卡片是否依然交替排列。
3. 学生分享实验结果,得出结论:无论奇数卡片和偶数卡片的顺序如何,它们都会交替排列。
四、实验拓展1. 教师提问:在生活中,我们还能找到奇数和偶数的例子吗?2. 学生分享生活中的奇数和偶数例子,如:桌子、椅子、书本、水果等。
3. 教师引导学生思考:为什么生活中有这么多奇数和偶数?4. 学生讨论,得出结论:奇数和偶数是自然界和人类社会中普遍存在的现象。
实验总结:本次趣味实验,让学生在轻松愉快的氛围中了解了奇数和偶数的概念,感受到了数学的乐趣。
通过动手操作,学生培养了观察能力和逻辑思维能力。
同时,实验拓展环节让学生将数学知识应用于生活,激发了学生的学习兴趣。
实验反思:1. 实验过程中,教师应注重引导学生观察、思考,培养学生的动手操作能力。
数学生活中的小实验报告

数学生活中的小实验报告引言数学是一门抽象而有趣的学科,它不仅存在于课本中,还融入到我们日常生活中的方方面面。
本文将介绍数学生活中的一些小实验,通过这些实验可以培养我们的数学思维能力和动手能力,增加对数学的兴趣和理解。
实验一:探索无穷数列实验目的通过构建一个简单的模型,观察和探索无穷数列的性质,加深对数学无穷的理解。
实验材料- 一张纸- 一支铅笔实验步骤1. 在纸上写下一个正整数,如1。
2. 在这个数的右边写上另一个正整数,即前一个数加1,如2。
3. 重复上一步的操作,不断写下下一个更大的正整数。
4. 观察无穷数列的变化。
实验结果通过实验,我们可以发现无穷数列是一个递增的数列,每个数都比前一个数大1。
这个数列是无限长的,其中每个正整数都被包含进去。
实验结论无穷数列代表了数学中“无穷”的概念,即没有边界和限制。
通过这个实验,我们可以更好地理解数学中的无穷性,并且可以将这个概念应用到更复杂的问题中。
实验二:探索质数的分布规律实验目的通过统计一定范围内的质数数量,观察质数的分布规律。
实验材料- 笔记本- 铅笔实验步骤1. 选择一个合适的范围,如1到100。
2. 逐个判断范围内的每个数是否为质数。
3. 统计质数的数量。
4. 重复上述步骤,选择不同范围进行实验。
实验结果通过实验,我们可以发现质数的分布并不是完全随机的。
在较小的范围内,质数似乎更为密集,而在较大的范围内,质数的数量稀疏。
同时,我们也可以观察到一些规律,比如2、3、5、7等质数经常出现在末尾。
实验结论根据实验结果,我们可以初步推断质数的分布并不是完全随机的,可能存在某种规律。
通过进一步的实验和研究,我们可以探索质数的分布规律,并找到更多关于质数性质的规律。
实验三:探索几何图形的面积和周长关系实验目的通过观察不同几何图形的面积和周长,探索它们之间的关系。
实验材料- 一张纸- 一支铅笔- 一把尺子实验步骤1. 选择一个几何图形,如正方形。
2. 用尺子测量正方形的边长,并计算出它的面积和周长。
数学实验综合实验报告

数学实验综合实验报告《数学实验综合实验报告》摘要:本实验旨在通过数学实验的方式,探索和验证数学理论,并通过实验数据的分析和处理,得出结论和结论。
本实验涉及到数学的多个领域,包括代数、几何、概率统计等。
通过实验,我们得出了一些有趣的结论和发现,验证了数学理论的正确性,并对数学知识有了更深入的理解。
一、实验目的1. 验证代数公式的正确性2. 探索几何图形的性质3. 分析概率统计的实验数据4. 探讨数学理论的应用二、实验方法1. 代数公式验证实验:通过代数运算和数值计算,验证代数公式的正确性。
2. 几何图形性质探索实验:通过几何构造和图形分析,探索几何图形的性质。
3. 概率统计数据分析实验:通过实验数据的收集和处理,分析概率统计的规律和特性。
4. 数学理论应用实验:通过实际问题的分析和解决,探讨数学理论在实际中的应用。
三、实验结果与分析1. 代数公式验证实验结果表明,代数公式在特定条件下成立,验证了代数理论的正确性。
2. 几何图形性质探索实验发现,某些几何图形具有特定的性质和规律,进一步加深了对几何学的理解。
3. 概率统计数据分析实验得出了一些概率统计的规律和结论,对概率统计理论有了更深入的认识。
4. 数学理论应用实验通过具体问题的分析和解决,验证了数学理论在实际中的应用性。
四、结论通过本次数学实验,我们验证了代数、几何、概率统计等数学理论的正确性,得出了一些有意义的结论和发现。
实验结果进一步加深了对数学知识的理解和应用,对数学理论的研究和发展具有一定的参考价值。
五、展望本次实验虽然取得了一些有意义的结果,但也存在一些不足之处,如实验方法的局限性、实验数据的局限性等。
未来可以进一步完善实验设计和方法,开展更深入的数学实验研究,为数学理论的发展和应用提供更多的支持和帮助。
《数学实验》实验报告——最小二乘法
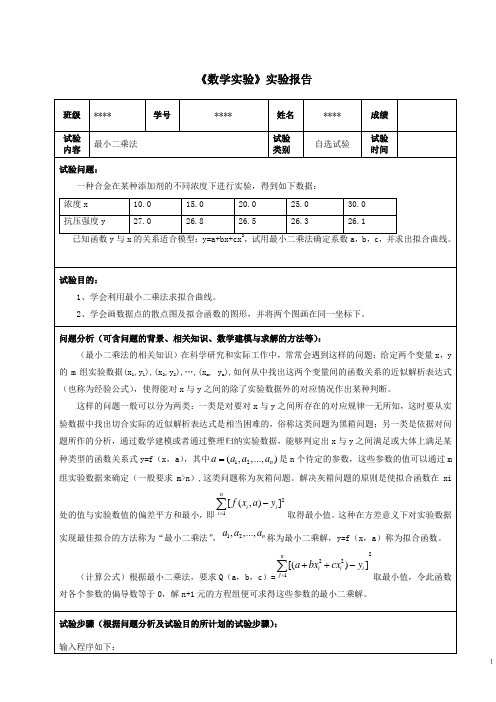
《数学实验》实验报告1x=Table[10.0+5.0*i,{i,0,4}];y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_] :=Sum[(a+b*x[[i]]+c*x[[i]]^2-y[[i]])^2,{i,1,5}]NSolve[{D[q[a,b,c],a]==0, D[q[a,b,c],b]==0,D[q[a,b,c],c]==0},{a,b,c}]t1=ListPlot[xy,PlotStyle->PointSize[0.02]];f[x_] :=27.56+ -0.0574286*x+0.000285714*x^2;t2=Plot[f[x],{x,5,35},AxesOrigin->{5,25}];Show[t1,t2]首先得到a,b,c三个值: {{a->27.56,b->-0.0574286,c->0.000285714}}然后得到同一坐标系下的数据点散点图及拟合函数的图形:试验过程(含详细试验步骤、程序清单及异常情况记录等)输入以下mathematica语句求解参数a,b,c:运行后可得解:2为求得数据点的散点图及拟合函数的图形,输入以下语句,并将两个图画在同一坐标下:运行得:3在最开始时,我输入的程序是这样的:x=Table[10.0+5.0*i,{i,0,4}];y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_] :=Sum[(a+b*x[[i]]+c*x[[i]]^2-y[[i]])^2,{i,1,5}]NSolve[{D[q[a,b,c],a]==0, D[q[a,b,c],b]==0,D[q[a,b,c],c]==0},{a,b,c}]t1=ListPlot[xy,PlotStyle->PointSize[0.02],DisplayFunction->Identity];f[x_] :=27.56+ -0.0574286*x+0.000285714*x^2;t2=Plot[f[x],{x,5,35},AxesOrigin->{5,25},DisplayFunction->Identity];Show[t1,t2, DisplayFunction->$ DisplayFunction]然而得到的结果没有图形(如下):我比照了老师的讲义,改动了“DisplayFunction->Identity”,可是,结果还是一样,没有图形。
数学实验典型案例

数学实验典型案例全文共四篇示例,供读者参考第一篇示例:数学实验是数学教学中不可或缺的一环,通过实验,学生可以更直观地认识数学知识,培养解决问题的能力和逻辑思维。
下面我们来看一些典型的数学实验案例,帮助学生更好地理解和掌握数学知识。
实验一:用三角形拼图探究三角形的性质这个实验旨在帮助学生探究三角形的性质。
教师让学生用拼图拼出不同形状的三角形,然后让学生观察三角形的属性,包括边长、角度、高度等。
通过观察和比较,学生可以发现不同的三角形之间的关系,了解三角形的性质和特点。
实验二:使用平衡秤探究平行线的性质这个实验旨在帮助学生探究平行线的性质。
教师可以准备一个平衡秤和一些不同长度的直线,让学生用平行线的方法来使平衡秤保持平衡。
通过实验,学生可以探究平行线的性质,包括同位角、内错角和同旁内角等。
这样可以让学生更深入地理解平行线的性质。
实验三:用图形和模型探究体积和表面积的关系这个实验旨在帮助学生探究体积和表面积的关系。
教师可以准备一些不同形状的图形和模型,让学生通过测量和计算来探究它们的体积和表面积之间的关系。
通过实验,学生可以发现不同形状的图形和模型之间的体积和表面积的规律,从而更好地理解这两个概念。
通过上述的数学实验案例,我们可以看到,数学实验是帮助学生深入理解和掌握数学知识的重要手段。
教师可以通过设计各种有趣的实验,激发学生的学习兴趣,培养学生的探究能力和解决问题的能力。
希望学生能够通过数学实验,更好地理解和运用数学知识,为未来的学习和生活打下坚实的基础。
【字数达到最低要求】第二篇示例:数学实验典型案例具有重要意义,不仅可以帮助学生巩固所学知识,还可以让他们通过实践探索数学规律,培养解决问题的能力。
下面将介绍几个经典的数学实验案例:一、随机实验与概率计算随机实验是概率论中的基本概念,通过实验可以帮助学生理解随机事件发生的规律。
可以进行抛硬币实验,记录正反面的次数,计算出正反面出现的概率分布;或者进行色子实验,统计各种点数出现的频率,从而了解点数的概率分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学实验一1, 立方曲线y=x 3>> x=-10:0.1:10; >> y=x.^3; >> plot(x,y)-10-8-6-4-2246810-1000-800-600-400-200020040060080010002.立方抛物线y=x 1/3>> x=-10:0.1:10; >> y=x.^(1/3); >> plot(x,y);-10-8-6-4-2024681000.511.522.53,高斯曲线y=2x e以参数方程表示的曲线;>> x=-10:0.1:10; >> y=exp(-x.^2); >> plot(x,y);>>-10-8-6-4-224681000.10.20.30.40.50.60.70.80.91以参数方程表示的曲线: 4,奈尔抛物线 x=t 3y=t 2(y=x 2/3)>> x=-10:0.1:10; >> y=x.^(2/3); >> plot(x,y);-10-8-6-4-20246810-3-2-10123455,半立方抛物线 x=t 2y=t 3(y 2=x 3)>> x=-10:0.1:10; >> y=x.^(3/2); >> plot(x,y);-10-8-6-4-20246810-5051015202530356,笛卡尔曲线 x=3at 2) , y=3at 2/(1+t 2) (x 3+y 3-3axy=0)>> t=-10:0.1:10; >> a=8;>> x=3*a*t./(1+t.^2);y=3*a*t.^2./(1+t.^2); >> plot(x,y);-15-10-505101505101520257,蔓叶线 x=at 2/(1+t 2),y=at 3/(1+t 2) (y 2=x 3/(a-x)) t=-10:0.1:10; >> a=2;>> x=a*t.^2./(1+t.^2);y=a*t.^3./(1+t.^2); >> plot(x,y);00.20.40.60.81 1.2 1.4 1.6 1.82-20-15-10-5051015208,摆线 x=a(t-sint), y=b(1-cost) >> a=10; >> b=15; >> t=-10:0.1:10;>> x=a*(t-sin(t));y=a*(1-cos(t)); >> plot(x,y);-150-100-5050100150024681012141618209,内摆线(星形线) x=acos 3t, y=asin 3t (x 2/3+y2/3=a2/3)>> t=-10:0.1:10; >> a=5;>> x=a*(cos(t)).^3; y=a*(sin(t)).^3; >> plot(x,y);-5-4-3-2-101234510,圆的渐伸线(渐开线)x=a(cost+tsint) , y=a(sint- tcost )t=-10:0.1:10;>> a=5;>> x=a.*(cos(t)+t.*sin(t));y=a.*(sin(t)-t.*cos(t));>> plot(x,y);-40-30-20-1010203040-50-40-30-20-100102030405011,空间螺线 x=acost , y=bsint , z=ct 。
t=-20:0.1:20; >> a=5;b=8;c=10;>> x=a.*cos(t);y=b.*sin(t);z=c.*t; >> plot3(x,y,z);-5510-200-100100200以极坐标方程表示的曲线: 12,阿基米德曲线 r=am ,r >=0 。
m=-20:0.1:20; >> a=1; >> r=a.*m;r>0;>> x=r.*cos(t);y=r.*sin(t); >> plot(x,y);-20-15-10-505101520-20-15-10-5510152013,对数螺线 r =e at。
>> t=-20:0.00001:20;>> a=1;>> r=exp(a.*t);>> x=r.*cos(t);y=r.*sin(t);>> plot(x,y);-0.500.51 1.52 2.5x 108-0.500.511.522.533.544.5x 10814,双纽线 r 2=a 2cos2t ((x 2+y 2)2=a 2(x 2-y 2))。
>> t=-20:0.00001:20;>> a=1;>> r=(a.^2.*cos(2.*t)).^(1/2);>> x=r.*cos(t);y=r.*sin(t);>> plot(x,y);-1-0.8-0.6-0.4-0.200.20.40.60.81-0.4-0.3-0.2-0.10.10.20.30.415,双纽曲线 r 2=a 2sin2t ((x 2+y 2)2=2a 2xy)>> t=-20:0.0001:20;>> a=1;>> r=(a.^2.*sin(2.*t)).^(1/2);>> x=r.*cos(t);y=r.*sin(t);>> plot(x,y);-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.20.20.40.60.8116.四叶玫瑰线 r=asin2t , r>=0 。
>> t=-20:0.0001:20;>> a=1;>> r=a.*sin(2.*t);>> x=r.*cos(t);y=r.*sin(t);>> plot(x,y);-0.8-0.6-0.4-0.200.20.40.60.8-0.8-0.6-0.4-0.20.20.40.60.817,三叶玫瑰线 r=a sin3t , r>=0>> t=-20:0.0001:20;>> a=1;>> r=a.*sin(3.*t);>> x=r.*cos(t);y=r.*sin(t);>> plot(x,y);-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.20.20.40.618 ,三叶玫瑰线 r= acos3t ,r>=0 。
>> t=-20:0.0001:20;>> a=1;>> r=a.*cos(3.*t);>> x=r.*cos(t);y=r.*sin(t);>> plot(x,y);-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.20.20.40.60.81数学实验二1,求下列极限(1),l i m x →∞(1-1/x)x>> syms x;>> limit((1-1/x)^x,x,inf)ans =exp(-1)(2),lim x →∞(x 3+3x )1/x>> syms x;>> limit((x^3+3^x)^(1/x),x,inf)ans =3(3),lim x →∞((x+2)1/2-2 (x+1)1/2+x 1/2) >> syms x;>> limit((x+2)^(1/2)-2*(x+1)^(1/2)+x^(1/2),x,inf)ans =(4)1lim x →(2/(x 2-1)-1/(x-1)) >> syms x;>> limit(2/(x^2-1)-1/(x-1),x,1)ans =-1/2(5)0lim x →x cot2x >> syms x;>> limit(x*cot(2*x),x,0)ans =1/2(6)lim x →∞((x 2+3x)1/2-x) >> syms x;>> limit((x^2+3*x)^(1/2)-x,x,inf)ans =3/2(7)lim x →∞(cos(m/x))x >> syms x;>> m=5;>> limit((cos(m/x))^x,x,inf)ans =1(8)1lim x →(1/x-1/(e x -1))>> syms x;>> limit(1/x-1/(exp(x)-1),x,1)ans =(exp(1)-2)/(exp(1)-1)(9)0lim x ((1+x)1/3-1)/x >> syms x;>> limit(((1+x)^(1/3)-1)/x,x,0)ans =1/32,做出函数f(x)=3x 2sin(x 3), -2<x<2 的图形 ,并指出大致单调区间;用diff 求f ’(x) ,并求出f (x )的确切的单调区间。
>> x=-2:0.001:2;y=3*x.^2.*sin(x.^3);>> plot(x,y);-2-1.5-1-0.500.51 1.52-15-10-551015由图形可得大致单调区间(-2,-1.7) (-1.3,1.3) (1.7,2)单调递增 (-1.7,1.3) (1.3,1.7)单调递增 >> syms x;>> diff(3*x.^2.*sin(x.^3),x,1) ans =6*x*sin(x^3)+9*x^4*cos(x^3) >> x=-0:0.001:2;>> y=6*x.*sin(x.^3)+9*x.^4.*cos(x.^3); >> plot(x,y) >>00.20.40.60.81 1.2 1.4 1.6 1.82-60-40-20020406080100120实验四1,(不定积分)用int 计算下列不定积分,并用diff 验证。
