从复数到三角函数公式
复数的三角形式与指数形式的相互转换方法

复数的三角形式与指数形式的相互转换方法复数的三角形式与指数形式是复数的两种常见表示方法,它们在数学和工程领域中经常被用到。
本文将介绍复数的三角形式和指数形式的定义及其相互转换方法。
一、复数的三角形式复数的三角形式是指由模和辐角表示的复数形式。
一个复数可以表示为a + bi的形式,其中a和b分别为实部和虚部,i为虚数单位。
复数的模表示复数到原点的距离,辐角表示复数与实轴正方向的夹角。
1. 复数的模一个复数z = a + bi的模可以用勾股定理求得,即|z| = √(a^2 + b^2)。
模表示复数在复平面上到原点的距离。
2. 复数的辐角复数z = a + bi的辐角可以用反正切函数求得,即θ = arctan(b/a),其中a≠0。
辐角表示复数与实轴正方向的夹角。
3. 复数的三角形式复数的三角形式可以表示为z = r(cosθ + isinθ),其中r为模,θ为辐角。
在这种形式下,复数z的实部为rcosθ,虚部为rsinθ。
二、复数的指数形式复数的指数形式是指由模和辐角的指数形式表示的复数。
复数的指数形式具有简洁的性质,在复杂运算和解析中常常更加方便。
1. 欧拉公式欧拉公式是表示复数的指数形式的重要公式,它可以表示为e^(iθ)= cosθ + isinθ。
这个公式将复数的指数形式与三角形式相联系。
2. 复数的指数形式复数的指数形式可以表示为z = re^(iθ),其中r为模,θ为辐角。
在这种形式下,复数z的实部为rcosθ,虚部为rsinθ。
三、复数的相互转换方法复数的三角形式和指数形式可以相互转换,下面介绍它们之间的转换方法。
1. 从三角形式到指数形式的转换将复数z = r(cosθ + isinθ)转换为指数形式,可以使用欧拉公式e^(iθ) = cosθ + isinθ。
因此,复数z可以表示为z = re^(iθ)。
2. 从指数形式到三角形式的转换将复数z = re^(iθ)转换为三角形式,可以利用指数形式的定义和欧拉公式。
高中三角函数所有公式大全

高中三角函数所有公式大全高中三角函数最全的公式如下:1+sin(a) = [sin(a/2)+cos(a/2)]^2; 1-sin(a) = [sin(a/2)-cos(a/2)]^2;三角函数是基本初等函数之一,是以角度(数学上最常用弧度制,下同)为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
也可以等价地用与单位圆有关的各种线段的长度来定义。
三角函数在研究三角形和圆等几何形状的性质时有重要作用,也是研究周期性现象的基础数学工具。
在数学分析中,三角函数也被定义为无穷级数或特定微分方程的解,允许它们的取值扩展到任意实数值,甚至是复数值。
常见的三角函数包括正弦函数、余弦函数和正切函数。
在航海学、测绘学、工程学等其他学科中,还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。
不同的三角函数之间的关系可以通过几何直观或者计算得出,称为三角恒等式。
三角函数一般用于计算三角形中未知长度的边和未知的角度,在导航、工程学以及物理学方面都有广泛的用途。
另外,以三角函数为模版,可以定义一类相似的函数,叫做双曲函数。
常见的双曲函数也被称为双曲正弦函数、双曲余弦函数等等。
三角函数(也叫做圆函数)是角的函数;它们在研究三角形和建模周期现象和许多其他应用中是很重要的。
三角函数通常定义为包含这个角的直角三角形的两个边的比率,也可以等价的定义为单位圆上的各种线段的长度。
更现代的定义把它们表达为无穷级数或特定微分方程的解,允许它们扩展到任意正数和负数值,甚至是复数值。
三角函数公式两角和公式sin(a+b)=sinacosb+cosasinbsin(a-b)=sinacosb-sinbcosacos(a+b)=cosacosb-sinasinbcos(a-b)=cosacosb+sinasinbtan(a+b)=(tana+tanb)/(1-tanatanb) tan(a-b)=(tana-tanb)/(1+tanatanb)ctg(a+b)=(ctgactgb-1)/(ctgb+ctga)ctg(a-b)=(ctgactgb+1)/(ctgb-ctga)倍角公式tan2a=2tana/(1-tan2a)ctg2a=(ctg2a-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a 半角公式sin(a/2)=√((1-cosa)/2)sin(a/2)=-√((1-cosa)/2)cos(a/2)=√((1+cosa)/2)cos(a/2)=-√((1+cosa)/2)tan(a/2)=√((1-cosa)/((1+cosa))tan(a/2)=-√((1-cosa)/((1+cosa))ctg(a/2)=√((1+cosa)/((1-cosa))ctg(a/2)=-√((1+cosa)/((1-cosa))和差化积2sinacosb=sin(a+b)+sin(a-b)2cosasinb=sin(a+b)-sin(a-b)2cosacosb=cos(a+b)-sin(a-b)-2sinasinb=cos(a+b)-cos(a-b)sina+sinb=2sin((a+b)/2)cos((a-b)/2 cosa+cosb=2cos((a+b)/2)sin((a-b)/2) tana+tanb=sin(a+b)/cosacosbtana-tanb=sin(a-b)/cosacosbctga+ctgbsin(a+b)/sinasinb-ctga+ctgbsin(a+b)/sinasinb正弦定理a/sina=b/sinb=c/sinc=2r注:其中r表示三角形的外接圆半径余弦定理b2=a2+c2-2accosb注:角b是边a和边c的夹角高中三角函数公式及诱导公式大全如下所示:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2k T +a )=sin ak∈z;cos(2k T + a )=cos ak∈z;tan(2k Tt +a )=tan ak∈z;cot(2k T + a )=cot akEz公式二:设α为任意角,T+a的三角函数值与α的三角函数值之间的关系:sin ( T + a )=-sin a;cos( T + a )=-cos a;tan( T + a )=tan a;cot ( T+a )=cot a公式三:任意角α与-a的三角函数值之间的关系:sin(- a )=-sin a;cos(- a )=cos a;tan(- a )=-tan a;cot(- a )=-cot a公式四:利用公式二和公式三可以得到T -a与a的三角函数值之间的关系:sin( T 一a )=sin a;cos ( T - a )=-cos a;tan ( T - a )=-tan a;cot ( T-a )=-cot a 1、公式一:设α为任意角,终边相同的角的同一三角函数的值相等sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)2、公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系sin(π+α)=-sinαcos(π+α)=-cosαcot(π+α)=cotα3、公式三:任意角α与-α的三角函数值之间的关系sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα4、公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系cos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα5、公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα6、公式六:π/2±α与α的三角函数值之间的关系sin(π/2+α)=cosαsin(π/2-α)=cosαcos(π/2+α)=-sinαcos(π/2-α)=sinαtan(π/2+α)=-cotαtan(π/2-α)=cotαcot(π/2+α)=-tanαcot(π/2-α)=tanα。
§6-4 复数三角形式运算

则有
(n ∈ N * )
这是复数三角形式的 n 次幂 (n ∈ N * ) 的运算法则,这个法则 叫做棣莫弗定理。 它表明:复数 n 次幂的模等于这个复数的模的 n 次幂, 它们辐角等于这个复数的辐角的 n 倍。也就是说,复数的 n * 次幂 ( n ∈ N ) ,是把模的 n 次幂作为幂的模,把辐角的 n 倍 作为幂的辐角。
证明 左边=
(cos 9θ + i sin 9θ ) (cos14θ + i sin14θ ) (cos 24θ + i sin 24θ )
= r1 ⋅ r2 cos (θ 1+ θ 2 ) + i sin (θ 1+ θ
2
) 。
r1 ( cosθ 1+ i sin θ
) ⋅ r2 ( cosθ 2+ i sin θ 2 ) = r1 ⋅ r2 cos (θ 1+ θ 2 ) + i sin (θ 1+ θ 2 )
复数三角形式运算复数的三角形式三角函数的复数形式三角函数复数形式复数的运算复数运算共轭复数的运算复数的四则运算复数运算法则matlab复数运算
6-4 复数三角形式的运算
一、乘法 设复数 z1 = r1 ( cosθ 1+ i sin θ
z1 ⋅ z 2 = r1 (cosθ 1+ i sin θ
1
)⋅ r2 (cosθ
由此例可以看出,一个非零复数的倒数,其模是原来 复数的模的倒数,其辐角是原来复数辐角的相反数。
例6 计算
解
如何用欧拉公式解决复数问题

如何用欧拉公式解决复数问题欧拉公式是数学中的一条重要公式,它可以将复数表示为三角函数的形式。
通过欧拉公式,我们可以更简单、更直观地处理复数问题。
在本文中,我将介绍欧拉公式的原理和应用,并通过实例来展示如何用欧拉公式解决复数问题。
一、欧拉公式的原理欧拉公式可以表示为:e^(ix) = cosx + isinx这里,e 是自然对数的底数,i 是虚数单位。
根据这个公式,我们可以将复数 z 表示为:z = a + bi其中,a 和 b 分别是复数的实部和虚部。
通过欧拉公式,复数 z 可以表示为:z = r * e^(iθ)其中,r 是复数的模,θ 是复数的辐角。
二、欧拉公式的应用欧拉公式在解决复数问题时具有广泛的应用。
下面,我将介绍两个常见的应用场景。
1.复数的乘法和除法利用欧拉公式,我们可以更方便地进行复数的乘法和除法。
例如,我们要计算复数 z1 = 2 + 3i 和复数 z2 = 4 - 5i 的乘积。
首先,将两个复数用欧拉公式表示为:z1 = r1 * e^(iθ1)z2 = r2 * e^(iθ2)然后,利用欧拉公式的乘法公式(cos相乘,sin相加),我们可以得到:z1 * z2 = (r1 * r2) * e^((iθ1 + iθ2))最后,将结果转换回直角坐标形式,即可得到复数的乘积。
同理,利用欧拉公式的除法公式,我们也可以计算复数的除法。
2.复数的幂次运算通过欧拉公式,我们还可以很方便地计算复数的幂次。
例如,我们要计算复数 z = 2 + 3i 的平方。
首先,将复数用欧拉公式表示为:z = r * e^(iθ)然后,利用欧拉公式的幂次公式,我们可以得到:z^n = r^n * e^(iθn)最后,将结果转换回直角坐标形式,即可得到复数的幂次。
三、实例演练为了更好地理解和应用欧拉公式,下面我将通过一个实例来演示如何用欧拉公式解决复数问题。
假设我们要计算复数 z = 1 + i 的平方。
首先,将复数用欧拉公式表示为:z = √2 * e^(iπ/4)然后,根据欧拉公式的幂次公式,计算平方:z^2 = (√2)^2 * e^(2 * iπ/4) = 2 * e^(iπ/2) = 2i最后,将结果转换回直角坐标形式,即可得到复数的平方为 2i。
从复数到三角函数公式

从复数到三角函数公式
复数是一种数学中的概念,它是由实数和虚数的和组成的。
实数是由负数和正数组成的,而虚数则是由由根号下的负数组成的。
复数可以表示为一个以实部和虚部相加的结果,其中实部代表着实数,而虚部代表着虚数。
因此,复数可以写为:
a + bi
其中a是实部,b是虚部,i表示虚数单位。
复数的三角函数公式可以用来表示一个复数在复平面上的位置。
它可以把复数转换成实数,也可以把实数转换成复数。
此公式也可以用来将极坐标中的点转换成直角坐标系。
三角函数公式如下:
z=r (cosθ + i sinθ)
其中z表示复数,r表示复数的模,cosθ和sinθ表示复数的实部和虚部。
实部和虚部是三角函数的函数值。
简而言之,复数的三角函数公式是一种把复数从极坐标表示法转换为直角坐标表示法的公式。
它是通过把复数的模和实部和虚部的三角函数函数值相乘来构建出来的。
只要知道从极坐标获得的r和θ值,就可以用这一公式来确定特定点的直角坐标。
三角函数与复数函数的关系

三角函数与复数函数的关系三角函数是数学中常见的函数之一,而复数函数则是运用复数进行运算的函数。
尽管它们在实际应用中的概念和运算方式有所不同,但三角函数和复数函数之间存在一定的关联和联系。
本文将从几何角度和数学运算的角度,讨论三角函数与复数函数的关系。
一、几何角度1. 正弦函数和余弦函数:正弦函数和余弦函数是三角函数中最基本的函数之一,它们可以用于表示角度与直角三角形边长之间的关系。
而复数则可以用于表示平面上的点和向量。
在直角坐标系下,复数的实部和虚部分别对应点的横坐标和纵坐标。
因此,可以将正弦函数和余弦函数与复数函数建立联系。
2. 正切函数和割函数:正切函数和割函数是三角函数中另外两个重要的函数。
正切函数可以表示角度与直角三角形斜边与相邻直角边之比,而割函数则表示角度与直角三角形斜边与对边之比。
复数的辐角可以表示平面上的向量与正实轴之间的夹角,在这个角度上取切函数和割函数的值与直角三角形中的值有一定的关系。
二、数学运算的角度1. 欧拉公式:欧拉公式是数学中的一个重要等式,它将三角函数与复数函数联系在一起。
欧拉公式表示为e^(ix) = cos(x) + i*sin(x),其中e为自然对数的底数,i为虚数单位。
欧拉公式表明,复数e^(ix)可以写成一个正弦函数和一个余弦函数的和。
这个公式不仅连接了三角函数和复数函数,还在数学中有广泛的应用。
2. 欧拉公式在复数运算中的应用:欧拉公式的一个重要应用是在复数运算中,它可以简化复数的乘法和幂运算。
通过使用欧拉公式,我们可以将复数写成模长和辐角的形式,从而更方便地进行复数运算。
同时,在复数平面上,欧拉公式还可以表示为一个旋转运算,即复数的乘法可以看作平面上的一个向量的旋转。
综上所述,三角函数与复数函数之间存在密切的关系。
从几何角度来看,三角函数可以用于描述角度与直角三角形边长之间的关系,而复数函数可以表示平面上的点和向量。
从数学运算角度来看,欧拉公式将三角函数与复数函数联系了起来,简化了复数运算。
三角函数和双曲函数公式表
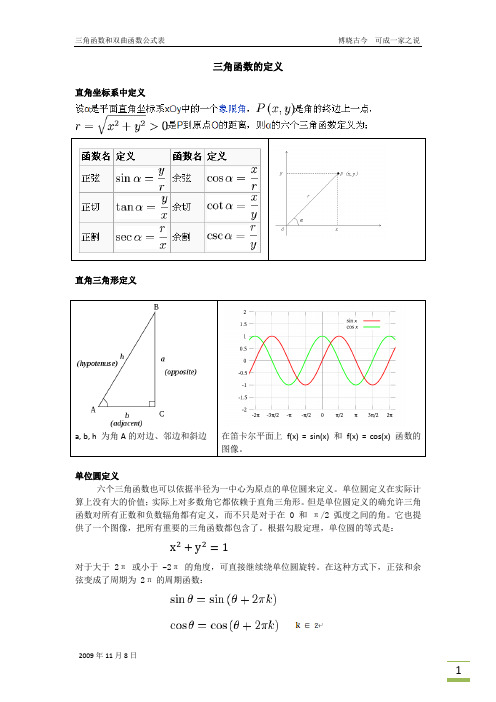
三角函数的定义直角坐标系中定义直角三角形定义a, b, h 为角A的对边、邻边和斜边在笛卡尔平面上f(x) = sin(x) 和f(x) = cos(x) 函数的图像。
单位圆定义六个三角函数也可以依据半径为一中心为原点的单位圆来定义。
单位圆定义在实际计算上没有大的价值;实际上对多数角它都依赖于直角三角形。
但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义,而不只是对于在 0 和π/2 弧度之间的角。
它也提供了一个图像,把所有重要的三角函数都包含了。
根据勾股定理,单位圆的等式是:x2+y2=1对于大于 2π或小于−2π的角度,可直接继续绕单位圆旋转。
在这种方式下,正弦和余弦变成了周期为 2π的周期函数:级数定义只使用几何和极限的性质,可以证明正弦的导数是余弦,余弦的导数是负的正弦。
(在微积分中,所有角度都以弧度来度量)。
我们可以接着使用泰勒级数的理论来证明下列恒等式对于所有实数x都成立:这些恒等式经常被用做正弦和余弦函数的定义。
它们经常被用做三角函数的严格处理和应用的起点(比如,在傅立叶级数中),因为无穷级数的理论可从实数系的基础上发展而来,不需要任何几何方面的考虑。
这样,这些函数的可微性和连续性便可以单独从级数定义来确立。
在这种形式的表达中,分母是相应的阶乘,分子称为“正切数”,它有一个组合解释:它们枚举了奇数势的有限集合的交错排列(alternating permutation)。
在这种形式的表达中,分母是对应的阶乘,而分子叫做“正割数”,有组合解释:它们枚举偶数势的有限集合的交错排列。
从复分析的一个定理得出,这个实函数到复数有一个唯一的解析扩展。
它们有同样的泰勒级数,所以复数上的三角函数是使用上述泰勒级数来定义的。
与指数函数和复数的联系可以从上述的级数定义证明正弦和余弦函数分别是复指数函数在它的自变量为纯虚数时候的虚数和实数部分:这个联系首先由欧拉注意到,叫做欧拉公式。
在这种方式下,三角函数在复分析的几何解释中变成了本质性的。
三角函数公式表

三角函数公式表三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系:平方关系:tanα ·cotα=1sinα ·cscα=1cosα ·secα=1 sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα sin2α+cos2α=11+tan2α=sec2α1+cot2α=csc2α(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin(-α)=-sinαcos(-α)=cosα tan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=——————1-tanα ·tanβtanα-tanβtan(α-β)=——————1+tanα ·tanβ2tan(α/2)sinα=——————1+tan2(α/2)1-tan2(α/2)cosα=——————1+tan2(α/2)2tan(α/2)tanα=——————1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式α+βα-βsinα+sinβ=2sin———·cos———2 2α+βα-βsinα-sinβ=2cos———·sin———2 2α+βα-βcosα+cosβ=2cos———·cos———2 2α+βα-βcosα-cosβ=-2sin———·sin———2 2 1sinα ·cosβ=-[sin(α+β)+sin(α-β)]21cosα ·sinβ=-[sin(α+β)-sin(α-β)]21cosα ·cosβ=-[cos(α+β)+cos(α-β)]21sinα ·sinβ=— -[cos(α+β)-cos(α-β)]2化asinα±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式集合、函数集合简单逻辑任一x∈A x∈B,记作A BA B,B A A=BA B={x|x∈A,且x∈B}A B={x|x∈A,或x∈B}c ard(A B)=card(A)+card(B)-card(A B)(1)命题原命题若p则q逆命题若q则p否命题若 p则 q逆否命题若 q,则 p(2)四种命题的关系(3)A B,A是B成立的充分条件B A,A是B成立的必要条件A B,A是B成立的充要条件函数的性质指数和对数(1)定义域、值域、对应法则(2)单调性对于任意x1,x2∈D若x1<x2 f(x1)<f(x2),称f(x)在D上是增函数若x1<x2 f(x1)>f(x2),称f(x)在D上是减函数(3)奇偶性对于函数f(x)的定义域内的任一x,若f(-x)=f(x),称f (x)是偶函数若f(-x)=-f(x),称f(x)是奇函数(4)周期性对于函数f(x)的定义域内的任一x,若存在常数T,使得f(x+T)=f(x),则称f(x)是周期函数(1)分数指数幂正分数指数幂的意义是负分数指数幂的意义是(2)对数的性质和运算法则loga(MN)=logaM+logaNlogaMn=nlogaM(n∈R)指数函数对数函数(1)y=ax(a>0,a≠1)叫指数函数(2)x∈R,y>0图象经过(0,1)a>1时,x>0,y>1;x<0,0<y<10<a<1时,x>0,0<y<1;x<0,y>1a> 1时,y=ax是增函数0<a<1时,y=ax是减函数(1)y=logax(a>0,a≠1)叫对数函数(2)x>0,y∈R图象经过(1,0)a>1时,x>1,y>0;0<x<1,y<00<a<1时,x>1,y<0;0<x<1,y>0a>1时,y=logax是增函数0<a<1时,y=logax是减函数指数方程和对数方程基本型logaf(x)=b f(x)=ab(a>0,a≠1)同底型logaf(x)=logag(x) f(x)=g(x)>0(a>0,a≠1)换元型 f(ax)=0或f (logax)=0数列数列的基本概念等差数列(1)数列的通项公式an=f(n)(2)数列的递推公式(3)数列的通项公式与前n项和的关系an+1-an=dan=a1+(n-1)da,A,b成等差 2A=a+bm+n=k+l am+an=ak+al等比数列常用求和公式an=a1qn_1a,G,b成等比 G2=abm+n=k+l aman=akal不等式不等式的基本性质重要不等式a>b b<aa>b,b>c a>ca>b a+c>b+ca+b>c a>c-ba>b,c>d a+c>b+da>b,c>0 ac>bca>b,c<0 ac<bca>b>0,c>d>0 ac<bda>b>0 dn>bn(n∈Z,n>1)a>b>0 >(n∈Z,n>1)(a-b)2≥0a,b∈R a2+b2≥2ab|a|-|b|≤|a±b|≤|a|+|b|证明不等式的基本方法比较法(1)要证明不等式a>b(或a<b),只需证明a-b>0(或a-b<0=即可(2)若b>0,要证a>b,只需证明,要证a<b,只需证明综合法综合法就是从已知或已证明过的不等式出发,根据不等式的性质推导出欲证的不等式(由因导果)的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
接著引入三倍角公式:
HPM 通訊第十七卷第九期第二版
(1) sin 3 3 sin 4 sin 3 。 (2) cos 3 4 cos 3 3 cos 。 證明: cos 3 i sin 3 e i ( 3 ) ( e i ) 3
2
cos
(2n 1) 2
HPM 通訊第十七卷第九期第三版
2 sin sin
n (n 1) sin 2 2
移項得 x
n n (n 1) (n 1) sin sin sin 2 2 ,即 sin sin 2 ... sin n 2 2 。 sin sin 2 2
從複數到三角函數公式 費爾茲獎首度出現女性數學家! 貝葉斯和貝氏定理
從複數到三角函數公式
陳敏晧 蘭陽女中 複數在數學各領域均有重大影響,本文章將討論如何以複數的形式來證明三角函數 的相關公式,由於複數具有極坐標形式,可以將角度做旋轉、長度做伸縮變換,這是傳 統幾何學在直角坐標平面難以突破的面向,因此,利用複數來證明三角函數公式往往會 有意想不到的收穫,也常使學習者見識到數學之美! 本文將使用到歷史法國數學家棣美弗(Abraham de Moivre, 1667-1754)於 1730 年發 表的棣莫弗公式,即若 z r (cos i sin ) ,則 z n r n (cos n i sin n ), n Z 。及歐拉 (Leonhard Euler, 1707-1783)在 1748 年所發表的歐拉公式: e i cos i sin 。 首先論證正弦與餘弦的和差角公式:
證明 2 :首先考慮積化和差與和差化積的公式,即
2 sin cos sin( ) sin( ), sin sin 2 sin cos 。 2 2
令 y cos cos 2 ... cos n ,將等式兩邊同乘 2 sin
2 cos cos 2 ... cos n
sin
第一種證明方法:不用複數概念。 1 首先考慮積化和差與和差化積的公式,即
2 sin sin cos( ) cos( ), cos cos 2 sin(
令 x sin sin 2 ... sin n ,將等式兩邊同乘 2 sin
HPM 通訊第十七卷第九期第一版
發行人:洪萬生(台灣師大數學系退休教授) 主編:蘇惠玉(西松高中)副主編:林倉億(台南一中) 助理編輯:黃俊瑋(台灣師大數學所研究生) 編輯小組:蘇意雯(台北市立教育大學)蘇俊鴻(北一女中) 黃清揚(福和國中)葉吉海(陽明高中) 陳彥宏(成功高中)陳啟文(中山女高) 王文珮(青溪國中)黃哲男(台南女中) 英家銘(台北醫學大學)謝佳叡(台灣師大數學系) 創刊日:1998 年 10 月 5 日 每月 5 日出刊 網址:.tw/~horng
cos i sin
3
(cos ) 3 3cos i sin 3 cos (i sin ) 2 i sin
2
3
cos 3 3 cos sin 2 i (3 cos 2 sin sin 3 ) cos 3 3 cos (1 cos 2 ) i 31 sin 2 sin sin 3 4 cos 3 3 cos i (3 sin 4 sin 3 )
) sin 。 2 2 2来自,即得2 sin
2
x 2 sin
2
sin 2 sin
2
sin 2 ... 2 sin
2
sin n
3 3 5 (2n 1) (2n 1) cos cos cos cos ... (cos ) cos 2 2 2 2 2 2 cos
比較兩複數的實部與虛部,即得 sin 3 3 sin 4 sin 3 ; cos 3 4 cos 3 3 cos 。 接著我們可以試著證明更複雜的三角函數公式:
1sin sin 2 ... sin n
sin
(n 1) n sin 2 2 。 sin 2 n (n 1) cos 2 2 。 sin 2
2
,即得
2 sin
2
y 2 sin
2
cos 2 sin
2
cos 2 ... 2 sin
2
cos n
2n 1 3 3 5 2n 1 (sin sin ) (sin( ) sin ) ... sin sin 2 2 2 2 2 2 2n 1 sin sin 2 2 2 sin sin
sin sin cos cos sin , cos cos cos sin sin 證明: cos( ) i sin( )
e i ( ) e i e i cos i sin (cos i sin ) (cos cos sin sin ) i (sin cos cos sin ) 比較兩複數的實部與虛部,即得
