第七章齿轮机构设计
机械设计基础讲义第七章齿轮传动

机械设计基础讲义第七章齿轮传动第7章齿轮传动基本要求:了解齿轮机构的类型和应⽤、齿廓啮合基本定律;掌握渐开线直齿圆柱齿轮的啮特性、正确啮合条件、连续传动条件等;熟悉渐开线齿轮各部分的名称、基本参数及⼏何尺⼨计算;重点:难点: 学时:§ 7-1 121 ⼈字齿轮传动斜齿圆柱齿轮传动齿轮与齿条传动内啮合齿轮传动外啮合齿轮传动)直齿圆柱齿轮2、空间齿轮机构蜗杆传动齿轮传动)交错轴齿轮传动(螺旋曲齿圆锥齿轮传动斜齿圆锥齿轮传动直齿圆锥齿轮传动传动)圆锥齿轮传动(伞齿轮§7-2 齿廓实现定传动⽐的条件∵ 21p p v v =⼜∴ C O v p 111ω= C O v p 222ω=∴ i 12=ω1/ω2=C O C O 12/上式表明,互相啮合的⼀对齿轮,在任⼀位置时的传动⽐,都与其连⼼线O 1O 2被其啮合齿廓在接触点处的公法线所分成的两段成反⽐。
这⼀定律称为齿廓啮合的基本定律。
过两齿廓啮合点所作的齿廓公法线与两轮连⼼线O 1O 2的交点C 称为啮合节点(简称节点)。
上式还表明,要使两齿轮作定传动⽐传动,则两齿廓必须满⾜的条件是:不论两齿廓在何位置接触,过接触点所作的两齿廓公法线必须与两齿轮的连⼼线相交于⼀定点。
当两齿轮作定传动⽐传动时,节点C 在轮1和轮2的运动平⾯上的轨迹分别是以O 1、O 2为圆⼼,以O 1 C 、O 2 C 为半径的两个圆,此圆称为节圆。
并且两节圆作纯滚动。
若两齿轮作变传动⽐传动时,节点C 在轮1和轮2的运动平⾯上的轨迹分别是两条⾮圆曲线,此曲线称为节线。
§7-3 渐开线的形成及其特性⼀、渐开线的形成1)基圆,半径⽤r b 表⽰2)展⾓,⽤θk 表⽰⼆、渐开线的特性1)?=AB BK2)渐开线上任⼀点的法线恒与基圆相切。
切点B 是点K 的曲率中⼼,⽽线段BK 是渐开线在点K 的曲率半径。
3)kb K r r OK OB ==αcos 4)渐开线的形状取决于基圆⼤⼩。
精密机械设计(裘祖荣) 第七章答案 齿轮传动
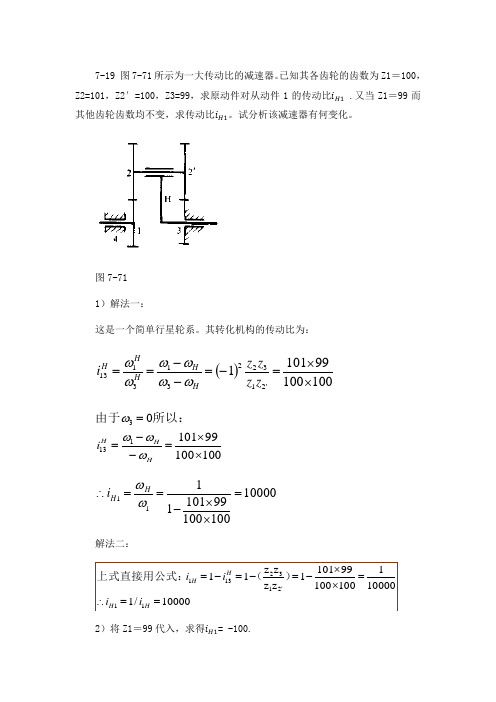
7-19 图7-71所示为一大传动比的减速器。
已知其各齿轮的齿数为Z1=100,Z2=101,Z2′=100,Z3=99,求原动件对从动件1的传动比i H1 .又当Z1=99而其他齿轮齿数均不变,求传动比i H1。
试分析该减速器有何变化。
图7-71 1)解法一:这是一个简单行星轮系。
其转化机构的传动比为:()100100991011'21322313113⨯⨯=-=--==z z z z i H H H HH ωωωωωω1001009910101133⨯⨯=--==H H Hi ωωωω所以:由于10000100100991011111=⨯⨯-==∴ωωH H i解法二:10000/1100001100100991011zz z z 11112132131==∴=⨯⨯-=-=-='H H HH i i i i )(上式直接用公式:2)将Z1=99代入,求得i H1= -100.3)齿轮1的转向从与原动件H 相同变为与原动件H 相反。
7-20 在图7-72示双螺旋桨飞机的减速器中,已知18,30,20,265421====z z z z ,及1n =15000r/min ,试求Q P n n 和的大小和方向。
(提示:先根据同心,求得3z 和6z 后再求解。
)图7-72解:由图可知n 3=n 6=0 根据同心条件:66202262213=⨯+=+=z z z 64253021866z z z =+=+⨯=1)1-2-3-P(H)组成行星轮系 i 13P=n 1−n p n 3−n p=15000−n p 0−n p=−z 3z 1=−6626解得n p =4239.5r/min (与n 1同向) n 4=n p =4239.5r/min 2)4-5-6-Q(H)组成行星轮系 i 46Q=n 4−n Q n 6−n Q=4239.5−n Q−n Q=−z 6z 4=−6630解得min /737.1324r n Q =(与n 1同向).7-21 在图7-73所示输送带的行星减速器中,已知:z 1=10, z 2=32, z 3=74, z 4=72, z 2,=30 及电动机的转速为1450r/min ,求输出轴的转速n 4。
第七章齿轮机构及齿轮传动

rb
cos K
(渐开线公式)
当k点取在分度圆上时:
rb
r cos
mz cos
2
cos k
rb rk
α是决定渐开线齿廓形状的一个基本参数
GB1356-88规定标准值α=20° 某些场合:α=14.5°、15°、22.5°、25°。
分度圆就是齿轮上 具有标准模数和标 准压力角的圆。
分度圆和节圆区别 与联系
1)、齿数z d zp
d zp
2)、模数m
表明:齿轮的大小和渐开线齿轮 形状都与齿数有关 (分度圆直径 d是绘制齿轮的重要参数)
d pz
定义模数 m p 或 p m
∴d=m z 单位:mm ; m 标准化。
rb
d mz
mz cos
2
r
cos
3)、分度圆压力角α
渐开线上一点k的向径:
rK
4、精密齿轮传动的设计要点
精密齿轮传动设计首先要根据主要要求,如精度、 强度、尺寸等等主要矛盾入手。设计合适的传动轮 系。 齿轮涉及到的基本问题: 1.齿轮传动类型的选择。 2.轮系总传动比、级数、各级传动比的分配。 3.齿轮模数和齿数的确定,及各几何尺寸的确定。 4. 齿轮材料的选择及强度设计。 5.传动精度分析和误差的计算。 6.传动力矩计算。 7.其他与装配有关的尺寸的计算等。
三、圆锥齿轮的几何关系
二、渐开线齿轮及其啮合特点
1、形成 当一直线n-n沿一个圆的圆周作纯滚动时,直线 上任一点K的轨迹
t
AK——渐开线 基圆,rb n-n:发生线
m n
K
m
rt
θK:渐开线AK段的展角
A
N
n
r O
第7章齿轮机构

(2)斜齿圆柱齿轮机构
(avi)
齿轮齿条传动
外啮合齿轮传动
特点:轮齿与其轴线倾斜;
传动平稳,适合于高速传动,
但有轴向力;有外啮合、内 (avi) 啮合和齿轮齿条传动类型条机构
(3)人字齿圆柱齿轮机构
特点:由两排旋 向相反的斜齿轮 对称组成,其轴 向力被相互抵消。 适合高速和重载 传动,但制造成 本较高。
3)搅起箱底沉淀的杂质,加剧轮齿的磨损。
§6-2 渐开线齿廓啮合传动的特点
一、渐开线的形成及其特性
1.渐开线的形成 当一直线沿半径为rb的
圆作纯滚动时,该直线上
渐开线
任一点K的轨迹称为该圆的 渐开线,该圆称为渐开线 的基圆,直线K-N称为渐开 线的发生线,角θK 称为渐 开线AK段的展角。
A
θK
rb
F
V
b. 与齿顶线平行的任一直线上具有相同的齿距p= p m。
c. 与齿顶线平行且齿厚s等于齿槽宽e的直线称为分度线, 它是计算齿条尺寸的基准线。
标准齿轮:具有标准模数、标准压 力角、标准齿顶高系数、标准顶隙 系数,且分度圆上齿厚等于齿槽宽
的齿轮。
2.渐开线标准直齿圆柱齿轮的几何尺寸
名称
i12
=
w1 w2
=
O2 P O1 P
=
r2 r1
(avi)
2. 可分性
O1
ω1
r′2
rb1
K N1 ′ P N2
rb2
r′1
ω2 O2
O1
ω1
r′2
rb1
N1 ′ K P N2
rb2
r′1
ω2 O2
i12
=
w1 w2
齿轮机构及其设计

齿轮机构及其设计齿轮机构是现代机械中应用最广泛的一种传动机构。
与其它传动机构相比,齿轮机构的优点是结构紧凑,工作可靠,效率高,寿命长,能保证恒定的传动比,而且其传动的功率与适用的速度范围达。
但是,其制造安装费用较高,及精度齿轮传动的振动噪声较大。
齿轮机构根据实现传动比的情况,分为定传动比和变传动比齿轮机构。
定传动比的圆形齿轮机构根据两传动轴线的相对位置,可分三类:平行轴齿轮机构(两齿轮的传动轴线平行)、相交轴齿轮机构(两齿轮的传动轴线相较于一点)、交错轴齿轮机构(两齿轮的传动轴线为空间任意交错位置)。
1.瞬时传动比两齿轮的传动比总等于齿数的反比,即n1/n2=z2/z1,但其瞬时传动比却与齿廓的形状有关。
按三心定理,公法线n-n与二齿轮连心线的交点C为二齿轮的相对速度瞬心,即二齿轮在C点的线速度应相等:ω1 O1C=ω2 O2C,由此得瞬时传动比і12:і12= ω1/ω2= O2C/ O1C=r2/r1该式说明,具有任意齿廓的二齿轮啮合时,其瞬时角速度的比值等于齿廓接触点公法线将其中心距分成两段长度的反比。
这就是齿廓啮合基本定律。
满足齿廓啮合基本定律的传动比为常数或按一定规律变化的一对齿廓称为共轭齿廓。
在齿轮机构中,相对速度瞬心C称为啮合节点,简称节点。
为实现定传动比传动,要求两齿廓在任何位置啮合时,其节点C都为中心线上的一个固定点,分别以O1、O2为圆心、以O1C 和O2C为半径的圆C1和C2,称为齿轮的节圆(注意非分度圆)。
故节圆是齿轮的相对瞬心线,齿轮的啮合传动相当于其两节圆作无滑动的纯滚动。
2.渐开线圆柱齿轮及其基本齿廓1)齿轮的各部分名称•齿顶圆(直径d a)•齿根圆(直径d f)•齿厚(分度圆处s,任意圆周处sі)•齿槽宽(分度圆处e,任意圆周处eі)•齿距(分度圆处p,任意圆周处pі=sі+eі)•分度圆(直径d,规定标准齿轮分度圆上的齿厚s与齿槽宽e相等,即s=e=1/2 p)•齿顶高(齿顶部分的径向高度h a)•齿根高(齿根部分的径向高度h f)•全齿高(齿顶圆与齿根圆之间的径向距离,h=h a+h f)。
机械原理阶段练习三与答案(7)

华东理工大学网络教育学院机械原理课程阶段练习三(第7章)第七章齿轮机构及其设计一:选择题1、渐开线直齿圆柱齿轮传动的可分性是指(B)不受中心距变化的影响。
A 节圆半径;B 传动比;C 啮合角。
2、齿轮经过正变位修正后,其分度圆同未修正时相比,是(A)。
A 相同;B 减少;C 增大。
3、对于渐开线齿轮而言,其模数决定齿轮的(C),而其分度圆上的压力角,确定了轮齿的(D)。
A 长短;B 厚度;C 大小;D 形状。
4、蜗杆传动的正确啮合条件中,应除去(C)。
A m a1= m t2;B a1= t2;C 1 = 2 ; D螺旋方向相同5、直齿圆柱齿轮的齿根圆(B)大于基圆。
A 一定;B 不一定;C 一定不。
6、渐开线直齿圆柱外齿轮轮廓根切发生在(C)场合。
A 模数较大;B 模数较小;C 齿数较少;D 齿数较多7、现要加工两只正常齿制渐开线标准直齿圆柱齿轮,其中齿轮1:m1 =2mm, z 1 =50;齿轮2:m2=4mm, z2=25。
这两只齿轮(C)加工。
A 可用同一把铣刀;B 可用同一把滚刀;C 不能用同有把刀具。
8、一对平行轴斜齿轮传动,起传动比i12(A)等于z v2/ z v1.A 一定;B 不一定;C 一定不。
9、模数m=2mm,压力角=20o,齿数z=20,齿顶圆直径d a=43.2mm,齿根圆直径d f =35.0mm的渐开线直齿圆柱齿轮是(C)齿轮。
A 标准;B 变位;C 非标准。
10、斜齿圆住齿轮基圆柱上的螺旋角b与分度圆上的螺旋角相比(B)。
A b >B b <C b =11、一对相啮合传动的渐开线齿轮,其压力角为(C),啮合角为(B)。
A 基圆上的压力角;B 节圆上的压力角;C 分度圆上的压力角;D 齿顶圆上的压力角。
12、在减速蜗杆传动中,用(D)来计算传动比i是错误的。
A i=1/2;B i=z1/z2;C i= n1/n2;D i=d2/d1. 13、蜗杆的标准模数是指(C )模数。
第七章-齿轮(机械学基础).

KN »AN
Ⅱ
O
渐开线方程
rk
rb
cos k
k tan k k
k in vk ,称 为 渐 开 线 函 数 。
上 式 即 为 以 K 为 参 数 的 渐 开 线 方 程 。 r b 已 知 , 连 续 给 定 K 则 r K 和 K 可 求 , 即 可 求 出 渐 开 线 上 各 点 的 极 坐 标 。
2
cosk
ON rb OK rk
渐开线上各点压力角不等,
rk k
渐开线在基圆上压力角为0, 离基圆越远,压力角越大
Ⅰ
KⅡ
N
rk k A
rb k
Ⅰ
O
7.3.2 渐开线的性质
Ⅰ
KⅡ
N N1
K1 A
Ⅱ
rb
Ⅰ
O
3、渐开线上任一点K的
法线切于基圆,切点N是 K的曲率中心。
A0, KKN
离基圆越远的点,曲率半 径越大。
人字齿轮
空间齿轮机构
圆锥齿轮
交错轴斜齿轮 蜗杆传动
7.1.1 平面齿轮机构 (1) 直齿圆柱齿轮
外齿轮啮合传动
(1) 直齿圆柱齿轮 内齿轮啮合传动
(1) 直齿圆柱齿轮 齿轮、齿条啮合传动
(2) 平行轴斜齿圆柱齿轮传动
(3) 人字齿轮啮合传动
7.1.2 空间齿轮机构
(1) 圆锥齿轮传动—直齿、曲齿、斜齿
7.3.2 渐开线的性质
K' K
K1' K1
A A'
4、同一基圆上任意两条 渐开线之间的法向距离相 等。
K1''
K'' A''
KK'K1K1'AA' KK ''K1K1''AA ''
第七章 齿轮传动

动画演示
齿轮传动
二.分度圆、模数和压力角
分度圆是齿轮各部分尺寸计 算的基准 分度圆直径d=zp/π, π为无 理数,则D无理数?工程上将比 值p/π规定为一些简单的值, 并使之标准化。这个比值称 为模数,用m表示 通常所说的齿轮的压力角α 是指其分度圆上的压力角。 α为标准值,其值为20º 齿轮上具有标准模数和标准 压力角的圆称为分度圆
齿轮传动
一.渐开线的形
成
一条直线L(称为发 生线(generating line))沿着半径为 rb的圆周(称为基 圆(base circle)) 作纯滚动时,直线 上任意点K的轨迹称 为该圆的渐开线 (involute)。
形成过程动画
齿轮传动
二.渐开线的性质
1) 发生线在基圆上滚过的线段
长度 KN 等于基圆上被滚过的 圆弧长度 AN ,即 KN AN 。 2) 渐开线上任一点的法线切于 基圆。 3)渐开线上的压力角
齿轮传动
齿轮基本尺寸的名称和符号 齿顶圆(da 和 ra) 齿距pi 四圆 齿根圆(df 和 rf) 分度圆(d 和 r) 基圆(db 和 rb) 齿顶高ha 齿距pi 三弧 齿厚si 齿根高hf 齿槽宽ei 齿厚si 齿槽宽ei 分度圆
齿顶圆 基圆
齿根圆
同一圆上
三高
pi si ei
rb
根切现象
根切机理
根切现象:当用齿条型刀具(或齿轮型刀具)加工齿轮时, 若被加工的齿数过少,刀具的齿顶线(或齿顶圆)就会超过 轮坯的啮合极限点N1,这时就会出现刀刃把轮齿根部的渐 开线齿廓切去一部份的现象
齿轮传动
渐开线齿廓的根切
2. 产生根切的原因
当刀具齿顶线与啮合线的交点超过 啮合极限点N之外,便将根部已切 制出的渐开线齿廓再切去一部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
渐开线齿廓的压力角
如图所示,点K为渐开线上任意一点,其向径用rk表示。若用此渐开线为齿轮的齿廓,当齿轮绕点O转动时,齿廓上点K速度的方向应垂直于直线OK,即沿直线mm。我们把法线BK与点K速度方向线mm之间所夹的锐角称为渐开线齿廓在该点的压力角,用αk表示,其大小等于∠KOB。
由△KOB可得:
(1)齿顶圆过齿轮各齿顶所作的圆,其直径和半径分别用da和ra表示。
(2)齿根圆过齿轮各齿槽底部的圆,其直径和半径分别用df和rf表示。
(3)分度圆齿顶圆和齿根圆之间的圆,是计算齿轮几何尺寸的基准圆其直径和半径分别用d和r表示。
(4)基圆形成渐开线的圆,其直径和半径分别用db和rb表示。
(5)齿顶高、齿根高及齿全高齿顶高为分度圆与齿顶圆之间的径向距离,用ha表示;齿根高为分度圆与齿根圆之间的径向距离,用hf表示;齿全高为齿顶圆与齿根圆之间的径向距离,用h表示,显然h=ha+hf。
2.承载能力大--在尺寸小、重量轻的前提下,要求轮齿的强度高、耐磨性好及寿命长。
7.2齿轮齿廓设计
7.2.1齿廓啮合基本定律
图示为一对作平面啮合的齿轮,两轮的齿廓曲线分别为G1和G2。设轮1绕轴O1以角速度ω1转动,轮2绕轴O2以角速度ω2转动,图中点K为两齿廓的接触点,过点K作两齿廓的公法线nn,公法线nn与连心线O1O2交于点C。由三心定理可知,点C是两轮的相对速度瞬心,故有:
(4)理解斜圆柱齿轮齿廓曲面的形成、基本参数与螺旋角的关系、当量齿轮及当量齿数的概念;理解平行轴斜齿轮传动运动设计的条件,并正确运用其几何尺寸公式进行计算;了解交错轴斜齿轮传动的特点。
(5)了解齿轮精度选择的方法,五种失效形式的特点、生成机理及予防或减轻损伤的措施;掌握齿轮材料选择要求、常用钢铁材料选用及其热处理特点。
渐开线的形成
如图示,当直线n-n沿圆周作纯滚动时,直线上任意一点K的轨迹AK称为该圆的渐开线。
这个圆称为基圆,其半径用rb表示;
直线n-n称为渐开线的发生线,
θk(=∠AOK)称为渐开线AK段的展角。
渐开线的性质
由渐开线的形成可知,渐开线具有下列性质:
1)发生线沿基圆滚过的长度,等于基圆上被滚过的弧长,即弦KB=弧AB。
上式表明:渐开线上各点的压力角是不同的,离基圆愈远(矢径rk愈大),其压力角愈大;渐开线起始点A的压力角为零。
由图可知:
渐开线上各点的曲率半径是不同的,离基圆愈远的点其曲率半径愈大;反之,则曲率半径愈小;渐开线在基圆上起始点A处的曲率半径为零。
渐开线函数
由图可得:
即:
上式表明:展角θk是压力角αk的函数称为渐开线函数。
4.中心距具有可分性
由上式可知:一对渐开线齿廓啮合的传动比决定于其基圆的大小,而齿轮一经设计加工好后,它们的基圆也就固定不变,因此当两轮的实际中心距略有偏差时,仍能保持原传动比,此特点称为渐开线齿廓啮合的可分性。这一特点对渐开线齿轮的制造、安装都是十分有利的。
7.3渐开线标准直齿圆柱齿轮机构
图示为直齿外齿轮的一部分。齿轮上每个凸起的部分称为齿,相邻两齿之间的空间称为齿槽。齿轮各部分的名称及符号规定如下:
平行轴齿轮传动机构(圆柱齿轮传动机构)
直齿
斜齿
曲齿
人字齿
齿轮齿条
内齿轮
相交轴齿轮传动机构(圆锥齿轮传动机构)
直齿
斜齿
曲线齿
交错轴齿轮传动机构
斜齿
蜗杆蜗轮
准双曲面齿轮
7.1.2传动的基本要求:
在齿轮传动机构的研究、设计和生产中,一般要满足以下两个基本要求:
1.传动平稳--在传动中保持瞬时传动比不变,冲击、振动及噪音尽量小。
齿轮机构主要缺点:制造及安装精度要求高,价格较贵,不宜用于两轴间距离较大的场合。
齿轮传动机构的分类:
按轴的相对位置
平行轴齿轮传动机构①
相交轴齿轮传动机构、交错轴齿轮传动机构②
按齿线相对齿轮体母线相对位置
直齿、斜齿、人字齿、曲线齿
按齿廓曲线
渐开线齿、摆线齿、圆弧齿
按齿轮传动机构的工作条件
闭式传动、开式传动、半开式传动③<
(6)熟练掌握齿轮传动的受力分析,特别是平行轴斜齿轮轴向力的大小和方向的确定,直齿锥齿轮传动轴向力与径向力的关系;理解几个载荷修正系数的意义及其影响因素,减小其影响的方法;
(7)熟练掌握直齿圆柱传动的齿面接触疲劳强度计算和齿根弯曲疲劳强度的计算基本理论依据,推导公式的思路,公式中各个参数和系数的意义,掌握其确定方法;参考示范例题,掌握齿轮传动设计的步骤,正确地进行直齿轮传动的强度设计计算;了解平行轴斜齿轮传动和直齿锥齿轮传动的当量齿轮的意义,掌握平行轴斜齿轮传动和直齿锥齿轮传动强度计算特点。
标准齿轮的几何尺寸计算公式详见付表
基本参数
(1)齿数z在齿轮整个圆周上轮齿的总数。
(2)模数m分度圆的周长=πd=zp,则有:
由于π是无理数,给齿轮的设计、制造及检测带来不便。为此,人为地将比值p/π取为一些简单的有理数,并称该比值为模数,用m表示,单位是mm。我国已制定了模数的国家标准,因此,分度圆直径d = mz,分度圆齿距p =πm。
由此可得:
在齿轮啮合原理中,将点C称为啮合节点,简称节点。i12称为传动比。
由以上分析可知:一对齿廓在任一位置啮合时,过接触点作齿廓公法线,必通过节点P,它们的传动比与连心线O1O2被节点C所分成两个线段成反比。这一规律称为齿廓啮合基本定律。
作固定传动比传动齿廓必须满足的条件
通常齿轮传动要求两轮作定传动比传动,则由式
(2)理解齿廓啮合基本定律,掌握渐开线齿廓的形成及其性质,并能在后续相关内容中运用;熟练掌握渐开线圆柱齿轮的基本参数、标准齿轮的几何尺寸计算,能够正确计算;掌握范成法切齿原理、标准齿轮和变位齿轮切制特点以及变位齿轮的尺寸变化。
(3)深入理解直齿轮传动运动设计应满足的六个条件及重合度、不根切最少齿数、无侧隙啮合方程等内容,并正确运用重合度等公式进行计算;掌握圆柱齿轮传动的几何尺寸计算及中心距变动系数、齿顶高变动系数等概念;了解标准齿轮传动、高度变位齿轮传动及角度变位齿轮传动的特点。
(2)渐开线上任一点的法线必与基圆相切。
(3)发生线与基圆的切点B为渐开线上点K的曲率中心,而线段BK是相应的曲率半径。
由图可知:
渐开线上各点的曲率半径是不同的,离基圆愈远的点其曲率半径愈大;反之,则曲率半径愈小;渐开线在基圆上起始点A处的曲率半径为零。
⑷渐开线的形状决定于基圆的大小。
如图示,基圆愈大,渐开线愈平直;当基圆半径趋于无穷大时,渐开线将成为一条垂直于N3K的直线。后面介绍的齿条的齿廓就是这种直线齿廓。
(6)齿厚、齿槽宽及齿距在半径为rk的圆周上,一个轮齿两侧齿廓之间的弧长称为该圆上的齿厚,用sk表示;在此圆周上,一个齿槽两侧齿廓之间的弧长称为该圆上的齿槽宽,用ek表示;此圆周上相邻两齿同侧齿廓之间的弧长称为该圆上的齿距,用pk表示,显然pk=sk+ek。分度圆上的齿厚、齿槽宽及齿距依次用s、e及p表示,p=s+e。基圆上的齿距又称为基节,用pb表示。
标准齿轮:基本参数取标准值,具有标准的齿顶高和齿根高,分度圆齿厚等于齿槽宽的直齿圆柱齿轮称为标准齿轮,不能同时具备上述特征的直齿轮都是非标准齿轮。标准齿轮的几何尺寸公式见下表。
7.3.4内齿轮和齿条
内齿轮
图为一直齿内齿轮的一部分,它与外齿轮的不同点是:
(1)内齿轮的齿廓是内凹的,其齿厚和齿槽宽分别对应于外齿轮的齿槽宽和齿厚。
(2)内齿轮的齿顶圆小于分度圆,齿根圆大于分度圆。
(3)为了使内齿轮与外齿轮组成的内啮合齿轮传动能正确啮合,内齿轮的齿顶圆必须大于基圆。
齿条
图为一标准齿条。当标准外齿轮的齿数增加到无穷多时,齿轮的基圆及其他圆都变成互相平行的直线,同侧渐开线齿廓也变成互相平行的斜直线齿廓,这样就形成标准齿条。
标准齿轮:基本参数取标准值,具有标准的齿顶高和齿根高,分度圆齿厚等于齿槽宽的直齿圆柱齿轮称为标准齿轮,不能同时具备上述特征的直齿轮都是非标准齿轮。
标准齿轮及其几何尺寸计算公式
由齿轮各部分名称的定义可以得到标准齿轮的几何尺寸计算公式,如(外齿轮):
分度圆直径d=mz
基圆直径db=dcosα
齿顶圆直径
齿根圆直径
工程上用invαk表示θk,即有
工程中已将不同压力角的渐开线函数计算出来制成表格以备查用,详见表2
如图示,若以渐开线起始点A的矢径OA为极轴,则渐开线上任意一点K的位置可用极坐标描述。联立(a)、(b)两式,可得渐开线的极坐标参数方程式为:
7.2.3渐开线齿廓的啮合特征
1.啮合线是一条定直线
图示为一对渐开线齿廓g1、g2在任意位置啮合,啮合接触点为点K。过点K作这对齿廓的公法线N1N2,根据渐开线的性质可知,公法线N1N2必同时与两基圆相切,即公法线N1N2为两基圆的一条内公切线。由于两基圆的大小和位置均固定不变,其内公切线只有一条。因此,不论两齿廓在任何位置啮合,它们的接触点一定在这条内公切线上(如图中的点K')。这条内公切线是接触点K的轨迹,称为啮合线,亦即一对渐开线齿廓的啮合线是一条定直线。
按齿面硬度
软齿面(≤350HB)、硬齿面(>350HB)
说明:
①平行轴齿轮传动机构又称为平面齿轮传动机构.
②相交轴齿轮传动机构和交错轴齿轮传动机构统称为空间齿轮传动机构.
③闭式传动的齿轮封闭在箱体内,润滑良好;开式传动的齿轮是完全外露的,不能保证良好润滑;半开式传动的齿轮浸在油池内,装有防护罩,不封闭。
第7章齿轮机构设计
本章以渐开线直齿圆柱齿轮传动为主线,阐述圆柱齿轮传动的运动设计和承载能力设计。运动设计主要包括啮合原理及啮合特点、基本参数和几何尺寸计算等内容;承载能力设计主要包括设计计算准则、齿轮失效、力分析和强度计算等内容。在此基础上,简明介绍直齿锥齿轮传动设计及齿轮润滑设计。
