湘教版九年级上册数学第三章 图形的相似 单元测试题
湘教版九年级上册数学《第3章图形的相似》单元测试题含答案
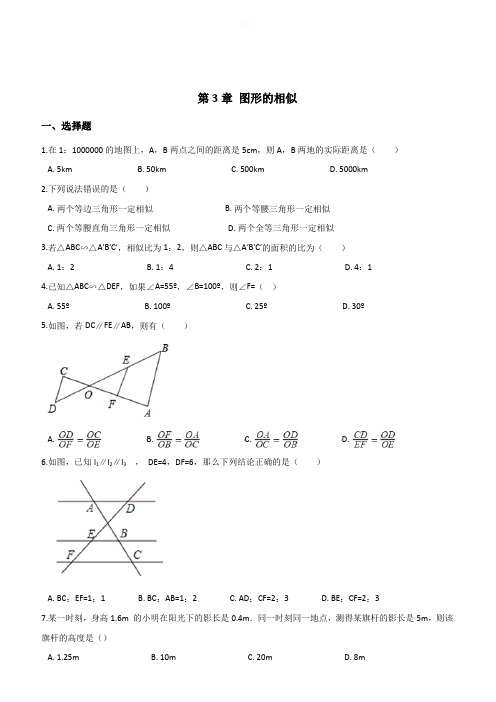
第3章图形的相似一、选择题1.在1:1000000的地图上,A,B两点之间的距离是5cm,则A,B两地的实际距离是()A. 5kmB. 50kmC. 500kmD. 5000km2.下列说法错误的是()A. 两个等边三角形一定相似B. 两个等腰三角形一定相似C. 两个等腰直角三角形一定相似D. 两个全等三角形一定相似3.若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为()A. 1:2B. 1:4C. 2:1D. 4:14.已知△ABC∽△DEF,如果∠A=55º,∠B=100º,则∠F=()A. 55ºB. 100ºC. 25ºD. 30º5.如图,若DC∥FE∥AB,则有()A. B. C. D.6.如图,已知l1∥l2∥l3,DE=4,DF=6,那么下列结论正确的是()A. BC:EF=1:1B. BC:AB=1:2C. AD:CF=2:3D. BE:CF=2:37.某一时刻,身高1.6m 的小明在阳光下的影长是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度是()A. 1.25mB. 10mC. 20mD. 8m8.如图,已知D、E分别是△ABC的AB、AC边上的点,DE∥BC,且S四边形DBCE=8S△ADE.那么AE:AC的值为()A. 1:8B. 1:4C. 1:3D. 1:99.如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A ,BC=3,AC=6,则CD的长为()A. 1B. 2C.D.10.如图,在▱ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于()A. 1:2B. 1:3C. 2:3D. 以上都不正确二、填空题11.若线段a,b,c,d成比例,其中a=3cm,b=6cm,c=2cm,则d=________ .12.如果两个相似三角形的相似比是1:3,那么这两个三角形面积的比是________.13.已知实数a,b,c满足a+b+c=10,且,则的值是________14.如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则=________ .15.如图,四边形ABCD与四边形EFGH位似,位似中心点是O,= ,则=________ .16.已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).①画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是________ ;②以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1________ ,点C2的坐标是________ ;③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标________ .17.如图,已知D ,E分别是△ABC的边BC和AC上的点,AE=2,CE=3,要使DE∥AB ,那么BC:CD应等于________.18.如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么=________ .19.如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=________米.20.一个等腰直角三角形和一个正方形如图摆放,被分割成了5个部分.①,②,③这三块的面积比依次为1:4:41,那么④,⑤这两块的面积比是________三、解答题21.如图,在△ABC中,点D在边AB上,满足且∠ACD=∠ABC,若AC=2,AD=1,求DB的长.22.如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,△ABE与△DEF相似吗?为什么?23.如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.24.已知:如图,.(1)求证:;(2)当时,求证:EC BC.25.在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.(1)感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;(3)应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为________.参考答案一、选择题B B BCD B C C C C二、填空题11.4cm12.1:913.14.15..16.(2,﹣2);;(1,0);(2a﹣3,2b﹣4)17.18.19.2.520.9:14三、解答题21.解∵∠ACD=∠ABC,∠BAC=∠CAD,∴△ADC∽△ACB.∴. ∵AC=2,AD=1,∴.∴DB=AB-AD=3.22.解:△ABE与△DEF相似.理由如下:∵四边形ABCD为正方形,∴∠A=∠D=90°,AB=AD=CD,设AB=AD=CD=4a,∵E为边AD的中点,CF=3FD,∴AE=DE=2a,DF=a,∴=2,=2,∴而∠A=∠D,∴△ABE∽△DEF.23.解:∵△PCD是等边三角形,∴∠PCD=60°,∴∠ACP=120°,∵△ACP∽△PDB,∴∠APC=∠B,又∠A=∠A,∴△ACP∽△ABP,∴∠APB=∠ACP=120°24.证明:(1)∵∴△ABC∽△DEF∴,(2)∵BAC=DAE∴BAD=CAE又∵∴∴△ABD∽△ACE∴ABD=ACE∵BAC=90°∴ABD+ACD=90°∴ACE+ACD=90°即EC BC.25.(1)证明:感知:如图①,∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠DAE+∠DEA=90°,∵EF⊥AE,∴∠AEF=90°,∴∠DEA+∠FEC=90°,∴∠DAE=∠FEC,∵DE=1,CD=4,∴CE=3,∵AD=3,∴AD=CE,∴△ADE≌△ECF(ASA)(2)探究:如图②,∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠DPE+∠DEP=90°,∵EF⊥PE,∴∠PEF=90°,∴∠DEP+∠FEC=90°,∴∠DPE=∠FEC,∴△PDE∽△ECF(3)2。
第3章 图形的相似数学九年级上册-单元测试卷-湘教版(含答案)

第3章图形的相似数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE,BD,且AE、BD交于点F,则S△DEF:S△ADF:S△BAF等于()A.4:10:25B.4:9:25C.2:3:5D.2:5:252、下列各组中的四条线段成比例的是()A.1cm、2cm、20cm、30cmB.1cm、2cm、3cm、4cmC.5cm、10cm、10cm、20cmD.4cm、2cm、1cm、3cm3、正方形ABCD的边长AB=2,E为AB的中点,F为BC的中点,AF分别与DE、BD相交于点M,N,则MN的长为( )A. B. ﹣1 C. D.4、已知,如图,E(﹣4,2),F(﹣1,﹣1).以O为位似中心,按比例尺1:2把△EFO 缩小,点E的对应点的坐标()A.(﹣2,1)B.(2,﹣1)C.(2,﹣1)或(﹣2,﹣1)D.(﹣2,1)或(2,﹣1)5、如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足= ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE= ;④S△DEF=4 ,其中正确的是()A.①②③B.②③④C.①②④D.①③④6、如图,在△ABC中,DE∥BC,,DE=4cm,则BC的长为()A.8 cmB.12 cmC.11 cmD.10 cm7、按如图所示的方法折纸,下面结论正确的个数()①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.A.1 个B.2 个C.3 个D.4 个8、如图,l1∥l2∥l3, BC=1,= ,则AB长为()A.4B.2C.D.9、若=,则的值为()A. B. C. D.10、如图,在矩形ABCD中,E,F分别是AD,AB边上的点,连接CE,DF,他们相交于点G,延长CE交BA的延长线于点H,则图中的相似三角形共有( )A.5对B.4对C.3对D.2对11、如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为()A.1:2B.1:4C.2:1D.4:112、如图,已知∠1=∠2,则添加下列一个条件后,仍无法判定△ABC∽△ADE的是()A.∠C=∠EB.∠B=∠ADEC.D.13、如图是著名画家达芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2a,则BE长为()A.(+1)aB.(﹣1)aC.(3﹣)aD.(﹣2)a14、如图,边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连接AH、FH,FH与AC交于点M,以下结论:①FH=2BH;②AC⊥FH;③S△ACF=1;④CE= AF;⑤=FG•DG,其中正确结论的个数为()A.2B.3C.4D.515、如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为()A.1B.C.2D.不确定二、填空题(共10题,共计30分)16、在中,AD是BC边上的高,,正方形EFGH的顶点E、F 分别在AB、AC上,H、G在BC上.那么正方形EFGH的边长是________.17、与相似且对应中线的比为3:5,则与面积的比为________.18、若,则=________.19、如图,已知矩形中,,,点M,分别在边,上,沿着折叠矩形,使点A,B分别落在E,F处,且点F在线段上(不与两端点重合),过点M作于点H,连接,给出下列判断:①;②折痕的长度的取值范围为;③当四边形为正方形时,N为的中点;④若,则折叠后重叠部分的面积为.其中正确的是________.(写出所有正确判断的序号).20、已知a、b、c、d是成比例线段,即=,其中a=3cm,b=2cm,c=6cm,则线段d=________ cm .21、如图,原点O是△ABC和△A’B’C’的位似中心,点A(1,0)与点A’(-2,0)是对应点,△ABC的面积是,则△A’B’C’的面积是________22、若x:y=1:2,则=________.23、如图,在直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,△AOB为正三角形,射线OC⊥AB,在OC上依次截取点P1, P2, P3,…,P n,使OP1=1,P1P2=3,P2P3=5,…,P n﹣1P n=2n﹣1(n为正整数),分别过点P1, P2, P3,…,P n向射线OA作垂线段,垂足分别为点Q1, Q2, Q3,…,Q n,则点Q n的坐标为________ .24、如图,已知等边△ABC,D是边BC的中点,过D作DE∥AB于E,连接BE交AD于D1;过D1作D1E1∥AB于E1,连接BE1交AD于D2;过D2作D2E2∥AB于E2,…,如此继续,若记S△BDE为S1,记为S2,记为S3…,若S△ABC面积为Scm²,则Sn=________cm²(用含n与S的代数式表示)25、 3月20日起,我国陆续公布了三星堆遗址考古最新发掘成果.地球表面纬度范围是0~90°,对其进行黄金分割,黄金分割点间地区特别适合人类生活,产生了包括三星堆在内的世界古文明,也囊括了大多发达国家.那么黄金地带纬度的范围是________.(黄金比为0.618)三、解答题(共5题,共计25分)26、,求的值.27、如图是一个铁夹子的侧面示意图,点是连接夹面的轴上一点,于点.这个侧面图是轴对称图形,直线是它的对称轴.已知,,.求点与点之间的距离.28、已知反比例函数y=(m为常数)的图象经过点A(-1,6).(1)求m的值;(2)如图,过点A作直线AC与函数y=的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.29、如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.30、某村计划在新农村改造过程中,拟筹资金2000元,计划在一块上、下底分别为10米、20米的梯形空地上种植花草(如图所示,),村委会想在地带与地带种植单价为10元的太阳花,当地带种满花后,已经花了500元,请你计算一下,若继续在地带种植同样的太阳花,资金是否够用?并说明理由.参考答案一、单选题(共15题,共计45分)1、B2、C3、C4、D5、C6、B8、C9、C10、B11、B12、D13、B14、C15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、29、。
湘教版九年级上册数学第三章图形的相似单元测试题

第三章图形的相像一、选择题1.以下说法中,错误的选项是A. 全部的等边三角形都相像B.和同一图形相像的两图形相像C. 全部的等腰直角三角形都相像D. 全部的矩形都相像2.已知△ABC∽△ DEF,若△ABC 与△DEF 的相像比为 3:4,则△ABC 与△DEF 的面积比为 ()A. 4:3B. 3:4C. 16:9 D. 9:163.如图, D 为的边BC上的一点,连结AD ,要使,应具备以下条件中的()A. B. AB 2=BD BC C. D. AC 2=CD CB4. 以下命题正确的选项是()A. 位似图形必定不是全等形B.相像比等于 1 的两个位似图形全等C. 两个位似图形的周长比等于相像比的平方D. 两个位似图形面积的比等相像比5.视力表对我们来说其实不陌生.如图是视力表的一部分,此中张口向上的两个“E”之间的变换是()A. 平移B.旋转C.对称 D.位似6.△ABC ∽△ DEF 且它们的面积比为,则周长比是()A. B. C.D.7.如图,在平行四边形 ABCD 中,假如点 M 为 CD 的中点, AM 与 BD 订交于点 N,若已知 S△DMN=3△ BAN等于(),那么 SA.6B.9C.12D. 38.如图,D、E 分别是△ABC 边 AB 、BC 上的点, DE∥AC,若 S△BDE:S△CDE =1:3,则的值为()A. B. C.D.9.如图,在△ABC 中,点 D,E 分别在 AB ,AC 上,且,则:()A. 1:2B. 1:4C. 1:8 D. 1:910.如图,在△ABC 中∠A=60°,BM ⊥AC 于点 M ,CN⊥AB 于点 N,P 为 BC边的中点,连结 PM,PN,则以下结论:①PM=PN;②;③△ PMN 为等边三角形;④当∠ ABC=45°时, BN=PC.此中正确的个数是()A. 1个B. 2个C. 3个 D. 4个11.如图,点,分别在的,边上,增添以下条件中的一个:①②③④⑤,,,,,使与必定相像的有().A. ①②④B.②④⑤C.①②③④D.①②③⑤二、填空题12.假如△∽△,且对应面积之比为,那么它们对应周长之比为________.13.已知△ABC ∽△ DEF,△ABC 比△ DEF 的周长比为 1:3,则△ ABC 与△DEF的面积之比为 ________14.已知在 Rt△ABC 中,∠C=90°,点 P、Q 分别在边 AB 、AC 上, AC=4,BC=AQ=3 ,假如△APQ 与△ ABC 相像,那么 AP 的长等于 ________.15.在平行四边形 ABCD 的边 AB 和 AD 上分别取点 E 和 F,使 AE=AB ,AF= AD ,连结 EF 交对角线 AC 于 G,则的值是________.16.如图,△ABC 中,∠C=90°,AC=6,BC=8,动点 P 从 A 点出发,以 1cm/s 的速度,沿 A﹣C﹣B 向 B 点运动,同时,动点 Q 从 C 点出发,以 2cm/s 的速度,沿 C﹣B﹣A 向 A 点运动,当此中一点运动到终点时,两点同时停止运动.设运动时间为 t 秒,当 t=________秒时,△PCQ 的面积等于 8cm2.17.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今日的话说,粗心是:如图,是一座边长为 200 步(“步”是古代的长度单位)的正方形小城,东门位于的中点,南门位于的中点,出东门 15 步的处有一树木,求出南门多少步恰巧看到位于处的树木(即点在直线上)?请你计算的长为________步.18.如图,要使△ABC 与△DBA 相像,则只要增添一个适合的条件是________(填一个即可) .19.如图, E 是□ABCD 的边 AD 上一点, AE= ED,CE 与 BD 订交于点 F,BD=10 ,那么 DF=________ .20.如图,在 Rt△ACB 中,∠ACB=90°,AC=BC ,D 是 AB 上的一个动点(不与点A,B 重合),连结CD,将CD 绕点C 顺时针旋转90°获得CE,连结DE,DE 与 AC 订交于点 F,连结 AE.以下结论:①△ ACE≌△ BCD;②若∠BCD=25°,则∠AED=65°;③DE2=2CF?CA;④若AB=3,AD=2BD ,则 AF=.此中正确的结论是________.(填写全部正确结论的序号)21 .如图,在正方形 ABCD 中,△BPC 是等边三角形, BP、CP 的延伸线分别交AD 于点 E、F,连结 BD、DP,BD 与 CF 订交于点 H.给出以下结论:①△ ABE≌△ DCF;②;③DP2=PH?PB;④.此中正确的选项是 ________ .(写出全部正确结论的序号)三、解答题22.如图,△ABC 的极点 A 是线段 PQ 的中点, PQ∥BC,连结 PC、QB,分别交 AB 、AC 于 M、N,连结 MN ,若 MN=1 ,BC=3,求线段 PQ 的长.23.如图,在平面直角坐标系中,已知点A(0 ,12),B(16,0),动点 P 从点 A 开始在线段 AO 上以每秒 1 个单位的速度向点O 挪动,同时点 Q 从点 B 开始在 BA 上以每秒 2 个单位的速度向点 A 挪动,设点 P、Q 挪动的时间为 t 秒。
湘教版九年级数学上册第3章 图形的相似 单元测试题(含答案)

第3章 图形的相似一、选择题(本大题共7小题,每小题4分,共28分) 1.以下列数据为长度的线段中,能成比例的是( ) A .3 cm ,6 cm ,8 cm ,9 cm B .3 cm ,5 cm ,6 cm ,9 cm C .3 cm ,6 cm ,7 cm ,9 cm D .3 cm ,6 cm ,9 cm ,18 cm2.已知△ABC ∽△A ′B ′C ′,AD ,A ′D ′分别是对应边BC ,B ′C ′上的高,且BC =10 cm ,B ′C ′=6 cm ,AD =7 cm ,则A ′D ′为( )A.163 cm B .12 cm C.215cm D .以上都不正确 3.在△ABC 中,D ,E 分别为边AB ,AC 的中点,则△ADE 与△ABC 的面积之比为( ) A.12 B.13 C.14 D.164.在△ABC 和△DEF 中,AB =AC ,DE =DF ,根据下列条件,能判定△ABC 和△DEF 相似的是( )A.AB DE =AC DFB.AB DE =BC EF C .∠A =∠E D .∠B =∠D 5.宽与长的比是5-12(约0.618)的矩形叫作黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图1,作正方形ABCD ,分别取AD ,BC 的中点E ,F ,连接EF .以点F 为圆心,以FD 的长为半径画弧,交BC 的延长线于点G .作GH ⊥AD ,交AD 的延长线于点H ,则图中下列矩形是黄金矩形的是( )图1A .矩形ABFEB .矩形EFCDC .矩形EFGHD .矩形DCGH6.如图2,已知△ABC ,任取一点O ,连接AO ,BO ,CO ,并取它们的中点D ,E ,F ,得△DEF ,则下列说法正确的个数是( )①△ABC 与△DEF 是位似图形;②△ABC 与△DEF 是相似图形;③△ABC 与△DEF 的周长比为1∶2;④△ABC 与△DEF 的面积比为4∶1.A .1B .2C .3D .4图2 图37.为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E ,标记好脚掌中心位置为B ,测得脚掌中心位置B 到镜面中心C 的距离是50 cm ,镜面中心C 距离旗杆底部D 的距离为4 m ,如图3所示.已知小丽同学的身高是1.54 m ,眼睛位置A 距离小丽头顶的距离是4 cm ,则旗杆DE 的高度为( )A .10 mB .12 mC .12.4 mD .12.32 m二、填空题(本大题共7小题,每小题5分,共35分) 8.已知ab =3,则a -b b=________.9.在△ABC 中,AB =6,AC =8,在△DEF 中,DE =4,DF =3,要使△ABC 与△DEF 相似,需添加一个条件是________.(写出一种情况即可)10.如图4,以点O 为位似中心,将△ABC 缩小得到△A ′B ′C ′,若AA ′=2OA ′,则△ABC 与△A ′B ′C ′的周长比为________.11.如果两个相似三角形的面积比是16∶9,那么它们对应的角平分线的比是________.图4 图512.如图5,在平面直角坐标系中,每个小方格的边长均为1,△AOB 与△A ′OB ′是以原点O 为位似中心的位似图形,且OA OA ′=32,点A ,B 都在格点上,则点B ′的坐标是________.13.如图6,为了测量一水塔的高度,小强用2 m 长的竹竿做测量工具,移动竹竿,使竹竿、水塔顶端的影子恰好落在地面上的同一点.此时,竹竿与这一点相距8 m ,与水塔相距32 m ,则水塔的高度为________m.图614.如图7,在Rt △ABC 中,∠C =90°,AC =6,BC =8,P ,Q 分别为边BC ,AB 上的两个动点,若要使△APQ 是等腰三角形且△BPQ 是直角三角形,则AQ =________.图7三、解答题(本大题共3小题,共37分)15.(10分)已知:如图8,△ABC 三个顶点的坐标分别为A (-2,-2),B (-5,-4),C (-1,-5).(1)在网格中画出△ABC 关于x 轴对称的△A 1B 1C 1;(2)以点O 为位似中心,将△ABC 放大为原来的2倍,得到△A 2B 2C 2,请在网格中画出△A 2B 2C 2,并写出点B 2的坐标.图816.(13分)如图9(示意图),小明把手臂水平向前伸直,手持长为a的小尺竖直,瞄准小尺的两端E,F,不断调整站立的位置,使站在点D处正好看到旗杆的底部和顶部.如果小明的手臂长l=40 cm,小尺的长a=20 cm,点D到旗杆底部的距离AD=25 m,求旗杆BA 的高度.图917.(14分)如图10,在正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,EF交AD的延长线于点E,交DC于点N.(1)求证:△ABM∽△EF A;(2)若AB=12,BM=5,求DE的长.图101.[答案] D 2.[答案] C 3.[答案] C 4.[答案] B5.[解析] D 设正方形ABCD 的边长为2,则CD =2,CF =1.在直角三角形DCF 中,DF =CF 2+CD 2=12+22=5,∴FG =5,∴CG =5-1,∴CGCD =5-12,∴矩形DCGH为黄金矩形.故选D.6.[解析] C 根据位似的性质得出①△ABC 与△DEF 是位似图形,②△ABC 与△DEF 是相似图形.∵△DEF 是将△ABC 的三边缩小为原来的12得到的,∴△ABC 与△DEF 的周长比为2∶1,故③错误.根据面积比等于相似比的平方,可知④△ABC 与△DEF 的面积比为4∶1.故选C.7.[解析] B 由题意可得AB =1.5 m ,BC =0.5 m ,DC =4 m ,△ABC ∽△EDC ,则ABDE =BC DC ,即1.5DE =0.54,解得DE =12(m).故选B. 8.[答案] 29.[答案] ∠A =∠D (答案不唯一) 10.[答案] 3∶1[解析] 由题意可知△ABC ∽△A ′B ′C ′, ∵AA ′=2OA ′,∴OA =3OA ′, ∴AC A ′C ′=OA O ′A ′=31,∴C △ABC C △A ′B ′C ′=AC A ′C ′=31. 故答案为3∶1. 11.[答案] 4∶3 12.[答案] (-2,43)[解析] 由题意得OA OA ′=32.又∵B (3,-2),∴点B ′的横坐标是3×(-23)=-2,点B ′的纵坐标是-2×(-23)=43,即点B ′的坐标是(-2,43).故答案为(-2,43).13.[答案] 1014.154或307 [解析] 在Rt △ABC 中,由勾股定理,得AB =10.应分情况讨论:①当AQ =PQ ,∠QPB =90°时.设AQ =PQ =x .由题意,得PQ ∥AC ,∴△BPQ ∽△BCA , ∴BQ BA =PQ CA ,∴10-x 10=x 6, ∴x =154,∴AQ =154.②当AQ =PQ ,∠PQB =90°时.设AQ =PQ =y . 由题意,得△BQP ∽△BCA ,∴PQ AC =BQ BC ,∴y 6=10-y 8,∴y =307. ③当AQ =AP ,∠PQB =90°时.设AQ =z . 由题意,得△BQP ∽△BCA ,BQ =10-z . BQ BC =BP BA ,10-z 8=BP 10,BP =12.5-1.25z . 在Rt △ACP 中,AC =6,AP =z ,BP =12.5-1.25z ,∴CP =8-(12.5-1.25z )=1.25z -4.5.由勾股定理,得(12.5-4.5z )2+62=z 2,解得z =10,∴此情况不存在.综上所述,满足条件的AQ 的值为154或307.15.解:(1)(2)画图如下图所示,B 2(10,8).16.解:过点C 作CH ⊥AB 于点H ,交EF 于点P ,则CH =AD =25 m ,CP =40 cm =0.4 m ,EF =20 cm =0.2 m.由题意,得EF ∥AB , ∴△CEF ∽△CBA ,∴EFBA=CPCH,即0.2BA=0.425,解得BA=12.5(m).答:旗杆BA的高度为12.5 m.17.解:(1)证明:∵四边形ABCD是正方形,∴AD∥BC,∴∠AMB=∠EAF.又∵EF⊥AM,∴∠AFE=90°,∴∠B=∠AFE,∴△ABM∽△EF A.(2)∵∠B=90°,AB=12,BM=5,∴AM=122+52=13.∵四边形ABCD为正方形,∴AD=AB=12.∵F是AM的中点,∴AF=FM=6.5.∵△ABM∽△EF A,∴BMF A=AMEA,即56.5=13EA,∴EA=16.9,∴DE=EA-AD=4.9.。
湘教版数学九年级上册单元测试(三)图形的相似

初中数学试卷单元测试 ( 三) 图形的相像(时间: 45 分钟满分: 100 分 )一、选择题 (本大题共 8 个小题,每题 3 分,共 24 分)1.假如 ab=cd ,则以下正确的选项是( )A.a ∶d=c ∶b ∶c=b ∶d C.a ∶b=c ∶d D.d ∶c=b ∶a2. 在比率尺为 1 ∶5 000 的地图上,量得甲、乙两地的距离为25 cm ,则甲、乙两地间的实质距离是 ( )A.1 250 kmB.125 kmC.12.5 kmD.1.25 km3.假如两个相像三角形的面积之比为9 ∶4,那么这两个三角形对应边上的高之比为( )A.9 ∶4∶2 C.2 ∶3 D.81 ∶164.以下命题是假命题的是( )A. 全部矩形都相像B.全部圆都相像C.全部正三角形都相像D.一个角是100 °的两个等腰三角形相像5.如图,已知 D , E 分别是△ABC 的 AB , AC 边上的点, DE∥BC,且 S△ADE∶S 四边形DBCE =1 ∶8,那么 AE∶AC 等于( )A.1 ∶9∶3 C.1 ∶8 D.1 ∶26.某学习小组在议论“变化的三角形”时,知道大三角形与小三角形是位似图形(如下图 ).则小三角形上的极点(a ,b) 对应于大三角形上的极点坐标为( )金戈铁制卷A.(-2a , -2b)B.(2a ,2b)C.(-2b , -2a)D.(-2a ,-b)7.如图,以下各式不可以说明△ ABC ∽△ADE 的是 ( )AD AE AD DE A. ∠ADE= ∠B B.∠AED= ∠C C.AC D. BCAB AB1 8.如图,将△ ABC 的三边减小为本来的,以下说法:2 ①△ABC 与△DEF 是位似图形;②△ ABC 与△DEF 是相像图形;③△ ABC 与△DEF 的周长之比为2 ∶1 ;④△ABC 与△DEF 的面积之比为 4 ∶1.此中正确的个数是 ( )A.1 个B.2 个C.3 个D.4 个二、填空题 (本大题共 6 个小题,每题3 分,共 18 分 ) 9.已知△ABC ∽△DEF ,且 AB = 1,则 S △ABC ∶S △DEF = . DE 2 a 3 a 10. 已知,则 . a b 5 b11. 如图,在 □ABCD 中, F 是 AD 延伸线上一点,连结 BF 交 DC 于点 E ,在不增添协助线的状况下,请写出图中一对相像三角形: .12. 如图,甲,乙两楼相距20 米,甲楼高 20 米,小明站在距甲楼 10 米的 A 处目测得点 A 与甲,乙楼顶 B 、 C 刚幸亏同向来线上,若小明的身高忽视不计,则乙楼的高度是米 .金戈铁制卷13. 若△ABC ∽△A ′B′C′,且AB= 3 ,△ABC 的周长为12 cm ,则△A ′B′C′的周长为cm. A'B' 414. 如图,△ABC 与△A′B′C′是位似图形,且极点都在格点上,则位似中心的坐标是.三、解答题 (共 58 分)15.(10分)如下图,矩形ABCD 与矩形 EFGH 相像吗?若相像,请加以证明,并求出相像比;若不相像,请说明原因 .16.(12分)如图,以点O 为位似中心,位似比为 2 ,画出△ABC 的位似△A ′B′C′.17.(12分)如图,在△ ABC中,DE∥BC,EF∥AB,求证:△ ADE∽△EFC.金戈铁制卷18.(12分)如图,∠C=90°,点D是AB的中点,DE⊥ AB于点D,交BC于点E,若AB=30,AC=18,求图中四边形 ADEC 的面积 .19. ( 12 分)如图,路灯(P 点 )距地面 8 米,身高 1.6 米的小明从距路灯的底部(O 点 )20 米的 A 点,沿 OA 所在的直线行走 14 米到 B 点时,身影的长度是变长了仍是变短了?变长或变短了多少米?参照答案1 311 .答案不独一,如△ DFE ∽△CBE 12 .60 13 .16 14 .(9, 0)9 . 10 .4 215 .矩形 ABCD 与矩形 EFGH 相像,相像比为 20 ∶13 ,原因:AB BC CD AD 20∵== = = ,且∠A= ∠B= ∠C= ∠D= ∠E= ∠F= ∠G= ∠H=90 °.EF FG GH EH 13∴矩形 ABCD ∽矩形 EFGH.16.图略 .17.∵DE∥BC,∴∠AED= ∠C.又∵EF∥AB ,∴∠A= ∠FEC.∴△ADE ∽△EFC.金戈铁制卷18 .在 Rt △ABC 中, BC = AB 2AC 2 = 24. 1 AB = 15. ∵点 D 是 AB 的中点,∴ BD =2∵∠BDE =∠C =90 °,∠B =∠B ,∴△BDE ∽△BCA ,∴ BD = BC ,∴DE = 45 ,DE CA 4∴S 四边形 ADEC = S △ABC -S △BDE = 1 ×18 ×24- 1 ×45 ×15 = 1315 . 2 2 4 819 .变短了 .∵∠MAC= ∠MOP=90 °,∠AMC= ∠OMP ,MA AC MA∴△MAC ∽△MOP .∴ OP ,即 8MO 20 MA.解得 MA=5.同原因△NBD ∽△NOP 可求得 NB=1.5.MA-NB=5-1.5=3.5( 米 ).即小明的身影变短了 3.5 米.金戈铁制卷。
【湘教版】九年级数学上册:第三章图形的相似单元检测试卷(含答案)

第三章《图形的相似》单元检测试卷1. 如果吐耳,那么兰的值是() y 4 X A.鱼 B.C. i4332. 下列各组中的四条线段成比例的是( A.工3, c=2,B. a=4, b=6, c=5, cMOC. <3—2,]5 D.日=2, Z J ^3,3. 己知,C 是线段仙的黄金分割点,AC<BC,若力员2,则殓()A. Vs - 1B.丄(V5+1)C. 3 ■码D. 1(V5 ・ 1)2 24. 如图,在厶ABC 中,DE//BC,翌AD&4,则氏的长是()DB Z对应边冴'的长是( )A. V2B. 2C. 3D. 46. 己知图(1) . (2)中各有两个三角形,其边长和角的度数己在图上 标注,图(2)中力3①交于。
点,对于各图中的两个三角形而言, 下列说法正确的是()A.只有(1)相似B.只有(2)相似一.选择(共10小A. 8B. 10C. 11D. 12C.都相似D.都不相似7. 在平行四边形肋①中,点厅是边肋上一点,且A 吕2ED,虑交对角线勿于点F,则里等于 FC8. 如图,身高1. 8刃的小超站在某路灯下,发现自己的影长恰好是3田,经测量,此时小超离路灯底部的距离是9呂则路灯离地而的高度是9. 如图,△创万与是以点。
为位似中心的位似图形,相似比为1: 2, Z^6Z>90° , CO=CD.若方(1,0),则点 C 的坐标为( )10. 如图,△個7中,点0在线段初上,且ABAD-AC,则下列结论一定1L 己知则业的值为 ________________________4 5 6aD. 9/z?A. (1,2)B. (1,1)C. (V2,V2)D. (2,1)正确的是( )A. A 前AC ・ BDB. AB ・AD^BD ・BCDAB ・AD=BDCD二填空题(共8小j3 2 3A E DB C( )第10题图12.如上图,己知点C是线段力万的黄金分割点,且BOAC.若S表示以虑为边的正方形面积,$表示长为AB.宽为的矩形面积,则S 与$的大小关系为_______________ .13.给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有 ___________ (填序号).14.把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩形纸片的长与宽之比为_____________ .15.己知ZiMCs△碑△力氏与△谢的相似比为4: 1,则△遊与△妙对应边上的高之比为 _____________ .16.如图,血^沪皿,眩〃用〃万C则S:免:5n= ______ .第16题图B C17.如图是小明设计用手电来测量都匀南沙州古城墙高度的示意图,点尸处放一水平的平而镜,光线从点力出发经过平而镜反射后刚好射到古城墙G?的顶端C处,已知ABLBD, CDJBD,且测得返1. 2米,B&L 8米,PM2米,那么该古城墙的高度是________________ 米(平面镜的厚度忽略不计).18.如图,在Rt'ABC中,ZACB=90°,①丄肋于点D, CD=2, BD=\,则AD的长是____________ , /IC的长是 ___________ .三•解答题(共6小题)19.如图,在边上为1个单位长度的小正方形网格中:(1)画出△力兀向上平移6个单位长度,再向右平移5个单位长度后的△ A.RG.(2)以点万为位似中心,将△肋C放大为原来的2倍,得到请在网格中画出(3)求△CGG的而积.■X20.已知:如图,△力氏中,,AB=A(=].f点。
湘教版九年级数学上册第3章 图形的相似测试题

湘教版九年级数学上册第3章 图形的相似测试题一、选择题(本大题共7小题,每题4分,共28分)1.5x =6y ,那么x y等于( ) A .5 B .6 C.56 D.652.C 是线段AB 的黄金联系点,且AB =6 cm ,那么BC 的长为( )A .(3 5-3)cmB .(9-3 5)cmC .(3 5-3)cm 或(9-3 5)cmD .(9-3 5)cm 或(6 5-6)cm3.如图3-Z -1,在四边形ABCD 中,AD ∥BC ,对角线AC ,BD 相交于点O ,AD =1,BC =4,那么△AOD 与△BOC 的面积之比等于( )A.12B.14C.18D.1164.以下选项中能判定△ABC ∽△DEF 的是( )A .∠A =45°,∠B =55°;∠D =45°,∠F =75°B .AB =5,BC =4,∠A =45°;DE =10,EF =8,∠D =45°C .AB =6,BC =5,∠B =40°;DE =5,EF =4,∠E =40°D .BC =4,AC =6,AB =9;DE =18,EF =8,DF =12图3-Z -1图3-Z -25.如图3-Z -2,线段AB 两个端点的坐标区分为A (6,6),B (8,2),以原点O 为位似中心,在第一象限内将线段AB 增加为原来的12后失掉线段CD ,那么端点C 的坐标为( ) A .(3,3) B .(4,3)C .(3,1)D .(4,1)6.如图3-Z -3,在△ABC 中,中线BE ,CD 相交于点O ,衔接DE ,以下结论:①DE BC=12;②S △DOE S △COB =12;③AD AB =OE OB ;④S △DOE S △ADE =13.其中正确的有( ) A .1个 B .2个 C .3个 D .4个图3-Z -3图3-Z -47.如图3-Z -4,在Rt △ABC 中,∠ABC =90°,AB =6,BC =8,∠BAC ,∠ACB 的平分线相交于点E ,过点E 作EF ∥BC 交AC 于点F ,那么EF 的长为( )A.52B.83C.103D.154二、填空题(本大题共4小题,每题4分,共16分)8.在比例尺为1∶40000的地图上,某条路途的长为7 cm ,那么该路途的实践长度是________ km.9.如图3-Z -5,在△ABC 中,MN ∥BC 区分交AB ,AC 于点M ,N .假定AM =1,MB =2,BC =3,那么MN 的长为________.10.在△ABC 中,AB =6,AC =5,点D 在边AB 上,且AD =2,点E 在边AC 上,当AE =________时,以A ,D ,E 为顶点的三角形与△ABC 相似.图3-Z -5图3-Z -611.如图3-Z -6,铁路道口的栏杆短臂长1 m ,长臂长16 m .当短臂端点下降0.5 m 时,长臂端点降低________m .(杆的宽度疏忽不计)三、解答题(本大题共5小题,共56分)12.(10分)如图3-Z -7所示,AD ,BE 区分是钝角三角形ABC 的边BC ,AC 上的高,求证:AD BE =AC BC. 图3-Z -713.(10分)如图3-Z -8,四边形ABCD 中,E ,F ,G 区分在AD ,BD ,CD 上,且EF ∥AB ,FG ∥BC .求证:△DEG ∽△DAC .图3-Z -814.(10分)如图3-Z -9,在10×10的正方形网格中,点A ,B ,C ,D 均在格点上,以点A 为位似中心画四边形AB ′C ′D ′,使它与四边形ABCD 位似,且位似比为2.(1)在图中画出四边形AB ′C ′D ′;(2)填空:△AC ′D ′是________三角形.图3-Z -915.(12分)为测量操场上旗杆的高度,设计的测量方案如图3-Z -10所示,标杆高度CD =3 m ,标杆与旗杆的水平距离BD =15 m ,人的眼睛距空中的高度EF =1.6 m ,人与标杆CD 的水平距离DF =2 m ,E ,C ,A 三点共线,求旗杆AB 的高度.图3-Z -1016.(14分)如图3-Z -11,四边形ABCD 中,AB =AC =AD ,AC 平分∠BAD ,点P 是AC 延伸线上一点,且PD ⊥AD .(1)证明:∠BDC =∠PDC ;(2)假定AC 与BD 相交于点E ,AB =1,CE ∶CP =2∶3,求AE 的长.图3-Z -11详解详析1.D2.C [解析] ∵C 是线段AB 的黄金联系点,且AB =6 cm ,∴BC =5-12AB =(3 5-3)cm 或BC =3-52AB =(9-3 5)cm.应选C.3.D [解析] 在梯形ABCD 中,AD ∥BC ,所以△AOD ∽△COB .又由AD =1,BC =4,依据相似三角形的面积比等于相似比的平方,即可求得△AOD 与△BOC 的面积之比.4.D 5.A6.C [解析] 由BE ,CD 均为△ABC 的中线可知,DE 为△ABC 的中位线,所以DE =12BC ,DE ∥BC ,所以DE BC =12,故①正确; 由DE ∥BC 可得△DOE ∽△COB ,所以S △DOE S △COB =(DE BC)2=14,故②错误;由DE ∥BC 可得AD AB =DE BC ,DE BC =OE OB ,所以AD AB =OE OB ,故③正确;由于DE ∥BC ,所以△ADE ∽△ABC ,所以S △ADE S △ABC =(DE BC )2=14,设△DOE 的高OH 为h ,DE =a ,那么BC =2a ,△BOC 的高为2h ,△ABC 的高为6h ,△ADE 的高为3h ,所以S △DOE S △ADE =12ah 12·a ·3h =13,故④正确.应选择C. 7.C [解析] 延伸FE 交AB 于点D ,作EG ⊥BC 于点G ,作EH ⊥AC 于点H ,∵EF ∥BC ,∠ABC =90°,∴FD ⊥AB .又∵EG ⊥BC ,∴四边形BDEG 是矩形.∵AE 平分∠BAC ,CE 平分∠ACB ,∴ED =EH =EG ,∠DAE =∠HAE ,∴四边形BDEG 是正方形.在△DAE 和△HAE中,∵⎩⎪⎨⎪⎧∠DAE =∠HAE ,∠ADE =∠AHE ,AE =AE ,∴△DAE ≌△HAE (AAS),∴AD =AH .同理△CGE ≌△CHE ,∴CG =CH .设BD =BG =x ,那么AD =AH =6-x ,CG =CH =8-x .∵AC =AB 2+BC 2=62+82=10,∴6-x +8-x =10,解得x =2,∴BD =DE =2,AD =4.∵DF ∥BC ,∴△ADF ∽△ABC ,∴AD AB =DF BC ,即46=DF 8,解得DF =163, 那么EF =DF -DE =163-2=103.应选C. 8.2.8 [解析] 设这条路途的实践长度为x ,那么140000=7x,解得x =280000 cm =2.8 km. 9.1 [解析] ∵MN ∥BC ,∴△AMN ∽△ABC ,∴AM AB =MN BC, 即11+2=MN 3,∴MN =1. 10.125或53 [解析] 当AE AD =AB AC时, ∵∠A =∠A ,∴△AED ∽△ABC ,此时AE =AB ·AD AC =6×25=125;当AD AE =AB AC时,∵∠A =∠A , ∴△ADE ∽△ABC ,此时AE =AC ·AD AB =5×26=53. 故答案为125或53. 11.812.证明:∵AD ,BE 是钝角三角形ABC 的高,∴∠ADC =∠BEC =90°.又∵∠DCA =∠BCE ,∴△DAC ∽△EBC ,∴AD BE =AC BC. 13.证明:∵EF ∥AB ,∴DE DA =DF DB. ∵FG ∥BC ,∴DG DC =DF DB , ∴DE DA =DG DC. 又∵∠EDG =∠ADC ,∴△DEG ∽△DAC .14.解:(1)如图,四边形AB ′C ′D ′即为所求作图形.(2)依据网格的特点,应用勾股定理可以求出AD ′=C ′D ′=210,应用勾股定理的逆定理可以得出∠AD ′C ′=90°,故△AC ′D ′是等腰直角三角形.15.解:如图,过点E 作EH ⊥AB 于点H ,交CD 于点G ,那么EF =DG =BH =1.6 m ,GH =BD =15 m ,EG =DF =2 m ,∴CG =CD -DG =3-1.6=1.4(m).∵CG ∥AH ,∴△ECG ∽△EAH ,∴CG AH =EG EH , 即1.4AH =22+15, 解得AH =11.9(m),∴AB =AH +BH =11.9+1.6=13.5(m).答:旗杆AB 的高度为13.5 m.16.解:(1)证明:∵AB =AD ,AC 平分∠BAD ,∴AC ⊥BD ,∴∠ACD +∠BDC =90°.∵AC =AD ,∴∠ACD =∠ADC ,∴∠ADC +∠BDC =90°.∵PD ⊥AD ,∴∠ADC +∠PDC =90°,∴∠BDC =∠PDC .(2)过点C 作CM ⊥PD 于点M , ∵∠BDC =∠PDC ,∴CE =CM .∵∠CMP =∠ADP =90°,∠P =∠P , ∴△CPM ∽△APD ,∴CM AD =PC P A. 设CM =CE =x .∵CE ∶CP =2∶3,∴PC =32x . ∵AB =AD =AC =1,∴x 1=32x 32x +1, 解得x =13(x =0不合题意,舍去), 故AE =1-13=23.。
九年级数学上第三章图形的相似单元试卷(湘教版教师用)

九年级数学上第三章图形的相似单元试卷(湘教版教师用)【易错题解析】湘教版九年级数学上册第三章图形的相似单元检测试卷一、单选题(共10题;共30分) 1.如果把三角形的三边按一定的比例扩大,则下列说法正确的是() A. 三角形的形状不变,三边的比变大 B. 三角形的形状变,三边的比变大 C. 三角形的形状变,三边的比不变 D. 三角形的形状不变,三边的比不变【答案】D 【考点】相似三角形的性质【解析】【分析】根据相似三角形的性质得出形状与各边的关系,从而分别分析得出答案.【解答】根据相似三角形的性质可得;如果把三角形的三边按一定的比例扩大.则三角形的形状不变,三边比不变.故选D.【点评】此题主要考查了相似性的性质,根据图形变化得出各边比例关系是解决问题的关键. 2.如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是() A. EG=4GC B. EG=3GC C. EG= GC D. EG=2GC 【答案】B 【考点】平行线分线段成比例【解析】【解答】∵DE∥FG∥BC,DB=4FB,∴ .故答案为:B 【分析】根据平行线分线段成比例即可得出答案。
3.若△ABC∽△A`B`C`,则相似比k等于()A. A′B′:AB B. ∠A: ∠A′ C. S△ABC:S△A′B′C′ D. △ABC周长:△A′B′C′周长【答案】D 【考点】相似三角形的性质【解析】【解答】根据相似三角形对应线段的比等于相似比,面积的比等于相似比的平方,周长的比等于相似比即可求解.∵△ABC∽△A′B′C′,∴相似比k=AB:A′B′=△ABC周长:△A′B′C′周长, = . 故答案为:D.【分析】由题意根据相似三角形对应线段的比等于相似比,面积的比等于相似比的平方,周长的比等于相似比即可求解。
4.对于线段a,b,如果a∶b=2∶3,那么下列四个选项一定正确的是( ) A. 2a=3b B. b-a=1 C. D. 【答案】C 【考点】比例的性质【解析】【解答】根据比值可得:A、2b=3a,则A不符合题意;B、设a=2k,则b=3k,a-b=k,则B不符合题意; C、,则C符合题意; D、,则D不符合题意,故答案为:C.【分析】(1)将比例式化为乘积式即可得2b=3a;(2)设a=2k,则b=3k,a-b=k,而k不一定等于1;(3)由等比性质可得;(4)由合比性质可得. 5.如图,△ABC∽△DEF,相似比为1∶2,若BC=1,则EF的长是()【答案】B 【考点】相似三角形的性质【解析】【解答】解:∵△ABC∽△DEF,相似比为1∶2 ∴ ∴EF=2 故答案为:B 【分析】根据相似三角形的性质及相似比,得出,即可求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章图形的相似
一、选择题
1.下列说法中,错误的是
A. 所有的等边三角形都相似
B. 和同一图形相似的两图形相似
C. 所有的等腰直角三角形都相似
D. 所有的矩形都相似
2.已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF 的面积比为()
A. 4:3
B. 3:4
C. 16:
9 D. 9:16
3.如图,D为的边BC上的一点,连接AD,要使,应具备下列条件中的()
A. B. AB2=BD BC C. D. AC2=CD CB
4. 下列命题正确的是()
A. 位似图形一定不是全等形
B. 相似比等于1的两个位似图形全等
C. 两个位似图形的周长比等于相似比的平方
D. 两个位似图形面积的比等相似比
5.视力表对我们来说并不陌生.如图是视力表的一部分,其中开口向上的两个“E”之间的变换是()
A. 平移
B. 旋转
C. 对
称 D. 位似
6.△ABC∽△DEF且它们的面积比为,则周长比是()
A. B. C.
D.
7.如图,在平行四边形ABCD中,如果点M为CD的中点,AM与BD相交于点N,若已知S△DMN=3,那么S△BAN等于()
A. 6
B. 9
C. 12
D. 3
8.如图,D、E分别是△ABC边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则的值为()
A. B. C.
D.
9.如图,在△ABC中,点D,E分别在AB,AC上,且,则:
( )
A. 1:2
B. 1:4
C. 1:
8 D. 1:9
10.如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC 边的中点,连接PM,PN,则下列结论:①PM=PN;②;③△PMN 为等边三角形;④当∠ABC=45°时,BN= PC.其中正确的个数是()
A. 1个
B. 2个
C. 3
个 D. 4个
11.如图,点,分别在的,边上,增加下列条件中的一个:
①,②,③,④,⑤,使与一定相似的有().
A. ①②④
B. ②④⑤
C. ①②③④
D. ①②③⑤
二、填空题
12.如果△∽△,且对应面积之比为,那么它们对应周长之比为________.
13.已知△ABC∽△DEF,△ABC比△DEF的周长比为1:3,则△ABC与△DEF 的面积之比为________
14.已知在Rt△ABC中,∠C=90°,点P、Q分别在边AB、AC上,AC=4,
BC=AQ=3,如果△APQ与△ABC相似,那么AP的长等于________.
15.在平行四边形ABCD的边AB和AD上分别取点E和F,使AE=AB,
AF=AD,连接EF交对角线AC于G,则的值是________.
16.如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s 的速度,沿A﹣C﹣B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C﹣B﹣A向A点运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t=________秒时,△PCQ的面积等于8cm2.
17.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门位于的中点,南门位于的中点,出东门15步的处有一树木,求出南门多少步恰好看到位于处的树木(即点
在直线上)?请你计算的长为________步.
18.如图,要使△ABC与△DBA相似,则只需添加一个适当的条件是________(填一个即可).
19.如图,E是□ABC D的边AD上一点,AE= ED,CE与BD相交于点F,BD=10,那么DF=________ .
20.如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:
①△ACE≌△BCD;②若∠BCD=25°,则∠AED=65°;③DE2=2CF•CA;④若AB=3 ,AD=2BD,则AF= .其中正确的结论是________.(填写所有正确结论的序号)
21 .如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
①△ABE≌△DCF;②;③DP2=PH•PB;④.
其中正确的是________ .(写出所有正确结论的序号)
三、解答题
22.如图,△ABC的顶点A是线段PQ的中点,PQ∥BC,连接PC、QB,分别交AB、AC于M、N,连接MN,若MN=1,BC=3,求线段PQ的长.
23.如图,在平面直角坐标系中,已知点A(0,12),B(16,0),动点P从点A开始在线段AO上以每秒1个单位的速度向点O移动,同时点Q从点B开始在BA 上以每秒2个单位的速度向点A移动,设点P、Q移动的时间为t秒。
⑴求直线AB的解析式;
⑵求t为何值时,△APQ与△AOB相似?
⑶当t为何值时,△APQ的面积为个平方单位?
⑷当t为何值时,△APQ的面积最大,最大值是多少?
24.甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.
已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)
25.如图,已知矩形OABC中,OA=2,AB=4,双曲线y=(k>0)与矩形两边AB、BC分别交于E、F.
(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,请证明△EGD∽△DCF,并求出k的值.
26.如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y= 的图象在第一象限内的交点为M,若△OBM的面积为1.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.。
