湖南大学工程热力学第4章理想气体热力过程(复习题)
工程热力学沈维道第4章 习题提示和答案

题 4-12 附图
提示和答案: 在 p − v 图和 T − s 图上, 随顺时针移动, n 增大。 可逆绝热膨胀 Δs1− 2s = 0 , 定温膨胀 Δs = 0.462kJ/(kg ⋅ K) ,多变膨胀 Δs = 0.1923kJ/(kg ⋅ K) 。 4-14 试证明理想气体在 T − s 图(如图 4-20)上的任意
可见温度变化范围很大时按定值比热容计算误差太大。
23
第四章 气体和蒸汽的热力过程
4-10
一体积为 0.15 m 3 的气罐,内装有 p1 = 0.55 MPa,t1 = 38 °C 的氧气,今对氧气
加热,其温度、压力都将升高,罐上装有压力控制阀,当压力超过 0.7 MPa 时阀门自动打 开,放走部分氧气,使罐中维持最大压力 0.7 MPa 。问当罐中氧气温度为 285 ℃时,共加 入多少热量?设氧气的比热容为定值, cV = 0.667 kJ/(kg ⋅ K) , c p = 0.917 kJ/(kg ⋅ K) 。 提示和答案: 初终态氧气氧气的质量 m1 =
wt , s =
4-6
1 M
( H m,1 − H m,2 ) = −138.21 × 103 J/kg 。
3 kg 空气从 p1 = 1 MPa 、 T1 = 900 K ,可逆绝热膨胀到 p2 = 0.1 MPa 。设比热
容为定值,绝热指数 κ =1.4,求: (1)终态参数 T2 和 v2 ; (2)过程功和技术功; (3) ΔU 和
的技术功
wt = − ∫ vdp = ∫ pdv + ( p1v1 − p2 v2 ) ,将过程功 ∫ pdv 的各关系式代入, p v v
v2
1
p2
1
v2
《工程热力学》第四章 总结及例题
U13 Q13 W13 649.4kJ 316.62kJ 965.52kJ
H13 nCpm T3 T1 U pV 965.52kJ 299.855 619.393 kPa 2m3 1604.6kJ
S13
n CVm
ln
T3 T1
R ln V3 V1
500mol 3 4.1868J/(mol K) ln 144.26K 4.56kJ/K 298K
Pa
10
1-2过程:由25 ℃,2m3 可逆绝热膨胀到1 atm 2-3过程:定温可逆压缩回到2 m3
理想气体等温过程 :热量=膨胀功=技术功
Q
Q12
Q23
Q23
WT 23
nRT
ln
V3 V2
500
mol 8.314
5
J/(mol K) 144.26
K ln
2 m3 5.906 m3
649.4 kJ
7
q h wt wt q h wt q (ha hb )
考虑过程等压 c a
a
q h c vdp
q ha hc
技术功:
wt q (ha hb )
8
例2 0.5 kmol某种单原子理想气体 ,由25 ℃,2m3 可逆绝热膨 胀到1 atm,然后在此状态的温度下定温可逆压缩回到2 m3。1) 画出各过程的p-v图及T-s图;2)计算整个过程的Q,W,ΔU, Δ H 及ΔS。
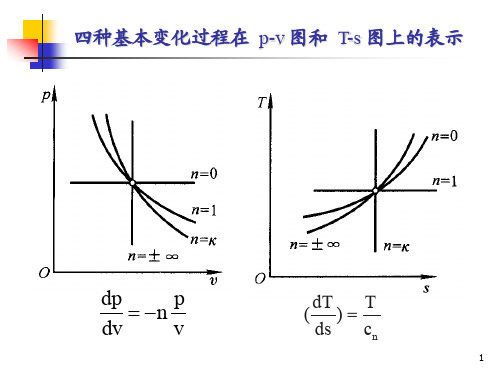
四种基本变化过程在 p-v 图和 T-s 图上的表示
dp n p dv v
dT T ( )
ds cn
1
p-v图和T-s图上的曲线簇
2
u,h,w,wt,q在p-v,T-s图上的变化趋势
u↑,h ↑(T ↑) w ↑(v ↑) wt ↑(p ↓) q ↑(s ↑)
《工程热力学》第四章 习题

Tp11(v1vv12)n0.10584k4g2=Kp2v2
RgT1
RgT2
T2
p2v2 Rg m
0.565106 0.013 287 0.058
441.25K
8
③
Q
mq
m
n
n 1
cv
(T2
T1)
3.21kJ
W
mw
2
pdV
1
n
1 1
(
p1V1
p2V2
)
8.58kJ
④ U mcv (T2 T1) 5.36kJ
3、初态为p1=0.1MPa,t1=40℃的空气,V1=0.052立 方米,在气缸中被可逆多变地压缩到p2=0.565MPa, V2=0.013立方米,试求该多变过程的多变指数n,压 缩后的温度t2,过程中空气和外界交换的功量和热 量,压缩过程中气体热力学能、焓和熵的变化。 1
1、在p-v图和T-s图上画出定比热容理想气体的可逆 定容加热过程、可逆定压加热过程、可逆定温加热 过程和可逆绝热膨胀过程。 1)可逆定容加热过程、可逆定压加热过程
v2n
T1v1n1
T2v2n1
T1 T2
vn1 2
vn1 1
1
vn1 2
vn1 1
,已知v2
v1
0 n1
5
3)n=1.6的膨胀过程,并判断q、w、△u的正负
此过程为放热,对外做功,内能减少
6
4) n=1.3的压缩过程,并判断q、w、△u的正负;
此过程为放热,外界对空气做功,内能增加。
7
3、初态为p1=0.1MPa,t1=40℃的空气,V1=0.052m3,
在气缸中被可逆多变地压缩到p2=0.565MPa, V2=0.013m3,试求该多变过程的多变指数n,压缩后 的温度t2,过程中空气和外界交换的功量和热量, 压缩过程中气体热力学能、焓和熵的变化。
第4章 热学 习题参考答案

Q1 W1 E1 950 J
B 到 C:
W2 0 E2 vCV ,m (TC TB ) 3( p CVC pBVB ) / 2 600 J Q2 W2 E2 600 J
C 到 A:
W3 p A (VA VC ) 100 J E3 vCV ,m (TA TC ) 3( p AVA pCVC ) / 2 150 J Q3 W3 E3 250 J
ca QT vRTc ln ca WTca QT
Va 3456 J Vb
(2) W WPab WVbc WTca 963J (3)
W 963 13.4% Q吸 3739.5 3456
W ( pa pc )(Vc Va ) 1.013 102 J
(4)
Pa Pd Ta Td
Pa Pb , Pc Pd ,Vb Vc
v RT v RT b c Ta Td
PbVb PcVc Ta Td
又 PV vRT
TaTc TbTd来自4-10 a 到 b 绝热
Q1 0
W1 E vCv,m (Ta Tb )
第 4 章 热力学基础 4-1(1) dW pdV (a 2 / V 2 )dV
W dW (a 2 / V 2 )dV a 2 (1 / V1 1 / V2 )
V1
V2
(2) p1V1 / T1 p2V2 / T2
T1 / T2 p1V1 / p2V2 V2 / V1
4-6(1)等体过程,V=常量,W=0
Q E W E M C p ,m (T2 T1 ) 623J M mol
工程热力学-第四章 习题

1、在p-v图和T-s图上画出定比热容理想气体的(1) 可逆定容加热过程、可逆定压加热过程;(2)可逆 定温加热过程和可逆绝热膨胀过程。
2、将满足空气下列要求的多变过程表示在p-v图和T-s 图上:1)空气升压、升温,又放热;2)空气膨胀、 升温,又吸热;3)n=1.6的膨胀过程,并判断q、 w、△u的正负;4) n=1.3的压缩过程,并判断q、 w、△u的正负;
W
mw
2
pdV
1
1 n 1
(
p1V1
p2V2
)
8.58kJ
④ U mcv (T2 T1) 5.36kJ
H mcp (T2 T1) 7.51kJ
S
m(cvIn
T2 T1
Rg In
v2 v1
)
0.0087kJ/K
9
v2n
T1v1n1
T2v2n1
T1 T2
v n 1 2
vn1 1
1
v n 1 2
v1n1,已知v2
v1
0 n1
5
3)n=1.6的膨胀过程,并判断q、w、△u的正负
此过程为放热,对外做功,内能减少
6
4) n=1.3的压缩过程,并判断q、w、△u的正负;
此过程为放热,外界对空气做功,内能增加。
3、初态为p1=0.1MPa,t1=40℃的空气, V1=0.052立方米,在气缸中被可逆多变地压缩到 p2=0.565MPa,V2=0.013立方米,试求该多变 过程的多变指数n,压缩后的温度t2,过程中空气和 外界交换的功量和热量,压缩过程中气体热力学能、1
1、在p-v图和T-s图上画出定比热容理想气体的可 逆定容加热过程、可逆定压加热过程、可逆定温加 热过程和可逆绝热膨胀过程。 1)可逆定容加热过程、可逆定压加热过程
工程热力学习题及答案1-5
第1章基本概念1.1 本章基本要求深刻理解热力系统、外界、热力平衡状态、准静态过程、可逆过程、热力循环的概念,掌握温度、压力、比容的物理意义,掌握状态参数的特点。
1.2 本章难点1.热力系统概念,它与环境的相互作用,三种分类方法及其特点,以及它们之间的相互关系。
2.引入准静态过程和可逆过程的必要性,以及它们在实际应用时的条件。
3.系统的选择取决于研究目的与任务,随边界而定,具有随意性。
选取不当将不便于分析。
选定系统后需要精心确定系统与外界之间的各种相互作用以及系统本身能量的变化,否则很难获得正确的结论。
4.稳定状态与平衡状态的区分:稳定状态时状态参数虽然不随时间改变,但是靠外界影响来的。
平衡状态是系统不受外界影响时,参数不随时间变化的状态。
二者既有所区别,又有联系。
平衡必稳定,稳定未必平衡。
5.状态参数的特性及状态参数与过程参数的区别。
1.3 例题例1:绝热刚性容器内的气体通过阀门向气缸充气。
开始时气缸内没有气体,如图1.1所示。
气缸充气后,气体推动气缸内的活塞向上移动,如图1.2所示。
设管道阀门以及气缸均可认为是绝热的。
若分别选取开口系统与闭口系统,试说明它们的边界应该如何划定?这些系统与外界交换的功量与热量又如何?解:(1)若以容器内原有的气体作为分析对象,属于闭口系统。
容器放气前,边界如图1.1中的虚线所示。
放气后边界如图1.2中的虚线所示。
气体对活塞作的功W是闭口系统与外界交换的功量。
气体通过活塞与外界交换的热量Q是此闭口系统的传热量。
图1.1 图1.2图1.3 图1.4(2)若以容器放气后残留在容器内的气体作为分析对象,同样也是闭口系统。
这时放气前的边界如图1.3中的虚线所示。
放气后的边界如图1.4的虚线表示。
残留气体对离开容器的那部分放逸气体所作的功,是本闭口系统与外界交换的功,残留气体与放逸气体之间交换的热量是本系统的传热量。
(3)类似地若以放逸气体为分析对象,同样也是闭口系统。
其边界将如图1.3和图1.4中的点划线所示。
湖南大学 工程热力学 第4章 理想气体热力过程(复习题)

第4章 理想气体热力过程及气体压缩4.1 本章基本要求熟练掌握定容、定压、定温、绝热、多变过程中状态参数p 、v 、T 、∆u 、∆h 、∆s 的计算,过程量Q 、W 的计算,以及上述过程在p -v 、T -s 图上的表示。
4.2 本章重点结合热力学第一定律,计算四个基本热力过程、多变过程中的状态参数和过程参数及在p -v 、T -s 图上表示。
本章的学习应以多做练习题为主,并一定注意要在求出结果后,在p -v 、T -s 图上进行检验。
4.3 例 题例1.2kg 空气分别经过定温膨胀和绝热膨胀的可逆过程,如图4.1,从初态1p =9.807bar,1t =300C 膨胀到终态容积为初态容积的5倍,试计算不同过程中空气的终态参数,对外所做的功和交换的热量以及过程中内能、焓、熵的变化量。
图4.1解:将空气取作闭口系对可逆定温过程1-2,由过程中的参数关系,得bar v v p p 961.151807.92112=⨯== 按理想气体状态方程,得111p RT v ==0.1677kg m /3125v v ==0.8385kg m /312T T ==573K 2t =300C 气体对外作的膨胀功及交换的热量为1211lnV V V p Q W T T ===529.4kJ 过程中内能、焓、熵的变化量为12U ∆=0 12H ∆=0 12S ∆=1T Q T=0.9239kJ /K 或12S ∆=mRln12V V =0.9238kJ /K 对可逆绝热过程1-2′, 由可逆绝热过程参数间关系可得kv v p p )(211'2= 其中22'v v ==0.8385kg m /3 故 4.12)51(807.9'=p =1.03barRv p T '''222==301K '2t =28C气体对外所做的功及交换的热量为)(11)(11'212211T T mR k V p V p k W s --=--==390.3kJ 0'=s Q过程中内能、焓、熵的变化量为kJ T T mc U v 1.390)(1212''-=-=∆ 或kJ W U 3.390212'-=-=∆kJ T T mc H p 2.546)(1212''-=-=∆ '12S ∆=0例2. 1kg 空气多变过程中吸取41.87kJ 的热量时,将使其容积增大10倍,压力降低为1/8,求:过程中空气的内能变化量,空气对外所做的膨胀功及技术功。
工程热力学第四章 习题解答

第四章 习题解答4-1 多变指数:()()2112ln ln 0.1250.9ln ln 0.1p p n v v ===()210.9 1.4110.91v n n q c T T u u n n κκ---=-=∆=∆---∴11408 kJ/kg 55u q ∆==⨯=40832 kJ/kg w q u =-∆=-=()21 1.4811.2 kJ/kg p h c T T u κ∆=-=⋅∆=⨯= 4011.228.8 kJ/kg s w q h =-∆=-=2211ln ln 1.01ln100.732ln 0.1250.822 kJ/kg Kp v v ps c c v p ∆=+=⨯+⨯=⋅ 4-2 ⑴1 1.4112 1.410.287423110.21 1.41 111.9 kJ/kg RT p w p κκκ--⎡⎤⎛⎫⎛⎫⨯⎢⎥=-=- ⎪ ⎪⎢⎥--⎝⎭⎝⎭⎢⎥⎣⎦= 0s ∆=⑵ ()()120.72342330088.25v w u c T T =-∆=-=⨯-=kJ/kg22113000.1lnln 1.0045ln 0.287ln 4230.5 0.117 kJ kg p T p s c R T p ∆=-=⋅-⋅=⑶1120.5ln 0.287ln195.4 kJ kg 0.2p w RT p ==⋅= 120.5ln 0.287ln 0.462 kJ kg K 0.2p s R p ∆==⨯=⋅⑷1112210.287423110.267.1121n n RT p w n p -⎡⎤⎡⎤⎛⎫⨯⎢⎥=-=-= ⎪⎢⎥⎢⎥--⎝⎭⎣⎦⎢⎥⎣⎦kJ/kg2221ln ln 1.005ln 0.723ln 0.20.35 kJ kg Kp v v ps c c v p ∆=+==-⋅4-3 ⑴ 21ln8.314373ln107140.6 kJ kmol v w RT v ==⨯= 21ln8.314ln1019.14 kJ K v s R v ∆==⨯=⋅ ⑵ 0w =21ln8.314ln1019.14 kJ K v s R v ∆==⨯=⋅ 4-4 210.12ln 50.2598ln 2.091 kJ K 0.6v S mR v ∆==⨯=-()303 2.091633.6 kJ Q W T S ==∆=⨯-=-0, 0H U ∆=∆=4-5 2211201.3286568.3 K 101.3p T T p ⎛⎫==⨯= ⎪⎝⎭()()210.287568.3286202.6 kJ kg 1.41v u c T T ∆=-=-=-()()21 1.40.287568.3286283.6 kJ kg 1.41p h c T T ⨯∆=-=-=-210.287586.3ln ln 0.493 kJ kg K 1.41286v T s c T ∆===⋅-4-6 ⑴ 21303 K T T ==120.3ln 60.287303ln 573.2 kJ 0.1p Q W mRT p ===⨯⨯⨯=⑵ 1 1.411.422110.1303221.4 K 0.3p T T p κκ--⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭ , 0Q = ()()120.2876303221.4351.3 kJ 1 1.41R W m T T κ=-=⨯-=--⑶ 1 1.211.222110.1303252.3 K 0.3n np T T p --⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭()()120.2876303252.3436.5 kJ 1 1.21R W m T T n =-=⨯-=--()()21 1.2 1.40.2876252.33031 1.21 1.41 218.3 kJv n Q m c T T n κ--=-=⨯⨯⨯----=4-7 ()()()()1221ln ln 0.60.12 1.30ln ln 0.8150.236p p n v v ===1116000.236493.4 K 0.287p v T R ⨯===2221200.815340.8 K 0.287p v T R ⨯===()()120.287493.4340.8146 kJ 1 1.31R w T T n =-=-=--()()21 1.3 1.40.287340.8493.411 1.31 1.4136.5 kJ/kgn R q T T n κκ--=⋅-=⋅⋅-----= ()()210.723340.8493.8109.5 kJ kg v u c T T ∆=-=⨯-=- ()()21 1.01340.8493.4154.1 kJ kg p h c T T ∆=-=⨯-=-22120.8150.12ln ln 1.01ln 0.723ln0.2360.6 0.089 kJ kg Kp v v p s c c v p ∆=+=⋅+⋅=⋅4-8 40200160 kJ kg u q w ∆=-=-=-211600.533 kJ kg K 373673v u c T T ∆-===⋅--()()()()()2121122112ln ln ln 16 1.491673ln ln ln 6373p p p p n v v p T p T ====⎛⎫⋅ ⎪⎝⎭()()121 1.4912000.327 kJ/kg K 673373n w R T T --⨯===⋅-- 0.5330.3270.86 kJ kg K p v c c R =+=+=⋅4-9 10.412122933454.7 K v T T v κ-⎛⎫==⨯= ⎪⎝⎭()()1120.287293454.7116 kJ 1 1.41R w T T κ=-=-=---2221ln 0.287454.7ln 3143.4 kJ vw RT v ==⨯⨯=12116143.427.4 kJ w w w =+=-+=4-10 ⑴ 333100 1.73583 K 0.2968p v T R ⨯=== 11.413232 1.735831265 K 0.25v T T v κ--⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭22120.296812651.5 MPa 0.25RT p p v ⨯====11227730.250.153 MPa 1265T v v T ==⨯=⑵ 定压过程:()()210.29681265773365 kJ kg 1 1.41R u T T κ∆=-=-=--()()210.29681265773146 kJ kg w R T T =-=⨯-=定熵过程:()()320.29685831265506 kJ kg 1 1.41R u T T κ∆=-=-=---506 kJ kg w u =-∆=4-11 ⑴ 31110.2875730.274 m 600RT v p ⨯===321330.2740.822 m kg v v ==⨯=11.4112121573369 K 3v T T v κ--⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭2220.2873690.129 MPa 0.822RT p v ⨯===310.274 v v ==3m kg223330.1290.387 MPa p v p v ==⨯= 32369T T ==K⑵ ()()1120.287573369146.41 1.41R w T T κ=-=-=--kJ kg32221ln 0.287369ln 116.43v w RT v ==⨯⨯=-kJ kg()1.293146.4116.438.8 kJ W mw ==⨯-=4-12 1112101.3ln101.3150ln 59250 kJ 5000p Q pV p ==⨯⨯=- 4-13 101.3256000.21550.2872733600pV mRT ⨯===⨯⨯ kg/s 1,120.1ln 0.21550.287293ln 37.8 kW 0.8s T p W mRTp ==⨯⨯=- 112,1 1.411.4111.40.2872930.8 0.2155151.3 kW 1.410.1s SRT p W m p κκκκ--⎡⎤⎛⎫⎢⎥=- ⎪⎢⎥-⎝⎭⎢⎥⎣⎦⎡⎤⨯⨯⎛⎫⎢⎥=⨯-=-⎪⎢⎥-⎝⎭⎣⎦4-14 1600 kg/h kg/s 6m== ⑴定温压缩11210.1ln 0.287293ln 25.1 kW 60.6s T p W mRTp ⋅==⨯⨯=- ⑵定熵压缩112,1 1.411.4111 1.40.2872930.6 132.8 kW 6 1.410.1s SRT p W m p κκκκ--⎡⎤⎛⎫⎢⎥=- ⎪⎢⎥-⎝⎭⎢⎥⎣⎦⎡⎤⨯⨯⎛⎫⎢⎥=⨯-=-⎪⎢⎥-⎝⎭⎣⎦⑶多变压缩 112,1 1.2211.22111 1.220.2872930.6 129.6 kW 6 1.2210.1n n s nnRT p W m n p --⎡⎤⎛⎫⎢⎥=- ⎪⎢⎥-⎝⎭⎢⎥⎣⎦⎡⎤⨯⨯⎛⎫⎢⎥=⨯-=- ⎪⎢⎥-⎝⎭⎣⎦4-15 压缩比2160.160p p ==,应采用二级压缩20.775 MPa p == ∵13322n nT p T p -⎛⎫= ⎪⎝⎭,2120T T '==℃ (冷却至初温)∴1 1.2511.2533226293441.90.775n np T T p --'⎛⎫⎛⎫==⨯= ⎪⎪⎝⎭⎝⎭K3168.8t =℃ 4-16 ()()()()()2121122112ln ln ln 0.50.1 1.130.5289ln ln ln 0.1348p p p p n v v p T p T ====⎛⎫⋅ ⎪⎝⎭111100400482.3 kg/min 8.04 kg/s 0.287289p V mRT ⨯====⨯ ()()12 1.130.2878.042893481 1.1311183 kWs nR W mnwm T T n ⨯==-=⨯---=- ()()21 1.13 1.48.040.7233482891 1.131 712.3 kW 42738 kJ/minv n Q m c T T n κ--=-=⨯⨯⨯---=-= 4-17 12111v p c p λ⎡⎤⎛⎫⎢⎥=-- ⎪⎢⎥⎝⎭⎣⎦⑴ n =1.4,11.40.510.0610.870.1v λ⎡⎤⎛⎫=--=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦⑵ n =1.25,11.250.510.0610.840.1v λ⎡⎤⎛⎫=--=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ ⑶ n =1.0,11.00.510.0610.760.1v λ⎡⎤⎛⎫=--=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦4-18 ()21w pw a n m c t m c T T ∆=--111100250297.3 kg/h 0.08258 kg/s 0.287293a p V m RT ⨯====⨯ ()()()2112 4.186846514297.3293423 0.705 kJ/kg Kw pw w pw n a a m c t m c t c m T T m T T ∆∆⨯⨯=-==--⨯-=-⋅111n v n n Rc c n n κκκ--==--- 1.40.2870.7051.411 1.200.2870.7051 1.41nn Rc n R c κκκ⨯+---===-+--1.211.2122114230.10.905 MPa 293n n T p p T --⎛⎫⎛⎫==⨯= ⎪⎪⎝⎭⎝⎭()()1211.20.2870.0825829342318.48 kW1.21s a s a anRW m w m nw m T T n ===--⨯=⨯-=-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章 理想气体热力过程及气体压缩4.1 本章基本要求熟练掌握定容、定压、定温、绝热、多变过程中状态参数p 、v 、T 、∆u 、∆h 、∆s 的计算,过程量Q 、W 的计算,以及上述过程在p -v 、T -s 图上的表示。
4.2 本章重点结合热力学第一定律,计算四个基本热力过程、多变过程中的状态参数和过程参数及在p -v 、T -s 图上表示。
本章的学习应以多做练习题为主,并一定注意要在求出结果后,在p -v 、T -s 图上进行检验。
4.3 例 题例1.2kg 空气分别经过定温膨胀和绝热膨胀的可逆过程,如图4.1,从初态1p =9.807bar,1t =300C ο膨胀到终态容积为初态容积的5倍,试计算不同过程中空气的终态参数,对外所做的功和交换的热量以及过程中内能、焓、熵的变化量。
图4.1解:将空气取作闭口系对可逆定温过程1-2,由过程中的参数关系,得bar v v p p 961.151807.92112=⨯==按理想气体状态方程,得111p RT v ==0.1677kg m /3 125v v ==0.8385kg m /312T T ==573K 2t =300C ο气体对外作的膨胀功及交换的热量为1211lnV V V p Q W T T ===529.4kJ 过程中内能、焓、熵的变化量为12U ∆=0 12H ∆=0 12S ∆=1T Q T=0.9239kJ /K 或12S ∆=mRln12V V =0.9238kJ /K 对可逆绝热过程1-2′, 由可逆绝热过程参数间关系可得kv v p p )(211'2= 其中22'v v ==0.8385kg m /3 故 4.12)51(807.9'=p =1.03barRv p T '''222==301K '2t =28C ο气体对外所做的功及交换的热量为)(11)(11'212211T T mR k V p V p k W s --=--==390.3kJ 0'=s Q过程中内能、焓、熵的变化量为kJ T T mc U v 1.390)(1212''-=-=∆或kJ W U 3.390212'-=-=∆kJ T T mc H p 2.546)(1212''-=-=∆ '12S ∆=0例2. 1kg 空气多变过程中吸取41.87kJ 的热量时,将使其容积增大10倍,压力降低为1/8,求:过程中空气的内能变化量,空气对外所做的膨胀功及技术功。
解:按题意 kg kJ q n /87.41= 1210v v = 1281p p = 空气的内能变化量:由理想气体的状态方程111RT V p = 222RT V p =得: 12810T T =多变指数 903.010ln 8ln )/ln()/ln(1221===v v p p n多变过程中气体吸取的热量11212141)(1)(T n kn c T T n k n c T T c q v vn n --=---=-= K T 1.571=气体内能的变化量kg kJ T T mc U v /16.8)(1212=-=∆空气对外所做的膨胀功及技术功:膨胀功由闭系能量方程kg kJ u q w n /71.331212=∆-=或由公式])(1[11112112nn p p RT n w ---=来计算技术功:kg kJ nw p pRT n n w nn /49.30])(1[112112112==--=-例3:一气缸活塞装置如图4.2所示,气缸及活塞均由理想绝热材料组成,活塞与气缸间无摩擦。
开始时活塞将气缸分为A 、B 两个相等的两部分,两部分中各有1kmol 的同一种理想气,其压力和温度均为p 1=1bar ,t 1=5℃。
若对A 中的气体缓慢加热(电热),使气体缓慢膨胀,推动活塞压缩B 中的气体,直至A 中气体温度升高至127℃。
试求过程中A 气体吸取的热量。
设气体56.120=v C kJ/(kmol ·K),874.200=p C kJ/(kmol ·K)。
气缸与活塞的热容量可以忽略不计。
解:取整个气缸内气体为闭系。
按闭系能量方程ΔU =Q -W因为没有系统之外的力使其移动,所以W =0则 B v B A v A B A T C n T C n U U U Q ∆+∆=∆+∆=∆=00 其中 1==B A n n kmol故 )(0B A v T T C Q ∆+∆= (1)在该方程A T ∆中是已知的,即1212T T T T T A A A A -=-=∆。
只有B T ∆是未知量。
当向A 中气体加热时,A 中气体的温度和压力将升高,并发生膨胀推动活塞右移,使B 的气体受到压缩。
因为气缸和活塞都是不导热的,而且其热容量可以忽略不计,所以B 中气体进行的是绝热过程。
又因为活塞与气缸壁间无摩擦,而且过程是缓慢进行的,所以B 中气体进行是可逆绝热压缩过程。
按理想气体可逆绝热过程参数间关系kk B p p T T 11212-⎪⎪⎭⎫⎝⎛=图4.2(2)由理想气体状态方程,得 初态时 111)(p T R n n V M B A +=终态时 2222)(p T R n T R n V B M B A M A +=其中V 1和V 2是过程初,终态气体的总容积,即气缸的容积,其在过程前后不变,故V 1=V 2,得22233)()(p T R n T R n p T R n n B M B A M A M B A +=+因为 1==B A n n kmol所以 1212122T T T T p p B A +=⎪⎪⎭⎫ ⎝⎛(3) 合并式(2)与(3),得kk A p p T T p p 11212122-⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛比值12p p 可用试算法求用得。
按题意已知: 1722732+=A T =445K ,52731+=T =278K40.088.2056.12111110=-=-=-=-p vo C C k k k 故 4.012122784452⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛p p p p计算得: 12p p =1.367 代式入(2)得K 315367.12784.011212=⨯=⎪⎪⎭⎫⎝⎛=-)(kk B p p T T代入式(1)得Q =12.56[(445-278)+(315-278)]=2562kJ例4:2kg 的气体从初态按多变过程膨胀到原来的3倍,温度从300℃下降至60℃,已知该过程膨胀功为100kJ ,自外界吸热20kJ ,求气体的c p 和c v 各是多少?现列出两种解法: 解1:由题已知:V 1=3V 2由多变过程状态方程式12112-⎪⎪⎭⎫ ⎝⎛=n V V T T即 1212ln ln1V V T T n =-494.1131ln 27330027360ln 1ln1212=+⎪⎭⎫⎝⎛++=+=V V lm T T n 由多变过程计算功公式:kJ 100)(1121=--=T T R n mW 故 )333573(2)1494.1(100)()1(21--=--=T T m n W R=0.1029kJ/kg ·K 式中 R c k R c c v p v -⋅=-=得 1-=k Rc v 代入热量公式 kJ 20)573333(11029.01494.1494.12)(1112=--⨯--⨯=--⋅--=k k T T k R n k n mQ 得 k =1.6175∴ K kJ/kg 1666.016175.11029.01⋅=-=-=k R c v c p =c v ·k=0.1666×1.6175=0.2695kJ/kg ·K解2:用解1中同样的方法求同n =1.494R=0.1029kJ/kg ·K由 )(12T T mc U v -=∆ 即 )(12T T mc W Q v -=-得K kJ/kg 167.0)573333(210020)(12⋅=--=--=T T m W Q c vKkJ/kg 2695.01029.0167.0⋅=+=+=Rc c v p例5:1kg 空气分两种情况进行热力过程,作膨胀功300kJ 。
一种情况下吸热380kJ ,另一情况下吸热210kJ 。
问两种情况下空气的内能变化多少?若两个过程都是多变过程,求多变指数,并将两个过程画在同一张p -v 图上。
按定比热容进行计算。
解:(1)求两个过程的内能变化。
两过程内能变化分别为:kJ/kg 80300380111=-=-=∆w q u kJ/kg 90300210222-=-=-=∆w q u(2)求多变指数。
K 6.111717.08011==∆=∆v c u T K 125717.09022-=-=∆=∆v c u T因为 T R nw ∆-=11图4.4 图4.5 2.如图4.5所示,234q 与 214q 谁大,234w 与 214w 谁大 4.5 自测题一、是非题1.气体从绝热容器中做自由膨胀,则气体的温度与压力变化的关系式为kk P P T T 11212-⎪⎪⎭⎫ ⎝⎛= ( )2.多变过程曲线上取任意两点的参数,所求得的多变指数n 的值都相同( )3.多变过程中,轴功与膨胀功之间存在下列关系Ws =nW ( ) 4.容积效率的大小只与余隙容积有关。
( ) 5.多变指数n 为负值的过程只能是放热过程。
( ) 6.在T -s 图上,任意两条可逆绝热过程线不能相交。
( ) 7.比热可能出现负值( )8.要得到较高的压力,不一定要采用多级压缩。
( )9.有余隙的压气机若能实现定温压缩,即使要达到较高的压力也不必采用多级压缩。
( )10.压缩1kg 气体所需的理论轴功,无论压缩与膨胀过程的多变指数是否相同,都与余隙容积的大小无关。
( )二、选择题1.某理想气体,经可逆定压过程对外作功W ,则其内能的变化量和与外界交换的热量分别为___。
A 无确定值B kwu =∆,w q =;Cw u =∆,kw q =D )1(-=∆κw u ,)1(-=κκwq 2.一个橡皮气球在太阳下被照晒,气球在吸热过程中膨胀,气球内的压力正比于气球的容积。
则气球内的气体进行的是___。
A 定压过程B 多变过程C 定温过程D 定容过程3.系统进行一个不可逆绝热膨胀过程后,欲使系统回复到初态,系统需要进行一个____ 过程A 可逆绝热压缩B 不可逆绝热压缩C 边压缩边吸热D 边压缩边放热4.理想气体n<0的多变膨胀过程具有 A q> 0 w>0 ∆u>0 B q<0 w>0 ∆u<0; C q>0 w>0 ∆u<0 D q<0 w>0 ∆u>0。
