五章导数和微分
《数学分析》考试大纲

《数学分析》考试大纲一、课程名称:数学分析二、适用专业: 数学与应用数学三、考试方法:闭卷考试四、考试时间:100分钟五、试卷结构:总分:100分,选择题15分,填空题15分,计算题40分,证明题30分。
六、参考书目:1、华东师范大学数学系编著,《数学分析》(上、下册),高等教育出版社,2010年第4版。
2、中国科学技术大学常庚哲史济怀编著,《数学分析教程》(上、下册),高等教育出版社,2003年第1版。
七、考试的基本要求:数学分析是数学与应用数学专业专升本入学考试中专业课考试内容,考生应理解和掌握《数学分析》中函数、极限、连续、微分学、积分学和级数的基本概念、基本理论、基本方法。
应具有抽象思维能力、逻辑推理能力、运算能力和空间想象能力,能运用所学知识正确拙推理证明,准确、简捷地计算。
能综合运用数学分析中的基本理论、基本方法分析和解决实际问题。
八、考试范围第一章实数集与函数(一)考核内容实数及其性质,绝对值与不等式。
区间与邻域,有界集与确界原理。
函数概念,函数的表示法。
函数的四则运算,复合函数,反函数,初等函数。
具有某些特性的函数:有界函数、单调函数、奇函数与偶函数、周期函数。
(二)考核知识点1、实数:实数的概念,实数的性质,绝对值与不等式;2、数集、确界原理:区间与邻域,有界集与无界集,上确界与下确界,确界原理;3、函数概念:函数的定义,函数的表示法(解析法、列表法、和图象法),分段函数;4、具有某些特征的函数:有界函数,单调函数,奇函数与偶函数,周期函数。
(三)考核要求1、了解实数域及性质;2、掌握几种不等式及应用;3、熟练掌握数域,上确界,下确界,确界原理;4、牢固掌握函数复合、基本初等函数、初等函数及某些特性(单调性、周期性、奇偶性、有界性等)。
第二章数列极限(一)考核内容数列。
数列极限的定义,无穷小数列。
收敛数列性质:唯一性、有界性、保号性、不等式性质、迫敛性、四则运算法则。
子列及子列定理。
第五章-微分方程

第五章 微分方程第一节 微分方程的基本概念 一、基本概念微分方程的定义:①凡是含有未知函数的导数(或微分)的方程,称为微分方程. ②未知函数是一元函数的微分方程称为常微分方程,未知函数是多元函数的微分方程称为偏微分方程.本书只讨论常微分方程,简称微分方程. 微分方程的阶、解与通解:微分方程中出现的未知函数最高阶导数的阶数,称为微分方程的阶.如果把函数)(x f y =代入微分方程后,能使方程成为恒等式,则称该函数为该微分方程的解.若微分方程的解中含有任意常数,且独立的任意常数的个数与方程的阶数相同,则称这样的解为微分方程的通解.初始条件与特解:用未知函数与其各阶导数在某个特定点的值作为确定通解中任意常数的条件,称为初始条件.满足初始条件的微分方程的解称为该微分方程的特解。
例1 课本294页 例1二、独立的任意常数线性相关与线性无关:设)(),(21x y x y 是定义在区间),(b a 的函数,若存在两个不全为零的数21,k k ,使得对于区间),(b a 的任一x ,恒有0)()(2211=+x y k x y k成立,则称函数)(),(21x y x y 在区间),(b a 线性相关,否则称为线性无关.显然,函数)(),(21x y x y 线性相关的充分必要条件是)()(21x y x y 在区间),(b a 恒为常数. 如果)()(21x y x y 不恒为常数,则)(),(21x y x y 在区间),(b a 线性无关.独立的任意常数:在表达式)()(2211x y C x y C y += (1C ,2C 为任意常数) 中,1C ,2C 为独立的任意常数的充分必要条件为)(1x y ,)(2x y 线性无关.例2 课本297页 例4第二节 可分离变量的微分方程 一、定义形如)()(d d y g x f xy= 的微分方程,称为可分离变量的方程.该微分方程的特点是等式右边可以分解成两个函数之积,其中一个仅是x 的函数,另一个仅是y 的函数,即)(),(y g x f 分别是变量y x ,的已知连续函数.二、求解方法可分离变量的微分方程)()(d d y g x f xy=的求解方法,一般有如下两步: 第一步:分离变量 x x f y y g d )(d )(=, 第二步:两边积分 ⎰⎰=x x f y y g d )(d )(.[例1]求微分方程ydy dx y xydy dx +=+2的通解.解先合并dx 与dy 的各项,得dx y dy x y )1()1(2-=- 设,01,012≠-≠-x y 分离变量得dx x dy y y 1112-=- 两端积分⎰⎰-=-dx x dy y y1112得 ||ln |1|ln |1|ln 2112C x y +-=- 于是 2212)1(1-±=-x C y 记,21C C ±=则得到题设方程的通解.)1(122-=-x C y注:在用分离变量法解可分离变量的微分方程的过程中, 我们在假定0)(≠y g 的前提下,用它除方程两边, 这样得到的通解, 不包含使0)(=y g 的特解. 但是, 有时如果我们扩大任意常数C 的取值围, 则其失去的解仍包含在通解中. 如在例2中,我们得到的通解中应该0≠C ,但这样方程就失去特解1±=y ,而如果允许0=C ,则1±=y 仍包含在通解22)1(1-=-x C y 中.[例2] 已知 ,tan 2cos )(sin 22x x x f +=' 当10<<x 时,求).(x f解设,sin 2x y =则,21sin 212cos 2y x x -=-=.1sin 1sin cos sin tan 22222yyx x x x x -=-==所以原方程变为,121)(y y y y f -+-='即.112)(yy y f -+-=' 所以 =)(y f ⎪⎪⎭⎫ ⎝⎛-+-y y 112dy 2y -=,)1ln(C y +-- 故 C x x x f +-+-=)]1ln([)(2).10(<<x第三节 线性微分方程 一、一阶线性微分方程定义 :形如)()(d d x Q y x P xy=+. 的微分方程,称为一阶线性微分方程,其中)(),(x Q x P 都是x 的已知连续函数,“线性”是指未知函数y 和它的导数y '都是一次的. 求解方法 :一阶线性微分方程)()(d d x Q y x P xy=+的求解方法,一般有如下两步: 第一步:先用分离变量法求一阶线性微分方程)()(d d x Q y x P xy=+所对应的齐次线性微分方程0)(d d =+y x P xy的通解⎰=-x x P c C y d )(e . 第二步:设⎰=-x x P x C y d )(e )(为一阶线性微分方程)()(d d x Q y x P xy=+的解,代入该方程后,求出待定函数)(x C .第三步: 将)(x C 代入⎰=-xx P x C y d )(e )(中,得所求一阶线性微分方程)()(d d x Q y x P xy=+的通解. 注:只要一阶线性微分方程是)()(d d x Q y x P xy=+的标准形式,则将⎰=-x x P x C y d )(e )(代入一阶线性微分方程后,整理化简后,必有)(e )(d )(x Q x C xx P =⎰'-,该结论可用在一阶线性微分方程的求解过程中,以简化运算过程. 一阶线性微分方程)()(d d x Q y x P xy=+的求解公式: ⎥⎦⎤⎢⎣⎡+⎰⎰=⎰-C x x Q y x x P x x P d e )(e d )(d )( (其中C 为任意常数). [例1] 求微分方程 y y x y x y xy d d d d 2+=+ 满足条件20==x y 的特解.解 这是可以分离变量的微分方程,将方程分离变量,有x x y y y d 11d 12-=-,两边积分,得=-⎰y y yd 12⎰-x x d 11,求积分得121ln 1ln 21C x y +-=-,1222)1ln(1ln C x y +-=-, 1222e )1(1C x y -=-,222)1(e 11-±=-x y C ,记 0e12≠=±C C ,得方程的解 22)1(1-=-x C y .可以验证 0=C 时,1±=y ,它们也是原方程的解,因此,式22)1(1-=-x C y 中的 C 可以为任意常数,所以原方程的通解为 22)1(1-=-x C y (C 为任意常数).代入初始条件 20==x y得 3=C ,所以特解为 22)1(31-=-x y .[例2] 求微分方程(1)xy yy +=',(2) x xy y x cos e 22=-'的通解.(1)解一 原方程可化为1d d +=xyx yx y ,令 x yu =, 则 1d d +=+u u x u x u ,即 x x u u u d d 12-=+ ,两边取积分 ⎰⎰-=+x x u u u d 1d )11(2, 积分得C x u uln ln ln 1-=-,将x y u =代入原方程,整理得原方程的通解为yx C y e = (C 为任意常数).解二 原方程可化为11d d =-x yy x 为一阶线性微分方程,用常数变易法.解原方程所对应的齐次方程01d d =-x yy x ,得其通解为 y C x =. 设y y C x )(=为原方程的解,代入原方程,化简得 1)(='y y C ,1ln)(C yy C =, 所以原方程的通解为 1ln C y y x=,即yx C ye = (C 为任意常数).(2)解一 原方程对应的齐次方程02d d =-xy xy 分离变量,得xy x y2d d =,x x yyd 2d =, 两边积分,得x x y y⎰⎰=d 2d ,C x y +=2ln ,)e ln(ln e ln ln 22x x C C y =+=,2e x C y =,用常数变易法.设2e )(x x C y =代入原方程,得 x x C x x cos e e )(22=',x x C cos )(=',C x x x x C +==⎰sin d cos )(,故原方程的通解为 )(sin e 2C x y x += (C 为任意常数).解二 这里x x P 2)(-=,x x Q x cos e )(2=代入通解的公式得)d e cos e (e d 2d 22⎰+⎰⋅⎰=---C x x y xx x x x=)d ecos e(e 222C x x x x x +⋅⎰-=)d cos (e 2C x x x +⎰=)(sin e 2C x x +(C 为任意常数).小结 一阶微分方程的解法主要有两种:分离变量法,常数变易法.常数变易法主要适用线性的一阶微分方程,若方程能化为标准形式 )()(x Q y x P y =+',也可直接利用公式C x x Q y xx P x x P +⎰⎰=⎰-d e )((e d )(d )()求通解.二、二阶常系数齐次线性微分方程定义:形如0=+'+''qy y p y的微分方程(其中q p ,均为已知常数,称为二阶常系数齐次线性微分方程. 求解方法:求解二阶常系数齐次线性微分方程,一般分为如下三步:第一步 写出方程0=+'+''qy y p y 的特征方程 02=++q pr r ,第二步 求出特征方程的两个特征根 1r ,2r ,第三步 根据下表给出的三种特征根的不同情形,写出0=+'+''qy y p y 的通解.[例3] 求微分方程02=+'-''y y a y 的通解.解 原方程对应的特征方程为 0122=+-ar r ,244222,1-±=a a r =12-±a a ,(1)当1>a ,即 1>a 或1-<a 时,特征方程有两个不相等的实根121-+=a a r ,122--=a a r ,故原方程的通解为xa a xa a C C y )1(2)1(122e e ---++=.(2)当1=a ,即1=a 或1-=a 时,特征方程有两个相等的实根 a r r ==21, 故原方程的通解为 axx C C y e )(21+=.(3)当1<a ,即 11<<-a 时,特征方程有两个共轭复根 22,11i a a r -±=,故原方程的通解为)1sin 1cos (e 2221x a C x a C y ax -+-=.三、二阶常系数非齐次线性微分方程定义:形如)(x f qy y p y =+'+''的微分方程(其中q p ,均为已知常数),称为二阶常系数非齐次线性微分方程.求解方法:求解二阶常系数非齐次线性微分方程, 一般分为如下三步:第一步 先求出非齐次线性微分方程)(x f qy y p y =+'+''所对应的齐次线性微分方程方程0=+'+''qy y p y 的通解c y ;第二步 根据下表设出非齐次线性微分方程)(x f qy y p y =+'+''的含待定常数的特解p y ,并将p y 代入非齐次线性微分方程)(x f qy y p y =+'+''解出待定常数,进而确定非齐次方程)(x f qy y p y =+'+''的一个特解p y ;第三步 写出非齐次线性微分方程)(x f qy y p y =+'+''的通解p c y y y +=.方程)(x f qy y p y =+'+''的特解p y 的形式表注:①表中的)(x P m 为已知的m 次多项式,)(x Q m 为待定的m 次多项式,如C Bx Ax x Q ++=22)( (C B A ,,为待定常数).②在设微分方程 xm x P qy y p y λe )(=+'+''的特解时,必须注意把特解p y 设全.如:2)(x x P m =,那么 2120)(b x b x b x Q m ++=,而不能设20)(x b x Q m =.另外,微分方程的特解都是满足一定初始条件的解,上面所求的特解p y 一般不会满足题设初始条件,因此需要从通解中找出一个满足该初始条件的特解.[例4] 求微分方程 xx y y e 4=-''满足初始条件00==x y,10='=x y 的特解.解 对应齐次方程的特征方程为 012=-r ,特征根 12,1±=r .故对应齐次微分方程的通解为 xx c C C y -+=e e 21.因为1=λ是特征方程的单根,所以设特解为 xP b x b x y e )(10+=,代入原方程得 x x b b b 4422010=++,比较同类项系数得 10=b ,11-=b ,从而原方程的特解为 xP x x y e )1(-=, 故原方程的通解为 =y xxC C -+ee 21x x x e )1(-+,由初始条件 0=x 时,0='=y y ,得 ⎩⎨⎧=-=+,2,02121C C C C从而11=C ,12-=C .因此满足初始条件的特解为 =y xx--ee x x x e )1(-+.[例5] 求微分方程 x y y y x2sin e 842=+'-''的通解.解 对应的齐次微分方程的特征方程 0842=+-r r ,特征根 i 222,1±=r .于是所对应的齐次微分方程通解为)2sin 2cos (e 212x C x C y x c +=.为了求原方程x y y y x2sin e842=+'-''的一个特解,先求x y y y )i 22(e 84+=+'-''(*)的特解.由于i 22+=λ是特征方程的单根,且1)(=x P m 是零次多项式。
数学分析5.5微分(含习题详解)

第五章导数和微分5 微分一、微分的概念定义1:设函数y=f(x)定义在点x0的某邻域U(x0)内. 当给x0一个增量△x,x0+△x∈U(x0)时,相应地得到函数的增量为△y=f(x0+△x)-f(x0). 如果存在常数A,使得△y能表示为△y=A△x +o(△x),则称函数f在点x0可微,并称上式中的第一项A△x为f在点x0的微分,记作:dy=A△x,或df(x)=A△x.当A≠0时,微分dy称为增量△y的线性主部。
定理5.10:函数f在点x0可微的充要条件是函数f在点x0可导,而且定义中的A=f’(x0).证:先证必要性:若f在点x0可微,则△y=A△x +o(△x),即=A+o(1),两边取极限得:f’(x0)==(A+o(1))=A.再证充分性:若f在点x0可导,则f在点x0的有限增量公式为:△y=f’(x0)△x+o(△x),根据微分的定义,f在点x0可微且有dy=f’(x0)△x.微分的几何意义:(如图)当自变量由x0增加到x0+△x时,函数增量△y= f(x0+△x)-f(x0)=RQ,而微分则是在点P处的切线上与△x所对应的增量,即dy=f’(x0)△x=RQ’,且==f’(x0)=0,所以当f ’(x 0)≠0时,=0. 即当x →x 0时线段Q ’Q 远小于RQ ’。
若函数y=f(x)在区间I 上每一点都可微,则称f 为I 上的可微函数.函数y=f(x)在I 上任一点x 处的微分记作dy=f ’(x)△x ,x ∈I. 特别地,当y=x 时,dy=dx=△x ,则微分也可记为dy=f ’(x)dx ,即 f ’(x)=,可见函数的导数等于函数微分与自变量微分的商。
因此导数也常称为微商。
二、微分的运算法则1、d[u(x)±v(x)]=du(x)±dv(x);2、d[u(x)v(x)]=v(x)du(x)+u(x)dv(x);3、d=;4、d(f ◦g(x))=f ’(u)g ’(x)dx ,其中u=g(x),或dy=f ’(u)du.例1:求y=x 2lnx+cosx 2的微分。
专升本(高数—)第五章多元函数微积分学PPT课件

第七节 二重积分的应用
*
2
考试点津:
• 本讲出题在18分—26分之间,本讲内容是 一元函数微分内容的延伸,一般在选择题、 填空题、解答题中出现。
• 本讲重点:
(1)二元函数的偏导数和全微分。
(2)二元函数的有关极值问题及应用。 (3)会计算二重积分
• 建议重点复习前几年考过的试题,把握考 试重心和知识点,重在模仿解题。
成人高考高数一辅导
•
College of Agriculture & Biological Engineering
*
1
第五章 多元函数微积分学 (11年考了22分)
第一节 多元函数、极限和连续 第二节 偏导数与全微分 第三节 二元函数的极值 第四节 二重积分的概念和性质 第五节 直角坐标系下二重积分的计算 第六节 极坐标系下二重积分的计算
可 以 证 明 ,一 元 函 数 关 于 极 限 的 运 算 法 则 仍 适 用 于 多 元 函 数 ,即 多 元 连 续 函 数 的 和 、差 、积 为 连 续 函 数 ,在 分 母 不 为 零 处 ,连 续 函 数 的 商 也 是 连 续 函 数 ,多 元 函 数 的 复 合 函 数 也 是 连 续 函 数 .由 此 还 可 得 出 如 下 结 论 : 一 切 多 元 初等函数在其定义区域内是连续的.
(4)最大值和最小值定理
在有界闭区域D上的多元连续函数,在D上至少取得它的最大 值和最小值各一次.
(5)介值定理
在有界闭区域D上的多元连续函数,如果在D上取得两个不同的
函数值,则它在D上取得介于这两值之间的任何值至少一次.分
(一) 偏导数
1. 偏导数的定义
定义 设函数 z f (x, y)在点(x0, y0 )的某一邻域内有 定义,当 y固定在 y0,而 x在 x0处有增量x时,相应地函 数有增量 f (x0 x, y0 ) f (x0, y0 ),如果极限
数学分析PPT课件第四版华东师大研制 第5章 导数和微分

证 当 x0 0 时,用归结原理容易证明 f (x) 在点 x0 不连续, 由定理 5.1, f (x) 在点 x0 不可导.
当 x0 = 0 时, 因为 D( x) 1,所以有
f (0) lim f ( x) f (0) lim xD( x) 0 .
x0 x 0
x 0
k lim f ( x) f ( x0 )
(2)
x x0
x x0
会是什么呢?
答: 它就是曲线在点 P 的切线 PT 的斜率.
前页 后页 返回
上面两个问题虽然出发点相异,但都可归结为同 一类型的数学问题: 求函数 f 在点 x0 处的增量 D y = f (x) – f (x0) 与自变量增量 D x = x – xo 之比 的极限. 这个增量比称为函数 f 关于自变量的平 均变化率,增量比的极限 (如果存在) 称为 f 在点 x0 处关于 x 的瞬时变化率(或简称变化率).
其上一点 P( x0, y0 ) 处的切线 PT. 为此我们在 P 的邻近取一 点 Q , 作曲线的割线 PQ ,这
条割线的斜率为
_
k
f (x)
f ( x0 ) .
x x0
y
Q
y f (x) •
T
P
•
O
x0 x x
点击上图动画演示
前页 后页 返回
设想一下,当动点 Q 沿此曲线无限接近点 P 时,k 的极限若存在,则这个极限
Dx
存在,则称该极限为 f (x) 在点 x0 的右导数, 记作
f( x0 ) . 类似地可以定义左导数 , 合起来即为:
前页 后页 返回
定义1 设函数 y =f (x) 在点 x0 的某邻域内有定
第五章多元函数微分学讲解

第五章 多元函数微分学知识点拔5.1 多元函数的概念一、二元函数的概念 1、二元函数的定义设在某一变化过程中,有三个变量y x ,和z ,如果对于变量y x ,在某一范围D 内任取一对数值,按照一定的对应法则,总有一个确定的值z 与它对应,则称变量z 是变量y x ,的二元函数,记作:),(y x f z =或),(y x z z =,其中y x ,称为自变量,z 称为因变量或称为y x ,的二元函数,变量y x ,取值范围D 称为该函数的定义域.2、二元函数的几何意义 二元函数),(y x f z =在几何上一般表示空间直角坐标系中的一个曲面.二、二元函数的极限 1、二元函数极限的定义设二元函数),(y x f z =在点),(000y x P 的某去心邻域内有定义,如果动点),(y x P 在该邻域内以任何方式无限地趋于点),(000y x P 时,函数),(y x f 总是无限地趋于一个常数A ,则称A 是函数),(y x f z =在),(y x P 趋于),(000y x P 时的极限(也称二重极限),记作A y x f y y X x =→→),(lim 0或A y x f y x y x =→),(lim),(),(00,若记点),(y x P 与点),(000y x P 之间的距离为20200)()(||y y x x PP -+-==ρ,则有A y x f =→),(lim 0ρ .注释:(1)极限的几何意义:当),(y x P 在),(000y x P 附近的某个范围内变化时,函数值),(y x f 与常数A 的距离恒小于任意给定的正数ε;(2)二元函数极限存在是指:动点P 必须以任意方式趋于点0P 时,),(y x f 都无限趋于常数A ,则二元函数的二重极限存在,但即使动点P 沿过0P 的无穷多条路径趋于0P 时极限都等于A ,也不能说明0P P →时,A y x f →),( .(3)二元函数极限不存在的判定方法:如果当点),(y x P 以两种不同的方式趋于点),(000y x P 时,函数),(y x f 分别趋于不同的常数,则可以断定函数),(y x f 在点),(000y x P 处的极限不存在。
5-5——华东师范大学数学分析课件PPT

v( x)d u( x) u( x)dv( x) v2(x)
函数 f 在点 x0 可微的充要条件是 f 在点 x0 可
导, 且 d f ( x) x x0 f ( x0)Δ x .
证 (必要性) 如果 f 在点 x0 可微, 据 (1) 式有
于是
Δy A o(1). Δx
f
(
x0
)
lim
Δ x 0
Δ Δ
y x
lim ( A o(1)) A ,
Δ x 0
(4) 式的写法会带来不少好处, 首先可以把导数看
成函数的微分与自变量的微分之商, 即
d y f ( x) ,
(5)
dx
所以导数也称为微商. 更多的好处将体现在后面
积分学部分中.
数学分析 第一章 实数集与函数
高等教育出版社
§5 微分
微分的概念
微分的 运算法则
高阶微分
微分在近似计算 中的应用
例1 d(x ) x 1 dx ;
d (sin x) cos x dx ; d (a x ) a x ln a dx .
数学分析 第一章 实数集与函数
高等教育出版社
§5 微分
微分的概念
微分的运算法则
微分的 运算法则
高阶微分
微分在近似计算 中的应用
由导数与微分的关系,可方便得出微分运算法则: 1. d (u( x) v( x)) du( x) dv( x); 2. d(u( x)v( x)) v( x)du( x) u( x)dv( x);
Δ S ( x x)2 x2 2x x ( x)2 由两部分组成 :
Δ x 的线性部分 2xΔx 和 Δ x 的高阶部分( Δ x)2. 因
高等数学第五章5
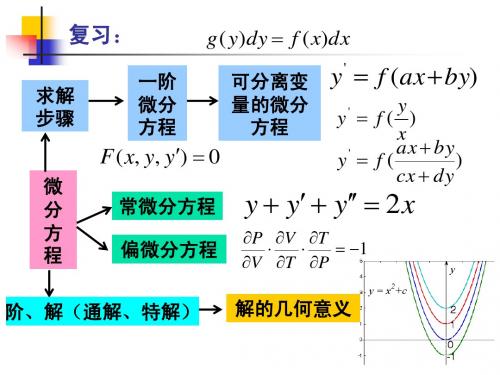
α ± iβ不是特征根
k =0
α ± iβ是单根
k =1
第5节 微分方程在医学医学问题
药物动力学模型
c(t ) = c0 e
− kt
k0 − kt x = (1 − e ) k
一、药物动力学模型
药物进入机体后,在随血液到达各个器官和 药物进入机体后, 组织的过程中,广泛采用房室模型 房室模型来研究药 组织的过程中,广泛采用房室模型来研究药 物在体内的吸收、分布、 物在体内的吸收、分布、代谢和排泄的时间 过程。 过程。 血药浓度:药物在血液中的浓度。 血药浓度:药物在血液中的浓度。血药浓度 的变化能够定量地反映出其他体液、 的变化能够定量地反映出其他体液、组织及 器官内药物水平的变化。 器官内药物水平的变化。 房室:就是机体的某一个部分。 房室:就是机体的某一个部分。假定血药浓 度在一个房室内是常数, 度在一个房室内是常数,在不同房室之间按 照一定规律转移。 照一定规律转移。
二、肿瘤生长模型
决定。 肿瘤的生长速率由当前 肿瘤的体积 V决定。
dV b = kV dt
表征肿瘤生长速 率的参数, 率的参数,也称 为形状参数
dV kt b = kV 当b = 1时, V = Ce dt 1− b 当b ≠ 1时, V = (1 − b)(kt + C )
肿瘤在 ∆t = t 2 − t1的增长情况
其特解为: 其特解为: ~ = x k eαx [Q ( x) cos βx + R ( x) sin βx] y
l l
其中 l = max{m, n}
l次多项式 次多项式
k由特征根的情况决定
~ = x k eαx [Q ( x) cos βx + R ( x) sin β x] y l l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4. 函数可导一定连续,但连续不一定可导;
5. 求导数最基本的方法: 由定义求导数.
6. 判断可导性
不连续,一定不可导.
直接用定义; 连续
看左右导数是否存在且相等.
思考题
函 数 f(x)在 某 点 x0处 的 导 数 f(x0) 与 导 函 数 f(x)有 什 么 区 别 与 联 系 ?
其运动路程为s = s(t),则物体在时刻 t 0 的
瞬时速度定义为
v(t0) lt i0m v lt i0m st lt i0m s(t0tt)s(t0)
速度反映了路程对时间变化的快慢程度
2.切线问题 割线的极限位置——切线位置
播放
y
如图, 如果割线MN绕点 M旋转而趋向极限位置 MT,直线MT就称为曲线 C在点M处的切线.
limylimf(x0 x)f(x0),
x x0
x0
x
称函f数 (x)在点 x0有无穷.导 (不数 可)导
例如,
y y3 x1
f(x)3 x1,
0
1
x
在x1处不可. 导
3.函数f(x)在连续点的左右 不导 存数 在都
(指摆动不 ), 则 定x0点不可. 导
例如, f(x)xsin1x, x0,
0, x0
y
1
-1/π 0 1/π
x
在x0处不可 . 导
4.若f(x0),且在x点 0的两个单侧导数 符号相, 反 则称x点 0为函数 f(x)的尖点 (不可导).点
y
y
yf(x)
o
x
yf(x)
o
x0
x
例8 讨论函数f (x)xsin1x, x0, 0, x0
在x0处的连续性与可. 导性
解
sin1 x
是有界函, 数lxim 0xsin1x0
关于导数的说明:
★ 导数概念是概括了各种各样的变化率而得出 的一个更一般、更抽象的概念,它撇开了变量 所代表的特殊意义,而纯粹从数量方面来刻画 变化率的本质
★ 点导数是因变x0量 处在 的点 变化 ,它率 反映因 了变量随自变量 而的 变变 化化 的快
慢程.度
★ xy是y在以 x0和x0x为端点的区间上
解 ylim loa(g xh )loax g
h 0
h
h
lim
loga
(1
) x
1
h0
h
x
x
1xlh im 0loag(1h x)h x
1 x
loga
e.
即 (lo axg )1 xloae g.
特别地
(lnx) 1 . x
例6 讨论f(函 x)x数 在 x0处的.可导
解 f(0h)f(0)h,
dy 或df(x)
dxxx0
dx
, xx0
即 y x x 0 l x 0 i x y m l x 0 ifm (x 0 x x ) f(x 0 )
其它形式 f(x 0) lh i0m f(x 0 h h )f(x 0).
f(x0)x l ix0 m f(xx ) x f0 (x0).
5.1 导数的概念
一、问题的提出
1.自由落体运动的瞬时速度问题
如图, 求t0时刻的瞬时速, 度
取一邻t0的 近时 于t,刻 运动时间 t,
平均速 v度 s t
s t
s0 t0
g 2
(t0
t).
当tt0时 , 取极限得
瞬
时v 速 lim g度 (0 tt) 2 t t0
gt0.
t0 t
t
上述求瞬时速度的方法对一般变速直线 运动也同样适用。设物体作变速直线运动,
定理 凡可导函数都是连续函数.
证 设函 f(x)在 数 x0 点 可, 导
limy x0x
f(x0)
y x
f(x0)
0( x 0 ) y f(x 0 ) x x
l x 0 i y m l x 0 i [ f m ( x 0 ) x x ] 0
函f(数 x )在x 0 连 点 . 续
f(0 )lif m (x )0f(x)在 x0处连 . 续
但x在 0处 x 0有 xy(0x)sixn01x0
sin
1 x
当 x0时 ,y在1和 1之间振荡而.极限不 x
f(x)在x0处不可 . 导
六、小结
1. 导数的实质: 增量比的极限;
2 .f ( x 0 ) a f ( x 0 ) f ( x 0 ) a ;
yf(x)
N
T
CM
极限位置即
ox0Leabharlann xxM N 0, NM 0.T设 M (x 0 ,y 0 )N ,(x ,y ).
割线 MN的斜率为 tan y y0 f(x) f(x0),
N 沿 C 曲 M 线 ,x x 0 , x x0
xx0
切线 MT的斜率为 ktan lim f(x)f(x0). x x0 xx0
42
2.物理意义 非均匀变化量的瞬时变化率.
变速直线运动:路程对时间的导数为物体的 瞬时速度.
v(t)lim sds. t0t dt
交流电路:电量对时间的导数为电流强度.
i(t)lim qdq. t0t dt
非均匀的物体:质量对长度(面积,体积)的导 数为物体的线(面,体)密度.
五、可导与连续的关系
例如,
(
x )
1
11
x2
2
1. 2x
( x 1 )
(1)x11
1 x2
.
例4 求函 f(x) 数 ax(a0 ,a1 )的.导数 解 (ax)lim axhax
h0 h ax limah 1
h0 h axlna.
即(ax)axln a .
特别地 (ex)ex.
例5 求y 函 lo ax ( 数 g a 0 ,a 1 )的.导数
h 0
h
h0 h
即(C )0.
例2 设函 f(x ) s数 ix ,n 求 (sx ) i及 n (sx ) ix n . 4
解 (sx i)n lis m ix n h ()sixn
h 0
h
h
limcos(x
h0
h) 2
sin 2
h
cx o . s
2 即(sx ) i n co x . s
思考题解答
由导数的定义知,f (x0)是一个具体的 数值, f (x)是由于f (x) 在某区间I 上每一 点都可导而定义在I 上的一个新函数,即 xI ,有唯一值f (x)与之对应,所以两
者的区别是:一个是数值,另一个是函数.两
者的联系是:在某点x0处的导数f (x0 )即是导 函数 f (x)在x0处的函数值.
x
lx i0m (x0 x x )(x0)f(x0)存,在
若 lim f(x0 x)f(x0)
x 0
x
lx i0m (x0 x x )(x0)f(x0)存,在
且 f ( x 0 ) f ( x 0 ) a ,
则f(x)在点x0可导,
且 f(x0)a.
三、由定义求导数(三步法)
f (x0 ) tan, (为倾角)o
yf(x)
T
M
x0
x
若 f(x0)0且有限 过 (x 时 0,f(x0)的 ) 切线方程为
y y 0 f( x 0 )x ( x 0 ).
法线方程为
yy0f(1x0)(xx0).
当 f(x0)0时
切线方程为
yf(x0)
法线方程为 xx0 当 f(x0) 时 切线方程为 xx0
第五章导数和微分
在许多实际问题中,需要从数量上研究变量的 变化速度。如物体的运动速度,电流强度,线密 度,比热,化学反应速度及生物繁殖率等,所有 这些在数学上都可归结为函数的变化率问题,即 导数。
本章将通过对实际问题的分析,引出微分学中 两个最重要的基本概念——导数与微分,然后再 建立求导数与微分的运算公式和法则,从而解决 有关变化率的计算问题。
步骤: ( 1 ) 求 y 增 f ( x x 量 ) f ( x );
(2 )算比 y f(x 值 x ) f(x );
x
x
(3)求极 y 限 lim y.
x 0 x
例1 求函 f(x ) C 数 (C 为)常 的数 .导数
解 f(x)lim f(xh )f(x)limCC 0.
注意: 该定理的逆定理不成立.
★ 连续函数不存在导数举例
1. 函数 f(x)连续 ,若f(x0)f(x0)则称x0点 为函f(数 x)的角,函 点数在角点 . 不
例如,
x2, x0
f(x)
,
x, x0
y
y x2
yx
0
x
在 x 0 处不 ,x 0 为 可 f(x )的 导 .角点
2.设函f数 (x)在点 x0连续 , 但
法线方程为 yf(x0)
例7 求等边双y曲1在 线点 (1,2)处的切线 x2
斜率 ,并写出在该点方 处程 的和 切法 线.线方
解 由导数的几何意义, 得切线斜率为
k y x1 2
(
1 ) x
x1 2
1 x2
x1 2
4.
所求切线方程为 y24(x1), 即 4xy40 .
2
法线方程为 y21(x1), 即 2 x 8 y 1 5 0 .
2.右导数:
f ( x 0 ) x lx 0 i 0 f m ( x x ) x f 0 ( x 0 ) l x i 0 f ( m x 0 x x ) f ( x 0 ) ;
★ 函 数 f(x )在 点 x 0处 可 导 左 导 数 f (x 0)和 右 导 数 f (x 0)都 存 在 且 相 等 .
