遗传算法的Matlab实现讲解ppt课件
遗传算法的原理及MATLAB程序实现.

1 遗传算法的原理1.1 遗传算法的基本思想遗传算法(genetic algorithms,GA)是一种基于自然选择和基因遗传学原理,借鉴了生物进化优胜劣汰的自然选择机理和生物界繁衍进化的基因重组、突变的遗传机制的全局自适应概率搜索算法。
遗传算法是从一组随机产生的初始解(种群)开始,这个种群由经过基因编码的一定数量的个体组成,每个个体实际上是染色体带有特征的实体。
染色体作为遗传物质的主要载体,其内部表现(即基因型)是某种基因组合,它决定了个体的外部表现。
因此,从一开始就需要实现从表现型到基因型的映射,即编码工作。
初始种群产生后,按照优胜劣汰的原理,逐代演化产生出越来越好的近似解。
在每一代,根据问题域中个体的适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。
这个过程将导致种群像自然进化一样,后代种群比前代更加适应环境,末代种群中的最优个体经过解码,可以作为问题近似最优解。
计算开始时,将实际问题的变量进行编码形成染色体,随机产生一定数目的个体,即种群,并计算每个个体的适应度值,然后通过终止条件判断该初始解是否是最优解,若是则停止计算输出结果,若不是则通过遗传算子操作产生新的一代种群,回到计算群体中每个个体的适应度值的部分,然后转到终止条件判断。
这一过程循环执行,直到满足优化准则,最终产生问题的最优解。
图1-1给出了遗传算法的基本过程。
1.2 遗传算法的特点1.2.1 遗传算法的优点遗传算法具有十分强的鲁棒性,比起传统优化方法,遗传算法有如下优点:1. 遗传算法以控制变量的编码作为运算对象。
传统的优化算法往往直接利用控制变量的实际值的本身来进行优化运算,但遗传算法不是直接以控制变量的值,而是以控制变量的特定形式的编码为运算对象。
这种对控制变量的编码处理方式,可以模仿自然界中生物的遗传和进化等机理,也使得我们可以方便地处理各种变量和应用遗传操作算子。
2. 遗传算法具有内在的本质并行性。
MATLAB遗传算法工具箱及应用(第二版)图文 (1)

第一章 遗传算法概述
考虑两个二进制父代串:
A=10010110 和 B=10111000 I是随机地在1到串长L减1之间(即[1,
在决策变量域中的染色体表现型已被编码,可以估计种 群的个体成员的特性或适应度。通过特征目标函数来估计个 体在问题域中的特性。在自然世界中,这就是个体在现行环 境中的生存能力。因此,目标函数建立的基础是在整个繁殖 过程中选择成对的个体进行交配。
第一章 遗传算法概述
在再生(复制)期间,每个个体均被计算适应度值,它来 自没有加工的原始特性度量,由目标函数给出。这个值用来 在选择中偏向更加适合的个体。相对整个种群,适应度高的 个体具有高的选中参加交配的概率,而适应度低的个体具有 相对低的选中概率。
第一章 遗传算法概述
1.2 遗传算法的特点
遗传算法具有如下优点: (1)对可行解表示的广泛性。遗传算法的处理对象不是参 数本身,而是针对那些通过参数集进行编码得到的基因个体。 此编码操作使得遗传算法可以直接对结构对象进行操作。所谓 结构对象,泛指集合、序列、矩阵、树、图、链和表等各种一 维或二维甚至多维结构形式的对象。这一特点使得遗传算法具 有广泛的应用领域。比如: ①通过对连接矩阵的操作,遗传算法可用来对神经网络或 自动机的结构或参数加以优化。 ②通过对集合的操作,遗传算法可实现对规则集合和知识 库的精炼而达到高质量的机器学习目的。 ③通过对树结构的操作,用遗传算法可得到用于分类的最 佳决策树。 ④通过对任务序列的操作,遗传算法可用于任务规划,而 通过对操作序列的处理,可自动构造顺序控制系统。
遗传算法Malab实例讲解PPT课件
else newpop(i,:)=pop(i); newpop(i+1,:)=pop(i+1);
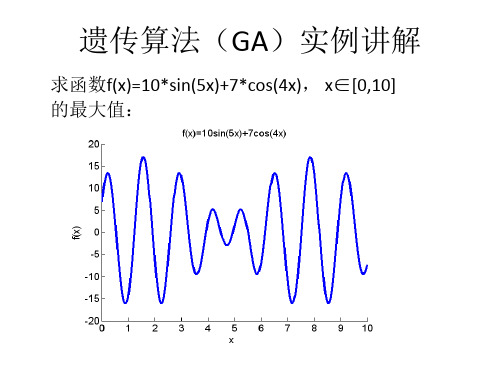
f(x)=10*sin(5x)+7*cos(4x), x∈[0,10]的最大值为: x1=1.5708 x2 =7.8540 F(x1)=f(x2)=17.0000
f(x)=10*sin(5x)+7*cos(4x) 的最大值
f1(x)=-f(x) -10*sin(5x)-7*cos(4x) 的最小值
if(ms(newin))<fitvalue(fitin) newpop(newin)=pop(fitin); newin=newin+1;
else fitin=fitin+1;
end end end
交叉
function [ newpop ] = crossover( pop,pc ) [px,py]=size(pop); newpop=ones(size(pop)); for i=1:2:px-1
if objvalue(i)+Cmin>0 temp=Cmin+objvalue(i);
else temp=0.0;
end fitvalue(i)= temp; end fitvalue=fitvalue';
end
选择
function [ newpop ] = selection( pop,fitvalue ) totalfit=sum(fitvalue); fitvalue=fitvalue/totalfit; fitvalue=cumsum(fitvalue); [px,py]=size(pop); ms=sort(rand(px,1)); fitin=1; newin=1; while newin<=px
《遗传算法详解》课件

遗传算法具有全局搜索能力、对问题 依赖性小、可扩展性强、鲁棒性高等 特点。
遗传算法的基本思想
初始化
随机生成一组解作为初始种群。
适应度评估
根据问题的目标函数计算每个解 的适应度值。
选择操作
根据适应度值的大小,选择优秀 的解进行遗传操作。
迭代更新
重复以上过程,直到满足终止条 件。
变异操作
对某些基因进行变异,增加解的 多样性。
《遗传算法详解》 ppt课件
• 遗传算法概述 • 遗传算法的基本组成 • 遗传算法的实现流程 • 遗传算法的优化策略 • 遗传算法的改进方向 • 遗传算法的未来展望
目录
Part
01
遗传算法概述
定义与特点
定义
遗传算法是一种模拟生物进化过程的 优化算法,通过模拟基因遗传和变异 的过程来寻找最优解。
Part
05
遗传算法的改进方向
混合遗传算法的研究
混合遗传算法
结合多种优化算法的优点,提高遗传算法的全局搜索能力和收敛速 度。
混合遗传算法的原理
将遗传算法与其他优化算法(如梯度下降法、模拟退火算法等)相 结合,利用各自的优势,弥补各自的不足。
混合遗传算法的应用
在许多实际问题中,如函数优化、路径规划、机器学习等领域,混 合遗传算法都取得了良好的效果。
自适应交叉率
交叉率控制着种群中新个体的产生速度。自适应交叉率可以根据种群中个体的适应度差 异进行调整,使得适应度较高的个体有更低的交叉率,而适应度较低的个体有更高的交 叉率。这样可以提高算法的搜索效率。
自适应变异率
变异率决定了种群中新个体的产生速度。自适应变异率可以根据种群中个体的适应度进 行调整,使得适应度较高的个体有更低的变异率,而适应度较低的个体有更高的变异率
遗传算法地原理及MATLAB程序实现

1遗传算法的原理1.1遗传算法的基本思想遗传算法(genetic algorithms , GA )是一种基于自然选择和基因遗传学原理,借鉴了生物进化优胜劣汰的自然选择机理和生物界繁衍进化的基因重组、突变的遗传机制的全局自适应概率搜索算法。
遗传算法是从一组随机产生的初始解(种群)开始,这个种群由经过基因编码的一定数量的个体组成,每个个体实际上是染色体带有特征的实体。
染色体作为遗传物质的主要载体,其内部表现(即基因型)是某种基因组合,它决定了个体的夕卜部表现。
因此,从一开始就需要实现从表现型到基因型的映射,即编码工作。
初始种群产生后,按照优胜劣汰的原理,逐代演化产生出越来越好的近似解。
在每一代,根据问题域中个体的适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。
这个过程将导致种群像自然进化一样,后代种群比前代更加适应环境,末代种群中的最优个体经过解码,可以作为问题近似最优解。
计算开始时,将实际问题的变量进行编码形成染色体,随机产生一定数目的个体,即种群,并计算每个个体的适应度值,然后通过终止条件判断该初始解是否是最优解,若是则停止计算输出结果,若不是则通过遗传算子操作产生新的一代种群,回到计算群体中每个个体的适应度值的部分,然后转到终止条件判断。
这一过程循环执行,直到满足优化准则,最终产生问题的最优解。
图1-1给出了遗传算法的基本过程。
1.2遗传算法的特点1.2.1遗传算法的优点遗传算法具有十分强的鲁棒性,比起传统优化方法,遗传算法有如下优点:1.遗传算法以控制变量的编码作为运算对象。
传统的优化算法往往直接利用控制变量的实际值的本身来进行优化运算,但遗传算法不是直接以控制变量的值,而是以控制变量的特定形式的编码为运算对象。
这种对控制变量的编码处理方式,可以模仿自然界中生物的遗传和进化等机理,也使得我们可以方便地处理各种变量和应用遗传操作算子。
2.遗传算法具有内在的本质并行性。
遗传算法及其MATLAB实现

P k
0.111180
Qk
0.111180
U2
U3 U4 U5 U6 U7 U8 U9 U10
17.370890
9.590546 29.106122 15.686001 11.900541 17.958717 19.763190 26.401669 10.252480
101111011111110
2、初始群体的产生
• 遗传算法是对群体进行的进 化操作,需要给其准备一些 起始搜索点的初始群体数据
• 初始群体太小时会产生病态 基因,且造成有效等位基因 先天缺乏 • 初始群体太大会导致结果难 以收敛且浪费资源,稳健性 下降 • 建议值0~100
假设初始种群中有10个个体,其染色体可随机生成如下:
5、新种群的交配(交叉运算)
• 交叉运算是遗传算法中产生新个体的主要操作过程,它以某一概率相互交互两个个体之间的部分染色体 • 先对群体进行随机配对,其次随机设置交叉点位置,最后再相互交换配对染色体之间的部分基因 • 交叉概率一般取0.4~0.99
①交配染色体数量的确定 交配染色体的数量等于染色体总量乘以交配概率。这里假设 交配概率 P c 为0.25,染色体总量为10条,所以 参加交配的染色 体数量为[2.5]条。符号[ ]表示取整,这里取整数2,即交配的染 色体数目为2条。 假定其分别对应U1~U10这10个个体,则其中低于交配概率0.25的U5和U7参加交配。这 样操作的原因是:交配概率越低,低于交配概率以下的随机数的数量就越少,所以参加交配 的染色体数量与交配概率可能会成正比。 ③在交配池发生交配 染色体U5和U7被选中作为交配的父辈,交配点的选择以随机数产生。交配的种类有单 点交配和多点交配,这里取单点交配。计算机随机生成一个介于0~32的整数。假设所产生 的整数为1,那么两个染色体自1位置开始分割,在染色体1位置右端部分进行交换而生成新 的子辈染色体,即 U5=[1 0011 0110 1001 0110 1000 0000 1011 1001] U7=[0 0111 0101 1100 1100 0000 0101 0100 1000] U5*=[1 0111 0101 1100 1100 0000 0101 0100 1000] U7*=[0 0011 0110 1001 0110 1000 0000 1011 1001]
Matlab与遗传算法ppt课件

StallTimeLimit
InitialPopulation PlotFcns
默认值 [0,1] 20 0.8 0.2 100 inf -inf
50
20
[] []
实现功能 初始种群生成区间 种群规模 交配概率 变异概率 超过进化代数时算法停止 超过运算时间限制时停止
最佳个体等于或小于适应度 阈值时算法停止
遗传算法的优点: 1. 与问题领域无关切快速随机的搜索能力。 2. 搜索从群体出发,具有潜在的并行性,可以进行多个个体的 同时比较. 3. 搜索使用评价函数启发,过程简单 4. 使用概率机制进行迭代,具有随机性。 5. 具有可扩展性,容易与其他算法结合。
求 m i n f( x ) 2 0 0 e 0 .0 5 x s i n ( x )x [ 2 ,2 ] ]
6
0.009857
164/33=5…32 5
32
0.003113
199/33=7…1 7
1
0.000946
329/33=10…32 10
32
0.001282
最终新种群染色体
U1
[1101101 1001]
U2
[1101101 1001]
U3
[0001100 1100]
U4
[1111110 1101]
4. 计算每个染色体被复制的累积概率
10
Q k Pk k 1
Hale Waihona Puke (3)选择新种群产生10个随机数:
0.301431,0.322062,0.766503, 0.881893,0.350871 0.538392, 0.177618,0.343242,0.032685,0.197577
第八章使用matlab遗传算法工具

:第八章使用MATLAB遗传算法工具最新发布的MATLAB Release 14已经包含了一个专门设计的遗传算法与直接搜索工具箱(Genetic Algorithm and Direct Search Toolbox,GADS)。
使用遗传算法与直接搜索工具箱,可以扩展MATLAB及其优化工具箱在处理优化问题方面的能力,可以处理传统的优化技术难以解决的问题,包括那些难以定义或不便于数学建模的问题,可以解决目标函数较复杂的问题,比如目标函数不连续、或具有高度非线性、随机性以及目标函数没有导数的情况。
本章节首先介绍这个遗传算法与直接搜索工具箱,其余各节分别介绍该工具箱中的遗传算法工具及其使用方法。
遗传算法与直接搜索工具箱概述本节介绍MATLAB的GADS(遗传算法与直接搜索)工具箱的特点、图形用户界面及运行要求,解释如何编写待优化函数的M文件,且通过举例加以阐明。
8.1.1 工具箱的特点GADS工具箱是一系列函数的集合,它们扩展了优化工具箱和MATLAB数值计算环境的性能。
遗传算法与直接搜索工具箱包含了要使用遗传算法和直接搜索算法来求解优化问题的一些例程。
这些算法使我们能够求解那些标准优化工具箱范围之外的各种优化问题。
所有工具箱函数都是MATLAB的M文件,这些文件由实现特定优化算法的MATLAB语句所写成。
使用语句】type function_name就可以看到这些函数的MATLAB代码。
我们也可以通过编写自己的M文件来实现来扩展遗传算法和直接搜索工具箱的性能,也可以将该工具箱与MATLAB的其他工具箱或Simulink结合使用,来求解优化问题。
工具箱函数可以通过图形界面或MATLAB命令行来访问,它们是用MATLAB语言编写的,对用户开放,因此可以查看算法、修改源代码或生成用户函数。
遗传算法与直接搜索工具箱可以帮助我们求解那些不易用传统方法解决的问题,譬如表查找问题等。
遗传算法与直接搜索工具箱有一个精心设计的图形用户界面,可以帮助我们直观、方便、快速地求解最优化问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab编程实现GA
❖ 选择复制
function [newpop]=selection(pop,fitvalue) %程序中采用赌轮盘选择法选择实现 totalfit=sum(fitvalue); %求适应值之和 fitvalue=fitvalue/totalfit; %单个个体被选择的概率 fitvalue=cumsum(fitvalue); %如 fitvalue=[1 2 3 4],则 cumsum(fitvalue)=[1 3 6 10]
pop=newpop;
end
fplot('2*x+10*sin(5*x)+7*cos(4*x)',[0 10])
hold on
plot(x,y,'r*') . hold off
Matlab编程实现GA
❖ 初始化(编码)
% initpop.m函数的功能是实现群体的初始化,popsize表示群体的大小, chromlength表示染色体的长度(二值数的长度),
.
Matlab编程实现GA
❖ 将二进制数转化为十进制数
将二进制数转化为十进制数 %产生 [2^n 2^(n-1) ... 1] 的行向量,然后求和,将二进制转化为十进制 function pop2=decodebinary(pop) [px,py]=size(pop); %求pop行和列数 for i=1:py
% 长度大小取决于变量的二进制编码的长度(在本例中取20位)。 %Name: initpop.m
function pop=initpop(popsize,chromlength) pop=round(rand(popsize,chromlength)); % rand随机产生每个单元为 {0,1}
行数为popsize,列数为chromlength的矩阵, % round对矩阵的每个单元进行取整。这样产生的初始种群。
量域 的数 objvalue=2*x+10*sin(5*x)+7*cos(4*x); %计算目标函数值
.
Matlab编程实现GA
❖ 计算个体的适应值
function fitvalue=calfitvalue(objvalue) global Cmin; fitvalue=objvalue-Cmin;
[px,py]=size(pop); ms=sort(rand(px,1)); %从小到大排列
fitin=1; newin=1; while newin<=px %蒙特卡洛方法抽样
if(ms(newin))<fitvalue(fitin) newpop(newin,:)=pop(fitin,:); newin=newin+1;
pop1(:,i)=2.^(py-i).*pop(:,i); end pop2=sum(pop1,2); %求pop1的每行之和
function pop2=decodechrom(pop,spoint,length) pop1=pop(:,spoint:spoint+length-1); pop2=decodebinary(pop1);
else fitin=fitin+1;
end
.
end
Matlab编程实现GA
❖ 交叉
function [newpop]=crossover(pop,pc) [px,py]=size(pop); newpop=ones(size(pop)); for i=1:2:px-1
if(rand<pc) cpoint=round(rand*py); newpop(i,:)=[pop(i,1:cpoint),pop(i+1,cpoint+1:py)]; newpop(i+1,:)=[pop(i+1,1:cpoint),pop(i,cpoint+1:py)];
.
Matlab编程实现GA
❖ 计算目标函数值
计算目标函数值 % calobjvalue.m函数的功能是实现目标函数的计算,其公式采用本文示
例仿真,可根据不同优化问题予以修改。 %遗传算法子程序 %Name: calobjvalue.m %实现目标函数的计算
function [objvalue]=calobjvalue(pop,chromlength,Xmax,Xmin) temp1=decodechrom(pop,1,chromlength); %将pop每行转化成十进制数 x=temp1*(Xmax-Xmin)/(2^chromlength-1); %将十进制域 中的数转化为变
.
Matlab编程实现GA
❖ 主程序
%遗传算法主程序 function My_GA global Cmin; Cmin=-10^6; popsize=50; %群体大小 Gene=20; chromlength=20; %字符串长
度(个体长度) pc=0.8; %交叉概率 pm=0.01; %变异概率 Xmax=10; Xmin=0;
个体及其适应值
x(i)=decodechrom(bestindividual,1,chromlength)*10/(2^chromlength-1); %最佳个体解码
y(i)=bestfit+Cmin; %最佳个体适应度 y_mean(i)=mean(fitvalue+Cmin); %第i代平均适应度
数学建模专题之
遗传算法的MATLAB实现
.
Contents I
1
Matlab编程实现GA
2
Matlab函数调用实现GA
3
Matlab工具箱实现GA
.数值函数
f(x)2x 1 0sin (5x)7co s(4x) m axf(x)?
x [0 ,1 0 ]
pop=initpop(popsize,chromlength); %随机产生初始群体 for i=1:Gene %20为迭代次数
[objvalue]=calobjvalue(pop,chromlength,Xmax,Xmin); %计算目标函数 fitvalue=calfitvalue(objvalue); %计算群体中每个个体的适应度 [newpop]=selection(pop,fitvalue); %复制 [newpop]=crossover(newpop,pc); %交叉 [newpop]=mutation(newpop,pm); %变异 [bestindividual,bestfit]=best(pop,fitvalue); %求出群体中适应值最大的
