立体几何证明垂直专项知识点及练习
专题4：立体几何中垂直关系的证明基础练习题
12．证明见解析
【分析】
在等腰三角形PAB中， 是 的中点，可得 ，利用线面垂直的判定定理可证 平面 ，利用线面垂直的性质定理，即可得证.
【详解】
证明：∵ 是 的中点， ，
∴ ，
∵ 底面 ，
∴ ，
又∵ ，即
∴ 平面 ，
∴ ，
∵ 平面 ， 平面 ，
∴ 平面 ，
∵ 平面 ，
∴ .
8．证明见解析
【分析】
由平面 ⊥平面 得到 ⊥平面 ，进一步得到 ⊥ ，再结合直径所对圆周角为直角得到 ⊥ ， ⊥平面 ，从而得到证明.
【详解】
由题设知，平面 ⊥平面 ，交线为 .
因为 ⊥ ， 平面 ，所以 ⊥平面 ，故 ⊥ .
因为 为 上异于 ， 的点，且 为直径，所以 ⊥ .
又 = ，所以 ⊥平面 .
∴点O为三角形ABC的垂心，∴BO⊥AC
又因PO⊥AC，所以AC⊥PBO
故PB⊥AC
考点：证明异面直线垂直．
7．见解析
【分析】
由已知中P为正方形ABCD所在平面外一点，PA⊥面ABCD，结合正方形的几何特征，我们易得到BC⊥平面PAB，由线面垂直的性质得到BC⊥AE，结合已知中AE⊥PB，及线面垂直的判定定理，得到AE⊥平面PBC，最后再由线面垂直的判定定理，即可得到AE⊥PC．
【点睛】
此题考查线面垂直的性质和判定的综合应用，利用线面垂直得线线垂直.
5．证明见解析
【分析】
先证直线 平面 ，再证平面 ⊥平面 .
【详解】
证明:∵ 是圆的直径， 是圆上任一点， ， ，
平面 ， 平面 ，
，又 ，
平面 ，又 平面 ，
平面 ⊥平面 .
【点睛】
立体几何之垂直问题知识点及题型总结 拔高教师版
目录立体几何之垂直问题 (2)模块一：垂直的判定与性质 (2)考点1：线面垂直的判定、性质及证明 (2)考点2：面面垂直的判定、性质及证明 (7)课后作业： (12)立体几何之垂直问题模块一：垂直的判定与性质考点1：线面垂直的判定、性质及证明例1.（1）（2019春•秦淮区期末）已知α，β，γ为平面，l ，m ，n 为直线，则下列哪个条件能推出(l β⊥ )A ．αβ⊥，n αβ=I ，1n ⊥B ．αγ⊥，βγ⊥，l α⊥C ．m α⊥，m β⊥，l α⊥D ．αγ⊥，l αγ=I ，βγ⊥【解答】解：对于A ，未说明l α⊂，故错误；对于B ，垂直同一平面的各平面的位置关系不确定，故错误； 对于C ，可确定//αβ，则l β⊥，故正确；对于D ，垂直同一平面的各平面的位置关系不确定，故错误； 故选：C ．线面垂直与面面垂直线面垂直：如果一条直线和一个平面相交于点，并且和这个平面内过点的任何直线都垂直，我们就说这条直线和这个平面互相垂直．点面距离：如果一条直线和平面垂直，则线与面的交点叫做垂足，垂线上任意一点到垂足间的线段，叫做这个点到这个平面的垂线段．垂线段的长度叫做这个点到平面的距离．判定定理：如果一条直线与平面内的两条相交直线垂直，则这条直线与这个平面垂直．推 论：如果两条平行直线中，有一条垂直于平面，那么另一条直面面垂直：如果两个相交平面的交线与第三个平面垂直，又这两个平面与第三个平 面相交所得的两条交线互相垂直，就称这两个平面互相垂直．判定判定定理：如果一个平面过另一个平面的一条垂线，则两个平面互相垂直． 线面垂直面面垂直定义定理定理定义（2）（2019春•漳州期中）已知m ，n 表示两条不同直线，α表示平面，下列说法中正确的是( )A ．若m α⊥，n α⊂，则m n ⊥B ．若//m α，//n α，则//m nC ．若m α⊥，m n ⊥，则//n αD ．若//m α，m n ⊥，则n α⊥【解答】解：对于A ，若m α⊥，n α⊂，根据线面垂直的性质可得m n ⊥；故正确； 对于B ，若//m α，//n α，则m 与n 可能相交、平行或者异面；故错误； 对于C ，若m α⊥，m n ⊥，则//n α或n α⊂，故错误；对于D ，若//m α，m n ⊥，则n 与α相交、平行或n α⊂，故错误． 故选：A ．例2.（1）（2018秋•唐山期末）如图，在以下四个正方体中，直线AB 与平面CDE 垂直的是( )A ．①②B ．②④C ．①③D ．②③【解答】解：在①中，AB 与CE 的夹角为45︒，∴直线AB 与平面CDE 不垂直，故①错误； 在②中，AB BC ⊥，AB CD ⊥，AB ∴⊥平面CDE ，故②正确；在③中，AB 与EC 的夹角为60︒，∴直线AB 与平面CDE 不垂直，故③错误； 在④中，AB DE ⊥，AB CE ⊥，AB ∴⊥平面CDE ，故④正确． 故选：B ．（2）（2019春•浉河区校级月考）如图，在直三棱柱111ABC A B C -中，1AB AC AA ===若11AC BC ⊥，则1(BC = )A ．B ．C ．D ．【解答】解：如图，连结1AC ，1AC AA =Q ， ∴直三棱柱111ABC A B C -的侧面11ACC A 为正方形，11AC AC ∴⊥，11AC BC ⊥Q ，111AC BC C =I ， 1A C ∴⊥平面1ABC ，1AC AB ∴⊥， 1AB AA ⊥Q ，111A C AA A =I ，AB ∴⊥侧面11ACC A ，1AB AC ∴⊥，故选：C ．（3）（2018秋•兴庆区校级期末）如图，AB 是O e 的直径，C 是圆周上不同于A ，B 的任意一点，PA ⊥平面ABC ，则四面体P ABC -的四个面中，直角三角形的个数有( )A ．4个B ．3个C ．2个D ．1个【解答】证明：AB Q 是圆O 的直径90ACB ∴∠=︒即BC AC ⊥，三角形ABC 是直角三角形又PA ⊥Q 圆O 所在平面，PAC ∴∆，PAB ∆是直角三角形．且BC 在这个平面内，PA BC ∴⊥ 因此BC 垂直于平面PAC 中两条相交直线，BC ∴⊥平面PAC ， PBC ∴∆是直角三角形．从而PAB ∆，PAC ∆，ABC ∆，PBC ∆中，直角三角形的个数是：4． 故选：A ．（4）（2019春•南昌期中）如图，在正方形ABCD 中，E 、F 分别是BC 、CD 的中点，G 是EF 的中点，现在沿AE 、AF 及EF 把这个正方形折成一个空间图形，使B 、C 、D 三点重合，重合后的点记为H ，那么，在这个空间图形中必有( )A ．AG EFH ⊥∆所在平面B ．AH EFH ⊥∆ 所在平面C ．HF AEF ⊥∆所在平面D ．HG AEF ⊥∆所在平面【解答】解：根据折叠前、后AH HE ⊥，AH HF ⊥不变，AH ∴⊥平面EFH ，B 正确； Q 过A 只有一条直线与平面EFH 垂直，A ∴不正确；AG EF ⊥Q ，EF AH ⊥，EF ∴⊥平面HAG ，∴平面HAG AEF ⊥，过H 作直线垂直于平面AEF ，一定在平面HAG 内， C ∴不正确；HG Q 不垂直于AG ，HG ∴⊥平面AEF 不正确，D 不正确．故选：B ．例3.（2019春•攀枝花期末）如图，在以A ，B ，C ，D ，E ，F 为顶点的多面体中，AF ⊥平面ABCD ，//DE AF ，//AD BC ，AB CD =，60ABC ∠=︒，22BC AD ==． （Ⅰ）请在图中作出平面DEG ，使得//BF 平面DEG ，并说明理由； （Ⅱ）证明：AC ⊥平面ABF ．【解答】解：（Ⅰ）如图，取BC 中点G ，连接DG ，EG ，则平面DEG 即为所求．22BC AD ==Q ，//AD BC ， //AD BG ∴且AD BG =．∴四边形ABGD 是平行四边形，则//AB DG ．AB ⊂/Q 平面DEG ，DG ⊂平面DEG ． //AB ∴平面DEG ．//AF DE Q ，AF ⊂/平面DEG ，DE ⊂平面DEG ，//AF ∴平面DEG ．AF ⊂Q 平面ABF ，AB ⊂平面ABF ，且AB AF A =I ．∴平面//ABF 平面DEG ．BF ⊂Q 平面ABF ，//BF ∴平面DEG ．（Ⅱ）由（Ⅰ）四边形ABGD 是平行四边形，则AB DG =，60DGC ABC ∠=∠=︒AB CD =Q ，CDG ∴∆是边长为1的正三角形． 1AD =Q ，120ADC ∠=︒，30ACD CAD ACB ∴∠=∠=∠=︒． 90BAC ∴∠=︒，即AC AB ⊥．AF ⊥Q 平面ABCD ，AC ⊂平面ABCD ． AC AF ∴⊥AF ⊂Q 平面ABF ，AB ⊂平面ABF ，AB AF A =I ． AC ∴⊥平面ABF ．考点2：面面垂直的判定、性质及证明例4.（1）（2019•衡阳三模）如图，在四面体ABCD 中，AD BD ⊥，截面PQMN 是矩形，则下列结论不一定正确的是( ) A ．平面BDC ⊥平面ADC B ．//AC 平面PQMN C ．平面ABD ⊥平面ADCD ．AD ⊥平面BDC【解答】解：由//PQ MN ，MN ⊂平面ADC ，PQ ⊂/平面ADC ，得//PQ 平面ADC ， 又PQ ⊂平面ABC ，平面ABC ⋂平面ADC AC =，//PQ AC ∴，同理，//QM BD ，//PQ AC ，//QM BD ，PQ OM ⊥，AC BD ∴⊥，又BD AD ⊥，BD ∴⊥平面ADC ，∴平面BDC ⊥平面ADC ，平面ABD ⊥平面ADC ，A ∴和C 选项均正确； 由//PQ AC ，得//AC 平面PQMN ，B ∴选项正确；Q 不能得到AD DC ⊥或AD BC ⊥，∴不能得到AD ⊥平面BDC ，故选项D 不一定正确．故选：D ．（2）（2018秋•潍坊期末）四面体PABC 中，PA PB PC ==，底面ABC ∆为等腰直角三角形，AC BC =，O 为AB 中点，请从以下平面中选出两个相互垂直的平面 ．（只填序号） ①平面PAB ②平面ABC ③平面PAC ④平面PBC ⑤平面POC【解答】解：Q 四面体PABC 中，PA PB PC ==， 底面ABC ∆为等腰直角三角形，AC BC =，O 为AB 中点，CO AB ∴⊥，PO AB ⊥，CO PO O =I ，AB ∴⊥平面POC ， AB ⊂Q 平面ABC ，∴平面POC ⊥平面ABC ， ∴两个相互垂直的平面为②⑤．故答案为：②⑤．（3）（2019春•雁峰区校级期末）如图，在三棱锥DABC 中，若AB CB =，AD CD =，E 是AC 的中点，则下列命题中正确的有 （写出全部正确命题的序号）． ①平面ABC ⊥平面ABD ； ②平面ABD ⊥平面BCD ；③平面ABC ⊥平面BDE ，且平面ACD ⊥平面BDE ； ④平面ABC ⊥平面ACD ，且平面ACD ⊥平面BDE ．【解答】解：因为AB CB =，且E 是AC 的中点，所以BE AC ⊥，同理有DE AC ⊥，于是AC ⊥平面BDE ．因为AC 在平面ABC 内，所以平面ABC ⊥平面BDE ．又由于AC ⊂平面ACD ，所以平面ACD ⊥平面BDE ，故答案为③．例5.（2019春•海安县校级期中）如图，在直三棱柱111ABC A B C -中，D ，E 分别为11A B ，11B C 的中点，点F 在侧棱1BB 上，且BD AF ⊥，AC AB ⊥．求证：（1）直线//DE 平面ACF ； （2）平面BDE ⊥平面ACF ．【解答】证明：（1）在直三棱柱111ABC A B C -中，11//AC AC ， 在三角形111A B C 中，D ，E 分别为1A 1B ，11B C 的中点，所以11//DE AC ，于是//DE AC ，又因为DE ⊂/平面ACF ，AC ⊂平面ACF ， 所以直线//DE 平面ACF ；（2）在直三棱柱111ABC A B C -中，1AA ⊥平面ABC 因为AC ⊂平面ABC ，所以1AA AC ⊥，又因为AC AB ⊥，1AA ⊂平面11ABB A ，AB ⊂平面11ABB A ，1AB AA A =I ， 所以AC ⊥平面11ABB A ．因为BD ⊂平面11ABB A ，所以AC BD ⊥．又因为BD AF ⊥，AC ⊂平面ACF ，AF ⊂平面ACF ，AC AF A =I ， 所以BD ⊥平面ACF ．因为直线BD ⊂平面BDE ，所以平面BDE ⊥平面ACF ．例6.（2019春•普宁市期末）如图所示，在四棱锥P ABCD -中，//AB CD ，AB AD ⊥，2CD AB =，平面PAD ⊥底面ABCD ，E 和F 分别是CD 和PC 的中点．求证：（1）//PA 平面BEF ； （2）平面BEF ⊥平面PCD ．【解答】证明：（1）连接AC ，交BE 于H ，可得四边形ABCE 为平行四边形， 且H 为AC 的中点，可得FH 为PAC ∆的中位线，可得//PA FH ，PA ⊂/平面BFE ，FH ⊂面BFE ，可得//PA 面BFE ；（2）平面PAD ⊥底面ABCD ，AB AD ⊥，可得AB ⊥平面PAD ， 即有AB PD ⊥，//AB CD ，可得CD PD ⊥， 由//EF PD ，由AB AD ⊥，2CD AB =，可得四边形ABED 为矩形，即有CD BE ⊥， 又CD PD ⊥，//FE PD ，可得CD FE ⊥，即有CD ⊥平面BFE ， 而CD ⊂平面PCD ，则平面BEF ⊥平面PCD ．例7.（2019春•宣城期末）如图，矩形ABCD 中，2AB BC =，以BD 为折痕把BDC ∆折起，使点C 到达点P 的位置．（1）若1BC =，求三棱锥P ABD -体积的最大值； （2）若PA PB ⊥，证明：平面PAB ⊥平面ABD ；【解答】解：（1）过P 作PO BD ⊥于O ，则PO BD PB PD =g g ，当PO ⊥平面ABD 时，三棱锥P ABD -体积最大， ∴三棱锥P ABD -体积的最大值为：（2）在PBD ∆中，PD PB ⊥， 又PA PB ⊥，PA PB P =I ，PA ，PD ⊂平面PAD ， PB ∴⊥平面PAD ，PB AD ⊥Q ，又AB AD ⊥，AB PB B =I ， AD ∴⊥平面PAB ，又AD ⊂平面ABD ，∴平面PAB ⊥平面ABD ．例8.（2019春•禅城区校级月考）如图，在三棱锥中，点E 、F 分别为AC 、AD 的中点． （1）求证：//EF 平面BCD ； （2）求证：平面EFB ⊥平面ABD ．【解答】证明：（1）在ACD ∆中，A Q ，F 是AC ，AD 的中点，//EF CD ∴，EF ⊂/Q 平面BCD ，CD ⊂平面BCD ， //EF ∴平面BCD ．（2）在ACD ∆中，AD CD ⊥，//EF CD ，EF AD ∴⊥，Q 在ABD ∆中，BA BD =，F 为AD 的中点，BF AD ∴⊥，EF ⊂Q 平面EFB ，BF ⊂平面EFB ，且EF BF F =I ， AD ∴⊥平面EFB ，AD ⊂Q 平面ABD ，∴平面EFB ⊥平面ABD ．课后作业：1.（2019春•秦淮区期末）已知α，β，γ为平面，l ，m ，n 为直线，则下列哪个条件能推出(l β⊥ )A ．αβ⊥，n αβ=I ，1n ⊥B ．αγ⊥，βγ⊥，l α⊥C ．m α⊥，m β⊥，l α⊥D ．αγ⊥，l αγ=I ，βγ⊥【解答】解：对于A ，未说明l α⊂，故错误；对于B ，垂直同一平面的各平面的位置关系不确定，故错误； 对于C ，可确定//αβ，则l β⊥，故正确；对于D ，垂直同一平面的各平面的位置关系不确定，故错误； 故选：C ．2.（2018秋•唐山期末）如图，在以下四个正方体中，直线AB 与平面CDE 垂直的是( )A ．①②B ．②④C ．①③D ．②③【解答】解：在①中，AB 与CE 的夹角为45︒，∴直线AB 与平面CDE 不垂直，故①错误； 在②中，AB BC ⊥，AB CD ⊥，AB ∴⊥平面CDE ，故②正确；在③中，AB 与EC 的夹角为60︒，∴直线AB 与平面CDE 不垂直，故③错误； 在④中，AB DE ⊥，AB CE ⊥，AB ∴⊥平面CDE ，故④正确． 故选：B ．3.（2019春•南昌期中）如图，在正方形ABCD 中，E 、F 分别是BC 、CD 的中点，G 是EF 的中点，现在沿AE 、AF 及EF 把这个正方形折成一个空间图形，使B 、C 、D 三点重合，重合后的点记为H ，那么，在这个空间图形中必有( )A ．AG EFH ⊥∆所在平面B ．AH EFH ⊥∆ 所在平面C ．HF AEF ⊥∆所在平面D ．HG AEF ⊥∆所在平面【解答】解：根据折叠前、后AH HE ⊥，AH HF ⊥不变，AH ∴⊥平面EFH ，B 正确； Q 过A 只有一条直线与平面EFH 垂直，A ∴不正确；AG EF ⊥Q ，EF AH ⊥，EF ∴⊥平面HAG ，∴平面HAG AEF ⊥，过H 作直线垂直于平面AEF ，一定在平面HAG 内， C ∴不正确；HG Q 不垂直于AG ，HG ∴⊥平面AEF 不正确，D 不正确．故选：B ．4.（2019春•南昌期中）如图，在正方形ABCD 中，E 、F 分别是BC 、CD 的中点，G 是EF 的中点，现在沿AE 、AF 及EF 把这个正方形折成一个空间图形，使B 、C 、D 三点重合，重合后的点记为H ，那么，在这个空间图形中必有( )A ．AG EFH ⊥∆所在平面B ．AH EFH ⊥∆ 所在平面C ．HF AEF ⊥∆所在平面D ．HG AEF ⊥∆所在平面【解答】解：根据折叠前、后AH HE ⊥，AH HF ⊥不变，AH ∴⊥平面EFH ，B 正确； Q 过A 只有一条直线与平面EFH 垂直，A ∴不正确；AG EF ⊥Q ，EF AH ⊥，EF ∴⊥平面HAG ，∴平面HAG AEF ⊥，过H 作直线垂直于平面AEF ，一定在平面HAG 内， C ∴不正确；HG Q 不垂直于AG ，HG ∴⊥平面AEF 不正确，D 不正确．故选：B ．5.（2019春•海安县校级期中）如图，在直三棱柱111ABC A B C -中，D ，E 分别为11A B ，11B C 的中点，点F 在侧棱1BB 上，且BD AF ⊥，AC AB ⊥．求证：（1）直线//DE 平面ACF ； （2）平面BDE ⊥平面ACF ．【解答】证明：（1）在直三棱柱111ABC A B C -中，11//AC AC ， 在三角形111A B C 中，D ，E 分别为1A 1B ，11B C 的中点，所以11//DE AC ，于是//DE AC ，又因为DE ⊂/平面ACF ，AC ⊂平面ACF ， 所以直线//DE 平面ACF ；（2）在直三棱柱111ABC A B C -中，1AA ⊥平面ABC 因为AC ⊂平面ABC ，所以1AA AC ⊥，又因为AC AB ⊥，1AA ⊂平面11ABB A ，AB ⊂平面11ABB A ，1AB AA A =I ， 所以AC ⊥平面11ABB A ．因为BD ⊂平面11ABB A ，所以AC BD ⊥．又因为BD AF ⊥，AC ⊂平面ACF ，AF ⊂平面ACF ，AC AF A =I ， 所以BD ⊥平面ACF ．因为直线BD ⊂平面BDE ，所以平面BDE ⊥平面ACF ．。
空间中的平行与垂直例题和知识点总结
空间中的平行与垂直例题和知识点总结在立体几何的学习中，空间中的平行与垂直关系是非常重要的内容。
理解和掌握这些关系，对于解决相关的几何问题具有关键作用。
下面我们通过一些例题来深入探讨，并对相关知识点进行总结。
一、平行关系（一）线线平行1、定义：如果两条直线在同一平面内没有公共点，则这两条直线平行。
2、判定定理：如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行。
例 1：在正方体 ABCD A₁B₁C₁D₁中，E，F 分别是 AB，BC 的中点，求证：EF∥A₁C₁。
证明：连接 AC，因为 E，F 分别是 AB，BC 的中点，所以 EF∥AC。
又因为正方体中，AC∥A₁C₁，所以 EF∥A₁C₁。
（二）线面平行1、定义：如果一条直线与一个平面没有公共点，则称这条直线与这个平面平行。
2、判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。
例 2：已知四棱锥 P ABCD 的底面是平行四边形，M 是 PC 的中点，求证：PA∥平面 MBD。
证明：连接 AC 交 BD 于 O，连接 MO。
因为四边形 ABCD 是平行四边形，所以 O 是 AC 的中点。
又因为 M 是 PC 的中点，所以MO∥PA。
因为 MO⊂平面 MBD，PA⊄平面 MBD，所以 PA∥平面MBD。
（三）面面平行1、定义：如果两个平面没有公共点，则称这两个平面平行。
2、判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。
例 3：在正方体 ABCD A₁B₁C₁D₁中，求证：平面 A₁BD∥平面 B₁D₁C。
证明：因为 A₁B∥D₁C，A₁D∥B₁C，且 A₁B 和 A₁D 是平面A₁BD 内的两条相交直线，D₁C 和 B₁C 是平面 B₁D₁C 内的两条相交直线，所以平面 A₁BD∥平面 B₁D₁C。
二、垂直关系（一）线线垂直1、定义：如果两条直线所成的角为 90°，则这两条直线垂直。
立体几何大题中的垂直证明方法 (1)
线面垂直的性质定理: 如果两条直线垂直于同一个平面,那么这两条直线平行.
1
2
• 三垂线定理&其逆定理 • 三垂线定理: • 平面内的一条直线,如果和穿过这也和这条斜线垂直. • 逆定理: • 如果平面内一条直线和穿过该平面的一条斜线垂直,
那么这条直线也垂直于这条斜线在平面内的射影. • 证明异面垂直.
立体几何大题中的垂直证明方法
一.线线垂直 如果两条直线相交于一点或经过平移后相交于一点, 并且交角为直角,则称这两条直线互相垂直. 垂直有相交垂直和异面垂直.
二.线面垂直
定义:如果一条直线和一个平面相交于点O,并且和这 个平面内过交点的任何直线都垂直,则称这条直线与 这个平面互相垂直.
这条直线叫做平面的垂线,这个平面叫做直线的垂面, 交点叫垂足.
立体几何线线垂直专题(史上最全)
立体几何垂直总结1、线线垂直的判断：线面垂直的定义：若一直线垂直于一平面，这条直线垂直于平面内所有直线。
补充：一条直线和两条平行直线中的一条垂直，也必垂直平行线中的另一条。
2、线面垂直的判断：（1）如果一直线和平面内的两相交直线垂直，这条直线就垂直于这个平面。
（2）如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面。
（3）一直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。
（4）如果两个平面垂直，那么在—个平面内垂直于交线的直线必垂直于另—个平面。
3、面面垂直的判断：一个平面经过另一个平面的垂线，这两个平面互相垂直。
证明线线垂直的常用方法：例1、（等腰三角形三线合一）如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。
求证：（1）⊥AB 平面CDE;（2）平面CDE ⊥平面ABC 。
证明：（1）BC AC CE AB AE BE =⎫⇒⊥⎬=⎭同理，AD BD DE AB AE BE =⎫⇒⊥⎬=⎭又∵CE DE E ⋂= ∴AB ⊥平面CDE （2）由（1）有AB ⊥平面CDE又∵AB ⊆平面ABC ， ∴平面CDE ⊥平面ABC例2、（菱形的对角线互相垂直、等腰三角形三线合一）已知四棱锥P ABCD -的底面是菱形．PB PD =，E 为PA 的中点．（Ⅰ）求证：PC ∥平面BDE ；（Ⅱ）求证：平面PAC ⊥平面BDE ．AEDBC例3、(线线、线面垂直相互转化)已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证：AD ⊥面SBC ．证明：90ACB ∠=∵° B C A C ∴⊥ 又SA ⊥面ABC S A B C ∴⊥ BC ∴⊥面SACBC AD ∴⊥ 又,SC AD SC BC C ⊥⋂=AD ∴⊥面SBC例4、(直径所对的圆周角为直角)如图2所示，已知PA 垂直于圆O 在平面，AB 是圆O 的直径，C 是圆O 的圆周上异于A 、B 的任意一点，且PA AC =，点E 是线段PC 的中点.求证：AE ⊥平面PBC .证明：∵PA ⊥O 所在平面，BC 是O 的弦，∴BC PA ⊥.又∵AB 是O 的直径，ACB ∠是直径所对的圆周角，∴BC AC ⊥.∵,PA AC A PA =⊂平面PAC ，AC ⊂平面PAC . ∴BC ⊥平面PAC ，AE ⊂平面PAC ，∴AE BC ⊥. ∵PA AC =，点E 是线段PC 的中点.∴AE PC ⊥. ∵PCBC C =,PC ⊂平面PBC ，BC ⊂平面PBC .∴AE ⊥平面PBC .例5、（证明所成角为直角）在如图所示的几何体中，四边形ABCD 是等腰梯形，AB ∥CD ，∠DAB ＝60°，AE ⊥BD ，CB ＝CD ＝CF . 求证：BD ⊥平面AED ； 证明 因为四边形ABCD 是等腰梯形，AB ∥CD ，∠DAB ＝60°，所以∠ADC ＝∠BCD ＝120°. 又CB ＝CD ，所以∠CDB ＝30°， 因此∠ADB ＝90°，即AD ⊥BD .又AE ⊥BD ，且AE ∩AD ＝A ，AE ，AD ⊂平面AED ，SDCBAACBPEO图2所以BD ⊥平面AED .例6、（勾股定理的逆定理）如图7－7－5所示，已知直三棱柱ABC —A 1B 1C 1中，△ABC 为等腰直角三角形，∠BAC ＝90°，且AB ＝AA 1，D 、E 、F 分别为B 1A 、C 1C 、BC 的中点． 求证：(1)DE ∥平面ABC ；(2)B 1F ⊥平面AEF .例7、（三垂线定理）证明：在正方体ABCD －A 1B 1C 1D 1中，A 1C ⊥平面BC 1D证明：连结ACB D AC ∵⊥∴ AC 为A 1C 在平面AC 上的射影∴⊥⊥⎫⎬⎭⇒⊥BD A C A C BC A C BC D11111同理可证平面练习；1、 如图在三棱锥P —ABC 中，AB ＝AC ，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上.证明：AP ⊥BC ；AC2、直三棱柱ABC －A 1B 1C 1中，AC ＝BC ＝12AA 1，D 是棱AA 1的中点，DC 1⊥BD .证明：DC 1⊥BC 。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)
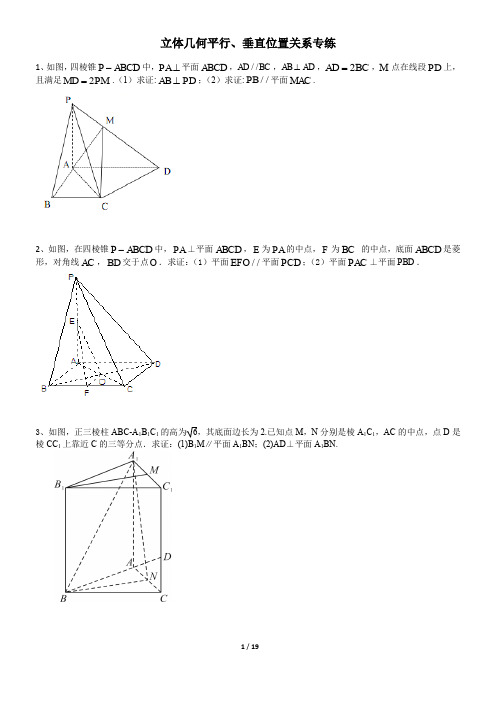
立体几何平行、垂直位置关系专练1、如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .2、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．3、如图，正三棱柱ABC-A 1B 1C 1的高为6，其底面边长为2.已知点M ，N 分别是棱A 1C 1，AC 的中点，点D 是棱CC 1上靠近C 的三等分点．求证：(1)B 1M ∥平面A 1BN ；(2)AD ⊥平面A 1BN.4、如图，等边三角形ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．(1)证明：CM⊥DE；(2)在边AC上找一点N，使CD∥平面BEN.5、如图，矩形ABCD所在平面与三角形ABE所在平面互相垂直，AE＝AB，M，N，H分别为DE，AB，BE 的中点．求证：(1)MN∥平面BEC；(2)AH⊥CE.6、如图，在三棱台ABCDEF中，CF⊥平面DEF，AB⊥BC.(1)设平面ACE∩平面DEF＝a，求证：DF∥a；(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在请确定点G的位置；若不存在，请说明理由．7、在三棱锥S ABC -中，平面SAB ⊥平面SBC ，AB BC ⊥，AS AB =，过A 作AF SB ⊥，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．（1）求证：平面EFG ∥平面ABC ．（2）求证：BC SA ⊥．8、如图，在直三棱柱111ABC A B C -中，AB BC ⊥，点D 为棱1C C 的中点，1AC 与1A D 交于点E ，1BC 与1B D 交于点F ，连结EF .求证：（1）//AB EF ；（2）平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．点，平面PAB ⊥底面ABCD ，90PAB ∠= ．求证：（1）//PB 平面AEC ；（2）平面PAC ⊥平面ABCD ．11、2.（2020·江苏省镇江高三二模）如图，三棱锥P ABC -中，点D ，E 分别为AB ，BC 的中点，且平面PDE ⊥平面ABC ．()1求证：//AC 平面PDE ；()2若2PD AC ==，PE =PBC ⊥平面ABC .12、（2020·江苏省建湖高级中学高三月考）如图，在四面体ABCD 中，,90AD BD ABC =∠= ，点,E F 分别为棱,AB AC 上的点，点G 为棱AD 的中点，且平面//EFG 平面BCD ．（1）求证：12EF BC =；（2）求证：平面EFD ⊥平面ABC ．点，PA ⊥平面ABCD .（1）求证：//PB 平面AEC ；（2）若四边形ABCD 是矩形且PA AD =，求证：AE ⊥平面PCD .14、（2020·江苏省高三二模）如图，在三棱柱111ABC A B C -中，侧面11ABB A ⊥底面ABC ，AB AC ⊥，E ，F 分别是棱AB ，BC 的中点.求证：（1）11AC ∥平面1B EF ；（2）1AC B E ⊥.15、（2020·江苏省连云港高三）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E 、F 分别为AD 、PB 的中点.（Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：//EF 平面PCD .16、（2020·江苏省苏州高三）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A1B 1∥平面DEC 1；（2）BE ⊥C 1E ．17、（2020·江苏省通州高三）如图，在三棱柱111ABC A B C -中，侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ；（2）求证:1C F ∥平面ABE ；18、（2020·江苏省高三三模）如图，三棱柱111ABC A B C -中，1BC B C =，O 为四边形11ACC A 对角线交点，F 为棱1BB 的中点，且AF ⊥平面11BCC B .（1）证明：//OF 平面ABC ；（2）证明：四边形11ACC A 为矩形.参考答案1．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .【解析】（1）∵四棱锥P ABCD -中，PA ⊥平面ABCD ，AB 平面ABCD ， ∴AB PA ⊥，又AB AD ⊥，,PA AD ⊂平面PAD ，PA AD A ⋂=， ∴AB ⊥面PAD .PD ⊂面PAD ，∴AB PD ⊥. （2）连结BD AC O ⋂=，连结MO ， ∵//AD BC ，2AD BC =，2DO BO ∴=,∵在PBD ∆中，2DM MP =，2DO BO =∴//PB MO ， 又PB ⊄面MAC ，MO ⊂面MAC ，∴//PB 面MAC .2．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ． 【详解】（1）因为在ΔPAC 中，E 为PA 的中点，O 为AC 的中点， 所以//EO PC又EO ⊄平面PCD ，PC ⊂平面PCD ， 所以//EO 平面PCD同理可证，//FO 平面PCD ，又EO FO O = ，EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD ．（2）因为PA ⊥平面ABCD ，BD ⊂平面ABCD ， 所以PA BD ⊥因为底面ABCD 是菱形，所以AC BD ⊥，又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
第8章立体几何专题4 垂直的证明常考题型专题练习——【含答案】
1垂直的证明【方法总结】1、证明线面垂直的方法：①利用线面垂直定义：如果一条直线垂直于平面内任一条直线，则这条直线垂直于该平面；②用线面垂直判定定理：如果一条直线与平面内的两条相交直线都垂直，则这条直线与平面垂直；③用线面垂直性质：两条平行线中的一条垂直于一个平面，则另一条也必垂直于这个平面．2、证明线线（或线面）垂直有时需多次运用线面垂直的定义和线面垂直的判定定理，实现线线垂直与线面垂直的相互转化．3、证明面面垂直一般要先找到两个面的交线，然后再在两个面内找能与交线垂直的直线，最后通过证明线面垂直证明面面垂直。
【分类练习】考向一 线面垂直例1、在四棱锥P ABCD -中，PA ⊥底面ABCD ，//AB CD ，AB BC ⊥，1AB BC ==，2DC =，点E 在PB 上求证：CA 平面PAD；【答案】(1)证明见解析；(2)2.【解析】(1)过A作AF⊥DC于F,则CF=DF=AF,所以∠DAC=90°,即AC⊥DA，又PA⊥底面ABCD，AC⊂面ABCD，所以AC⊥PA，因为PA、AD⊂面PAD，且PA∩AD=A，所以AC⊥平面PAD.例2、如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.11（1）证明：BE ⊥平面EB 1C 1；解析：（1）由已知得，11B C ⊥平面11ABB A ，BE ⊂平面11ABB A ，故11B C ⊥BE ．又1BE EC ⊥，所以BE ⊥平面11EB C ．例3、如图，在三棱柱111ABC A B C -中，1CC ⊥平面ABC ，D ，E ，F ，G 分别为1AA ，AC ，11A C ，1BB 的中点C 1B 1A 1GFE DCBA求证：AC ⊥平面BEF ；1【解析】(1)在三棱柱111ABC A BC -中，∵1CC ⊥平面ABC ， ∴四边形11A ACC 为矩形．又E ，F 分别为AC ，11A C 的中点， ∴AC ⊥EF ． ∵AB BC =． ∴AC ⊥BE ， ∴AC ⊥平面BEF ．例4、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，CD ⊥AD ，BC ∥AD ，12BC CD AD ==.（Ⅰ）求证：BD ⊥平面PAB ；【解析】因为PA ⊥平面ABCD ，BD ⊂平面ABCD ， 所以BD ⊥PA .在直角梯形ABCD 中，12BC CD AD ==，由题意可得2AB BDBC==，所以222AD AB BD=+，所以BD AB⊥.因为PA AB A=，所以BD⊥平面PAB.【巩固练习】1、如图，在三棱柱ABC－A1B1C1中，AB＝AC，A1在底面ABC的射影为BC的中点，D 是B1C1的中点．证明：A1D⊥平面A1BC；【答案】见解析【解析】证明：设E为BC的中点，连接A1E，AE.由题意得A1E⊥平面ABC，所以A1E⊥AE.11因为AB ＝AC ，所以AE ⊥BC.故AE ⊥平面A 1BC.连接DE ，由D ，E 分别为B 1C 1，BC 的中点，得DE ∥B 1B 且DE ＝B 1B，从而DE ∥A 1A 且DE ＝A 1A ，所以AA 1DE 为平行四边形．于是A 1D ∥AE. 因为AE ⊥平面A 1BC ，所以A 1D ⊥平面A 1BC.2．（2019·上海格致中学高三月考）如图，在四棱锥P ABCD -中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD DC =，E 是PC 的中点，作EF PB ⊥交PB 于点F .（1）证明：PA ∥平面EDB ； （2）证明：PB ⊥平面EFD .【答案】（1）详见解析；（2）详见解析.【解析】（1）设AC 与BD 相交于O ，连接OE ，由于O 是AC 中点，E 是PC 中点，所以OE 是三角形PAC 的中位线，所以//PA OE ，而PA ⊂平面EDB ，OE ⊂平面EDB ，1所以PA ∥平面EDB.（2）由于PD ⊥底面ABCD ，所以PD BC ⊥，由于,BC CD PD CD D ⊥⋂=，所以BC ⊥平面PCD ，所以BC DE ⊥.由于DP DC =且E 是PC 中点，所以DE PC ⊥，而PC BC C ⋂=，所以DE ⊥平面PBC ，所以DE PB ⊥.依题意EF PB ⊥，DE EF E =，所以PB ⊥平面EFD .3．（2019·江苏高三月考）如图，在四棱锥P ABCD -中，四边形ABCD 是平行四边形，AC ，BD 相交于点O ，OP OC =，E 为PC 的中点，PA PD ⊥.（1）求证：//PA 平面BDE ； （2）求证：PA ⊥平面PCD 【答案】（1）详见解析（2）详见解析 【解析】（1）连结OE .1因为四边形ABCD 是平行四边形，AC ，BD相交于点O ，所以O 为AC 的中点. 因为E 为PC 的中点，所以//OE PA .因为OE ⊂平面BDE ，PA ⊄平面BDE ，所以//PA 平面BDE .（2）因为OP OC =，E 为PC 的中点，所以OE PC ⊥. 由（1）知，//OE PA ，所以PA PC ⊥.因为PA PD ⊥，PC ， PD ⊂平面PCD ，PC PD P ⋂=，所以PA ⊥平面PCD .考向二 面面垂直例1、如图，在四棱锥P ABCD -中，已知底面ABCD 为矩形，且2AB =，1BC =，E ，F 分别是AB ，PC 的中点，PA DE ⊥.旗开得胜1(1)求证：//EF 平面PAD ； (2)求证：平面PAC ⊥平面PDE ． 【答案】（1）详见解析（2）详见解析【解析】证明：(1)取PD 中点G ，连AG ，FG ，F ，G 分别是PC ，PD 的中点//FG CD ∴，且12FG CD = 又E 为AB 中点//AE CD ∴，且12AE CD =//AE FG ∴，AE FG =四边形AEFG 为平行四边形//EF AG ∴，又EF ⊄平面PAD ，AG ⊂平面PAD //EF ∴平面PAD(2)设AC DE H =由AEHCDH ∆∆及E 为AB 中点旗开得胜1得12AH AE CH CD == 又2AB =，1BC =3AC ∴=，1333AH AC ==23AH AB AE AC ∴==又BAD ∠为公共角GAE BAC ∴∆∆90AHE ABC ∴∠=∠=︒即DE AC ⊥又DE PA ⊥，PAAC A =DE ⊥平面PAC ，又DE ⊂平面PDE∴平面PAC ⊥平面PDE例2、如图，边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直，M 是CD上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC ；MD CBA【解析】(1)由题设知，平面CMD ⊥平面ABCD ，交线为CD ．因为BC⊥CD，BC⊂平面ABCD，所以BC⊥平面CMD，故BC⊥DM．因为M为CD上异于C，D的点，且DC为直径，所以DM⊥CM．又BC CM=C，所以DM⊥平面BMC．而DM⊂平面AMD，故平面AMD⊥平面BMC．例3、如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，∠ABC=3π，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=AD，点M在线段EF上。
专题20立体几何中的平行与垂直问题(解析版)
专题20 立体几何中的平行与垂直问题一、题型选讲题型一、线面平行与垂直知识点拨：证明直线与平面的平行与垂直问题，一定要熟练记忆直线与平面的平行与垂直判定定理和性质定理，切记不可缺条件。
直线与平面的平行有两种方法：一是在面内找线；二是通过面面平行转化。
直线与平面垂直关键是找两条相交直线例1、（2019南通、泰州、扬州一调）如图，在四棱锥PABCD中，M, N分别为棱PA, PD的中点.已知侧面PAD丄底面ABCD,底面ABCD是矩形，DA=DP.求证：（1）MN〃平面PBC；MD丄平面PAB.【证明】（1）在四棱锥P-ABCD中，M, N分别为棱PA, PD的中点，所以MN〃AD.（2分）又底面ABCD是矩形，所以BC〃AD.所以MN〃BC.（4分）又BC U平面PBC，MN Q平面PBC，所以MN〃平面PBC. （6分）（2）因为底面ABCD是矩形，所以AB丄AD.又侧面PAD丄底面ABCD，侧面PAD n底面ABCD=AD, AB U底面ABCD，所以AB丄侧面PAD.（8分）又MD U侧面PAD，所以AB丄MD.（10分）因为DA=DP,又M为AP的中点，从而MD丄PA. （12分）又PA，AB在平面PAB内，PA n AB=A，所以MD丄平面PAB.（14分）例2、（2019扬州期末）如图所示，在三棱柱ABCA1B1C1中，四边形AA1B1B为矩形，平面AA1B1B丄平面ABC,点E，F分别是侧面AA1B1B，BB1C1C对角线的交点.（1）求证：EF〃平面ABC；（2）求证：BB］丄AC.规范解答（1）在三棱柱ABCA1B1C1中，四边形AA1B1B,四边形BB1C1C均为平行四边形，E, F分别是侧面AA1B1B, BB1C1C对角线的交点，所以E, F分别是AB1，CB1的中点，所以EF〃AC.（4分）因为EF Q平面ABC, AC U平面ABC，所以EF〃平面ABC.（8分）（2）因为四边形AA1B1B为矩形，所以BB1丄AB.因为平面AA1B1B丄平面ABC,且平面AA1B1B n平面ABC=AB, BB1U平面AA1B1B, 所以BB1丄平面ABC.（12分）因为AC U平面ABC，所以BB1丄AC.（14分）例3、（2019南京、盐城二模）如图，在三棱柱ABCA1B1C1中，AB=AC, A1C丄BC］, AB］丄BC1，D, E 分别是AB1和BC的中点.求证：（1）DE〃平面ACC1A1；（2）AE丄平面BCC1B1.A _________ c,规范解答⑴连结A1B，在三棱柱ABCA1B1C1中，AA1#BB1且AA1=BB1，所以四边形AA1B1B是平行四边形．又因为D是AB1的中点，所以D也是BA1的中点.（2分）在厶BA1C中，D和E分别是BA1和BC的中点，所以DE〃A］C.又因为DE G平面ACC1A1，A1C U平面ACC1A1，所以DE〃平面ACC1A1.（6分）（2）由（1）知DE〃A］C，因为A1C丄BC” 所以BC］丄DE.（8 分）又因为BC］丄AB1，AB1H DE=D，AB1，DE U平面ADE，所以BC1丄平面ADE.又因为AE U平在ADE,所以AE丄BC1.（10分）在厶ABC中，AB=AC，E是BC的中点，所以AE丄BC.（12分）因为AE丄BC1，AE丄BC，BC1H BC=B，BC1，BC U平面BCC1B1，所以AE丄平面BCC1B1. （14 分）例4、（2019苏锡常镇调研）如图，三棱锥DABC中，已知AC丄BC，AC丄DC，BC=DC，E，F 分别为BD，CD 的中点．求证：（1）EF〃平面ABC；（2）BD丄平面ACE.所以EF 〃平面ABC.（6分）（2）因为AC丄BC，AC丄DC，BC H DC = C，BC，DC U平面BCD所以AC丄平面BCD，（8分）因为BD U平面BCD，所以AC丄BD，（10分）因为DC=BC，E为BD的中点，所以CE丄BD，（12分）因为AC n CE = C, AC，CE U平面ACE，所以BD丄平面ACE.（14分）例5、（2019苏州三市、苏北四市二调）如图，在直三棱柱ABCA1B1C1中，侧面BCC1B1为正方形，A1B1 丄B1C1•设A1C与AC1交于点D, B1C与BC1交于点E.求证：（1） DE〃平面ABB1A1；（2） BC］丄平面A1B1C.规范解答（1）因为三棱柱ABCA1B1C1为直三棱柱，所以侧面ACC1A1为平行四边形．又A1C 与AC1 交于点D,所以D为AC]的中点，同理，E为BC]的中点•所以DE〃AB.（3分）又AB U平面ABB]A], DE G平面ABB]A], 所以DE〃平面ABB]A].（6分）（2）因为三棱柱ABCA]B]C]为直三棱柱，所以BB]丄平面A]B]C]. 又因为A]B]U平面A]B]C],所以BB]丄A]B i.（8分）又A]B]丄B]C], BB], B]C] U 平面BCC]B], BB]n B]C1=B1，所以A]B]丄平面BCC]B].（10 分）又因为BC]U平面BCC]B1，所以A]B丄BC].（12分）又因为侧面BCC]B1为正方形，所以BC]丄BQ.又A1B1n B1C=B1，A1B1，B1C U平面A1B1C, 所以BC1丄平面A1B1C.（14分）例6、（2017苏北四市一模）如图，在正三棱柱ABCA1B1C1中，已知D, E分别为BC, B1C1的中点，点F 在棱CC1上，且EF丄CD.求证：（1）直线A1E〃平面ADC1；⑴证法1连结ED,因为D, E分别为BC, B1C1的中点，所以B&/BD且B1E=BD, 所以四边形BBDE是平行四边形，（2分）所以BB/DE且BB1=DE. 又BB]〃AA]且BB]=AA], 所以AA/DE且AA1=DE, 所以四边形AA]ED是平行四边形，所以A]E〃AD.（4分）又因为AE G平面ADC, AD U平面ADC，所以直线AE〃平面ADC.（7分）1 1 1畀 ------ 1B证法2连结ED,连结A1C, EC分别交AC” DC1于点M, N,连结MM,则因为D, E分别为BC,B1C1的中点，所以C1E^CD且C、E=CD,所以四边形C1EDC是平行四边形，所以N是CE的中点.（2分）因为A1ACC1为平行四边形，所以M是A1C的中点，（4分）所以MN//A\E.又因为A]E G平面ADC，MN U平面ADC，，所以直线Af〃平面ADC、.（7分）（2）在正三棱柱ABCA1B1C1中，BB]丄平面ABC.又AD U平面ABC，所以AD丄BB、.又A ABC是正三角形，且D为BC的中点，所以AD丄BC.（9分）又BB，，BC U 平面BBCC，，BB1A BC=B，所以AD丄平面B,BCC,，又EF U平面BBCC，所以AD丄EF.（11分）又EF丄CD，CD，AD U平面ADC,，C,D A AD=D，所以直线EF丄平面ADC,.（14分）题型二、线面与面面平行与垂直证明平面与平面的平行与垂直问题，一定要熟练记忆平面与平面的平行与垂直判定定理和性质定理，切记不可缺条件。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
立体几何证明------垂直
一.复习引入
1.空间两条直线的位置关系有：_________,_________,_________三种。
2.（公理4）平行于同一条直线的两条直线互相_________.
3.直线与平面的位置关系有_____________,_____________,_____________三种。
4.直线与平面平行判定定理:如果_________的一条直线和这个平面内的一条直线平行，
那么这条直线和这个平面平行
5.直线与平面平行性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这
个平面相交，那么_________________________.
6.两个平面的位置关系:_________,_________.
7.判定定理1：如果一个平面内有_____________直线都平行于另一个平面，那么这两
个平面平行.
8.线面垂直性质定理：垂直于同一条直线的两个平面________.
9.如果两个平行平面同时和第三个平面相交，那么它们的________平行.
10.如果两个平面平行，那么其中一个平面内的所有直线都_____于另一个平面. 二．知识点梳理
知识点一、直线和平面垂直的定义与判定
定义判定
语言描述如果直线l和平面α内的任意一条直
线都垂直，我们就说直线l与平面
互相垂直，记作l⊥α一条直线与一个平面内的两条相交直线都垂直，则这条直线与该平面垂直.
图形
条件b为平面α内的任一直线，而l对这
一直线总有l⊥αl⊥m，l⊥n，m∩n＝B，m⊂α，n⊂α
结论l⊥αl⊥α
要点诠释：定义中“平面内的任意一条直线”就是指“平面内的所有直线”，这与“无数条直线”不同（线线垂直线面垂直）
性质
语言描述一条直线垂直于一个平面，那么这条
直线垂直于这个平面内的所有直线
垂直于同一个平面的两条直线平行.
图形
E
D
A
条件
结论
知识点三、二面角 Ⅰ.二面角：从一条直线出发的两个半平面所组成的图形叫二面角（dihedral angle ）. 这条直线叫做二
面角的棱，这两个半平面叫做二面角的面. 记作二面角AB αβ－－. （简记P AB Q －－）
二面角的平面角的三个特征:
ⅰ. 点在棱上 ⅱ. 线在面内 ⅲ.
与棱垂直
Ⅱ.二面角的平面角：在二面角αβ－l －的棱l 上任取一点O ，以点O 为垂足，在半平面,αβ内分别作垂直于棱l 的射线OA 和OB ，则射线OA 和OB 构成的AOB ∠叫做二面角的平面角. 作用：衡量二面角的大小；范围：000180θ<<.
知识点四、平面和平面垂直的定义和判定
定义 判定 文字描述 两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面垂直.
一个平面过另一个平面的垂线，则这
两个平面垂直 图形
结果
α∩β=l α-l-β=90o α⊥β
（垂直问题中要注意题目中的文字表述，特别是“任何”“ 随意”“无数”等字眼） 三．常用证明垂直的方法
立体几何中证明线面垂直或面面垂直都可转化为线线垂直，而证明线线垂直一般有以下的一些方法： （1） 通过“平移”。
（2） 利用等腰三角形底边上的中线的性质。
（3） 利用勾股定理。
（4） 利用直径所对的圆周角是直角
(1) 通过“平移”,根据若则a //b,且b⊥平面α,a⊥平面α
1．在四棱锥P-ABCD 中，△PBC 为正三角形，AB ⊥平面PBC ，AB ∥CD ，AB=2
1
DC ，中点为PD E . 求证：AE ⊥平面PDC.
O A C
B P
.
2．如图，四棱锥P －ABCD 的底面是正方形，PA ⊥底面ABCD ， ∠PDA=45°，点E 为棱AB 的中点．求证：平面PCE ⊥平面PCD ；
（2）利用等腰三角形底边上的中线的性质
3、在三棱锥P ABC -中，2AC BC ==，90ACB ∠=o ，AP BP AB ==，
PC AC ⊥．
（Ⅰ）求证：PC AB ⊥；
（3）利用勾股定理
4.如图，四棱锥P ABCD -的底面是边长为1
的正方形，,1,PA CD PA PD ⊥==
求证:PA ⊥平面ABCD ；
（4）利用直径所对的圆周角是直角
5、如图，AB 是圆O 的直径，C 是圆周上一点，P A ⊥平面ABC .
（1）求证：平面P AC ⊥平面PBC ；
_ D
_ C
_ B
_ A
_ P
（第2题
A
C
B
P
课堂及课后练习题：
1.判断下列命题是否正确，对的打“√”，错误的打“×”。
（1）垂直于同一直线的两个平面互相平行 （ ） （2）垂直于同一平面的两条直线互相平行 （ ）
（3）一条直线在平面内，另一条直线与这个平面垂直，则这两条直线垂直（ ）
2.已知直线
a,b
和平面α
，且,,a b a α⊥⊥则
b
与α
的位置关系是
________________________________________________.
3.如图所示，在四棱锥P ABCD -中，AB PAD ⊥平面,//AB CD ,PD AD =,E 是PB 的中点，F 是CD 上的点，且1
2
DF AB =
,PH 为PAD ∆中AD 边上的高。
（1）证明：PH ABCD ⊥平面；
4.如图所示, 四棱锥P -ABCD 底面是直角梯形
,,2,BA AD CD AD CD AB PA ⊥⊥=⊥底面ABCD ,
E 为PC 的中点, P A ＝AD 。
证明: BE PDC ⊥平面;
5.如图，在三棱锥P ABC -中，⊿PAB 是等边三角形，∠P AC =∠
PBC =90 º 证明：AB ⊥PC
C
A
D
B
O
E
6.如图，四面体ABCD 中，O 、E 分别是BD 、BC 的中点，
2, 2.CA CB CD BD AB AD ====== （1）求证：AO ⊥平面BCD ； （2）求异面直线AB 与CD 所成角的大小；
7.如图，四棱锥S ABCD -中，BC AB ⊥,BC CD ⊥，侧面SAB 为等边三角形，2,1AB BC CD SD ====．证明：SD SAB ⊥平面;
8.如图，在圆锥PO 中，已知PO =2，⊙O 的直径2AB =,C 是狐AB 的中点，D 为AC 的中点．证明：平面POD ⊥平面PAC ;
课堂及课后练习题答案： 1
（1） √ （2） √ （3）√ 2.b//b αα⊂或者 3.
证明：因为PH 为PAD ∆中AD 边上的高，所以PH AD ⊥，又因为AB PAD ⊥平面，所以AB PH ⊥，
=AB AD A I ，所以PH ABCD ⊥平面
4.分析：取PD 的中点F ，易证AF//BE, 易证A F ⊥平面PDC ，从而BE PDC ⊥平面 .
5.证明：因为PAB ∆是等边三角形，90PAC PBC ∠=∠=︒, 所以Rt PBC Rt PAC ∆≅∆,可得AC BC =。
如图，取AB 中点D ，连结PD ,CD , 则PD AB ⊥,CD AB ⊥, 所以AB ⊥平面PDC ,
所以AB PC ⊥。
6.（1）证明：连结OC
,,.BO DO AB AD AO BD ==∴⊥Q ,,.BO DO BC CD CO BD ==∴⊥Q 在AOC ∆中，由已知可得1, 3.AO CO == 而2,AC =
222,AO CO AC ∴+=90,o AOC ∴∠=即.AO OC ⊥
,BD OC O =Q I AO ∴⊥平面BCD
7.
（I ）取AB 中点E ，连结DE ，则四边形BCDE 为
矩形，DE=CB=2，连结SE ，则, 3.SE AB SE ⊥=
又SD=1，故222
ED SE SD =+，
所以DSE ∠为直角。
由,,AB DE AB SE DE SE E ⊥⊥=I ， 得AB ⊥平面SDE ，所以AB SD ⊥。
SD 与两条相交直线AB 、SE 都垂直。
所以SD ⊥平面SAB 。