EOF在大气科学中的应用,eof介绍
EOF分析及其应用

EOF分析及其应用
一、EOF分析是什么
EOF分析(Empirical Orthogonal Function Analysis)是一种常用
的时间-空间统计分析方法,它是由把空间上的一维观测或多维观测数据
矩阵投影到一个更特别的模型空间中,然后对该模型空间中的变换数据进
行分析从而推算出有关的特征参数的一种分析方法。
二、EOF分析的原理
EOF分析由英国天文学家Harold E. Jeffreys (1891-1989)于
1931年提出。
它利用最小二乘估计法,把空间上一维或多维观测的数据
矩阵投影在一个特定的模型空间中,然后对该模型空间中变换的数据进行
分析,从而推算出有关的特征参数。
EOF分析的核心理论是“变换空间”,即给定一个多维空间Vn,找出一个低维变换空间Vm具有一定的特殊性质(如基Vm上的每一列向量的模具有最小值,它们张成一个最小的模型空
间上),使得数据在其中具有最好的表示,且在该变换空间中可以表示出
空间统计分布的特性。
三、EOF分析的应用
(1)短时间强对流预报
短时间强对流预报是一种有效的大气环境监测技术,它依据大气各层
能量释放特征进行短时间的天气预报。
EOF方法运用了空间观测数据,可
以对大气能量释放做出准确的模拟分析,从而预测出未来几小时内这一区
域内的强对流天气预报。
(2)大气环流异常研究。
eof的用法

eof的用法EOF 是英文 End of File 的缩写,意为“文件结束”。
它在计算机领域中经常用来表示在读取文件时的文件结束标记。
下面将详细介绍 EOF 的用法和相关知识。
在计算机编程中,EOF是一个特殊的值或标记,用于指示已经到达文件的末尾。
在文件读取过程中,通常使用一个循环来逐行读取文件的内容,当读取到EOF时,循环将停止执行,表示文件已经读取完毕。
EOF的定义和使用方式与编程语言和文件读取库有关,下面以C语言为例进行说明。
在 C 语言中,EOF 定义在 stdio.h 头文件中,其值通常为 -1、当调用读取函数(如 getchar 或 fscanf)时,如果读取到了文件的末尾,这些函数将返回 EOF 值。
因此,可以通过检查函数的返回值是否为 EOF来判断是否读取到了文件的末尾。
下面是一个简单的示例程序,演示了如何使用EOF进行文件读取:```c#include <stdio.h>int main。
FILE某 file = fopen("e某ample.t某t", "r"); // 打开文件if (file == NULL)printf("文件打开失败\n");return 1;}int c;while ((c = fgetc(file)) != EOF) // 逐字符读取文件内容,直到文件结束putchar(c); // 输出字符}fclose(file); // 关闭文件return 0;```在上述示例中,程序首先打开了一个名为 "e某ample.t某t" 的文件。
然后,通过循环读取文件内容,直到读取到 EOF。
在每次循环中,将读取的字符通过 putchar 函数输出到屏幕上。
最后,关闭文件并返回。
以上就是使用 EOF 进行文件读取的简单示例。
需要注意的是,EOF仅表示文件的结束,并不能同时表示文件读取是否成功。
EOF是什么?

EOF是什么?作者:阮一峰日期: 2011年11月12日我学习C语言的时候,遇到的一个问题就是EOF。
它是end of file的缩写,表示"文字流"(stream)的结尾。
这里的"文字流",可以是文件(file),也可以是标准输入(stdin)。
比如,下面这段代码就表示,如果不是文件结尾,就把文件的内容复制到屏幕上。
int c;while ((c = fgetc(fp)) != EOF) {putchar (c);}很自然地,我就以为,每个文件的结尾处,有一个叫做EOF的特殊字符,读取到这个字符,操作系统就认为文件结束了。
但是,后来我发现,EOF不是特殊字符,而是一个定义在头文件stdio.h的常量,一般等于-1。
#define EOF (-1)于是,我就困惑了。
如果EOF是一个特殊字符,那么假定每个文本文件的结尾都有一个EOF(也就是-1),还是可以做到的,因为文本对应的ASCII 码都是正值,不可能有负值。
但是,二进制文件怎么办呢?怎么处理文件内部包含的-1呢?这个问题让我想了很久,后来查了资料才知道,在Linux系统之中,EOF根本不是一个字符,而是当系统读取到文件结尾,所返回的一个信号值(也就是-1)。
至于系统怎么知道文件的结尾,资料上说是通过比较文件的长度。
所以,处理文件可以写成下面这样:int c;while ((c = fgetc(fp)) != EOF) {do something}这样写有一个问题。
fgetc()不仅是遇到文件结尾时返回EOF,而且当发生错误时,也会返回EOF。
因此,C语言又提供了feof()函数,用来保证确实是到了文件结尾。
上面的代码feof()版本的写法就是:int c;while (!feof(fp)) {c = fgetc(fp);do something;}但是,这样写也有问题。
fgetc()读取文件的最后一个字符以后,C语言的feof()函数依然返回0,表明没有到达文件结尾;只有当fgetc()向后再读取一个字符(即越过最后一个字符),feof()才会返回一个非零值,表示到达文件结尾。
EOF分析方法范文

EOF分析方法范文EOF(End-of-File)分析方法是一种用于处理文件结尾标记的方法。
在计算机科学和信息技术领域,EOF通常用于表示文件的结尾。
当程序读取文件时,它会继续读取直到遇到EOF标记,表示已经读取到文件的结尾。
EOF分析方法就是通过检测EOF标记,来判断文件是否已经读取到结尾。
1.引言随着计算机技术的不断发展,文件处理在计算机科学和信息技术领域起着至关重要的作用。
在处理文件时,EOF分析方法可以帮助我们判断文件是否已经读取到结尾,从而避免读取不必要的数据或产生错误。
2.EOF标记在绝大多数操作系统中,EOF标记通常表示为文件的结尾。
当程序读取文件时,它会不断地读取数据,直到遇到EOF标记。
EOF标记的具体表示方式在不同的操作系统中有所不同,例如在Windows中,EOF标记通常表示为一个特殊字符(Ctrl+Z),而在Unix和Linux中,EOF标记则表示为一个换行符(\n)。
EOF分析方法的关键在于正确检测EOF标记的存在。
3.读取文件的方法在实际应用中,EOF分析方法可以与其他文件读取方法结合使用。
常用的文件读取方法有逐行读取、按字符读取和按块读取等。
-逐行读取:逐行读取文件是一种常见的读取方法。
通过循环读取每一行数据,直到遇到EOF标记。
-按字符读取:按字符读取文件是一种细粒度的读取方法。
通过逐个字符读取数据,并判断是否遇到EOF标记。
-按块读取:按块读取文件是一种高效的读取方法。
通过指定缓冲区的大小,一次读取多个字符,并判断是否遇到EOF标记。
无论使用哪种读取方法,都需要注意正确判断EOF标记的存在,并在读取到EOF标记后及时终止读取操作。
4.EOF分析方法在文件处理中的应用-文件读取:在读取文件时,EOF分析方法帮助我们判断是否遇到文件的结尾。
根据不同的读取方法,可以在读取到EOF标记后进行不同的处理,例如输出读取到的数据、关闭文件等。
-文件复制:在文件复制过程中,EOF分析方法可以帮助我们判断源文件是否读取到结尾,从而及时终止读取操作。
实验报告二 经验正交分解
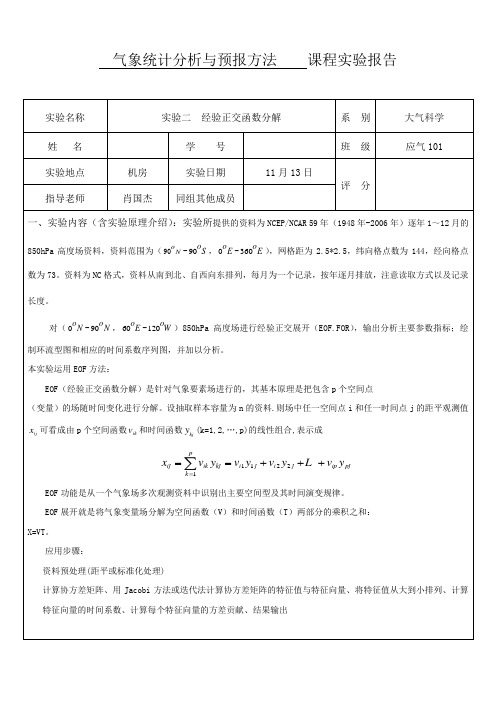
气象统计分析与预报方法 课程实验报告实验名称 实验二 经验正交函数分解系 别 大气科学 姓 名 学 号 班 级应气101实验地点 机房 实验日期 11月13日评 分指导老师肖国杰同组其他成员一、实验内容(含实验原理介绍):实验所提供的资料为NCEP/NCAR 59年(1948年-2006年)逐年1~12月的850hPa 高度场资料,资料范围为(90N-90S ,0E -360E ),网格距为2.5*2.5,纬向格点数为144,经向格点数为73。
资料为NC 格式,资料从南到北、自西向东排列,每月为一个记录,按年逐月排放,注意读取方式以及记录长度。
对(0N -90N ,60E -120W )850hPa 高度场进行经验正交展开(EOF.FOR ),输出分析主要参数指标;绘制环流型图和相应的时间系数序列图,并加以分析。
本实验运用EOF 方法:EOF (经验正交函数分解)是针对气象要素场进行的,其基本原理是把包含p 个空间点(变量)的场随时间变化进行分解。
设抽取样本容量为n 的资料.则场中任一空间点i 和任一时间点j 的距平观测值ij x 可看成由p 个空间函数ik v 和时间函数kj y (k=1,2,…,p)的线性组合,表示成11221pij ikkj i j i j ip pj k x vy v y v y v y ===+++∑EOF 功能是从一个气象场多次观测资料中识别出主要空间型及其时间演变规律。
EOF 展开就是将气象变量场分解为空间函数(V )和时间函数(T )两部分的乘积之和: X=VT 。
应用步骤:资料预处理(距平或标准化处理)计算协方差矩阵、用Jacobi 方法或迭代法计算协方差矩阵的特征值与特征向量、将特征值从大到小排列、计算特征向量的时间系数、计算每个特征向量的方差贡献、结果输出二、实验目的:经验正交函数分解(EOF)是统计天气分析中气象要素场最基础的研究模型,是必须理解和掌握的方法之一,是后续课程中许多气象要素场的计算结果的理解的基础理论,也是毕业设计和论文中的基本分析方法。
梅雨锋云系的模态研究Ⅰ:主导模态

梅雨锋云系的模态研究Ⅰ:主导模态覃丹宇;黄勇;李博;方宗义【摘要】利用经验正交函数(EOF)分解方法,对1998~2008年梅雨活跃期共16次过程每3h间隔的静止卫星云顶亮温(也称相当黑体亮度温度,即Black Body Temperature,以下简称TBB)的距平场进行计算,获得了梅雨锋云系的主要模态.经检验,前7个模态为独立模态,方差贡献分别为7.78%、5.83%、5.20%、4.27%、4.19%、3.62%和3.36%.这7个独立模态反映梅雨期间云系主要的异常特征.各模态相似云图中的云系与气候态相比出现位置偏移与形状变化,表明梅雨锋云系随主导环流系统的演变而发生断裂、减弱、消散、重建的过程.从各模态相应的大气环流配置来看,气候态梅雨锋云系对应的大气环流为三阻型梅雨形势.另外7个主导模态的大气环流基本可以划分为两类,一类为阻塞高压型,中高纬地区存在阻塞高压活动,在第2模态正位相,第4模态负位相,第5模态正位相和第6模态正、负位相以及第7模态正位相对应的500 hPa环流形势上都可以看到这一特点;另一类为槽脊型,中高纬地区阻塞高压活动不明显,等高线为一槽两脊或两槽—脊型分布,与这种环流形势相关的模态有第1模态正、负位相,第2模态负位相,第3模态负位相,第4模态正位相,第5模态负位相和第7模态负位相.【期刊名称】《大气科学》【年(卷),期】2014(038)004【总页数】19页(P700-718)【关键词】梅雨锋;云系;卫星;EOF【作者】覃丹宇;黄勇;李博;方宗义【作者单位】中国气象局中国遥感卫星辐射测量和定标重点开放实验室,北京100081;国家卫星气象中心,北京100081;安徽省气象科学研究所安徽省大气科学与卫星遥感重点实验室,合肥230001;中国气象局中国遥感卫星辐射测量和定标重点开放实验室,北京100081;国家卫星气象中心,北京100081;国家卫星气象中心,北京100081【正文语种】中文【中图分类】P4051 引言梅雨是东亚季风区夏季典型的天气和气候现象,是从我国江淮流域一直到日本南部每年 6~7月常常出现的一段持续的、大范围的、降水次数较频繁的连阴雨天气(大气科学辞典,1994)。
EOF分析及其应用最新

EOF分析及其应用最新
EOF(End of File)指的是在计算机中表示文件结束的标记。
在计算
机科学中,EOF有着广泛的应用。
下面是EOF分析及其应用的最新内容。
1.EOF在文件读取中的应用:
在文件读取过程中,EOF的出现可以用来检测文件是否已经到达结尾。
当读取到文件的末尾时,EOF标记将被置位,进而告知程序文件已经读取
完毕。
这对于读取未知长度的文件非常有用,因为它可以确保程序不会尝
试读取文件超出末尾的字符。
2.EOF在网络通信中的应用:
在网络通信中,EOF用于判断一次数据传输是否已经完成。
在一次通
信中,数据可能会被分成多个数据包进行传输,而EOF被用来标志着数据
的结束。
当接收方收到EOF标记时,它将知道该数据包已经接收完整,并
可以继续处理数据。
3.EOF在压缩算法中的应用:
在压缩算法中,EOF被用来标志着原始文件的结束。
当压缩文件被解
压缩时,EOF标记将告知解压缩器已经解压缩到达原始文件的末尾。
4.EOF在数据库操作中的应用:
在数据库操作中,EOF被用作一个指示器,用来检查查询语句是否已
经遍历完所有的结果。
当查询的结果集遍历完毕时,EOF标记将被置位,
程序可以据此判断查询结果是否为空,或者是否还有更多的结果待处理。
总之,EOF在计算机科学的许多领域都有着重要的应用。
它不仅可以
用来检测文件的结束,还可以用于网络通信、压缩算法以及数据库操作等
方面。
了解EOF的基本概念和应用,有助于开发高效、安全和可靠的软件系统。
EOF分析

对角线上的元素为奇异值),奇异值与特征根成倍数关
1 • 如果矩阵C = n XX T ,C 的特征根为λ,则有
• 如果矩阵C = XX T ,C 的特征根为λ,则有
√ = nλ; √ = λ;
由于该方法是直接对矩阵X 进行分解,所以对内存的要求远小于方法1。计算速度 很快。 两种方法对比练习。
显著性检验
-2.20 -4.40
1.80 0.60
-1.20 -0.40
[U,S,V]=svd(X); 得到 U= 0.19 0.98 0.98 -0.19 S= 6.49 0 0 0 0 0 4.23 0 0 0 V= 0.66 -0.49 0.56 0.02 0.67 0.63 -0.73 -0.31 0.53 0.14 0.39 0.03 -0.10 -0.26 -0.02 EOF=U; PC=S*V’; 得到PC= 4.28 -2.07
1 外,EOF和PC都具有正交性的特点,可以证明 n P C × P C T = ∧;即不同的PC之
间相关为0。E × E T = I 。I为对角单位矩阵,即对角线上值为1,其他元素都 为0。这表明各个模态之间相关为0,是独立的。 由上面的计算过程可以看出,EOF分析的核心是计算矩阵C 的特征根和特征向 量。计算矩阵特征根和特征向量的方法很多,下面具体给出Matlab中进行EOF分 析的两种不同的方法。具体步骤可参考下面两个框图中的实例。 方法1:调用[EOF,E]=eig(C),其中EOF为计算得到的空间特征向量,E为特 征根。然后计算主成分P C = EOF T × X 。需要指出的时,当数据量很大时,例 如分析高分辨率的资料(如1km分辨率的NDVI资料),空间范围很大维数m很容易 超过数万个点,则矩阵C 的维数是个巨大量,需要占用大量内存,也会导致计算 速度异常缓慢。而且很可能超出计算机的计算极限而死机。 方法2:直接对矩阵X 进行奇异值分解 X=U 其中 系。 43 为奇异值对交阵( VT
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最近做了一些数据分析,用到EOF分解,但是并没有发现网上有中文的相关资源,个人认为这个东西的理解对搞物理海洋和大气科学的人还是非常重要的,这里谈点自己的理解,也请大家多批评指正。
EOF Decomposition即正交经验函数分解,英文也常用PCA(Pri ncipal Components Analysis)即主成分分析。
撒一把芝麻在地上,让你用个尽可能小的椭圆把它们圈起来。
这个椭圆的长轴,就是这堆芝麻的第一主成分,所谓first leading EOF,也叫Mode-1,短轴呢,就是第二主成分了。
如果这群芝麻撒得特听话,基本排成一条线,你的椭圆就会特别扁,这时候长轴就特别能描述这群芝麻的特点。
理想化一下,芝麻们就排成一直线,椭圆就理想成Ax+B了。
长轴和短轴差别越大,即长轴的“方差贡献”越大,描述地越好。
这是最简单的对EOF的理解。
说起将EOF用在大气海洋,不可不提的一个人就是John Kutzbach,U niv.Wisconsin-Madison的senior scientist。
以前的EOF是一个纯数学概念,和海洋大气并不搭界,而Kutzbach第一个把EOF引入海洋大气界,开始彻底改变人们对数据分析和物理现象的认识。
Kutzbach 是个很有传奇色彩的人物,有很多开创性的工作。
比如虽然大家公认Wallace是Arctic Oscillation的提出者,其实Kutzbach很早就发现了AO的存在。
再比如Earth's Climate System概念的提出及学科系统的完善,他也是功不可没。
Ruddiman著Earth's Climate:Past and Future的时候,第一句话就是献给Kutzbach,极高地评价他headed
the effort to make the study of Earth's climate a science.还有很多鲜为人知的故事,在此不表。
总之,我们要饮水思源的。
对海洋大气四维时空数据做EOF分解,不仅能找到Mode-1、Mode-2、Mode-3……还可以把针对每一个Mode把时间和空间分离,也就是把这个4D场进而分成一个1D时间场和一个3D空间场(因为z通常设为常数,所以实际常为x-y的2D平面场)。
这时,每一个Mode都有其方差贡献,并对应一个spatial pattern(空间分布)和一个time series
(时间序列)。
先来看方差贡献(Variance Contribution)。
不妨画个柱状图看看,就拿右边这张图说事儿吧,这是全球降水的前5个Mode的方差贡献。
你看第一和第二根就分得特别开,第二和第三马马虎虎,第三和第四就差得很小了,往后更是越来越接近。
这说明Mode-1和Mode-2还是可以用的,第三往后的尾巴就扔掉吧。
大家注意到,这里Mode-1方差贡献仅有9.5%,并不是个好例子,如果做SST,Mode-1的方差贡献会大到30~40%。
因为降水的海上观测资料时间短且至今并不理想,加上其本身的时空变化就非常大,能explain9.5%已然很好了。
再看空间分布,也就是常说的EOF1,EOF2等等。
空间分布每个点的值的大小表示其variation,如果值越大,可以理解成这个点特别活泼,总
是跳开平均值特别远。
其正负没有绝对意义,只表示相对的正反位相。
下左图是冬季北半球SLP(Sea Level Pressure)的EOF1,很明显的A O(Arctic Oscillation)pattern。
对于海洋大气,EOF1常看到的是ENS O pattern,EOF2开始就能看到其他的pattern了,比如经典的马鞍形PDO(Pacific Decadal Oscillation)。
Winter SLP EOF-1Winter SLP PC-
1
再看时间序列,也就是常说的PC1,PC2等等。
这条高高低低的曲线,表示的是这些variation在时间上的变动规律,有时也画条形图。
一些h igh amplitude代表的是一些extreme events,比如82/83、97/98这些强El Nino事件就是从SST的PC1上看出来的。
在零线以上或者以下,则表示其在该时间上是正位相或负位相,比如上右图,是和SLP EOF1对应的时间序列,从50年代到90年代AO就经常keep在零线以上,
说明它常以正位相的形式存在,这时如果看看它的spatial pattern,果然一像个暖色的帽子扣在北极上。
但是90年代以后AO就常以负位相出现了,我们说Climate Shift了。
理解EOF要特别注意两点,就是EOF只是一种纯数学的分解,并不一定和物理意义完全对应。
有时一个强物理机制可以在好几个mode中出现,而且一个mode中也会有很多物理机制在起作用,所以在理解的时候不能生拉硬扯非要和什么pattern挂钩。
第二,海洋大气的EOF1常常是ENSO的pattern,如果想看Decadal以上的东西,可以先滤掉EN SO,再做EOF。
常用的是FTF(Fourier Transform Function)和wav elet,你要嫌麻烦可以用running mean(呵呵我不推
荐)。
1.主成分分析原理介绍(该部分选自胡基福老师的《气象统计原理与方法》)
为了直观理解主成分定义,设研究对象有x1与x2两个变量(指标)(个人认为如果真想区分EOF和PCA,指标这个词是可以帮助理解的),共观测了n次,样本数据排列为
x11,x12, (x1)
x21,x22, (x2)
现以x1与x2分别为坐标轴,对n对资料作相关点聚图。
可见,由于x 1与x2的相关关系,使n个点的分布情况大致成一椭圆形(如图1所
示)。
显然,椭圆的长轴方向反映了n个点的主要变化趋势,可作为新变量y1,椭圆的短轴反映了n个点变化的次要趋势,可作为新变量y2。
新变量y1与y2有如下特征:
1)新变量y1与y2相关关系很小(互相独立)
2)n个点在新变量y1方向上离散度最大,而在y2方向上离散度最小。
图1
因此,新变量y1与y2综合反映了原变量x1与x2的信息,是相互独立的,而且是按方差贡献(离散度)大小排列的,所以y1称为x1与x2的第一主成分,y2称为x1与x2的第二主成分。
这种变量变换结果相当于在原坐标系中旋转一个角度θ,使新坐标y1在椭圆长轴方向上,y2在椭圆的短轴方向上。
即使原变量x1与x2的离散度在新坐标中重新分配,y1占绝大部分,而y2占小部分,但是其总和是相等的,例如:
(55%)(45%)80%)(20%)
可见我们若只取第一主成分y1来代替原变量x1与x2,进行分析就可以达到80%的精度,从而达到降维分析的目的,这就是主成分分析的意义。
(两个指标变一个)
2.个人理解
上面是主成分分析的意义,用一个新变量代替两个旧变量,降维~(或许不应该叫变量)
先抛开EOF的具体分析方法,改用带气象海洋的特点,把上面的工作做一遍,看能发现什么:两个空间点x1与x2(起码一条,不再是指标),n次观测(长度为n的时间序列)
x11,x12, (x1)
x21,x22, (x2)
以x1与x2分别为坐标轴,对n对资料作相关点聚图。
还是那个椭圆,还是y1与y2
y1=x1cosθ+x2sinθ
y2=x2cosθ-x1sinθ
这个是很容易得到的。
θ是两坐标系间的夹角。
现在我们看图2:
图2
红点是一个测点。
蓝色的x1与x2就是原始的数据。
现在走出PCA的路线。
不写y1与y2的表达式了,把x1与x2分别用y1与y2表示,(对原数据影响力依次减小的项)就是:
x1=y1cosθ-y2sinθ
x2=y2cosθ+y1sinθ
这样实际上是把原数据写成了两项和的形式。
这是一个时刻的点,然后所有的点上面的式子就应该是
x1n=y1ncosθ-y2nsinθ
x2n=y2ncosθ+y1nsinθ
或者换个写法,就全明白了
x1(t)=y1(t)cosθ-y2(t)sinθ
x2(t)=y2(t)cosθ+y1(t)sinθ
很好理解,θ是只与空间有关的,y1(t)、y2(t)是只和时间有关的(在椭圆上不同的点不同)。
这就是两个空间点时间序列的EOF分解~把两个点扩展成n个点,那么点聚图就变成了n维,就有n个模态,椭圆就变成了椭球或者然后我们不知名的椭某某,式子就写成了y1到yn与θ的表达式。
y几的那一项就是第几模态,因为y1到yn的影响逐渐减小的。
简单说,我现在理解EOF就是在把原数据拆成若干项和的形式,每项反映原数据的程度依次降低。
而且每项时间导数空间导数的组成也就好理解了(有上面的表达式),就说当时间系数变化定数时,空间系数绝对值越大,这个点数据的变化程度越大(不同空间点的比较)。
同样空间系数固定时,时间系数变化越大,不同时刻数据变化越大(不同时间点的比较)在这样理解的基础上空间系数分布和时间系数曲线图就好看了。
而且该方法与物理意义不对应,纯是数学方法,有上面的表达式,也好理解了。
