第三章结晶动力学和热力学精品PPT课件
合集下载
金属材料第三章结晶
第三章金属的结晶金属由液态转变为固态的过程称为凝固，由于固态金属是晶体，故又把凝固称为结晶。
§3.1 结晶的过程和条件一、液态金属的结构特点金属键：导电性，正电阻温度系数近程有序：近程规则排列的原子集团结构起伏：近程规则排列的原子集团是不稳定的，处于时聚时散，时起时伏，此起彼伏，不断变化和运动之中，称为结构起伏。
结晶的结构条件：当近程规则排列的原子集团达到一定的尺寸时，可能成为结晶核心称为晶核, 即由液态金属的结构起伏提供了结晶核心。
结构起伏是金属结晶的结构条件。
二、结晶过程形核：液相中出现结晶核心即晶核；晶核长大：晶核形成后不断长大，同时新晶核不断形成并长大；不断形核、不断长大；晶体形成：各晶核相互碰撞，形成取向各异、大小不等的等轴晶粒组成的多晶体形核与长大是晶体形成的一般规律。
单晶体与多晶体三、结晶的过冷现象用热分析法获得液态金属在缓慢冷却时温度随时间的变化关系，即冷却曲线。
由冷却曲线可知，结晶时有过冷现象：实际结晶温度Tn低于理论结晶温度Tm的现象称为过冷。
液态金属过冷是结晶的必要条件。
过冷度：△T=Tm-Tn, 其大小除与金属的性质和纯度有关外，主要决定于冷却速度，一般冷却速度愈大，实际结晶温度愈低，过冷度愈大。
四、结晶的热力学条件热力学：研究热现象中物态转变和能量转换规律的学科，主要研究平衡状态的物理、化学过程。
热力学第二定律：在等温等压下，自发过程自动进行的方向是体系自由焓降低的方向，这个过程一直进行到自由焓具有最低值为止，称为最小自由焓原理。
利用最小自由焓原理分析结晶过程。
两相自由焓差是相变的驱动力。
金属结晶的热力学条件：固相自由焓必须低于液相自由焓。
热力学条件与过冷条件的一致性。
§3.2 形核的规律形核方式：均匀形核（自发形核）与非均匀形核（非自发形核）。
一、均匀形核均匀形核：当液态金属很纯净时，在相当大的过冷度下，固态晶核依靠液相内部的结构起伏直接从液相中自发形成。
第三章结晶动力学与结晶热力学
此外还有小角激光散射法、动态X射线衍射法、 光学解偏振法等。
DSC方法
随结晶程度增加，放热量增多，随结晶速率 增加，放热速率增大。通过测量结晶放热速率随 时间的变化可以了解结晶过程的情况。
结 晶
开始结晶
放t=0Biblioteka 热速率结晶结束 t=t∞
基线
mW
t
聚合物等温结晶的DSC曲线
t /min
ΔH∞——结晶开始到结晶完成的放热量；
平均值E的增量为：
dE N2rdr dr
设水波前进速度（球晶生长
速度）为v，则有：
r
r Vt
P
drVdt
d E N 2rd N r 2V 2 td t
对上式积分即可得到m的平均值E与t的关系：
E vt
t
Ed EN2rdrN2V2td tN2tv 2
0
0
0
1V cexpN(2tv2)
—— 一次性成核、晶核密度为N并且二维生长时， 结晶体系内的非晶部分与时间的关系
只有满足 t 的r/条v 件所产生的
水波才能通过P点。
dr r P
因此：
d EI(t r)2rd r
v
对上式积分：
v
E
tI(tr)2rd rIv2t3
0
v
3
代入式 1VcP(0)eE
1Vc
exp 1(Iv2t3)
3
2. 对于形成三维球晶的情况
2rd r4r2dr
(1) 对于晶核同时形成体系
v
E
tN4r2dr4Nv3t3
0
3
(2) 对于晶核不断形成体系
N——单位体积的晶 核数
EvtI(tr)4r2drIv3t4
DSC方法
随结晶程度增加，放热量增多，随结晶速率 增加，放热速率增大。通过测量结晶放热速率随 时间的变化可以了解结晶过程的情况。
结 晶
开始结晶
放t=0Biblioteka 热速率结晶结束 t=t∞
基线
mW
t
聚合物等温结晶的DSC曲线
t /min
ΔH∞——结晶开始到结晶完成的放热量；
平均值E的增量为：
dE N2rdr dr
设水波前进速度（球晶生长
速度）为v，则有：
r
r Vt
P
drVdt
d E N 2rd N r 2V 2 td t
对上式积分即可得到m的平均值E与t的关系：
E vt
t
Ed EN2rdrN2V2td tN2tv 2
0
0
0
1V cexpN(2tv2)
—— 一次性成核、晶核密度为N并且二维生长时， 结晶体系内的非晶部分与时间的关系
只有满足 t 的r/条v 件所产生的
水波才能通过P点。
dr r P
因此：
d EI(t r)2rd r
v
对上式积分：
v
E
tI(tr)2rd rIv2t3
0
v
3
代入式 1VcP(0)eE
1Vc
exp 1(Iv2t3)
3
2. 对于形成三维球晶的情况
2rd r4r2dr
(1) 对于晶核同时形成体系
v
E
tN4r2dr4Nv3t3
0
3
(2) 对于晶核不断形成体系
N——单位体积的晶 核数
EvtI(tr)4r2drIv3t4
第三章 晶体生长
A
B
图3-11 共晶系相图
LE ⇄(C + D)
第二节 相图及其在晶体生长中的应用
• 共晶反应过程
具有共晶成分的合金溶液，温度降到E点 时，开始同时从液体中开始析出成分为C的α 相和成分为D的β相，两相的相对含量可以用 杠杆定律求出
A
B
继续降温，最终形成α相和β相的机械混合物 ，但是晶体的总体成分仍是共晶成分。 形成的两相混合物具有显微组织特征。
①两种组分中金属原子或离子的半径必须接近，其半径差要小于15% ，否则，不同大小的原子或离子产生的晶格畸变将很大，以致影响 固溶度； ②两种组分必须具有相同的晶体结构，否则固体中将出现不同结构 的相，或固溶度仅限于一定范围； ③金属原子必须具有相同的价电子数，否则价电子数之差有可能导 致形成化合物而不形成固溶体； ④金属原子必须具有几乎相同的电负性，如果两种金属具有显著地 电负性差，则将倾向于形成金属间化合物。
L L+ L+
相图分析
相和相区与共晶相似 包晶线PDC：该线成分对应的合金在该 温度下发生包晶反应。该反应是液相L 包着固相, 新相β在L与α的界面 上形核，并向L和两个方向长大。
+
图3-12 包晶系相图
第二节 相图及其在晶体生长中的应用
• 包晶反应过程
第二节 相图及其在晶体生长中的应用
下面以凝固结晶为例说明形核过程： 短程有序（Short range order）：由于液态金属中有序原子集团的尺 寸很小，所以把液态金属结构的特点概括为短程有序（长程无序）， 通常用团簇结构cluster来表征。 晶胚（Embryo）：温度降低至熔点以下时，这些近程有序的原子集 团就成为均匀形核的晶胚，尺寸会增大。晶胚内部原子呈晶态有序 排列，而外层原子与液体中不规则排列的原子相接触构成界面。 晶核（Nucleus）：当具备结晶条件时，大于一定尺寸的晶胚就会成 为晶核。
晶格动力学讲稿PPT课件
i
3N
mi i
aijQ j
（2） （3）
T
1 2
3N i 1
• j1
Qi2
V
1 2
3N
2 i
Qi2
i 1
（4）
第26页/共68页
由分析力学的一般办法，由动能和势能可以直接写出拉格朗日函数
L T : V :
（5） （6）
:
Pi
L
•
•
Qi
（7）
的解为： 3N个相互无关的方程，各H简••Q正i 12坐3i标N1描P述i2 独 立i2的Q简i2 谐振动。其中任意简正坐标
（7）
u Ae qna表示第n个原子i振q动n的a位相因t 子。 n
整体上看，每个原子的振动位相各不相同，相邻的原子为相差为qa，因此（7）式代 表了一种全部原子都以同一频率，同一振幅。相邻原子的振动位相差均为qa的集体 振动模式——格波。因为是简谐近似，所以也称维简谐格波。
格波是晶体中全体原子都参与的一种简单的集体振动模式格波——晶格振动的 简正模。
因为q介于
之间。
,
a a
2 l
a Na a
即因此N，只由取一Nl 个维不单N同原的子值组。成的一维晶格，q只能取N个不同的值。
2
2
l
第10页/共68页
q只对应一个格波。q取N个不同的值，对应N
个 ，因此，独立的格波函数为N。 晶格振动频率数目=晶体的自由度数。
3 一维双原子晶体的振动
作用力为 n n1
根据牛顿定理，得到第n个原子的运动方程为
n1 n
， n n1
（n6）1 n
••
m n n1 n n n1 n1 n1 2n
晶格振动和晶体的热学性质精品PPT课件
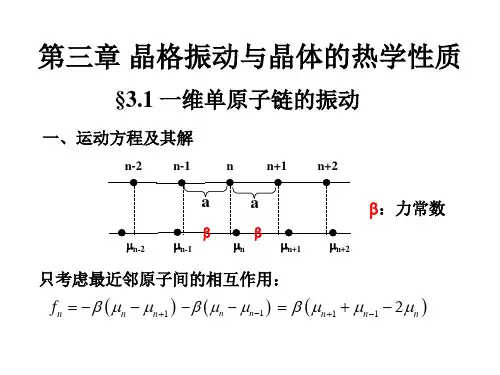
(q)
nn+)(00M
=c0q
2mcos+12aq m M2m2
ei12aq 2Mmcos
aq
q
光波： ＝c0q， c0为光速
对于实际晶体， ＋(0)在1013 ~ 1014Hz，对应于远 红外光范围。离子晶体中光学波的共振可引起对远红外 光在 ＋(0)附近的强烈吸收。
久期方程：
2
Mm
M
m
M
2
m2
2Mm
cos
aq
＝
M Mm
m
1
1
4 Mm
M m2
sin 2
1 2
aq
q
a
a
两个色散关系即有两支格波：（＋：光学波； －：声学波）
π nn
Aei12aq B
2cos 12aq ei12aq 2M2
M
2mcos12 aqei12aq m M2m22Mmcosaq
j
• 一种格波即一种振动模式称为一种声子， nj：声子数。
•
当电子或光子与晶格振动相互作用时，总是以
E
N j=1
nj
1 2
为 j
单元交换能量。
• 声子具有能量 q ，也具有准动量 Mn nn12n ，但它不能
脱离固体而单独存在，并不是一种真实的粒子, 只是一 种准粒子。
• 声子的作用过程遵从能量守恒和准动量守恒。
当q0时，＋，原胞中两种原子振动位相完全相反。
i 1 aq
M
2
2mcos
1 2
aqe
2
m2 2Mmcosaq
M
m
Rei
离子晶体在某种光波的照射下，光波的电场可以激发这 种晶格振动，因此，我们称这种振动为光学波或光学支。
第三章液态金属结晶的基本原理 上
Δ T ≈ 0.2T m
有效形核 温度
平衡状态下
(G V ) TTm L m Tm Sm 0 Sm
Lm Tm L T T L m T 所以： G V L m TSm m m Tm Tm
式中 T 为过冷度。对于给定金属，熔化潜热Lm和熔点Tm均为 定值，故GV仅与 T 有关。因此液态金属（合金）凝固的驱动力 是由过冷度提供的。
2 LC Vs Tm r* L T
16 3 VS Tm G LC 3 LT
4 3 GV G r 4r 2 SL 3 VS
2
3.2.1 均匀形核
能量起伏：系统中微小区域的能量偏离平均能量水平而高 低不一的现象。（是结晶的必要条件之三）。 高能原子附上低能晶胚，释放能量，提供形核功。 另一方面，液体中存在“结构起 r 伏”的原子集团，其统计平均尺寸 r°随温度降低（ΔT 增大）而增大， r°与 r* 相交，交点的过冷度即为 均质形核的临界过冷度ΔT*（约为 0.18-0.20Tm）。 形 成 临 界 晶 核 （ r* ） 时 的 过 冷 度 (△T*). △T≥△T*是结晶的必要条件。
dGV d PdV VdP TdS SdT
（3.4）
而
d q A
式中q-系统从外界吸收的热量；A-系统对外界所作的功。 在恒温下 q TdS 在只有膨胀功时 A PdV
所以 代入（3.4）得： 在恒压条件下dP=0 所以
d q A TdS PdV
3.2.1 均匀（自发）形核
下面我们从以下 均质生核的基础理论 ： 1)过冷液相中的相起伏提供固相晶核的晶胚； 四个方面进行分析：
2)晶胚在过冷的均匀熔体中一出现本身就包含
《晶格动力学讲稿》课件
晶格动力学的经典理论模型
01
02
03
弹性力学模型
将晶格视为弹性连续体， 通过弹性力学理论来描述 晶格的动力学行为。
哈密顿量模型
将晶格中的原子或分子的 运动视为经典力学中的粒 子运动，通过哈密顿量来 描述晶格的动力学行为。
牛顿运动方程
通过牛顿运动方程来描述 晶格中原子或分子的运动 ，可以更精确地描述晶格 的动力学行为。
晶格振动与声子
晶格振动模式
晶格是由原子或分子构成的周期性结构，原子或分子的相对位置发生变化时会产生晶格振 动。晶格振动模式可以分为光学模式和声学模式。
声子与能量传递
声子在晶格中传播时，会与其他粒子发生相互作用，传递能量和动量。声子是晶格中能量 传递的重要载体。
声子的统计性质
在热力学平衡状态下，声子遵循Bose-Einstein统计分布，表现出粒子数的涨落和热辐射 等特性。了解声子的统计性质对于理解晶格动力学的热力学性质和相变机制具有重要意义 。
材料力学性质的预测
弹性模量
晶格动力学理论可以用于预测材料的弹性模量，通过分析晶 格振动对材料宏观力学性能的影响，可以计算出弹性模量的 大小。
强度与韧性
利用晶格动力学的理论模型，可以预测材料的强度和韧性， 了解材料在不同受力条件下的力学行为和破坏机制。
06
未来研究方向与展望
新型计算方法的探索
机器学习算法的应用
基态求解
密度泛函理论的核心是求解多电 子系统的基态，常用的方法有 Kohn-Sham方法和HartreeFock方法等。
交换关联泛函
密度泛函理论中，需要选择合适 的交换关联泛函来描述电子间的 相互作用，不同的泛函会导致不 同的计算结果。
05
第三章 凝固热力学与动力学
体中的“能量起伏”提供。
能量起伏是结晶的必要条件之三
第三章 凝固热力学与动力学
20
五、形核率
形核率：是单位体积中、单位时间内形成的晶核数目。
I
C
exp
G KT
A
exp
G KT
ΔT*～0.2Tm
第三章 凝固热力学与动力学
21
第三节 非均质形核
一、非均质形核形核功 二、非均质形核形核条件
第三章 凝固热力学与动力学
又因为SL＞SS，所以：
G
T
P
L
＞
G
T
P
S
即：液相自由能G随温度上升而下降的斜率大于固相G的斜率。
第三章 凝固热力学与动力学
8
G = H- ST，所以：ΔGV =GS-GL =（HS- SST ）-（HL- SLT ）
=（HS- HL ）-T（SS- SL ）
即
ΔGV = ΔH - TΔS
G
16
3
3 SL
VS Tm H m T
2
液相中形成球形晶胚时自由能变化
过冷度ΔT 越大，ΔG* 越小。
第三章 凝固热力学与动力学
17
三、临界过冷度
r 22SL SLVVsS Tm
HGm V T
r
r*
rº
过冷是结晶的必要条件之一
0
ΔT* ΔT
第三章 凝固热力学与动力学
18
回四忆、：结实构际起液态伏金与属能结量构？起伏
第三章 凝固热力学与动力学
11
三、溶质平衡分配系数（K0）
定义：恒温T*下固相合金成分浓度C*s与液相合
金成分浓度C*L 达到平衡时的比值。
能量起伏是结晶的必要条件之三
第三章 凝固热力学与动力学
20
五、形核率
形核率：是单位体积中、单位时间内形成的晶核数目。
I
C
exp
G KT
A
exp
G KT
ΔT*～0.2Tm
第三章 凝固热力学与动力学
21
第三节 非均质形核
一、非均质形核形核功 二、非均质形核形核条件
第三章 凝固热力学与动力学
又因为SL＞SS，所以：
G
T
P
L
＞
G
T
P
S
即：液相自由能G随温度上升而下降的斜率大于固相G的斜率。
第三章 凝固热力学与动力学
8
G = H- ST，所以：ΔGV =GS-GL =（HS- SST ）-（HL- SLT ）
=（HS- HL ）-T（SS- SL ）
即
ΔGV = ΔH - TΔS
G
16
3
3 SL
VS Tm H m T
2
液相中形成球形晶胚时自由能变化
过冷度ΔT 越大，ΔG* 越小。
第三章 凝固热力学与动力学
17
三、临界过冷度
r 22SL SLVVsS Tm
HGm V T
r
r*
rº
过冷是结晶的必要条件之一
0
ΔT* ΔT
第三章 凝固热力学与动力学
18
回四忆、：结实构际起液态伏金与属能结量构？起伏
第三章 凝固热力学与动力学
11
三、溶质平衡分配系数（K0）
定义：恒温T*下固相合金成分浓度C*s与液相合
金成分浓度C*L 达到平衡时的比值。
第3章 液态金属凝固热力学与动力学ppt课件
过冷是凝固的必要条件
2018/11/21 8
二、液态金属的凝固过程
相变动力学理论： 高能态的液态原子变成低 能态的固态原子，必须越 过能态更高的高能态△GA 区。只有液态金属中那些 具有较高能态的原子（被 激活的原子）才能越过高 能态的界面变成固体中的 原子，完成凝固。△GA称 动力学能障。
2018/11/21 9
10
2018/11/21
液态金属的凝固过程：（1）生核； （2）长大。 首先体系通过能量起伏作用在某些微区内 克服能障形成稳定的新相小质点—晶核，然后 固液界面逐渐向液相内推移，使晶核长大，直 到所有液态金属全转变成金属晶体。
2018/11/21
11
三、液态合金凝固过程中的溶质再分配
1、概念：合金析出的固相中溶质含量不同于其周围液 相内溶质含量的现象，叫溶质再分配。 溶质再分配系数 K0 ：恒温T*下固相合金成分浓度 C*s与液相合金成分浓度C*L 达到平衡时的比值。
2018/11/21
14
第二节 均质形核
生核方式：（1）均质形核（自发生核）； （2）非均质形核（异质形核，非自发生核）。 1、概念 均质形核：依靠液态金属内部自身的结构自发地形核。 2、特点 1）在熔体各处几率相同； 2）固液界面由生核过程提供； 3）热力学能障大，需驱动力大； 4）理想的液态金属。
2018/11/21
15
3、均匀形核的能量变化——形核功 “结构起伏”的尺寸、大小与温度有关。 温度越低，“结构起伏”尺寸越大。 当温度降到熔点以下时，这种晶胚（原子团）的 尺寸较大。
晶胚内部的原子组成晶态的规则排列，其外层原 子与液体金属中不规则排列的原子接触，构成界 面。
第三章结晶动力学与结晶热力学PPT课件
第三章 结晶动力学与结晶热力学
§3-1 聚合物的结晶过程 §3-2 聚合物结晶动力学
§3-3 聚合物结晶热力学
§3-1 聚合物的结晶过程
一、聚合物的结晶能力
聚合物结晶的必要条件： ——链结构具有对称性或者立构规整性 聚合物结晶的充分条件： ——结晶温度位于玻璃化转变温度和结晶熔 融温度之间
自由基聚合产物——结构单元及构型的无规排列使 分子链立构规整性受到破坏，一般没有结晶能力； 配位聚合产物——分子链具有立构规整性，表现出 较强的结晶能力，通常可以结晶。其中全同立构体 结晶能力强于间同立构体，全反式聚合物结晶能力 强于全顺式聚合物，等规度高的结晶能力强于等规 度低的。 缩聚产物——不存在结构单元键接方式和立体构型 问题，但大多数缩聚物的分子链具有对称结构，可 以结晶。
lgt
Avrami指数——与成核机理和晶体生长方式有关的 常数，等于生长的空间维数和成核过 程的时间维数之和。 不同成核方式和生长类型的Avrami指数 生长方式 均相成核 异相成核
三维生长（球晶）
二维生长43;1=3
n=3+0=3
n=2+0=2
一维生长（针状晶体）
n=1+1=2
E——0到t时刻通过任意点P的水波数的平均值。
1. 在薄层熔体形成二维晶体的情况
雨水滴落到水面上相当于形成晶核，而水波的扩 展相当于二维晶体的生长。 当m=0时，意味着所有的晶体生长面都不经过P点。 即P点仍处于非晶态的几率为：
P(0) e
E
假设此时结晶部分所占的体积分数为Vc，非晶部 分所占的体积分数则为：
n=1+0=1
Avrami方程应用时存在的两个问题
1）测定出的Avrami指数n不是整数 （A）存在对时间有依赖性的初期成核作用； （B）结晶过程中均相成核和异相成核同时存在； 2 ）用 Avrami 方程作图时直线的最后部分与实验点 发生偏离——二次结晶 （A）球晶表面未接触部分的继续增长； （B）球晶内部的结构调整使结晶进一步完善；
§3-1 聚合物的结晶过程 §3-2 聚合物结晶动力学
§3-3 聚合物结晶热力学
§3-1 聚合物的结晶过程
一、聚合物的结晶能力
聚合物结晶的必要条件： ——链结构具有对称性或者立构规整性 聚合物结晶的充分条件： ——结晶温度位于玻璃化转变温度和结晶熔 融温度之间
自由基聚合产物——结构单元及构型的无规排列使 分子链立构规整性受到破坏，一般没有结晶能力； 配位聚合产物——分子链具有立构规整性，表现出 较强的结晶能力，通常可以结晶。其中全同立构体 结晶能力强于间同立构体，全反式聚合物结晶能力 强于全顺式聚合物，等规度高的结晶能力强于等规 度低的。 缩聚产物——不存在结构单元键接方式和立体构型 问题，但大多数缩聚物的分子链具有对称结构，可 以结晶。
lgt
Avrami指数——与成核机理和晶体生长方式有关的 常数，等于生长的空间维数和成核过 程的时间维数之和。 不同成核方式和生长类型的Avrami指数 生长方式 均相成核 异相成核
三维生长（球晶）
二维生长43;1=3
n=3+0=3
n=2+0=2
一维生长（针状晶体）
n=1+1=2
E——0到t时刻通过任意点P的水波数的平均值。
1. 在薄层熔体形成二维晶体的情况
雨水滴落到水面上相当于形成晶核，而水波的扩 展相当于二维晶体的生长。 当m=0时，意味着所有的晶体生长面都不经过P点。 即P点仍处于非晶态的几率为：
P(0) e
E
假设此时结晶部分所占的体积分数为Vc，非晶部 分所占的体积分数则为：
n=1+0=1
Avrami方程应用时存在的两个问题
1）测定出的Avrami指数n不是整数 （A）存在对时间有依赖性的初期成核作用； （B）结晶过程中均相成核和异相成核同时存在； 2 ）用 Avrami 方程作图时直线的最后部分与实验点 发生偏离——二次结晶 （A）球晶表面未接触部分的继续增长； （B）球晶内部的结构调整使结晶进一步完善；
液态金属凝固热力学及动力学 ppt课件
过冷度 T TK GL x
ppt课件
17
2、树枝晶方式生长
S/L前沿为负的温度梯度：GL=dT/dx<0
过冷度 T TK GL x
ppt课件
18
二、晶体微观长大方式
1、Jackson 因子
Gs x(1 x) x ln x (1 x) ln(1 x) NK BTm
*
Δ T 均≈0.2T0 Δ T 非′ Δ T 非″ I 非′ I 非″
* *
I均 I 非″ ΔT
I均
(a)
(b)
ΔT
ppt课件
11
3. 影响因素 （1）过冷度 （2）形核基底的性质 点阵畸变，可用点阵错配度δ 来衡量
a S aC aC
CS
当δ ≤0.05时，称完全共格界面，其界面能σ 较低，衬底促进非均匀形核的能力很强。
V2=K2exp(-B/ΔTK )
3）小平面生长成多面体晶体，棱角发明。 “微观上光滑，宏观上粗糙（长大后)”
ppt课件 22
（3）从缺陷处生长 位错、挛晶处——天然的台阶
1）螺旋位错
ppt课件
23
（3）从缺陷处生长
2）旋转挛晶生长 3）反射挛晶生长
(a) (b) 图 通过孪晶生长机制
(a)石墨的旋转孪晶及其生长台阶(b)面心立方晶体反射孪晶及其凹角边界
液态金属凝固热力学及动力学
Thermodynamics and kinetics of solidification
pp均质生核）
1、热力学条件： G<0, 过程自发进行
Gv GL GS ( H L TS L ) ( H S TSS ) H TS
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
收缩变的非常缓慢，往往结晶终了的时间
是不明确的。
17
（2） 光学解偏振法
利用球晶的光学双折射性质进行测定 熔融聚合物试样，光学各向同性，透明 结晶聚合物试样，光学各向异性，不透明 时间 ，结晶度 ，解偏振光的强度 ，作图
18
（3）DSC
19
Endotherm Up
ΔHt ΔH
0
2
4
6
Time /min
均相成核: 结晶单元的自我成核 异相成核: 结晶单元以外的因素成核
晶粒的生长（Growth）
高分子链扩散到晶核或晶体表面进行生长，可以在原有 表面进行扩张生长，也可以在原有表面形成新核而生长
14
测试方法
体积变化——膨胀剂法 热效应——示差扫描量热法DSC 观察晶体生长——偏光显微镜法PLM
9
（E）缩聚聚合物，虽然结构复杂，不存在立体 异构的现象，化学结构也有相同的对称性，还有 氢键，所以都具有结晶能力
例如：PBT, PET, PC, PA66等
O
O
C
C H 2 COC H 2 C H 2 4
O
n
O
O
H
H
C
C H 2 C N 4
C H 2
N
6n
10
（2） 其它结构因素
分子间氢键，使分子间力增大，分子变得刚硬， 结晶能力上升！
第四节 聚合物的结晶动力学 Crystallization kinetics of polymers
1
结晶行为和结晶动力学
结晶条件 非晶态
结晶性聚合物
聚
晶态
合
物
非结晶性聚合物
分子结构的对 称性和规整性
结晶条件，如 温度和时间等
2
晶迭的形成
a amorphous c crystalline L long period
DSC curve for PE isothermal crystallization
RelativeCrystallinity X(t):
相对结晶度
X(t) Ht H
20
（4） 偏光显微镜PLM
Diameter (μm)
55 50 45 40 35 30 25 20 15 10
5 0
0
121℃ 123℃ 124℃ 125℃
c a L
3
一、 分子结构与结晶能力、结晶速度 （1） 链的对称性和规整性
分子链的对称性越高, 规整性越好, 越容 易规则排列形成高度有序的晶格
（A）结晶能力强：PE和PTFE 均能结晶， PE 的结晶度高达95%， 而且结晶速度极快
4
CH 3
CH2 C n CH 3
Cl
CH2 C
n
Cl
O CH2 n
支化越多，分子链规整性下降，结晶能力下降！ 交联越多，分子链不规整，结晶能力下降！
11
分子量过大，影响链段的重排能力，结晶速率 下降，结晶能力下降！ 无规和交替共聚物一般无结晶能力！（EPR） 嵌段和接枝共聚物有各自的晶区！
12
二、 结晶速度与测量方法 结晶过程
成核
增长
聚合物结晶过程主要分为两步: 晶核的形成（Nucleation） 常见有两种成核机理:
n=3+0=3
n=2+0=2
n=1+0=1
24
lg[-lnVt -V]=lgK+nlgt V0 -V
lg[-ln Vt -V ] V0 -V
次期结晶: 结晶后 期偏离Avrami方 程
斜率为n 截距为lgK
T3 T2 T1
主期结晶: 可用 Avrami方程描 述前期结晶
lgt
25
由等温结晶的Avrami作图研究发现：
200
400
600
800
1000
1200
Crystallization Time (s)
G R t
21
三、 Avrami方程
结晶过程
成核
增长
（1） 聚合物的等温结晶动力学
Avrami Equation
Vt -V =exp(-Ktn) Avrami指数
V0 -V
结晶速率常数
膨胀计法
ht -h =exp(-Ktn) h0 -h
6
无规高分子是否一定不能结晶?
PVC: 自由基聚合产物，氯原子电负性较大，分子链上相 邻的氯原子相互排斥， 彼此错开， 近似于间同立构， 因 此具有微弱的结晶能力， 结晶度较小(约5%)。 PVA: 自由基聚合的聚乙酸乙烯基酯水解而来，由于羟基 体积小，对分子链的几何结构规整性破坏较小， 因而具 有结晶能力，结晶度可达60%。
DSC法 1 -X t= 1 - H t 1 A t= e x p (-K tn )
H A
23
Avrami指数n = 空间维数 + 时间维数
生长类型
三维生长 (球状晶体) 二维生长 (片状晶体) 一维生长 (针状晶体)
均相成核
n=生长维数+1
n=3+1=4
n=2+1=3
n=1+1=2
异相成核
n=生长维数
结晶初、中期，结晶过程符合方程； 结晶后期，实际结晶过程偏离Avrami方程，
聚异丁烯PIB 聚偏二氯乙烯PVDC 聚甲醛POM
对称性取代的烯类高聚物，结构简单源自对称 性好，均能结晶5通常，全同和间同立构聚合可以结晶， 全同立构的结晶能力比间同立构的强， 等规度高的结晶能力比等规度低的强， 无规共聚通常使结晶能力下降。
通常，自由基聚合得到无规立构聚合物； 定向聚合得到等规立构聚合物
顺式： 分子间距较大，重复周期长， 不易结晶，室温下弹性好， 很好的橡胶（BR）。
反式： 分子链结构较规整，重复周期短， 易结晶，室温下弹性差， 很好的塑料。
8
（C） 分子链的适当柔顺性，有利于结晶， 分子链太柔，结晶速率很小， 分子链太刚硬，重排能力很小，很难重为结晶态。
（D） 拉伸作用有利于结晶，即在拉伸力的作用下，结 晶聚合物往往表现出再结晶的现象。 如天然橡胶的拉伸结晶。
15
（1） 体积膨胀计
规定: 体积收缩一半所需时间的倒数作为该
温度下的结晶速度。
表示结晶过程中试样
体积收缩的大小
h0 ht ~ t
h
1
ht - h h0 - h
0.5
G=
1 t1
2
温度 恒定
0
t1/2
t
16
反S形曲线
（1）结晶初期，体积变化较为缓慢（存在诱导
期）；
（2）结晶中期，速度加快；
（3）结晶后期，体积变化逐渐减慢，最后体积
聚三氟氯乙烯: 自由基聚合产物，具有不对称碳原子且无 规， 但由于氯原子与氟原子体积相差不大，仍具有较强的 结晶能力，结晶度可达90%。
7
（B）全顺式、全反式、双烯类1，4加成聚合物， 链结构规整，也可以结晶，但因为链柔性太大， Tm很低，结晶速度很小。 聚1，4—丁二烯
等同周期：0.81nm 等同周期：0.48nm