高一数学上册专题训练题5

合集下载

【必刷题】2024高一数学上册数学竞赛基础专项专题训练(含答案)

【必刷题】2024高一数学上册数学竞赛基础专项专题训练（含答案）试题部分一、选择题：1. 已知函数f(x) = x² 2x + 1，那么f(x)在区间（∞，1）上的单调性是（）A. 单调递增B. 单调递减C. 先单调递增后单调递减D. 先单调递减后单调递增2. 下列等比数列中，公比为2的是（）A. 1, 2, 4, 8, 16B. 2, 4, 6, 8, 10C. 1, 3, 9, 27, 81D. 3, 6, 12, 24, 483. 设集合A={x|1≤x≤3}，集合B={x|x²2x3=0}，则A∩B的结果是（）A. {1, 2}B. {2, 3}C. {1, 3}D. {2}4. 若向量a=(2, 3)，向量b=(1, 2)，则向量a与向量b的夹角是（）A. 30°B. 45°C. 60°D. 90°5. 已知函数g(x) = |x1|，那么g(x)在x=1处的导数是（）A. 0B. 1C. 1D. 不存在6. 下列函数中，奇函数是（）A. y = x²B. y = x³C. y = |x|D. y = 2x7. 在平面直角坐标系中，点P(2, 3)关于原点对称的点是（）A. (2, 3)B. (2, 3)C. (2, 3)D. (2, 3)8. 若复数z满足|z1|=1，则z在复平面上的对应点位于（）A. 圆心在(1,0)，半径为1的圆上B. 圆心在(0,1)，半径为1的圆上C. 圆心在(1,0)，半径为1的圆上D. 圆心在(0,1)，半径为1的圆上9. 已知等差数列{an}的前n项和为Sn，若a1=1，d=2，则S4的值为（）A. 16B. 20C. 24D. 2810. 若函数h(x) = (x+1)/(x1)的值域为（∞，1）∪(1，+∞），则x的取值范围是（）A. (∞，1)∪(1，+∞）B. (∞，1)∪(1，+∞）C. (∞，1)∪(1，1)D. (1，+∞）二、判断题：1. 任何两个实数的和仍然是一个实数。

人教A版高一数学必修第一册全册复习训练题卷含答案解析(52)

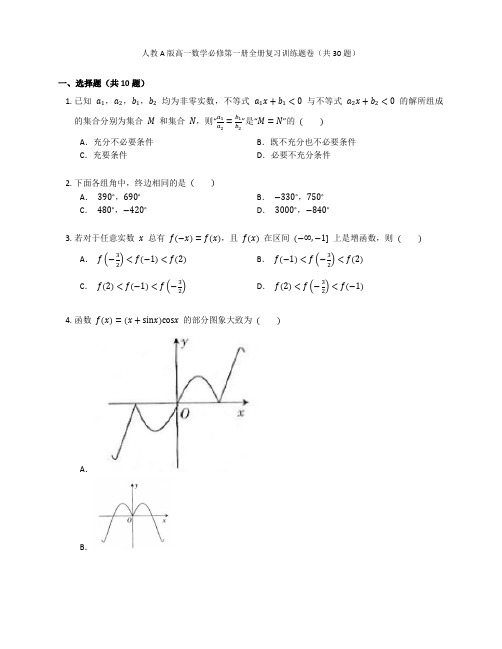
人教A 版高一数学必修第一册全册复习训练题卷（共30题）一、选择题（共10题）1. 已知 a 1，a 2，b 1，b 2 均为非零实数，不等式 a 1x +b 1<0 与不等式 a 2x +b 2<0 的解所组成的集合分别为集合 M 和集合 N ，则“a 1a 2=b 1b 2”是“M =N ”的 ( )A ．充分不必要条件B ．既不充分也不必要条件C ．充要条件D ．必要不充分条件2. 下面各组角中，终边相同的是 ( ) A ． 390∘，690∘ B ． −330∘，750∘ C ． 480∘，−420∘D ． 3000∘，−840∘3. 若对于任意实数 x 总有 f (−x )=f (x )，且 f (x ) 在区间 (−∞,−1] 上是增函数，则 ( ) A ． f (−32)<f (−1)<f (2) B ． f (−1)<f (−32)<f (2) C ． f (2)<f (−1)<f (−32)D ． f (2)<f (−32)<f (−1)4. 函数 f (x )=(x +sinx )cosx 的部分图象大致为 ( )A ．B ．C．D．5.集合A={x∣ −1<x<3}，B={x∣ x2+x−6<0,x∈Z}，则A∩B=( )A．(−1,2)B．(−3,3)C．{0,1}D．{0,1,2}6.已知集合A={x∣ 1≤x<3}，B={x∣ x2≤4}，则A∩B=( )A．{x∣ 1≤x<2}B．{x∣ −2≤x<1}C．{x∣ 1≤x≤2}D．{x∣ 1<x≤2}7.已知cos(π2+α)=√33(−π2<α<π2)，则sin(α+π3)=( )A．3√2−√36B．3√2+√36C．√6−36D．√6+368.设集合M={x∈R∣ 0≤x≤2}，N={x∈R∣ −1<x<1}，则M∩N=( )A．{x∣ 0≤x≤1}B．{x∣ 0≤x<1}C．{x∣ 1<x≤2}D．{x∣ −1<x≤2}9. 式子 a√−1a 经过计算可得 ( ) A ． √−a B ． √a C ． −√a D ． −√−a10. 设集合 A ={x∣ −1<x ≤1}，B ={−1,0,1,2}，则 A ∩B = ( )A ． {−1,0,1}B ． {−1,0}C ． {0,1}D ． {1,2}二、填空题（共10题）11. 已知集合 A =(−2,3)，B =[−1,4]，则集合 A ∩B = ．12. 已知 a >0，b >0，则 a 2+4+4ab+4b 2a+2b的最小值为．13. 若 (3−2m )12>(m +1)12，则实数 m 的取值范围为．14. 若 cosα=13，则 sin (α−π2)= ．15. 若角 α 终边经过点 P (−1,2)，则 tanα= ．16. 二次函数 y =ax 2+bx +c (x ∈R ) 的部分对应值如表：x−3−2−101234y 60−4−6−6−406则不等式 ax 2+bx +c >0 的解集是．17. 已知 a >b >0，则 a +4a+b +1a−b 的最小值为．18. 若 π2<α<π 且 cosα=−13，则 tanα= ．19. 如果 α∈(π2,π)，且 sinα=45，那么 sin (α+π4)+cos (α+π4)= ．20. 已知函数 f (x )=1+∣x∣−x 2(−2<x ≤2)．用分段函数的形折表示该函数为；该函数的值域为．三、解答题（共10题）21.画出下列函数的图象，并根据图象说出函数y=f(x)的单调区间及在每一单调区间上的单调性．(1) y=x2−5x−6；(2) y=9−x2．22.数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养．因为运算，数的威力无限；没有运算，数就只是一个符号．对数运算与指数幂运算是两类重要的运算．(1) 对数的运算性质降低了运算的级别，简化了运算，在数学发展史上是伟大的成就．对数运算性质的推导有很多方法．请同学们根据所学知识推导如下的对数运算性质：如果a>0，且a≠1，M>0，那么log a M n=nlog a M(n∈R)．(2) 请你运用上述对数运算性质计算lg3lg4(lg8lg9+lg16lg27)的值．(3) 因为210=1024∈(103,104)，所以210的位数为4（一个自然数数位的个数，叫做位数）．请你运用所学过的对数运算的知识，判断20192020的位数．（注：lg2019≈3.305）．23.回答下列问题：(1) 将log232=5化成指数式；(2) 将3−3=127化成对数式；(3) 已知log4x=−32，求x；(4) 已知log2(log3x)=1，求x．24.写出下列命题的否定，并判断其否定的真假：(1) p：不论m取何实数，方程x2+mx−1=0必有实根；(2) ∀x,y∈R，x2+y2+2x−4y+5=0．25.已知集合A={x∣2−a≤x≤2+a}，B={x∣∣x≤1或x≥4}．(1) 当a=3时，求A∩B；(2) 若A∩B=∅，求实数a的取值范围．26.已知函数f(x)=log a(x+2)−1，其中a>1．(1) 若f(x)在[0,1]上的最大值与最小值互为相反数，求a的值．(2) 若f(x)的图象不经过第二象限，求a的取值范围．27.求2π3的六个三角比的值．28.子集（1）对于两个集合A和B，如果集合A中都属于集合B（若a∈A，则a∈B），那么集合A叫做集合B的子集，记作或，读作“ ”或“ ”．可用文氏图表示为（2）子集的性质：①A⊆A，即任何一个集合是它本身的子集；②∅⊆A，即空集是任何集合的子集．问题：集合A是集合B的子集的含义是什么？,b}，Q={0,a+b,b2}，且P=Q．求a2018+b2019的值．29.已知集合P={1,ab30.已知集合A={x∣ 1≤x≤2}，B={x∣ 1≤x≤a,a≥1}．(1) 若A⫋B，求a的取值范围；(2) 若B⊆A，求a的取值范围．答案一、选择题（共10题） 1. 【答案】D【解析】取 a 1=b 1=1，a 2=b 2=−1，则可得 M =(−∞,−1)，N =(−1,+∞)，M ≠N ，因此不是充分条件，而由 M =N ，显然可以得到 a 1a 2=b 1b 2，所以是必要条件．故选D ．【知识点】充分条件与必要条件2. 【答案】B【解析】因为 390∘=360∘+30∘，690∘=720∘−30∘，所以 390∘ 与 690∘ 终边不同，A 错误；因为 −330∘=−360∘+30∘，750∘=720∘+30∘，所以 −330∘ 与 750∘ 终边相同，B 正确；因为 480∘=360∘+120∘，−420∘=−360∘−60∘，所以 480∘ 与 −420∘ 终边不同，C 错误；因为 3000∘=2880∘+120∘，−840∘=−720∘−120∘，所以 3000∘ 与 −840∘ 终边不同，D 错误．故选B ．【知识点】任意角的概念3. 【答案】D【解析】由 f (−x )=f (x ) 可得 f (x ) 为偶函数，且在 (−∞,1] 上单增，由偶函数性质可知其在区间 [1,+∞) 上，因为 f (−32)=f (32)，f (−1)=f (1)，所以 f (2)<f (−32)<f (−1)．【知识点】函数的单调性4. 【答案】D【解析】因为函数 f (x ) 为奇函数，故排除B ，又因为当 x ∈(0,π2) 时，f (x )>0，当 x ∈(π2,π)时，f (x )<0，故排除C ，A ．【知识点】函数的奇偶性、函数图象5. 【答案】C【解析】 B ={x∣ x 2+x −6<0,x ∈Z }={x∣ −3<x <2,x ∈Z }={−2,−1,0,1}，又 A ={x∣ −1<x <3}，所以 A ∩B ={0,1}，故选C ．【知识点】交、并、补集运算6. 【答案】C【知识点】二次不等式的解法、交、并、补集运算7. 【答案】A【解析】因为cos(π2+α)=−sinα=√33，所以sinα=−√33，所以−π2<α<0，所以cosα=√63，所以sin(α+π3)=sinαcosπ3+cosαsinπ3 =−√33×12+√63×√32=3√2−√36,故选A．【知识点】两角和与差的正弦8. 【答案】B【解析】因为M={x∈R∣ 0≤x≤2}，N={x∈R∣ −1<x<1}，所以M∩N={x∣ 0≤x<1}．【知识点】交、并、补集运算9. 【答案】D【解析】因为√−1a 成立，所以a<0，所以a√−1a=−√−a2a=−√−a．故选D．【知识点】幂的概念与运算10. 【答案】C【解析】A∩B={0,1}．【知识点】交、并、补集运算二、填空题（共10题）11. 【答案】[−1,3)【知识点】交、并、补集运算12. 【答案】 4【解析】由a 2+4+4ab+4b 2a+2b=(a+2b )2+4a+2b=(a +2b )+4a+2b ，因为 a >0，b >0，所以 a +2b >0，4a+2b >0，所以 (a +2b )+4a+2b≥2√(a +2b )⋅4a+2b=4，当且仅当 a +2b =2 时取等号，即a 2+4+4ab+4b 2a+2b的最小值为 4．【知识点】均值不等式的应用13. 【答案】 [−1,23)【知识点】幂函数及其性质14. 【答案】 −13【知识点】诱导公式15. 【答案】 −2【知识点】任意角的三角函数定义16. 【答案】 (−∞,−2)∪(3,+∞)【知识点】二次不等式的解法17. 【答案】 3√2【解析】 4a+b +1a−b =22a+b +12a−b ≥(2+1)2(a+b )+(a−b )=92a ，所以 a +4a+b +1a−b≥a +92a≥2√a ⋅92a=3√2，当且仅当 {2a+b=1a−b,a =92a,即 a =3√22，b =√22时等号成立．【知识点】均值不等式的应用18. 【答案】 −2√2【知识点】同角三角函数的基本关系19. 【答案】 −3√25【知识点】两角和与差的余弦、两角和与差的正弦20. 【答案】 f(x)={1−x,−2<x ≤01,0<x ≤2； [1,3)【解析】 f (x )=1+∣x∣−x 2(−2<x ≤2)，当 −2<x ≤0 时，f (x )=1−x ；当 0<x ≤2 时，f (x )=1．所以函数 f (x )={1−x,−2<x ≤01,0<x ≤2，函数 f (x ) 的图象如图所示：根据图象，得函数 f (x ) 的值域为 [1,3)．【知识点】分段函数、函数的值域的概念与求法三、解答题（共10题） 21. 【答案】(1) 图略．函数 y =x 2−5x −6 在 (−∞,52] 上单调递减，在 [52,+∞) 上单调递增． (2) 函数 y =9−x 2 在 (−∞,0] 上单调递增，在 [0,+∞) 上单调递减．【知识点】函数的单调性22. 【答案】(1) (a m )n =a mn ， log a (a m )n =log a a mn ， log a (a m )n =mn ，令 a m =M ，则 m =log a M ，则 log a M n =nlog a M ．(2) lg3lg4(lg8lg9+lg16lg27)=lg32lg2(3lg22lg3+4lg23lg3)=34+23=1712． (3) lg20192020=2020lg2019≈2020×3.305=6676.1，所以20192020≈106676.1∈(106676,106677)，所以20192020位数为6677．【知识点】对数的概念与运算23. 【答案】(1) 因为log232=5，所以25=32．(2) 因为3−3=127，所以log3127=−3．(3) 因为log4x=−32，所以x=4−32=22×(−32)=2−3=18．(4) 因为log2(log3x)=1，所以log3x=2，即x=32=9．【知识点】对数的概念与运算24. 【答案】(1) ¬p：存在一个实数m，使方程x2+mx−1=0没有实数根．因为该方程的判别式Δ=m2+4>0恒成立，所以¬p为假命题．(2) ¬p：∃x,y∈R，x2+y2+2x−4y+5≠0．因为x2+y2+2x−4y+5=(x+1)2+(y−2)2，当x=0，y=0时，x2+y2+2x−4y+5≠0成立，所以¬p为真命题．【知识点】全（特）称命题的概念与真假判断、全（特）称命题的否定、复合命题的概念与真假判断25. 【答案】(1) 当a=3时，A={x∣−1≤x≤5}，B={x∣∣x≤1或x≥4}，所以A∩B={x∣∣−1≤x≤1或4≤x≤5}．(2) ①若A=∅，则2−a>2+a，解得a<0，满足A∩B=∅；②若A≠∅，则2−a≤x≤2+a，所以a≥0．因为A∩B=∅，所以{2−a>1,2+a<4,解得0≤a<1．综上，实数a的取值范围是(−∞,1)．【知识点】交、并、补集运算26. 【答案】(1) 函数f(x)=log a(x+2)−1的定义域是(−2,+∞)．因为a>1，所以f(x)=log a(x+2)−1是[0,1]上的增函数．所以f(x)在[0,1]上的最大值是f(1)=log a3−1；最小值是f(0)=log a2−1．依题意，得log a3−1=−(log a2−1)，解得a=√6．(2) 由（1）知，f(x)=log a(x+2)−1是(−2,+∞)上的增函数．在f(x)的解析式中，令x=0，得f(0)=log a2−1，所以，f(x)的图象与y轴交于点(0,log a2−1)．依题意，得f(0)=log a2−1≤0．解得a≥2．【知识点】函数的最大（小）值、对数函数及其性质27. 【答案】sin2π3=√32，cos2π3=−12，tan2π3=−√3，cot2π3=−√33，sec2π3=−2，csc2π3=23√3．【知识点】任意角的三角函数定义28. 【答案】（1）任何一个元素；A⊆B；B⊇A；A包含于B；B包含A（2）集合A中的任何一个元素都是集合B中的元素，即由x∈A能推出x∈B．例如{0,1}⊆{−1,0,1}，则由0∈{0,1}能推出0∈{−1,0,1}．【知识点】包含关系、子集与真子集29. 【答案】−1．【知识点】集合相等30. 【答案】(1) 若A⫋B，由下图可知，a>2．(2) 若B⊆A，由下图可知，1≤a≤2．【知识点】包含关系、子集与真子集11。

上海市高一数学上学期周练05-人教版高一全册数学试题

某某市2016-2017学年高一数学上学期周练05一. 填空题1. 下列不等式的解为：①2560x x -+<，②2560x x -++<2. 写出命题：若2017x y +≠，则2016x ≠或1y ≠的等价命题3. 已知：11a b -≤+≤，且13a b ≤-≤，则3a b -的取值X 围为4. 不等式20ax bx a ++<(0)ab >的解集是空集，则222a b b +-的取值X 围是5. 不等式20ax bx c ++>的解集是1(,3)2-，则不等式20cx bx a ++<的解集为 6. 已知12a ≥，22()f x a x ax c =-++，对于任意[0,1]x ∈，()1f x ≤恒成立，则实数c 的取值X 围是7. 已知实数,x y 满足2241x y xy ++=，则2x y +的最大值为8. 若不等式2051x px ≤++≤恰好有一个实数值为解，则p =9. 若下列三个方程：24430x ax a +-+=，22(1)0x a x a +-+=，2220x ax a +-=中至少有一个方程有实根，则a 的取值X 围是10. 已知,,a b c 为互不相等的整数，则22224()()a b c a b c ++-++的最小值为11. 已知,a b R ∈，关于x 的方程432210x ax x bx ++++=存在一个实根，则22a b +的最小值为二. 选择题1. 集合{|41,}A x x k k Z ==+∈，{|42,}B x x k k Z ==+∈，{|43,}C x x k k Z ==+∈ 若a A ∈，b B ∈，c C ∈，则（）A. abc A ∈B. abc B ∈C. abc C ∈D. abc AB C ∉ 2. 设a 和b 都是非零实数，则不等式a b >和11a b>同时成立的充要条件是（） A. 0a b >> B. 0a b >> C. 0a b >> D. 以上答案均不对3. 假设n 是不小于3的正整数，n 个给定的实数12,,,n x x x ⋅⋅⋅具有如下性质：对任意一个二次函数()y f x =，数12(),(),,()n f x f x f x ⋅⋅⋅中至少有三个数相同，则下列对于12,,,n x x x ⋅⋅⋅的判断中，正确的是（）A. 至少有三个数是相同的B. 至少有两个数是相同的C. 至多有三个数是相同的D. 至多有两个数是相同的4. 当一个非空数集F 满足“如果,a b F ∈，则,,a b a b ab F +-∈，且0b ≠时，a F b∈” 时，我们称F 就是一个数域，以下四个关于数域的命题：① 0是任何数域的元素；② 若数域F 有非零元素，则2016F ∈；③ 集合{|3,}P x x k k Z ==∈是一个数域；④ 有理数集是一个数域；其中真命题有（）个A. 0B. 1C. 2D. 3三. 解答题1. 解关于x 的不等式[(3)1](1)0m x x +-+>()m R ∈；2.（1）是否存在实数p ，使得40x p +<是220x x -->成立的充分不必要条件？如果存在，求出p 的取值X 围，如果不存在，说明理由；（2）是否存在实数p ，使得40x p +<是220x x -->成立的必要不充分条件？如果存在，求出p 的取值X 围，如果不存在，说明理由；3. 已知集合22{|410813,,}A t t a ab b a b a Z b Z ==++--+∈∈，对于任意的x A ∈， y A ∈，判断元素xy 与集合A 的关系，并证明你的结论；4. 已知二次函数()y f x =的二次项系数是1，并且一次项系数和常数项都是整数，若(())0f f x =有四个不同的实数根，并且在数轴上四个根成等距排列，试求二次函数()y f x =的解析式，使得其所有项的系数和最小；参考答案一. 填空题1. (2,3)、(,1)(6,)-∞-+∞2. 若2016x =且1y =，则2017x y +=3. [1,7]4. 4[,)5-+∞ 5. 1(2,)3- 6. 34c ≤ 8. 4p =± 9. 32a ≤-或1a ≥- 10. 2 11. 8二. 选择题1. B2. A3. B4. D。

专题05 函数：定义域归类大全-2023学年高一数学培优练(人教A版2019第一册)(解析版)

专题5函数：定义域归类大全目录【题型一】开偶次方根函数定义域............................................................................................................................2【题型二】解绝对值函数不等式求定义域................................................................................................................3【题型三】抽象函数定义域1：(x)→f(g(x))型.........................................................................................................4【题型四】抽象函数定义域2：f(g(x))→f(x)型........................................................................................................6【题型五】抽象函数定义域3：f(g(x))→f(h （x ）)型..............................................................................................7【题型六】抽象函数定义域4：f(x)→f(g（x）)+f(h（x）).............................................................................8【题型七】抽相与具体函数混合型............................................................................................................................9【题型八】嵌入型（内外复合）函数型定义域......................................................................................................11【题型九】恒成立含参型..........................................................................................................................................12【题型十】对数函数定义域......................................................................................................................................14【题型十一】定义域：解指数函数不等式..............................................................................................................15【题型十二】正切函数定义域................................................................................................................................16【题型十三】解正弦函数不等式求定义域..............................................................................................................17【题型十四】解余弦函数不等式求定义域..............................................................................................................18【题型十五】求分段函数定义域..............................................................................................................................20【题型十六】实际应用题中的定义域应用..............................................................................................................21培优第一阶——基础过关练......................................................................................................................................23培优第二阶——能力提升练......................................................................................................................................26培优第三阶——培优拔尖练.. (30)综述：常考函数的定义域：1.()()00f x f x ⇒≠⎡⎤⎣⎦；②.()()10f x f x ⇒≠；③()0f x ⇒≥；④.()()log 0a f x f x ⇒>；⑤.()()tan ,2f x f x k k Z ππ⇒≠+∈；⑥.实际问题中，需根据实际问题限制范围.【题型一】开偶次方根函数定义域【典例分析】（2021·福建·厦门市海沧中学高一期中）函数()f x =的定义域为（）A ．[]0,3B ．[]1,3C ．[)3,+∞D ．(]1,3【答案】D【分析】根据二次根式的性质及二次不等式的解法即可得出结果.【详解】解：由题意可得()3010x x x ⎧-≥⎨->⎩，解得13x <≤.1.（2022·全国·高一专题练习）已知函数()f x =(,1]-∞，则实数a 的取值集合为（）A ．{1}B ．(,1]-∞C ．[1,)+∞D ．(,1)(1,)-∞⋃+∞【答案】A【分析】求出函数的定义域，对比即可得出.【详解】由0a x -≥可得x a ≤，即()f x 的定义域为(,]a -∞，所以1a =，则实数a 的取值集合为{}1.故选：A.2.（2022·山东·临沂二十四中高一阶段练习）函数31y x =的定义域是（）A ．(],1-∞B ．()()1,00,1-U C ．[)(]1,00,1- D ．(]0,1【答案】C【分析】函数定义域满足23100x x ⎧-≥⎨≠⎩，求解即可【详解】由题，函数定义域满足23100x x ⎧-≥⎨≠⎩，解得[)(]1,00,1x ∈- .故选：C3.（2022·全国·高一专题练习）函数()0(1)f x x =-的定义域为（）A ．2,3⎛⎫+∞ ⎪⎝⎭B ．()2,11,3∞⎛⎫⋃+ ⎪⎝⎭C ．()2,11,3∞⎡⎫⋃+⎪⎢⎣⎭D ．2,3⎡⎫-+∞⎪⎢⎣⎭【答案】B【分析】根据二次根式的被开方数大于等于0，分式的分母不为0，以及零次幂的底数不等于0，建立不等式组，求解即可.【详解】解：由已知得32>010x x -⎧⎨-≠⎩，解得2>3x 且1x ≠，所以函数()0(1)f x x =-的定义域为()2,11,3∞⎛⎫⋃+ ⎪⎝⎭，故选：B.【题型二】解绝对值函数不等式求定义域【典例分析】.（2022·江苏·高一）函数y =）A ．()0,∞+B ．(),0∞-C ．()()0,11,+∞ D ．()()(),11,00,-∞-⋃-⋃+∞【答案】C【分析】根据0次幂的底数不等于0，偶次根式的被开方数非负，分母不等于0列不等式，解不等式即可求解.【详解】由题意可得：1000x x x x x ⎧-≠⎪+≥⎨⎪+≠⎩，解得：0x >且1x ≠，所以原函数的定义域为()()0,11,+∞ ，1.（2022·广东·广州六中高一期末）函数y ___________.【答案】[2,0)-【分析】利用根式、分式的性质求函数定义域即可.【详解】由解析式知：240||0x x x ⎧-≥⎨-≠⎩，则220x x -≤≤⎧⎨<⎩，可得20x -≤<，∴函数的定义域为[2,0)-.故答案为：[2,0)-.2.（2021·江苏·常州市第二中学高一期中）函数()f x =________．【答案】13,22⎡⎤-⎢⎥⎣⎦##1322x x ⎧⎫-≤≤⎨⎬⎩⎭【分析】根据解析式的形式得到关于x 的不等式，解不等式后可得函数的定义域.【详解】解：由题设可得2120x --≥，即122x -≤，故2122x -≤-≤，所以1322x -≤≤，故答案为：13,22⎡⎤-⎢⎥⎣⎦.3.（2021·北京市第九中学高一期中）函数y =________．【答案】(,1][2,)-∞⋃+∞【分析】满足函数有意义的条件，即2310x --≥，解得定义域.【详解】由题知，2310x --≥，解得2x ≥或1x ≤，故函数的定义域为：(,1][2,)-∞⋃+∞故答案为：(,1][2,)-∞⋃+∞【题型三】抽象函数定义域1：(x)→f(g(x))型【典例分析】（2022·江西·修水中等专业学校模拟预测）已知函数()y f x =的定义域为[]1,5-，则函数()221y f x =-的定义域为（）A ．[]0,3B ．[]3.3-C ．[D ．[]3,0-【答案】C【分析】由题可知解21215x -≤-≤即可得答案.【详解】解：因为函数()y f x =的定义域为[]1,5-，所以，21215x -≤-≤，即203x ≤≤，解得x ≤≤所以，函数()221y f x =-的定义域为[故选：C基本规律已知()f x 的定义域为[,]a b ，求(())f g x 的定义域：解不等式()a g x b ≤≤即可得解【变式训练】1.（2022·全国·高一专题练习）已知()()013x f x x-=-，则()1f x +的定义域为（）A ．()(),11,3-∞⋃B ．()(),22,4-∞⋃C ．()(),00,2-∞ D ．(),2-∞【答案】C【分析】先求得()f x 的定义域，然后将1x +看作一个整体代入计算即可.【详解】由题可知：10330x x x -≠⎧⇒<⎨->⎩且1x ≠所以函数定义域为{3x x <且}1x ≠令13x +<且11x +≠，所以2x <且0x ≠所以()(),00,2x ∈-∞ ，所以()1f x +的定义域为()(),00,2-∞ 故选：C2.（2015·上海·闵行中学高一期中）已知函数()1y f x =+的定义域为[]23-，，则函数()21y f x =-的定义域为（）A ．502⎡⎤⎢⎥⎣⎦，B ．[]14-，C ．5522⎡⎤-⎢⎥⎣⎦，D ．3722⎡⎤-⎢⎥⎣⎦，【答案】C【分析】先求1x +取值范围，再根据两函数关系得21x -取值范围，解得结果为所求定义域.【详解】因为函数()1y f x =+的定义域为[]23-，，所以1[1,4]x +∈-，因此55[1,4]02||51222x x x ∈-∴≤≤∴≤≤--即函数()21y f x =-的定义域为5522⎡⎤-⎢⎥⎣⎦，故选：C3.（2018·江西·南康中学高一期中）已知函数()f x 的定义域为[3,)+∞，则函数1(1)f x+的定义域为（）A ．4(,]3-∞B ．4(1,]3C ．1(0,]2D ．1(,]2-∞【答案】C【分析】由已知函数定义域，可得113x+≥，求解分式不等式得答案．【详解】解：∵函数()f x 的定义域为[3,)+∞，∴由113x +≥，得12x ≥，则102x <≤．∴函数1(1)f x +的定义域为1(0,]2．故选：C ．【题型四】抽象函数定义域2：f(g(x))→f(x)型【典例分析】（2023·全国·高一专题练习）已知函数22211x x y f x x ⎛⎫+-= ⎪+-⎝⎭的定义域是[)1,+∞，则函数()y f x =的定义域是_______．【答案】(]1,2【分析】令()()222111x x g x x x x +-=≥+-，根据函数值域的求解方法可求得()g x 的值域即为所求的()f x 的定义域.【详解】令()()222111x x g x x x x +-=≥+-，则()()222111111111x x x x g x x x x x x x x+-+==+=+≥+-+--+，1y x x =- 在[)1,+∞上单调递增，10x x∴-≥，10111x x∴<≤-+，()12g x ∴<≤，f x ∴的定义域为(]1,21,21.（2019·陕西·渭南市尚德中学高一阶段练习）若函数(1)f x -的定义域为[1,2]-，那么函数()f x 中的x 的取值范围是________.【答案】[2,1]-【分析】根据函数(1)f x -的定义域求出()f x 的定义域即可．【详解】解：函数(1)f x -的定义域为[1-，2]，即12x -≤≤211x ∴-≤-≤1[2x ∴-∈-，1]，故函数()f x 的定义域为[2,1]-，故答案为：[2,1]-.2.（2020·山西·太原五中高一阶段练习）若函数(21)f x -的定义域为[0,1]，则函数()f x 的定义域为（）A ．[1,0]-B ．[3,0]-C ．[0,1]D ．[1,1]-【答案】D【解析】由函数(21)f x -的定义域为[0,1]，可求出1211-≤-≤x ，令x 代替21x -，可得11x -≤≤，即可求出函数()f x 的定义域.【详解】因为函数(21)f x -的定义域为[0,1]，由01x ，得1211-≤-≤x ，所以()y f x =的定义域是[1,1]-，故选：D3.（2023·全国·高一专题练习）已知()21f x -的定义域为⎡⎣，则()f x 的定义域为（）A ．[]22-,B ．[]0,2C ．[]1,2-D ．⎡⎣【答案】C【分析】由x ≤≤2x -.【详解】因为2(1)f x -的定义域为[，所以x ≤≤所以2112x -≤-≤，所以()f x 的定义域为[1,2]-．故选：C【题型五】抽象函数定义域3：f(g(x))→f(h （x ）)型【典例分析】（2022·全国·高一课时练习）函数()3=-y f x 的定义域为[]4,7，则()2y f x =的定义域为（）A ．()1,4B ．[]1,2C ．()()2,11,2--⋃D ．[][]2,11,2-- 【答案】D【分析】利用抽象函数的定义域解法结合一元二次不等式的解法即可求解.【详解】解：因为函数()3=-y f x 的定义域为[]4,7所以47x ≤≤即134x ≤-≤所以214x ≤≤解得：[][]2,11,2x ∈--⋃所以()2y f x =的定义域为[][]2,11,2-- 故选：D.1.（2021·辽宁·沈阳市第一中学高一期中）函数()1f x +的定义域为[]1,2-，则函数()2f x 的定义域为（）A ．1,12⎡⎤-⎢⎥⎣⎦B ．1,12⎡⎤⎢⎥⎣⎦C ．31,2⎡⎤⎢⎥⎣⎦D ．13,22⎡⎤⎢⎥⎣⎦【答案】D【分析】当[]1,2x ∈-得到[]1,13x +∈，根据123x ≤≤解得答案.【详解】函数()1f x +的定义域为[]1,2-，即[]1,2x ∈-，故[]0,2x ∈，[]1,13x +∈.123x ≤≤，解得13,22x ⎡⎤∈⎢⎥⎣⎦.故选：D.2.（2022·全国·高一课时练习）若函数()22f x -的定义域为[]1,3-，则函数()f x 的定义域为______；若函数()23f x -的定义域为[)1,3，则函数()13f x -的定义域为______.【答案】[]2,7-22,33⎛⎤-⎥⎝⎦【分析】根据抽象函数定义域求解即可.【详解】因为函数()22f x -的定义域为[]1,3-，即13x -≤≤，所以209x ≤≤，2227x -≤-≤，故函数()f x 的定义域为[]2,7-.因为函数()23f x -的定义域为[)1,3，即13x ≤<，所以1233x -≤-<，则函数()f x 的定义域为[)1,3-，令1133x -≤-<，得2233x -<≤，所以函数()13f x -的定义域为22,33⎛⎤- ⎥⎝⎦.故答案为:[]2,7-，22,33⎛⎤- ⎥⎝⎦3.（2022·黑龙江·牡丹江市第三高级中学高一阶段练习）(21)f x -的定义域为[0,1)，则(13)f x -的定义域为（）A ．(2,4]-B ．12,2⎛⎤- ⎥⎝⎦C ．20,3⎛⎤ ⎥⎝⎦D ．10,6⎛⎤⎥⎝⎦【答案】C【分析】先由[0,1)x ∈，求出21x -的范围，可求出()f x 的定义域，而对于相同的对应关系，21x -的范围和13x -相同，从而可求出(13)f x -的定义域.【详解】因为01x ≤<，所以022x ≤<，所以1211x -≤-<，所以()f x 的定义域为[1,1)-，所以由1131x -≤-<，得203x <≤，所以(13)f x -的定义域为20,3⎛⎤⎥⎝⎦，故选：C 【题型六】抽象函数定义域4：f(x)→f(g（x）)+f(h（x）)【典例分析】（2021·全国·高一单元测试）已知函数()f x 的定义域为()0,1，若10,2c ⎛⎫∈ ⎪⎝⎭，则函数()()()g x f x c f x c =++-的定义域为（）A ．(),1c c --B ．(),1c c -C ．()1,c c -D ．(),1c c +【答案】B【分析】由已知函数的定义域有0101x c x c <+<⎧⎨<-<⎩，即可求复合函数的定义域.【详解】由题意得：0101x c x c <+<⎧⎨<-<⎩，即11c x c c x c-<<-⎧⎨<<+⎩，又10,2c ⎛⎫∈ ⎪⎝⎭，∴1c x c <<-．故选：B1.（2021·安徽蚌埠·高一期末）已知函数()f x 的定义域是[]0,2，则函数()1122g x f x f x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭的定义域是（）A ．13,22⎡⎤⎢⎥⎣⎦B ．15,22⎡⎤⎢⎥⎣⎦C ．13,22⎡⎤-⎢⎥⎣⎦D ．[]0,2【答案】A【解析】根据函数定义域的性质进行求解即可.【详解】因为函数()f x 的定义域是[]0,2，所以有：102132122022x x x ⎧≤+≤⎪⎪⇒≤≤⎨⎪≤-≤⎪⎩.故选：A2.（2020·安徽·繁昌皖江中学高一期中）已知函数()f x 的定义域为[0,4]，求函数2(3)()y f x f x =++的定义域为（）A ．[2,1]--B ．[1,2]C ．[2,1]-D ．[1,2]-【答案】C【分析】根据抽象函数的定义域得到关于x 的不等式组，解出即可【详解】函数()f x 的定义域为[0,4]，所以函数2(3)()y f x f x =++的定义域满足：203404x x ≤+≤⎧⎨≤≤⎩解得3122x x -≤≤⎧⎨-≤≤⎩，即21x -≤≤所以函数2(3)()y f x f x =++的定义域为[2,1]-故选：：C3.（2021·江西·黎川县第一中学高一阶段练习）若函数()y f x =的定义域是[0,1]，则函数()()(2)(01)F x f x a f x a a =+++<<的定义域是（）A ．1,22a a -⎡⎤-⎢⎥⎣⎦B ．,12a a ⎡⎤--⎢⎥⎣⎦C ．[,1]a a --D ．1,2a a -⎡⎤-⎢⎥⎣⎦【答案】A【分析】根据抽象函数定义域的求法列不等式组，解不等式组求得()F x 的定义域.【详解】依题意101102122a x a x a a a x a x ⎧-≤≤-⎧≤+≤⎪⎪⇒⎨⎨-≤+≤-≤≤⎪⎪⎩⎩，由于01a <<，所以111101222a a a a a -----=>⇒->，0222a a a a a ⎛⎫---=-<⇒-<- ⎪⎝⎭，所以由1122a x aa a x -≤≤-⎧⎪⎨--≤≤⎪⎩解得122a a x --≤≤.所以()F x 的定义域为1,22a a -⎡⎤-⎢⎣⎦.故选：A【题型七】抽相与具体函数混合型【典例分析】（2022·黑龙江·铁人中学高一期末）已知函数()22f x -的定义域为{}|1x x <，则函数()211f x x --的定义域为（）A ．(,1)-∞B ．(,1)-∞-C ．()(),11,0-∞--U D ．()(),11,1-∞-- 【答案】D【分析】先求出()f x 的定义域，再根据分母不为零和前者可求题设中函数的定义域.【详解】因为函数()22f x -的定义域为{}|1x x <，故220x -<，所以()f x 的定义域为(),0-∞，故函数()211f x x --中的x 需满足：21010x x -<⎧⎨-≠⎩，故1,1x x <≠-，故函数()211f x x --的定义域为()(),11,1-∞-- ，故选：D.1.（2021·河南·高一期中）已知函数()21y f x =-的定义域是[]2,3-，则y =是（）A ．[]2,5-B ．(]2,3-C ．[]1,3-D ．(]2,5-【答案】D【分析】根据给定复合函数求出()f x 的定义域，再列式求解作答.【详解】因函数()21y f x =-的定义域是[]2,3-，即()21f x -中[]2,3x ∈-，则21[5,5]x -∈-，因此，y =5520x x -≤≤⎧⎨+>⎩，解得25x -<≤，所以y =(]2,5-.故选：D2.（2022·全国·高一专题练习）设()f x 22x f f x ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭的定义域为．A ．（－4,0)∪（0,4)B ．（－4，－1)∪（1,4)C ．（－2，－1)∪（1,2)D ．（－4，－2)∪（2,4)【答案】B【详解】试题分析：要使函数有意义，则2>02x x +-解得22x ∈-（，），22x f f x ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭有意义，须确保两个式子都要有意义，则222{222x x-<<-<<⇒4114x ∈--⋃（，）（，），故选B .考点：1.函数的定义域；2.简单不等式的解法.3.2021·江西·赣州市赣县第三中学高一阶段练习）若函数()1f x +的定义域为[]1,15-，则函数()2f x g x =）A ．[]1,4B ．(]1,4C ．[]1,14D ．(]1,14【答案】B【分析】首先根据函数()1f x +的定义域求出函数()y f x =的定义域，然后再列出()2f x g x =x 所满足的条件，从而可求出函数()2f x g x =.【详解】因为函数()1f x +的定义域为[]1,15-，所以115x -≤≤，所以0116x ≤+≤，所以函数()y f x =的定义域为[]0,16，所以要使函数()2f x g x =201610x x ⎧≤≤⎨->⎩，解得14x <≤，所以函数()2f x g x =(]1,4.故选：B ．【题型八】嵌入型（内外复合）函数型定义域【典例分析】（2021·全国·高一课时练习）已知()11f x x =+，则()()f f x 的定义域为（）A ．{}|2x x ≠-B ．{}|1x x ≠-C ．{1x x ≠-且}2x ≠-D ．{0x x ≠且}1x ≠-【答案】C【分析】利用分母不为0及复合函数的内层函数不等于0求解具体函数定义域【详解】因为1()1f x x =+，所以1x ≠-，又因为在(())f f x 中，()1f x ≠-，所以111x ≠-+，所以2x ≠-，所以(())f f x 的定义域为{1x x ≠-且}2x ≠-.故选：C1.（2020·江西省临川第二中学高一阶段练习）已知函数()f x 的定义域为(0,1]，()g 2x x =+，那么()()f g x 的定义域是（）A ．(2,3]B ．[0,1)C ．(0,1]D ．(2,1]--【答案】D【解析】本题首先可根据题意得出()01g x <≤，然后通过计算即可得出结果.【详解】因为函数()f x 的定义域为(0,1]，()g 2x x =+，所以函数()()f g x 需要满足()01g x <≤，即021x <+≤，解得21x -<≤-，()()f g x 的定义域是(2,1]--，故选：D.2.（2020·全国·高一）设()11f x x-＝，则()f f x ⎡⎤⎣⎦＝________.【答案】1x x-(0x ≠，且1x ≠)【分析】将()f x 的解析表达式中的x 用()f x 替换，然后化简整理即得，注意根据原函数的定义域确定复合函数()()f f x 的定义域【详解】∵()11f x x=-，∴()()1111111111x 1x f f x x f x x x-⎡⎤===⎣⎦------＝.由于()11f x x =-中1x ≠，∴()f f x ⎡⎤⎣⎦中()1f x ≠，即111x≠-，∴0x ≠，且1x ≠，故答案为：1x x-(0x ≠，且1x ≠)【题型九】恒成立含参型【典例分析】（2022·全国·高一专题练习）若函数()f x =的定义域为R ，则a 的范围是（）A ．[0,4]B ．[0,4)C ．D ．(0,4)【答案】A【分析】根据给定条件，可得210ax ax ++≥，再分类讨论求解作答.【详解】依题意，R x ∀∈，210ax ax ++≥成立，当0a =时，10≥成立，即0a =，当0a ≠时，2Δ40a a a >⎧⎨=-≤⎩，解得04a <≤，因此得04a ≤≤，所以a 的范围是[0,4].故选：A1.（2021·四川·遂宁中学高一阶段练习）已知函数()f x =的定义域是R ，则m的取值范围是（）A ．04m ≤<B ．01m ≤≤C ．4m ≥D ．04m ≤≤【答案】A【分析】对m 分0,0m m =≠两种情况讨论得解.【详解】解：由题得210mx mx ++≠的解集为R .当0m =时，10≠，符合题意；当0m ≠时，240,04m m m ∆=-<∴<<.综合得04m ≤<.故选：A2.（2022·全国·高一专题练习）已知y =的定义域是R ，则实数a 的取值范围是()A．⎛ ⎝⎭B．⎫⎪⎪⎝⎭C．33,22⎛⎛⎫-∞+∞ ⎪⎝⎭⎝⎭D．3322⎛-+ ⎝⎭【答案】D【分析】结合函数特征和已知条件可得到21(1)04ax a x +-+>解集为R ，当0a =时，可得到与已知条件矛盾；当0a ≠时，结合一元二次函数图像即可求解.【详解】由题意可知，21(1)04ax a x +-+>的解集为R ，①当0a =时，易知211(1)044ax a x x +-+=-+>，即14x <，这与21(1)04ax a x +-+>的解集为R 矛盾；②当0a ≠时，若要21(1)04ax a x +-+>的解集为R ，则只需21(1)4y ax a x =+-+图像开口向上，且与x 轴无交点，即判别式小于0，即20(1)0a a a >⎧⎨∆=--<⎩a <<综上所述，实数a的取值范围是33,22⎛+ ⎝⎭.故选：D.3.（2021·广东·深圳市南山外国语学校（集团）高级中学高一阶段练习）若函数()f x =R ，则实数m 的取值范围是（）A ．(0,4B ．[)0,4C ．[]0,4D ．(]0,4【答案】B【分析】由题意可知224mx mx ++>0的解集为R ，分0m =，0m <，0m >三种情况讨论，即可求解.【详解】解：函数的定义域为R ，即不等式的解集224mx mx ++>0的解集为R 当0m =时，得到40>，显然不等式的解集为R ；当0m <时，二次函数224y mx mx =++开口向下，函数值y 不恒大于0，故不等式的解集不可能为R ；当0m >时，二次函数224y mx mx =++开口向上，由不等式的解集为R ，等到二次函数与x 轴没有交点，24160m m ∆=-<，解得04m <<；综上所述，实数m 的取值范围[)0,4.故选：B【题型十】对数函数定义域【典例分析】（2020·黑龙江哈尔滨·高一阶段练习（理））函数y =R ，则实数a 的取值范围是A ．[0,)+∞B ．[1,0)(0,)-⋃+∞C ．(,1)-∞-D ．[1,1)-【答案】A【详解】当0a =时，y =R ;当0a ≠时，函数的值域为R ，则221ax x +-的开口向上，且判别式大于等于零，即0{440a a >+≥，解得0a >.故实数a 的取值范围是[0,)+∞.故选：A.1.（2022·山东·枣庄市第三中学高一开学考试）已知函数()f x 的定义域为()0,1，则()12log 21y f x ⎡⎤=-⎢⎥⎣⎦的定义域为___________.【答案】3,14⎛⎫⎪⎝⎭【分析】根据()f x 的定义域，求得()12log 21x -的取值范围，由此求得x 的取值范围，也即求得函数()12log 21y f x ⎡⎤=-⎢⎥⎣⎦的定义域.【详解】由于函数()f x 的定义域为()0,1，所以()12log 2011x <-<，即()111222log log 21lo 112g x -<<，由于12log y x =在定义域上递减，所以12112x <-<，解得314x <<.所以函数()12log 21y f x ⎡⎤=-⎢⎥⎣⎦的定义域为3,14⎛⎫ ⎪⎝⎭.故答案为：3,14⎛⎫⎪⎝⎭2.（2021·山东省实验中学高一阶段练习）函数()f x =的定义域为___________.【答案】(]1,3##{|13}x x <≤【分析】由函数的解析式中含有二次根式和对数式，可由二次根式的被开方数非负及对数式的真数大于零联立不等式组，解之即可.需注意不等式的定义域须写成集合或区间形式.【详解】解：由题意可得，自变量x 须满足不等式组：41log (1)0210x x ⎧--≥⎪⎨⎪->⎩41log (1)210x x ⎧-≤⎪⇔⎨⎪->⎩1210x x -≤⎧⇔⎨->⎩13x ⇔<≤所以函数()f x ={|13}x x <≤.故答案为：{|13}x x <≤.3.（2019·黑龙江·哈九中高一阶段练习（文））已知集合{}10A x x =->，22log 1x B x y x ⎧⎫-==⎨⎬+⎩⎭，则()A B =R ð（）A ．[)0,1B ．()1,2C ．(]1,2D ．[)2,+∞【答案】C【分析】求出集合A 、B ，再利用补集和交集的定义可求出集合()R A B ð.【详解】{}()101,A x x =->=+∞ ，()()222log 0,12,11x x B x y xx x ⎧⎫⎧⎫--===>=-∞-⋃+∞⎨⎬⎨⎬++⎩⎭⎩⎭，则[]1,2R B =-ð，因此，()(]1,2R A B = ð.故选：C.【题型十一】定义域：解指数函数不等式【典例分析】（2022·全国·高一专题练习）已知函数()f x =[)2,+∞，则=a _________．【答案】4【分析】由已知可得不等式20x a -≥的解集为[)2,+∞，可知2x =为方程20x a -=的根，即可求得实数a 的值.【详解】由题意可知，不等式20x a -≥的解集为[)2,+∞，则220a -=，解得4a =，当4a =时，由240x -≥，可得2242x ≥=，解得2x ≥，合乎题意.故答案为：4.1.（2023·全国·高一专题练习）已知函数()ln f x x =()2f x 的定义域为（）A ．()01，B ．()12，C ．(]04，D ．(]02，【答案】D【分析】通过求解f (x )的定义域，确定f (2x )的中2x 的范围，求出x 范围，就可确定f (2x )定义域【详解】要使函数()ln f x x =+01620xx >⎧⎨-≥⎩，解得04x <≤，()f x 的定义域为(]0,4，由024x <≤，解得02x <≤，()2f x 的定义域为(]0,2，故选D.2.（2022·全国·高一专题练习）函数()f x =___________.【答案】(,0]-∞【分析】根据具体函数的定义域求法，结合指数函数的单调性求解.【详解】解：由1102x ⎛⎫-≥ ⎪⎝⎭，得011122⎛⎫⎛⎫≥= ⎪ ⎪⎝⎭⎝⎭x ，所以0x ≤，所以函数的定义域为(,0]-∞，故答案为：(,0]-∞3.（2022·全国·高一专题练习）函数y ________.【答案】(－∞，－2]∪[2，＋∞)【分析】根据开偶数次方根号里的数大于等于零，结合指数函数的单调性解之即可得解.【详解】由题意有22390x --≥，即22233x -≥，所以222x -≥，即24x ≥，所以2x ≥或2x -≤，故所求函数的定义域为(－∞，－2]∪[2，＋∞).故答案为：(－∞，－2]∪[2，＋∞).【题型十二】正切函数定义域【典例分析】（2022·安徽·泾县中学高一开学考试）函数()f x 的定义域为___________.【答案】|,Z 44x k x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭【分析】根据开偶数次发，根号里的数大于等于零，解正切函数不等式即可得解.【详解】解：由21tan 0x -≥，有1tan 1x -≤≤，可得ππππ44k x k -+≤≤，k ∈Z ，所以函数()f x 的定义域为|,Z 44x k x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭.故答案为：|,Z 44x k x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭.1.（2022·云南昭通·高一期末）函数3tan 24y x π⎛⎫=-- ⎪⎝⎭的定义域为___________.【答案】5|,Z 82k x x k ππ⎧⎫≠+∈⎨⎬⎩⎭【分析】先得到使函数有意义的关系式32,Z 42x k k πππ-≠+∈，求解即可.【详解】若使函数有意义，需满足：32,Z 42x k k πππ-≠+∈，解得5,Z 82k x k ππ≠+∈；故答案为：5|,Z 82k x x k ππ⎧⎫≠+∈⎨⎬⎩⎭2.（2022·全国·高一课时练习）函数tan(6)4y x π=+的定义域为________．【答案】{|,Z}624k x x k ππ≠+∈【分析】由6,Z 42x k k πππ+≠+∈，即得.【详解】由题意，要使函数tan(6)4y x π=+的解析式有意义，自变量x 须满足：6,Z 42x k k πππ+≠+∈，解得,Z 624k x k ππ≠+∈，故函数tan(6)4y x π=+的定义域为{|,Z}624k x x k ππ≠+∈，故答案为：{|,Z}624k x x k ππ≠+∈【题型十三】解正弦函数不等式求定义域【典例分析】（2022·北京八中高一期中）函数()2()lg 14sin f x x =-的定义域为________.【答案】,,66k k k Zππππ⎛⎫-++∈ ⎪⎝⎭【分析】根据对数的真数大于0，解不等式即可得出答案.【详解】由题意得：214sin 0x ->，所以sin 1122x <-<，所以,66k x k k Z ππππ-+<<+∈，函数()f x 的定义域为：,,66k k k Zππππ⎛⎫-++∈ ⎪⎝⎭1.（2023·全国·高一专题练习）函数y =___________.【答案】5(2,2Z)66k k k ππππ++∈【分析】根据给定条件，列出不等式，解正弦不等式即可作答.【详解】依题意，1sin 02x ->，即1sin 2x >，解得522,Z 66k x k k ππππ+<<+∈，所以所求定义域为5(2,2Z)66k k k ππππ++∈.故答案为：5(2,2Z)66k k k ππππ++∈2.（2023·全国·高一专题练习）函数()f x =________________．【答案】(][]4,0,ππ-- 【分析】根据f(x )解析式列出不等式组，解不等式组即可得到定义域﹒【详解】()f x = 2sin 0160x x ⎧∴⎨->⎩ ，解得22,44k x k k Zx πππ+∈⎧⎨-<<⎩ ，对于22,k x k k Z πππ+∈ ，当0k =时，0x π ，当1k =时，23x ππ ，当1k =-时，2x ππ-- ，当2k =-时，43x ππ-- ，∴不等式组的解为：4x π-<- 或0.x π ()f x ∴的定义域为][(4,0,.ππ⎤--⋃⎦故答案为：][(4,0,.ππ⎤--⋃⎦3..（2023·全国·高一专题练习）函数()f x =的定义域为__________.【答案】5{|22,}44x k x k k Z ππππ-≤≤+∈【分析】由二次根式中被开方数非负，结合正弦函数性质可得．【详解】由题意10x ≥，sin 2x ≤，所以52244k x k ππππ-≤≤+，k Z ∈．故答案为：5{|22,}44x k x k k Z ππππ-≤≤+∈．【题型十四】解余弦函数不等式求定义域【典例分析】（2022·陕西省安康中学高一期末）函数1()ln cos 2f x x ⎛⎫=- ⎪⎝⎭的定义域为_______________．【答案】ππ2π,2π,33⎛⎫-+∈ ⎪⎝⎭k k k Z【分析】由题可知，解不等式1cos 2x >即可得出原函数的定义域.【详解】对于函数1()ln cos 2f x x ⎛⎫=- ⎪⎝⎭，有1cos 02x ->，即1cos 2x >，解得()ππ2π2π33-<<+∈k x k k Z ，因此，函数1()ln cos 2f x x ⎛⎫=- ⎪⎝⎭的定义域为ππ2π2π,33x k x k k ⎧⎫-<<+∈⎨⎬⎩⎭Z .故答案为：ππ2π,2π,33⎛⎫-+∈ ⎪⎝⎭k k k Z .【提分秘籍】基本规律余弦函数定义域是全体实数，本身没有限制。

高一数学上学期周练(五)

２0１７—２018学年上期高一数学周练(五)一。

选择题:１、下列四个集合中,空集是( )A、B、{0｝Ｃ、或 D、2、给定映射f:在映射f下,(3,1)的原像为( )A。

(1,3) B。

(5,5) C、(3,1) D。

(１,1)3、下列对应是从集合S到T的映射的是( )A、S=｛0,1,４,9},Ｔ＝｛-3,-2,－１,0,１,2,3｝,对应法则是开平方Ｂ、S=Ｎ,T={—１,1},对应法则是,C、Ｓ＝{0,1,2,５｝,,对应法则是取倒数Ｄ、,对应法则是４、与函数y=x+1相同的函数是( )(A) (B)y=t+１(Ｃ) (D)５、定义在R上的函数ｆ(ｘ)满足:对任意的,有,则( )A。

f(3)＜f(2)〈f(4) Ｂ、 f(１)〈f(２)〈ｆ(3) C、 f(-2)<ｆ(1)＜ｆ(3) Ｄ、f(3)〈f(1)＜f(0)1０、假如函数在区间上单调递减,那么实数ａ的取值范围是 ( )A。

B。

Ｃ。

Ｄ。

7、下列函数中,在区间(０,1)上是增函数的是( )A、Ｂ、ｙ=3-x C。

D、8、关于不等式的解集为,,则a＝( )A、 B、 C、 D、9、已知函数f(ｘ)的定义域是,且满足f(xy)＝=f(x)+f(y), ｆ=1,假如关于0＜x<ｙ,都有f(x)＞f(y),不等式的解集为( )A、ﻩB、C。

Ｄ、［—1,4］１０、已知在R上恒满足ｆ(x)＜0,则实数a的取值范围是( )A、－4<ａ<0 B。

C。

D、１1、关于x的不等式(mx—1)(x－2)<０的解为,则m的取值范围是( )(A)m〈 (Ｂ)m〉0 (C)0＜m〈 <m＜212、已知函数,若f(x)在R上是增函数,则实数a的取值范围是( )A。

B、 C、 D、［1,２］二。

填空题:１３、已知:A=｛(x,ｙ)｜x+y=0},B＝{(x,y)｜ｘ-y=2},则A∩B＝、1４、函数y＝f(ｘ)的图象如图所示,则函数f(x)的单调递增区间是______＿_、15、若ｆ(x)＝与g(x)＝在区间(1,2)上都是增函数,则a的取值范围是____＿__＿、1６、函数在区间［0,m]上的最大值为2,最小值为1,则m的取值范围是、三、解答题:17。

2020-2021学年高一数学上学期周练试题(五)

2020-2021学年高一数学上学期周练试题（五）一、选择题．请把答案直接填涂在答题卡相应位置上．1．“”是“”的（）A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件2．设，，则等于（）A. B. C. D.3．已知，则的大小关系为（）A． B． C． D．4．已知，（且），则的取值范围为（）A. B. C. D.5．函数的图象大致是（）A． B． C． D．6．已知函数，则不等式解集为（）A. B. C. D.7.若函数在区间上为减函数，则实数的取值范围为（）A． B． C． D．8．设，若有三个不同的实数根，则实数的取值范围是（）A． B． C． D．二、多选题：（每小题给出的四个选项中，不止一项是符合题目要求的，请把正确的所有选项填涂在答题卡相应的位置上）9．设，下列判断正确的是（）A． B． C． D．10．下列个函数中是奇函数的有（）A． B． C． D．11．若，则下列结论正确的有（）A．若，则B．C．若，则D．若，则12．对于函数，下列说法正确的有（）A．是偶函数B．是奇函数C．在区间上是减函数，在区间上是增函数D．没有最小值二、填空题．请把答案直接填写在答题卡相应位置上．13．函数且恒过定点．14.若函数为奇函数，则= ____________．15．已知，则函数的最大值为__ ____．16．已知的值域为R，那么a的取值范围是．三、解答题．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．17．计算：（1）；（2）；（3）求函数y＝log（x+1）（16﹣4x）的定义域．18．已知函数，设．（1）判断函数的奇偶性，并说明理由．（2）求函数的单调区间．（3）求函数的值域（不需说明理由）19.已知函数．（1）若，求不等式的解集；（2）若为偶函数，求的值．20．某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数与听课时间之间的关系满足如图所示的曲线。

高一数学上册期末复习训练试题

高一数学上册期末复习训练试题数学（五）编校：李茂生1、设集合}7,5,3,1{},5,4,2,1{},80|{==≤≤∈=T S x N x U ，则()U SC T ={}4,2 ．2、直线y x b =+平分圆228280x y x y +-++=的周长，则b =（ -5 ）3、已知圆的半径为2，圆心在x 轴的正半轴上，且圆与直线3x + 4y +4 = 0相切，则圆的标准方程是____22(2)4x y -+=___________________ 4．函数x x f 2log 1)(-=的定义域是 ]2,0( .5、已知3121311.1,9.0,9.0===c b a ，则c b a ,,按从小到大顺序排列为 c a b << 6、已知幂函数的图象过点)2,2(，则它的单调增区间为 [)+∞,0 ； 7、幂函数()αx x f =的图象经过点⎪⎭⎫⎝⎛--81,21，则满足()27=x f 的x 的值是 3 8、已知直角三角形的两直角边长分别为3cm 和4cm ，则以斜边为轴旋转一周所得几何体的表面积为 845π。

9、若函数()()log 1a f x x =+()0,1a a >≠的定义域和值域都为[]0,1，则a = 2 。

10. 已知偶函数在区间上单调递增，则满足的x 取值范围是 .11．函数)13lg(13)(2++-=x xx x f 的定义域是（—13，1）．12．函数f (x )＝|log a x |(0<a <1)的单调减区间是（0，1）．13、（16分）已知()f x 为R 上的偶函数，当0x ≥时，()2x f x e =（1）当0x <时，求()f x 的解析式；（2）当0m >时，比较(1)f m -与(3)f m -的大小；（3）求最小的整数(1)m m >，使得存在实数t ，对任意的[1,]x m ∈，都有()2f x t ex +≤。

高一上册数学试卷模拟题

高一上册数学试卷模拟题一、选择题（每题5分，共10题）1. 设集合A = {xx^2 - 3x + 2 = 0}，B={1, 2}，则A与B的关系是（）- A. A⊂neqq B- B. A = B- C. A⊃neqq B- D. A∈ B解析：解方程x^2 - 3x + 2 = 0，即(x - 1)(x - 2)=0，解得x = 1或x = 2。

所以A={1, 2}，因为A和B元素完全相同，所以A = B，答案为B。

2. 函数y=√(x - 1)的定义域为（）- A. (-∞,1]- B. (1,+∞)- C. [1,+∞)- D. (-∞,1)解析：要使根式有意义，则根号下的数非负，即x - 1≥0，解得x≥1，所以定义域为[1,+∞)，答案为C。

3. 已知函数f(x)=2x + 3，则f( - 1)的值为（）- A. 1.- B. -1.- C. 5.- D. -5.解析：将x=-1代入f(x)=2x + 3，得f(-1)=2×(-1)+3 = 1，答案为A。

4. 下列函数中，在(0,+∞)上为增函数的是（）- A. y=-x + 1- B. y=(1)/(x)- C. y = x^2- D. y=-x^2解析：- 对于y=-x + 1，一次项系数-1<0，在R上为减函数，在(0,+∞)上也是减函数。

- 对于y=(1)/(x)，在(0,+∞)上，y随x增大而减小，是减函数。

- 对于y = x^2，其图象开口向上，对称轴为y轴，在(0,+∞)上为增函数。

- 对于y=-x^2，图象开口向下，在(0,+∞)上为减函数。

所以答案为C。

5. 若log_a2，则a的取值范围是（）- A. (0,1)- B. (1,+∞)- C. (0,+∞)- D. (-∞,0)解析：因为对数函数y = log_ax，当a>1时，函数单调递增；当0 < a < 1时，函数单调递减。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

立体几何专题训练
一、选择题
1.（2009年广东卷文）给定下列四个命题：
①若一个平而内的两条直线与另一个平面都平行，那么这两个平面相
互平行；
②若一个平而经过另一个平面的垂线，那么这两个平面相互垂直；
③垂直于同一直线的两条直线相互平行；
④若两个平而垂直，那么一个平而内与它们的交线不垂直的直线与另
一个平而也不垂直.
其中，为真命题的是
A.①和②
B.②和③
C.③和④
D.②和④
2. （2009广东卷理）给定下列四个命题，
①若一个平面內的两条直线与另一个平面都平行，那么这两个平面相互平行；
②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；
③垂直于同一直线的两条直线相互平行；
④若两个平酝垂直，那么一个平面內与它们的交线丕垂直的直线与另一个平酝也不垂直.
其中，为真命题的是
A.①和②
B.②和③
C.③和④
D.②和⑷
3.（2009浙江卷理）在三棱柱ABC-A^C,中，各棱长相等，侧援垂直于底而，点D是侧面BB”的中心，则AD与平而BBQC所成角的大小是（）A・ 30 B. 45’ C. 60 D. 90
4.（2009浙江卷文）设是两个不同的平面，/是一条直线，以下命题正确的是（）
A.若/丄丄0,贝Ij/u0
B.若〃/a,a//0,则/u0
C. 若 /丄 a.a//0,贝 I” 丄0
D.若
l//a.a 丄0,贝 lj/丄 0
5.（2009北京卷文）若正四棱柱ABCD-A^C ｝D ｝的底面边长为1, AB ｛与底而
ABCD 成60°角,则AC 到底面ABCD 的距离为
A.逅
B. 1 3 D. 也
14. （2009江西卷文）如图，在四而体43CD 中,
截而PQMN 是正方形，则在下列命题中，错误的为
A. AC 丄 BD
B. AC// 截而 PQMN
C. AC = BD D ・异而直线PM 与3D 所成的角为45 18. （2009全国卷I
［理）己知正四棱柱ABCD-qQCQ 中，M = 2AB, E
为中点，则异面直线BE 与cq 所成的角的余弦值为
C. >/2
D.
20.（2009宁夏海南卷理）如图，正方体A3CD-MCQ 的棱线长为1,
线段上有两个动点E, F,
下列结论中错误的是
（A ） AC 丄8E
（B ） EF//平面ABCD
（C ）三棱锥A-BEF 的体积为定值
（D ）异而直线AE3F 所成的角为定值 10 5 10 则
5. （2009江苏卷）设&和
为不重合的两个平面，给出下列命题:
（1）若Q 内的两条相交直线分别平行于0内的两条直线，则&平行于
0；
（2）若。

外一条直线/与o 内的一条直线平行，贝I"和a 平行；
（3）设◎和0相交于直线/,若&内有一条直线垂直于/,则&和0垂直；
（4）直线/与&垂直的充分必要条件是/与&内的两条直线垂直。

上面命题中，真命题的序号（写出所有真命题的序号）. 二、填空题
1. （2009浙江卷理）若某几何体的三视图
（单位：期）如图所示，
则此几何体的体积是 __________ .
2. （2009浙江卷理）如图，在长方形A3CD
中，43 = 2, BC = 1, E 为DC 的中点，F 为线
段EC （端点除外）上一动点.现将A4FD 沿
AF 折起，使平而4BQ 丄平而A3C.在平而
ABD 内过点D 作QK 丄AB, K 为垂足.
设AK = t,贝办的取值范围是 ____________
2009年高考数学试题分类汇编立体几何（2）正视图
（第门
题）
8. （2009安徽卷文）在空间直角坐标系中，已知点A （1, 0, 2）, 轴
上，且、I 到A 与到B 的距离相等，则M 的坐标是 _________ 。

11.（ 2009四川卷文）如图，己知正三棱柱 ABC-
A^C,的各条棱长都相等，M 是侧棱Cq 的中点，则异
而直线和BM 所成的角的大小是 O
三、解答题
4. （2009浙江卷文）（木题满分14分）如图，DC 丄平面ABC, EB//DC , AC = BC = EB = 2DC = 2, ZACB = 120J , 分别为 AE,AB 的中点.(I)
5. （2009北京卷文）（本小题共14分）如
图，四棱锥P-ABCD 的底而是正方形, PD 丄底
jfUBCD ，点E 在棱PB 上.
（I ）求证：平面AEC 丄平面PDB ；
（II ）当PD = dB 且E 为PB 的中点时, 求AE
与
平而PDB 所成的角的大小.
B(l, -3, 1),点 M 在 y
证明:
W3
8. （2009全国卷II 文）（本小题满分12分）
如图，直三棱柱ABC-A]B]Ci 中，AB 丄AC,D 、E 分别为AAi 、B|C 的中点，DE 丄平而BCCi
（I ）证明：AB=AC
（II ）设二而角A-BD-C 为60。

,求B]C 与平面BCD 所成的角的
大小
22. （2009湖南卷文）（本小题满分12分）
如图3,在正三棱柱ABC-A^C,中，点D 是的中点，点E 在AC 上，且DE 丄A]E.
（I ）证明：平而AQE 丄平面ACCR ；
（II ）求直线AD 和平而AQE 所成角的正
弦值。

C.
A
27. （2009陕西卷文）（本小题满分12分）
如图，直三棱柱ABC-A/C 中，AB二1, AC = A\ =^3 , ZABC=60°.
（I）证明：AB ± A{C；
（II ）求二面角A一A]C—B的大小。

D。