邱关源电路4版全习题详细讲解1~6章
(完整版)邱关源电路教材重点分析兼复习纲要-武汉大学电路

第一章电路模型和电路定律,第二章电阻电路的等效变换,第三章电阻电路的一般分析,第四章电路定理。
这四章是电路理论的基础,全部都考,都要认真看,打好电路基础。
第一章1-2电流和电压的参考方向要注意哈,个人认为搞清楚方向是解电路最重要的一步了,老师出题,喜欢把教材上常规的一些方向标号给标反,这样子,很多式子就得自己重推,这也是考验你学习能力的方式,不是死学,比如变压器那章,方向如果标反,式子是怎样,需要自己推导一遍。
第二章都要认真看。
第三章3-1 电路的图。
图论是一门很重要的学科,电路的图要好好理解,因为写电路的矩阵方程是考试重点,也是送分题,而矩阵方程是以电路图论为基础的。
第四章4-7对偶原理。
自己看一下,懂得什么意思就行了。
其他小节都是重点,特别是特勒跟和互易。
这几年真题第一题都考这个知识点。
第五章含有运算放大器的电阻电路。
这个知识点是武大电路考试内容,一定要懂,虚短和虚断在题目中是怎么用的,多做几个这章的题就很清楚了。
5-2 比例电路的分析。
这一节真题其实不怎么常见,跟第三节应该是一个内容,还是好好看一下吧。
第六章储能元件。
亲,这是电路基础知识,老老实实认真看吧。
清楚C和L的能量计算哦。
第七章一阶电路和二阶电路的时域分析。
一阶电路的都是重点,二阶电路的时域分析,其实不怎么重要,建议前期看一下,从来没有出现过真性二阶电路让考生用时域法解的,当然不是不可以解,只是解微分方程有点坑爹,而且基本上大家都是要背下来那么多种情况的解。
所以,这章的课后习题中,二阶的题用时域解的就不用做了,一般后面考试都是用运算法解。
7-1 7-2 7-3 7-4 都是重点,每年都考。
好好看。
7-5,7-6,两节,看一下即可,其实也不难懂,只是很难记。
7-7,7-8很重要,主要就是涉及到阶跃和冲激两个函数的定义和应用,是重点。
7-9,卷积积分,这个方法很有用,也不难懂,不过我没看过也不会用也不会做,每次遇到题目都是死算,建议好好研究下卷积。
电路分析基础(第四版)课后答案第1章ppt课件

1.8 求图示各电路中的电压U。 题解1.8图
解 图(a):U=1×3-2=1 V 图(b): 在图示电路中设电压U1的参考方向, 如题解1.8
图(b)所示。 应用电阻串并联等效及分压关系式, 得电压
(24)//3 U1(24)//3196V
所以
U2 44U13 264V
图(c): 在图示电路中设电流I1、 I2的参考方向, 如题解 1.8图(c)所示。 由电阻串联等效及欧姆定律, 得电流
1.11 图示直流电路, 图中电压表、 电流表均是理想的, 并已知电压表读数为30 V。
(1) (2) 电压源Us产生的功率Ps为多少?
题解1.11图
解 用短路线将图示电路中两处接地点连在一起,并设 a、 b点, 电流I、 I1、 I2参考方向, 如题解 1.11图所示。 由图可见, 电流表所在支路的10 kΩ电阻同与电压表相并的 30 kΩ电阻是串联关系。 因电压表读数是30 V, 所以
图(b): 在图示电路中设节点a及电流I1、I2、I3、I4的参 考方向,如题解1.10图(b)所示。 应用电阻串并联等效, 得
电流
I1[4//44]5/1/6//6153A
由3个相等电阻并联分流, 得
I2I313I11331A
再由2个电阻并联分流, 得电流
I44 44I31 210.5A
对节点a应用KCL, I=I2+I4=1+0.5=1.5 A
图(c)电路中, 设电流I1、 I2、 I3如题解1.7图(c)所示。 应用电阻串并联等效, 得电流
I13//61 22 1//613A 再应用电阻并联分流公式, 得
I23 66I13 232A
61 I3126I1331A
对节点a应用KCL, I=I2-I3=2-1=1 A
电路分析基础第四版课后习题答案
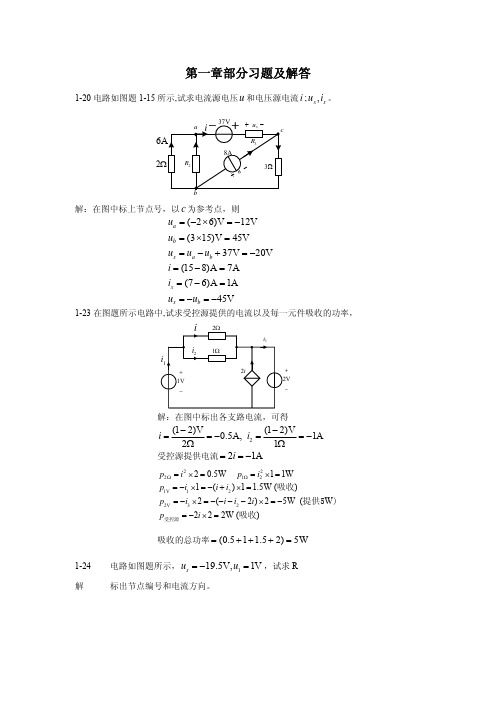
i
i1
+ 1V −
2Ω
i3
i2
1Ω
2i
+ 2V −
解:在图中标出各支路电流,可得
(1 − 2)V (1 − 2)V = −0.5A, i2 = = −1A 2Ω 1Ω 受控源提供电流 = 2i = −1A i=
p2 Ω = i 2 × 2 = 0.5W
为确定 R,需计算 i4 ,
uce = ucd + ude = 0 ⇒ ude = −ucd = −10u1 = −10V
故
i3 =
udc = −2.5A, i4 = is − i3 = (−3.5 + 2.5)A = −1A 4 R = 0Ω 由此判定
1-33
试用支路电流法求解图题所示电路中的支路电流 i1 , i2 , i3 。
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
⎧25i1 − 20i2 − 5i3 = 50 ⎪ 代入并整理得: ⎨−5i1 + 9i2 − 4i3 = 0 解得 ⎪−5i − 4i + 10i = 0 2 3 ⎩ 1
受控源电压 受控源功率
⎧i1 = 29.6A ⎨ ⎩i2 = 28A
i2
3Ω
i3
gu
2−5
解
设网孔电流为 i1 , i2 , i3 ,则 i3 = − gu A = −0.1u A ,所以只要列出两个网孔方程
27i1 − 18i2 = 42 −18i1 + 21i2 − 3(−0.1u A ) = 20
因 u A = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
邱关源《电路》笔记及课后习题(电路定理)【圣才出品】

第4章电路定理4.1 复习笔记一、叠加定理叠加定理:在线性电路中,任一支路的电流或电压,等于每一独立电源单独作用于电路时在该支路所产生的电流或电压的代数和。
应用方法:给出电路中变量的参考方向;画出各独立源单独作用时的等效电路;在等效电路中求出相应的待求电压电流变量或中间变量;运用叠加定理求出原电路中的待求电压电流变量。
注:①该定理只适用于线性电路;②计算元件的功率时不可应用叠加的方法;③在各个独立电源单独作用时,不作用的电压源短路,不作用的电流源开路;各分电路在叠加计算时电压和电流的参考方向可取为与原电路相同方向,取代数和时注意各分量的正负号。
二、替代定理给定任意一个线性电阻电路,如果第j条支路的电压u j和电流i j已知,那么这条支路就可以用一个具有电压等于u j的独立电压源,或者一个具有电流等于i j的独立电流源来代替,替代后的电路中的全部电压和电流均将保持原值,如图4-1-1所示。
图4-1-1三、戴维宁定理和诺顿定理1.一个线性含源一端口网络如图4-1-2(a)所示,对外电路来说,可以用一个电压源和电阻的串联组合来等效替代,这一等效电路称为戴维宁等效电路,如图4-1-2(b)所示。
电压源的电压等于该一端口网络的开路电压u oc,而电阻等于该一端口网络中所有独立源为零值时的等效电阻R eq。
图4-1-22.一个线性含源一端口网络N,可以等效为一个电流源和电阻的并联组合,这样的等效电路称为诺顿等效电路,如图4-1-2(c)所示。
电流源的电流等于该网络N的短路电流i sc,并联电阻R eq等于该网络中所有独立源为零值时所得网络N0的等效电阻R eq。
3.应用戴维宁定理和诺顿定理求解电路,一般按以下步骤进行:(1)求解含源端口的开路电压u oc或短路电流i sc。
(2)求解端口的输入电阻R eq,有如下两种方法:①利用开路电压与短路电流之比R eq=U oc/i sc;②将含源一端口网络中所有独立源置零,求解其对应的R eq。
电路课件 第一章(第四版 邱关源 高等教育出版社)

U
A
UAB
B
3. 关联参考方向
元件或支路的u,i 采用相同的参考方向称之为关联参考 方向。反之,称为非关联参考方向。
i + U
关联参考方向
i +
U
非关联参考方向
例
i
+
A U B
电压电流参考方向如图中所标,问:对A 、B两部分电路电压电流参考方向关联否?
答: A 电压、电流参考方向非关联;
B 电压、电流参考方向关联。
解得电流
t0 0 t 1s 1 t 2s t 2s t0 0 t 1s 1 t 2s t 2s
0 1
电源波形
i/A
1
2 t /s
-1
1
2 t /s
p( t ) u( t )i ( t ) 0 2t 2t 4 0 t0 0 t 1s 1 t 2s t 2s
0 -2
2
p/W
吸收功率
例
3. 集总参数电路
由集总元件构成的电路 集总元件 集总条件 假定发生的电磁过程都集中在元件内部进行
d
1.2 电流和电压的参考方向
(reference direction)
电路中的主要物理量有电压、电流、电荷、磁链、能 量、电功率等。在线性电路分析中人们主要关心的物理量 是电流、电压和功率。
t 若u ( ) 0
t
1 2 1 2 Cu ( t ) q (t ) 0 2 2C
从t0到 t 电容储能的变化量:
1 1 1 2 1 2 2 2 WC Cu ( t ) Cu ( t 0 ) q (t ) q (t 0 ) 2 2 2C 2C
邱关源《电路》笔记和课后习题(含考研真题)详解-第一章至第二章【圣才出品】

圣才电子书 十万种考研考证电子书、题库视频学习平台
理想电压源的符号如图 1-1-4(a)所示。其特点是其两端电压总能保持一定或一定的 时间函数,且电压值大小由电压源本身决定,与流过它的电流值无关,如图 1-1-4(b)所 示。
图 1-1-4(a)
图 1-1-4(b) 说明:a.电压源为一种理想模型;b.与电压源并联的元件,其端电压为电压源的值; c.理想电压源的功率从理论上来说可以为无穷大。 ②理想电流源 理想电流源的符号如图 1-1-5(a)所示。其特点是输出电流总能保持一定或一定的时 间函数,且电流值大小由电流源本身决定,与外部电路及它的两端电压值无关,如图 1-1-5
电阻元件、电源元件和受控电源元件是常用的电路元件。电路元件可分为无源元件及有 源元件两大类。
1.无源元件及其伏安特性 表 1-1-2 无源元件及其伏安特性
功率和能量比较: (1)电阻元件 P=ui=Ri2=u2/R≥0(关联参考方向);
W t Ri2 d t0 电阻是耗能元件。 (2)电容元件
5 / 81
圣才电子书 十万种考研考证电子书Fra bibliotek题库视频学习平台
P=ui=Cu(du/dt)(u,i 取关联参考方向);吸收功率,电容是无源元件。
WC C
ut2 udu 1 Cu 2
ut1
2
t2
1 Cu 2 2
t1
WC t2 WC t1
电容是储能元件。
2 / 81
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 1-1-2 电压的参考方向 3.关联参考方向 对于一个元件或支路来说:如果指定元件的电流的参考方向是从电压参考极性的“+” 指向“-”,即两者的参考方向一致,则把电流和电压的这种参考方向称为关联参考方向; 反之称为非关联参考方向。如图 1-1-3 所示,对 A 而言,u 和 i 为非关联方向;对 B 而言, u 和 i 为关联方向。
电路分析基础第四版课后习题第一章第二章第三章第四章答案
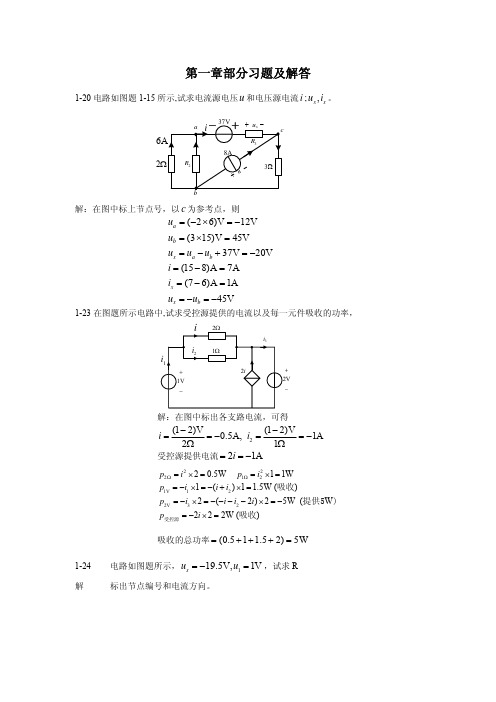
+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ,列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示,试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向,
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
电路复习总结(一到八章)邱关源

5种基本的理想电路元件:电阻元件:表示消耗电能的元件。
电感元件:表示产生磁场,储存磁场能量的元件。
电容元件:表示产生电场,储存电场能量的元件。
电压源和电流源:表示将其他形式的能量转变成电能的元件。
规定正电荷的 运动方向为电流的实际方向对于复杂电路或电路中的电流随时间变化时,电流的实际方向往往很难事先判断。
任意假定一个正电荷运动的方向即为电流的参考方向。
u, i 取关联参考方向p=ui 表示元件吸收的功率p>0 吸收正功率 (实际吸收) u, i 取非关联参考方向p = ui 表示元件发出的功率p>0 发出正功率 (实际发出)电压源的功率电压、电流参考方向非关联电流(正电荷 )由低电位向高电位移动,外力克服电场力作功,电源发出功率。
S 0 p u i =>发出功率,起电源作用基尔霍夫电流定律 (KCL)在集总参数电路中,任意时刻,对任意结点流出(或流入)该结点电流的代数和等于零。
基尔霍夫电压定律 (KVL)在集总参数电路中,任一时刻,沿任一回路,所有支路电压的代数和恒等于零。
等效电路:1.电阻串联iR i R R i R i R i R u n n k eq 11)(=++=++++=knk k n k R R R R R R >=++++=∑=11eq2.电阻并联i = i1+ i2+ …+ ik+ …+in=u/R1 +u/R2 + …+u/Rn =u(1/R1+1/R2+…+1/Rn)=uGeqk nR R R R R G R <+++==eq 21eq eq 1111即Y →△的变换条件为213133113232233212112R R R R R R R R R R R R R R R R R R ++=++=++=△→Y 的变换条件为312312233133123121223231231231121R R R R R R R R R R R R R R R R R R ++=++=++=1.理想电压源的串联和并联串联nS1S2Sn S 1k k u u u u u ==+++=∑并联2S 1S u u u ==2. 理想电流源的串联和并联 并联∑=+⋅⋅⋅++=kn i i i i i S S S21S串联2S 1S i i i ==实际电源的两种模型及其等效变换1. 实际电压源iR u u S S -=2. 实际电流源S S R ui i -=实际电压源、实际电流源两种模型可以进行等效变换,所谓的等效是指端口的电压、电流关系在转换过程中保持不变。
