高考理科数学常用公式大全
高中数学必备必考公式大全

高考数学必备必考公式大全一、集合1.并集的运算A∪B={x|x∈A,或x∈B}2. 并集的运算性质(1) A∪A=A(2)A∪∅=A(3)A∪B=B∪A(4) A∪B=A⇔B⊆A3. 交集的运算A∩B={x|x∈A,且x∈B}4. 交集的运算性质(1)A∩A=A(2)A∩∅=∅(3)A∩B=B∩A(4)A∩B=A⇔A⊆B5. 补集的运算∁U A={x|x∈U,且x∉A}6. 补集的运算性质(1) ∁U (∁U A)=A(2) ∁U U=∅,∁U∅=U(3)A∪(∁U A)=U,A∩(∁U A)=∅(4) ∁U (A∩B)=( ∁U A)∪(∁U B), ∁U (A∪B)=( ∁U A)∩(∁U B)二、函数与导数公式1. 有理数指数幂的运算性质(1)a r a s=a r+s(a>0,r,s∈Q)(2)=a r-s(a>0,r,s∈Q)(3)(a r)s=a rs(a>0,r,s∈Q)(4)(ab)r=a r b r(a>0,b>0,r∈Q)2.对数运算公式(1)对数的运算性质如果a>0,且a≠1,M>0,N>0,那么:log a(M·N)=log a M+log a N;log a=log a M-log a N;log a M n=n log a M(n∈R)(2)对数恒等式a log aN =N(a>0,且a≠1,N>0)(3)对数运算的换底公式log a b=(a>0,且a≠1;c>0,且c≠1;b>0)(4)换底公式的变形log a b·log b a=1,即log a b=lo b n=log a blog N M==(5)换底公式的推广log a b·log b c·log c d=log a d3.求导公式及运算法则(1)基本初等函数的导数公式a.若f(x)=c(c为常数),则f'(x)=0.b.若f(x)=x n(n∈Q*),则f'(x)=nx n-1.c.若f(x)=sin x,则f'(x)=cos x.d.若f(x)=cos x,则f'(x)=-sin x.e.若f(x)=a x,则f'(x)=a x ln a.f.若f(x)=e x,则f'(x)=e x.g.若f(x)=log a x,则f'(x)=.h.若f(x)=ln x,则f'(x)=.(2)导数运算法则a.[f(x)±g(x)]'=f'(x)±g'(x)b.[f(x)·g(x)]'=f'(x)g(x)+f(x)g'(x)c.[]'=(g(x)≠0)(3)复合函数的导数(理)设y=f(u),u=φ(x),则y'x=y'u u'x或记作f '[φ(x)]=f '(u)φ'(x).特别地,[f (ax +b )] '=a f' (ax+b).4.定积分的运算性质(理)(1)b a ⎰kf (x )d x=k b a ⎰f (x )d x (k 为常数)(2) b a ⎰[f (x )±g (x )]d x=b a ⎰f (x )d x±b a ⎰g (x )d x (3)b a ⎰f (x )d x=-a b ⎰f (x )d x(4)c a ⎰f (x )d x=b a ⎰f (x )d x+cb ⎰f (x )d x (a<b<c )三、三角函数1. 同角关系:(1)平方关系:sin 2α+cos 2α=1.(2)商的关系:=tan α(α≠+k π,k ∈Z ). 2. 诱导公式:奇变偶不变,符号看象限。
高考数学必考必背公式全集

一、对数运算公式。
log log m n a a n b b m =log log log a a a M M N N-=1. log 10a = 2. log 1a a = 3. log log log a a a M N MN += 4. 5.log log n a a M n M =6. 7. log a M a M =8. 9. 10. 二、 三角函数运算公式。
1. 同角关系:2. 诱导公式:奇变偶不变,符号看象限。
3. 两角和差公式:sin()sin cos sin cos αβαβαα±=± cos()cos cos sin sin αβαβαβ±=二倍角公式:sin 22sin cos ααα= 2222cos 2cos sin 2cos 112sin ααααα=-=-=-4. 辅助角公式:)sin(cos sin 22ϕθθθ++=+b a b a ,其中,2||,tan ,0πϕϕ<=>a b a 5. 降幂公式(二倍角余弦变形):6.角函数定义:角α中边上任意一点P 为),(y x ,设r OP =||则:,cos ,sin rxr y ==ααx y=αtan 三、 三角函数图像与性质。
四、 解三角形公式。
1. 正弦定理2. 余弦定理3. 三角形面积公式 A bc B ac C ab S sin 21sin 21sin 21===4..三角形的四个“心”; 重心:三角形三条中线交点.sin tan cos ααα=22sin cos 1αα+=21cos 2cos 2αα+=21cos 2sin 2αα-=log log log a b a N N b=1log log b a a b =1log log a a Mn=2222222222cos 2cos 2cos a b c bc Ab ac ac B c a b ab C=+-=+-=+-22tan tan 21tan ααα=-外心:三角形三边垂直平分线相交于一点. 内心:三角形三内角的平分线相交于一点.垂心:三角形三边上的高相交于一点.六、向量公式。
高中数学常用公式大全

高中数学常用公式大全一、集合。
1. 集合的基本运算。
- 交集:A∩ B = {xx∈ A且x∈ B}- 并集:A∪ B={xx∈ A或x∈ B}- 补集:∁_UA = {xx∈ U且x∉ A}(U为全集)2. 集合元素个数关系。
- n(A∪ B)=n(A)+n(B)-n(A∩ B)(n(A)表示集合A的元素个数)二、函数。
1. 函数的定义域。
- 分式函数y = (f(x))/(g(x)),g(x)≠0。
- 偶次根式函数y=sqrt[n]{f(x)}(n为偶数),f(x)≥slant0。
2. 函数的单调性。
- 设x_1,x_2∈[a,b],x_1 < x_2- 对于函数y = f(x),若f(x_1),则y = f(x)在[a,b]上单调递增;若f(x_1)>f(x_2),则y = f(x)在[a,b]上单调递减。
3. 函数的奇偶性。
- 对于函数y = f(x),定义域关于原点对称。
- 若f(-x)=f(x),则y = f(x)是偶函数;若f(-x)= - f(x),则y = f(x)是奇函数。
4. 一次函数y=kx + b(k≠0)- 斜率k=(y_2 - y_1)/(x_2 - x_1)。
5. 二次函数y = ax^2+bx + c(a≠0)- 对称轴x =-(b)/(2a),顶点坐标(-(b)/(2a),frac{4ac - b^2}{4a})。
- 当a>0时,函数开口向上,在x =-(b)/(2a)处取得最小值frac{4ac -b^2}{4a};当a < 0时,函数开口向下,在x=-(b)/(2a)处取得最大值frac{4ac -b^2}{4a}。
6. 指数函数y = a^x(a>0,a≠1)- 性质:当a > 1时,函数在R上单调递增;当0 < a < 1时,函数在R上单调递减。
7. 对数函数y=log_ax(a>0,a≠1)- 性质:当a > 1时,函数在(0,+∞)上单调递增;当0 < a < 1时,函数在(0,+∞)上单调递减。
高三数学公式归纳大全

数学考试主要考察大家的公式运用情况,所以要想数学考出好成绩,一定要牢牢记住数学公式。
今天老师就给大家总结了整个高中都会用到的数学公式,一共有五十条,大家一定要熟背哦~1 . 适用条件[直线过焦点],必有ecosA=(x-1)/(x+1),其中A为直线与焦点所在轴夹角,是锐角。
x为分离比,必须大于1。
注:上述公式适合一切圆锥曲线。
如果焦点内分(指的是焦点在所截线段上),用该公式;如果外分(焦点在所截线段延长线上),右边为(x+1)/(x-1),其他不变。
2 . 函数的周期性问题(记忆三个)(1)若f(x)=-f(x+k),则T=2k;(2)若f(x)=m/(x+k)(m不为0),则T=2k;(3)若f(x)=f(x+k)+f(x-k),则T=6k。
注意点:a.周期函数,周期必无限b.周期函数未必存在最小周期,如:常数函数。
c.周期函数加周期函数未必是周期函数,如:y=sinxy=sin派x相加不是周期函数。
3 . 关于对称问题(无数人搞不懂的问题)总结如下(1)若在R上(下同)满足:f(a+x)=f(b-x)恒成立,对称轴为x=(a+b)/2(2)函数y=f(a+x)与y=f(b-x)的图像关于x=(b-a)/2对称;(3)若f(a+x)+f(a-x)=2b,则f(x)图像关于(a,b)中心对称4 . 函数奇偶性(1)对于属于R上的奇函数有f(0)=0;(2)对于含参函数,奇函数没有偶次方项,偶函数没有奇次方项(3)奇偶性作用不大,一般用于选择填空5 . 数列爆强定律(1)等差数列中:S奇=na中,例如S13=13a7(13和7为下角标);(2)等差数列中:S(n)、S(2n)-S(n)、S(3n)-S(2n)成等差(3)等比数列中,上述2中各项在公比不为负一时成等比,在q=-1时,未必成立(4)等比数列爆强公式:S(n+m)=S(m)+q²mS(n)可以迅速求q6 . 数列的终极利器,特征根方程首先介绍公式:对于an+1=pan+q(n+1为下角标,n为下角标),a1已知,那么特征根x=q/(1-p),则数列通项公式为an=(a1-x)p²(n-1)+x,这是一阶特征根方程的运用。
高中理科数学公式大全完整版

高中理科数学公式大全完整版高中理科数学公式大全完整版一、数学公式1、圆的面积 S=πR²2、圆周长 C=2πR3、圆柱体 V=πR²h4、圆锥体 V=πR²h/35、圆周角 a=∠C×π6、勾股定理 c²=a²+b²7、正弦定理 a/sinA=b/sinB=c/sinC=2R8、余弦定理 b²=a²+c²-2accosB9、弧长公式 l=n/180×π×r²10、扇形面积 s=n/360×π×r²11、弓形面积 s=[(b-a)×h]/212、三角形面积 s=√[p(p-a)(p-b)(p-c)] 其中 p=(a+b+c)/213、重心定理三条中线的交点叫重心,重心分中线为2:1(顶点到重心)14、平行四边形性质:平行四边形对边相等;平行四边形对角相等;平行四边形对角线互相平分;平行四边形内角和外角和都为360度。
15、平行四边形判定:一组对边平行且相等的四边形为平行四边形;两组对边分别相等的四边形为平行四边形;对角线互相平分的四边形为平行四边形;两组对角分别相等的四边形为平行四边形。
16、菱形性质:菱形四边都相等;菱形对角线互相垂直;菱形内角和都为360度;菱形是轴对称图形,有四条对称轴。
17、菱形判定:一组邻边相等的平行四边形是菱形;对角线互相垂直的平行四边形是菱形;四条边都相等的四边形是菱形;两条对角线分别平分各自对角的四边形为菱形。
18、正方形性质:正方形的四边都相等;正方形的四个角都是直角;正方形的对角线相等并互相垂直平分;正方形的邻边互相垂直;正方形的内角和外角和都为360度。
19、正方形判定:邻边相等的矩形是正方形;有一个角是直角的菱形是正方形;对角线互相垂直的矩形是正方形。
20、等腰梯形性质:等腰梯形两腰相等;等腰梯形两底角相等;等腰梯形的两条对角线相等。
高中数学总结——常用公式与推论

高中数学总结——公式与推论(理科)张皓翔成都二十中一.关于函数1. 抽象函数的周期(1)f(a±x)=f(b±x) T=|b-a|(2)f(a±x)=-f(b±x) T=2|b-a|(3)f(x-a)+f(x+a)=f(x) T=6a(4)f(x-a)=f(x+a) T=2a(5)f(x+a)=-f(x) T=2a2.奇偶函数概念的推广及其周期:(1)对于函数f(x),若存在常数a,使得f(a-x)=f(a+x),则称f(x)为广义(Ⅰ)型偶函数,且当有两个相异实数a,b同时满足时,f(x)为周期函数T=2|b-a|(2)若f(a-x)=-f(a+x),则f(x)是广义(Ⅰ)型奇函数,当有两个相异实数a,b同时满足时,f(x)为周期函数T=2|b-a|3.抽象函数的对称性(1)若f(x)满足f(a+x)+f(b-x)=c则函数关于(,)成中心对称(充要)(2)若f(x)满足f(a+x)=f(b-x)则函数关于直线x=成轴对称(充要)4.洛必达法则,设连续可导函数f(x)和g(x)5.常见奇函数(1). y=sinx y=tanx(2). y=x n(n∈2k+1 k∈Z)(3). y=lg(√1+x2−x)−x→y=lg√1+(ax2)±ax y=lg b−axb=ax(4). f(x)=a x−1(a>0 且 a≠1)a x+1(5). f(x)=|x+a|−|x−a|6.抽象函数模型(1).f(x+y)=f(x)+f(y) f(x)=kx(2).f(x+y)=f(x)f(y) f(x)=a x)=f(x) -f(y) f(x)=log a x(3).f(xy)=f(x)+f(y) f(xy二、三角函数1.三角形恒等式(1)在△中,(2)正切定理&余切定理:在非Rt△中,有tanA+tanB+tanC=tanAtanBtanC(3)(4)(5)2.任意三角形射影定理(又称第一余弦定理):在△ABC中a=bcosC+ccosB;b=ccosA+acosC;c=acosB+bcosA3. 任意三角形内切圆半径r=(S为面积),外接圆半径欧拉不等式:R>2r4.梅涅劳斯定理如下图,E.D.F三点共线的充要条件是5.塞瓦定理如下图,AD、BE、CF三线共点的充要条件是6. 斯特瓦尔特定理:如下图,设已知△ABC及其底边上B、C两点间的一点D,则有A²DC+AC²BD-AD²BC=BC DC BD7、和差化积公式(只记忆第一条)sinα+sinβ=2sin cossinα-sinβ=2cos sincosα+cosβ=2cos coscosα-cosβ=-2sin sin8、积化和差公式sinαsinβ=-cosαcosβ=sinαcosβ=cosαsinβ=9、万能公式10.三角混合不等式:若x∈(0,),sinx<x<tanx当x→0时sinx x tanx11.海伦公式变式如下图,图中的圆为大三角形的内切圆,大三角形三边长分别为a.b.c,大三角形面积为12.双曲函数定义双曲正弦函数sinhx=,双曲余弦函数coshx=易知(1)奇偶性:sinhx为奇函数,coshx为偶函数(2)导函数:(sinhx)’=coshx,(coshx)’=sinhx(3)两角和:sinh(x+y)=sinhxcoshy+coshxsinhycosh(x+y)=coshxcoshy+sinhxsinhy(4)复数域:sinh(ix)=isin(x)cosh(ix)=icos(x)(5)定义域:x∈R(6)值域:sinhx∈R,coshx∈[1,+∞)13.三角形三边a.b.c成等差数列,则14.三角形不等式(1)在锐角△中,(2)在△中,(3)在△中,sinA>sinB cos2A>cos2B15.ASA的面积公式:三、数列(所有通过递推关系得出通项后都要检验首项)1.A n+1=kA n+f(n)两边同除以k n+1,构造数列{},通过累加法得出通项公式2. A n+1=kA n+C设一常数x,A n+1+x=k(A n+x)A n+1 =kA n+(k-1)x则(k-1)x=C,求出x=,得到等比数列{},公比为k3.不动点法:形如A n+1=(d≠0,当d=0时,则是第二种情况),设函数f(x)=,x=的根称为f(x)的不动点,(1)若函数f(x)有2个不动点α,β则数列{}是一个等比数列,A’n==,A n=(2)若函数f(x)只有一个不动点α则数列{}数一个等差数列,A’n=(3)若函数f(x)没有不动点,则数列{A n}是周期数列,周期自己找4.特征方程法:形如A n+2=pA n+1+qA n称为二阶递推数列,我们可以用它的特征方程x²-px-q=0的根来求它的通项公式(1)若方程有两根x1,x2,则A n=x1n-1+x2n-1 (,可根据题目确定)(2)若只有一个根x0A n=(+n)x0n-1(,可根据题目确定)5.变系数一阶递推数列四、不等式1.权方和不等式(赫德尔不等式推出)当且仅当2.黎曼和-定积分不等式级数与定积分之间的关系设可积函数f(x)当f(x)为减时,当f(x)为增时,3.琴生不等式函数的平均数与平均数的函数之间的关系当f(x)为凹函数,即f’’(x)>0时当f(x)为凸函数,即f’’(x)<0时当且仅当x1=x2=∧=x n时,等号成立4.卡尔松不等式5.排序不等式当且时,其中以上可概括为顺序和≥乱序和≥倒序和5.切比雪夫总和不等式(排序不等式推出)当a n与b n逆序时当a n与b n顺序时不等式反向6.舒尔不等式(Schur不等式)x t(x-y)(x-z)+y t(y-x)(y-z)+z t(z-x)(z-y)≥0当x=y=z时,等号成立配Schur法(Schur分拆法)三元齐三次对称轮换式f(x,y,z)≥0的充要条件是因为f(x,y,z)=a+b+cxyz 三元齐四次对称轮换式f(x,y,z)≥0的充要条件是因为f(x,y,z)=三元齐五次对称轮换式f(x,y,z)≥0的充要条件是因为f(x,y,z)=7.常用对数不等式当x〉-1时,当且仅当x=0时等号成立8.伯努利不等式当x≥-1,n≥0时或n为正偶数,x∈R时(1+x)n≥1+nx当n=0或1,或x=0时等号成立9.uvw法和pqr法(解决三元对称轮换式)uvw法:令a+b+c=3u,ab+bc+ca=3v2,abc=w3,得到新不等式pqr法:令a+b+c=p ,ab+bc+ca=q ,abc=r,得到新不等式当a.b.c为非负实数时,用uvw法;当a,b,c∈R时,用pqr法10.SOS法(配方法)不解释11.拉格朗日乘数法(解决条件极值问题)已知f(x,y,z)=0,求F(x,y,z)的极值构造拉格朗日函数L=F(x,y,z)+λf(x,y,z)对F(x,y,z)分别关于x,y,z,λ求偏导,得到四元方程组,其中对F(x,y,z)关于λ求偏导所得方程即f(x,y,z)=0解四元方程组所得解,即F(x,y,z)的极值点,从而算出极值。
高考数学必背必记公式
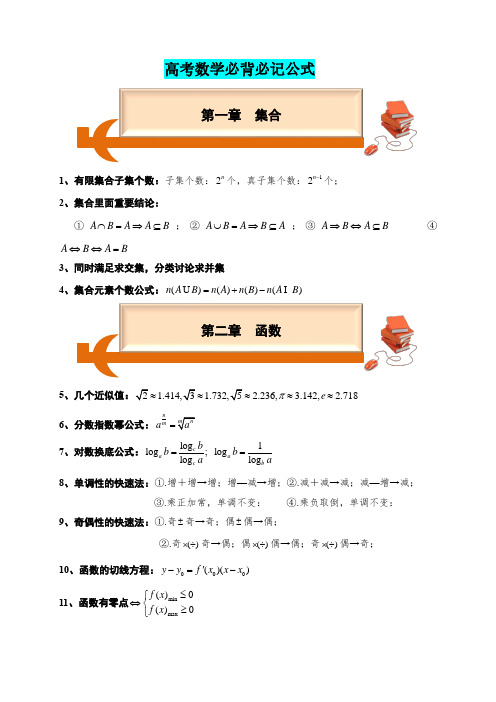
高考数学必背必记公式1、有限集合子集个数:子集个数:2n 个,真子集个数:12n −个;2、集合里面重要结论:①A B A A B ⋂=⇒⊆;②A B A B A ⋃=⇒⊆;③A B A B ⇒⇔⊆ ④A B A B ⇔⇔=3、同时满足求交集,分类讨论求并集4、集合元素个数公式:()()()()n A B n A n B n A B =+−U I5、几个近似值:2 1.414,3 1.732,5 2.236, 3.142, 2.718e π≈≈≈≈≈6、分数指数幂公式:n m n ma a = 7、对数换底公式:log 1log ;log log log c a a c b b b b a a ==8、单调性的快速法:①.增+增→增;增—减→增;②.减+减→减;减—增→减;③.乘正加常,单调不变: ④.乘负取倒,单调不变:9、奇偶性的快速法:①.奇±奇→奇;偶±偶→偶;②.奇()⨯÷奇→偶;偶()⨯÷偶→偶;奇()⨯÷偶→奇;10、函数的切线方程:000()()y y f x x x '−=−11、函数有零点min max ()0()0f x f x ≤⎧⇔⎨≥⎩第一章 集合第二章 函数12、函数无零点max min ()0()0f x f x ⇔≤≥或13、函数周期性:()()f a x f b x +=+的周期Tb a =−; 14、函数对称性:()()f a x f b x +=−的对称轴2a bx +=; 15、抽象函数对数型:若()()()f xy f x f y =+,则()log a f x x =; 16、抽象函数指数型:若()()()f x y f x f y +=,则()x f x a =; 17、抽象函数正比型:若()()()f x y f x f y +=+,则()f x kx =; 18、抽象函数一次型:若()f x c '=,则()f x cx b =+; 19、抽象函数导数型:若()()f x f x '=,则()x f x ke =或()0f x =;20、两个重要不等式:1ln(1)1(0)ln 1x x e x x x e x x x ⎧≥+⇒+≤≤−==⎨≤−⎩当且仅当时“”成立21、洛必达法则:()()()()limlim x ax a f x f x g x g x →→'='(当()0()0f x g x ∞→∞或时使用) 22、恒成立问题:max min(1)()()(2)()()a f x a f x a f x a f x ≥⇔≥<⇔<23、证明()()f x g x >思路:思路1:(1)()()()()0h x f x g x h x =−⇔>(常规首选方法)思路2:min max ()()f x g x >(思路1无法完成)24、等差数列通项公式:1(1)n a a n d =+− 25、等差数列通项公式:11()(1)22n n n a a n n S na d +−==+ 26、等比数列通项公式:11n n a a q −=27、等比数列通项公式:11(1)11n n n a a qa q S q q+−==−−第三章 数列28、等差数列的性质:若m n p q +=+,则m n p q a a a a +=+ 29、等比数列的性质:若m n p q +=+,则m n p q a a a a = 30、等差中项:若,,a A b 成等差数列,则2A a b =+ 31、等比中项:若,,a G b 成等比数列,则2G ab = 32、裂项相消法1:若111(1)1n n nn −++=,则有1111n n T n n =−=++ 33、裂项相消法2:若1111(2)22n n n n −++⎛⎫= ⎪⎝⎭,则有1111(1)2212n T n n =+−−++ 34、裂项相消法3:若111111n nnn a a d a a ++=−⎛⎫⎪⎝⎭,则有11111()nn T d a a +=− 35、裂项相消法4:若1111(21)(21)22121n n n n −+−−+⎛⎫= ⎪⎝⎭,则有11(1)221n T n =−+ 36、错位相减法求和通式:1112()1(1)1n n n n dq b b a b q a b T q q q −=+−−−−37、三角函数的定义:正弦:sin y r α=;余弦:cos x r α=;正切:tan yxα=;其中:22r x y =+38、诱导公式:π倍加减名不变,符号只需看象限;半π加减名要变,符号还是看象限。
高考数学公式理科总结

高考数学公式理科总结高考数学公式理科总结数学作为高考的一门科目,深受大多数理科生的青睐。
因为无论是数学的思维锻炼还是需要掌握的数学公式,都是高考备考不可或缺的一部分。
今天,我们就来总结一下理科数学中常用的数学公式及其应用。
一、代数部分1.一元二次方程公式:ax²+bx+c=0,求根公式为x=(-b±√b²-4ac)/2a。
应用:用于求解一元二次方程,例如求解公路修建所需要的材料和成本等。
2.等比数列公式:an=a1q^(n-1)(其中a1为首项,q为公比,an为第n项)。
应用:用于解决各种与成长或增长相关的问题,如人口增长、利润的增长等。
3.排列组合公式:排列公式为A(n,m)=n!/(n-m)!,组合公式为C(n,m)=n!/m!(n-m)!。
应用:用于处理不同的复杂问题,例如排列组合问题、选择问题、不重复随机抽样问题等。
二、几何部分1.三角函数公式:sinθ=对边/斜边,cosθ=邻边/斜边,tanθ=对边/邻边。
应用:用于三角函数问题,例如角度求解、三角函数值等。
2.圆公式:圆的面积公式为A=πr²,圆的周长公式为C=2πr。
应用:用于解决圆形问题,例如圆周运动、圆的切线、圆的切点等。
3.立体几何公式:三棱锥表面积公式为S=ab+a√(a²+b²+c²-2abcosA),三棱锥体积公式为V=1/3abh。
应用:用于解决空间几何问题,例如三棱锥表面积和体积的计算等。
三、概率统计部分1.样本调查公式:样本调查中常用的统计量有平均数、中位数、众数、方差、标准差、相关系数、回归方程等。
应用:用于处理随机事件、样本调查、统计数据等问题。
2.基本概率公式:P(A)=m/n,其中m表示事件A的样本点个数,n表示整个样本点个数。
应用:用于基本的统计概率问题,例如计算事件发生的概率等。
3.正态分布公式:正态分布的概率密度函数为f(x)=1/σ√2πexp(-(x-μ)²/(2σ²))。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考理科常用数学公式总结1.德摩根公式 ();()U U U U U U C A B C A C B C A B C A C B ==.2.U U A B A A B B A B C B C A =⇔=⇔⊆⇔⊆U A C B ⇔=ΦU C A B R ⇔=3.()()card A B cardA cardB card A B =+-()()card A B C cardA cardB cardC card A B =++-()()()()card A B card B C card CA card ABC ---+.4.二次函数的解析式的三种形式 ①一般式2()(0)f x ax bx c a =++≠;② 顶点式2()()(0)f x a x h k a =-+≠;③零点式12()()()(0)f x a x x x x a =--≠.5.设[]2121,,x x b a x x ≠∈⋅那么[]1212()()()0x x f x f x -->⇔[]1212()()0(),f x f x f x a b x x ->⇔-在上是增函数;[]1212()()()0x x f x f x --<⇔[]1212()()0(),f x f x f x a b x x -<⇔-在上是减函数.设函数)(x f y =在某个区间内可导,如果0)(>'x f ,则)(x f 为增函数;如果0)(<'x f ,则)(x f 为减函数. 6.函数()y f x =的图象的对称性:①函数()y f x =的图象关于直线x a =对称()()f a x f a x ⇔+=-(2)()f a x f x ⇔-=.②函数()y f x =的图象关于直线2a bx +=对称()()f a mx f b mx ⇔+=-()()f a b mx f mx ⇔+-=. 7.两个函数图象的对称性:①函数()y f x =与函数()y f x =-的图象关于直线0x =(即y 轴)对称.②函数()y f mx a =-与函数()y f b mx =-的图象关于直线2a bx m+=对称.③函数)(x f y =和)(1x f y -=的图象关于直线y=x 对称. 8.分数指数幂mn a =(0,,a m n N *>∈,且1n >).1m n m na a -=(0,,a m n N *>∈,且1n >).9. log (0,1,0)b a N b a N a a N =⇔=>≠>.10.对数的换底公式 log log log m a m N N a =.推论 log log m n a a nb b m =.11.11,1,2n n n s n a s s n -=⎧=⎨-≥⎩( 数列{}n a 的前n 项的和为12n n s a a a =+++).12.等差数列的通项公式*11(1)()n a a n d dn a d n N =+-=+-∈;其前n 项和公式 1()2n n n a a s +=1(1)2n n na d -=+211()22d n a d n =+-. 13.等比数列的通项公式1*11()n n n aa a q q n N q-==⋅∈;其前n 项的和公式11(1),11,1n n a q q s q na q ⎧-≠⎪=-⎨⎪=⎩或11,11,1n n a a qq q s na q -⎧≠⎪-=⎨⎪=⎩.14.等比差数列{}n a :11,(0)n n a qa d a b q +=+=≠的通项公式为1(1),1(),11n n n b n d q a bq d b q d q q -+-=⎧⎪=+--⎨≠⎪-⎩;其前n 项和公式为(1),11(),1111n n nb n n d q s d q db n q q q q +-=⎧⎪=-⎨-+≠⎪---⎩. 15.分期付款(按揭贷款) 每次还款(1)(1)1nn ab b x b +=+-元(贷款a 元,n 次还清,每期利率为b ).16.同角三角函数的基本关系式 22sin cos 1θθ+=,tan θ=θθcos sin ,tan 1cot θθ⋅=.17.正弦、余弦的诱导公式212(1)sin ,sin()2(1)s ,nn n co απαα-⎧-⎪+=⎨⎪-⎩ 212(1)s ,s()2(1)sin ,nn co n co απαα+⎧-⎪+=⎨⎪-⎩18.和角与差角公式sin()sin cos cos sin αβαβαβ±=±;cos()cos cos sin sin αβαβαβ±=;tan tan tan()1tan tan αβαβαβ±±=.22sin()sin()sin sin αβαβαβ+-=-(平方正弦公式); 22cos()cos()cos sin αβαβαβ+-=-.sin cos a b αα+=)αϕ+(辅助角ϕ所在象限由点(,)a b 的象限决定,tan baϕ= ).19.二倍角公式 sin 2sin cos ααα=.2222cos 2cos sin 2cos 112sin ααααα=-=-=-.22tan tan 21tan ααα=-. 20.三角函数的周期公式 函数sin()y x ωϕ=+,x ∈R 及函数cos()y x ωϕ=+,x ∈R(A,ω,ϕ为常数,且A ≠0,ω>0)的周期2T πω=;函数tan()y x ωϕ=+,,2x k k Z ππ≠+∈(A,ω,ϕ为常数,且A ≠0,ω>0)的周期T πω=. 21.正弦定理2sin sin sin a b cR A B C===. 22.余弦定理2222cos a b c bc A =+-;2222cos b c a ca B =+-; 2222cos c a b ab C =+-.23.面积定理(1)111222a b c S ah bh ch ===(a b c h h h 、、分别表示a 、b 、c 边上的高).(2)111sin sin sin 222S ab C bc A ca B ===.(3)22(||||)()OAB S OA OB OA OB ∆=⋅-⋅.24.三角形内角和定理 在△ABC 中,有()222C A BA B C C A B πππ+++=⇔=-+⇔=-222()C A B π⇔=-+. 25.平面两点间的距离公式,AB d =||AB AB AB =⋅=11(,)x y ,B 22(,)x y ). 26.向量的平行与垂直 设a =11(,)x y ,b =22(,)x y ,且b ≠0,则 a b ⇔b =λa 12210x y x y ⇔-=. a ⊥b(a ≠0)⇔a ·b=012120x x y y ⇔+=.27.线段的定比分公式 设111(,)P x y ,222(,)P x y ,(,)P x y 是线段12P P 的分点,λ是实数,且12PP PP λ=,则121211x x x y y y λλλλ+⎧=⎪⎪+⎨+⎪=⎪+⎩⇔121OP OP OP λλ+=+⇔12(1)OP tOP t OP =+-(11t λ=+). 28.三角形的重心坐标公式 △ABC 三个顶点的坐标分别为11A(x ,y )、22B(x ,y )、33C(x ,y ),则△ABC 的重心的坐标是123123(,)33x x x y y y G ++++. 29.点的平移公式 ''''x x h x x h y y k y y k⎧⎧=+=-⎪⎪⇔⎨⎨=+=-⎪⎪⎩⎩''OP OP PP ⇔=+ (图形F 上的任意一点P(x ,y)在平移后图形'F 上的对应点为'''(,)P x y ,且'PP 的坐标为(,)h k ). 30.常用不等式:(1),a b R ∈⇒222a b ab +≥(当且仅当a =b 时取“=”号).(2),a b R +∈⇒2a b+≥(当且仅当a =b 时取“=”号). (3)3333(0,0,0).a b c abc a b c ++≥>>>(4)柯西不等式22222()()(),,,,.a b c d ac bd a b c d R ++≥+∈ (5)b a b a b a +≤+≤-31.极值定理 已知y x ,都是正数,则有(1)如果积xy 是定值p ,那么当y x =时和y x +有最小值p 2;(2)如果和y x +是定值s ,那么当y x =时积xy 有最大值241s .32.一元二次不等式20(0)ax bx c ++><或2(0,40)a b ac ≠∆=->,如果a 与2ax bx c ++同号,则其解集在两根之外;如果a 与2ax bx c ++异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间. 121212()()0()x x x x x x x x x <<⇔--<<; 121212,()()0()x x x x x x x x x x <>⇔--><或.33.含有绝对值的不等式 当a> 0时,有22x a x a a x a <⇔<⇔-<<.22x a x a x a >⇔>⇔>或x a <-. 34.无理不等式(1()0()0()()f x g x f x g x ≥⎧⎪>⇔≥⎨⎪>⎩. (22()0()0()()0()0()[()]f x f x g x g x g x f x g x ≥⎧≥⎧⎪>⇔≥⎨⎨<⎩⎪>⎩或. (32()0()()0()[()]f x g x g x f x g x ≥⎧⎪⇔>⎨⎪<⎩. 35.指数不等式与对数不等式 (1)当1a >时,()()()()f x g x a a f x g x >⇔>; ()0log ()log ()()0()()a a f x f x g x g x f x g x >⎧⎪>⇔>⎨⎪>⎩.(2)当01a <<时,()()()()f x g x a a f x g x >⇔<;()0log ()log ()()0()()a a f x f x g x g x f x g x >⎧⎪>⇔>⎨⎪<⎩36.斜率公式 2121y y k x x -=-(111(,)P x y 、222(,)P x y ). 37.直线的四种方程(1)点斜式 11()y y k x x -=- (直线l 过点111(,)P x y ,且斜率为k ). (2)斜截式 y kx b =+(b 为直线l 在y 轴上的截距).(3)两点式 112121y y x x y y x x --=--(12y y ≠)(111(,)P x y 、222(,)P x y (12x x ≠)). (4)一般式 0Ax By C ++=(其中A 、B 不同时为0).38.两条直线的平行和垂直 (1)若111:l y k x b =+,222:l y k x b =+①121212,l l k k b b ⇔=≠;②12121l l k k ⊥⇔=-.(2)若1111:0l A x B y C ++=,2222:0l A x B y C ++=,且A 1、A 2、B 1、B 2都不为零,①11112222A B C l l A B C ⇔=≠;②1212120l l A A B B ⊥⇔+=; 39.夹角公式 2121tan ||1k kk k α-=+.(111:l y k x b =+,222:l y k x b =+,121k k ≠-)12211212tan A B A B A A B B α-=+(1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠).直线12l l⊥时,直线l 1与l 2的夹角是2π. 40.点到直线的距离 d =(点00(,)P x y ,直线l :0Ax By C ++=).41. 圆的四种方程(1)圆的标准方程 222()()x a y b r -+-=.(2)圆的一般方程 220x y Dx Ey F ++++=(224D E F +->0).(3)圆的参数方程 cos sin x a r y b r θθ=+⎧⎨=+⎩.(4)圆的直径式方程 1212()()()()0x x x x y y y y --+--=(圆的直径的端点是11(,)A x y 、22(,)B x y ).42.椭圆22221(0)x y a b a b +=>>的参数方程是cos sin x a y b θθ=⎧⎨=⎩.43.椭圆22221(0)x y a b a b +=>>焦半径公式 )(21c a x e PF +=,)(22x c a e PF -=.44.双曲线22221(0,0)x y a b a b -=>>的焦半径公式21|()|a PF e x c =+,22|()|a PF e x c=-.45.抛物线px y 22=上的动点可设为P ),2(2y py或或)2,2(2pt pt P P (,)x y ,其中22y px =.46.二次函数2224()24b ac b y ax bx c a x a a-=++=++(0)a ≠的图象是抛物线:(1)顶点坐标为24(,)24b ac b a a --;(2)焦点的坐标为241(,)24b ac b a a -+-;(3)准线方程是2414ac b y a--=.47.直线与圆锥曲线相交的弦长公式AB=1212|||AB x x y y ==-=-(弦端点A ),(),,(2211y xB y x ,由方程⎩⎨⎧=+=0)y ,x (F bkx y 消去y 得到02=++c bx ax ,0∆>,α为直线AB 的倾斜角,k 为直线的斜率). 48.圆锥曲线的两类对称问题:(1)曲线(,)0F x y =关于点00(,)P x y 成中心对称的曲线是00(2-,2)0F x x y y -=. (2)曲线(,)0F x y =关于直线0Ax By C ++=成轴对称的曲线是22222()2()(,)0A Ax By C B Ax By C F x y A B A B++++--=++. 49.“四线”一方程 对于一般的二次曲线220Ax Bxy Cy Dx Ey F +++++=,用0x x代2x ,用0y y 代2y ,用002x y xy +代xy ,用02x x +代x ,用02y y+代y 即得方程 0000000222x y xy x x y yAx x B Cy y D E F ++++⋅++⋅+⋅+=,曲线的切线,切点弦,中点弦,弦中点方程均是此方程得到.50.共线向量定理 对空间任意两个向量a 、b (b ≠0 ),a ∥b ⇔存在实数λ使a =λb .51.对空间任一点O 和不共线的三点A 、B 、C ,满足OP xOA yOB zOC =++, 则四点P 、A 、B 、C 是共面⇔1x y z ++=. 52. 空间两个向量的夹角公式 cos 〈a ,b 〉=(a =123(,,)a a a ,b =123(,,)b b b ).53.直线AB 与平面所成角sin||||AB marc AB m β⋅=(m 为平面α的法向量).54.二面角l αβ--的平面角cos ||||m n arc m n θ⋅=或cos ||||m narc m n π⋅-(m ,n 为平面α,β的法向量).55.设AC 是α内的任一条直线,且BC ⊥AC ,垂足为C ,又设AO 与AB 所成的角为1θ,AB 与AC 所成的角为2θ,AO 与AC 所成的角为θ.则12cos cos cos θθθ=. 56.若夹在平面角为ϕ的二面角间的线段与二面角的两个半平面所成的角是1θ,2θ,与二面角的棱所成的角是θ,则有22221212sin sin sin sin 2sin sin cos ϕθθθθθϕ=+- ;1212||180()θθϕθθ-≤≤-+(当且仅当90θ=时等号成立).57.空间两点间的距离公式 若A 111(,,)x y z ,B 222(,,)x y z ,则 ,A B d =||AB AB AB =⋅=58.点Q 到直线l 距离h =(点P 在直线l 上,直线l 的方向向量a =PA ,向量b =PQ ).59.异面直线间的距离 ||||CD n d n ⋅=(12,l l 是两异面直线,其公垂向量为n ,C D 、分别是12,l l 上任一点,d 为12,l l 间的距离).60.点B 到平面α的距离 ||||AB n d n ⋅=(n 为平面α的法向量,AB 是经过面α的一条斜线,A α∈).61.异面直线上两点距离公式 d =(两条异面直线a 、b 所成的角为θ,其公垂线段'AA 的长度为h.在直线a 、b 上分别取两点E 、F ,'A E m =,AF n =,EF d =). 62. 2222123l l l l =++222123cos cos cos 1θθθ⇔++=(长度为l 的线段在三条两两互相垂直的直线上的射影长分别为123l l l 、、,夹角分别为123θθθ、、)(立几中长方体对角线长的公式是其特例).63. 面积射影定理 'cos S S θ=(平面多边形及其射影的面积分别是S 、'S ,它们所在平面所成锐二面角的为θ). 64.欧拉定理(欧拉公式) 2V F E +-=(简单多面体的顶点数V 、棱数E 和面数F)65.球的半径是R ,则其体积是343V R π=,其表面积是24S R π=.66.分类计数原理(加法原理)12n N m m m =+++.67.分步计数原理(乘法原理)12n N m m m =⨯⨯⨯.68.排列数公式 m n A =)1()1(+--m n n n =!!)(m n n -.(n ,m ∈N *,且m n ≤).69.排列恒等式 (1)1(1)m m n n A n m A -=-+;(2)1m mn n n A A n m-=-;(3)11m m n n A nA --=; (4)11n n n n n n nA A A ++=-;(5)11m m m n n n A A mA -+=+. 70.组合数公式 mnC =m n m mA A =m m n n n ⨯⨯⨯+-- 21)1()1(=!!!)(m n m n -⋅(n ,m ∈N *,且m n ≤).71.组合数的两个性质(1) m n C =mn n C - ;(2) m n C +1-m n C =m n C 1+72.组合恒等式(1)11m m n n n m C C m --+=;(2)1m m n n n C C n m -=-;(3)11mm nn n C C m--=; (4)∑=nr rn C 0=n 2;(5)1121++++=++++r n r n r r r r r r C C C C C .73.排列数与组合数的关系是:m mn n A m C =⋅! .74.二项式定理 nn n r r n r n n n n n n nn b C b a C b a C b a C a C b a ++++++=+--- 222110)( ; 二项展开式的通项公式:rr n r nr b a C T -+=1)210(n r ,,, =. 75.等可能性事件的概率()m P A n=. 76.互斥事件A ,B 分别发生的概率的和P(A +B)=P(A)+P(B).77.n 个互斥事件分别发生的概率的和P(A 1+A 2+…+A n )=P(A 1)+P(A 2)+…+P(A n ).78.独立事件A ,B 同时发生的概率P(A ·B)= P(A)·P(B). 79.n 个独立事件同时发生的概率 P(A 1· A 2·…· A n )=P(A 1)· P(A 2)·…· P(A n ).80.n 次独立重复试验中某事件恰好发生k 次的概率()(1).k kn k n nP k C P P -=- 81.离散型随机变量的分布列的两个性质:(1)0(1,2,)i P i ≥=;(2)121P P ++=.82.数学期望1122n n E x P x P x P ξ=++++83.数学期望的性质:(1)()()E a b aE b ξξ+=+;(2)若ξ~(,)B n p ,则E np ξ=. 84.方差()()()2221122n n D x E p x E p x E p ξξξξ=-⋅+-⋅++-⋅+85.标准差σξ=ξD .86.方差的性质(1)()22()D E E ξξξ=-;(2)()2D a b a D ξξ+=;(3)若ξ~(,)B n p ,则(1)D np p ξ=-.87.正态分布密度函数()()()222,,x f x x μσ--=∈-∞+∞式中的实数μ,σ(σ>0)是参数,分别表示个体的平均数与标准差.88.标准正态分布密度函数()()22,,x f x x -=∈-∞+∞.89.对于2(,)N μσ,取值小于x 的概率()x F x μσ-⎛⎫=Φ ⎪⎝⎭.()()()12201x x P x x P x x x P <-<=<<()()21F x F x =- 21x x μμσσ--⎛⎫⎛⎫=Φ-Φ ⎪ ⎪⎝⎭⎝⎭.90.回归直线方程 y a bx =+,其中()()()1122211n ni i i i i i nn i i i i x x y y x y nx y b x x x nx a y bx====⎧---⎪⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑. 91.相关系数 ()()niix x y y r --=∑ ()()niix x y y --=∑|r|≤1,且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小.92.特殊数列的极限 (1)0||1lim 11||11n n q q q q q →∞<⎧⎪==⎨⎪<=-⎩不存在或.(2)1101100()lim ()()k k k k tt t n t t kk t a n a n a a k t b n b n b b k t ---→∞-⎧<⎪+++⎪==⎨+++⎪⎪>⎩不存在 .(3)()111lim11nn a q a S q q→∞-==--(S 无穷等比数列}{11n a q - (||1q <)的和).93.0lim ()x x f x a →=⇔00lim ()lim ()x x x x f x f x a -+→→==.这是函数极限存在的一个充要条件.94.函数的夹逼性定理 如果函数f(x),g(x),h(x)在点x 0的附近满足:(1)()()()g x f x h x ≤≤;(2)0lim (),lim ()x x x x g x a h x a →→==(常数),则0lim ()x x f x a →=.本定理对于单侧极限和∞→x 的情况仍然成立.95.两个重要的极限 (1)0sin lim 1x x x →=;(2)1lim 1xx e x →∞⎛⎫+= ⎪⎝⎭(e=2.718281845…). 96.)(x f 在0x 处的导数(或变化率或微商)00000()()()limlim x x x x f x x f x yf x y x x=∆→∆→+∆-∆''===∆∆. 97.瞬时速度00()()()lim limt t s s t t s t s t t tυ∆→∆→∆+∆-'===∆∆. 98.瞬时加速度00()()()lim limt t v v t t v t a v t t t∆→∆→∆+∆-'===∆∆. 99.)(x f 在),(b a 的导数()dy df f x y dx dx ''===00()()lim limx x y f x x f x x x∆→∆→∆+∆-==∆∆. 100.函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率)(0x f ',相应的切线方程是))((000x x x f y y -'=-.101.几种常见函数的导数 (1) 0='C (C 为常数). (2) '1()()n n x nx n Q -=∈. (3) x x cos )(sin ='. (4) x x sin )(cos -='.(5) x x 1)(ln =';ea x xa log 1)(log ='. (6) x x e e =')(; a a a x x ln )(='.102.复合函数的求导法则 设函数()u x ϕ=在点x 处有导数''()x u x ϕ=,函数)(u f y =在点x 处的对应点U 处有导数''()u y f u =,则复合函数(())y f x ϕ=在点x处有导数,且'''x u x y y u =⋅,或写作'''(())()()x f x f u x ϕϕ=.103.可导函数)(x f y =的微分dx x f dy )('=. 104.,a bi c di a c b d +=+⇔==.(,,,a b c d R ∈)105.复数z a bi =+的模(或绝对值)||z =||a bi +106.复数的四则运算法则(1)()()()()a bi c di a c b d i +++=+++; (2)()()()()a bi c di a c b d i +-+=-+-;(3)()()()()a bi c di ac bd bc ad i ++=-++;(4)2222()()(0)ac bd bc ada bi c di i c di c d c d +-+÷+=++≠++.107.复平面上的两点间的距离公式12||d z z =-=(111z x y i =+,222z x y i =+).108.向量的垂直 非零复数1z a bi =+,2z c di =+对应的向量分别是1OZ ,2OZ ,则12OZ OZ ⊥⇔12z z ⋅的实部为零⇔21z z 为纯虚数⇔2221212||||||z z z z +=+ ⇔2221212||||||z z z z -=+⇔1212||||z z z z +=-⇔0ac bd +=⇔12z iz λ= (λ为非零实数).109.实系数一元二次方程的解 实系数一元二次方程20ax bx c ++=,①若240b ac ∆=->,则1,22b x a -±=;②若240b ac ∆=-=,则122bx x a==-;③若240b ac ∆=-<,它在实数集R 内没有实数根;在复数集C 内有且仅有两个共轭复数根240)x b ac =-<.。
