平衡二叉树的操作演示 Microsoft Office Word 文档
平衡二叉树的手动调整方法
平衡⼆叉树的⼿动调整⽅法看书左旋右旋看着懵逼,不懂往左旋转往右旋转到底是怎么个旋转法。
总结了⼀个万能的⼿动调整⽅法,不⽤记忆什么LL,LR,RL,RR的形式,通吃。
当新插⼊⼀个节点,导致不平衡,进⾏⼿动调整。
步骤有四步:1。
找到最⼩不平衡⼦树(和其根节点)2。
从根节点出发,沿插⼊路径找三个节点。
3。
调整这三个节点。
(找出中位数,让中位数作为根节点,其余两个⼀左⼀右)4。
剩下的节点,左右⼦树的位置保持不变,再找到最后⼀个节点的插⼊位置。
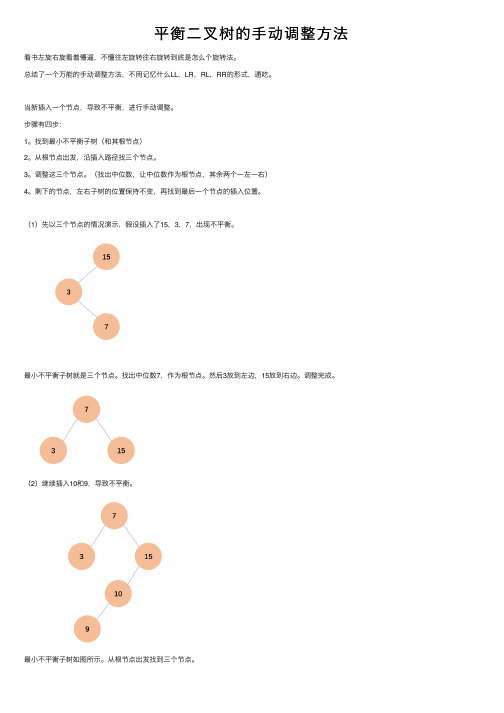
(1)先以三个节点的情况演⽰,假设插⼊了15,3,7,出现不平衡。
最⼩不平衡⼦树就是三个节点。
找出中位数7,作为根节点。
然后3放到左边,15放到右边。
调整完成。
(2)继续插⼊10和9,导致不平衡。
最⼩不平衡⼦树如图所⽰。
从根节点出发找到三个节点。
调整这三个节点的位置,⽅法和上⾯⼀样,把中位数10作为根节点。
(3)继续插⼊8导致不平衡,以及最⼩不平衡⼦树。
7是根节点。
从7开始,找到7,10,9三个节点。
调整这三个。
让9做根节点,7在左,10在右。
对于剩下的节点,左右⼦树位置保持不变。
3仍然在最左,15仍然在最右。
然后再找到8应该插在哪⾥就⾏了。
调整完成。
复述⼀遍⽅法:1。
找到最⼩不平衡⼦树(和其根节点)2。
从根节点出发,沿插⼊路径找三个节点。
3。
调整这三个节点。
(找出中位数,让中位数作为根节点,其余两个⼀左⼀右)4。
剩下的节点,左右⼦树的位置保持不变,再找到最后⼀个节点的插⼊位置。
这套⽅法万能,不⽤记书上的四种样式。
详解平衡二叉树
一、平衡二叉树的概念平衡二叉树(Balanced binary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的,所以又称为AVL树。
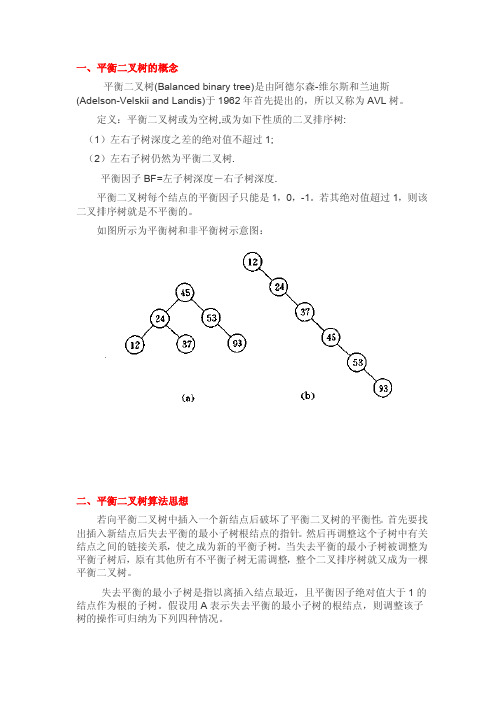
定义:平衡二叉树或为空树,或为如下性质的二叉排序树:(1)左右子树深度之差的绝对值不超过1;(2)左右子树仍然为平衡二叉树.平衡因子BF=左子树深度-右子树深度.平衡二叉树每个结点的平衡因子只能是1,0,-1。
若其绝对值超过1,则该二叉排序树就是不平衡的。
如图所示为平衡树和非平衡树示意图:二、平衡二叉树算法思想若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。
首先要找出插入新结点后失去平衡的最小子树根结点的指针。
然后再调整这个子树中有关结点之间的链接关系,使之成为新的平衡子树。
当失去平衡的最小子树被调整为平衡子树后,原有其他所有不平衡子树无需调整,整个二叉排序树就又成为一棵平衡二叉树。
失去平衡的最小子树是指以离插入结点最近,且平衡因子绝对值大于1的结点作为根的子树。
假设用A表示失去平衡的最小子树的根结点,则调整该子树的操作可归纳为下列四种情况。
1)LL型平衡旋转法由于在A的左孩子B的左子树上插入结点F,使A的平衡因子由1增至2而失去平衡。
故需进行一次顺时针旋转操作。
即将A的左孩子B向右上旋转代替A作为根结点,A向右下旋转成为B的右子树的根结点。
而原来B的右子树则变成A的左子树。
(2)RR型平衡旋转法由于在A的右孩子C 的右子树上插入结点F,使A的平衡因子由-1减至-2而失去平衡。
故需进行一次逆时针旋转操作。
即将A的右孩子C向左上旋转代替A作为根结点,A向左下旋转成为C的左子树的根结点。
而原来C的左子树则变成A的右子树。
(3)LR型平衡旋转法由于在A的左孩子B的右子数上插入结点F,使A的平衡因子由1增至2而失去平衡。
故需进行两次旋转操作(先逆时针,后顺时针)。
即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置,然后再把该D结点向右上旋转提升到A结点的位置。
平衡二叉树操作演示.doc

平衡二叉树操作演示.数据结构实习报告题目:平衡二叉树的操作演示班级:信息管理与信息系统11-平衡二叉树的操作演示班级:信息管理与信息系统11:崔佳学号:201101050903完成日期:2013.06.25一、需求分析1. 初始,平衡二叉树为空树,操作界面给出两棵平衡二叉树的显示、查找、插入、删除、销毁、合并两棵树,几种选择。
其中查找、插入和删除操作均要提示用户输入关键字。
每次插入或删除一个节点后都会更新平衡二叉树的显示。
2. 平衡二叉树的显示采用凹入表形式。
3.每次操作完毕后都会给出相应的操作结果,并进入下一次操作,知道用户选择退出二、概要设计1.平衡二叉树的抽象数据类型定义:ADT BalancedBinaryTree{ 数据对象D:D是具有相同特性的数据元素的集合。
各个数据元素均含有类型相同,可唯一标志的数据元素的关键字。
数据关系R:数据元素同属一个集合。
基本操作P:InitA VL(BSTree T) 操作结果:构造一个空的平衡二叉树T DestroyA VL(BSTree T) 初始条件:平衡二叉树T存在操作结果:销毁平衡二叉树T SearchA VL(BSTree T,int key) 初始条件:平衡二叉树T存在,key为和关键字相同类型的给定值操作结果:若T中存在关键字和key相等的数据元素,则返回指向该元素的指针,否则为空InsertA VL(BSTree T,int key,Status taller) 初始条件:平衡二叉树T存在,key和关键字的类型相同操作结果:若T中存在关键字等于key的数据元素则返回,若不存在则插入一个关键字为key的元素DeleteA VL(BSTree T,int key,Status lower) 初始条件:平衡二叉树T存在,key和关键字的类型相同操作结果:若T中存在关键字和key相同的数据元素则删除它}ADT BalancedBinaryTree2.本程序包含二个模块1)主程序模块:void main(){ 接收命令;While(“命令”!=“退出”){ 处理命令;清屏并得新打印提示信息;接收下一条命令;}}2)平衡二叉树基本操作实现平衡二叉树的抽象数据类型的各函数原型。
平衡二叉树(AVLtree)

平衡⼆叉树(AVLtree)⼆叉查找树在极端情况下会演变成⼀棵只有⼀侧⼦孩⼦的树,例如每个⾮叶⼦只有左孩⼦或者右孩⼦,这时候在查找的时候就需要遍历这棵树来找到⽬标值,它的快速搜索价值就体现不出来了,如果这棵搜索树在构建的时候,能够平衡左右⼦树的⾝⾼差,使得左右⼦树⾝⾼差不超过1,那它的搜索效率就是O(lgn),平衡⼆叉树就是这样的树,它有以下特点:1、左右⼦树的⾼度差不超过12、左右⼦树都是平衡⼆叉树,空节点也视其为⼀棵平衡⼆叉树以上有点递归定义问题的意思,平衡⼆叉树的关键特性是其任何⼀个节点为根的左右⼦树⾼度差不能超过1,因为有这个特性限制,所以在创建平衡⼆叉树的时候如果发现这个平衡被打破了,需要对树进⾏旋转操作,以恢复其平衡的性质,具体的旋转有以下⼏种情况:1、LL类型旋转(单向向右):这种情况下是某个节点的左孩⼦的左⼦树导致该节点失衡,需要对该节点进⾏向右旋转,如下图:如上图,值为3的节点,当它只有⼀个左孩⼦2时,此时左右孩⼦的⾼度差是1,当再插⼊1时,它的左右孩⼦的⾼度差变成了2,需要对其进⾏右旋:LL_Rotate(node): leftNode=node.left;//待旋转节点的左孩⼦ leftRightNode=leftNode;//待旋转节点的左孩⼦的右孩⼦ leftNode.right=node;//更新左孩⼦节点,将⾃⼰作为作为左孩⼦的右节点,即上图中3变成了2的右孩⼦ node.left=leftRightNode;//更新⾃⼰的左孩⼦, node.height=max(node.left.height,node.right.height)+1;//更新⾼度 leftNode.height=max(leftNode.left.height,leftNode.right.height)+1;//跟新新的根节点⾼度,需要先更新node节点... return leftNode;//返回左孩⼦替代⾃⼰的位置,⽐如上图中,2替代了3的位置2、RR类型旋转(单向向左):这种情况下是某个节点的右孩⼦的右⼦树导致该节点失衡,需要对该节点进⾏向左旋转,如下图:如上图,因为3的插⼊,根节点1的平衡因⼦变成2,需要对1进⾏左旋,⽅向与LL完全相反:RR_Rotate(node): rightNode=node.right;//获取右孩⼦ rightLeftNode=rightNode.left;//获取右孩⼦的左孩⼦ rightNode.left=node;//更新右孩⼦ node.right=rightLeftNode; node.height=max(node.left.height,node.right.height)+1; rightNode.height=max(rightNode.left.height,right.right.height)+1; return rightNode;//返回3、LR类型旋转(先左后右):这种情况下是某个节点的左孩⼦的右⼦树导致该节点失衡,需要对该节点的左孩⼦进⾏左旋,然后再对其进⾏右旋,如下图:如上图,节点值为8的节点的左孩⼦,因为6的插⼊,导致8节点失衡,需要先对左孩⼦4进⾏左旋,由6替代4的位置,再对8进⾏右旋,由6替代8:Left_Right_Rotate(node): node.left=LL_Rotate(node.left);//对左孩⼦左旋 return RR_Rotate(node);//对⾃⼰进⾏右旋4、RL类型旋转(先右后左):这种情况下是某个节点的右孩⼦的左⼦树导致该节点失衡,需要对该节点的右孩⼦进⾏右旋,然后再对其进⾏左旋,如下图:如上图,4的平衡因⼦因为其右孩⼦7新增了⼀个左孩⼦节点6⽽打破,需要对节点7先右旋,再对4进⾏左旋,同LR完全相反,伪代码如下:Right_Left_Rotate(node): node.right=RR_Rotate(node.right);//对右孩⼦进⾏右旋 return LL_Rotate(node);//对⾃⾝进⾏左旋节点的⾼度的获取:Get_Height(node): if node==null: return 0; leftHeight=Get_Height(node.left); rightHeight=Get_Height(node.right); return max(leftHeight,rightHeight)+1;平衡因⼦的获取,某个节点的平衡因⼦是由左右⼦树的⾼度差决定的:Get_Factor(node): return Get_Height(node.left)-Get_Height(node.right);节点的平衡调整,涉及到左旋、右旋、左右旋转、右左旋转:balance(node): if node==null return null; //左⼦树导致不平衡 if getFactor(node)==2 : //左孩⼦的左⼦树导致不平衡 if getFactor(node.left)==1: node=LL_Rotate(node) else: //左孩⼦的右⼦树导致不平衡 node=Left_Right_Rotate(node); //右⼦树导致不平衡 else if getFactor(node)==-2: 右⼦树的右孩⼦导致不平衡 if getFactor(node.right)==-1: node=RR_Rotate(node); else //右孩⼦的左⼦树导致不平衡 node=Right_Left_Rotate(node); //返回旋转后的节点 return node;树的插⼊操作:insert_val(node,val): if node==null: return new Node(val); //这⾥是⼀个递归创建过程 if val<node.val: node.left=insert_val(node.left,val); node.left.parent=node; else node.right=insert_val(node.right,val); node.right.parent=node; //返回调整后的节点 return balance(node);树的删除操作,删除操作有点复杂,需要找到那个替代⾃⼰的节点,其⽅法就是寻找删除节点的左⼦树的最⼤值;如果待删除节点没有左⼦树,则需要寻找右⼦树的最⼩值,如果待删除的节点是叶⼦节点,则直接删除即可:delete_node(node,val): if node==null: return;//没有找到,直接返回 if val < node.val: delete_node(node.left,val); else if val > node.val: delete_node(node.right,val); else: //寻找到了⽬标节点 //⽬标节点是叶⼦节点 if node.left==null && node.right==null: parent=node.parent; //待删除的节点是根节点 if parent==null: root=null; else if parent.left==node: parent.left=null; else: //删除节点 parent.right=null; else if node.left!=null: left=node.left maxNode=left while left!=null: maxNode=right; left=left.right; node.val=maxNode.val delete_node(node.left,node.val); else: //与上⾯node.left!=null中的left相反,将left修改为right balance(node);//调节树的平衡以上AVL树的构建分析完毕,其中关键点为节点的平衡操作,创建和删除节点时使⽤到了递归操作,算是⼀个设计技巧,如下为完整的⽰例代码:package avl;import java.util.ArrayList;import java.util.List;/*** AVL 树的定义*/public class AVLTree {//根节点Node root=null;/*** 插⼊新值* @param val* @return*/public AVLTree insertVal(int val){if(root==null){root=new Node(val);}else{insertVal(root,val);}return this;* 节点的插⼊* @param node* @param val* @return*/private Node insertVal(Node node,int val){if(node==null){node=new Node(val);return node;}if(val<node.val){Node left=insertVal(node.left,val);node.left=left;left.parent=node;}else{Node right=insertVal(node.right,val);node.right=right;right.parent=node;}//调整节点node=balance(node);return node;}/*** 删除节点* @param val*/public void deleteVal(int val){deleteVal(root,val);}private void deleteVal(Node node,int val){//没有找到,直接返回if(node==null){return;}else if(val<node.val){deleteVal(node.left,val);balance(node);}else if(val>node.val){deleteVal(node.right,val);balance(node);}else{//叶⼦节点,直接删除if(node.left==null && node.right==null){Node parent=node.parent;if(parent==null){root=null;}if(parent.left==node){parent.left=null;}else{parent.right=null;}}else{//如果左⼦树不为空,寻找其最⼤的后继节点if(node.left!=null){Node left=node.left;Node maxNode=left;//注意这⾥是怎么找最⼤的后继节点的while(left!=null){maxNode=left;left=left.right;}node.val=maxNode.val;deleteVal(node.left,maxNode.val);balance(node);}else{Node right=node.right;Node maxNode=right;while(right!=null){maxNode=right;right=right.left;}node.val=maxNode.val;deleteVal(node.right,maxNode.val);balance(node);}}}* 平衡节点的操作动作* @param node* @return*/private Node balance(Node node){if(node==null){return null;}if(getFactor(node)==2){if(getFactor(node.left)==1){node= LL_Rotate(node);}else{node= LR_Rotate(node);}}else if(getFactor(node)==-2){if(getFactor(node.right)==-1){node= RR_Rotate(node);}else{node= RL_Rotate(node);}}return node;}/*** 获取节点的⾼度* @param node* @return*/private int getHeight(Node node){if(node==null){return0;}int left=getHeight(node.left);int right=getHeight(node.right);int max=Math.max(left,right);return max+1;}/*** 获取节点的平衡因⼦* @param node* @return*/private int getFactor(Node node){if(node==null){return0;}return getHeight(node.left)-getHeight(node.right); }/*** 先右后左* @param node* @return*/private Node RL_Rotate(Node node){Node right=LL_Rotate(node.right);node.right=right;right.parent=node;return RR_Rotate(node);}/*** 先左后右* @param node* @return*/private Node LR_Rotate(Node node){Node left=RR_Rotate(node.left);node.left=left;left.parent=node;return LL_Rotate(node);}/*** 单向左旋* @param node* @return*/private Node RR_Rotate(Node node){Node right=node.right,parent=node.parent; Node rightLeft=right.left;right.left=node;node.parent=right;node.right=rightLeft;if(rightLeft!=null){rightLeft.parent=node;}right.parent=parent;if(parent!=null){if(parent.left==node){parent.left=right;}else{parent.right=right;}}else{root=right;}return right;}/*** 单向右旋* @param node* @return*/private Node LL_Rotate(Node node){Node left=node.left,parent=node.parent; Node leftRight=left.right;left.right=node;node.parent=left;node.left=leftRight;if(leftRight!=null){leftRight.parent=node;}left.parent=parent;if(parent!=null){if(parent.left==node){parent.left=left;}else{parent.right=left;}}else{root=left;}return left;}/*** 先序遍历* @param node*/public void preOrder(Node node){if(node!=null){System.out.print(node);preOrder(node.left);preOrder(node.right);}}/*** 中序遍历* @param node*/public void inOrder(Node node){if(node!=null){inOrder(node.left);System.out.print(node);inOrder(node.right);}}/*** 后序遍历* @param node*/public void postOrder(Node node){if(node!=null){postOrder(node.left);postOrder(node.right);System.out.print(node);}}/*** 按层遍历树*/public void printByLevel(){System.out.println("=========================");List<Node> temp=new ArrayList<>();if(root!=null){temp.add(root);}while(temp.size()>0){List<Node> nodes=new ArrayList<>();temp.stream().forEach(obj-> {System.out.print(obj);if(obj.left!=null){nodes.add(obj.left);}if(obj.right!=null){nodes.add(obj.right);}});System.out.println();temp.clear();temp.addAll(nodes);}}public static void main(String[] args) {AVLTree tree=new AVLTree();tree.insertVal(1).insertVal(2).insertVal(3).insertVal(4).insertVal(5).insertVal(7).insertVal(6); tree.printByLevel();tree.deleteVal(6);tree.printByLevel();tree.deleteVal(4);tree.printByLevel();}}class Node{public int val;public Node left,right,parent;public Node(int val){this.val=val;}@Overridepublic String toString() {return val+"";}}View Code。
C#与数据结构--树论--平衡二叉树(AVLTree)

C#与数据结构--树论--平衡⼆叉树(AVLTree)介绍我们知道在⼆叉查找树中,如果插⼊元素的顺序接近有序,那么⼆叉查找树将退化为链表,从⽽导致⼆叉查找树的查找效率⼤为降低。
如何使得⼆叉查找树⽆论在什么样情况下都能使它的形态最⼤限度地接近满⼆叉树以保证它的查找效率呢?前苏联科学家G.M. Adelson-Velskii 和 E.M. Landis给出了答案。
他们在1962年发表的⼀篇名为《An algorithm for the organization of information》的⽂章中提出了⼀种⾃平衡⼆叉查找树()。
这种⼆叉查找树在插⼊和删除操作中,可以通过⼀系列的旋转操作来保持平衡,从⽽保证了⼆叉查找树的查找效率。
最终这种⼆叉查找树以他们的名字命名为“AVL-Tree”,它也被称为平衡⼆叉树(Balanced Binary Tree)。
这⾥所说的平衡使我们想到了中庸之道,但有句话说得好,“中不偏,庸不易”。
学会这种平衡术是⼀个相当痛苦的过程。
什么是平衡为了保证平衡,AVL树中的每个结点都有⼀个平衡因⼦(balance factor,以下⽤BF表⽰),它表⽰这个结点的左、右⼦树的⾼度差,也就是左⼦树的⾼度减去右⼦树的⾼度的结果值。
AVL树上所有结点的BF值只能是-1、0、1。
反之,只要⼆叉树上⼀个结点的BF的绝对值⼤于1,则该⼆叉树就不是平衡⼆叉树。
图1演⽰了平衡⼆叉树和⾮平衡⼆叉树。
AVL树的构造如何构造⼀棵平衡⼆叉树呢?动态地调整⼆叉查找树平衡的⽅法为:每插⼊⼀个结点后,⾸先检查是否破坏了树的平衡性,如果因插⼊结点⽽破坏了⼆叉查找树的平衡,则找出离插⼊点最近的不平衡结点,然后将该不平衡结点为根的⼦树进⾏旋转操作,我们称该不平衡结点为旋转根,以该旋转根为根的⼦树称为最⼩不平衡⼦树。
失衡状态可归纳为4种,它们对应着4种旋转类型。
下⾯使⽤了Flash动画演⽰了这四种旋转类型,请确保你的电脑安装了Flash8.0以上版本的播放器,并且浏览器允许使⽤Flash。
平衡二叉树

Vocabulary
树 tree 子树 subtree 森林 forest 根 root 叶子 leaf 结点 node 深度 depth 层次 level 双亲 parents 孩子 children 兄弟 brother 祖先 ancestor 子孙 descentdant
性质4
具有n个结点的接近完全二叉树的深度为
证明:假设深度为k,则根据性质2和接近完全 二叉树的定义有
性质5
如果对一棵有n个结点的接近完全二叉树(其深度为log2n+1,下取 整)的结点按层序编号(从第1层到第log2n+1层,每层从左到右), 则对任一结点i(1≤i≤n),有 (1)如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双 亲PARENT(i)是结点[ i/2]。 (2)如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩 子LCHILD(i)是结点2i (3)如果2i+l>n,则结点i无右孩 子;否则其右孩子只RCHILD(i) 是结点2i+1
A B C D
E
F Right subtree
Left subtree
Rotate the tree clockwise by 45
A
N
45
B E K
NCBiblioteka FNNDN
G
NN
H M
NN
I
N
J
NN
L
NN
Element Left Right
Left
Right
Several binary trees
depth of ni ::= length of the unique path K from the root to ni. Depth(root) = 0.
平衡二叉树用法
平衡二叉树用法平衡二叉树,这可是个挺有趣的东西呢。
就像是一群小伙伴排队,得保持一种很和谐的状态。
咱先说说啥是平衡二叉树吧。
你可以把它想象成一个特殊的树状结构,这棵树里的每个节点呢,就像一个个小家庭。
它有个特点,就是左右两个子树的高度差不能太大,不然就像一个人两条腿不一样长,走路就不稳当了。
要是左边的子树长得特别高,右边的子树矮矮的,那就不平衡了,就像盖房子一边地基深一边地基浅,很容易出问题的。
那平衡二叉树有啥用呢?嘿,用处可大了去了。
比如说你要在一大堆数据里找一个特定的数据,就像在一个装满东西的大仓库里找一个小零件。
如果没有平衡二叉树这种巧妙的结构,你可能得翻遍整个仓库,累个半死还不一定找得到。
但是有了平衡二叉树呢,就好像仓库里有了很清晰的分区和索引,你可以很快地定位到那个小零件所在的区域,然后轻松找到它。
这在计算机处理数据的时候,能节省好多时间和资源呢。
再打个比方,平衡二叉树就像是一个超级有条理的图书管理员。
你想要找一本书,这个管理员能很快根据书的类别、编号之类的信息,在图书馆的书架里准确找到那本书。
要是没有这种条理,那图书馆就乱成一团,找本书得费好大劲儿。
在实际的编程或者数据处理中,平衡二叉树的用法可不少。
当你有很多数据需要不断地插入、删除和查找的时候,平衡二叉树就像一个贴心的小助手。
比如说一个游戏里,要记录每个玩家的等级、得分之类的信息。
这些信息一直在变化,一会儿有新玩家加入,等级信息要插入,一会儿玩家升级了得分变了,要更新信息,还有的时候要查看某个玩家的具体数据。
如果用平衡二叉树来管理这些数据,就像有个小秘书把一切都安排得井井有条。
你看啊,要是没有平衡二叉树这种结构,数据多了以后,查找数据就会变得特别慢,就像你在一个没有交通规则的马路上开车,到处都是乱哄哄的,根本走不动。
而平衡二叉树就像是给数据的世界建立了交通规则,让一切都变得顺畅起来。
不过呢,平衡二叉树也不是那么好伺候的。
要想让它一直保持平衡的状态,就像要让一个调皮的孩子一直乖乖听话一样难。
平衡二叉树
6.6 平衡二叉树(AVL树)★3◎4平衡二叉树、一棵空树,或者是具有下列性质的二叉排序树:它的左子树和右子树都是平衡二叉树,且左子树和右子树高度之差(平衡因子)的绝对值不超过1。
在平衡二叉树上插入或删除结点后,可能使树失去平衡,因此,需要对失去平衡的树进行平衡化调整。
设a 结点为失去平衡的最小子树根结点,对该子树进行平衡化调整归纳起来有以下4种情况:(1)左单旋转(LL)型调整(在a的右孩子的右子树上插入结点,使得a结点的平衡因子从﹣1变成﹣2)如图6-5(a)为插入前的子树。
其中,B为结点a的左子树,D、E分别为结点c的左右子树,B、D、E三棵子树的高均为h。
图6-5(a)所示的子树是平衡二叉树。
在图6-5(a)所示的树上插入结点x,如图6-5(b)所示。
结点x插入在结点c的右子树E上,导致结点a的平衡因子绝对值大于1,以结点a为根的子树失去平衡。
【调整策略】调整后的子树除了各结点的平衡因子绝对值不超过1外,还必须是二叉排序树。
由于结点c的左子树D可作为结点a的右子树,将结点a为根的子树调整为左子树是B,右子树是D,再将结点a为根的子树调整为结点c的左子树,结点c为新的根结点,如图6-5(c)所示。
【平衡化调整操作判定】沿插入路径检查三个点a、c、E,若它们处于与“\”直线同一个方向,则要作左单旋转,即以结点c为轴逆时针旋转。
(2)右单旋转(RR)型调整(在a的左孩子的左子树上插入结点,使得a结点的平衡因子从1变成2)RR型调整与LL型调整类似,沿插入路径检查三个点a、c、E,若它们处于与“/”直线同一个方向,则要做右单旋转,即以结点c为轴顺时针旋转,如图6-6所示。
(3)先左后右双向旋转(LR)型调整(在a的左孩子的右子树上插入结点,使得a 结点的平衡因子从1变成2)如图6-7(a)为插入前的子树,根结点a的左子树比右子树高度高1,待插入结点x将插入到结点b的右子树上,并使结点b的右子树高度增加1,从而使结点a的平衡因子的绝对值大于1,导致结点a为根的子树平衡被破坏,如图6-7(b)、图6-7(c)所示。
实验四 平衡二叉树演示
实验四平衡二叉树演示1.问题定义及需求分析1.1课题目的和任务问题描述:利用平衡二叉树设计动态查找表。
实验要求:设计平衡二叉树的动态演示的模拟程序。
1)采用平衡二叉树存储结构。
2)完成平衡二叉树的创建、查找、插入和删除的演示操作。
3)可以考虑两棵平衡二叉树的合并。
1.2数据形式输入数据形式:通过键盘输入数据输入值的范围:树中元素的值为float型,范围为1.2e-38至3.4e+38;树的名称为char类型数据,可以输入字母,数字和符号,但是长度必须在20位以内;对菜单进行操作时,输入数据长度必须在200以内,且有效的输入数据为0至7,其中0为退出程序,1至7为对应菜单的操作选项。
输出数据形式:输出到显示器。
1.3程序功能创建平衡二叉树存储结构,通过平衡因子,使二叉排序树达到平衡,提供平衡二叉树的创建、查找和删除,树中元素的查找、插入和删除等基本功能,可以实现创建多棵平衡二叉树,并且能够进行两棵树的合并。
通过平衡二叉树,能够使树时刻保持平衡,从而提高在树中遍历数据的速度,具有重要意义。
1.4测试数据1 //创建平衡二叉树2 //输入创建树的个数t1 //输入第一个树的名称5 //输入第一个树中元素的个数5 26 8 9 //依次输入各个元素t2 //输入第二个树的名称5 //输入第二个树中元素的个数3 14 10 7 //依次输入各个元素5 //层次遍历输出第一个树的结构图t1 //操作树名5 //层次遍历输出第二个树的结构图t2 //操作树名3 //插入元素操作t1 //操作树名1 //插入元素个数7 //依次插入元素5 //层次遍历输出树的结构图t1 //操作树名4 //删除元素操作t2 //操作树名1 //删除元素个数7 //依次删除元素5 //层次遍历输出树的结构图t2 //操作树名6 //合并两个树操作t1 t2 //操作树名5 //层次遍历输出树的结构图t1 //操作树名2 //查询元素操作t1 //操作树名5 //需要查询的元素(该元素树中存在)2 //查询元素操作t1 //操作树名11 //需要查询的元素(该元素树中不存在)7 //删除二叉平衡树操作t1 //操作树名2 //查询操作t1 //操作树名(会提示该树不存在,说明删除树成功)0 //退出程序2.概要设计2.1抽象数据类型需要定义一个树的结构类型,其中包含数据类型,它的左右孩子指针,以及平衡因子,平衡因子的取值为-1,0,1三种,分别对应树的右边高(RH),平衡(EH)和左边高(LH)三种情形,通过平衡因子的判别,来调整树的高度使其达到平衡;另外需要用到双向链表的数据结构,以及队列的数据结构。
平衡二叉树的定义及基本操作(查找、插入、删除)及代码实现
平衡⼆叉树的定义及基本操作(查找、插⼊、删除)及代码实现⽂章⽬录平衡⼆叉树的定义 为了避免树的⾼度增长过快,降低⼆叉排序树的性能,我们规定在插⼊和删除⼆叉树结点时,要保证在任意结点的左、右⼦树⾼度差的绝对值不超过1,将这样的树称为平衡⼆叉树(Balanced Binary Tree),简称平衡树(AVL)。
此外,AVL树⼜称为⾼度平衡的⼆叉查找树。
定义结点左⼦树与右⼦树的⾼度差为该结点的平衡因⼦,则平衡⼆叉树结点的平衡因⼦的值只可能是-1,0或1 。
平衡⼆叉树可定义为:或者是⼀棵空树,或者是具有下列性质的⼆叉树:它的左⼦树和右⼦树都是平衡⼆叉树,且左⼦树和右⼦树的⾼度差的绝对值不超过1。
平衡⼆叉树的结点类型描述:typedef struct AVLNode{int data;//数据域int bf;//平衡因⼦struct AVLNode *lchild,*rchild;//指针域}AVLNode,*AVLTree;平衡⼆叉树的查找 平衡⼆叉树上进⾏查找的过程与⼆叉排序树相同,详细完整代码请参照。
因此,在查找过程中,与给定值进⾏⽐较的关键字个数不超过树的深度。
可以证明,含有n个结点的平衡⼆叉树的最⼤深度为O(log n),因此平衡⼆叉树的平均查找长度为O(log n)。
22平衡⼆叉树的平衡旋转 ⼆叉排序树保证平衡的基本思想如下: 每当在⼆叉排序树中插⼊(或删除)⼀个结点时,⾸先检查其插⼊路径上的结点是否因为此次操作导致了不平衡。
若导致了不平衡,则先找到插⼊路径上离插⼊结点最近的平衡因⼦的绝对值⼤于1的结点A,再对以A为根的⼦树,在保持⼆叉排序树特性的前提下,调整各结点的位置关系,使之重新达到平衡。
⼀般可将失去平衡后进⾏调整的规律归纳为下列四种情况:LL平衡旋转,RR平衡旋转,LR平衡旋转,RL平衡旋转。
LL平衡旋转(右单旋转) 由于在结点A的左孩⼦(L)的左⼦树(L)上插⼊了新结点,A的平衡因⼦由1增⾄2,导致了以A为根的⼦树失去平衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目:平衡二叉树操作的演示一、需求分析1. 初始,平衡二叉树为空树,操作界面给出两棵平衡二叉树的显示、查找、插入、删除、销毁、合并两棵树,几种种选择。
其中查找、插入和删除操作均要提示用户输入关键字。
每次插入或删除一个节点后都会更新平衡二叉树的显示。
2. 平衡二叉树的显示采用凹入表形式。
3. 每次操作完毕后都会给出相应的操作结果,并进入下一次操作,直到用户选择退出程序。
二、概要设计1.平衡二叉树的抽象数据类型定义:ADT BalancedBinaryTree{数据对象D:D是具有相同特性的数据元素的集合。
各个数据元素均含有类型相同,可唯一标志的数据元素的关键字。
数据关系R:数据元素同属一个集合。
基本操作P:InitA VL(BSTree& T)操作结果:构造一个空的平衡二叉树TDestroyA VL(BSTree& T)初始条件:平衡二叉树T存在操作结果:销毁平衡二叉树TSearchA VL(BSTree T,int key)初始条件:平衡二叉树T存在,key为和关键字相同类型的给定值操作结果:若T中存在关键字和key相等的数据元素,则返回指向该元素的指针,否则为空InsertA VL(BSTree& T,int key,Status& taller)初始条件:平衡二叉树T存在,key和关键字的类型相同操作结果:若T中存在关键字等于key的数据元素则返回,若不存在则插入一个关键字为key的元素DeleteA VL(BSTree& T,int &key,Status& lower)初始条件:平衡二叉树T存在,key和关键字的类型相同操作结果:若T中存在关键字和key相同的数据元素则删除它}ADT BalancedBinaryTree2.本程序包含二个模块1)主程序模块:在文件A VLTree.cpp中,主要实现与用户的交互,以及对平衡二叉树基本操作调用。
Void main(){接收命令;While(“命令”!=“退出”){处理命令;清屏并得新打印提示信息;接收下一条命令;}}2)平衡二叉树基本操作在头文件A VLTree.h中,实现平衡二叉树的抽象数据类型的各函数原型。
各模块间的调用关系如下:主程序模块三、详细设计1. 根据题目要求和平衡二叉树的操作特点,平衡二叉树采用整数链式存储结构,并实现在头文件AVL.h中。
――――――基本操作的函数原型――――――#define LH 1 //左高#define EH 0 //等高#define RH -1 //右高#define TRUE 1#define FALSE 0#define ERROR 0#define OK 1typedef int Status;typedef int ElemType; //本程序处理数据对象为整型typedef struct BSTNode{ElemType data;int bf;struct BSTNode *lchild,*rchild;}BSTNode,*BSTree;――――――――内部操作――――――――1)平衡二叉树基本操作实现//构造平衡二叉树TStatus InitAVL(BSTree &T){T=NULL;return OK;}//对以*p为根的二叉树作左旋处理,处理之后p指向新的树根结点//即旋转处理之前的右子树的根结点void L_Rotate(BSTree &p){BSTree rc;rc=p->rchild;p->rchild=rc->lchild;rc->lchild=p; p=rc;}//对以*p为根的二叉树作右旋处理,处理之后p指向新的树根结点//即旋转处理之前的左子树的根结点void R_Rotate(BSTree &p){BSTree lc;lc=p->lchild;p->lchild=lc->rchild;lc->rchild=p; p=lc;}//对以指针T所指结点为根的二叉树作右平衡处理//本算法结束时T指向新的根结点void LeftBalance(BSTree &T){BSTree lc,rd;lc=T->lchild;switch(lc->bf){case LH:T->bf=lc->bf=EH;R_Rotate(T); break;case RH:rd=lc->rchild;switch(rd->bf){case LH:T->bf=RH; lc->bf=EH; break;case EH:T->bf=lc->bf=EH; break;case RH:T->bf=EH; lc->bf=LH; break;}rd->bf=EH;L_Rotate(T->lchild);R_Rotate(T);}}//对以指针T所指结点为根的二叉树作右平衡处理//本算法结束时T指向新的根结点void RightBalance(BSTree& T){BSTree rc,rd;rc=T->rchild;switch(rc->bf){case RH: T->bf=rc->bf=EH;L_Rotate(T);break;case LH: rd=rc->lchild;switch(rd->bf){case RH:T->bf=LH; rc->bf=EH; break;case EH:T->bf=rc->bf=EH; break;case LH:T->bf=EH; rc->bf=RH; break;}rd->bf=EH;R_Rotate(T->rchild);L_Rotate(T);}}//查找关键字为key的结点//如有返回指向此结点的指针,如无返回空Status SearchA VL(BSTree T,int e){if(!T) return ERROR;if(T->data==e){printf("\t结果: %d[%d]\n\t",T->data,T->bf);return OK;}else{if(T->lchild)if(SearchA VL(T->lchild,e))return OK;if(T->rchild)if(SearchA VL(T->rchild,e))return OK;return ERROR;}}//若在平衡的二叉排序树中不存在和e相同的关键字的结点,则插入一个数据元素为e的新结点并返回1,否则返回0。
//若因插入而使二叉排序树失去平衡,则做平衡旋转处理//布尔变量taller反映T长高与否Status InsertAVL(BSTree &T,ElemType e,Status &taller){if(!T){T=(BSTree)malloc(sizeof(BSTNode));T->data=e;T->lchild=T->rchild=NULL;T->bf=EH;taller=TRUE;}else{if(e==T->data){taller=FALSE; return FALSE;}if(e<T->data){if(!InsertAVL(T->lchild,e,taller)) return FALSE;if(taller)switch(T->bf){case LH:LeftBalance(T); taller=FALSE; break;case EH:T->bf=LH; taller=TRUE; break;case RH:T->bf=EH; taller=FALSE; break;}}else{if(!InsertA VL(T->rchild,e,taller)) return FALSE;if(taller)switch(T->bf){case RH:RightBalance(T); taller=FALSE; break;case EH:T->bf=RH; taller=TRUE; break;case LH:T->bf=EH; taller=FALSE; break;}}}return TRUE;}//打印空格void Printblank(int i){while(i >=0){printf(" ");i--;}}//以凹入表的形式显示平衡二叉树Tvoid ViewTree(BSTree T,int i){if(T){ Printblank(i); printf("%d[%d]\n",T->data,T->bf);} else{ Printblank(i); printf("NULL\n"); return; } ViewTree(T->lchild,i+5);ViewTree(T->rchild,i+5);}//销毁平衡二叉树void DestroyAVL(BSTree &T){if(T){if(T->lchild)DestroyA VL(T->lchild);if(T->rchild)DestroyA VL(T->rchild);free(T);T=NULL;}}//连接二叉树T2到T1中Status CombineA VL(BSTree &T1,BSTree& T2){Status taller;if(!T2)return TRUE;if(T2->lchild) CombineA VL(T1,T2->lchild);if(T2->rchild) CombineA VL(T1,T2->rchild);if(!InsertAVL(T1,T2->data,taller)) return FALSE;return TRUE;}//从二叉排序树中删除结点p,并重接它的左或右子树Status Delete(BSTree& p,int &e,int &flag){BSTree q,s;if(!p->rchild){q=p;if(p->lchild){p->lchild->bf=p->bf;e=p->lchild->data;}p=p->lchild;free(q);flag=1;}else if(!p->lchild){q=p;p->rchild->bf=p->bf;e=p->rchild->data;p=p->rchild;free(q);flag=1;}else{q=p; s=p->lchild;while(s->rchild){q=s; s=s->rchild;}p->data=s->data;if(q!=p)q->rchild=s->lchild;else {q->lchild=s->lchild;p->bf=RH;}e=q->data;free(s);}return TRUE;}//若二叉排序树T中存在关键字等于e的数据元素时,则删除该数据元素结点//并返回TRUE,否则返回FALSEStatus DeleteBST(BSTree& T,int &e,int &flag){if(!T)return FALSE;else{if(e==T->data)return Delete(T,e,flag);else if(e<T->data) {if(!DeleteBST(T->lchild,e,flag)) return FALSE;return TRUE;}else {if(!DeleteBST(T->rchild,e,flag)) return FALSE;return TRUE;}}}void DelBalance(BSTree& T,int e, Status &lower,int &flag) {if(!T){lower=TRUE; return;}if(e==T->data){if(flag==1)switch(T->bf){case RH:case LH:T->bf=EH; lower=TRUE; break;}else switch(T->bf){case RH:lower=FALSE; break;case EH:T->bf=LH; lower=FALSE; break;case LH:LeftBalance(T); lower=TRUE; break;}return ;}if(e<T->data){DelBalance(T->lchild,e,lower,flag);if(lower)switch(T->bf){case LH:T->bf=EH; lower=TRUE; break;case EH:T->bf=RH; lower=FALSE; break;case RH:RightBalance(T); lower=TRUE; break;}}if(e>T->data){DelBalance(T->rchild,e,lower,flag);if(lower)switch(T->bf){case RH:T->bf=EH; lower=TRUE; break;case EH:T->bf=LH; lower=FALSE; break;case LH:LeftBalance(T); lower=TRUE; break;}}return ;}//删除平衡二叉树结点Status DeleteA VL(BSTree &T,int &e,Status &lower){ int flag=0;if(!DeleteBST(T,e,flag)) return FALSE;else DelBalance(T,e,lower,flag);return TRUE;}2)主函数Main及其它辅助函数的实现/*主函数*/#include "A VLTree.h"void main(){system("color 3f");void Print(); void About();BSTree T,t,p; int e,s; Status taller,lower;InitAVL(T); InitA VL(t); InitA VL(p);Print();scanf("%d",&s);while(s!=8){switch(s){case 1: //显示printf("按凹入表形式打印二叉树结构:\n");printf("T:\n");PrintTree(T,1);printf("t:\n");PrintTree(t,1);break;case 2: //查找printf("\t选择树(1,2):");scanf("%d",&s);printf("\t关键字(整数):");scanf("%d",&e);if(s==1) s=SearchA VL(T,e);if(s==2) s=SearchA VL(t,e);if(!s) printf("\t查找失败\n\t");break;case 3: //插入printf("\t选择树(1-T,2-t):");scanf("%d",&s);printf("\t关键字(整数):");scanf("%d",&e);if(s==1){InsertA VL(T,e,taller);printf("T:\n");PrintTree(T,1);}if(s==2){InsertA VL(t,e,taller);printf("t:\n");PrintTree(t,1);}break;case 4: //删除printf("\t选择树(1-T,2-t):");scanf("%d",&s);printf("\t关键字(整数):");scanf("%d",&e);if(s==1)if(DeleteA VL(T,e,lower))printf("\t删除成功\n\t");elseprintf("\t删除失败\n\t");if(s==2)if(DeleteA VL(t,e,lower))printf("\t删除成功\n\t");elseprintf("\t删除失败\n\t");break;case 5: //合并if(CombineA VL(T,t))printf("\t合并成功\n");elseprintf("\t合并失败\n");printf("合并后T:\n");PrintTree(T,1);break;case 6: //销毁printf("\t选择树(1,2):");scanf("%d",&s);if(s==1) DestroyA VL(T);if(s==2) DestroyA VL(t);printf("\t销毁成功\n\t");break;}system("pause");Print();scanf("%d",&s);}}void Print(){system("cls");printf(" ※※※※平衡二叉树操作演示※※※※\n");printf("\n");printf(" **************菜单**************** \n");printf(" * 1. 显示* \n");printf(" * 2. 查找* \n");printf(" * 3. 插入* \n");printf(" * 4. 删除* \n");printf(" * 5. 合并* \n");printf(" * 6. 销毁* \n");printf(" * 7. 退出* \n");printf(" ********************************** \n");printf("请选择:\n");}3)函数之间的调用关系图:PrintTreeDeleteR_Rotate L_Rotate四、调试分析1. 本程序设计到二衡二叉树主要操作的几个函数大部分采用递归的形式实现。
