宁夏银川九中高三上学期第一次月考——数学文数学(文)
《精编》宁夏银川一中高三数学上学期第一次月考试题新人教A版 文.doc

xy-1127π 3π银川一中2021届高三年级第一次月考数 学 试 卷〔文〕第一卷一、选择题〔本大题共12小题,每题5分,总分值60分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.〕 1.集合}111|{≥-+=x x x M ,集合}032|{>+=x x N ,那么=⋂N M C R )(( ) A .(-1,23) B .(-1,23] C .[-1,23) D .[-1,23] 2.α是第二象限角,且sin(53)-=+απ,那么tan2α的值为( ) A .54 B .723- C .724- D .924- 3.以下函数中,在其定义域是减函数的是( ) A. 12)(2++-=x x x f B. x x f 1)(=C. ||)41()(x x f = D. )2ln()(x x f -= 4. 以下函数中,最小正周期为π,且图象关于直线x=3π对称的函数是( )A .y=2sin(2x+3π) B .y=2sin(2x-6π)C .y=2sin(32π+x ) D .y=2sin(2x-3π) 5. 函数xx x f 2)1ln()(-+=的零点所在的大致区间是〔 〕 A .〔3,4〕 B .〔2,e 〕 C .〔1,2〕 D .〔0,1〕6.二次函数4)(2+-=ax x x f ,假设)1(+x f 是偶函数,那么实数的值为( ) A. -1B. 1C. -2D. 27. 2||,0)(sin(πϕωϕω<>+=x y )的图象的一局部图形如以下列图,那么函数的解析式为( ) A .y=sin(x+3π) B .y=sin(x-3π)C .y=sin(2x+3π)D .y=sin(2x-3π)8. 设a 为实数,函数f (x )=x 3+ax 2+(a -2)x 的导数是)('x f ,且)('x f 是偶函数,那么曲线y =f (x )在原点处的切线方程为( )A .y =-2xB .y =3xC .y =-3xD .y =4x9. 将函数y=sin(2x+4π)的图象向左平移4π个单位,再向上平移2个单位,那么所得图象的函数解析式是( ) A .y=2cos 2(x+8π) B .y=2sin 2(x+8π)C .y=2-sin(2x-4π) D .y=cos2x10.函数⎩⎨⎧≤<+-<≤---=)10(1)01(1)(x x x x x f ,那么1)()(->--x f x f 的解集为( )A .(-∞,-1)∪(1,+∞) B. [-1,-21)∪(0,1] C .(-∞,0)∪(1,+∞) D. [-1,-21]∪(0,1) 11.对于任意的实数a 、b ,记max{a,b}=⎩⎨⎧<≥)()(b a b b a a .假设F(x)=max{f(x),g(x)}(x ∈R),其中函数y=f(x)(x ∈R)是奇函数,且在x=1处取得极小值-2,函数y=g(x) (x ∈R)是正比例函数,其图象与x ≥0时的函数y=f(x)的图象如以下列图,那么以下关于函数y=F(x)的说法中,正确的选项是( ) A .y=F(x)为奇函数 B .y=F(x)有极大值F(-1)C .y=F(x)的最小值为-2,最大值为2D .y=F(x)在(-3,0)上为增函数12.设函数⎪⎩⎪⎨⎧<-≥-=)2(1)21()2()2()(x x x a x f x 是R 上的单调递减函数,那么实数a 的取值范围为( )A .(-∞,2)B .(-∞,813] C .(0,2) D .[813,2) 二.填空题:〔本大题共4小题,每题5分。
宁夏银川九中2015届高三上学期第一次月考试题 文科综合试题
绝密★启用前宁夏银川九中2015届高三上学期第一次月考试题文科综合试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号框涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号框。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷和草稿纸上无效。
4.考试结束,将本试卷和答题卡一并交回。
5.本试卷共12页,如遇缺页、漏页、字迹不清等情况,考生须及时报告监考老师。
第Ⅰ卷本卷共35小题。
每小题4分,共140分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
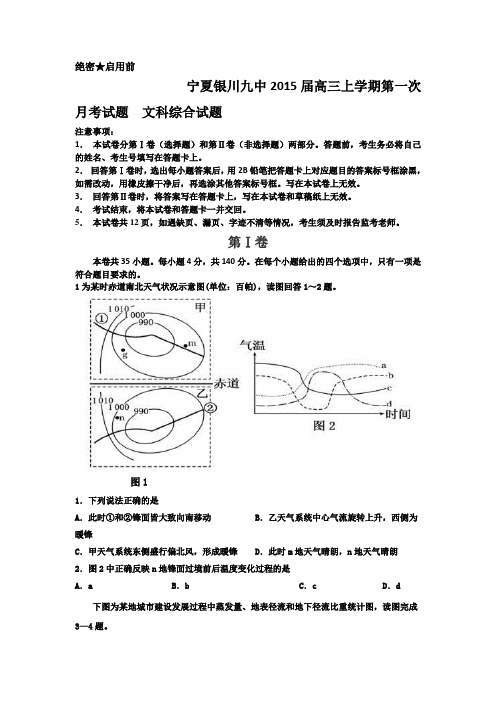
1为某时赤道南北天气状况示意图(单位:百帕),读图回答1~2题。
图11.下列说法正确的是A.此时①和②锋面皆大致向南移动 B.乙天气系统中心气流旋转上升,西侧为暖锋C.甲天气系统东侧盛行偏北风,形成暖锋 D.此时m地天气晴朗,n地天气晴朗2.图2中正确反映n地锋面过境前后温度变化过程的是A.a B.b C.c D.d下图为某地城市建设发展过程中蒸发量、地表径流和地下径流比重统计图,读图完成3—4题。
3.该城市地表径流和地下径流的比重变化的原因主要是A.降水量减少B.硬化地面增加C.过度开采地下水D.水资利用率低4.下列措施对缓解图示变化趋势作用不大的是A.增加城市绿地面积B.保护城市湿地生态系统C.完善城市排水系统D.限制建筑物的高度下图中①—④箭头表示洋流的流向。
读图回答5—6题。
5.关于图中①~④洋流的叙述正确的是A.①洋流的形成与气压带风带季节性北移有关B.②洋流反映了该海域8月洋流的流向C.③洋流按成因分类属于补偿流D.④洋流流经的两岸地区为热带雨林带6.当赤道以北海域洋流流向为②时,下列叙述正确的是A.我国河流多为丰水期B.非洲热带草原一片枯黄C.北太平洋副热带高压势力强盛D.亚欧大陆等温线向低纬凸出热岛强度是指中心城区比郊区气温高出的数值大小,下图是某大城市热岛强度日变化示意图。
宁夏回族自治区银川一中2021届高三上学期第一次月考数学(文)试题含有答案

银川一中2021届高三年级第一次月考文 科 数 学命题人:注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,务必将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、已知集合M ={x |-4<x <2},N ={x |x 2-x -6<0},则M ∩N =( )A .{x |-4<x <3}B .{x |-4<x <-2}C .{x |-2<x <2}D .{x |2<x <3}2、设x ∈R ,则“x 3>8”是“|x |>2”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 3、函数y =)1lg(322+++-=x x x y 的定义域为( )A .(-1,3]B .(-1,0)∪(0,3]C .[-1,3]D .[-1,0)∪(0,3]4、下列函数中,在区间(0,+∞)上单调递增的是( )A .y =x 12 B .y =2-xC .y =log 12x D .y =1x5、已知f (x )=a 2-32x +1是R 上的奇函数,则f (a )的值为( )A .76B .13C .25D .236、设a =0.80.7,b =0.80.9,c =1.20.8,则a ,b ,c 的大小关系是( )A .a >b >cB .b >c >aC .c >a >bD .c >b >a7、若sin α=-513,且α为第四象限角,则tan α的值等于( )A .125B .-125C .512D .-5128、某食品的保鲜时间y (单位:小时)与储藏温度x (单位:C )满足函数关系e kx b y+= (e =2.718为自然对数的底数,,k b 为常数).若该食品在0C 的保鲜时间是192h 小时,在22C 的保鲜时间是48h ,则该食品在33C 的保鲜时间是( ). A. 16hB. 20hC. 24hD. 21h9、设x R ∈,定义符号函数10sgn 0010x x x x ,,,>⎧⎪==⎨⎪-<⎩,则( ).A .{}sgn x x x = B .{}sgn x x x =C .{}sgn x x x =D .{}sgn x x x=10、若1sin α+1cos α=3,则sin αcos α=( )A .-13B .13C .-13或1D .13或-111、已知函数f (x )=⎩⎪⎨⎪⎧log 12x ,x >12+36x ,x ≤1,则f [f (12)]=( )A .3B .4C .-3D .3812.已知定义在(0,+∞)上的函数)(x f ,)('x f 是)(x f 的导函数,满足0)()('<-x f x xf ,且2)2(=f ,则0)(>-x x e e f 的解集是( ) A .),0(2eB .),2(ln +∞C .)2ln ,(-∞D .),(2+∞e二、填空题:(本大题共4小题,每小题5分,共20分)13、已知函数()()01xf x a b a a =+>≠,的定义域和值域都是[]10-,,则a b +=_____.14、若cos(π4-α)=35,则sin 2α=________.15、若f (x )=-12(x -2)2+b ln x 在(1,+∞)上是减函数,则b 的取值范围是_______.16、已知f (x )=⎩⎪⎨⎪⎧|lg x |,x >02|x |,x ≤0,则函数y =2f 2(x )-3f (x )+1的零点个数是________.三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答。
宁夏银川一中高三年级第一次月考(数学文).pdf

银川一中2012届高三年级第一次月考 数 学 试 卷(文) 2011.08 命题人:尹向阳 第Ⅰ卷 一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.设函数y=的定义域为M,集合N={y|y=x2,x∈R},则M∩N=( ) A. B.N C.[1,+∞) D.M 2.函数y=的定义域为( ) A.(,1) B.(,+∞) C.(1,+∞) D.(,1)∪(1,+∞) 3.对命题“x0∈R,x02-2x0+4≤0”的否定正确的是( ) A.x0∈R,x02-2x0+4>0 B.x∈R,x2-2x+4≤0 C.x∈R,x2-2x+4>0 D.x∈R,x2-2x+4≥0 4.已知直线:x+ay+6=0和:(a-2)x+3y+2a=0,则∥的充要条件是a=( ) A.3 B.1 C.-1 D.3或-1 5.函数y=的值域是( ) A.[0,+∞) B.(0,4] C.[0,4) D.(0,4) 6.下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是( ) A.y=x3 B.y=C.y=2|x| D.y=cosx 7.已知定义域为R的函数f(x)在区间(4,+∞)上为减函数,且函数y=f(x+4)为偶函数,则( ) A.f(2)>f(3) B.f(2)>f(5) C.f(3)>f(5) D.f(3)>f(6) 8.已知函数f(x)=,若f(2-x2)>f(x),则实数x的取值范围是( ) A.(-∞,-1)∪(2,+∞) B.(-∞,-2)∪(1,+∞) C.(-1,2) D.(-2,1) 9.若函数y=ax与y=-在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是( ) A.增函数 B.减函数 C.先增后减 D.先减后增 10.函数y=2x-x2的图象大致是( ) A B C D 11.某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x-0.15x2和L2=2x,其中x为销售量(单位:辆),若该公司在这两地共销售15辆车,则能获得的最大利润为( ) A.45.606 B.45.6 C.45.56 D.45.51 12.函数f(x)的定义域为D,若对于任意x1,x2∈D,当x10,则函数y=的最小值为________. 15.已知3a=5b=A,且,则A=________。
宁夏银川九中高三数学第一次模拟考试试题 文 新人教A版

宁夏银川九中2014届高三数学第一次模拟考试试题 文 新人教A 版一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.设常数a ∈R ,集合()(){}|10A x x x a =--≥,{}|1B x x a =≥-.若AB =R ,则a 的取值范围为( )A .(),2-∞B .(],2-∞C .()2,+∞D .[)2,+∞ 2 .设A,B 为直线y x =与圆221x y += 的两个交点,则||AB =( )A .1BCD .2 3.函数121()()2xf x x =-的零点个数为( )A .0B .1C .2D .3 4.设斜率为2的直线l 过抛物线2(0)y ax a =≠的焦点F,且和y 轴交于点A,若△OAF(O 为坐标原点)的面积为4,则抛物线方程为( ).A.24y x =±B.28y x =±C. 24y x =D. 28y x =5 .已知数列{}n a 的前n 项和为n S ,11a =,12n n S a +=,则n S =( )A .12n -B .132n -⎛⎫ ⎪⎝⎭C .123n -⎛⎫ ⎪⎝⎭D .112n - 6.从装有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概率是( )A.110B.310C.35D.9107.若函数[]()sin(0,2)3x f x ϕϕπ+=∈是偶函数,则ϕ=( ).A .2πB .23πC .32πD .53π 8.已知圆C 与直线x -y =0 及x -y -4=0都相切,圆心在直线x +y =0上,则圆C 的方程为( ).(A )22(1)(1)2x y ++-= (B) 22(1)(1)2x y -++=(C) 22(1)(1)2x y -+-= (D) 22(1)(1)2x y +++=9.如果不等式2()0f x ax x c =-->的解集为{|21}x x -<<, 那么函数()y f x =-的大致图象是( )10.过椭圆22221x y a b+=(0a b >>)的左焦点1F 作x 轴的垂线交椭圆于点P ,2F 为右焦点,若1260F PF ∠=,则椭圆的离心率为( ).A .2B .3C .12D .13 11.已知双曲线)0(12222>=-b by x 的左、右焦点分别是1F 、2F ,其一条渐近线方程为x y =,点),3(0y P 在双曲线上.则1PF ·2PF =( ).A. -12B. -2C. 0D. 412.某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .28+B .30+C .56+D .60+第Ⅱ卷二、填空题:请把答案填在题中横线上(本大题共4个小题,每小题5分,共20分)。
届高三上学期第一次月考数学(文)试题(附答案)

宁夏育才中学高三年级第一次月考数学 (文科)命题人:(试卷满分 150 分,考试时间为 120 分钟)第Ⅰ卷(共60分)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、若A={}|10x x +>,B={}|30x x -<,则AB = ( )A .(-1,+∞)B .(-∞,3) C.(-1,3) D.(1,3) 2.下列函数中,既是偶函数又在+∞(0,)单调递增的函数是( )A. 3y x =B. 1y x =+C. 21y x =-+D. 2x y -= 3.“1cos 2x =”是“2,3x k k Z ππ=+∈”的 条件( ) A 充分不必要B .必要不充分C .充要D .既不充分也不必要4. 11、设a =3.02,b=23.0,c=lo 2g 0.3, ,则a ,b,c 的大小关系( )A. a <b <cB. b <c <aC. c < b <aD. c <a <b5. 幂函数y=f(x)的图象经过点(4,12),则f(14)的值为( ) A.1B.4C.2D.36. 已知4cos 5α=-,且(,)2παπ∈,则tan()4πα-等于( ) A .17-B .7-C .71D .77.设()ln f x x x =,若0'()2f x =,则0x =( ) A. 2eB.e C.ln 22D. ln 2 8. 若将函数2sin 2y x =的图像向左平移12π个单位长度,则平移后图象的对称轴为( )A.()26k x k Z ππ=-∈ B 、()26k x k Z ππ=+∈ C 、()212k x k Z ππ=-∈ D 、()212k x k Z ππ=+∈9.函数()()xx x f 21ln -+=的零点所在的大致区间是( ) A.(0,1)B. (1,2)C. (2,3)D.(3,4)10.ABC ∆的内角A B C 、、的对边分别是a b c 、、,若2B A =,1a =,b =则c = ( ) A.B .2CD .111.若函数()f x kx Inx =-在区间()1,+∞单调递增,则k 的取值范围是( )A.(],2-∞- B . (],1-∞- C.[)2,+∞ D.[)1,+∞12.已知函数()y f x =的周期为2,当[1,1]x ∈-时2()f x x =,那么函数()y f x =的图象与函数|lg |y x =的图象的交点共有( )A .10个B .9个C .8个D .1个第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置. 13.在ABC 中且2,45,1===∆ABC S B a ,则△ABC 的外接圆的直 径为_____14.曲线32y x x =-在点(1,-1)处的切线方程是. 15.设函数)2(0,0,R,(x ) x sin((x) f πφωφω∈>∈+=A 的部分图象如右图所示,则f (x)的表达式 .16.给出下列说法:①命题“若α=6π,则sin α=21”的否命题是假命题; ②命题p:∃x 0∈R,使sinx 0>1,则p:∀x ∈R,sinx ≤1;③“ϕ=2π+2k π(k ∈Z)”是“函数y=sin(2x+ϕ)为偶函数”的充要条件;④命题p:∃x 0∈(0,2π),使sinx 0+cosx 0=21,命题q:在△ABC 中,若sinA>sinB,则A>B,那么命题(p)∧q 为真命题. 选出正确的命题 _____三.解答题:本大题共5个小题,满分70分. 解答应写出文字说明、证明过程或演算步骤. 17、(本小题满分10分)已知函数()24(0)2(0)12(0)x x f x x x x ⎧->⎪==⎨⎪-<⎩,(1)画出函数()f x 图像;(2)当43x -≤<时,求()f x 取值的集合.18.(本题满分12分)已知2tan ,02-=<<-x x π. 错误!未找到引用源。
宁夏回族自治区银川市2021届高三上学期第一次月考数学(文)试卷

文科数学命题人:注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,务必将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、已知集合M ={x |-4<x <2},N ={x |x 2-x -6<0},则M ∩N =( )A .{x |-4<x <3}B .{x |-4<x <-2}C .{x |-2<x <2}D .{x |2<x <3}2、设x ∈R ,则“x 3>8”是“|x |>2”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 3、函数y =)1lg(322+++-=x x x y 的定义域为( )A .(-1,3]B .(-1,0)∪(0,3]C .[-1,3]D .[-1,0)∪(0,3]4、下列函数中,在区间(0,+∞)上单调递增的是( )A .y =x 12 B .y =2-x C .y =log 12xD .y =1x5、已知f (x )=a 2-32x +1是R 上的奇函数,则f (a )的值为( )A .76B .13C .25D .236、设a =0.80.7,b =0.80.9,c =1.20.8,则a ,b ,c 的大小关系是( )A .a >b >cB .b >c >aC .c >a >bD .c >b >a7、若sin α=-513,且α为第四象限角,则tan α的值等于( )A .125B .-125C .512D .-5128、某食品的保鲜时间y(单位:小时)与储藏温度x(单位:C )满足函数关系e kx b y +=(e =2.718为自然对数的底数,,k b 为常数).若该食品在0C 的保鲜时间是192h 小时,在22C 的保鲜时间是48h ,则该食品在33C 的保鲜时间是(). A.16hB.20hC.24hD.21h9、设x R ∈,定义符号函数10sgn 0010x x x x ,,,>⎧⎪==⎨⎪-<⎩,则().A .{}sgn x x x = B .{}sgn x x x =C .{}sgn x x x =D .{}sgn x x x=10、若1sin α+1cos α=3,则sin αcos α=( ) A .-13B .13C .-13或1D .13或-111、已知函数f (x )=⎩⎪⎨⎪⎧log 12x ,x >12+36x ,x ≤1,则f [f (12)]=( )A .3B .4C .-3D .3812.已知定义在(0,+∞)上的函数)(x f ,)('x f 是)(x f 的导函数,满足0)()('<-x f x xf ,且2)2(=f ,则0)(>-x x e e f 的解集是() A .),0(2eB .),2(ln +∞C .)2ln ,(-∞D .),(2+∞e二、填空题:(本大题共4小题,每小题5分,共20分)13、已知函数()()01xf x a b a a =+>≠,的定义域和值域都是[]10-,,则a b +=_____.14、若cos(π4-α)=35,则sin2α=________.15、若f (x )=-12(x -2)2+b ln x 在(1,+∞)上是减函数,则b 的取值范围是_______.16、已知f (x )=⎩⎪⎨⎪⎧|lg x |,x >02|x |,x ≤0,则函数y =2f 2(x )-3f (x )+1的零点个数是________.三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答。
宁夏银川市第九中学高三数学上学期第一次月考试题 文

银川九中2016届高三第一次月考数学试卷(文)一、选择题(本大题共12小题,每小题5分,共60分)1.设集合M ={x |x ≥0,x ∈R },N ={x |x 2<1,x ∈R },则M ∩N =( )A .[0,1]B .[0,1)C .(0,1]D .(0,1) 2.函数y =1lnx -1的定义域为( ) A .(1,+∞) B .[1,+∞) C .(1,2)∪(2,+∞)D .(1,2)∪[3,+∞)3.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )A .y =e xB .y =sin xC .y =xD .y =ln x 24.若曲线y =f (x )在点(x 0,f (x 0))处的切线方程为3x -y +1=0,则( )A .f ′(x 0)<0B .f ′(x 0)>0C .f ′(x 0)=0D .f ′(x 0)不存在5.“x >0”是“3x 2>0”成立的( )A .充分不必要条件B .必要不充分条件C .既不充分也不必要条件D .充要条件6.函数f (x )=1x-6+2x 的零点一定位于区间( )A .(3,4)B .(2,3)C .(1,2)D .(5,6)7.已知f (x )=⎩⎪⎨⎪⎧f x -5,x ≥0,log 2-x ,x <0,则f (2 016)等于( )A .-1B .0C .1D .28.若命题“∃x 0∈R ,使得x 20+mx 0+2m -3<0”为假命题,则实数m 的取值范围是( )A .[2,6]B .[-6,-2]C .(2,6)D .(-6,-2) 9.函数f (x )=1+log 2x 与g (x )=21-x在同一直角坐标系下的图像大致是( )10.函数f (x )=x 2+|x -2|-1(x ∈R )的值域是( )A .[34,+∞)B .(34,+∞)C .[-134,+∞)D .[3,+∞)11.若函数f (x )=x 2+ax +1x 在(12,+∞)上是增函数,则实数a 的取值范围是( )A .[-1,0]B .[-1,+∞)C .[0,3]D .[3,+∞)12.已知函数f (x )满足:①定义域为R ;②对任意x ∈R ,有f (x +2)=2f (x );③当x ∈[-1,1]时,f (x )=1-x 2.若函数g (x )=⎩⎪⎨⎪⎧e xx ≤0,ln x x >0,则函数y =f (x )-g (x )在区间[-5,5]上零点的个数是( )A .7B .8C .9D .10二、填空题(本大题共4小题,每小题5分,共20分)13.已知f (2x +1)=3x -2,且f (a )=4,则a 的值是________. 14.若log a (a 2+1)<log a 2a <0,则实数a 的取值范围是________.15.已知曲线y =-13x 3+2与曲线y =4x 2-1在x =x 0处的切线互相垂直,则x 0的值为________.16.已知偶函数y =f (x )满足条件f (x +1)=f (x -1),且当x ∈[-1,0]时,f (x )=3x+49,则f (log 135)的值等于________.三、解答题(本大题共6小题,共70分)17.(本小题满分12分)函数f (x )对一切实数x ,y 均有f (x +y )-f (y )=(x +2y +1)x 成立,且f (1)=0.(1)求f (0)的值; (2)求f (x )的解析式.18.(本小题满分12分)已知函数f (x )=ax 2+b ln x 在x =1处有极值12.(1)求a ,b 的值;(2)判断函数y =f (x )的单调性并求出单调区间.19.(本小题满分12分) 已知函数f (x )=⎩⎪⎨⎪⎧x +22, x <0,4, x =0,x -22, x >0.(1)写出f (x )的单调区间; (2)若f (x )=16,求相应x 的值.20.(本小题满分12分) 已知p :指数函数f (x )=(2a -6)x在R 上是单调减函数;q :关于x 的方程x 2-3ax +2a 2+1=0的两根均大于3,若p 或q 为真,p 且q 为假,求实数a 的取值范围.21.(本题满分12分) 已知函数f (x )=ln x , g (x )=(x -a )2+(ln x -a )2.(1)求函数f (x )在A (1,0)处的切线方程;(2)若g ′(x )在[1,+∞)上单调递增,求实数a 的取值范围; (3)证明:g (x )≥12.(选考题)请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁夏银川九中2018届高三上学期第一次月考数学(文)试题本试卷满分150分(注:班级.姓名.学号.座位号一律写在装订线以外规定的地方,卷面不得出现任何标记) 一、 选择题(本大题共12小题,每小题5分)1.已知集合(){}lg 3A x y x ==+,{}2B x x =≥,则AB =( )A. (3,2]-B.(3,)-+∞C.[2,)+∞D.[3,)-+∞ 2.已知命题:1≤∈x cos R x ,有对任意,则A .1≥∈⌝x cos R x p ,使:存在B .1≥∈⌝x cos R x p ,有:对任意C .1>∈⌝x cos R x p ,使:存在D .1>∈⌝x cos R x p ,有:对任意 3.已知向量,,若与共线,则( )4.曲线在点处的切线的倾斜角为( )A .30°B .45°C .60°D .120° 5.若角α的终边在直线y =2x 上,则的值为( ) A .0 B. 34 C .1 D. 546.把函数图象上各点的横坐标缩短到原来的倍(纵坐标不变),再将图象向右平移个 单位,那么所得图象的一条对称轴方程为( )。
A . B . C . D . 7.下列说法错误..的是 ( ) A .命题“若,则中至少有一个为零”的否定是:“若,则都不为零”. B .对于命题,使得;则是,均有.C .命题“若,则方程有实根”的逆否命题为:“若方程无实根,则”. D“”是“”的充分不必要条件.8.已知向量,.若向量的夹角为,则实数=( )(A ) (B ) (C )0 (D )9. 已知分别是△的三个内角所对的边长,若,,,则(A )1 (B ) (C ) (D )10. 函数的零点所在的一个区间是A. (18,14)B. (14,12)C. (12,1) D. (1,2)11.函数在区间的简图是( )12.设函数()log (2)a f x x a =-+在区间上恒为正值,则实数的取值范围是A .B .C .D .二、填空题(本大题共4小题,每小题5分)13.已知向量,,若,则实数的值为=________.14.已知函数f (x )=ln(1+x )-ax 的图象在x =1处的切线与直线x +2y -1=0平行,则实数a 的值为______.15.若,则的值是 ___________.16.函数f (x )=sin ⎝⎛⎭⎫2x -π3(x ∈R)的图象为C ,以下结论正确的是________.(写出所有正确结论的编号)①图象C 关于直线x =11π12对称; ②图象C 关于点⎝⎛⎭⎫2π3,0对称; ③ 函数f (x )在区间⎝⎛⎭⎫-π12,5π12内是增函数;④由y =sin 2x 的图象向右平移π3个单位长度可以得到图象C .三、解答题(解答应写出文字说明、证明过程或求解演算步骤)17.(本题满分12分)设向量()()3sin ,sin ,cos ,sinx ,0,.2a x x b x x π⎡⎤==∈⎢⎥⎣⎦(I )若,求的值;(II )设函数,求的最大值。
18.(本题满分12分)在中,角的对边分别为,且满足()()B a c A b -+=πcos 2cos(Ⅰ)求角的大小;(Ⅱ)若,的面积为,求的值.19.(本题满分12分)已知函数f(x)=Asin(ωx +φ) (A>0,ω>0,|φ|<π2)在一个周期内的图象如图所示. (1)求函数的解析式;(2)设0<x<π,且方程f(x)=m 有两个不同的实数根,求实数m 的取值范围以及这两个根的和.20.(本题满分12分)已知函数f (x )=x 3-3ax 2+2bx 在点x =1处有极小值-1 (1)求a 、b 的值;(2)讨论函数f(x)的单调性.21.(本题满分12分)已知函数c bx x x x f ++-=2321)(。
(Ⅰ)若在是增函数,求b 的取值范围;(Ⅱ)若在时取得极值,且时,恒成立,求c 的取值范围。
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分,解答时请写清题号.22.(本小题满分10分)选修4-4:极坐标系与参数方程在直角坐标系xOy 中,直线L 的参数方程为(t 为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为.(Ⅰ)求圆C 的圆心到直线L 的距离;(Ⅱ)设圆C 与直线L 交于点A 、B .若点P 的坐标为(3,),求|PA|+|PB|.23.(本小题满分10分)选修4-5:不等式选讲 已知函数()|21||23|.f x x x =++- (1)求不等式的解集;(2)若关于x 的不等式的解集非空,求实数的取值范围.参考答案二、填空题:13. 14.1 15.-2- 16.①②③ 三、解答题:17.(本题满分12分)设向量()()3sin ,sin ,cos ,sinx ,0,.2a x x b x x π⎡⎤==∈⎢⎥⎣⎦(I )若,求的值;(II )设函数,求的最大值。
解:(I )由2222)(sin )4sin ax x x =+=,222(cos )(sin )1b x x =+=,及 又1[0,],sin 22x x π∈=从而,所以 ……4分(II )2()cos sin f x a b x x x =⋅=⋅+1112cos 2sin(2)2262x x x π-+=-+.……8分 当[0.]sin 2- 1.326x x πππ=∈时,()取最大值 所以…10分18.在中,角的对边分别为,且满足()()B a c A b -+=πcos 2cos (Ⅰ)求角的大小;(Ⅱ)若,的面积为,求的值.解: (Ⅰ))cos (sin )cos (sin 2cos sin B A B C A B -+-= ………………………2分 B C B A A B cos sin 2cos sin cos sin -=+∴B C B A cos sin 2)sin(-=+ …………………………4分…………………………6分(Ⅱ)32321sin 21=⨯==ac B ac S …………………………8分 又212)(cos 22222=+-+=-+=ac ac c a B ac c a b …………………10分 …………………12分19.已知函数f(x)=Asin(ωx +φ) (A>0,ω>0,|φ|<π2)在一个周期内的图象如图所示.(1)求函数的解析式;(2)设0<x<π,且方程f(x)=m 有两个不同的实数根,求实数m 的取值范围以及这两个根的和.解 (1)观察图象,得A =2,T =⎝ ⎛⎭⎪⎫11π12-π6×43=π.∴ω=2πT =2,∴f(x)=2sin(2x +φ).∵函数经过点⎝ ⎛⎭⎪⎫π6,2, ∴2sin ⎝ ⎛⎭⎪⎫2×π6+φ=2, 即sin⎝ ⎛⎭⎪⎫π3+φ=1. 又∵|φ|<π2,∴φ=π6, ∴函数的解析式为f(x)=2sin ⎝ ⎛⎭⎪⎫2x +π6. …………… 6分 (2)∵0<x<π,∴f(x)=m 的根的情况,相当于f(x)=2sin ⎝ ⎛⎭⎪⎫2x +π6与g(x)=m 的交点个数情况,且0<x<π,∴在同一坐标系中画出y =2sin ⎝ ⎛⎭⎪⎫2x +π6和y =m(m ∈R)的图象.由图可知,当-2<m<1或1<m<2时,直线y =m 与曲线有两个不同的交点,即原方程有两个不同的实数根.∴m 的取值范围为-2<m<1或1<m<2; …………… 9分当-2<m<1时,此时两交点关于直线x =23π对称,两根和为43π;当1<m<2时,此时两交点关于直线x =π6对称,两根和为π3. …………… 12分20.已知函数f (x )=x 3-3ax 2+2bx 在点x =1处有极小值-1. (1)求a 、b 的值;(2)讨论函数f(x)的单调性.解析:(1)f (1)=1-3a +2b =-1,又f ′(x )=3x 2-6ax +2b , ∴f ′(1)=3-6a +2b =0,∴a =13,b =-12.(2)f (x )=x 3-x 2-x ,∴f ′(x )=3x 2-2x -1=(3x +1)(x -1). 当x <-13或x >1时,f ′(x )>0;当-13<x <1时,f ′(x )<0.∴f (x )的单调增区间为(-∞,-13)和(1,+∞),单调减区间为(-13,1).21.已知函数c bx x x x f ++-=2321)(。
(Ⅰ)若在是增函数,求b 的取值范围;(Ⅱ)若在时取得极值,且时,恒成立,求c 的取值范围。
解;(1),∵在是增函数, ∴恒成立,∴,解得. ∵时,只有时,,∴b 的取值范围为.……4分 (2)由题意,是方程的一个根,设另一根为,则 ∴ ∴,…………………………………6分∵对时,恒成立,∴,解得或,故c 的取值范围为…………………………………………………………12分22. (本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线L 的参数方程为(t 为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为.(Ⅰ)求圆C的圆心到直线L的距离;(Ⅱ)设圆C与直线L交于点A、B.若点P的坐标为(3,),求|PA|+|PB|.(Ⅰ)由,可得,即圆C的方程为.由可得直线l的方程为.所以,圆C的圆心到直线l的距离为.5分(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得,即.由于△=.故可设t1、t2是上述方程的两个实根,所以,又直线l过点,故由上式及t的几何意义得.10分23.已知函数()|21||23|.f x x x=++-(1)求不等式的解集;(2)若关于x的不等式的解集非空,求实数的取值范围.。
