2018年上海市普通高等学校春季招生统一文化考试数学试卷及答案
2018年上海市春考数学试卷(含答案)
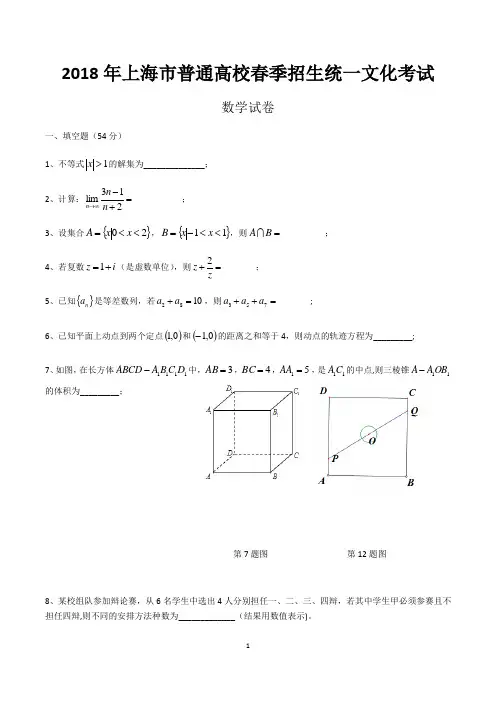
2018年上海市普通高校春季招生统一文化考试数学试卷一、填空题(54分)1、不等式1>x 的解集为______________;2、计算:_________213lim=+-∞→n n n ;3、设集合{}20<<=x x A ,{}11<<-=x x B ,则________=B A ;4、若复数i z +=1(是虚数单位),则______2=+zz ; 5、已知{}n a 是等差数列,若1082=+a a ,则______753=++a a a ;6、已知平面上动点到两个定点()0,1和()0,1-的距离之和等于4,则动点的轨迹方程为_________;7、如图,在长方体1111D C B A ABCD -中,3=AB ,4=BC ,51=AA ,是11C A 的中点,则三棱锥11OB A A -的体积为_________;第7题图 第12题图8、某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为_____________(结果用数值表示)。
9、设R a ∈,若922⎪⎭⎫ ⎝⎛+x x 与92⎪⎭⎫ ⎝⎛+x a x 的二项展开式中的常数项相等,则_______=a ;10、设R m ∈,若是关于的方程0122=-++m mx x 的一个虚根,则-z 的取值范围是________;11、设0>a ,函数()()1,0),sin()1(2∈-+=x ax x x x f ,若函数12-=x y 与()x f y =的图像有且仅有两个不同的公共点,则的取值范围是__________;12、如图,在正方形ABCD 的边长为米,圆的半径为1米,圆心是正方形的中心,点、分别在线段AD 、上,若线段PQ 与圆有公共点,则称点在点的“盲区”中,已知点以1。
5米/秒的速度从出发向移动,同时,点以1米/秒的速度从出发向移动,则在点从移动到的过程中,点在点的盲区中的时长均为_____秒(精确到0。
2018年上海市普通高等学校春季招生统一文化考试数学试卷

2018年上海市普通高等学校春季招生统一文化考试数学试卷一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)1.不等式||1x >的解集为__________.2.计算:31lim 2n n n →∞-=+__________. 3.设集合{|02}A x x =<<,{|11}B x x =-<<,则A B =__________.4.若复数z i i =+(i 是虚数单位),则2z z+=__________. 5.已知{}n a 是等差数列,若2810a a +=,则357a a a ++=__________.6.已知平面上动点P 到两个定点(1,0)和(1,0)-的距离之和等于4,则动点P 的轨迹为 __________.7.如图,在长方形1111B ABC A C D D -中,3AB =,4BC =,15AA =, O 是11A C 的 中点,则三棱锥11A AOB -的体积为__________.第7题图 第12题图8.某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、 四辩.若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为__________.9.设a R ∈,若922x x ⎛⎫+ ⎪⎝⎭与92a x x ⎛⎫+ ⎪⎝⎭的二项展开式中的常数项相等,则a =__________. 10.设m R ∈,若z 是关于x 的方程2210x mx m -+=+的一个虚根,则||z 的取值范围是__________.11.设0a >,函数()2(1)sin()f x x x ax =+-,(0,1)x ∈,若函数21y x =-与()y f x = 的图象有且仅有两个不同的公共点,则a 的取值范围是__________. 12.如图,正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲 区”中.已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度 从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长约为__________秒(精确到0.1)二、选择题(本大题共有4题,满分20分,每题5分)13.下列函数中,为偶函数的是( )(A )2y x -= (B )13y x =(C )12y x -= (D )3y x = 14.如图,在直三棱柱111AB A B C C -的棱虽在的直线中,与直线1BC异面的直线条数为( )(A )1 (B )2(C )3 (D )415.记n S 为数列{}n a 的前n 项和.“{}n a 是递增数列”是“n S 为递增数列”的( )(A )充分非必要条件 (B )必要非充分条件 (C )充要条件 (D )既非充分也非必要条件16.已知A 、B 为平面上的两个定点,且|2|AB =.该平面上的动线段PQ 的端点P 、Q ,满足||5AP ≤,6AB AP ⋅=,2AQ AP =-,则动线段PQ 所形成图形的面积为( )(A )36 (B )60 (C )81 (D )108三、解答题(本大题共有5题,满分76分,第17~19题每题14分,20题16分,21题18分)17.(本题满分14分,第1小题满分6分,第2小题满分8分)已知cos y x =.(1)若3(1)f α=,且[0,]απ∈,求()3f πα-的值; (2)求函数(2)2()y f x f x =-的最小值.18. (本题满分14分,第1小题满分6分,第2小题满分8分)已知a R ∈,双曲线222:1x y aΓ-=.(1)若点(2,1)在Γ上,求Γ的焦点坐标; (2)若1a =,直线1y kx =+与Γ相交于A 、B 两点,且线段AB 中点的横坐标为1,求实数k 的值.19.(本题满分14分,第1小题满分7分,第2小题满分7分)利用“平行于圆锥曲线的母线截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥视为圆锥)在广告牌上投影出其标识,如图1所示,图2是投影出的抛物线的平面图,图3是一个射灯的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,OC AB ⊥于C ,3AB =米, 4.5OC =米.(1)求抛物线的焦点到准线的距离; (2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到0.01°).图1 图2图320.(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分) 设0a >,函数1()12x f x a =+⋅. (1)若1a =,求()f x 的反函数1()f x -;(2)求函数()()y f x f x ⋅-=的最大值(用a 表示);(3)设()()(1)g x f x f x =--.若对任意(,0]x ∈-∞,)(()0g x g ≥恒成立,求a 的取值范围.21.(本题满分18分,第1小题满分3分,第2小题满分6分,第3小题满分9分) 若{}n c 是递增数列,数列{}n a 满足:对任意*n N ∈,存在*m N ∈,使得10m n m n a c a c +-≤-,则称{}n a 是{}n c 的“分隔数列”.(1)设2n c n =,1n a n =+,证明:数列{}n a 是{}n c 的“分隔数列”;(2)设4n c n =-,n S 是{}n c 的前n 项和,31n n d c -=,判断数列{}n S 是否是数列{}n d 的分隔数列,并说明理由;(3)设1n n c aq -=,n T {}n c 的前n 项和,若数列{}n T 是{}n c 的分隔数列,求实数a 、q 的取值范围.。
上海春考

2018年上海市春季高考数学试卷一. 填空题(本大题共12题,满分54分,第1~6题每题4分,第7~12题每题5分) 1. 不等式||1x >的解集为2. 计算:31lim2n n n →∞-=+3. 设集合{|02}A x x =<<,{|11}B x x =-<<,则A B =I4. 若复数1i z =+(i 是虚数单位),则2z z+=5. 已知{}n a 是等差数列,若2810a a +=,则357a a a ++=6. 已知平面上动点P 到两个定点(1,0)和(1,0)-的距离之和等于4,则动点P 的轨迹方程为7. 如图,在长方体1111ABCD A B C D -中,3AB =,4BC =,15AA =,O 是11AC 的中点,则三棱锥11A AOB -的体积为8. 某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为 (结果用数值表示)9. 设a ∈R ,若292()x x +与92()a x x+的二项展开式中的常数项相等,则a =10. 设m ∈R ,若z 是关于x 的方程2210x mx m ++-=的一个虚根,则||z 的取值范围是11. 设0a >,函数()2(1)sin()f x x x ax =+-,(0,1)x ∈,若函数21y x =-与()y f x =的图像有且仅有两个不同的公共点,则a 的取值范围是12. 如图,正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中,已知点P 以米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长约为 秒(精确到)二. 选择题(本大题共4题,每题5分,共20分) 13. 下列函数中,为偶函数的是( )A. 2y x -=B. 13y x = C. 12y x -= D. 3y x =14. 如图,在直三棱柱111ABC A B C -的棱所在的直线中,与直线1BC 异面的直线的条数为( ) A. 1 B. 2 C. 3 D. 415. 设n S 为数列{}n a 的前n 项和,“{}n a 是递增数列”是“{}n S 是递增数列”的( ) A. 充分非必要条件 B. 必要非充分条件 C. 充要条件 D. 既非充分又非必要条件16. 已知A 、B 为平面上的两个定点,且||2AB =u u u r,该平面上的动线段PQ 的端点P 、Q ,满足||5AP ≤u u u r ,6AP AB ⋅=u u u r u u u r ,2AQ AP =-u u u r u u u r,则动线段PQ 所形成图形的面积为( )A. 36B. 60C. 72D. 108三. 解答题(本大题共5题,共14+14+14+16+18=76分) 17. 已知cos y x =.(1)若1()3f α=,且[0,]απ∈,求()3f πα-的值; (2)求函数(2)2()y f x f x =-的最小值.18. 已知a R ∈,双曲线222:1x y aΓ-=.(1)若点(2,1)在上,求Γ的焦点坐标;(2)若1a =,直线1y kx =+与Γ相交于A 、B 两点,且线段AB 中点的横坐标为1,求实数k 的值.19. 利用“平行于圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥为圆锥)在广告牌上投影出其标识,如图1所示,图2是投影射出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,OC AB ⊥于C ,3AB =米, 4.5OC =米.(1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到°).(图1) (图2) (图3)20. 设0a >,函数1()12xf x a =+⋅. (1)若1a =,求()f x 的反函数1()f x -;(2)求函数()()y f x f x =⋅-的最大值(用a 表示);(3)设()()(1)g x f x f x =--,若对任意(,0]x ∈-∞,()(0)g x g ≥恒成立,求a 取值范围.21. 若{}n c 是递增数列,数列{}n a 满足:对任意*n N ∈,存在*m N ∈,使得10m nm n a c a c +-≤-,则称{}n a 是{}n c 的“分隔数列”.(1)设2n c n =,1n a n =+,证明:数列{}n a 是{}n c 的分隔数列;(2)设4n c n =-,n S 是{}n c 的前n 项和,32n n d c -=,判断数列{}n S 是否是数列{}n d 的分隔数列,并说明理由;(3)设1n n c aq -=,n T 是{}n c 的前n 项和,若数列{}n T 是{}n c 的分隔数列,求实数a 、q 的取值范围.参考答案一. 填空题1. (,1)(1,)-∞-+∞U2. 33. (0,1)4. 25. 156.22143x y += 7. 5 8. 180 9. 4 10. )+∞11. 1119(,]66ππ12.二. 选择题13. A 14. C 15. D 16. B三. 解答题 17.(1;(2)32-. 18.(1),(;(219.(1)14;(2)°. 20、解析:(1)()()1,011log )(11log 112212∈⎪⎭⎫ ⎝⎛-=⇒⎪⎪⎭⎫ ⎝⎛-=⇒-=-x x x f y x y x ; (2)()()xx x x x a a a a y 2122211211⋅++=⋅+⋅⋅+=-,设02>=t x, 则()111222+++=+++=a taat at a at ty ,因为0>a ,所以a taat 2≥+,当且仅当1=t 时取等号,所以12122++≥+++a a a t a at ,即()⎥⎦⎤ ⎝⎛+∈211,0a y ; (3)()223222221122+⋅+⋅-=⋅+-⋅+=xx x x a t a a a a x g ,设t x=2,因为()0,∞-∈x , 所以()1,0∈t ,则()att a a t g 322++-=,若a t t t a 222=⇒=,1°当12≥a 时,即20≤<a ,a t t a y 322++=单调递减,所以()+∞++∈,232a a y , 则()⎪⎭⎫⎝⎛++-∈0,232a a a a g ,且()2302++-=a a a g ,故满足()()0g x g ≥,符合题意; 2°当120<<a 时,即2>a ,则a a a aa t t a y 322322322+=+⋅≥++=, 则()()0,322-∈a g ,因为()()02log 2min g a g x g ≠⎪⎪⎭⎫⎝⎛=,故不符合题意,舍去; 综上:(]2,0∈a 。
2018年上海春季招生统一文化考试数学(含答案)

C9k x9k
a2k x2k
C9k ak x93k ,k
3,
常数项为C93a3 a 4
10.设 m R ,若 z 是关于 x 的方程 x2 mx m2 1 0 的一个虚根,则 | z | 的取值范围
是__________.
答案:( 3 ,+) 3
解析:
法一:设z a bi,(b 0)代入方程得:(a bi)2 +m(a bi) m2 1 0,即 a2 b2 ma m2 1 0, 2ab mb 0
(B)60
(C)81
(D)108
本题考查向量的投影,因为 AP 5,所以P点在以A为圆心半径为5的圆面上, 又AP AB 6= AB AP cos ,所以 AP cos =3,根据题意作图如下:
三、解答题(本大题共有 5 题,满分 76 分,第 17~19 题每题 14 分,20 题 16 分, 21 题 18 分)
3/7
仅供学习交流、勿做商用!
答案:A
14.如图,在直三棱柱 ABC A1B1C1 的棱虽在的直线中,与直线 BC1
异面的直线条数为( )
(A)1
(B)2
(C)3
(D)4
答案:C
15.记 Sn 为数列{an}的前 n 项和.“{an}是递增数列”是“ Sn 为递增数列”的( )
(A)充分非必要条件
答案: C31C53P33 180
9.设 a R
,若
x2
2 x
9
与
x
a x2
9
的二项展开式中的常数项相等,则 a
2018年上海春考数学试卷

2018年上海市普通高等学校春季招生统一文化考试数学试卷一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每 题5分)1.不等式 lxl>1的解集为3n -1 2.计算: lim -------- =.n—厂 n 23.设集合 A={xl0cx£2},B={xl —1cxc1},则 AC B = .4.若复数2Z =1 • i ( i 是虚数单位),则z ■z5•已知{a .}是等差数列,若a 2 a^ 10,则a 3 a s a 7 =6 .已知平面上动点P 到两个定点(1,0)和(-1,0)的距离之和等于 4,则动点P 的轨迹为7•如图,在长方形 ABCD —ABQU 中,AB=3,BC =4,AA =5, O 是 A 1C 1 的中点,则三棱锥A-AOB 1的体积为 ______________10.设m • R ,若z 是关于x 的方程x 2 mx m 20的一个虚根, 是 __________ .11.设 a 0,函数 f (x) =x 2(1 -x)sin( ax),x (0,1),若函数 y =2x T 与 y = f (x)四辩.若其中学生{ 229.设 a R ,若 I x< x与X •刍 的二项展开式中的常数项相等, x 2则|z|的取值范围第12题图的图象有且仅有两个不同的公共点,则a 的取值范围是 ___________ .12•如图,正方形 ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段 AD 、CB 上,若线段PQ 与圆0有公共点,则称点Q 在点P 的盲区”中•已知点P 以1. 5米/秒的速度从 A 出发向D 移动,同时,点 Q 以1米/秒的速 度 从C 出发向B 移动,则在点 P 从A 移动到D 的过程中,点 Q 在点P 的盲区中的时长约为 _____________ 秒(精确到0. 1)15.记S n 为数列{a n }的前n 项和.{a n }是递增数列"是 S 为递增数列"的()(A )充分非必要条件 (B )必要非充分条件 (C )充要条件(D )既非充分也非必要条件T16.已知A 、B 为平面上的两个定点, 且| AB | =2 .该平面上的动线段 PQ 的端点P 、Q ,满足| AP F 5, AP A^ 6, AQ = -2AP ,则动线段PQ 所形成图形的面积为()(A) 36 (B) 60 (C) 81三、解答题(本大题共有5题,满分76分,第17~佃题每题14分,20题16分,21题18分)17. (本题满分14分,第1小题满分6分,第2小题满分8分)二、选择题(本大题共有 4题,满分20分,母题5分)13•下列函数中,为偶函数的是()2(A ) y =x1(B ) y = x 3 1(C ) y=x^3(D ) y =x14•如图,在直三棱柱 ABC-ABG 的棱所在的直线中,与直线 BG异面的直线条数为( )(A ) 1(B ) 2 (C ) 3(D ) 4(D) 108已知y =cosx .⑴若f(»3,且一[°C,求(巧)的值;(2)求函数y二f (2x)-2f(x)的最小值.18.(本题满分14分,第1小题满分6分,第2小题满分8分)2X 2已知a • R,双曲线-I, -讨=1.a(1)若点(2,1)在丨上,求-的焦点坐标;(2)若a =1,直线y =kx • 1与丨相交于A、B两点,且线段AB中点的横坐标为1, 求实数k 的值.19.(本题满分14分,第1小题满分7分,第2小题满分7分)利用平行于圆锥曲线的母线截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥视为圆锥) 在广告牌上投影出其标识,如图1所示,图2是投影出的抛物线的平面图,图3是一个射灯的直观图,在图2与图3中,点O、A、B在抛物线上,OC是抛物线的对称轴,OC_AB于C , AB=3米,0C =4.5米.(1)求抛物线的焦点到准线的距离;圆锥的母线与轴的夹角的大小(精确到0. 01°.(2)在图3中,已知0C平行于圆锥的母线SD , AB、DE是圆锥底面的直径,求图3设a -0,函数f(x)二20.(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)(1) 若a =1,求f (x)的反函数f J (x);(2) 求函数y 二f(x) ・f(-x)的最大值(用a 表示);(3) 设 g(x) =f (x) -f (x -1).若对任意 x (-::,0] , g(x)_g(O)恒成立,求 a 的 取值范围.21. (本题满分18分,第1小题满分3分,第2小题满分6分,第3小题满分9分)若{C n }是递增数列,数列{a n }满足:对任意n • N *,存在m • N *,使得 為一 C n< 0 ,am -C n 卅则称{a n }是{q }的分隔数列”(1) 设C n =2n , a n = n ,1,证明:数列 佝}是G }的分隔数列”(2) 设c n = n- 4 , S n 是{c n }的前n 项和,d n =务」,判断数列{S n }是否是数列{d n } 的分隔数列,并说明理由;n_ ________________________________________(3)设C n =aq , T n 是{C n }的前n 项和,若数列{人}是{q }的分隔数列,求实数a 、 q 的取值范围.、填空题;0 :: ax :: a 11 二12. 4.4提示:以A 为原点建立坐标系,设时刻为t ,则P(0,1.5t),Q(20, 20-t),0岂t 乞403,化简得(8—t)x —8y+12t=020-020—t —1.5t、选择题16. BP(x, y)的轨迹为线段 x =3,-4乞y 空4 , AP 扫过的三角形面积为12,则利用相似三角形可知AQ 扫过的面积为48,因此和为60参考答案1. (」:,-1)U(1,2. 33.(0,1)4. 25. 156.2 2x y ‘ 1437. 5 8. 180 9. 411.11二 19二提示:2x -1—X = 2(1-x)sin( ax)—1 x -1 二 2(1 -x)sin( ax) = sin(ax)二 27 二 11二 7二11■:11 ■:ax , , 2-, 2二,4二,4 二,||( 6 6 6 6 6 6 x -0y —1.5t 则 I PQ :点0(10,10)到直线PQ 的距离|(8-t)10-80 创胡,化简得 3t 2 愀-128_0 .(8 -1)2 83即于『3,则0十邑旦1=心二J:4.413. A 14. C15. D提示:建系 A(0,0), B(2,0),则三、解答题32a —,(t =2X (0,1]) 22 a t 3at因为-a<0,所以当X=0,t=1时,分母取到最小值从而分式值取到最小值,(3)a 0q _2【a A 0 ②当q .1时,G18.(1) (_ .3,0) ; (2)19.(1) 1 1 ; (2) 9.59 420.(1) 1 1 f —(x)Jog ? —.x(0 ::: X ::: 1) ;( 2)y1 2 ( x = 0时取最值);1 2a a 2提示:g(X )=1 y 2X「1 a 2X」-a=__X__2a 2 2X X . 3a2X21. (1)证明:存在m = 2n ,此时一 n N ,c n = 2n :: a m = 2n 1 :: c n2n 2 证毕(2)不是•反例:n =4时,m 无解;提示:因为{aq n4}为递增数列,因此a 0或者…q 10 ::①当a 0时,0 cq v1~n N *,c n <0,因此 IH ::: T2 :::可=q ::: 9C 3111因此不存在C 2 ^T m ::.C3,不合题意。
2018年上海市春考数学试卷

上海市教育考试院保留版权2018年春考数学第1页(共4页)2018年上海市普通高校春季招生统一文化考试数学试卷考生注意:1.本场考试时间120分钟.试卷共4页,满分150分,答题纸共2页.2.作答前,在答题纸正面填写姓名、准考证号,反面填写姓名.将核对后的条形码贴在指定位置.3.所有作答必须涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题,用黑色字迹钢笔、水笔或圆珠笔作答非选择题.一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)考生应在答题纸相应编号的空格内直接填写结果.1.不等式||1x >的解集为.2.计算:31lim 2n n n →∞-=+.3.设集合{|02}A x x =<<,{|11}B x x =-<<,则A B = .4.若复数1i z =+(i 是虚数单位),则2z z +=.5.已知{}n a 是等差数列,若2810a a +=,则357a a a ++=.6.已知平面上动点P 到两个定点(1,0)和(1,0)-的距离之和等于4,则动点P 的轨迹方程为.7.如图,在长方体1111ABCD A B C D -中,3AB =,4BC =,15AA =,O 是11A C 的中点,则三棱锥11A A OB -的体积为.8.某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为.(结果用数值表示)9.设a ∈R ,若922x x ⎛⎫+ ⎪⎝⎭与92a x x ⎛⎫+ ⎪⎝⎭的二项展开式中的常数项相等,则a =.10.设m ∈R ,若z 是关于x 的方程2210x mx m ++-=的一个虚根,则||z 的取值范围是.2018年春考数学第2页(共4页)11.设0a >,函数()2(1)sin()f x x x ax =+-,(0,1)x ∈,若函数21y x =-与()y f x =的图像有且仅有两个不同的公共点,则a 的取值范围是.12.如图,正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中,已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长约为.二、选择题(本大题共有4题,满分20分,每题5分)每题有且只有一个正确答案,考生应在答题纸的相应位置,将代表正确选项的小方格涂黑.13.下列函数中,为偶函数的是().(A)2y x -=(B)13y x =(C)12y x -=(D)3y x =14.如图,在直三棱柱111ABC A B C -的棱所在的直线中,与直线1BC 异面的直线的条数为().(A)1(B)2(C)3(D)415.设n S 为数列{}n a 的前n 项和,“{}n a 是递增数列”是“{}n S 是递增数列”的().(A)充分非必要条件(B)必要非充分条件(C)充要条件(D)既非充分又非必要条件16.已知A 、B 为平面上的两个定点,且||2AB = ,该平面上的动线段PQ 的端点P 、Q ,满足||5AP ≤,6AP AB ⋅= ,2AQ AP =- ,则动线段PQ 所形成图形的面积为().(A)36(B)60(C)72(D)108三、解答题(本大题满分76分)本大题共有5题,解答下列各题必须在答题纸的相应位置写出必要的步骤.17.(本题满分14分,第1小题满分6分,第2小题满分8分)已知函数()cos f x x =.(1)若1()3f α=,且[0,π]α∈,求π3f α⎛⎫- ⎪⎝⎭的值;(2)求函数(2)2()y f x f x =-的最小值.2018年春考数学第3页(共4页)18.(本题满分14分,第1小题满分6分,第2小题满分8分)已知a ∈R ,双曲线222:1x y aΓ-=.(1)若点(2,1)在上,求Γ的焦点坐标;(2)若1a =,直线1y kx =+与Γ相交于A 、B 两点,且线段AB 中点的横坐标为1,求实数k 的值.19.(本题满分14分,第1小题满分6分,第2小题满分8分)利用“平行于圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥为圆锥)在广告牌上投影出其标识,如图1所示,图2是投影射出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,OC AB ⊥于C ,3AB =米, 4.5OC =米.(1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到0.01°).20.(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)设0a >,函数1()12x f x a =+⋅.(1)若1a =,求()f x 的反函数1()f x -;(2)求函数()()y f x f x =⋅-的最大值(用a 表示);(3)设()()(1)g x f x f x =--,若对任意(,0]x ∈-∞,()(0)g x g ≥恒成立,求a 的取值范围.图1图3图22018年春考数学第4页(共4页)21.(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分)若{}n c 是递增数列,数列{}n a 满足:对任意*n ∈N ,存在*m ∈N ,使得10m n m n a c a c +--≤,则称{}n a 是{}n c 的“分隔数列”.(1)设2n c n =,1n a n =+,证明:数列{}n a 是{}n c 的分隔数列;(2)设4n c n =-,n S 是{}n c 的前n 项和,32n n d c -=,判断数列{}n S 是否是数列{}n d 的分隔数列,并说明理由;(3)设1n n c aq -=,n T 是{}n c 的前n 项和,若数列{}n T 是{}n c 的分隔数列,求实数a 、q 的取值范围.。
2018年上海市普通高等学校招生统一考试数学真题试题及参考答案(上海卷)
【试题级别】高三
【试题地区】上海
【试题来源】2018年高考数学真题试卷(上海卷)
15.(2018•上海)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA₁是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点,以AA₁为底面矩形的一边,则这样的阳马的个数是()
A.4
B.8
C.12
D.16
【答案】D
【解析】【解答】以AA1取矩形分别讨论,找到AA1所在矩形个数,并根据每个矩形可做4个阳马的基本位置关系,可得答案为D。
故答案为:D。
【分析】以AA1为底边的直四棱锥,运用线面垂直关系判定的方法分析图形中基本元素及其相互关系解答即可。
【题型】单选题
【考查类型】高考真题
【试题来源】2018年高考数学真题试卷(上海卷)。
2018年普通高等学校招生上海市数学真题卷(含答案)
(C) 3 3
(D)0【答案】 B
【知识点】函数的概念【考查能力】空间想象能力
【解析】点 (1, f (1)) 在直线 x = 1 上,把直线进行旋转可得旋转后的直线,这样进
行下去直到回到 (1, f (1)) 点可知 f (1) = 3 2
17. 已知圆锥的顶点为 P ,底面圆心为 O ,半径为 2,
2
2
【知识点】直线的交点坐标与距离公式
【解析】数形结合,转化单位圆上圆心角为 60o的两点到直线 x + y -1 = 0 的距离
之和,可求得最大值为 2 + 3 。
13. 设 P 是椭圆 x2 + y2 = 1 上的动点,则 P 到该椭圆的两个焦点的距离之和为(
).
53
(A) 2 2
(B) 2 3
O
B
A
M
(2)若
f
æ çè
p 4
ö ÷ø
=
3 +1,求方程 f ( x) = 1-
2 在区间[-p ,p ] 上的解.
1)、由偶函数可知 f (-x) = f (x) 得 a = 0 。
(2)、 f (p ) = 3 +1Þ a = 3 , f (x) = 2sin(2x + p ) +1, \sin(2x + p ) = - 2 ,在
(C) 2 5
(D) 4 2 【答案】 C
14. 已知 a Î R ,则“ a > 1”是“ 1 < 1 ”的(
).
a
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)既非充分又非必要条件【答案】 A
15. 《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设 AA1 是正六 棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点,以 AA1 为底面矩形的一边,
上海普通高等学校春季招生统一文化考试数学试卷
12.如图,正方形 的边长为20米,圆 的半径为1米,圆心是正方形的中心,点 、 分别在线段 、 上,若线段 与圆 有公共点,则称点 在点 的“盲区”中.已知点 以1.5米/秒的速度从 出发向 移动,同时,点 以1米/秒的速度从 出发向 移动,则在点 从 移动到 的过程中,点 在点 的盲区中的时长约为__________秒(精确到0.1)
(3)设 , 的前 项和,若数列 是 的分隔数列,求实数 、 的取值范围.
二、选择题(本大题共有4题,满分20分,每题5分)
13.下列函数中,为偶函数的是( )
(A) (B)
(C) (D)
14.如图,在直三棱柱 的棱虽在的直线中,与直线
异面的直线条数为( )
(A)1(B)2
(C)3(D)4
15.记 为数列 的前 项和.“ 是递增数列”是“ 为递增数列”的( )
(A)充分非必要条件(B)必要非充分条件
上海普通高等学校春季招生统一文化考试数学试卷
2018年上海市普通高等学校春季招生统一,满分54分,第1~6题每题4分,第7~12题每题5分)
1.不等式 的解集为__________.
2.计算: __________.
3.设集合 , ,则 __________.
(C)充要条件(D)既非充分也非必要条件
16.已知 、 为平面上的两个定点,且 .该平面上的动线段 的端点 、 ,满足 , , ,则动线段 所形成图形的面积为( )
(A)36(B)60(C)81(D)108
三、解答题(本大题共有5题,满分76分,第17~19题每题14分,20题16分,21题18分)
最新上海市春考数学试卷(含答案)
2018年上海市普通高校春季招生统一文化考试数学试卷一、填空题(54分)1、不等式1>x 的解集为______________;2、计算:_________213lim=+-∞→n n n ;3、设集合{}20<<=x x A ,{}11<<-=x x B ,则________=B A ;4、若复数i z +=1(i 是虚数单位),则______2=+zz ; 5、已知{}n a 是等差数列,若1082=+a a ,则______753=++a a a ;6、已知平面上动点P 到两个定点()0,1和()0,1-的距离之和等于4,则动点P 的轨迹方程为_________;7、如图,在长方体1111D C B A ABCD -中,3=AB ,4=BC ,51=AA ,O 是11C A 的中点,则三棱锥11OB A A -的体积为_________;第7题图 第12题图8、某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为_____________(结果用数值表示)。
9、设R a ∈,若922⎪⎭⎫ ⎝⎛+x x 与92⎪⎭⎫ ⎝⎛+x a x 的二项展开式中的常数项相等,则_______=a ;10、设R m ∈,若z 是关于x 的方程0122=-++m mx x 的一个虚根,则-z 的取值范围是________;11、设0>a ,函数()()1,0),sin()1(2∈-+=x ax x x x f ,若函数12-=x y 与()x f y =的图像有且仅有两个不同的公共点,则a 的取值范围是__________;12、如图,在正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中,已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长均为_____秒(精确到0.1). 二.选择题(20分)13. 下列函数中,为偶函数的是( )A 2-=x y B 31x y = C 21-=xy D 3x y =14. 如图,在直三棱柱111C B A ABC -的棱所在的直线中,与直线1BC 异面的直线的条数为( ) A 1 B 2 C 3 D 415. 若数列}{n a 的前n 项和,“}{n a 是递增数列”是“}{n S 是递增数列”的( ) A 充分不必要条件 B 必要不充分条件 C 充要条件 D 即不充分也不必要条件16、已知A 、B 是平面内两个定点,且2=→AB ,该平面上的动线段PQ 的两个端点P 、Q 满足:5≤→AP ,6=⋅→→AB AP ,→→-=AP AQ 2,则动线段PQ 所围成的面积为( )A 、50B 、60C 、72D 、108三、解答题(14+14+14+16+18=76分) 17、已知x x f cos )(=(1).若31)(=αf ,且],0[πα∈,求)3(πα-f 的值; (2).求函数)(2)2(x f x f y -=的最小值;18、已知R a ∈,双曲线1:222=-Γy ax(1).若点)1,2(在Γ上,求Γ的焦点坐标;(2).若1=a ,直线1+=kx y 与Γ相交于B A ,两点,若线段AB 中点的横坐标为1,求k 的值;19.利用“平行与圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理;某公司用两个射灯(射出的光锥视为圆锥)在广告牌上投影出其标识,如图1所示,图2投影出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,AB OC ⊥于C ,3=AB 米,5.4=OC 米.(1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到01.0).20.设0>a ,函数xa x f 211)(⋅+=(1).若1=a ,求)(x f 的反函数)(1x f -(2)求函数)()(x f x f y -⋅=的最大值,(用a 表示)(3)设=)(x g )1()(--x f x f ,若对任意)0()(],0,(g x g x ≥-∞∈恒成立,求a 的取值范围?21.若}{n c 是递增数列,数列}{n a 满足:对任意*,N m R n ∈∃∈,使得01≤--+n m nm c a a a ,则称}{n a 是}{n c 的“分隔数列”(1)设1,2+==n a n c n n ,证明:数列}{n a 是}{n c 的分隔数列;(2)设n n S n c ,4-=是}{n c 的前n 项和,23-=n n c d ,判断数列}{n S 是否是数列}{n d 的分隔数列,并说明理由;(3)设n n n T aq c ,1-=是}{n c 的前n 项和,若数列}{n T 是}{n C 的分隔数列,求实数q a ,的取值范围?2018年上海市普通高校春季招生统一文化考试数学试卷参考答案:一、填空题:1、()()+∞-∞-,11, ;2、3;3、()1,0;4、2;5、15;6、13422=+y x ;7、5;8、180; 9、4;10、⎪⎪⎭⎫⎝⎛∞+,33;11、⎥⎦⎤⎝⎛619611ππ,;12、4.4; 二、选择题:13、A ;14、C ;15、D ;16、B ; 三、解答题:17、(1)6621+;(2)23-; 18、(1)()()0,30,3-,;(2)215-; 19、(1)41;(2)59.9; 20、解析:(1)()()1,011log )(11log 112212∈⎪⎭⎫ ⎝⎛-=⇒⎪⎪⎭⎫ ⎝⎛-=⇒-=-x x x f y x y x ; (2)()()xx x x x a a a a y 2122211211⋅++=⋅+⋅⋅+=-,设02>=t x, 则()111222+++=+++=a taat at a at ty ,因为0>a ,所以a taat 2≥+,当且仅当1=t 时取等号,所以12122++≥+++a a a t a at ,即()⎥⎦⎤ ⎝⎛+∈211,0a y ; (3)()223222221122+⋅+⋅-=⋅+-⋅+=xx x x a t a a a a x g ,设t x=2,因为()0,∞-∈x , 所以()1,0∈t ,则()att a a t g 322++-=,若a t t t a 222=⇒=,1°当12≥a 时,即20≤<a ,a t t a y 322++=单调递减,所以()+∞++∈,232a a y , 则()⎪⎭⎫⎝⎛++-∈0,232a a a a g ,且()2302++-=a a a g ,故满足()()0g x g ≥,符合题意;2°当120<<a 时,即2>a ,则a a a aa t t a y 322322322+=+⋅≥++=, 则()()0,322-∈a g ,因为()()02log 2ming a g x g ≠⎪⎪⎭⎫⎝⎛=,故不符合题意,舍去; 综上:(]2,0∈a 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年上海市普通高等学校春季招生统一文化考试
数学试卷
一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)
1.不等式||1x >的解集为__________. 2.计算:31
lim
2
n n n →∞-=+__________.
3.设集合{|02}A x x =<<,{|11}B x x =-<<,则A B =__________.
4.若复数z i i =+(i 是虚数单位),则2
z z
+
=__________. 5.已知{}n a 是等差数列,若2810a a +=,则357a a a ++=__________.
6.已知平面上动点P 到两个定点(1,0)和(1,0)-的距离之和等于4,则动点P 的轨迹为
__________.
7.如图,在长方形1111B ABC A C D D -中,3AB =,4BC =,15AA =, O 是11AC 的 中点,则三棱锥11A AOB -的体积为__________.
第7题图 第12题图
8.某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、 四辩.若其中学生
甲必须参赛且不担任四辩,则不同的安排方法种数为__________.
9.设a R ∈,若9
22x x ⎛⎫+ ⎪⎝
⎭与9
2a x x ⎛⎫+ ⎪⎝⎭的二项展开式中的常数项相等,则a =__________.
10.设m R ∈,若z 是关于x 的方程2
2
10x mx m -+=+的一个虚根,则||z 的取值范围
是__________.
11.设0a >,函数()2(1)sin()f x x x ax =+-,(0,1)x ∈,若函数21y x =-与()y f x =
的图象有且仅有两个不同的公共点,则a 的取值范围是__________.
12.如图,正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、
Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲
区”
中.已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度从
C 出发向B 移动,则在点P 从A 移动到
D 的过程中,点Q 在点P 的盲区中的时长约为
__________秒(精确到0.1)
二、选择题(本大题共有4题,满分20分,每题5分)
13.下列函数中,为偶函数的是( ) (A )2
y x -= (B )13
y x =
(C )1
2
y x
-=
(D )3
y x =
14.如图,在直三棱柱111AB A B C C -的棱虽在的直线中,与直线1BC 异面的直线条数为( ) (A )1 (B )2
(C )3
(D )4
15.记n S 为数列{}n a 的前n 项和.“{}n a 是递增数列”是“n S 为递增数列”的( ) (A )充分非必要条件 (B )必要非充分条件
(C )充要条件
(D )既非充分也非必要条件
16.已知A 、B 为平面上的两个定点,且|2|AB =.该平面上的动线段PQ 的端点P 、Q , 满足||5AP ≤,6AB AP ⋅=,2AQ AP =-,则动线段PQ 所形成图形的面积为( )
(A )36
(B )60
(C )81
(D )108
三、解答题(本大题共有5题,满分76分,第17~19题每题14分,20题16分,21题18分)
17.(本题满分14分,第1小题满分6分,第2小题满分8分)
已知cos y x =.
(1)若3(1)f α=
,且[0,]απ∈,求()3
f π
α-的值; (2)求函数(2)2()y f x f x =-的最小值.
18. (本题满分14分,第1小题满分6分,第2小题满分8分) 已知a R ∈,双曲线22
2:1x y a
Γ-=.
(1)若点(2,1)在Γ上,求Γ的焦点坐标;
(2)若1a =,直线1y kx =+与Γ相交于A 、B 两点,且线段AB 中点的横坐标为1,
求实数k 的值.
19.(本题满分14分,第1小题满分7分,第2小题满分7分)
利用“平行于圆锥曲线的母线截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两
个射灯(射出的光锥视为圆锥)在广告牌上投影出其标识,如图1所示,图2是投影出的抛物线的平面图,图3是一个射灯的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,OC AB ⊥于C ,3AB =米, 4.5OC =米. (1)求抛物线的焦点到准线的距离;
(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求
圆锥的母线与轴的夹角的大小(精确到0.01°).
图1 图2 图3 20.(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)
设0a >,函数1
()12x
f x a =
+⋅.
(1)若1a =,求()f x 的反函数1
()f x -;
(2)求函数()()y f x f x ⋅-=的最大值(用a 表示);
(3)设()()(1)g x f x f x =--.若对任意(,0]x ∈-∞,)(()0g x g ≥恒成立,求a 的
取值范围.
21.(本题满分18分,第1小题满分3分,第2小题满分6分,第3小题满分9分)
若{}n c 是递增数列,数列{}n a 满足:对任意*
n N ∈,存在*
m N ∈,使得
1
0m n
m n a c a c +-≤-,
则称{}n a 是{}n c 的“分隔数列”. (1)设2n c n =,1n a n =+,证明:数列{}n a 是{}n c 的“分隔数列”;
(2)设4n c n =-,n S 是{}n c 的前n 项和,31n n d c -=,判断数列{}n S 是否是数列{}
n d 的分隔数列,并说明理由;
(3)设1
n n c aq
-=,n T {}n c 的前n 项和,若数列{}n T 是{}n c 的分隔数列,求实数a 、
q 的取值范围.
参考答案
一、填空题
1.(,1)
(1,)-∞-+∞
2.3
3.(0,1)
4.2 5.15
6.22
143
x y +=
7.5 8.180 9.4
10.)+∞ 11.1119(,]66
ππ
12.4.4
二、选择题
13.A
14.C
15.D
16.B
三、解答题
17.(1)
16+;(2)3
2
-
18.(1)(1,0),(1,0)-;(2. 19.(1)
1
4
;(2)9.59︒. 20.(1)1
2
1()log (01)x f
x x x --=<<;(2)2
1
12max y a a =++(0x =时取最值);
(3)
21.(1)证明略;(2)不是.反例:4n =时,m 无解;(3)0
2
a q ≥>⎧⎨⎩.。
