房山区初三数学二模答案2020.6
7房山答案

房山区九年级数学二模答案 2020.6二、填空题(本题共16分,每小题2分)9.1- ; 10.1.3 ; 11.),(15-; 12. 222+2+=b +a b ab a )(; 13.8; 14.2S ; 15.222-20=6+)(x x ;16.同圆或等圆半径相等,三边相等的三角形是等边三角形,等边三角形的内角是60°,一条弧所对的圆周角是它所对圆心角的一半.(直径所对的圆周角是直角,正弦定义,三角函数值)三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28,每小题7分)17.解: 1-2+30sin 4+51-18°1-)(1-2+21×4+5-23= ………………………………………………4分4-24=……………………………………………………… 5分18. 解不等式①:……………………………………………………1分 得-3<x ……………………………………………………2分解不等式②: ……………………………………………………3分 得-5>x ……………………………………………………4分不等式组的解集是 3-<<5-x ………………………………………………5分19.证明:∵BD 平分∠ABC∴∠ABD =∠CBD ………………………………………………1分 ∵DE ∥AB∴∠ABD =∠BDE ………………………………………………2分 ∴∠CBD =∠BDE ………………………………………………3分 ∴EB = ED ………………………………………………4分 ∵F 是BD 中点∴EF 平分∠BED ………………………………………………5分 20.x x 2<3+34+2<1-x x ACB0=3)-(1)-(x x3= 1=21x x ,……………………………………2分 (2) 由题意得0≠k , ……………………………………3分0>12-16=Δk ……………………………………4分∴34<k ∴34<k 且 0≠k …………………………………5分21.(1)证明:∵CE =CD ,CF =CB∴四边形DBEF 是平行四边形 ………………………………………………1分 DE =2CD ,BF =2BC ∵菱形ABCD 中, CD = CB∴ DE = BF ………………………………………………2分 ∴四边形DBEF 是矩形 ………………………………………………3分 (2)∵AB =5∴BF =10∵菱形ABCD 中, 53=∠cos ABD ,∠DBF =∠ABD ∴53=∠cos DBF∵∠BDF =90°∴DB =6 ………………………………………………4分 ∴DF = 8 ………………………………………………5分22. (1)把3=x 代入1-=x y 得2=y ∴),(23A 又)0(>=x xky 图象过点),(23A 解得6=k ……………………………………………1分当n = 4时, ),(34B ),(234C 23=PC ,23=BC ………………………………………3分 ② 1≤<0n 或 4≥n ………………………………5分23. (1)DE 与⊙O 相切 ………………………………1分连接OD 、CD 、OE∵ BC 为⊙O 的直径∴∠CDA =∠CDB =90° ∵E 是AC 中点 ∴ED =EC∵OC =O D ,OE =O E ∴ΔOCE ≌ΔO DE∴∠O DE =∠OCE =90°………………………………2分 ∴O D ⊥DE∴DE 与⊙O 相切 ………………………………3分 (2)∵∠ACB =90°,AB =10,BC =6∴AC =8,CE =4, OC =3 ………………………………4分 ∵DE 、CE 与⊙O 相切 ∴DE=CE ,∠CEO =∠DEO∴O E ⊥CD ………………………………5分 ∴ OE =5∵CF OE CE OC •=•∴512=CF ∴59=OF ………………………………6分24. (1) 11 ………………………………2分(2) 如图 ………………………………3分(3) 8 ………………………………4分 (4) ①② ………………………………6分 25. (1) (cm)x12 3 4 5 6 (cm) 4.475.245.865.965.484.72 4.00 (cm)6.005.865.233.982.461.06………………………………2分(2)………………………………4分(3)AM 的长度约为 2.98cm 或1.50cm ………………………………6分 26.(1)对称轴-1=22-=aax ……………………………………1分(2)∵4AB把(1,0)代入表达式:0=c +2a +a 得:a 3-=c ……………3分 ∴ C (0,-3a ) ∴ D (0,-3a+1), 31D y a =-+ …………………………4分(3)当0a >时将点()4,4P -代入抛物线223y ax ax a =+-得:41683a a a =--, 45a =∴当45a ≥时,抛物线与线段PD 只有一个交点 …………………5分当0a <时抛物线的顶点为()1,4a -- 当44a -=时1a =- …………………6分综上所述,当45a ≥或1a =-时,抛物线与线段PD 只有一个交点.27.(1)① 过点D 作DF ⊥AC 于F ……………………………………1分 ∵30DBA =︒∠ ∴BD DF 21=∵以AC 为斜边作等腰ADC Rt Δ ∴FC AF =∴AC DF 21= ∴AC BD = ……………………………………2分② ∵ 等腰ADC Rt Δ与等腰Rt BED △中AC BD =∴DE DC =, 45=∠=∠CDE FDC ∵30DBA =︒∠∴ 60=∠FDB , 15=∠CDB ∴ 60=∠CDE∴CDE Δ是等边三角形 ……………………………………3分 ∵DE EB =∴EB EC = ……………………………………4分(2)法1. 添加辅助线 ……………………………5分证出ADB Δ≌CDG Δ ……………………………6分 ∴ 45=∠=∠A DCG∴ 90=∠GCB ∵EB EG =∴ EB EC = ………………………………7分法2. 添加辅助线 ……………………………5分证出ADB Δ⁓GDE Δ …………………………6分 ∴ 45=∠=∠A DGE∴GE 平分DGC ∠∴GE 是DC 的中垂线∴ EB EC ED == ………………………………7分法3. 添加辅助线 ……………………………5分证出 45=∠EDB =∠EFB ……………………6分∴FE 是DC 的中垂线∴ EB EC ED == ……………………7分 28.(1)①类似以上作答,只要弧上所有点都出现在三角形内部,均给分.………………………………2分②当2OB =时,Rt ABC △的形内弧最长,此时弧长=π=.(学生不必画出图象)………………………………3分(2)当圆心在x 轴下方时,此时最长形内弧与线段DF ,EF 相切∵1DOF DOM △∽△∴21OF OM OD ⋅=∴14OM = ∴4M y ≤- ………………………………4分当圆心在x 轴上方时,此时最长形内弧与x 轴相切∵2EGM HEG △∽△∴22HG HM HE ⋅=∴52EH =∴252EM =∴52M y ≥………………………………5分综上所述,4M y ≤-或52M y ≥(3)当4G x ≤-时,此时最长形内弧与x 轴相切∵1GOP GHO △∽△ ∴143GP = ∴143P y ≥当40G x -<<时,此时最长形内弧与线段OM 相切解得243P y ≥当04G x <<时,此时最长形内弧与线段MG 相切解得3433P y ≥………………………………6分当4G x ≥时,此时最长形内弧与线段MG 相切解得433P y ≤-………………………………7分综上所述,43P y ≥23P y ≤。
北京市房山区初三二模数学试卷及参考答案2020.6

北京市房山区初三二模数学试题及参考答案2020.6学校班级姓名考号考生须知1.本试卷共11页,共三道大题,28道小题,满分100分。
考试时间120分钟。
2.在试卷和答题卡上认真填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,请将本试卷、答题卡和草稿纸一并交回。
一、选择题(本题共16分,每小题2分)下面1-8题均有四个选项,其中符合题意的选项只有..一个.1. 在迎来庆祝新中国成立70周年之后,对于中国而言,2020年又将是一个新的时间坐标.过去40年,中国完成了卓越的经济转型,八亿两千万人成功脱贫,这是人类发展史上具有里程碑意义的重大成就.将820000000用科学记数法表示为()A. 8.2 ×109B. 0.82 ×109C. 8.2 ×108D. 82 ×1072. 如图是某个几何体的三视图,该几何体是()A.长方体B.三棱柱C.正方体D.圆柱3.实数a,b在数轴上的对应点的位置如图所示,则正确的结论是()A.|b|<a B.﹣a<b C.a+b>0 D.|a|>b4.《北京市生活垃圾管理条例》对生活垃圾分类提出更高要求,于2020年5月1日起施行,施行的目的在于加强生活垃圾管理,改善城乡环境,保障人体健康.下列垃圾分类标志,是中心对称图形的是()A B C D5. 李老师是一位运动达人,他通过佩戴智能手环来记录自己一个月(30天)每天所走的步数,并绘制成如下统计表:在每天所走的步数这组数据中,众数和中位数分别是( ) A .1.6,1.5 B .1.7,1.6 C .1.7,1.7 D .1.7,1.55 6. 如图,在□ABCD 中,延长AD 至点E ,使AD=2DE ,连接BE 交CD 于点F ,交AC 于点G ,则AGCG的值是()A .32B .31C .21D .437. 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果:抛掷次数“正面向上”的频率100.450.550100150200250300350400下面有三个推断:①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;GFDAE③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45. 其中合理的是( ) A .①B .②C .①②D .①③8.2020年是5G 爆发元年,三大运营商都在政策的支持下,加快着5G 建设的步伐.某通信套餐 类型 月费(元/月) 套餐内包含内容套餐外资费 国内数据流量(GB ) 国内主叫(分钟) 国内流量 国内主叫 套餐1 12830200每5元1GB ,用满3GB 后每3元1GB ,不足部分按照0.03元/MB 收取0.19 元/分钟套餐2 158 40 300 套餐3 198 60 500 套餐423880600小武每月大约使用国内数据流量49GB ,国内主叫350分钟,若想使每月付费最少,则他应预定的套餐是( )A .套餐1B .套餐2C .套餐3D .套餐4二、填空题(本题共16分,每小题2分) 9. 若分式1-1+x x 值为0,则x 的值是 .10.如图,扇形AOB ,通过测量、计算,得弧AB 的长约为 cm. (π取3.14 ,结果保留一位小数)11. 如图,若在象棋棋盘上建立直角坐标系,使“帥”位于 点(-3,-2),“炮”位于点(-2.0),则“兵”位于的点的坐 标为 .AB O已知:平面内一点A . 求作:∠A ,使得∠A =30°.作法:如图,(1)作射线AB ;(2)在射线AB 上取一点O ,以O 为圆心,OA 为半径作圆,与射线AB 相交于点C ; (3)以C 为圆心,OC 为半径作弧,与⊙O 交于点D ,作射线AD . 则∠DAB 即为所求的角.12. 如图,一个大正方形被分成两个正方形和两个一样的矩形,请根据 图形,写出一个含有a ,b 的正确的等式______________________.13. 如果4=+n m ,那么代数式nm mn m n m +2•)2++(22的值为 . 14. 已知一组数据1x ,2x ,3x ,…,n x 的方差是2S ,那么另一组数据3-1x ,3-2x ,3-3x ,…,3-n x 的方差是 .15. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”如图,我们用点A ,B ,C 分别表示竹梢,竹根和折断处,设折断处离地面的高度BC 为x 尺,则可列方程为_________________ . 16. 下面是“作一个30°角”的尺规作图过程.请回答:该尺规作图的依据是_______________________________________ .三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,,第27-28题,每小题7分)17. 计算:1-2+30sin 4+51-18°1-)(18. 解不等式组:19. 如图,在△ABC 中,BD 平分∠ABC 交AC 于点D ,DE ∥AB 交BC 于点E ,F 是BD 中点. 求证:EF 平分∠BED .20.已知关于x 的一元二次方程0=3+4-2x kx 有两个不相等的实数根. (1)当k =1时,求此方程的根;(2)若此方程有两个不相等的实数根,求k 的取值范围.21. 如图,菱形ABCD 中, 分别延长DC ,BC 至点E ,F ,使CE =CD ,CF =CB ,联结DB ,BE ,EF ,FD .(1)求证:四边形DBEF 是矩形;(2)若AB =5,53=∠cos ABD ,求DF 的长.2x<1)+(3x .2+<21-x x FEACBACFD22. 在平面直角坐标系xOy 中,反比例函数)0(>=x xky 的图象与直线1-=x y 交于点 A (3,m ) (1)求k 的值(2)已知点P (n ,0)(n > 0),过点P 作垂直于x 轴的直线,交直线1-=x y 于点B ,交函数)0(>=x xky 图象于点C . ①当n = 4时,判断线段PC 与BC 的数量关系,并说明理由;②若PC ≤BC ,结合图象,直接写出n 的取值范围.23. 如图,在△ABC 中,∠ACB =90°,以BC 为直径的⊙O 交AB 于点D ,E 是AC 中点, 连接DE .(1)判断DE 与⊙O 的位置关系并说明理由;(2)设CD 与OE 的交点为F ,若AB =10,BC =6,求OF 的长.24. GDP 是指一个国家(或地区)在一定时期内生产活动的最终成果,常被公认为是衡量经济状况的最佳指标. 截止2020年4月27日,对除西藏外的30个省区市第一季度有关GDP 的数据进行收集、整理、描述和分析.下面给出了部分信息:a.各省区市GDP 数据的频数分布直方图,如图24-1(数据分成6组,各组是,,,,,):EDCOAxy–1123456–1123456AOb.2020年第一季度GDP 数据在8≤<4x 这一组的是:4.6 4.95.0 5.1 5.3 5.46.37.4 7.5 7.8 7.8c.30个省区市2020年第一季度及2019年GDP 增速排名统计图,如图24-2:d.北京2020年第一季度GDP 数据约为7.5千亿,GDP 增速排名为第22.根据以上信息,回答下列问题:(1)在30个省区市中,北京2020年第一季度GDP 的数据排名第_______.(2)在30个省区市2020年第一季度及2019年GDP 增速排名统计图中,请在图中用“○”图24-1图24-2圈出代表北京的点.(3)2020年第一季度GDP增速排名位于北京之后的几个省份中,2019年GDP增速排名的最好成绩是第_______.(4)下列推断合理的是_______.①与2019年GDP增速排名相比,在疫情冲击下,2020年全国第一季度增速排名,部分省市有较大下滑,如D代表的湖北排名下滑最多.②A、B、C分别代表的新疆、广西、青海位于西部地区,多为人口净流出或少量净流入,经济发展主要依靠本地劳动力供给,疫后复工复产效率相对较高,相对于2019年GDP增速排名位置靠前.25.已知线段AB = 6cm,点M是线段AB上一动点,以AB为直径作⊙O,点C是圆周上一点且AC = 4cm,连接CM,过点A做直线CM的垂线,交⊙O于点N,连接CN,设AM的长为xcm,线段AN 的长为cm,线段CN 的长为cmNO BAMC小华同学根据学习函数的经验,,分别对函数y1,y2,随自变量x的变化而变化的规律进行了探究.下面是小华同学的探究过程,请补充完整:(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:x(cm)0 1 2 3 4 5 6 (cm) 4.47 5.24 5.86 5.96 4.72 4.00 (cm) 6.00 5.86 5.23 3.98 2.46 1.06 0 请你补全表格的相关数值,保留两位小数.(2)在同一平面直角坐标系xOy 中,描出补全后的表中各组数值所对应的点(x ,y 1),(x ,y 2),并画出函数 y 1,y 2的图象(函数y 2的图象如图,请你画出y 1的图象)(3)结合画出的函数图象,解决问题:当ΔCAN 是等腰三角形时时,AM 的长度约为______________cm .(保留两位小数)26.在平面直角坐标系中,已知抛物线22y ax ax c =++与x 轴交于点A 、B ,且4AB =.抛物线与y 轴交于点C ,将点C 向上移动1个单位得到点D . (1)求抛物线对称轴;(2)求点D 纵坐标(用含有a 的代数式表示);(3)已知点()4,4P -,若抛物线与线段PD 只有一个交点,求a 的取值范围.27. 点C 为线段AB 上一点,以AC 为斜边作等腰ADC Rt Δ,连接BD ,在ABD Δ外侧,以BD 为斜边作等腰Rt BED △,连接EC . (1)如图1,当30DBA =︒∠时: ① 求证:AC BD =;② 判断线段EC 与EB 的数量关系,并证明;A图1(2) 如图2,当°45<∠<°0DBA 时,EC 与EB 的数量关系是否保持不变? 对于以上问题,小牧同学通过观察、实验,形成了解决该问题的几种思路:想法1: 尝试将点D 为旋转中心. 过点D 作线段BD 的垂线,交BE 延长线于点G ,连接CG ;通过证明三角形ADB Δ≌CDG Δ全等解决以上问题;想法2: 尝试将点D 为旋转中心. 过点D 作线段AB 的垂线,垂足为点G ,连接EG .通过证明ADB Δ∽GDE Δ解决以上问题;想法3:尝试利用四点共圆. 过点D 作AB 垂线段DF ,连接EF ,通过证明D 、F 、B 、E 四点共圆,利用圆的相关知识解决以上问题.请你参考上面的想法,证明EC =EB (一种方法即可)图2EA C28. 过三角形的任意两个顶点画一条弧,若弧上的所有点都在该三角形的内部或边上,则称该弧为三角形的“形内弧”.(1)如图,在等腰Rt ABC △中,90A =︒∠,2AB AC ==. ① 在下图中画出一条Rt ABC △的形内弧;② 在Rt ABC △中,其形内弧的长度最长为____________.ABC(2)在平面直角坐标系中,点()2,0D -,()2,0E ,()0,1F ,点M 为DEF △形内弧所在圆的圆心. 求点M 纵坐标M y 的取值范围;(3)在平面直角坐标系中,点(2,M ,点G 为x 轴上一点. 点P 为OMG △最长形内弧所在圆的圆心,求点P 纵坐标P y 的取值范围.北京市房山区初三二模数学试题及参考答案 2020.6一、选择题(本题共16分,每小题2分)二、填空题(本题共16分,每小题2分)9.1- ; 10.1.3 ; 11.),(15-; 12. 222+2+=b +a b ab a )(;13.8; 14.2S ; 15.222-20=6+)(x x ; 16.同圆或等圆半径相等,三边相等的三角形是等边三角形,等边三角形的内角是60°,一条弧所对的圆周角是它所对圆心角的一半.(直径所对的圆周角是直角,正弦定义,三角函数值)三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28,每小题7分) 17.解:1-2+30sin 4+51-18°1-)(1-2+21×4+5-23= ………………………………………………4分4-24=……………………………………………………… 5分18. 解不等式①: ……………………………………………………1分 得-3<x ……………………………………………………2分解不等式②: ……………………………………………………3分 得-5>x ……………………………………………………4分不等式组的解集是 3-<<5-x ………………………………………………5分19.证明:∵BD平分∠ABC∴∠ABD =∠CBD ………………………………………………1分 ∵DE ∥AB∴∠ABD =∠BDE ………………………………………………2分 ∴∠CBD =∠BDE ………………………………………………3分 ∴EB = ED ………………………………………………4分 ∵F 是BD 中点∴EF 平分∠BED ………………………………………………5分 20.x x 2<3+34+2<1-x x AC(1) 当k =1时,此方程为0=3+4-2x x ……………………………………1分0=3)-(1)-(x x3= 1=21x x ,……………………………………2分 (2) 由题意得0≠k , ……………………………………3分0>12-16=Δk ……………………………………4分∴34<k ∴34<k 且 0≠k …………………………………5分21.(1)证明:∵CE =CD ,CF =CB∴四边形DBEF 是平行四边形 ………………………………………………1分 DE =2CD ,BF =2BC ∵菱形ABCD 中, CD = CB∴ DE = BF ………………………………………………2分 ∴四边形DBEF 是矩形 ………………………………………………3分 (2)∵AB =5∴BF =10∵菱形ABCD 中, 53=∠cos ABD ,∠DBF =∠ABD ∴53=∠cos DBF ∵∠BDF =90°∴DB =6 ………………………………………………4分 ∴DF = 8 ………………………………………………5分22. (1)把3=x 代入1-=x y 得2=y ∴),(23A又)0(>=x xky 图象过点),(23A 解得6=k ……………………………………………1分 (2)① PC = BC ……………………………………………2分当n = 4时, ),(34B ),(234C 23=PC ,23=BC ………………………………………3分 ② 1≤<0n 或 4≥n ………………………………5分23. (1)DE 与⊙O 相切 ………………………………1分连接OD 、CD 、OE∵ BC 为⊙O 的直径∴∠CDA =∠CDB =90° ∵E 是AC 中点 ∴ED =EC ∵OC =O D ,OE =O E ∴ΔOCE ≌ΔO DE∴∠O DE =∠OCE =90°………………………………2分 ∴O D ⊥DE∴DE 与⊙O 相切 ………………………………3分 (2)∵∠ACB =90°,AB =10,BC =6∴AC =8,CE =4, OC =3 ………………………………4分 ∵DE 、CE 与⊙O 相切 ∴DE=CE ,∠CEO =∠DEO∴O E ⊥CD ………………………………5分 ∴ OE =5∵CF OE CE OC •=•∴512=CF ∴59=OF ………………………………6分24. (1) 11 ………………………………2分(2) 如图 ………………………………3分(3) 8 ………………………………4分 (4) ①② ………………………………6分 25. (1) (cm)x12 3 4 5 6 (cm) 4.475.245.865.965.484.72 4.00 (cm)6.005.865.233.982.461.06………………………………2分(2)………………………………4分(3)AM 的长度约为 2.98cm 或1.50cm ………………………………6分 26.(1)对称轴-1=22-=aax ……………………………………1分(2)∵4AB =A (-3,0),B (1,0) ……………………………………2分 把(1,0)代入表达式:0=c +2a +a 得:a 3-=c ……………3分 ∴C (0,-3a )∴ D (0,-3a+1), 31D y a =-+ …………………………4分(3)当0a >时将点()4,4P -代入抛物线223y ax ax a =+-得:41683a a a =--, 45a =∴当45a ≥时,抛物线与线段PD 只有一个交点 …………………5分当0a <时抛物线的顶点为()1,4a -- 当44a -=时1a =- …………………6分综上所述,当45a ≥或1a =-时,抛物线与线段PD 只有一个交点.27.(1)① 过点D 作DF ⊥AC 于F ……………………………………1分 ∵30DBA =︒∠ ∴BD DF 21=∵以AC 为斜边作等腰ADC Rt Δ ∴FC AF =∴AC DF 21= ∴AC BD = ……………………………………2分② ∵ 等腰ADC Rt Δ与等腰Rt BED △中AC BD =∴DE DC =,ο45=∠=∠CDE FDC ∵30DBA =︒∠∴ο60=∠FDB ,ο15=∠CDB ∴ο60=∠CDE∴CDE Δ是等边三角形 ……………………………………3分 ∵DE EB =∴EB EC = ……………………………………4分(2)法1. 添加辅助线 ……………………………5分证出ADB Δ≌CDG Δ ……………………………6分 ∴ο45=∠=∠A DCG∴ο90=∠GCB ∵EB EG =∴ EB EC = ………………………………7分法2. 添加辅助线 ……………………………5分证出ADB Δ⁓GDE Δ …………………………6分 ∴ο45=∠=∠A DGE∴GE 平分DGC ∠ ∴GE 是DC 的中垂线∴ EB EC ED == ………………………………7分法3. 添加辅助线 ……………………………5分证出ο45=∠EDB =∠EFB ……………………6分∴FE 是DC 的中垂线∴ EB EC ED == ……………………7分 28.(1)①类似以上作答,只要弧上所有点都出现在三角形内部,均给分.………………………………2分②当2OB =时,Rt ABC △的形内弧最长,此时弧长=π=.(学生不必画出图象)………………………………3分(2)当圆心在x 轴下方时,此时最长形内弧与线段DF ,EF 相切∵1DOF DOM △∽△∴21OF OM OD ⋅=∴14OM = ∴4M y ≤- ………………………………4分当圆心在x 轴上方时,此时最长形内弧与x 轴相切∵2EGM HEG △∽△∴22HG HM HE ⋅=∴52 EH=∴252EM=∴52My≥………………………………5分综上所述,4My≤-或52My≥(3)当4Gx≤-时,此时最长形内弧与x轴相切∵1GOP GHO△∽△∴143GP=∴143Py≥当40Gx-<<时,此时最长形内弧与线段OM相切解得243Py≥21 当04G x <<时,此时最长形内弧与线段MG 相切解得343P y ≥ ………………………………6分 当4G x ≥时,此时最长形内弧与线段MG 相切解得433P y ≤- ………………………………7分综上所述,43P y ≥23P y ≤。
2020届北京中考数学二模试卷(房山区)

2020届北京中考数学二模试卷(房山区)下面1-8题均有四个选项,其中符合题意的选项只有一个.1.在迎来庆祝新中国成立70周年之后,对于中国而言,2020年又将是一个新的时间坐标.过去40年,中国完成了卓越的经济转型,八亿两千万人成功脱贫,这是人类发展史上具有里程碑意义的重大成就.将820000000用科学记数法表示为( ) A.98.210⨯B.90.8210⨯C.88.210⨯D.78210⨯2.如图是某个几何体的三视图,该几何体是( )A.长方体 C.正方体B.三棱柱 D.圆柱3.实数,a b 在数轴上的对应点的位置如图所示,则正确的结论是( )A. b a <B. a b -<C. 0a b +>D. a b >4.《北京市生活垃圾管理条例》对生活垃圾分类提出更高要求,于2020年5月1日起施行,施行的目的在于加强生活垃圾管理,改善城乡环境,保障人体健康.下列垃圾分类标志,是中心对称图形的是( )5.李老师是一位运动达人,他通过佩戴智能手环来记录自己一个月(30天)每天所走的步数,并绘制成如右统计表: 在每天所走的步数这组数据中,众数和中位数分别是( ) A.1.6,1.5B.1.7,1.6C.1.7,1.7D.1.7,1.556.如图,在ABCD Y 中,延长AD 至点E ,使2AD DE ,连接BE 交CD 于点F ,交AC 于点G ,则CGAG的值是() A. 23B.13C.12D.347.如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果下面有三个推断:①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.其中合理的是( ) A.①B.②C.①②D.①③8. 2020年是5G 爆发元年,三大运营商都在政策的支持下,加快着5G 建设的步伐.某通信公司实行的5G 畅想套餐,部分套餐资费标准如下:套餐类型 月费(元/月)套餐内包含内容 套餐外资费 国内数据流量(GB ) 国内主叫(分钟) 国内流量国内主叫 套餐1 128 30 200 每5元1GB ,用满3GB 后每3元1GB ,不足部分按照0.03元/MB 收取0.19元/分钟套餐2 158 40 300 套餐3 198 60 500 套餐423880600他应预定的套餐是( ) A.套餐1 B.套餐2 C.套餐3D.套餐4二、填空题(本题共16分,每小题2分) 9. 若分式11x x +-值为0,则x 的值是 .10. 如图,扇形AOB ,通过测量、计算,得»AB 的长约为.cm (π取3.14,结果保留一位小数)11.如图,若在象棋棋盘上建立直角坐标系,使“帅”位于点(32)--,,“炮”位于点()2,0-,则“兵”位于的点的坐标为.12.如图,一个大正方形被分成两个正方形和两个一样的矩形,请根据图形,写出一个含有a b ,的正确的等式.13.如果4m n +=,那么代数式222(2)m n m n m m n+++g 的值为14.已知一组数据123,,,n x x x x gg g ,的方差是2S ,那么另一组数据1233,3,3,3n x x x x ----gg g ,的方差是 .15.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”尺),现被风折断,竹梢触地面处与竹根的距译文:“有一根竹子,原高二丈(1丈10A B C分别表示竹梢,离为6尺,问折断处离地面的高度为多少尺?”如图,我们用点,,竹根和折断处,设折断处离地面的高度BC为x尺,则可列方程为16.下面是“作一个30︒角”的尺规作图过程.已知:平面内一点A.求作:∠A,使得∠A=30°作法:如图,(1)作射线AB;(2)在射线AB上取一点O,以O为圆心,OA为半径作圆,与射线AB相交于点C;(3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.则∠DAB即为所求的角.该尺规作图的依据是三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28题,每小题7分)17.114sin3015-+o()18.解不等式组:3(1)2,12.2x xxx+<⎧⎪⎨-<+⎪⎩19.如图,在ABCV中,BD平分ABC∠交AC于点,//D DE AB交BC于点,E F是BD 中点.求证:EF平分BED∠.20.已知关于x的一元二次方程2430kx x-+=.(1)当1k=时,求此方程的根;(2)若此方程有两个不相等的实数根,求k的取值范围.21.如图,菱形ABCD 中,分别延长,DC BC 至点,E F ,使,CE CD CF CB ==,连接,,,.DB BE EF FD(1)求证:四边形DBEF 是矩形; (2)若355AB cos ABD =∠=,,求DF 的长.22.在平面直角坐标系xOy 中,反比例函数()0ky x x=>的图象与直线1y x =-交于点()3A m ,(1)求k 的值(2)已知点()(),00P n n >,过点P 作垂直于x 轴的直线,交直线1y x =-于点B ,交函数()0ky x x=>于点C . ①当4n =时,判断线段PC 与BC 的数量关系,并说明理由; ②若PC BC ≤,结合图象,直接写出n 的取值范围.23.如图,在90ABC ACB ∠=︒V 中,,以BC 为直径的O e 交AB 于点,D E 是AC 中点,连接DE .(1)判断DE 与O e 的位置关系并说明理由;(2)设CD 与OE 的交点为F ,若10,6AB BC ==,求OF 的长.24.GDP 是指一个国家(或地区)在一定时期内生产活动的最终成果,常被公认为是衡量经济状况的最佳指标.截止2020年4月27日,对除西藏外的30个省区市第一季度有关GDP 的数据进行收集、整理、描述和分析.下面给出了部分信息:a.各省区市GDP 数据的频数分布直方图,如图24-1(数据分成6组,各组是04,488121216,1620,2024x x x x x x <≤<≤<≤<≤<≤<≤,,):b.2020年第一季度GDP 数据在这一组的是:4.6 4.95.0 5.1 5.3 5.46.37.4 7.5 7.8 7.8 c.30个省区市2020年第一季度及2019年GDP 增速排名统计图,如图24-2: d.北京2020年第一季度GDP 数据约为7.5千亿,GDP 增速排名为第22.根据以上信息,回答下列问题:(1)在30个省区市中,北京2020年第一季度GDP的数据排名第.(2)在30个省区市2020年第一季度及2019年GDP增速排名统计图中,请在图中用“O”圈出代表北京的点(3)2020年第一季度GDP增速排名位于北京之后的几个省份中,2019年GDP增速排名的最好成绩是第.(4)下列推断合理的是.①与2019年GDP增速排名相比,在疫情冲击下,2020年全国第一季度增速排名,部分省市有较大下滑,如D代表的湖北排名下滑最多.、、分别代表的新疆、广西、青海位于西部地区,多为人口净流出或少量净流②A B C入,经济发展主要依靠本地劳动力供给,疫后复工复产效率相对较高,相对于2019年GDP增速排名位置靠前.25.已知线段6AB cm =,点M 是线段AB 上一动点,以AB 为直径作O e ,点C 是圆周上一点且4AC cm =,连接CM ,过点A 做直线CM 的垂线,交O e 于点N ,连接CN ,设线段AM 的长为xcm ,线段AN 的长为1y cm ,线段CN 的长为2y cm .小华同学根据学习函数的经验,分别对函数12,y y ,随自变量x 的变化而变化的规律进行了探究.下面是该同学的探究过程,请补充完整:(1)按照下表中自变量x 的值进行取点、画图、测量,分别得到了12,y y 与x 的几组对应值:(2)在同一平面直角坐标系xOy 中,描出补全后的表中各组数值所对应的点()()12,,x y x y ,,并画出函数12,y y的图象(函数2y 的图象如图,请你画出1y 的图象)V是等腰三角形时,AM的长度约为(3)结合画出的函数图象,解决问题:当CANcm.26.在平面直角坐标系中,已知抛物线22y ax ax c =++与x 轴交于点,A B ,且4AB =.抛物线与y 轴交于点C ,将点C 向上移动1个单位得到点D . (1)求抛物线对称轴;(2)求点D 纵坐标(用含有a 的代数式表示);(3)已知点()4,4P -,若抛物线与线段PD 只有一个公共点,求a 的取值范围.27.点C 为线段AB 上一点,以AC 为斜边作等腰Rt ADC V ,连接BD ,在Rt ABD V 外侧,以BD 为斜边作等腰Rt BED V ,连接EC . (I)如图1,当30DBA ∠=︒时: ①求证:AC BD =;②判断线段EC 与EB 的数量关系,并证明;(2)如图2,当045DBA ︒<∠<︒时,EC 与EB 的数量关系是否保持不变?对于以上问题,小牧同学通过观察、实验,形成了解决该问题的几种思路:想法1:尝试将点D 为旋转中心,过点D 作线段BD 垂线,交BE 延长线于点G , 连接CG ;通过证明ADB CDG V V ≌解决以上问题;想法2:尝试将点D 为旋转中心,过点D 作线段AB 垂线,垂足为点G ,连接EG .通过证明ADB GDE V V ∽ 解决以上问题;想法3:尝试利用四点共圆,过点D 作AB 垂线段DF ,连接EF ,通过证明D F BE 、、、四点共圆,利用圆的相关知识解决以上问题.请你参考上面的想法,证明EC EB =(一种方法即可)28.过三角形的任意两个顶点画一条弧,若弧上的所有点都在该三角形的内部或边上,则称该弧为三角形的“形内弧”.(1)如图,在等腰Rt ABC V 中,902A AB AC ∠=︒==,. ①在下图中画出一条Rt ABC V 的形内弧; ②在Rt ABC V 中,其形内弧的长度最长为.(2)在平面直角坐标系中,点()()()2,02001D E F -,,,,.点M 为DEF V 形内弧所在圆的圆心.求点M 纵坐标M y 的取值范围;(3)在平面直角坐标系中,点(M ,点G 为x 轴上一点点P 为OMG V 最长形内弧所在圆的圆心,求点P 纵坐标p y 的取值范围.。
2020年北京市房山区初三二模数学试卷及参考答案2020.6

北京市房山区初三下学期第二次统一测试数学二模试题及参考答案2020年6月一、选择题(本题共16分,每小题2分)下面1-8题均有四个选项,其中符合题意的选项只有..一个.1. 在迎来庆祝新中国成立70周年之后,对于中国而言,2020年又将是一个新的时间坐标.过去40年,中国完成了卓越的经济转型,八亿两千万人成功脱贫,这是人类发展史上具有里程碑意义的重大成就.将820000000用科学记数法表示为()A. 8.2 ×109B. 0.82 ×109C. 8.2 ×108D. 82 ×1072. 如图是某个几何体的三视图,该几何体是()A.长方体B.三棱柱C.正方体D.圆柱3.实数a,b在数轴上的对应点的位置如图所示,则正确的结论是()A.|b|<a B.﹣a<b C.a+b>0 D.|a|>b4.《北京市生活垃圾管理条例》对生活垃圾分类提出更高要求,于2020年5月1日起施行,施行的目的在于加强生活垃圾管理,改善城乡环境,保障人体健康.下列垃圾分类标志,是中心对称图形的是()A B C D5. 李老师是一位运动达人,他通过佩戴智能手环来记录自己一个月(30天)每天所走的步数,并绘制成如下统计表:在每天所走的步数这组数据中,众数和中位数分别是( ) A .1.6,1.5 B .1.7,1.6 C .1.7,1.7 D .1.7,1.55 6. 如图,在□ABCD 中,延长AD 至点E ,使AD=2DE ,连接BE 交CD 于点F ,交AC 于点G ,则AGCG的值是()A .32B .31C .21D .437. 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果:抛掷次数“正面向上”的频率100.450.550100150200250300350400下面有三个推断:①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45. 其中合理的是( )GFDAEA .①B .②C .①②D .①③8.2020年是5G 爆发元年,三大运营商都在政策的支持下,加快着5G 建设的步伐.某通套餐 类型 月费(元/月) 套餐内包含内容套餐外资费 国内数据流量(GB ) 国内主叫(分钟) 国内流量 国内主叫套餐1 12830200每5元1GB ,用满3GB 后每3元1GB ,不足部分按照0.03元/MB 收取0.19 元/分钟套餐2 158 40 300 套餐3 198 60 500 套餐423880600小武每月大约使用国内数据流量49GB ,国内主叫350分钟,若想使每月付费最少,则他应预定的套餐是( )A .套餐1B .套餐2C .套餐3D .套餐4二、填空题(本题共16分,每小题2分)9. 若分式1-1+x x 值为0,则x 的值是 .10.如图,扇形AOB ,通过测量、计算,得弧AB 的长约为 cm. (π取3.14 ,结果保留一位小数)11. 如图,若在象棋棋盘上建立直角坐标系,使“帥”位于 点(-3,-2),“炮”位于点(-2.0),则“兵”位于的点的坐 标为 .12. 如图,一个大正方形被分成两个正方形和两个一样的矩形,请根据AB O已知:平面内一点A . 求作:∠A ,使得∠A =30°.作法:如图,(1)作射线AB ;(2)在射线AB 上取一点O ,以O 为圆心,OA 为半径作圆,与射线AB 相交于点C ; (3)以C 为圆心,OC 为半径作弧,与⊙O 交于点D ,作射线AD . 则∠DAB 即为所求的角.图形,写出一个含有a ,b 的正确的等式______________________.13. 如果4=+n m ,那么代数式nm mn m n m +2•)2++(22的值为 . 14. 已知一组数据1x ,2x ,3x ,…,n x 的方差是2S ,那么另一组数据3-1x ,3-2x ,3-3x ,…,3-n x 的方差是 .15. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”如图,我们用点A ,B ,C 分别表示竹梢,竹根和折断处,设折断处离地面的高度BC 为x 尺,则可列方程为_________________ . 16. 下面是“作一个30°角”的尺规作图过程.请回答:该尺规作图的依据是_______________________________________ .三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,,第27-28题,每小题7分)17. 计算:1-2+30sin 4+51-18°1-)(18. 解不等式组:19. 如图,在△ABC 中,BD 平分∠ABC 交AC 于点D ,DE ∥AB 交BC 于点E ,F 是BD 中点. 求证:EF 平分∠BED .20.已知关于x 的一元二次方程0=3+4-2x kx 有两个不相等的实数根. (1)当k =1时,求此方程的根;(2)若此方程有两个不相等的实数根,求k 的取值范围.21. 如图,菱形ABCD 中, 分别延长DC ,BC 至点E ,F ,使CE =CD ,CF =CB ,联结DB ,BE ,EF ,FD .(1)求证:四边形DBEF 是矩形;(2)若AB =5,53=∠cos ABD ,求DF 的长.2x<1)+(3x .2+<21-x x FEACBACFDE22. 在平面直角坐标系xOy 中,反比例函数)0(>=x xky 的图象与直线1-=x y 交于点 A (3,m ) (1)求k 的值(2)已知点P (n ,0)(n > 0),过点P 作垂直于x 轴的直线,交直线1-=x y 于点B ,交函数)0(>=x xky 图象于点C .①当n = 4时,判断线段PC 与BC 的数量关系,并说明理由;②若PC ≤BC ,结合图象,直接写出n 的取值范围.23. 如图,在△ABC 中,∠ACB =90°,以BC 为直径的⊙O 交AB 于点D ,E 是AC 中点, 连接DE .(1)判断DE 与⊙O 的位置关系并说明理由;(2)设CD 与OE 的交点为F ,若AB =10,BC =6,求OF 的长.24. GDP 是指一个国家(或地区)在一定时期内生产活动的最终成果,常被公认为是衡量经济状况的最佳指标. 截止2020年4月27日,对除西藏外的30个省区市第一季度有关GDP 的数据进行收集、整理、描述和分析.下面给出了部分信息:a.各省区市GDP 数据的频数分布直方图,如图24-1(数据分成6组,各组是,,,,,):EDCOAxy–1123456–1123456AOb.2020年第一季度GDP 数据在8≤<4x 这一组的是:4.6 4.95.0 5.1 5.3 5.46.37.4 7.5 7.8 7.8c.30个省区市2020年第一季度及2019年GDP 增速排名统计图,如图24-2:d.北京2020年第一季度GDP 数据约为7.5千亿,GDP 增速排名为第22.根据以上信息,回答下列问题:(1)在30个省区市中,北京2020年第一季度GDP 的数据排名第_______.(2)在30个省区市2020年第一季度及2019年GDP 增速排名统计图中,请在图中用“○”图24-1图24-2圈出代表北京的点.(3)2020年第一季度GDP增速排名位于北京之后的几个省份中,2019年GDP增速排名的最好成绩是第_______.(4)下列推断合理的是_______.①与2019年GDP增速排名相比,在疫情冲击下,2020年全国第一季度增速排名,部分省市有较大下滑,如D代表的湖北排名下滑最多.②A、B、C分别代表的新疆、广西、青海位于西部地区,多为人口净流出或少量净流入,经济发展主要依靠本地劳动力供给,疫后复工复产效率相对较高,相对于2019年GDP增速排名位置靠前.25.已知线段AB = 6cm,点M是线段AB上一动点,以AB为直径作⊙O,点C是圆周上一点且AC = 4cm,连接CM,过点A做直线CM的垂线,交⊙O于点N,连接CN,设AM的长为xcm,线段AN 的长为cm,线段CN 的长为cmNO BAMC小华同学根据学习函数的经验,,分别对函数y1,y2,随自变量x的变化而变化的规律进行了探究.下面是小华同学的探究过程,请补充完整:(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:x(cm)0 1 2 3 4 5 6 (cm) 4.47 5.24 5.86 5.96 4.72 4.00 (cm) 6.00 5.86 5.23 3.98 2.46 1.06 0 请你补全表格的相关数值,保留两位小数.(2)在同一平面直角坐标系xOy 中,描出补全后的表中各组数值所对应的点(x ,y 1),(x ,y 2),并画出函数 y 1,y 2的图象(函数y 2的图象如图,请你画出y 1的图象)(3)结合画出的函数图象,解决问题:当ΔCAN 是等腰三角形时时,AM 的长度约为______________cm .(保留两位小数)26.在平面直角坐标系中,已知抛物线22y ax ax c =++与x 轴交于点A 、B ,且4AB =.抛物线与y 轴交于点C ,将点C 向上移动1个单位得到点D . (1)求抛物线对称轴;(2)求点D 纵坐标(用含有a 的代数式表示);(3)已知点()4,4P -,若抛物线与线段PD 只有一个交点,求a 的取值范围.27. 点C 为线段AB 上一点,以AC 为斜边作等腰ADC Rt Δ,连接BD ,在ABD Δ外侧,以BD 为斜边作等腰Rt BED △,连接EC . (1)如图1,当30DBA =︒∠时: ① 求证:AC BD =;② 判断线段EC 与EB 的数量关系,并证明;A图1(2) 如图2,当°45<∠<°0DBA 时,EC 与EB 的数量关系是否保持不变? 对于以上问题,小牧同学通过观察、实验,形成了解决该问题的几种思路:想法1: 尝试将点D 为旋转中心. 过点D 作线段BD 的垂线,交BE 延长线于点G ,连接CG ;通过证明三角形ADB Δ≌CDG Δ全等解决以上问题;想法2: 尝试将点D 为旋转中心. 过点D 作线段AB 的垂线,垂足为点G ,连接EG .通过证明ADB Δ∽GDE Δ解决以上问题;想法3:尝试利用四点共圆. 过点D 作AB 垂线段DF ,连接EF ,通过证明D 、F 、B 、E 四点共圆,利用圆的相关知识解决以上问题.请你参考上面的想法,证明EC =EB (一种方法即可)图2EA C28. 过三角形的任意两个顶点画一条弧,若弧上的所有点都在该三角形的内部或边上,则称该弧为三角形的“形内弧”.(1)如图,在等腰Rt ABC △中,90A =︒∠,2AB AC ==. ① 在下图中画出一条Rt ABC △的形内弧;② 在Rt ABC △中,其形内弧的长度最长为____________.ABC(2)在平面直角坐标系中,点()2,0D -,()2,0E ,()0,1F ,点M 为DEF △形内弧所在圆的圆心. 求点M 纵坐标M y 的取值范围;(3)在平面直角坐标系中,点(2,M ,点G 为x 轴上一点. 点P 为OMG △最长形内弧所在圆的圆心,求点P 纵坐标P y 的取值范围.北京市房山区初三下学期第二次统一测试数学二模试题及参考答案2020年6月二、填空题(本题共16分,每小题2分)9.1- ; 10.1.3 ; 11.),(15-; 12. 222+2+=b +a b ab a )(; 13.8; 14.2S ; 15.222-20=6+)(x x ; 16.同圆或等圆半径相等,三边相等的三角形是等边三角形,等边三角形的内角是60°,一条弧所对的圆周角是它所对圆心角的一半.(直径所对的圆周角是直角,正弦定义,三角函数值)三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28,每小题7分) 17.解:1-2+30sin 4+51-18°1-)(1-2+21×4+5-23= ………………………………………………4分4-24=……………………………………………………… 5分18. 解不等式①:……………………………………………………1分 得-3<x……………………………………………………2分解不等式②: ……………………………………………………3分得-5>x ……………………………………………………4分不等式组的解集是 3-<<5-x ………………………………………………5分 19.证明:∵BD 平分∠ABC∴∠ABD =∠CBD ………………………………………………1分x x 2<3+34+2<1-x x B∵DE ∥AB∴∠ABD =∠BDE ………………………………………………2分 ∴∠CBD =∠BDE ………………………………………………3分 ∴EB = ED ………………………………………………4分 ∵F 是BD 中点∴EF 平分∠BED ………………………………………………5分 20.(1) 当k =1时,此方程为0=3+4-2x x ……………………………………1分0=3)-(1)-(x x3= 1=21x x ,……………………………………2分 (2) 由题意得0≠k , ……………………………………3分0>12-16=Δk ……………………………………4分∴34<k ∴34<k 且 0≠k …………………………………5分 21.(1)证明:∵CE =CD ,CF =CB∴四边形DBEF 是平行四边形 ………………………………………………1分 DE =2CD ,BF =2BC ∵菱形ABCD 中, CD = CB∴ DE = BF ………………………………………………2分 ∴四边形DBEF 是矩形 ………………………………………………3分 (2)∵AB =5∴BF =10∵菱形ABCD 中, 53=∠cos ABD ,∠DBF =∠ABD ∴53=∠cos DBF ∵∠BDF =90°∴DB =6 ………………………………………………4分 ∴DF = 8 ………………………………………………5分22. (1)把3=x 代入1-=x y 得2=y ∴),(23A 又)0(>=x xky 图象过点),(23A 解得6=k ……………………………………………1分 (2)① PC = BC ……………………………………………2分当n = 4时, ),(34B ),(234C 23=PC ,23=BC ………………………………………3分 ② 1≤<0n 或 4≥n ………………………………5分23. (1)DE 与⊙O 相切 ………………………………1分连接OD 、CD 、OE∵ BC 为⊙O 的直径∴∠CDA =∠CDB =90° ∵E 是AC 中点 ∴ED =EC∵OC =O D ,OE =O E ∴ΔOCE ≌ΔO DE∴∠O DE =∠OCE =90°………………………………2分 ∴O D ⊥DE∴DE 与⊙O 相切 ………………………………3分 (2)∵∠ACB =90°,AB =10,BC =6∴AC =8,CE =4, OC =3 ………………………………4分 ∵DE 、CE 与⊙O 相切 ∴DE=CE ,∠CEO =∠DEO∴O E ⊥CD ………………………………5分 ∴ OE =5∵CF OE CE OC •=•∴512=CF ∴59=OF ………………………………6分24. (1) 11 ………………………………2分(2) 如图 ………………………………3分(3) 8 ………………………………4分 (4) ①② ………………………………6分 25. (1) (cm)x12 3 4 5 6 (cm) 4.475.245.865.965.484.72 4.00 (cm)6.005.865.233.982.461.06………………………………2分(2)………………………………4分(3)AM 的长度约为 2.98cm 或1.50cm ………………………………6分 26.(1)对称轴-1=22-=aax ……………………………………1分(2)∵4AB =A (-3,0),B (1,0) ……………………………………2分把(1,0)代入表达式:0=c +2a +a 得:a 3-=c ……………3分∴ C (0,-3a )∴ D (0,-3a+1), 31D y a =-+ …………………………4分(3)当0a >时将点()4,4P -代入抛物线223y ax ax a =+-得:41683a a a =--, 45a =∴当45a ≥时,抛物线与线段PD 只有一个交点 …………………5分当0a <时抛物线的顶点为()1,4a -- 当44a -=时1a =- …………………6分综上所述,当45a ≥或1a =-时,抛物线与线段PD 只有一个交点.27.(1)① 过点D 作DF ⊥AC 于F ……………………………………1分 ∵30DBA =︒∠ ∴BD DF 21=∵以AC 为斜边作等腰ADC Rt Δ ∴FC AF =∴AC DF 21= ∴AC BD = ……………………………………2分② ∵ 等腰ADC Rt Δ与等腰Rt BED △中AC BD =∴DE DC =,ο45=∠=∠CDE FDC ∵30DBA =︒∠∴ο60=∠FDB ,ο15=∠CDB ∴ο60=∠CDE∴CDE Δ是等边三角形 ……………………………………3分 ∵DE EB =∴EB EC = ……………………………………4分(2)法1. 添加辅助线 ……………………………5分证出ADB Δ≌CDG Δ ……………………………6分 ∴ο45=∠=∠A DCG∴ο90=∠GCB ∵EB EG =∴ EB EC = ………………………………7分法2. 添加辅助线 ……………………………5分证出ADB Δ⁓GDE Δ …………………………6分 ∴ο45=∠=∠A DGE∴GE 平分DGC ∠ ∴GE 是DC 的中垂线∴ EB EC ED == ………………………………7分法3. 添加辅助线 ……………………………5分证出ο45=∠EDB =∠EFB ……………………6分∴FE 是DC 的中垂线∴ EB EC ED == ……………………7分 28.(1)①类似以上作答,只要弧上所有点都出现在三角形内部,均给分.………………………………2分②当2OB =时,Rt ABC △的形内弧最长,此时弧长=π=.(学生不必画出图象)………………………………3分(2)当圆心在x 轴下方时,此时最长形内弧与线段DF ,EF 相切∵1DOF DOM △∽△ ∴21OF OM OD ⋅= ∴14OM = ∴4M y ≤- ………………………………4分当圆心在x 轴上方时,此时最长形内弧与x 轴相切∵2EGM HEG △∽△ ∴22HG HM HE ⋅= ∴52EH =∴252EM =∴52M y ≥………………………………5分综上所述,4M y ≤-或52M y ≥(3)当4G x ≤-时,此时最长形内弧与x 轴相切∵1GOP GHO △∽△ ∴143GP = ∴143P y ≥ 当40G x -<<时,此时最长形内弧与线段OM 相切解得243P y ≥当04G x <<时,此时最长形内弧与线段MG 相切解得3433P y ≥ ………………………………6分 当4G x ≥时,此时最长形内弧与线段MG 相切解得423P y ≤ ………………………………7分综上所述,433P y ≥或33P y ≤-。
2020-2021学年北京市房山区中考数学第二次模拟试题及答案解析

最新北京市房山中考二模数学试卷一、单选题(共10小题)1.小星同学在“百度”搜索引擎中输入“中国梦,我的梦”,可以搜索到与之相关的结果的条数约为61700000,将61700000用科学记数法表示为()A.617×105B.6.17×106C.6.17×107D.0.617×108考点:科学记数法和近似数、有效数字答案:C试题解析:用科学计数法表示较大的正数时,一般形式为a×10n.其中1≤a<10,n为正整数.确定n的值时,要把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,所以a=6.17,n=7.2.实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是()A.b B.d C.a D.c考点:实数大小比较答案:D试题解析:由于a<b<0<c<d,则3.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.考点:中心对称与中心对称图形答案:B试题解析:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形;轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。
而A是轴对称图形,C与D是中心对称图形。
4.小明掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,那么向上一面的点数大于4的概率为()A.B.C.D.考点:概率及计算答案:C试题解析:骰子共有6个点数,其中点数大于4的有5,6两种情况,则5.如果一个正多边形的每个外角为72°,那么这个正多边形的边数为()A.5B.6C.7D.8考点:多边形的内角与外角答案:C试题解析:由正多边形的每个外角为72°,该正多边形的每个内角为180°-72°=108°.故这个多边形的内角和为n×108°,又因为正n边形的内角和为(n-2)×180°,设该多边形的边数为n,则(n-2)×180°=n×108°,解得:n=5.6.如图,AB是⊙O的直径,C、D两点在⊙O上,如果∠C=40°,那么∠ABD的度数为()A.40°B.90°C.80°D.50°考点:圆周角定理及推论答案:D试题解析:根据题意得7.国家气象局监测2015年某日24小时PM2.5的值,其中6个时刻的数值如下表,则这组数据的中位数和平均数分别是()A.331;332.5B.329;332.5C.331;332D.333;332考点:平均数、众数、中位数答案:A试题解析:把六个数从小到大排序:324,325,329,333,342,342,则中位数为(329+333)÷2=331,平均数为(324+325+329+333+342+342)÷6=332.58.直线与双曲线(k≠0)在同一坐标系中的大致图象是()A.B.C.D.考点:反比例函数与一次函数综合答案:C试题解析:根据题意得:当k>0时,双曲线位于一,三象限,而直线位于一,三,四象限;当k<0时,双曲线位于二,四象限,而直线位于一,二,四象限。
2020年北京市房山区中考数学二模试卷

2020年北京市房山区中考数学二模试卷
一、选择题下面1-8题均有四个选项,其中符合题意的选项只有一个.
1.(2分)在迎来庆祝新中国成立70周年之后,对于中国而言,2020年又将是一个新的时间坐标.过去40年,中国完成了卓越的经济转型,八亿两千万人成功脱贫,这是人类发展史上具有里程碑意义的重大成就.将820000000用科学记数法表示为()
A.8.2×109B.0.82×109C.8.2×108D.82×107
2.(2分)如图是某个几何体的三视图,该几何体是()
A.长方体B.三棱柱C.正方体D.圆柱
3.(2分)实数a,b在数轴上的对应点的位置如图所示,则正确的结论是(
A.|b|<a B.﹣a<b C.a+b>0D.|a|>b
4.(2分)《北京市生活垃圾管理条例》对生活垃圾分类提出更高要求,于2020年5月1日起施行,施行的目的在于加强生活垃圾管理,改善城乡环境,保障人体健康.下列垃圾分类标志,是中心对称图形的是()
A.B.C.D.
5.(2分)李老师是一位运动达人,他通过佩戴智能手环来记录自己一个月(30天)每天所走的步数,并绘制成如图统计表,在每天所走的步数这组数据中,众数和中位数分别是()。
北京市房山区2019-2020学年中考二诊数学试题含解析
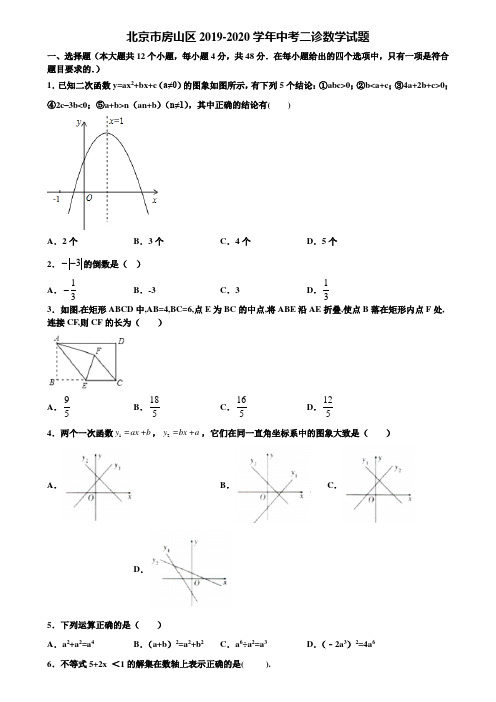
北京市房山区2019-2020学年中考二诊数学试题一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知二次函数y=ax 2+bx+c (a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c ;③4a+2b+c>0;④2c –3b<0;⑤a+b>n (an+b )(n≠1),其中正确的结论有( )A .2个B .3个C .4个D .5个2.3--的倒数是( ) A .13-B .-3C .3D .133.如图,在矩形ABCD 中,AB=4,BC=6,点E 为BC 的中点,将ABE 沿AE 折叠,使点B 落在矩形内点F 处,连接CF,则CF 的长为( )A .95B .185C .165D .1254.两个一次函数1y ax b =+,2y bx a =+,它们在同一直角坐标系中的图象大致是( )A .B .C .D .5.下列运算正确的是( ) A .a 2+a 2=a 4B .(a+b )2=a 2+b 2C .a 6÷a 2=a 3D .(﹣2a 3)2=4a 66.不等式5+2x <1的解集在数轴上表示正确的是( ).A.B.C.D.7.如图,AB是⊙O的直径,AB=8,弦CD垂直平分OB,E是弧AD上的动点,AF⊥CE于点F,点E 在弧AD上从A运动到D的过程中,线段CF扫过的面积为()A.4π+33B.4π+343C.43π+343D.43π+338.如图,边长为2a的等边△ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是()A.12a B.a C.32a D.3a9.如图,已知△ADE是△ABC绕点A逆时针旋转所得,其中点D在射线AC上,设旋转角为α,直线BC与直线DE交于点F,那么下列结论不正确的是()A.∠BAC=αB.∠DAE=αC.∠CFD=αD.∠FDC=α10.比较417363)A.417363B.436317C363417D17363 411.一个不透明的布袋里装有5个红球,2个白球,3个黄球,它们除颜色外其余都相同,从袋中任意摸出1个球,是黄球的概率为()A.310B.15C.12D.71012.二次函数y=ax2+bx+c(a≠0)和正比例函数y=﹣13x的图象如图所示,则方程ax2+(b+13)x+c=0(a≠0)的两根之和()A.大于0 B.等于0 C.小于0 D.不能确定二、填空题:(本大题共6个小题,每小题4分,共24分.)13.如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C,若∠ACB=30°,AB=3,则阴影部分的面积是___.14.函数32xyx=-中,自变量x的取值范围是______15.如图△ABC中,AB=AC=8,∠BAC=30°,现将△ABC绕点A逆时针旋转30°得到△ACD,延长AD、BC交于点E,则DE的长是_____.16.在平面直角坐标系中,已知线段AB的两个端点的坐标分别是A(4,-1)、B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2),则点B′的坐标为________.17.某航空公司规定,乘客所携带行李的重量x(kg)与运费y(元)满足如图所示的函数图象,那么每位乘客最多可免费携带____kg的行李.18. “五一劳动节”,王老师将全班分成六个小组开展社会实践活动,活动结束后,随机抽取一个小组进行汇报展示.第五组被抽到的概率是___.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)如图,已知抛物线234y ax ax a =+-与x 轴负半轴相交于点A ,与y 轴正半轴相交于点B ,OB OA =,直线l 过A 、B 两点,点D 为线段AB 上一动点,过点D 作CD x ⊥轴于点C ,交抛物线于点 E . (1)求抛物线的解析式;(2)若抛物线与x 轴正半轴交于点F ,设点D 的横坐标为x ,四边形FAEB 的面积为S ,请写出S 与x 的函数关系式,并判断S 是否存在最大值,如果存在,求出这个最大值;并写出此时点E 的坐标;如果不存在,请说明理由.(3)连接BE ,是否存在点D ,使得DBE V 和DAC V 相似?若存在,求出点D 的坐标;若不存在,说明理由.20.(6分)如图,小明在一块平地上测山高,先在B 处测得山顶A 的仰角为30°,然后向山脚直行60米到达C 处,再测得山顶A 的仰角为45°,求山高AD 的长度.(测角仪高度忽略不计)21.(6分)解方程: +=1.22.(8分)如图,AB 是⊙O 的一条弦,E 是AB 的中点,过点E 作EC ⊥OA 于点C ,过点B 作⊙O 的切线交CE 的延长线于点D . (1)求证:DB=DE;(2)若AB=12,BD=5,求⊙O 的半径.23.(8分)图1是一商场的推拉门,已知门的宽度2AD =米,且两扇门的大小相同(即AB CD =),将左边的门11ABB A 绕门轴1AA 向里面旋转37︒,将右边的门11CDD C 绕门轴1DD 向外面旋转45︒,其示意图如图2,求此时B 与C 之间的距离(结果保留一位小数).(参考数据:sin370.6︒≈,cos370.8︒≈,2 1.4≈)24.(10分)如图,在4×4的正方形方格中,△ABC 和△DEF 的顶点都在边长为1的小正方形的顶点上. 填空:∠ABC= °,BC= ;判断△ABC 与△DEF 是否相似,并证明你的结论.25.(10分)如图,抛物线2y ax 2ax c =-+(a≠0)交x 轴于A 、B 两点,A 点坐标为(3,0),与y 轴交于点C (0,4),以OC 、OA 为边作矩形OADC 交抛物线于点G .求抛物线的解析式;抛物线的对称轴l 在边OA (不包括O 、A 两点)上平行移动,分别交x 轴于点E ,交CD 于点F ,交AC 于点M ,交抛物线于点P ,若点M 的横坐标为m ,请用含m 的代数式表示PM 的长;在(2)的条件下,连结PC ,则在CD 上方的抛物线部分是否存在这样的点P ,使得以P 、C 、F 为顶点的三角形和△AEM 相似?若存在,求出此时m 的值,并直接判断△PCM 的形状;若不存在,请说明理由.26.(12分)某初中学校组织200位同学参加义务植树活动.甲、乙两位同学分别调查了30位同学的植树情况,并将收集的数据进行了整理,绘制成统计表1和表2: 表1:甲调查九年级30位同学植树情况 每人植树棵数 7 8 9 10 人数36156表2:乙调查三个年级各10位同学植树情况 每人植树棵数 678910人数363126根据以上材料回答下列问题:(1)关于于植树棵数,表1中的中位数是 棵;表2中的众数是 棵; (2)你认为同学 (填“甲”或“乙”)所抽取的样本能更好反映此次植树活动情况; (3)在问题(2)的基础上估计本次活动200位同学一共植树多少棵? 27.(12分)如图,在平面直角坐标系xOy 中,直线16y k x =+与函数()20k y x x=>的图象的两个交点分别为A (1,5),B . (1)求1k ,2k 的值;(2)过点P (n ,0)作x 轴的垂线,与直线16y k x =+和函数()20k y x x=>的图象的交点分别为点M ,N ,当点M 在点N 下方时,写出n 的取值范围.参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.B 【解析】 【分析】①观察图象可知a <0,b >0,c >0,由此即可判定①;②当x=﹣1时,y=a ﹣b+c 由此可判定②;③由对称知,当x=2时,函数值大于0,即y=4a+2b+c >0,由此可判定③;④当x=3时函数值小于0,即y=9a+3b+c <0,且x=﹣2b a =1,可得a=﹣2b,代入y=9a+3b+c <0即可判定④;⑤当x=1时,y 的值最大.此时,y=a+b+c ,当x=n 时,y=an 2+bn+c ,由此即可判定⑤. 【详解】①由图象可知:a <0,b >0,c >0,abc <0,故此选项错误; ②当x=﹣1时,y=a ﹣b+c <0,即b >a+c ,故此选项错误;③由对称知,当x=2时,函数值大于0,即y=4a+2b+c >0,故此选项正确; ④当x=3时函数值小于0,y=9a+3b+c <0,且x=﹣2b a =1即a=﹣2b ,代入得9(﹣2b)+3b+c <0,得2c <3b ,故此选项正确;⑤当x=1时,y 的值最大.此时,y=a+b+c ,而当x=n 时,y=an 2+bn+c ,所以a+b+c >an 2+bn+c ,故a+b >an 2+bn ,即a+b >n (an+b ),故此选项正确. ∴③④⑤正确. 故选B . 【点睛】本题主要考查了抛物线的图象与二次函数系数之间的关系,熟知抛物线的图象与二次函数系数之间的关系是解决本题的关键. 2.A 【解析】 【分析】先求出33--=-,再求倒数. 【详解】 因为33--=- 所以3--的倒数是13- 故选A考核知识点:绝对值,相反数,倒数. 3.B 【解析】 【分析】连接BF ,由折叠可知AE 垂直平分BF ,根据勾股定理求得AE=5,利用直角三角形面积的两种表示法求得BH=125,即可得BF=245 ,再证明∠BFC=90°,最后利用勾股定理求得CF=185.【详解】连接BF ,由折叠可知AE 垂直平分BF ,∵BC=6,点E 为BC 的中点, ∴BE=3, 又∵AB=4, ∴222243AB BE +=+=5,∵1122AB BE AE BH ⋅=⋅, ∴1134522BH ⨯⨯=⨯⨯, ∴BH=125,则BF=245,∵FE=BE=EC , ∴∠BFC=90°, ∴2222246()5BC BF -=-185 .故选B . 【点睛】本题考查的是翻折变换的性质、矩形的性质及勾股定理的应用,掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键. 4.B 【解析】 【分析】根据各选项中的函数图象判断出a 、b 的符号,然后分别确定出两直线经过的象限以及与y 轴的交点位置,解:由图可知,A、B、C选项两直线一条经过第一三象限,另一条经过第二四象限,所以,a、b异号,所以,经过第一三象限的直线与y轴负半轴相交,经过第二四象限的直线与y轴正半轴相交,B选项符合,D选项,a、b都经过第二、四象限,所以,两直线都与y轴负半轴相交,不符合.故选:B.【点睛】本题考查了一次函数的图象,一次函数y=kx+b(k≠0),k>0时,一次函数图象经过第一三象限,k<0时,一次函数图象经过第二四象限,b>0时与y轴正半轴相交,b<0时与y轴负半轴相交.5.D【解析】【分析】根据完全平方公式、合并同类项、同底数幂的除法、积的乘方,即可解答.【详解】A、a2+a2=2a2,故错误;B、(a+b)2=a2+2ab+b2,故错误;C、a6÷a2=a4,故错误;D、(-2a3)2=4a6,正确;故选D.【点睛】本题考查了完全平方公式、同底数幂的除法、积的乘方以及合并同类项,解决本题的关键是熟记公式和法则.6.C【解析】【分析】先解不等式得到x<-1,根据数轴表示数的方法得到解集在-1的左边.【详解】5+1x<1,移项得1x<-4,系数化为1得x<-1.本题考查了在数轴上表示不等式的解集:先求出不等式组的解集,然后根据数轴表示数的方法把对应的未知数的取值范围通过画区间的方法表示出来,等号时用实心,不等时用空心. 7.A 【解析】 【分析】连AC ,OC ,BC .线段CF 扫过的面积=扇形MAH 的面积+△MCH 的面积,从而证明120AMH ∠︒=即可解决问题. 【详解】如下图,连AC ,OC ,BC ,设CD 交AB 于H ,∵CD 垂直平分线段OB , ∴CO =CB , ∵OC =OB , ∴OC =OB =BC , ∴60ABC ∠︒=, ∵AB 是直径, ∴90ACB ∠︒=, ∴30CAB ∠︒=,∵90AFC AHC ∠∠︒==,∴点F 在以AC 为直径的⊙M 上运动,当E 从A 运动到D 时,点F 从A 运动到H ,连接MH , ∵MA =MH ,∴30MAH MHA ∠∠︒== ∴120AMH ∠︒=, ∵3AC =∴CF 扫过的面积为221203(23)(23)433360ππ⨯=+, 故选:A . 【点睛】本题主要考查了阴影部分面积的求法,熟练掌握扇形的面积公式及三角形的面积求法是解决本题的关键. 8.A【解析】【分析】取CB 的中点G ,连接MG ,根据等边三角形的性质可得BH=BG ,再求出∠HBN=∠MBG ,根据旋转的性质可得MB=NB ,然后利用“边角边”证明∴△MBG ≌△NBH ,再根据全等三角形对应边相等可得HN=MG ,然后根据垂线段最短可得MG ⊥CH 时最短,再根据∠BCH=30°求解即可.【详解】如图,取BC 的中点G ,连接MG ,∵旋转角为60°,∴∠MBH+∠HBN=60°,又∵∠MBH+∠MBC=∠ABC=60°,∴∠HBN=∠GBM ,∵CH 是等边△ABC 的对称轴,∴HB=12AB , ∴HB=BG ,又∵MB 旋转到BN ,∴BM=BN ,在△MBG 和△NBH 中,BG BH MBG NBH MB NB ⎧⎪∠∠⎨⎪⎩===,∴△MBG ≌△NBH (SAS ),∴MG=NH ,根据垂线段最短,MG ⊥CH 时,MG 最短,即HN 最短,此时∵∠BCH=12×60°=30°,CG=12AB=12×2a=a , ∴MG=12CG=12×a=2a ,∴HN=2a , 故选A .【点睛】本题考查了旋转的性质,等边三角形的性质,全等三角形的判定与性质,垂线段最短的性质,作辅助线构造出全等三角形是解题的关键,也是本题的难点.9.D【解析】【分析】利用旋转不变性即可解决问题.【详解】∵△DAE 是由△BAC 旋转得到,∴∠BAC=∠DAE=α,∠B=∠D ,∵∠ACB=∠DCF ,∴∠CFD=∠BAC=α,故A ,B ,C 正确,故选D .【点睛】本题考查旋转的性质,解题的关键是熟练掌握旋转不变性解决问题,属于中考常考题型.10.C【解析】【分析】根据且【详解】解:易得:4 故选C.【点睛】本题主要考查开平方开立方运算。
房山区初三二模数学试卷及答案

D.C.B.A.房山区2011年九年级学题统一练习(二)一、选择题(本大题共32分,每小题4分): 1.-3的相反数等于A .3B .-3C .31 D .-312.上海世博会永久地标建筑世博轴获“全球生态建筑奖”,该建筑占地面积约为104500平方米.其中104500这个数用科学记数法表示为A .1.045610⨯ B .0.1045 510⨯ C .10.45410⨯ D .1.045510⨯ 3.下列说法正确的是A .3B .对角线相等的四边形是矩形C .近似数0.2050有4个有效数字D .两个底角相等的梯形一定是等腰梯形 4.如果正多边形的每个外角等于40°,则这个正多边形的边数是 A .10 B .9 C .8 D .75.已知两圆的半径分别为3cm ,和5cm , 圆心距是6cm ,则两圆的位置关系 A .相离 B .外切 C .相交 D .内切6.如图所示,电路图上有A 、B 、C 三个开关和一个小灯泡,闭合开关C 或者同时闭合开关A 、B ,都可使小灯泡发光.现在任意闭合其中一个开关,则小灯泡发光的概率等于 A .14 B .13 C .23 D .127.对于一组数据:75,73,75,71,76,下列说法正确的是A .这组数据的平均数是75B .这组数据的方差是3.2C .这组数据的中位数是74D .这组数据的众数是76 8.将如图所示的白纸只沿虚线剪开,用裁开的纸片和白纸上的阴影部分围成一个立体模型,以阴影部分为底面放在桌面上,下面四个示意图中,只有一个符合上述要求,那么这个示意图是二、填空题(本大题共16分,每小题4分):CDF EBA 9.若分式121x x +-有意义,则x_____________. 10.因式分解:39x x -=______________.11.如图,正方形ABCD 的边长为4cm ,正方形AEFG 的边长为1cm .如果正方形AEFG 绕点A 旋转,那么C 、F 两点之间的最小距离是____________.12.如图,正方形ABCD ,E 为AB 上的动点,(E 不与A 、B 重合)联结DE ,作DE 的中垂线,交AD 于点F . (1)若E 为AB 中点,则DFAE= . (2)若E 为AB 的n 等分点(靠近点A), 则DFAE= . 三、解答题(本大题共30分,每小题5分) 13.(本小题满分5分)计算:01(π4)tan 602----. 解:14.(本小题满分5分)解不等式5122(43)x x --≤,并把它的解集在数轴上表示出来. 解:15.(本小题满分5分)已知:如图,在△ABC 中,∠ACB=90°点D 是AB 的中点,延长BC 到点F , 延长CB 到点E ,使CF=BE ,联结DE 、DC 、DF .求证:DE=DF . 证明:16.(本小题满分5分)已知2(2)(2)40x x x y ---+=,求代数式2x -解:FEDCAy-52x 13-4123-1-2-3-1-2O17.(本小题满分5分)列方程或方程组解应用题:九年级(1)班的学生周末乘汽车到游览区游览,游览区到学校120千米,一部分学生乘慢车先行,出发1小时后,另一部分学生乘快车前往,结果他们同时到达,已知快车速度是慢车速度的1.5倍,求慢车的速度. 解:18.(本小题满分5分)已知反比例函数y = kx 的图象与二次函数y =ax 2+x -1的图象相交于点A (2,2)(1)求反比例函数与二次函数的解析式;(2)设二次函数图象的顶点为B ,判断点B 是否在反比例函数的图象上,并说明理由;(3)若反比例函数图象上有一点P ,点P 的横坐标为1,求△AOP 的面积. 解:(1)(2)(3)四、解答题(本大题共20分,每小题5分): 19.(本小题满分5分)在△ABC 中,AB=AC ,∠BAC=120°,过点C 作CD ∥AB ,且CD=2AB ,联结BD ,BD=2.求△ABC 的面积. 解:D C20.(本小题满分5分)已知:如图,在Rt ABC △中,90C ∠=,点O 在AB 上,以O 为圆心,OA 长为半径的圆与AC AB ,分别交于点D E ,,且CBD A ∠=∠.(1)判断直线BD 与O 的位置关系,并证明你的结论;(2)若2BC =,BD =52,求ADAO的值.解:(1)判断:证明:(2)21.(本小题满分5分)“校园手机”现象越来越受到社会的关注.“春节”期间,小记者刘凯随机调查了我区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:D BD CB A图① 图②(1)求这次调查的家长人数,并补全图①; (2)求图②中表示家长“赞成”的圆心角的度数;(3)从这次接受调查的学生中,随机抽查一个,恰好是“无所谓”态度的学生的概率是多少? 解:(1)(3) 22.(本小题满分5分)已知菱形纸片ABCD 的边长为8,∠A=60°,E 为AB 边上的点,过点E 作EF ∥BD 交AD 于点F .将菱形先沿EF 按图1所示方式折叠,点A 落在点A '处,过点A '作GH ∥BD 分别交线段BC 、DC 于点G 、H,再将菱形沿GH 按图1所示方式折叠,点C 落在点C '处, C G '与C 'H 分别交A E '与A F '于点M 、N .若点C '在△A 'EF 的内部或边上,此时我们称四边形A MC N ''(即图中阴影部分)为“重叠四边形”.图1 图2 备用图(1)若把菱形纸片ABCD 放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A 、B 、C 、D 、E 恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形A MC N ''的面积;(2)实验探究:设AE 的长为m ,若重叠四边形A MC N ''存在.试用含m 的代数式表示重叠四边形A MC N ''的面积,并写出m 的取值范围(直接写出结果,备用图供实验,探究使用). 解:(1)重叠四边形A MC N ''的面积为 ;(2)用含m 的代数式表示重叠四边形A MC N ''的面积为______________;m 的取值范围为_____________.五、解答题(本大题共22分,其中第23小题7分,第24小题7分,第25小题8分): 23.(本小题满分7分)已知:二次函数y=22(2)x n m x m mn +-+-. (1)求证:此二次函数与x 轴有交点;(2)若m-1=0,求证方程22(2)0x n m x m mn +-+-=有一个实数根为1;(3)在(2)的条件下,设方程22(2)0x n m x m mn +-+-=的另一根为a,当x=2时,关于n 的函数1y nx am=+与222(2)y x n m ax m mn =+-+-的图象交于点A 、B (点A 在点B 的左侧),平行于y 轴的直线L 与1y nx am =+、222(2)y x n m ax m mn =+-+-的图象分别交于点C 、D ,若CD=6,求点C 、D 的坐标.(1)证明:(2)解:(3)解:24.(本小题满分7分)如图,已知二次函数()220y ax ax c a =-+<的图象与x 轴负半轴交于点A (-1,0),与y轴正半轴交与点B ,顶点为P ,且OB=3OA ,一次函数y=kx+b 的图象经过A 、B . (1)求一次函数解析式; (2)求顶点P 的坐标; (3)平移直线AB 使其过点P ,如果点M在平移后的直线上,且3tan 2OAM ∠=,求点M 坐标; (4)设抛物线的对称轴交x 轴与点E ,联结AP 交y 轴与点D ,若点Q 、N 分别为两线段PE 、PD 上的动点,联结QD 、QN ,请直接写出QD+QN 的最小值. 解:(1)(2)(3)(4) 25.(本小题满分8分)如图,在平面直角坐标系中,点O 是坐标原点,四边形AOCB 是梯形,AB ∥OC ,点A 在y 轴上,点C 在x 轴上,且2OA 80-=(),OB =OC . (1)求点B 的坐标;(2)点P 从C 点出发,沿线段CO 以5个单位/秒的速度向终点O 匀速运动,过点P 作PH ⊥OB ,垂足为H ,设△HBP 的面积为S (S≠0),点P 的运动时间为t 秒,求S 与t 之间的函数关系式(直接写出自变量t 的取值范围); (3)在(2)的条件下,过点P 作PM ∥CB 交线段AB 于点M ,过点M 作MR ⊥OC ,垂足为R ,线段MR 分别交直线PH 、OB 于点E 、G ,点F 为线段PM 的中点,联结EF .①判断EF 与PM 的位置关系; ②当t 为何值时,2EG =?解:(1)(2)(3)房山区2011年九年级数学统一练习(二)答案及评分标准二、 填空题:9. 12≠; 10. (+3)(3)x x x -; 11. 12.251,42n n + .三、解答题:13.解:原式=112- -----------------------------------------------------------4分=32- ----------------------------------------------------------------------5分 14.解:去括号:5x-1286x ≤- --------------------------------------------------------------1分移项: 58126x x -≤- ------------------------------------------------------------------2分 合并同类项:36x -≤ ---------------------------------------------------------------------3分 系数化1:2x ≥- --------------------------------------------------------------------4分 这个不等式的解集在数轴上表示如下:数轴表示(略) ----------------------------------------------5分 15.证明:∵在△ABC 中,∠ACB=90°,点D 是AB 的中点∴CD=BD ------------------------------------------------------------1分 ∴∠DCE=∠DBF------------------------------------------------------2分 ∵CF=BE , ∴CE = BF ---------------------------------3分 ∴△DCE ≌△DBF------------------------------------4分∴DE=DF . -------------------------------------------------5分 16.解:∵2(2)(2)40x x x y ---+=∴222240x x x y --++= --------------------------------------------------2分 ∴2x y -= ---------------------------------------------------3分 当2x y -=时,222x xy y -+=2()x y - ---------------------------------------------------4分 =4 ----------------------------------------------------------------5分 17.解:设慢车的速度为x 千米/小时,则快车速度为1.5x 千米/小时,由题意得:12012011.5x x-= -------------------------------2分 解得: x=40 ------------------------------4分 经经验x=40是所列方程的根,且符合题意 ------------------5分 答:慢车的速度为40千米/小时.18.解:(1)∵反比例函数y = kx的图象与二次函数y =ax 2+x -1的图象相交于点A (2,2) ∴k =4 ,a =14∴反比例函数的解析式为:4y x =二次函数的解析式为:2114y x x =+- ------------------------------------2分(2)∵二次函数2114y x x =+-的图象的顶点为B (-2,-2),在4y x= 中,当x=-2时,y=422=-- ∴顶点B (-2,-2)在反比例函数的图象上----------------------------------------------3分 (3)∵点P 在4y x=的图象上,且点P 的横坐标为1 ∴P (1,4) ------------------------------------------------------------------------- 4分FEDCA∴AOP 3S ∆= ------------------------------------------------------------------------ 5分19.解:过点B 作BE ⊥AC 交CD 于E ,过点A 作AF ⊥CB 于F∵CD ∥AB ,AB=AC , ∴四边形ABEC 是菱形---------------------------------------1分∴BE=CE=AB∵∠BAC=120° ∴∠ABC=30°,∠ABE=60°,∠BED=60° ∵CD=2AB ,BD=2∴△ABC 是等边三角形 ,AB=2 --------------------------------------------------------------------2分 在△ABF 中,∠AFB=90°, ∠ABC=30°,AB =2 ∴AF=1 ---------------------------------------------------------------------------3分 ∴-------------------------------------------------------------------------------4分 ∴△ABC-------------------------------------------------------------------------------5分20.解:(1)直线BD 与O 相切.------------------------------------------------------------------1分证明:如图1,连结OD .OA OD =,∴A ADO ∠=∠.90C ∠=, ∴90CBD CDB ∠+∠=.又CBD A ∠=∠,∴90ADO CDB ∠+∠=. ∴90ODB ∠=. ∴直线BD 与O 相切. ---------------------------------------------------------------------------2分(2)解法一:如图1,连结DE .90C ∠=, 2BC =,BD =52∴4cos 5BC CBD BD ∠==. ---------------------------------------------------------------------------3分AE 是O 的直径, ∴90ADE ∠=.∴cos ADA AE=. ∵CBD A ∠=∠, ∴AD AE =BC BD =45.----------------------------------------------------------------------------------------4分 ∵AE=2AO ∴AD AO =85---------------------------------------------------------------------------------------------------5分 F E A BCD解法二:如图2,过点O 作OH AD ⊥于点H . ∴12AH DH AD ==. ∴cos AH A AO = 90C ∠=, 2BC =,BD =52 ∴4cos 5BC CBD BD ∠==.-------------------------------------------------------------------------- 3分∵CBD A ∠=∠, ∴AHAO =BCBD =45.-------------------------------------------------------------------------------------4分 ∴ADAO =85 -----------------------------------------------------------------------------------------5分21.解:(1)家长人数为80÷20%=400 ----------------------------------------1分正确补图① -----------------------------------------------------------2分(2)表示家长“赞同”的圆心角度数为︒=︒⨯3636040040--------------------3分(3)学生持“无所谓”态度的人数为30人,调查的学生数为140+30+30=200人-------------------------------------------4分学生恰好持“无所谓”态度的概率是15.0303014030=++ -----------------5分22.解:(1)重叠四边形A MC N ''的面积为 32; - -----------------------------------2分(2)用含m 的代数式表示重叠四边形A MC N ''的面积为 2m -823)(;-----4分m 的取值范围为 316≤m <8 ----------------------------5分23.(1)证明:令0y =,则有22(2)0x n m x m mn +-+-=△=222(2)4()n m m mn n ---= -----------------------------------------------------------1分∵20n ≥∴△≥0 -----------------------------------------------2分∴二次函数y=22(2)x n m x m mn +-+-与x 轴有交点(2)解:解法一:由101m m -==得,方程22(2)0x n m x m mn +-+-=可化为 2(2)10x n x n +-+-=解得:11x x n ==-或 -------------------------------------------------------------------3分∴方程22(2)0x n m x m mn +-+-=有一个实数根为1 ----------------------------------4分解法二:由101m m -==得,方程22(2)0x n m x m mn +-+-=可化为 2(2)10x n x n +-+-=当x=1时,方程左边=1+(n-2)+1-n=0方程右边=0∴左边=右边 -----------------------------------------------------------3分∴方程22(2)0x n m x m mn +-+-=有一个实数根为1 -------------------4分(3)解:方程22(2)0x n m x m mn +-+-=的根是:121,1x x n ==- ∴1a n =-当x =2时,11y n =+,22251y n n =-++ ----------------------------------5分设点C (,1b b +)则点D (2,251b b b -++)∵CD=6 , ∴221(251)62b 51(1)6b b b b b +--++=-++-+=或∴31b b ==-或 -----------------------------------------------------------6分∴C 、D 两点的坐标分别为C (3,4),D (3,-2)或C (-1,0),D (-1,-6)------7分24.解:(1)∵A (-1,0),∴OA=1∵OB=3OA ,∴B (0,3)----------------------------------------------------------------------------1分∴图象过A 、B 两点的一次函数的解析式为:y=3x+3 -----------------------------------------2分(2)∵二次函数()220y ax ax c a =-+<的图象与x 轴负半轴交与点A (-1,0),与y 轴正半轴交与点B (0,3), ∴c=3,a=-1∴二次函数的解析式为:223y x x =-++ ------------------------------------------------------3分∴抛物线223y x x =-++的顶点P (1,4)-----------------------------------------------------4分(3)设平移后的直线的解析式为:3y x b =+∵直线3y x b =+过P (1,4)∴b=1∴平移后的直线为31y x =+∵M 在直线31y x =+,且3tan 2OAM ∠=设M (x,3x+1)① 当点M 在x 轴上方时,有31312x x +=+,∴13x = ∴11(,2)3M --------------------------------------------------------------------5分 ②当点M 在x 轴下方时,有31312x x +-=+,∴59x =- ∴25(,9M -23-) ----------------------------------------------------------------6分 (4)作点D 关于直线x=1的对称点D’,过点D’作D’N ⊥PD 于点N-----------------------------------------------------------7分25.解:(1)如图1,过点B 作BN ⊥OC ,垂足为N∵2OA 80-+=(),OB=OC ∴OA=8,OC=10 -------------------------------1分∴OB=OC=10, BN=OA=8 ∴.6==22BN -OB ON∴B(6,8) ----------------------------------------------2分(2)如图1,∵∠BON=∠POH, ∠ONB=∠OHP=90°.∴△BON ∽△POH ∴PHBN OH ON PO BO == ∵PC=5t. ∴OP=10-5t. ∴OH=6-3t. PH=8-4t.∴BH=OB-OH=10-(6-3t)=3t+4 ∴1646)48)(43(2++-=-+=t t t t 21S ------------------------------------ 3分 ∴t 的取值范围是:0≤t <2 ------------------------------------------4分(3)①EF ⊥PM ----------------------------------------------------5分∵MR ⊥OC ,PH ⊥OB∴∠RPM+∠RMP=90°,∠HPD+∠HDP=90°∵OC=OB ∴∠OCB=∠OBC.∵BC ∥PM∴∠RPM=∠HDP ,∴∠RMP=∠HPD ,即:∠ EMP=∠HPM∴EM=EP∵点F 为PM 的中点 ∴EF ⊥PM ----------6分②如图2过点B 作BN′⊥OC ,垂足为 N′,BN′=8,CN′=4∵BC ∥PM,MR ⊥OC∴△MRP ≌△B N′C∴PR=C N′=4设EM=x,则EP=x在△PER 中,∠ERP=90°,RE=MR-ME=8-x有222(8)4x x --=,∴x=5∴ME=5∵△MGB ∽△N′BO ∴ON MB B N MG '=' ∵ PM ∥CB ,AB ∥OC∴四边形BMPC 是平行四边形. ∴ BM=PC=5t.第一种情况:当点G 在点E 上方时(如图2)∵EG=2,∴MG=EM-EG=5-2=3 ∴3586t = ∴t=209 --------------------7分第二种情况:当点G 在点E 下方时(如图3) MG=ME+EG=5+2=7, ∴7586t = ,∴t=2021 -------------------------------------------8分 ∴当t=209或2021时,EG =2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
房山区九年级数学二模答案 2020.6
二、填空题(本题共16分,每小题2分)
9.1- ; 10.1.3 ; 11.),(15-; 12. 2
2
2
+2+=b +a b ab a )(; 13.8; 14.2
S ; 15.2
2
2
-20=6+)(x x ;
16.同圆或等圆半径相等,三边相等的三角形是等边三角形,等边三角形的内角是60°,一条弧所对的圆周角是它所对圆心角的一半.(直径所对的圆周角是直角,正弦定义,三角函数值)
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28,每小题7分) 17.解:
1
-2+
30sin 4+5
1-18°1
-)(
1
-2+21
×4+5-23= ………………………………………………4分
4-24=
……………………………………………………… 5分
18. 解不等式①:
……………………………………………………1分 得-3<x ……………………………………………………2分
解不等式②: ……………………………………………………3分 得-5>x ……………………………………………………4分
不等式组的解集是 3-<<5-x ………………………………………………
5分
19.
证明:∵BD 平分∠ABC
∴∠ABD =∠CBD ………………………………………………1分 ∵DE ∥AB
∴∠ABD =∠BDE ………………………………………………2分 ∴∠CBD =∠BDE ………………………………………………3分 ∴EB = ED ………………………………………………4分 ∵F 是BD 中点
∴EF 平分∠BED ………………………………………………5分
x x 2<3+34+2<1-x x A
C
20.
(1) 当k =1时,此方程为0=3+4-2
x x ……………………………………1分
0=3)-(1)-(x x
3= 1=21x x ,
……………………………………2分 (2) 由题意得0≠k , ……………………………………3分
0>12-16=Δk ……………………………………4分
∴34
<
k ∴3
4
<k 且 0≠k …………………………………5分
21.
(1)证明:∵CE =CD ,CF =CB
∴四边形DBEF 是平行四边形 ………………………………………………1分 DE =2CD ,BF =2BC ∵菱形ABCD 中, CD = CB
∴ DE = BF ………………………………………………2分 ∴四边形DBEF 是矩形 ………………………………………………3分 (2)∵AB =5
∴BF =10
∵菱形ABCD 中, 53
=∠cos ABD ,
∠DBF =∠ABD ∴5
3=
∠cos DBF ∵∠BDF =90°
∴DB =6 ………………………………………………4分 ∴DF = 8 ………………………………………………5分
22. (1)把3=x 代入1-=x y 得2=y ∴)
,(23A 又)0(>=
x x
k
y 图象过点)
,(23A 解得6=k ……………………………………………1分 (2)① PC = BC ……………………………………………2分
当n = 4时, )
,(34B ),(2
3
4C 23=
PC ,2
3
=BC ………………………………………3分 ② 1≤<0n 或 4≥n ………………………………5分
23. (1)DE 与⊙O 相切 ………………………………1分
连接OD 、CD 、OE
∵ BC 为⊙O 的直径
∴∠CDA =∠CDB =90° ∵E 是AC 中点 ∴ED =EC
∵OC =O D ,OE =O E ∴ΔOCE ≌ΔO DE
∴∠O DE =∠OCE =90°………………………………2分 ∴O D ⊥DE
∴DE 与⊙O 相切 ………………………………3分 (2)∵∠ACB =90°,AB =10,BC =6
∴AC =8,CE =4, OC =3 ………………………………4分 ∵DE 、CE 与⊙O 相切 ∴DE=CE ,∠CEO =∠DEO
∴O E ⊥CD ………………………………5分 ∴ OE =5
∵CF OE CE OC •=•
∴512=CF ∴5
9
=OF ………………………………6分
24. (1)11 ………………………………2分
(2)如图………………………………3分
(3)8 ………………………………4分
(4)①②………………………………6分
25. (1)
x01 2 3 4 5 6 (cm)
(cm) 4.47 5.24 5.86 5.96 5.48 4.72 4.00 (cm) 6.00 5.86 5.23 3.98 2.46 1.06 0
………………………………2分(2)
………………………………4分(3)AM的长度约为 2.98cm或1.50cm ………………………………6分
26.(1)对称轴-1=22-
=a
a
x ……………………………………1分
(2)∵4AB =
A (-3,0),
B (1,0) ……………………………………2分 把(1,0)代入表达式:0=c +2a +a 得:a 3-=c ……………3分 ∴
C (0,-3a )
∴ D (0,-3a+1), 31D y a =-+ …………………………4分
(3)当0a >时
将点()4,4P -代入抛物线223y ax ax a =+-得:
41683a a a =--, 45
a =
∴当4
5
a ≥
时,抛物线与线段PD 只有一个交点 …………………5分
当0a <时
抛物线的顶点为()1,4a -- 当44a -=时
1a =- …………………6分
综上所述,当4
5
a ≥
或1a =-时,抛物线与线段PD 只有一个交点.
27.(1)
① 过点D 作DF ⊥AC 于F ……………………………………1分 ∵30DBA =︒∠ ∴BD DF 2
1=
∵以AC 为斜边作等腰ADC Rt Δ ∴FC AF =
∴AC DF 2
1= ∴AC BD = ……………………………………2分
② ∵ 等腰ADC Rt Δ与等腰Rt BED △中AC BD =
∴DE DC =,ο45=∠=∠CDE FDC ∵30DBA =︒∠
∴ο60=∠FDB ,ο15=∠CDB ∴ο60=∠CDE
∴CDE Δ是等边三角形 ……………………………………3分 ∵DE EB =
∴EB EC = ……………………………………4分
(2)法1. 添加辅助线 ……………………………5分
证出ADB Δ≌CDG Δ ……………………………6分 ∴ο45=∠=∠A DCG
∴ο90=∠GCB ∵EB EG =
∴ EB EC = ………………………………7分
法2. 添加辅助线 ……………………………5分
证出ADB Δ⁓GDE Δ …………………………6分 ∴ο45=∠=∠A DGE
∴GE 平分DGC ∠ ∴GE 是DC 的中垂线
∴ EB EC ED == ………………………………7分
法3. 添加辅助线 ……………………………5分
证出ο45=∠EDB =∠EFB ……………………6分
∴FE 是DC 的中垂线
∴ EB EC ED == ……………………7分 28.
(1)①
类似以上作答,只要弧上所有点都出现在三角形内部,均给分.
………………………………2分
②当2OB =时,Rt ABC △的形内弧最长,此时弧长=π=.(学生不必画出图象)
………………………………3分
(2)当圆心在x 轴下方时,此时最长形内弧与线段DF ,EF 相切
∵1DOF DOM △∽△
∴2
1OF OM OD ⋅=
∴14OM = ∴
4
M y ≤- ………………………………4分
当圆心在x 轴上方时,此时最长形内弧与x 轴相切
∵2EGM HEG △∽△
∴2
2HG HM HE ⋅=
∴
5
2 EH=
∴
2
5
2
EM=
∴
5
2
M
y≥
………………………………5分
综上所述,4
M
y≤-或
5
2
M
y≥
(3)当4
G
x≤-时,此时最长形内弧与x轴相切
∵1
GOP GHO
△∽△
∴
1
43
GP=
∴
1
43
P
y≥
当40
G
x
-<<时,此时最长形内弧与线段OM相切
解得
2
43
P
y≥
当04G x <<时,此时最长形内弧与线段MG 相切
解得343
P y ≥
………………………………6分
当4G x ≥时,此时最长形内弧与线段MG 相切
解得433P y ≤-
………………………………7分
综上所述,43P y ≥23
P y ≤。
