(完整)2010-2011《信号与系统A》期末考试试卷及答案,推荐文档
2010-2011《信号与系统A》期末考试试卷及答案,推荐文档

1 0.25z 1 1 1.1z 1 0.3z 2
1
H (z)
1 0.25 z (1 0.5z 1 )(1 0.6 z 1)
( 2) H (z)
1 0.25z 1 1 1.1z 1 0.3z 2
Y ( z) X ( z)
Y ( z) 1.1z 1Y (z) 0.3z 2Y ( z) X ( z) 0.25z 1 X (z)
y( n) 1.1y(n 1) 0.3 y(n 2) x(n) 0.25x(n 1)
(t ) ,求复合系统的冲激响应 h( t ) 。
x(t )
y(t)
h1( t)
h2 (t )
h3 (t)
h1 (t ) h(t ) u(t) u(t)* (t 1)*[ (t)] 解:
u(t) u(t)* (t 1) u(t ) u(t 1)
四、(10 分)求周期矩形脉冲信号的傅立叶级数(指数形式) ,并大概画出其频谱图。
(1) f (2t) 的波形
(2) f (t 2)u(t 2) 的波形
f (t) 1
-1
0
1
t
解: (1)
f 2t
1
1
1
t
2
2
(2)
f t 2ut 2
1
t
0
1
2
3
三、(10 分)如图所示,该 LTI 系统由多个子系统组成,各子系统的冲激响应分别为:
h1(t ) u(t), h2 (t) (t 1), h3(t)
-2ωm
2ωm
(8 分)
Ys ( jw )
-4ωm
-2ωm
w
2ωm
4ωm
七、(10 分)考查如图所示的离散时间 LTI 稳定系统;
《信号与系统》期末试题A卷

云南大学2014至2015学年下学期 信息学院电子信息科学与技术、电子信息工程、通信工程专业2013级《信号与系统》期末试卷A (闭卷) 满分:100分 考试时间:120分钟 任课教师:梁虹 普园媛 尉洪 周浩 专业: 学号: 姓名:分)1、连续时间信号与系统的基本分析方法有 分析法, 分析法和 分析法。
2、离散时间信号)k (f 作用于单位序列响应为)k (h 的系统,其零状态响应为 。
3、连续时间系统单位阶跃响应)t (g 与单位冲激响应)t (h 的关系是 。
4、由频率响应分别为)j (H 1ω和)j (H 2ω的两子系统串联而成的系统频率响应)j (H ω= 。
5、若连续时间系统的激励信号为)(t f ,零状态响应为)t (y zs ,则系统无失真传输的频域条件为 。
6、周期信号频谱的特点为 、谐波性和收敛性。
7、t t f 0cos )(ω=,其傅里叶变换为 。
8、信号)( )cos()(0 t t et f tεωα-=的拉普拉斯变换为 。
9、sT e Z =建立了s 平面与z 平面之间的映射关系,由此,s 平面的 对应于z 平面的单位圆内,s 平面的 对应于z 平面的单位圆,s 平面的 对应于z平面的单位圆外。
10、描述某离散时间系统的差分方程为()()()())1k (f 2k f 2k y 611k y 61k y -+=----,则该系统的系统函数)z (H = ,该系统的频率响应函数)e (H j θ= 。
二、简述题(共20 分,每题5分)1、给出三个常用信号的傅里叶变换对。
2、介绍傅里叶变换的频移特性及其应用意义。
3、简述连续时间系统的单位冲激响应h(t),系统频率响应H(jw),系统函数H(s)的概念及其相互关系。
4、简述傅里叶变换的时域卷积定理和频域卷积定理。
三、分析作图题(每小题10 分,共20分)1、某一有限频带信号)t 6cos()t 3cos(35)t (f ππ++=,用π15w s =的冲激函数序列进行取样,(1)画出)t (f 及取样信号)t (f s 在频率区间)23,23(ππ-的频谱图,分析该信号采样时的奈奎斯特频率?(2)若希望由)t (f s 恢复原信号)t (f ,请设计恢复系统,并给出对应理想低通滤波器的相关参数。
《信号与系统》期末试卷与答案

《信号与系统》期末试卷与答案第 2 页 共 14 页《信号与系统》期末试卷A 卷班级: 学号:__________ 姓名:________ _ 成绩:_____________一. 选择题(共10题,20分) 1、n j n j een x )34()32(][ππ+=,该序列是 。
A.非周期序列B.周期3=NC.周期8/3=N D. 周期24=N2、一连续时间系统y(t)= x(sint),该系统是 。
A.因果时不变B.因果时变C.非因果时不变D. 非因果时变3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u e t h t ,该系统是 。
A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定第 3 页 共 14 页4、若周期信号x[n]是实信号和奇信号,则其傅立叶级数系数a k 是 。
A.实且偶 B.实且为奇 C.纯虚且偶 D. 纯虚且奇5、一信号x(t)的傅立叶变换⎩⎨⎧><=2||02||1)(ωωω,,j X ,则x(t)为 。
A.tt 22sin B.tt π2sin C.tt 44sin D.ttπ4sin6、一周期信号∑∞-∞=-=n n t t x )5()(δ,其傅立叶变换)(ωj X 为 。
A.∑∞-∞=-k k )52(52πωδπB.∑∞-∞=-k k)52(25πωδπC. ∑∞-∞=-k k )10(10πωδπ D.∑∞-∞=-k k)10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ,则x[n]奇部的傅立叶变换为 。
第 4 页 共 14 页A. )}(Re{ωj e X jB.)}(Re{ωj e X C.)}(Im{ωj e X jD.)}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ,则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 。
A. 500B. 1000C. 0.05D. 0.0019、一信号x(t)的有理拉普拉斯共有两个极点s=-3和s=-5,若)()(4t x et g t=,其傅立叶变换)(ωj G 收敛,则x(t)是 。
信 与系统期末考试试卷有详细答案

《 信号与系统 》考试试卷(时间120分钟)1. 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =,则该系统为线性、时不变、因果。
(是否线性、时不变、因果?) 2. 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。
5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常 数相频特性为_一过原点的直线(群时延)。
6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7. 若信号的3s F(s)=(s+4)(s+2),求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8. 为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9. 已知信号的频谱函数是))00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。
10. 若信号f(t)的211)s (s )s (F +-=,则其初始值=+)(f 0 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分, 6题15分,共60分)1.信号)t (u e )t (f t-=21,信号⎩⎨⎧<<=其他,01012t )t (f ,试求)t (f *)t (f 21。
《信号与系统》期末试卷A卷与答案.pptx

0
y(t)
1 t2 2
Tt
1 T2
1
2 t Tt
2
3T2
2
2
0
t 0 0t T
T t 2T 2T t 3T 3T t
3、(3×4 分=12 分)
j dX ( j / 2)
(1)
tx(2t) 2
d
(1t)x(1t) x(1t) tx(1t)
(2) X ( j)e j j d [X ( j)e j] jX ' ( j)e j d
(3)
t
dx(t) dt
X ( j)
dX ( j) d
第 页 4共 6 页
学海无 涯
4、(5 分)解 :
s2
1 2s 2
s2 2s 2
s2 2s 2
F (s) es 2(s 1) es (s 1)2 1
f (t) (t 1) 2e(t 1) cos(t 1)u(t 1)
学海无涯
《信号与系统》期末试卷 A 卷
班级:
学号:
姓名:
_ 成绩:
一. 选择题(共 10 题,20 分)
j( 2 )n
j( 4 )n
1、 x[n] e 3 e 3 ,该序列是
A.非周期序列 B.周期 N 3
D。
C.周期 N 3/ 8
CDCC
D. 周期 N 24
2、一连续时间系统y(t)= x(sint),该系统是
3
3
(b)若系统因果,则Re{s} 2,h(t) 1 e2tu(t)-1 et u(t) 4分
3
3
(c)若系统非稳定非因果,则Re{s} -1,h(t) 1 e2t u(t) 1 et u(t) 4分
2010-2011(2)《信号与系统A》期末考试试卷A(new)答案

班 级 学 号 姓 名t(C )连续、非周期频谱; (D )离散、非周期频谱。
7.欲使信号通过线性系统不产生失真,则该系统应具有( )(A )幅频特性为线性,相频特性也为线性; (B )幅频特性为线性,相频特性为常数; (C )幅频特性为常数,相频特性为线性; (D )系统的冲激响应为0()()h t ku t t =-。
8.周期矩形脉冲的谱线间隔与( ) (A )脉冲幅度有关 (B )脉冲宽度有关 (C )脉冲周期有关(D )周期和脉冲宽度有关9. 已知Z 变换Z 1311)]([--=zn x ,收敛域3<z ,求逆变换得x (n )为( ) (A ))(3n u n (B ))(3n u n -- (C ))(3n u n -- (D ))1(3---n u n10. 某系统的系统函数为H (s ),若同时存在频响函数H (j ω),则该系统必须满足条件( ) (A )时不变系统 (B )因果系统 (C )稳定系统 (D )线性系统二、画图题.(10分)一连续时间信号()x t 如图所示,请画出下面信号并给以标注。
(1)(5分)(4/2)x t -。
(2) (5分)[()()]()x t x t u t +-。
1-12()x t -2 -1 0 1 2 t1-12()x t --2 -1 0 1 2 t13()()()x t x t u t +-⎡⎤0 1 2 t解:(1)(5分)(4/2)x t -(2) (5分)[()()]()x t x t u t +-。
解:三、(10分)如图所示,该LTI 系统由多个子系统组成,各子系统的冲激响应分别为:12()(1)(2),()(1),h t u t u t h t t δ=---=-,求复合系统的冲激响应()h t 。
解:12()[()()]()[()(1)(2)](1)(1)(2)(3)h t t h t h t t u t u t t t u t u t δδδδ=+*=+---*-=-+---四、(15分)已知某系统的频响特性()H j ω及激励信号的频谱()F j ω如题图所示,s (t )(1)画出()y t 的频谱()Y j ω,并写出()Y j ω的表示式; (2) 若()cos 200p t t =,画出()s y t 的频谱()s Y j ω;(x ()t(3) 若()()20n p t t n πδ+∞=-∞=-∑,画出()sy t 的频谱()sY j ω,并写出()sY j ω的表示式。
信号与系统a答案
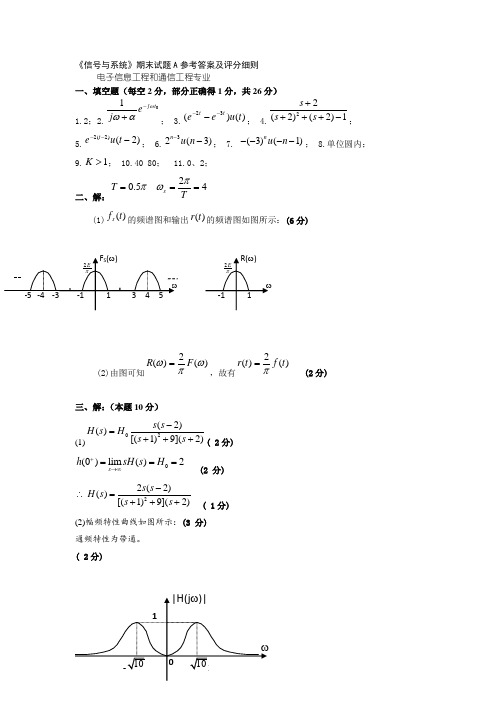
《信号与系统》期末试题A 参考答案及评分细则电子信息工程和通信工程专业 一、填空题(每空2分,部分正确得1分,共26分)1.2;2.01t j ej ωαω-+; 3.)()(32t u eett---; 4.22(2)(2)1s s s ++++-;5.)2()2(2---t u et ; 6.32(3)n u n --; 7. (3)(1)n u n ----; 8.单位圆内;9.1K >; 10.40 80; 11.0、2;二、解:425.0===TT s πωπ(1))(t f s 的频谱图和输出)(t r 的频谱图如图所示:(6分)(2)由图可知)(2)(ωπωF R =,故有)(2)(t f t r π=(2分)三、解:(本题10分)(1)2(2)()[(1)9](2)s s H s H s s -=+++( 2分)0(0)lim ()2s h sH s H +→∞=== (2 分)22(2)()[(1)9](2)s s H s s s -∴=+++ ( 1分)(2)幅频特性曲线如图所示:(3 分) 通频特性为带通。
( 2分)四、解:3212()()(2)zH z z z -=-- (1)收敛域的三种情况:2z >12z <122z << (2分)(2) 12()2z zH z z z =--- (2分)2z >时 12()[()2]()nnh n u n =- 系统因果不稳定 (2分) 12z <时 12()[()2](1)nn h n u n =-+-- 系统非因果不稳定 (2分)122z <<时12()()()2(1)nnh n u n u n =+-- 系统非因果稳定 (2分)五、求解各题1.(1)电路的S 域模型为:525)(2++=s s s H (3分)极、零点图如图所示: (2分)极点位于左半平面系统是稳定系统。
安徽大学2010-2011信号A及答案

安徽大学20 10 —20 11 学年第 2 学期《 信号与系统 》考试试卷(A 卷)(闭卷 时间120分钟)一、填空题(每小题2分,共10分) 1. 对于一个因果系统()n h 来说,当0<n 时,()n h _________。
2. 若激励信号为()t x ,响应信号为()t y ,则无失真传输的条件是_________。
3. 如果一个系统函数的极点位于左半平面,零点位于右半平面,而且零点与极点对于_________互为镜像,那么我们称这种系统函数为全通函数。
4. 若系统的单位冲激响应为()t h ,单位阶跃响应为()t g ,则二者的关系为_____________。
5. 设()n x 是一序列且[)+∞-∈,5n ,则它的收敛域是________。
二、选择题(每小题2分,共10分)1.已知()t f ,为求()at t f -0()0,0>t a 应按( )运算求得正确结果。
A. ()at f -左移0t B. ()at f 右移0t C. ()at f 左移a t 0 D. ()at f -右移a t 02. 对于信号f (t )及单位冲激信号)(t δ,则()()=-⎰+∞∞-0t t t f δ( )。
A.()0f B.()t f C. ()0t f D.03. 已知()t f 的拉氏变换为()F s ,则1()2f t 的拉式变换是( )。
A.()22s F B. ()s F 22C. ()212-s FD. ()2s e s F -4. 由S 平面与Z 平面的映射关系ST e Z =可知,S 平面的垂直带区域[]()21σσσ,∈映射为Z 平面上的( )区域。
A .环状的 B.某个圆以内 C.某个圆以外 D.带状的院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------5. 带通滤波器的品质因数Q 定义为( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) f (2t) 的波形
(2) f (t 2)u(t 2) 的波形
f (t) 1
-1
0
1
t
解:(1)
f 2t
1
t
1
1
2
2
(2)
f t 2ut 2
1
t
0
1
2
3
三、(10 分)如图所示,该 LTI 系统由多个子系统组成,各子系统的冲激响应分别为:
h1(t) u(t), h2 (t) (t 1), h3(t) (t) ,求复合系统的冲激响应 h(t) 。
F[
k
j(w kws )]
Fs ( jw)
x(t)
h1 (t )
h2 (t)
y(t)
h3 (t)
h1 (t )
h(t) u(t) u(t) * (t 1) *[ (t)]
解:
u(t) u(t) * (t 1) u(t) u(t 1)
四、(10 分)求周期矩形脉冲信号的傅立叶级数(指数形式),并大概画出其频谱图。
a0
1 T1
西南交通大学 2010-2011 学年第(1)学期考试试卷
密封装订线
姓名
学号
密封装订线
课程代码 3122400 课程名称 信号与系统 A 考试时间 120 分钟
题号 一 二 三 四 五 六 七 八 九 十 总成绩 得分
阅卷教师签字: 一、选择题:(20 分) 本题共 10 个小题,每题回答正确得 2 分,否则得零分。每小题所给答案中只有一个是正确 的。
)
(A)时不变系统
(B)因果系统
(C)稳定系统
(D)线性系统
7. 理想不失真传输系统的传输函数 H(jω)是 (
)。
(A) Ke j 0 t
(B) Ke j t0
(C) Ke j t0 u( c ) u( c )
(D) Ke j0 t0 ( t0 ,0 ,c , k 为常数)
8.已知 f (t) F ( j) ,则信号 y(t) f (t) (t 5) 的频谱函数 Y ( j) 为(
1. 连续周期信号 f(t)的频谱 F ( j) 的特点是( )
(A)周期、连续频谱; (C)连续、非周期频谱;
(B)周期、离散频谱; (D)离散、非周期频谱。
2.欲使信号通过线性系统不产生失真,则该系统应具有(
)
(A)幅频特性为线性,相频特性也为线性;
(B)幅频特性为线性,相频特性为常数;
(C)幅频特性为常数,相频特性为线性;
(D)系统的冲激响应为 h(t) ku(t t0 ) 。
3.周期矩形脉冲的谱线间隔与( )
(A)脉冲幅度有关
(B)脉冲宽度有关
(C)脉冲周期有关
(D)周期和脉冲宽度有关
4.
已知
Z
变换
Z[
x(n)]
1
1 3z
1
,收敛域
z
3 ,求逆变换得 x(n)为(
)
(A) 3n u(n)
(B) 3n u(n)
dy2 (t) dy(t) 2 y(t) x(t)
dt 2
dt
(1) 求该系统的系统函数 H (s) ,并画出 H (s) 的零极点图;
(2) 求系统是稳定的情况下,系统的单位冲激响应 h(t) ;
(3) 求系统是因果的情况下,系统的单位冲激响应 h(t) ; (4)画出系统直接型实现的模拟框图。 解:
(A) y(t 3) (B) y(t 4) (C) y(t 7) (D) y(t 1)
二、画图题.(15 分)
(1)(5 分)令 x(n) u(n) u(n 5) ,计算并画出它的奇部和偶部。
解:
Ev {x(n)}
1 [x(n) 2
x(n)]
1 u(n) u(n 5) u(n) u(n 5)
)。
(A) f (5)e j5
(B) F ( j )e j5
(C) f (5)
(D) F ( j)
9.下列系统中可逆系统是( (A) y(t) x(t 4)
(C) y(n) nx(n)
)。
(B) y(t) cosx(t)
(D) y(n) x(n)x(n 1)
10. 已知 y(t) x(t) h(t) ,则 x(t 3) h(t 4) ( )。
(C) 3n u(n)
(D) 3n u(n 1)
5.
若对
f(t)进行理想取样,其奈奎斯特取样频率为
fs,则对
f
1 ( 3
t
2) 进行取样,其奈奎斯
特取样频率为(
)。
班级
密封装订线
(A)3fs
(B)
1 3
fs
(C)3(fs-2)
(D)
1( 3
fs
2)
6.
某系统的系统函数为 H(s),若同时存在频响函数 H(jω),则该系统必须满足条件(
T1
2 T1
2
f (t)dt 1 T1
2 2
Edt
E T1
2分
an
2E n
n sin( )
T1
2E T1
n Sa(
T1
)
E1
Sa( n1 2
)
3分
F (n1 )
2E n1T1
sin
n1
2
E T1
Sa
n1
2
2分
五、(20 分)一连续时间 LTI 系统的输入和输出,由下列微分方程表征:
谱 Fs ( j ) 的频谱示意图。 (3) 若用同样的采样间隔对 f (2t) 进行采样,得到采样信号 fs (2t) 。试画出 fs (2t) 的频谱示意
图。
F ( j )
1
m
Байду номын сангаас
解:(1)
ws 2wm 20rad / s
fs
ws 2
10
Hz
1 Ts=f=s s10
(2) Fs (
jw)
1 Ts
2
1
s
1 s
2
六、(15 分)设 f (t) 是频带有限的信号,其频谱如图所示,频带宽度m 10 rad / s 。 (1) 求 f (t) 的奈奎斯特采样频率s , fs ,奈奎斯特采样间隔Ts 。 (2) 若用奈奎斯特采样间隔Ts 对信号进行采样,得到采样信号 fs (t) ,画出采样信号 fs (t) 的频
(1)H (s) 1 = 1/ 3 - 1/ 3 ,极点-1,2 s2 s 2 s 2 s 1
(2)若系统稳定,则-1,-Re{s} 2 h(t) 1 e2tu(t) 1 etu(t)
3
3
(3)若系统因果,则,Re-{s} 2 h(t) 1 e2tu(t) 1 etu(t)
3
3
(4) x(t)
2
Od {x(n)}
1 [x(n) 2
x(n)]
1 u(n) u(n 5) u(n) u(n 5)
2
Ev{x(n)}
1 0.5
-4 -3 -2-1 0 1 2 3 4
Od {x(n)}
0.5 -4 -3 -2-1 0 1 2 3 4
-0.5
2. (10 分)已知信号 f (t) 波形如图所示,试给出下列函数的波形。
