系泊系统建模
系泊系统问题模型分析
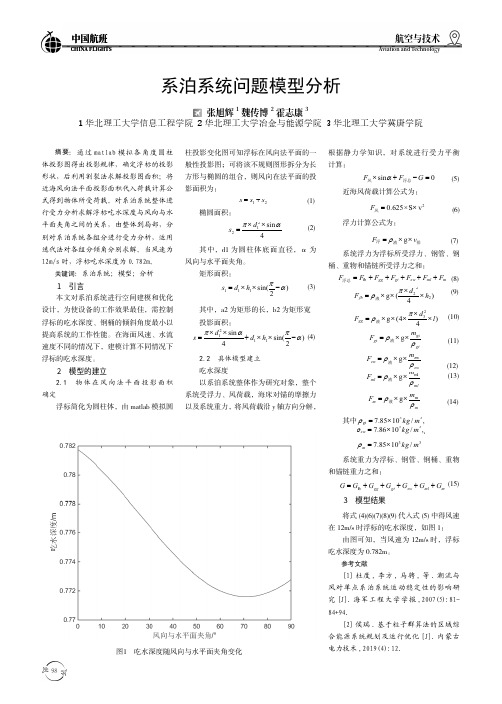
Ffb
=
ρ液
×g
×
π (
× d22 4
×
h2 )
(9)
Fgg
=
ρ液
×g×(4× π
× d32 4
×l)
(10)
Fgt
=
ρ液
×g×
mgt ρ gt
(11)
Fzw
=
ρ液
×g×
mzw ρ zw
(12)
Fml
=
ρ液
×g×
mml ρml
(13)
Fm
=
ρ液
×g×
mm ρm
(14)
其中 ρgt = 7.85×103 kg / m3, ρzw = 7.86 ×103 kg / m3, ρm ρgt = 7.85×103 kg / m3, ρzw = 7.86 ×103 kg / m3, ρm = 7.85×103 kg / m3
98
中国航班
CHINA FLIGHTS
航空与技术
Aviation and Technology
系泊系统问题模型分析
张旭辉 1 魏传博 2 霍志康 3 1 华北理工大学信息工程学院 2 华北理工大学冶金与能源学院 3 华北理工大学冀唐学院
摘 要: 通 过 matlab 模 拟 各 角 度 圆 柱 体投影图得出投影规律,确定浮标的投影 形状,后利用割裂法求解投影图面积;将 近海风向法平面投影面积代入荷载计算公 式得到物体所受荷载。对系泊系统整体进 行受力分析求解浮标吃水深度与风向与水 平面夹角之间的关系,由整体到局部,分 别对系泊系统各组分进行受力分析,运用 迭代法对各组分倾角分别求解。当风速为 12m/s 时,浮标吃水深度为 0.782m。
系泊系统的设计-系泊系统数学建模

系泊系统的设计:系泊系统数学建模系泊系统的设计摘要本文对系泊系统的设计问题进行了分析,给出合理的假设,建立优化模型,巧妙地解决了题目中所提出的问题。
针对问题一,首先采用集中质量的多边形近似法对单点系泊系统进行静力学分析,结合单点浮标系统特性,建立单点浮标的静力学模型,并对其算法进行改进,使算法能够迭代修正浮标受到的浮力。
其次通过适当的假设列出平衡方程并求解,得出锚链各节点处张力的递推公式,利用MATLAB软件迭代验证,最后得到了较为准确的结果。
针对问题二,基于问题一建立的模型,得出在题设条件下,浮标系统已不处于最优工作状态,须通过改变重物球来对系统进行调节。
计算出临界条件下重物球的质量,利用MATLAB 拟合得到的重物球重力与钢桶倾斜角度之间的关系曲线,得出对重物球进行调整的范围。
针对问题三,首先求得极端环境条件下钢桶倾角仍满足约束条件时候的重物球质量,然后通过合理的假设,在问题一建立的模型基础上,改变算法的迭代约束条件,从而得出不同情况下钢桶、钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
关键词:系泊系统;集中质量的多边形近似法;MATLAB;迭代一、问题的重述1.1问题的背景随着各国不断加大对海洋事业的投入以及不断深入对海底观测领域的探索,各海洋研究机构和海洋管理部门都相继建立了符合自身业务需求的海洋观测系统,其中浮标系统、系泊系统和水声通讯系统组成了近浅海观测网的传输节点。
而影响其系泊系统工作效果的因素很多,例如水流力、海风和水深等。
系泊系统的设计问题就是根据这些影响因素确定锚链的型号、长度和重物球的质量,使得系泊系统处于最佳工作状态。
从国家海洋资源战略角度来讲,研究各因素对系泊系统的不同影响显得尤为重要。
1.2问题的提出问题一:将该型传输节点布放在水深18m、海床平坦、海水密度为1.025×103kg/m3的静止海域时,选用II型电焊锚链22.05m,质量为1200kg的重物球,分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
系泊系统的设计数学建模

系泊系统的设计数学建模以系泊系统的设计数学建模为标题,我们来探讨一下该系统的数学建模方法。
系泊系统是指将船只或其他浮动物体固定在水中的一种装置。
在设计系泊系统时,需要考虑到多种因素,如风、波浪、潮流等。
为了确保系泊系统的安全性和稳定性,需要进行数学建模,以便分析和预测系统的行为。
我们可以考虑船只与锚之间的力学关系。
船只受到来自风、波浪和潮流等外力的作用,而锚通过拉力将船只固定在水中。
我们可以使用牛顿第二定律来描述船只的运动状态。
假设船只的质量为m,加速度为a,外力的合力为F,那么可以得到以下公式:F = ma。
接下来,我们需要考虑锚链的力学特性。
锚链是连接船只和锚的重要部分,它承受着船只在水中的运动引起的张力。
我们可以使用弹簧模型来描述锚链的特性。
假设锚链的弹性系数为k,长度为l,弹性形变为x,那么可以得到以下公式:F = kx。
除了船只和锚链的力学特性,我们还需要考虑水流的影响。
水流会给船只和锚链施加额外的力,从而影响系统的稳定性。
我们可以使用流体力学的知识来描述水流的特性。
假设水流的速度为v,密度为ρ,船只的受力面积为A,那么可以得到以下公式:F = ρAv。
在数学建模中,我们还需要考虑到船只的姿态稳定性。
船只在水中的姿态受到风、波浪和潮流等因素的影响,如果船只的姿态不稳定,就会导致系泊系统的不稳定。
我们可以使用刚体力学的知识来描述船只的姿态稳定性。
假设船只的质量矩阵为I,角加速度为α,扭矩为τ,那么可以得到以下公式:τ = Iα。
我们还需要考虑到船只与锚链之间的相互作用。
船只的运动会引起锚链的张力变化,而锚链的形变又会对船只的运动产生影响。
我们可以使用动力学的知识来描述船只和锚链之间的相互作用。
假设船只和锚链之间的相互作用力为F,船只的加速度为a,锚链的弹性形变为x,那么可以得到以下公式:F = ma = kx。
通过以上的数学建模,我们可以对系泊系统的行为进行分析和预测。
我们可以通过求解上述公式,得到船只、锚链和水流之间的关系,并进一步优化系统的设计,以提高系统的安全性和稳定性。
系泊系统的多目标优化模型

系泊系统的多目标优化模型韩林晟;许玳瑜;梁杨;覃思义【摘要】针对海上浮标系泊系统,基于机理分析和力学分析得到了给定锚链型号与链长、重物球质量、海域环境(风流与海流)等系统参数下,对于声纳钢桶倾角的影响规律.在此基础上对系统各个部分进行了受力分析,并由此建立静力学平衡方程.以理论水深与实际水深的差值为优化目标,以静力学平衡方程为约束条件建立了优化模型;调节重物球,建立以重物球质量、浮标的吃水深度、游动区域半径及钢桶的倾斜角度尽可能小为优化目标,以钢桶倾角、锚链与海床的夹角要求以及静力学平衡方程为约束条件建立了多目标优化模型.在给定的实际环境参数条件下,对系泊系统进行了计算设计.【期刊名称】《实验科学与技术》【年(卷),期】2017(015)002【总页数】6页(P4-9)【关键词】系泊系统设计;静力学方程;力学分析;多目标优化【作者】韩林晟;许玳瑜;梁杨;覃思义【作者单位】电子科技大学数学学院,四川成都611731;电子科技大学数学学院,四川成都611731;电子科技大学数学学院,四川成都611731;电子科技大学数学学院,四川成都611731【正文语种】中文【中图分类】X328;O29建设海洋观测网是衡量一个国家海洋综合实力的重要工作。
近浅海观测网的传输节点由浮标系统、系泊系统和水声通信系统组成。
某型传输节点的浮标系统可简化为底面直径2 m、高2 m的圆柱体;其系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成;其水声通信系统安装在封闭圆柱形钢桶内。
这样的传输节点一般要求:1)锚链与海床的夹角不超过16°,否则锚会被拖行;2)钢桶竖直时,水声通信设备的工作效果最佳,当倾斜角度超过5°时,工作效果较差。
在系泊系统的设计中,需确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
系泊系统设计是建立海洋观测的重要环节,其核心问题在于如何在给定传输节点布放位置及其周边海域环境的条件下,建立数学模型,设计选择锚链型号、长度,以及悬挂重物球的质量等参数,使得系统中的钢桶、浮标等满足观测条件。
单点系泊系统的模拟建模

- 13 -高 新 技 术0 引言南海某油田水深117 m。
在浮式生产储卸油装置(Floating Production Storage and Offloading,FPSO)单点系泊系统的常规年检过程中发现,其9条系泊钢缆均有不同程度的断丝(如图1所示),并且个别配重链与四角板的连接断开(如图2所示)。
为了保证生产的安全,业主决定先解脱FPSO,然后再更换系泊系统的锚腿。
图1 系泊钢缆断丝图2 配重链与四角板连接断开该系泊系统及其油田设施由FPSO、STP 单点转塔、9条系泊锚腿、2条柔性立管和2条电缆组成。
其中,STP 的东北方向和西南方向各有1条柔性立管和1条电缆。
该立管和电缆先跨过中水浮桥(Mid Water Arch,MWA),再铺设到海床,最后分别与东北方向和西南方向的平台进行连接;立管将各自平台所产的原油输送到FPSO,并用电缆给FPSO 输送电力。
立管、电缆和9条系泊锚腿与STP 单点的中心对称,9条锚腿中每3条锚腿组成1簇,簇与簇之间间隔120 °,每簇内的锚腿之间相隔5 °。
整个系泊系统的模型布置图如图3所示。
单条系泊锚腿的组成图如图4所示,其具体组成和尺寸见表1。
在系泊更换施工期间,FPSO 进坞维修,FPSO 不在位。
该系泊系统更换项目的主要工作包括以下4个:1) 对该系泊系统的9条锚腿进行更换。
2) 对吸力桩和STP 的上阳极进行修复。
3) 弃置8条旧锚腿(将8条旧锚腿丢弃至油田区域海底的指定区域)。
4) 对1条锚腿进行回收并检测其断丝和腐蚀情况。
其中,不更换下锚链,也就是不更换与吸力桩连接的桩链,对其进行重复利用。
为了缩短项目工期,让油田尽快复产,在该项目中采用3条船在系泊系统的3个扇区进行同步作业。
系泊系统是开采海洋石油的常见方式之一,与系泊系统有关的海油工程项目较多。
,张人公等人[1]给出了西江油田BTM 及其软管回收弃置的方案,邹佳星等人[2]评估了某系泊系统的剩余强度。
系泊系统的设计数学建模差分法

模型假设假设所有的材料都是普通钢材,,普通钢材的密度直接按照铁的密度计算,即所有材料密度为7.9×103kg/m3。
问题分析问题总分析:本题最关键的就是讨论出系泊系统中各个参数之间的关系。
我们把系泊系统中的锚链、钢管和钢桶的每一段,都看作是一条理想的杆,再对每一段杆进行受力分析,通过对每根杆分析受力平衡和力矩平衡,得出递推关系,建立差分方程;再利用二分法确定差分方程的初值,从而解出每段杆各个参数的值。
问题一的分析:先对每段理想的杆进行受力分析,和力矩平衡分析,得到拉力以及夹角的差分递推关系,得T的大小和方向,就能计算得到整个系泊系统的状态。
再知只要知道第一根杆受到的拉力1分析第一根理想杆即浮标的受力情况,得知它受到的拉力又由浮标吃水深度f决定,最后利用二分法确定f,从而得到整个系泊系统的状态。
问题二的分析:在问题一的假设上,风速变为36m/s,利用同样的方法求解,求得海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
为使得钢桶的倾斜角度不超过5度,锚链在锚点与海床的夹角不超过16度,我们从1200逐步增加重物球的重量,观察两个角度的大小变化,得到重物球质量的下限;接着再考虑浮标的吃水深度问题,因浮标不能完全浸入水中,计算得到重物球的质量的上限。
问题三的分析:要考虑风力、水流力和水深情况下的系泊系统设计,就是要确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
为了确定锚链的型号,先分析在极端情况,即水深20m,海水速度为1.5m/s,风速36m/s的情况下的锚链在锚点与海床的夹角为16度附近需要锚链长度较短的锚链。
再以这个最短锚链长度为例,求对应的重物球质量范围,使得锚链在锚点与海床的夹角不超过16度,钢桶的倾斜角度不超过5度,并使得浮标不能完全浸没在水中。
最后给出一个特定取值状态下系泊系统的状态。
符号说明模型建立与求解模型准备:对第i根杆的受力进行分析,如图1:图1将受力分析图简化成图2:图2i B F 为第i 根杆受到的重力i G 和浮力i B 的合力,定义竖直向上的方向为正方向,则i B F 为负值。
数学建模A题系泊系统设计

系泊系统的设计摘要对于问题一,建立模型一,已知题目给出的锚链长度与其单位长度的质量,得到悬链共210环。
对各节锚链,钢桶,四节钢管受力分析得出静力平衡方程,使用分段外推法,可以得到静力平衡下的迭代方程。
其中锚对锚链的拉力大小方向为输入变量,迭代的输出变量为浮标的位置和对钢管的拉力,在给定的风速下,输入和输出满足关系2)2(25.1cos 水v h T -=α,αθcos cos 11T T =,通过多层搜索算法得出最符合的输入输出值,即可得到给定风速下浮标的吃水深度,浮标拉力、锚链与海床夹角。
利用MATLAB 软件编程求解模型得到:风力12m/s 时,钢桶与竖直方向上的角度1.9863度,从下往上四节钢管与竖直方向夹角为1.9652度、1.9592度、1.9532度、1.9472度,浮标吃水0.7173m ,以锚为圆心浮标的游动区域16.5125m ,锚链末端切线与海床的夹角3.8268度。
风力24m/s 时,锚链形状,钢桶与竖直方向上的夹角3.9835度,从下往上四节钢管与竖直方向夹角为3.9420度、3.9301度、3.9183度、3.9066度,浮标吃水0.7244m ,以锚为圆心浮标的游动区域18.3175m 。
锚链末端切线与海床夹角15.9175度。
对于问题二的第一小问,使用模型一求解,当风速36m/s 时,锚链末端切线与海床夹角26.3339度,浮标吃水0.7482m ,浮标游动区域为以锚为圆心半径为18.9578m 的圆形区域,从下往上四节钢管与竖直方向倾斜角度为8.4463度、8.4225度、8.3989度、8.3753度,钢桶与竖直方向倾斜角度为8.5294度。
为满足问题二的要求,在模型一的基础上把重物球质量作为变量,建立模型二,将钢桶倾斜角小于5度和锚链前端夹角小于16度当做两个约束条件,通过MATLAB 编程求解得到满足约束条件要求的重物球质量取值范围为3700kg 到5320kg 。
系泊系统的设计数学建模

系泊系统的设计数学建模以系泊系统的设计数学建模为标题,本文将介绍系泊系统设计中的数学建模方法和相关原理。
系泊系统是指用于固定船舶或浮动结构物的一种装置,常用于码头、船坞、海上石油平台等场所。
在设计系泊系统时,需要考虑到各种因素,如海浪、风力、船舶质量等。
数学建模是一种将现实问题转化为数学模型的方法,通过建立适当的数学模型,可以对系泊系统进行分析和优化设计。
对于系泊系统中的海浪和风力等外部环境因素,可以使用波浪理论和风力学原理进行数学建模。
波浪理论可以描述海浪的传播和幅度,通过建立波浪模型可以计算出海浪对系泊系统的作用力。
风力学原理可以描述风力对系泊系统的作用,通过建立风力模型可以计算出风力对系泊系统的作用力。
这些外部环境因素的数学建模可以帮助设计者预测系泊系统在不同环境条件下的稳定性。
对于系泊系统中的船舶质量和系泊装置的特性,可以使用力学原理进行数学建模。
船舶质量可以分解为重力和浮力两部分,通过建立重力和浮力模型可以计算出船舶的质量。
系泊装置的特性可以通过建立弹性力学模型来描述,可以计算出系泊装置对船舶的支撑力和阻尼力。
这些力学模型的数学建模可以帮助设计者评估系泊系统的稳定性和可靠性。
对于系泊系统的优化设计,可以使用优化算法进行数学建模。
优化算法可以通过建立目标函数和约束条件,来寻找最优的系泊系统设计方案。
通过数学建模和优化算法,设计者可以在考虑各种因素的基础上,找到最合适的系泊系统设计方案,以提高系统的稳定性和安全性。
系泊系统的设计数学建模是一种重要的工具和方法,可以帮助设计者在考虑各种因素的基础上,进行系统的分析和优化设计。
通过建立适当的数学模型和使用优化算法,可以提高系泊系统的稳定性和可靠性,为实际工程应用提供科学依据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
系泊系统建模 Prepared on 22 November 2020系泊系统的设计摘要本文通过建立数学模型,对系泊系统的传输节点示意图进行受力分析,建立了静力学模型,并通过增加风力、水流力等对系泊系统进行更优化的设计。
对于问题一,在海平面处于静止状态下,对风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标吃水深度和浮标游动区域的计算,首先对锚链运用微元法对其中一节进行分析,再对其他物体进行受力分析和力矩平衡,得到静力学平衡的方程组,使用MATLAB对其求解,可得锚链形状(见图1和图2)其它求解结果:风速12m/s时,钢桶的倾斜角度为°,从上到下的倾斜角度为°°°°,吃水深度为(m),游动区域为(m)。
风速24m/s时,钢桶的倾斜角度为°,从上到下的倾斜角度为°°°°,吃水深度为(m),游动区域为(m)。
对于问题二,在风速为36m/s时,钢桶和各节钢管的倾斜角度、锚链形状、和浮标游动区域的计算问题,首先利用问题1中的算法求解出结果,发现在风速为36m/s时,钢桶的倾斜角度超过了5度,锚链在锚点与海床的夹角超过了16度,调节重物球的质量为3000kg,其调节前和调节后36m/s的求解结果,调节前:钢桶的倾斜角度为°从上到下的倾斜角度为°°°°,游动区域为(m)。
调节后:钢桶的倾斜角度为°从上到下的倾斜角度为°°°°,游动区域为(m)。
对于问题三,在考虑风力和水流力的情况下,本文基于风力和水流力为一对阻力的基础上,在布放点水的深度变化下,首先分别对浮标、钢管、钢桶及重物球系统进行受力分析,重新建立静力学模型,再利用软件进行求解出在水深为下,钢桶、钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域(结果见文中),同时推出更合理的系泊系统的设计。
关键词:系泊系统的设计静力学模型单目标优化力学方程组1问题重述问题背景近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成(如图1所示)。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体,浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg,锚链选用无档普通链(链环中间没有档撑的0型环)环,近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节,每节长度1m,直径为50mm,每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度,否则锚会被拖行,致使节点移位丢失。
水声通讯系统安装在一个长1m、外径30cm的密封圆柱形钢桶内,设备和钢桶总质量为100kg。
钢桶上接第4节钢管,下接电焊锚链。
钢桶竖直时,水声通讯设备的工作效果最佳。
若钢桶倾斜,则影响设备的工作效果。
钢桶的倾斜角度(钢桶与竖直线的夹角)超过5度时,设备的工作效果较差。
为了控制钢桶的倾斜角度,钢桶与电焊锚链链接处可悬挂重物球。
问题提出问题一:假设海水静止时,在题中所给的浮标、钢管、钢桶、重物球、锚链、锚的相关数据,分别别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
问题二:在问题1的假设下,计算海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量,使得钢桶的倾斜角度不超过5度,锚链在锚点与海床的夹角不超过16度。
问题三:由于潮汐等因素的影响,布放海域的实测水深介于16m~20m之间。
布放点的海水速度最大可达到s、风速最大可达到36m/s。
请给出考虑风力、水流力和水深情况下的系泊系统设计,分析不同情况下钢桶、钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
2问题分析问题要求锚链末端与锚的连接处的切线方向与海床的夹角不超过16度,否则锚会被拖行,且对于钢桶的倾斜角度超过5度时,设备的工作效果较差,为此,我们要通过确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度与游动区域及钢桶的倾斜角度尽可能小。
问题1的分析问题要求在海水静止时,分别计算海面为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
为此,首先对传输节点示意图进行整体分析进而分析浮标的受力情况,由立体几何中的相关知识平面直角坐标系,对浮标、钢管、锚链、钢桶及重物球系统进行局部受力分析,然后通过牛顿第一定律保持平衡静止,进而建立了静力学模型。
对于吃水深度,通过水的深度来计算,而浮标的游动区域,通过各个物体在水平方向的投影长度求解出游动区域半径,然后利用MATLAB软件,求解出风速为12m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域,风速为24m/s以此类推。
问题2的分析问题2是在问题1的假设下,求出风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域;首先利用问题1的模型进行求解,发现钢桶的倾斜角度超过5度,锚链在锚点与海床的夹角超过16度,为此,可将问题2建立一个优化模型,并对所建立的模型,,在满足钢桶的倾斜角度不超过5度、锚链在锚点与海床的夹角不超过16度的情况下,利用MATLAB软件求解出尽可能小的浮标吃水深度、钢桶倾斜角度及游动区域所对应的的重物球质量。
问题3的分析对于问题三,因为受到潮汐等因素的影响,布放点的海水速度最大可达到s、风速最大可达到36m/s,为此,在考虑风力、水流力和水深情况下的系泊系统的设计,本文将在第一问的基础上,加上风力、水流力和水深情况,再对各个物体进行受力分析,重新建立静力学模型。
然后,以此模型为背景,设计出更加合理的系泊系统。
3模型假设1.假设海水的密度是分布均匀的。
2.假设各个深度的水流的流速近似相等。
3.假设不考虑锚链自身的弹性伸长。
4.假设所用的重力加速度为m。
5. 假设一切阻力忽略不计。
4定义与符号说明浮标的吃水深度重力加速度重物球的质量钢桶的重力钢桶与竖直方向的角度单位长度锚链的质量浮标游动区域半径浮标游动区域重物球的质量5模型的建立与求解问题一的解答稳定后的系泊系统可以分为锚、锚链、钢桶和重物球、钢管、浮标五个部分标五个部分,如图为系泊系统的结构图:、图1系泊系统结构图下面对浮标、钢管、钢桶和重物球、锚链依次进行分析(一) 浮标的受力分析如图1所示,浮力在风速为v 的情况下处于平衡状态,且对于浮力收到4个力作用。
图2浮力的受力图其中,风F 为风速引起的力,浮F 为在水中的浮力,其方向竖直向上,1F 为钢管对浮标的作用力,G 为浮标的重力,s 为物体在风向法平面的投影面积(m 2),h 为浮标的高度,假设浮标的吃水深度为吃h ,由阿基米德原理可知,有如下关系:针对浮标而言,当其处于受力平衡时,其受力方程如下所示:(二) 四根钢管的受力分析图3钢管的受力分析由图2可知,对于第一节钢管的受力平衡为:其中,l 为钢管的长度,2F 为第二节钢管对第一节钢管的作用力。
而对于其他钢管的受力分析以及力矩平衡,可以以此类推: 第二节钢管的受力和力矩平衡分析: 第三节钢管的受力和力矩平衡分析: 第四节钢管的受力和力矩平衡分析:(三) 对钢桶的受力分析图4钢桶与重物球的受力分析图3的受力和力矩平衡状态如下:其中,球G 为重物球(铁球,密度为7900m kg /)的质量,桶G 为钢桶的质量,5F 为锚链对钢桶的作用力,4F 为钢管对钢桶的作用力,β为钢桶与竖直方向的角度。
(四) 对锚链的受力分析:利用微元法对锚链其中一节进行分析图5锚链的受力分析图其中,2T 为锚对锚链的作用力,2γ为作用力与水平面的夹角,mg 为AB 这一节的重力。
则对于B 点的受力分析如下:γγsin sin 22T T mg =+(1) γγcos cos 22T T =(2)利用)2()1(可得:2222cos sin tan γγγT T mg +=(3) 由坐标系可知:γtan =dxdy(4) 联合(3)、(4)可知:2222cos sin γγT T mg dx dy+=对于锚链,a l m ω=其中,ω为单位长度锚链的质量,a l 为AB 的长度。
则有:2222cos sin γγωT T g l dx dya +=(5) 有弧长公式:222)()()(dy dx dL += 得:dx dxdy dL 2)(1+=对其进行积分可得:dx dxdy L ⎰+=2)(1代入(5)可得: 令k dxdy=则有: 对x 进行求导: 然后对x 和k 进行分离: 求解可得:1222cos )1ln(C x T gk k +=++γω(6)又因为)1ln(arcsin 2++=x x hx 代入(6)中得:对上式变量分离并积分得到锚链的曲线方程为:基于以上对各物体的受力分析,便可得出所求问题的方程。
1.吃水深度的计算:对于吃水深度,我们利用整个系统在水中的深度减去除浮标以外的各物体在竖直方向的高度,其公式如下:其中,c y 为锚链的高度,H 为水的深度。
2.游动区域的计算针对浮标的游动区域,可以把浮标行走的区域看成圆形区域,在风力达到最大且方向保持不变时,游动区域半径达到最大,而半径的长度就为各个物体在水平方向的投影区域,其中锚链在水平方向的距离为x ,则浮标的游动区域半径R 如下:再利用圆的面积公式2r S π=便可得出浮标的游动区域。
模型一的求解与结果分析为求解当选用II 型电焊锚链,选用的重物球的质量为1200kg 。
现将该型传输节点布放在水深18m 、海床平坦、海水密度为×103kg/m 3的海域。
在海平面静止时,海面风速为12m/s 和24m/s 时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域,利用所建立的静力学模型,通过MATLAB 软件便可求解。
针对12m/s 和24m/s 时钢桶和各节钢管的倾斜角度、浮标的吃水深度和游动区域如表1所示当v为12m/s时,锚链的形状由图4可见:图612m/s的锚链形状由图4可知,当风速为12m/s时,锚链有一部分拖地,其拖地长度为,故锚链与锚的倾斜角度为0度。
当风速为24m/s时的锚链形状(锚链不拖地)为:图724m/s时锚链的形状问题二的解答由题目可知,当锚链末端与锚的链接处的切线方向与海床的夹角超过16度,锚就会被拖行,钢桶竖直时,水声通讯设备的工作效果最佳,若钢桶倾斜则影响设备的工作效果。
当钢桶与竖直方向的夹角即倾斜角超过5度时,设备工作效果较差,为此,我们建立以钢桶的倾斜角度尽可能小为目标函数,并以重物球的质量范围、钢桶的倾斜角度不超过5度为约束条件的优化模型如下:m为重物球的质量,对所选取得变量进行其中, 为钢桶的倾斜角度,球无量钢化处理,再利用MATLAB软件进行求解并对结果进行比较和分析。
