网络课程结构力学作业

网络学院结构力学练习册答案

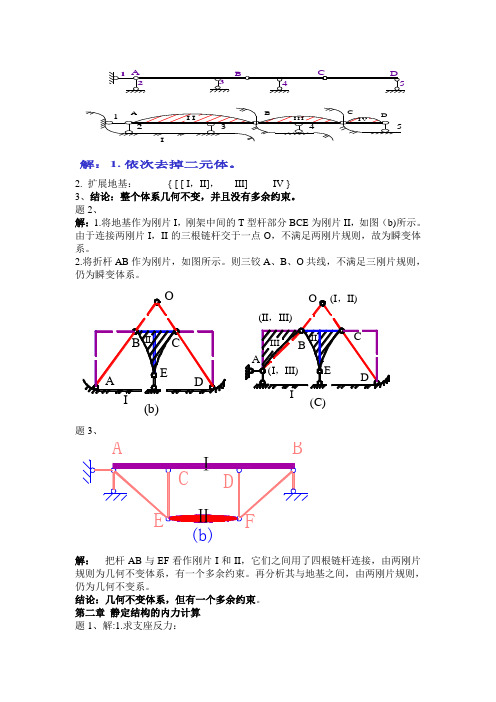
解：1. 依次去掉二元体。

2. 扩展地基： { [ [ I ，II]， III] IV } 3、结论：整个体系几何不变，并且没有多余约束。

题2、解：1.将地基作为刚片I ，刚架中间的T 型杆部分BCE 为刚片II ，如图（b)所示。

由于连接两刚片I ，II 的三根链杆交于一点O ，不满足两刚片规则，故为瞬变体系。

2.将折杆AB 作为刚片，如图所示。

则三铰A 、B 、O 共线，不满足三刚片规则，仍为瞬变体系。

(b)(C)题3、(b)解：把杆AB 与EF 看作刚片I 和II ，它们之间用了四根链杆连接，由两刚片规则为几何不变体系，有一个多余约束。

再分析其与地基之间，由两刚片规则，仍为几何不变系。

结论：几何不变体系，但有一个多余约束。

第二章静定结构的内力计算题1、解:1.求支座反力：14KN/m4KNA2.绘内力图：193.校核内力图：由内力图特征和结点、杆件平衡。

37k N28k N4kN19k NN DEDAN题2、解:1.求支座反力：80kN 80kNH 2.绘弯矩图:120由M 图可知：对称结构作用正对称荷载，弯矩图正对称。

题3、提示：1、求支座反力：2、判断零杆和已知轴力杆：3、求其余各杆轴力：第三章静定结构的位移计算题1、解：1.建立虚设状态，如图：2.分别求两种状态各杆轴力：3.由公式计算位移：题2、解：1）画实际状态弯矩图： 2）建立虚设状态并作其弯矩图：题3、第四章力法题1、第五章位移法题1、第六章力矩分配法题1、题2、第七章影响线题1、题2解：第八章结构的动力计算题1、题2、题3、第九章矩阵位移法题1、题2、题3、。

《结构力学二》平时作业-2021年华南理工大学网络教育

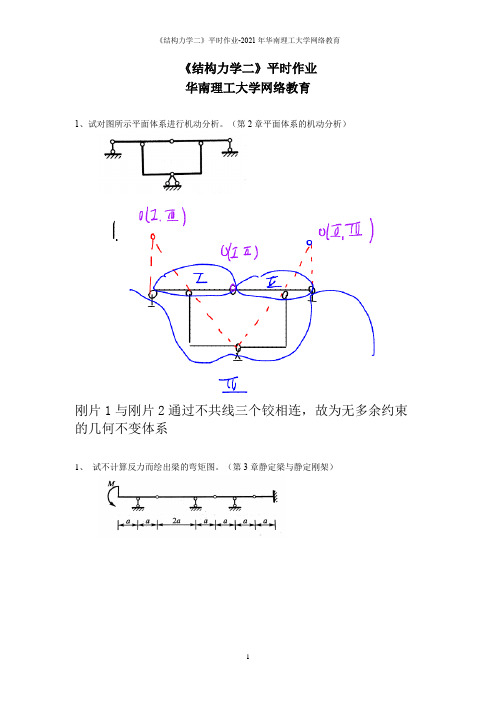
《结构力学二》平时作业华南理工大学网络教育1、试对图所示平面体系进行机动分析。

（第2章平面体系的机动分析）刚片1与刚片2通过不共线三个铰相连，故为无多余约束的几何不变体系1、试不计算反力而绘出梁的弯矩图。

（第3章静定梁与静定刚架）2、作图所示结构的M 图,并求a 杆的轴力。

q=20kN/m 。

（第3章静定梁与静定刚架）q解：正对称，取半结构3、图所示抛物线三铰拱的轴线方程为24()fy x l x l =-，试求截面K 的内力。

（第4章静定拱）4、试用截面法计算图示桁架中指定杆件的内力。

（第5章静定平面桁架）5、作图所示结构的M图，并求链杆的轴力。

（第5章静定平面桁架）6、图所示简支刚架支座B下沉b，试求C点水平位移。

（第6章结构位移计算）7、图所示结构的支座B 发生了水平位移30mm a =（向右），40mm b =（向下），0.1rad ϕ=。

已知各杆的46400cm I =，210GPa E =。

试：（a ）作M 图；（b ）求D 点竖向位移及F 点水平位移。

（第7章力法）8、用力法计算，并绘图示结构的M图。

EI=常数。

（第7章力法）9、用力法计算图示结构，作其M图。

EI=常数。

（第7章力法）l10、用位移法计算图所示结构，并作M 图。

EI =常数。

（第8章位移法）q11、已知图示结构B 点的转角ϕB EI =6411/()，各杆EI =常数,作M 图。

P=8kN,q=12kN/m 。

（第8章位移法）12、试用位移法计算刚架，绘制弯矩图。

E=常数。

（第8章位移法）13、试用力矩分配法计算图示刚架，并绘制M图所示。

E=常数。

（第9章渐近法）14、用力矩分配法计算并作图示结构M 图所示。

EI =常数。

（第9章渐近法）615、试作图示伸臂梁LRB C SC B SB SB F M F M F F 、、、、和影响线。

（第11章影响线及其应用）。

北交《结构力学》在线作业一答案

北交《结构力学》在线作业一-0003试卷总分:100 得分:0一、单选题(共15 道试题,共30 分)1.机动法作静定梁影响线应用的原理为（）。

A.变形条件B.虚功原理C.平衡条件D.叠加原理正确答案:B2.传递系数与（）有关。

A.近端的支承条件B.远端的支承条件C.杆件的线刚度D.B+C正确答案:B3.A.AB.BC.CD.D正确答案:B4.静定结构在支座移动时，会产生（）。

A.内力B.应力C.刚体位移D.变形正确答案:C5.A.AB.BC.CD.D正确答案:D6.A.AB.BC.CD.D正确答案:B7.A.AB.BC.CD.D正确答案:B8.力法方程是沿基本未知量方向的（）。

A.力的平衡方程B.位移为零方程C.位移协调方程D.力的平衡及位移为零方程正确答案:C9.A.AB.BC.CD.D正确答案:B10.A.AB.BC.CD.D正确答案:B11.A.AB.BC.CD.D正确答案:D12.A.AB.BC.CD.D正确答案:A13.力矩分配法是以（）为基础的渐近法。

A.力法B.位移法C.迭代法D.力法与位移法的联合正确答案:B14.A.AB.BC.CD.D正确答案:C15.移动荷载的定义是（）。

A.大小、方向、作用位置随时间改变的荷载B.大小不变、方向及作用位置随时间改变的荷载C.方向不变，大小及作用位置随时间改变的荷载D.大小、方向不变，作用位置随时间改变的荷载正确答案:B二、多选题(共20 道试题,共40 分)1.用无剪力分配法计算时，结构中的杆件应该是（）。

A.无侧移的杆B.剪力静定杆C.梁式杆D.链杆正确答案:AB2.关于位移法基本未知量，下列叙述正确的有（）。

A.铰处弯矩为零，故铰处角位移不作为基本未知量（因为非独立量）B.弯曲刚度无穷大杆件两端的转角不需作为基本未知量，当柱子平行且承受水平荷载作用时，结点处不产生转动，即结点转角为零C.静定部分可由平衡条件求出其内力，故该部分结点处的角位移和线位移不需作为基本未知量D.可将原结构改变为铰结体系，用附加链杆方法使该铰结体系成为几何不变体系时，所加链杆数目即为结点线位移未知数目正确答案:ABCD3.支座移动对静定结构不会产生（）。

(完整版)结构力学课堂作业

联结三个刚片的铰结点，相当的约束个数为：2个； 3个； 4个；4aa66367337db72. 图示体系为：A. 几何不变无多余约束；B. 几何不变有多余约束；C. 几何常变；D. 几何瞬变。

3. 图示体系为：A.几何不变无多余约束；B. 几何不变有多余约束；C. 几何常变D. 几何瞬变。

?4aa66367337db74.图示，体系是:A. 无多余联系的几何不变体系；B. 有多余联系的几何不变体系；C. 几何可变体系D. 瞬变体系。

)D. 答题:D.（已提交）4aa66367337db7答题:D.（已提交）A. B. 答题: D.（已提交）4aa66367337db7C. ED.（已提交）5. 图示体系为几何不变体系，且其多余联系数目为 A. 1 ; B. 2 ; C. 3 ； C. * D.（已提交）6.图示体系内部几何组成分析的正确结论是A. 几何不变且有两个多余联系；B. 几何不变且有一个多余联系；C. 几何不变且无多余联系；D. 几何瞬变体系（O:）D.（已提交）7.图示体系的几何组成为A.几何不变，无多余约束；B. 几何不变，有多余约束；C. 瞬变体系；D. 常变体系D.（已提交）8. 图示体系的几何组成为答题:4aa66367337db7D. 4。

'■答题：I D答题:4aa66367337db7C答题:4aa66367337db7 A. 几何不变，无多余约束；B. 几何不变，有多余约束；C. 瞬变体系；D. 常变体系。

4aa66367337db7答题:「A9.在图示体系中，A. 5、6、9 ；B. 5、6、7 ；C. 3、6、8 ；D. 1、6、7 oA.视为多余联系的D.（已提交）根链杆应是D.（已提交）10. 图示体系是几何不变体系。

4aa66367337db7F答题: 错.（已提交）11. 图示体系按三刚片法则分析，）三铰共线，故为几何瞬变体系。

结构力学_在线作业_1

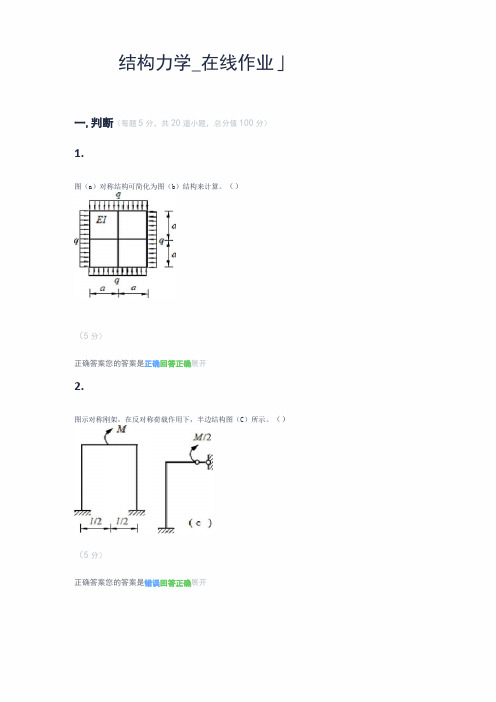
结构力学_在线作业」一,判断（每题5分，共20道小题，总分值100分）1.图（a）对称结构可简化为图（b）结构来计算。

（）（5分）正确答案您的答案是正确回答正确展开2.图示对称刚架，在反对称荷载作用下，半边结构图（C）所示。

（）（5分）正确答案您的答案是错误回答正确展开3.图示简支斜梁，在荷载P作用下，若改变B支座链杆方向，则梁的内力将是M、N 不变，Q改变。

（）（5分）正确答案您的答案是错误回答正确展开4.计算图示桁架中指定杆件内力，各杆EA=常数，N2= P/2o（）（5分）正确答案您的答案是正确回答正确展开5.图（a）所示桁架结构可选用图（b）所示的体系作为力法基本体系。

（）（5分）正确答案您的答案是正确回答正确展开图示对称结构，EI=常数;较简便的力法基本结构如图所示。

（）由对称性覆=0（5分）正确答案您的答案是正确回答正确展开6.图示结构中杆AC由于加热伸长了A则杆AB的变形是0。

（）（5分）正确答案您的答案是正确回答正确展开7.图示结构EI=常数，求K点的竖向位移时，由图乘法得:八用（1/EI）x y四。

（）⑨1（5分）正确答案您的答案是错误回答正确展开8.图示体系的几何组成为几何不变，无多余联系。

（）（5分）正确答案您的答案是正确回答正确展开9.图示为一刚架的力法基本体系，E=常数。

其司2为EI/8。

（）2 -lOkNAn（5分）正确答案您的答案是错误回答正确展开10.图示刚架，EI=常数，B点的竖向位移（I）为Pl/ （6EI）。

（）*4（5分）正确答案您的答案是错误回答正确展开（5分）正确答案您的答案是错误回答正确展开/ 1120 I-- --------------------------- ---------- - ---- *4^ ------------ *-1 （5分）正确答案您的答案是正确回答正确展开11.图示简支斜梁，在荷载P 作用下，若改变B 支座链杆方向，则梁的内力将是M 不变，Q 、N 改变。

《结构力学》在线作业二

结构力学在线作业二1. 引言结构力学是土木工程领域中一门重要的学科，它研究物体在外力作用下的力学行为。

本文主要介绍结构力学在线作业二的内容。

2. 问题描述在线作业二主要涉及以下问题：2.1. 悬臂梁的计算有一个悬臂梁，长为L，截面面积为A，弹性模量为E。

求解以下问题：•悬臂梁在端点受到的力、弯曲力和剪力分别是多少？•悬臂梁的最大弯矩是多少？2.2. 杆的轴向变形计算有一个杆长为L，截面积为A，弹性模量为E。

求解以下问题：•杆在两端受到的力是多少？•杆的伸长量是多少？•杆的轴向应变是多少？3. 解决方法为了解决上述问题，我们可以使用结构力学中的公式和理论知识。

具体的解决方法如下：3.1. 悬臂梁的计算方法悬臂梁是一种常见的结构，在计算其受力情况时，可以使用以下公式：•力：根据受力平衡条件，可以得到悬臂梁的端点受力。

•弯曲力：使用弯曲力-剪力曲线的关系，可以得到悬臂梁上任意一点的弯曲力。

•剪力：使用剪力-剪力曲线的关系，可以得到悬臂梁上任意一点的剪力。

•最大弯矩：通过对弯曲力求导数并令导数为零，可以求得弯曲力的最大值，即悬臂梁的最大弯矩。

3.2. 杆的轴向变形计算方法杆的轴向变形计算需要使用以下公式和理论知识：•力：根据受力平衡条件，可以得到杆的两端受力。

•伸长量：使用胡克定律，可以得到杆的伸长量。

•轴向应变：使用应变-应力关系，可以得到杆的轴向应变。

4. 计算实例为了更好地理解解决方法，我们进行以下计算实例：4.1. 悬臂梁计算实例已知悬臂梁的长度L=5m，截面面积A=0.1m^2，弹性模量E=200GPa。

根据悬臂梁的计算方法，我们可以得到以下结果：•端点受力为0N，弯曲力为0N，剪力为0N。

•最大弯矩为0N*m。

4.2. 杆的轴向变形计算实例已知杆的长度L=3m，截面面积A=0.05m^2，弹性模量E=100GPa。

根据杆的轴向变形计算方法，我们可以得到以下结果：•两端受力为0N。

•伸长量为0m。

结构力学(一)·平时作业2020春华南理工大学网络教育答案

结构力学(一)·平时作业2020春华南理工大学网络教育答案1.叙述结构力学在实际工程领域中的作用。

答：建筑物、构筑物或其他工程对象中支承和传递荷载而起骨架作用的部分称为工程结构。

例如，房屋建筑中由基础、柱、剪力墙梁、板及其他构件组成的结构体系，水工建筑物中的大坝和闻门，公路和铁路桥梁、隧道和涵洞，飞机、汽车中的受力骨架等，都是工程结构的典型例子。

2.简单列举平面体系机动分析的基本方法，并举例说明其中一种方法的使用方法。

答：平面体系机动分析的基本方法：几何不变体系、几何可变体系。

几何不变体系：三刚片规则、二元体规则、两刚片规则。

两刚片规则：两个钢片用一个铰和一个不通过该铰的链杆连接，组成几何不变体系。

几种常用的分析途径（1）去掉二元体，将体系化简单，然后再分析。

（2）如上部体系与基础用满足要求的三个约束相联可去掉基础，只分析上部。

（3）当体系杆件数较多时，将刚片选得分散些，用链杆组成的虚铰相连，而不用单铰相连。

（4）由一基本刚片开始，逐步增加二元体，扩大刚片的范围，将体系归结为两个刚片或三个刚片相连，再用规则判定。

（5）由基础开始逐件组装。

（6）刚片的等效代换：在不改变刚片与周围的连结方式的前提下，可以改变它的大小、形状及内部组成。

即用一个等效(与外部连结等效)刚片代替它。

3.举例说明利用结点法和截面法计算静定桁架内力的基本步骤。

答：以静定桁架为例：结点法是以结点为隔离体,一次求得两个未知力（单杆）；截面法通常截取的隔离体包含两个节点及以上,以此可求得3个未知力（单杆）.结点法用通常来求所有杆内力,一般从两个未知力杆结点开始,而截面法通常用来求指定杆内力.结点法：（1）求支座反力；（2）依次截取各结点，画出受力图，由平衡条件求其未知轴力。

截面法：（1）求反力（同静定梁）；（2）作截面（用平截面，也可用曲截面）截断桁架，取隔离体；（3）①选取矩心，列力矩平衡方程（力矩法）；②列投影方程（投影法）；（4）解方程。

西南大学网络教育在线作业答案[0729]《结构力学》

结构力学1：[论述题]简答题1、简述刚架内力计算步骤。

答：（1）求支座反力。

简单刚架可由三个整体平衡方程求出支座反力，三铰刚架及主从刚架等，一般要利用整体平衡和局部平衡求支座反力。

（2）求控制截面的内力。

控制截面一般选在支承点、结点、集中荷载作用点、分布荷载不连续点。

控制截面把刚架划分成受力简单的区段。

运用截面法或直接由截面一边的外力求出控制截面的内力值。

（3）根据每区段内的荷载情况，利用"零平斜弯”及叠加法作出弯矩图。

作刚架Q、N图有两种方法，一是通过求控制截面的内力作出；另一种方法是首先作出M 图；然后取杆件为分离体，建立矩平衡方程，由杆端弯矩求杆端剪力；最后取结点为分离体，利用投影平衡由杆端剪力求杆端轴力。

当刚架构造较复杂（如有斜杆），计算内力较麻烦事，采用第二种方法。

（4）结点处有不同的杆端截面。

各截面上的内力用该杆两端字母作为下标来表示，并把该端字母列在前面。

（5）注意结点的平衡条件。

2、简述计算结构位移的目的。

答：(1) 验算结构的刚度。

校核结构的位移是否超过允许限值，以防止构件和结构产生过大的变形而影响结构的正常使用。

(2) 为超静定结构的内力分析打基础。

超静定结构的计算要同时满足平衡条件和变形连续条件。

(3) 结构制作、施工过程中也常需先知道结构的位移。

3、如何确定位移法基本未知量。

答：（1）在刚结点处加上刚臂。

（2）在结点会发生线位移的方向上加上链杆。

（3）附加刚臂与附加链杆数目的总和即为基本未知量数目。

确定线位移的方法（1）由两个已知不动点所引出的不共线的两杆交点也是不动点。

（2）把刚架所有的刚结点（包括固定支座）都改为铰结点，如此体系是一个几何可变体系，则使它变为几何不变体系所需添加的链杆数目即等于原结构的线位移数目。

4、简述力法的基本思路。

答：力法的基本思路：将超静定结构的计算转化为静定结构的计算，首先选择基本结构和基本体系，然后利用基本体系与原结构之间在多余约束方向的位移一致性和变形叠加列出力法典型方程，最后求出多余未知力和原结构的内力。