《结构力学》课后作业参考答案 (5)
结构力学结构力学第三版王焕定第5章习题及参考答案

4-1 答:可用解除约束、暴露未知力和求计算自由度的方法判断超静定次数。
(a )7次;(b )3次;(c )3次;(d )4次;(e )7次;(f )10次;(g )7次;(h )6次;(i )21次。
4-2 (a) 答:一次超静定,可如下做单位与荷载弯矩图:可由图乘求系数,由力法方程求解并由叠加做弯矩图:1111P 23111041P1P 01P 11d 3d 838ll X M l x EI EIM M ql x EI EI ql X M M X M δ∆δ∆+===−====+∑∫∑∫本题也可将B 处解除约束变成铰,以简支梁为基本体系,两者工作量相当(从略)。
这说明力法由于基本体系不唯一,对应解法也不唯一,只要不出错都可获得问题的解答,真实解答是唯一的。
ql 22 A B M P 图 q A lA /8M 图在上述荷载及单位弯矩图下,可图乘求系数、建立力法方程并求解,最后叠加出最终弯矩图,有关过程如下:2211P P2P 122P 1P 22211211222212112121118,816,36,300M X M X M M l F X l F X EI l F EI l EI l EI l X X X X P P P ++===−=∆=∆=====∆++=∆++δδδδδδδδ 本题也可利用对称性,在轴力为零前提下按一次超静定结构计算(过程参见(c )题),最终结果完全一样。
P M P 图 1F P l /8F P l /8 B A M 图21M 图F P l /44-2(c) 答:横向荷载轴力为零,可按一次求解(实际(b )可用对称性化成本题形式)由单位、荷载弯矩图苛求习俗,建立力法方程并求解,叠加可得最终弯矩图如下。
11P P 1P111P 1111220X M M l F X EI lF EI l X P +=−==∆==∆+δδ 考虑到本题荷载及杆长是上题(b )对称性后的一倍,可将两者结果一样。
结构力学课后习题答案

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学第5章答案(完整版)
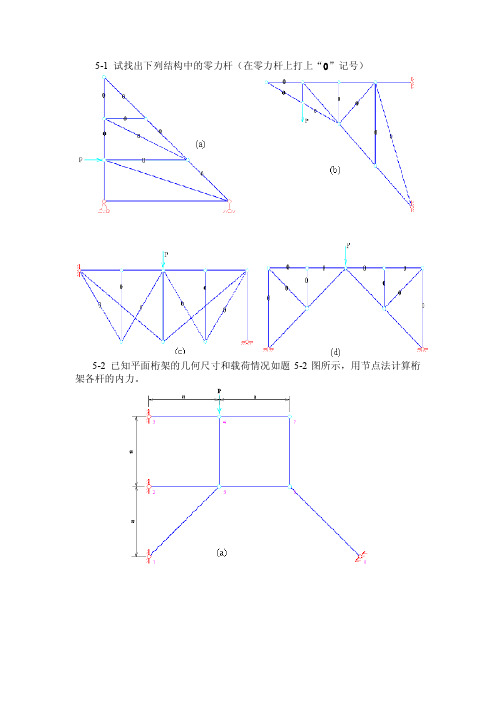
5-1试找出下列结构中的零力杆(在零力杆上打上“0”记号)5-2 已知平面桁架的几何尺寸和载荷情况如题5-2图所示,用节点法计算桁架各杆的内力。
解:(a)、零力杆:74,76,65,68,43分析节点4,得P N -=45分析节点5,得 2- 1P N P N ==552,(b)、零力杆:26,61,63,48,83,85,37,71分析节点7:P N -=75 分析节点5:5254P N =1221233234434554N N N N N N N N =======(c)、支座反力:均为0分析节点1: P N P N 2,31512-== 分析节点2: P N P N 2,32523== 分析节点3: P N 235-= 分析节点4: 04543==N N (d)、零力杆:12,15,52,83,43,49支座反力:P R P R P R y x y 3.1,8.0,3.2223=-==分析节点5: P N 8.056-=分析节点6: P N P N -=-=6267,8.0 分析节点9: P N P N 6.0,26.09893=-= 分析节点8: P N 6.087=分析节点3: P N P N 1.1,27.13237=-= 分析节点7: P N 23.072-=5-3 用分解成平面桁架的方法求如题5-3图所示空间桁架各杆的内力。
解:零力杆:26,48,34,24,28122152316213337317383N P a N P P cN P N P N P N P NP ==-=-=-===-3 5-4 已知平面桁架的几何尺寸和受载情况如题5-4图所示。
求图中用粗线所示的杆件①,②,③的内力。
解:(a)、零力杆如图所示1340,3P M N ==∑由得 3210,M N P ==-∑由得310,3y F N P ==∑由得 (b)、2140,2M N P ==∑由得230,x F N P ==-∑由得250,y F N ==∑由得(c)、支座反力:均为0,结构简化为:PN F P N F PN M x y 31,032,032,03213====-==∑∑∑得由得由得由5-5 求如题5-5图所示平面桁架的内力。
结构力学课后习题答案
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
题3-1图3-2 试不计算反力而绘出梁的M 图。
题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
题4-1图4-2 作图示刚架的M 图。
(b)(a)20kN40kN20kN/m40kN(b)5kN/m40kN(a)(c)(b)(a)题4-2图4-3 作图示三铰刚架的M 图。
题4-3图4-4 作图示刚架的M 图。
题4-4图4-5 已知结构的M 图,试绘出荷载。
P(e)(d)(a)(b)(c)/4kN(b)(a)(a)(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
题4-6图习题55-1 图示抛物线三铰拱轴线方程,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程,求截面K 的弯矩。
题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(e)(g)(h)P(d)(c)(a)(b)(f)x x l l fy )(42-=x x l lfy )(42-=C题6-1图6-2 用结点法计算图示桁架中各杆内力。
题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(b)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学全部作业参考答案

1:[论述题]1、(本题10分)作图示结构的弯矩图。
各杆EI相同,为常数。
图参考答案:先对右下铰支座取整体矩平衡方程求得左上活动铰支座反力为0,再对整体竖向投影平衡求得右下铰支座竖向反力为0;再取右下直杆作为隔离体可求出右下铰支座水平反力为m/l(向右),回到整体水平投影平衡求出左下活动铰支座反力为m/l(向左)。
反力求出后,即可绘出弯矩图如图所示。
图2:[填空题]2、(本题3分)力矩分配法适用于计算无结点超静定刚架。
参考答案:线位移3:[单选题]7、(本题3分)对称结构在对称荷载作用下,内力图为反对称的是A:弯矩图B:剪力图C:轴力图D:弯矩图和剪力图参考答案:B4:[填空题]1、(本题5分)图示梁截面C的弯矩M C = (以下侧受拉为正)图参考答案:F P a5:[判断题]4、(本小题2分)静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
参考答案:错误6:[判断题]3、(本小题 2分)在温度变化与支座移动因素作用下静定与超静定结构都有内力。
参考答案:错误7:[判断题]1、(本小题2分)在竖向均布荷载作用下,三铰拱的合理轴线为圆弧线。
参考答案:错误8:[论述题]2、(本小题10分)试对下图所示体系进行几何组成分析。
参考答案:结论:无多余约束的几何不变体系。
9:[单选题]1、(本小题3分)力法的基本未知量是A:结点角位移和线位移B:多余约束力C:广义位移D:广义力参考答案:B10:[单选题]2、(本小题3分)静定结构有温度变化时A:无变形,无位移,无内力B:有变形,有位移.无内力C:有变形.有位移,有内力D:无变形.有位移,无内力参考答案:B11:[判断题]2、(本小题2分)几何可变体系在任何荷载作用下都不能平衡。
参考答案:错误12:[判断题]5、(本小题2分) 按虚荷载原理所建立的虚功方程等价于几何方程。
参考答案:正确13:[单选题]3、(本小题3分)变形体虚功原理A:只适用于静定结构B:只适用于线弹性体C:只适用于超静定结构D:适用于任何变形体系参考答案:D14:[单选题]4、(本小题3分)由于静定结构内力仅由平衡条件决定,故在温度改变作用下静定结构将A:产生内力B:不产生内力C:产生内力和位移D:不产生内力和位移参考答案:B15:[单选题]5、(本小题3分)常用的杆件结构类型包括A:梁、拱、排架等B:梁、拱、刚架等C:梁、拱、悬索结构等D:梁、刚架、悬索结构等参考答案:B16:[单选题]6、(本题3分)图示计算简图是图A:为无多余约束的几何不变体系。
同济大学 结构力学课后习题及答案解析(完整版)

(c) (d)
(e) (f)
(g) (h)
2-5 试从两种不同的角度分析图示体系的几何构造。 (a)
(b)
同济大学朱慈勉 结构力学 第 3 章习题答案 3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a) A
FP
B
C
FPa
D
E
F
a
a
a
a
a
(b) 2kN/m
10kN
A
2m
6m
B
C
2m
D
4m
2m
1
1
2a
1
2
2
M1
6-4 试用力法计算图示结构,并绘其内力图。 (a)
6m
20kN/m
B
1.75EI
C
D
EI
A
6m
3m
解:基本结构为:
20kN/m
X1
6 1
M1
6 810
810
Mp
11X1 1p 0
M M1X1 M p
(b) E
2a
4a
C
D
q
EI=常数
A
B
4a
4a
解:基本结构为:
X1
计算 M 1 ,由对称性知,可考虑半结构。
(c)
15kN
20kN/m
A
B
C
D
E
F
2m 2m 3m
3m
3m
4m
(d)
6kN·m
4kN·m
A 3m
B
C
D
2m 2m
E 2m 2m
A
4kN
FG
H
2m 2m 2m
结构力学课后习题答案
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学 第五章 作业参考答案
结构力学 第五章习题 参考答案2005级 TANG Gui-he (整理)5-1 试用结点法计算图示桁架各杆的内力。
5-2 试用结点法计算图示桁架各杆的内力。
解:由整体平衡条件可解得支座反力 F A =1.5F F B =1.5F 取结点A 为隔离体,如图,用数解法可解得 F A C =-2.12F F A B =1.5F 同理,依次取结点B 、C 、 D 、E 为隔离体,并由对称性可得各杆的内力如图。
4 * 8m60k N60k N6M 2MA B C D E FG H 解:由 M H =0 可得支座F a y=75kN.由 F Y=0 得 F h y=45kN 取 A 结点为隔离体,利用数解法可得 F N AB=-100kN. F NAC=125kN. 再取 C 点为隔离体,利用投影法和力平衡 可得 F N BC=-50,F NCE=103.1kN.同理依次取 B , D , E , G , F 可得各杆内力(如图所标)AC-60k N -90k N -100k N 45k N75k N125k N 75k N 42.4k N61.8k N 103.1k N -60k N -50k N -30k N55-4试判断图示桁架中的零杆。
解:图中红色的杆件为零杆在杆中标有 为零杆其中用到K 型和T 型结构判断原理5-5试用截面法计算图示桁架中指定杆件的内力。
2解:(1)求出支座竖向反力为2.5F (↑),(2)作截面I -I ,由∑M A=0得: 2.5F ×15-10F -5F +6F N 1=0 → F N 1=-3.75F (3)由∑M B=0得: 2.5F ×10-F ×5-F N 2×6=0 → F N 2=3.33F (4)利用勾股定理求出A B 杆长7.8F N 4x =5F N 4/3.84 由∑M C=0得: 2.5F ×10-5F +F N 1×6+6×5F N 4/7.8=0 → F N 4=0.65F (5)取结点B 为分析对象,由∑F Y=0得: F N 4×6/7.8+F N 3=0 → F N 3=-0.5F5-6试用截面法计算图示桁架中指定杆件的内力。
结构力学章节习题及参考答案
结构力学章节习题及参考答案第1章绪论(无习题)第2章平面体系的机动分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W<0,则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6)(b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6)(c)图,故原体系是几何可变体系。
()(a)(b)(c)习题2.1(6)图习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题2.2(6)图(7) 习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题2.2(7)图习题2.3 对习题2.3图所示各体系进行几何组成分析。
(a)(b)(c)(d)(e)(f)习题2.3图(h)第3章(g)静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
《结构力学》课后习题答案__重庆大学出版社
第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构力学 第七章习题 参考答案TANG Gui-he7-2 试作图示超静定梁的M 、S F 图。
解:(1 (2)根据位移条件,得:11110P X δ+∆= (3)做出基本结构的各单位内力图和荷载内力图。
311112()233l l l l EI EI δ==g g g311155(222648P Fl l l Fl EI EI∆=−=−g g g(4)求解出多余未知力。
1516FX ⇒=(5)按照叠加法做出最后弯矩图和剪力图(如下图)。
11P M M X M =+M PBALMM 图AB 3F L /16F L /4图AB11F /165F /16F S7-3 试作图示超静定梁的M 、S F 图。
基本体系(2)根据位移条件,得:11110P X δ+∆=(3)做出基本结构的各单位内力图和荷载内力图。
112122(1)233l l EI EI δ==g g g g 21111()24216P Fl Fl l EI EI∆==g g g(4)求解出多余未知力。
1332FlX =−⇒ (5)按照叠加法做出最后弯矩图和剪力图(如下图)。
11P M M X M =+M PMABCF L /4M 图3F L /32ABC图F S3F /3213F /3219F /327-4 试作图示超静定梁的M 、S F 图。
q =2k N /mq =2k N /m1基本体系解:(1 (2)根据位移条件,得:11110P X δ+∆=(3)做出基本结构的各单位内力图和荷载内力图。
1116112279(2992339339)(33)356235EI EI EIδ=++++=g g g g g g g g g g 116293112291[(298123938199)(69)][(93)3(3)3]5632233421377 4P EI EI EI+∆=−+++−−−=−g g g g g g g g g g g g g g (4)求解出多余未知力。
1 6.17 kN X =⇒(5)按照叠加法做出最后弯矩图和剪力图(如下图)。
11P M M X M =+MMM 图(N m)图(k N )F S177-5 试用力法分析图示刚架,绘制M 、S F 、N F 图。
qq解:(1)该结构为二次超静定结构,拆除B 点多余联系,得到基本体系。
(2)根据位移条件,得:111122*********P P X X X X δδδδ++∆=++∆= (3)做出基本结构的各单位内力图和荷载内力图。
3111124[()()]233l l l l l l l EI EIδ=+=g g g g g g3122111()22l l l l EI EI δδ===g g g322112()233l l l l EI EI δ==g g g22241112215[()()()]22323828P ql ql ql ql l l l l l l EI EI ∆=−+−=−g g g g g g g g g g24211()224P ql ql l l EI EI∆=−=−g g g(4)求解出多余未知力。
1237328ql X ql X =⇒ =(5)按照叠加法做出最后弯矩图和剪力图(如下图)。
1122P M M X M X M =++ACBq L /22q L /2M P4q L /73q L /287-6图示刚架E =常数,52n =,试作其M 图,并讨论n 增大和减少时,M 图如何变化。
q =15k N /mq解:(1)该结构为一次超静定结构,拆除B 点多余联系,得到基本体系。
(2)根据位移条件,得:11110P X δ+∆= (3)做出基本结构的各单位内力图和荷载内力图。
1111121211360(66)6(610)6(144)23EI nEI EI nδ=+=+g g g g g g g g 111127500(10187.5)63P nEI nEI ∆=−=−g g (4)求解出多余未知力。
17500kN 360144n X n+⇒= 当52n =时,110.42 kN X =(5)按照叠加法做出最后弯矩图和剪力图(当52n =时,弯矩如下图)。
11P M M X M =+当n 增大时,AC 和BD 杆件弯矩减少,CD 跨中弯矩增大,当n =∞时,BD 杆相当于简支梁。
157-7 作刚架的M 图。
解:(1)该结构为二次超静定结构,拆除B 点多余联系,得到基本体系。
(2)根据位移条件,得:1111221211222200P P X X X X δδδδ++∆=++∆= (3)做出基本结构的各单位内力图和荷载内力图。
11212126[(33)3(36)3]23EI EI δ=+=g g g g g g 12210δδ==22212144(66)623EI EI δ==g g g111756(1683)32P EI EI ∆=−=−g g g2131260[261683168]6P EI EI∆=−+=−g g g (4)求解出多余未知力。
1268.75X X ==⇒ (5)按照叠加法做出最后弯矩图(如下图)。
1122P M M X M X M =++187-8 作刚架的M 图。
解:(1(2)根据位移条件,得:11110P X δ+∆= (3)做出基本结构的各单位内力图和荷载内力图。
112121230[(33)3(32)2]2323EI EI δ=+=g g g g g g 121248(23)1223P EI EI∆=−=−g g g(4)求解出多余未知力。
18kN 5X =⇒(5)按照叠加法做出最后弯矩图如下。
11P M M X M =+7-9 试求图示桁架各杆的内力,各杆EA 相同。
解:(1)该结构为一次超静定结构,拆开一根多余杆件,得到基本体系。
(2)根据位移条件,得:11110P X δ+∆=(3)做出基本结构的各单位内力图和荷载内力图。
11114112](2a a EA EA EA δ=+=+g g g g g g 11()P F a EA ∆=−=gg (4)求解出多余未知力。
10.146X F =−⇒(5)按照叠加法做出最后弯矩图如下。
11N N N P F F X F =+22N1F 图NF 图N P7-12图示组合结构210/A I l =,试按去掉CD 杆和切断CD 杆两种不同的基本体系,以建立典型方程进行计算,并讨论当0A →和A →∞时的情况。
解:(1)该结构为一次超静定结构。
(2)根据位移条件,得:11110P X δ+∆=(3)做出基本结构的各单位内力图和荷载内力图。
23111112132()2223260l l l l l EA EI EIδ=+=g g g g g311122()22326P l Fl Fl l EA EI∆=−=−g g g g g(4)求解出多余未知力。
11013X F =−⇒ (5)按照叠加法做出最后弯矩图如下。
11N N N P F F X F =+(6)根据位移条件,得:111112P X l X EA δ+∆=−g (7)做出基本结构的各单位内力图和荷载内力图。
3111122()22326l l l l EI EI δ==g g g g311122()22326P l Fl Fl l EA EI∆=−=−g g g g g(8)求解出多余未知力。
11013X F =−⇒7-13 试计算图示排架,作M 图。
8C D8C D解:(1)该结构为一次超静定结构,切断CD 杆多余联系,得到基本体系。
(2)根据位移条件,得:11110P X δ+∆=(3)做出基本结构的各单位内力图和荷载内力图。
11116112279(2992339339)(33)3256235EI EI EI δ=++++=g g g g g g g g g g g 1113972610252P EI EI+∆==g g g (4)求解出多余未知力。
1 1.29 kN X −⇒=(5)按照叠加法做出最后弯矩图和剪力图(如下图)。
11P M M X M =+8D8C DE A ->8CD7-18 试计算对称结构的M 图。
EI =常数。
qq解:(1)按照对称性取半结构之后,该结构为二次超静定结构,得到基本体系。
(2)根据位移条件,得:111122*********0P PX X X X δδδδ++∆=++∆= (3)做出基本结构的各单位内力图和荷载内力图。
311112()233l l l l EI EIδ==g g g g212212l EI δδ==2213[(1)111]22l l l EI EI δ=+=g g g241113()3248P ql ql l l EI EI ∆=−=−g g g 23211()1326P ql ql l EI EI∆=−=−g g g(4)求解出多余未知力。
324112223212512328 336226ql l l ql X X X EI EI EI qll l ql X X X EIEI EI=+= =−+=⇒ (5)按照叠加法做出最后弯矩图(如下图)。
1122P M M X M X M =++q q 3636M 图解方程组可用计算器来求解!结构力学 第七章 习题 参考答案7-26 结构的温度变化如图所示,EI =常数,截面对称于形心轴,其高度/10h l =,材料的线膨胀系数为α。
试:(a )结构的M 图;(b )求杆端A 的转角。
解:(1)该结构为一次超静定结构,去掉支座B 水平多余联系,得到基本体系。
(2)根据位移条件,得:11110t X δ+∆= (3)做出基本结构的各单位内力图和荷载内力图。
3112122()233l l l l EI EIδ==g g g g111255(255)1(1)22()2(/10)2320t N tF tl M dsh l l l lααααα∆∆=+−×+=−××−××××=−∑∑(4)求解出多余未知力。
12480EIX l α=⇒ (5)按照叠加法做出最后弯矩图和剪力图(如下图)。
11M M X =(6)求A 转角1111148021255(255)1 ()(1)()232(/10)2 60 ()c t N A y tF tl M ds EI hEI l l l l l l EI l l l ωαααααα∆∆=++−×+=++×××+×××+×=∑∑∑∫g g g 顺时针4L华南农业大学 水利与土木工程学院(College of water conservancy and Civil Engineering, SCAU )7-30 图示结构支座B 发生了水平位移30mm() a =向右,40mm() b =向下,0.01rad ϕ=,已知各杆的46400cm I =,E=210GPa 。
