《电磁场与电磁波》期末考试试题A卷
华中师范大学2018电磁场与电磁波期末试卷A

=0E 说明静电场做功与路径无关。
院(系):专业:年级:学生姓名:学号:-------------------------------------------------密----------------------------------封-----------------------------线---------------------------------------------------------第 1 页(共 页) A =) 0 j2πˆe z x E e -=化方向为 产生全透射现象时,入射波为ˆ(,)x E z t e =------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------得分评阅人四、简答题:(3小题,每题5分,共15分)1.电磁波的相速度是如何定义的?自由空间中的相速度是多少?试比较分析理想介质和导电媒质中相速度的不同之处?电磁波的等相位面在空间中的移动速度称为相位速度,简称相速。
在自由空间中相速的值为3乘以10的8次方米每秒2.写出无源自由空间中复矢量的麦克斯韦方程中的两个旋度方程。
3.设自由空间中平面电磁波的电场为ˆ(,)cos(-)mxE z t e E t kz=ω,简述其传播特性。
波是横向的,波的传播方向与场的方向相互垂直,被称为TEM波。
传播时不发生任何旋转,传播方向固定。
场向量大小满足E=cB,说明电磁波中起主要作用的往往是电场力。
j ˆe y kz H e -=------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------第 3 页(共 页) j20πˆz x E e e -=的均匀平面波从由空气垂直入射到理想介质4r =,r μ求反射系数和透射系数;。
电磁场与电磁波期末试题2010A

北京工业大学电控学院2009――2010学年第 2 学期《电磁场与电磁波》 课程试卷A适用专业: 电子工程、通信工程 考试方式:闭卷 考试时间 :2009年6 月 29 日班级学号 姓名: 成绩 得分登记(由阅卷教师填写)考生须知:答卷前务必首先写清班级学号和姓名,否则无成绩;一、简答题(30分)1.写出静电场的电位泊松方程,并给出其两种理想介质分界面的边界条件。
2ρϕε∇=-; 在两种完纯介质分界面上电位满足的边界条件:12ϕϕ= 1212snnϕϕεερ∂∂-=-∂∂2.讨论均匀平面波在无界空间传播时本征阻抗与波阻抗的区别。
3.写出均匀平面波在无界良导体中传播时相速的表达式。
4.写出时谐电磁场条件下亥姆霍兹方程。
5.写出传输线输入阻抗公式。
6.证明电场矢量和磁场矢量垂直。
证明:任意的时变场(静态场是时变场的特例)在一定条件下都可以通过Fourier展开为不同频率正弦场的叠加。
垂直。
也与垂直与垂直。
与乘定义,可知根据E H H X∴=⨯-=⨯-∂∂-=⨯∇B B E B E k B j E k j tBE ωω7.写出线性各向同性的电介质、磁介质和导电介质的本构关系式。
EJ H B EDσμε=== 8.写出均匀平面波在两介质分界面的发射系数和投射系数表达式。
9.写出对称天线的归一化方向函数。
10.解释TEM 、TE 、TM 波的含义。
二、计算题1. (10分)已知矢量222()()(2)x y z x axz xy by z z czx xyz =++++-+-E e e e ,试确定常数a 、b 、c 使E 为无源场。
解 由(2)(2)(122)0x az xy b z cx xy ∇=++++-+-= E ,得2,1,2a b c ==-=-2.已知标量函数22223326u x y z x y z =+++--。
(1)求u ∇;(2)在哪些点上u ∇等于零。
解 (1)(23)(42)(66)xyzx y z u u u u x y z xyz∂∂∂∇=++=++-+-∂∂∂e e e e e e ;(2)由(23)(42)(66)0x y z u x y z ∇=++-+-=e e e ,得 32,12,1x y z =-==3. 两块很大的平行导体板,板间距离为d ,且d 比极板的长和宽都小得多。
北邮2020春电磁场与电磁波期末试题

北京邮电大学2019-2020年第二学期期末考试电磁场与电磁波试题(开卷,A )已知:-12091==8.8510(/)3610F m επ⨯⨯,70=410(/)H m μπ-⨯一、(15分) 相距无穷远的不带电孤立导体球壳A 与孤立导体球B ,其中球壳A 的内径为b ,外径为a ,内外径之间为理想导体,r b <及r a >处为真空;导体球B 半径为与球壳A 的外径相同。
在球壳A 中,距离中心c (c b <)处存在一电量为Q 的点电荷。
将导体球B 从无穷远处移动到球壳A 处,并与球壳A 充分接触后再移动到无穷远处,试求:在整个移动导体球B 的过程中外力所作的功。
(提示:可考虑功能原理)二(10分)、太阳能电池板的能量转化效率为30%,一个2.5平方米的太阳能电池板供一个1000瓦的灯泡照明,假设太阳光是线偏振的单色平面波,试估计太阳光的电场与磁场的振幅。
三(15分)、设一平行大地的双导体传输线, 距地面高度为h, 导体半径为a, 二轴线间的距离为d (a<<d, a<<h )。
考虑地面影响时, 试计算两导线的电位分布及电容。
如题三图所示。
题三图四(15分)、一个长方形导体盒,各边尺寸分别是a ,b ,c ,各周界之间相互绝缘,每个面的电位函数如题四图所示,试求导体盒内部的电位函数。
题四图五(10分)、证明:对于良导体导体内单位宽度断面的表面电流:J s =H 0,期中H 0为导体表面的切向磁场强度。
六、(15分)一右旋圆极化波垂直入射到位于z=0的理想导体板上,其电场强度的复数表示式为0()j z x y i E E e j e e β→→-=-求:(1) 确定反射波的极化方式,说明原因;(2) 求导体板上的感应电流;(3) 求总电场的瞬时表达式。
七(10分)、设在波导中沿z 轴传播的电磁波的形式为: 022c c πππcos sin e j zz x E m m n E E x y k x k a a b βγγ-∂-⎛⎫⎛⎫⎛⎫==- ⎪ ⎪ ⎪∂⎝⎭⎝⎭⎝⎭试以此分析并说明相移常数β和波数k 之间的关系。
电磁场与电磁波期末考试试题A卷

《电磁场与电磁波》期末考试试题A卷一:(16分)简答以下各题:1.写出均匀、理想介质中,积分形式的无源(电流源、电荷源)麦克斯韦方程组;(4分)d d d d d 0d 0l S l S S S t t ∂⎧⋅=⋅⎪∂⎪∂⎪⋅=-⋅⎪∂⎨⎪⋅=⎪⎪⋅=⎪⎩⎰⎰⎰⎰⎰⎰D H l S B E l S D S B S2. 假设两种理想介质间带有面密度为S ρ的自由电荷,写出这两种介质间矢量形式的交变电磁场边界条件;(4分)()()()()12121212000S ρ⋅-=⎧⎪⋅-=⎪⎨⨯-=⎪⎪⨯-=⎩n D D n B B n E E n H H3. 矩形金属波导中采用TE 10模(波)作为传输模式有什么好处(3点即可);(4分)4. 均匀平面波从媒质1(1,1=,1=0)垂直入射到与媒质2(2,2=,2=0)的边界上。
当1与2的大小关系如何时,边界上的电场振幅大于入射波电场振幅?当1与2的大小关系如何时,边界上的电场振幅小于入射波电场振幅?(4分)答:(1)电场在边界上振幅与入射波振幅之比是1+R ,所以问题的关键是判的R 的正负。
第一问答案1<2,第二问答案1>2二、(16分)自由空间中平面波的电场为:()120e j t kx z ω+=πE e ,试求:1. 与之对应的H ;(5分)2. 相应的坡印廷矢量瞬时值;(5分)3. 若电场存在于某一均匀的漏电介质中,其参量为(0ε, 0μ,σ),且在频率为9kHz 时其激发的传导电流与位移电流幅度相等,试求电导率σ。
(6分)解:1.容易看出是均匀平面波,因此有()()()j j 01120e e 120t kx t kx x x z y ωωπηπ++⎛⎫-=⨯=-⨯⋅= ⎪⎝⎭e H E e e e (A/m )或者直接利用麦克斯韦方程也可以求解:()j 0e j t kx y ωωμ+∇⨯==-E H e2.若对复数形式取实部得到瞬时值,则()120cos z t kx =πω+E e ,()cos y t kx =ω+H e ,()()()2120cos cos 120cos z y x t kx t kx t kx πωωπω⎡⎤=⨯=+⨯+=-+⎡⎤⎣⎦⎣⎦S E H e e e (W/m 2)。
电磁场与波期末考试试题A卷含答案

莆田学院期末考试试卷 (A )卷2011 — 2012 学年第 一 学期课程名称: 电磁场与波 适用年级/专业: 09/电信 试卷类别 开卷( ) 闭卷(√) 学历层次 本科 考试用时 120分钟《.考生..注意:答案要全部抄到答题纸上,做在试卷上不给分.......................》.一、填空题(每空2分,共30分)1.给定两个矢量z y x a a a A 32-+=,z y a a B +-=4,则矢量A 的单位矢量为 ① ,矢量B A ⋅= ② 。
2.高斯散度定理的积分式为 ① ,它广泛的用于将一个封闭面积分变成等价的体积分,或者将一个体积分变成等价的封闭面积分。
3.已知任意一个矢量场A ,则其旋度的散度为 ① 。
4.介质中恒定磁场的基本方程的积分式为 ① , ② , ③ 。
5.一个半径为a 的接地导体球,一点电荷q 位于距球心d 处,则其镜像电荷带电量为 ① ,位置位于 ② ;当点电荷q 向无限远处运动时,其镜像电荷向 ③ 运动。
6.标量场2),,(x xyz z y x +=ψ通过点P(1,1,2)的梯度为① 。
7.引入位移电流的概念后,麦克斯韦对安培环路定律做了修正,其修正后的微分式是 ① ,其物理含义是: ② 。
8.自由空间传播的电磁波,其磁场强度)sin(z t H a H m y βω-=,则此电磁波的传播方向是 ① ,磁场强度复数形式为 ② 。
二、单项选择题(每小题2分,共20分)1.自由空间中的平行双线传输线,导线半径为a ,线间距为D ,则传输线单位长度的电容为 。
A .)ln(1aaD C -=πε B. )ln(201aa D C -=πε C. )ln(2101a a D C -=πε2.如果某一点的电场强度为零,则该点的电位为 。
A.一定为零 B.不一定为零 C.为无穷大3.真空中一个电流元在某点产生的磁感应强度dB 随该点到电流元距离变化的规律为 。
09下电磁场与电磁波试卷A.

09-10第二学期华侨大学 《电磁场与电磁波》A 类 试卷班 级___________________ 考试日期 2010 年 7 月 14 日 姓 名___________________学 号______________________一、 请求矢量ˆˆˆr xxyy zz =++在球坐标系下的表达式。
(8分) 二、 电子绕氢原子核作半径0.05纳米的圆周运动,计算ω和T 。
(8分) 三、 请给出无源非均匀空间电场散度表达式,并证明当n z εα=时(α,n 为常数),电场为z 方向时满足:E nE z ∇⋅=-( E 为电场幅度)。
(12分)四、 自由空间(0z >)中分布磁感应强度ˆˆˆ1.50.80.6B x y zmT =++,求下半空间(100rμ=)中磁感应强度及各个区域中的磁化电流密度。
(12分) 五、 求如图系统电容值。
(10分)半径a=10cm b=20cm c=30cm六、 在无损耗的线性、各向同性媒质中,电场强度()E r 的波动方程为()()220E r E r ωμε∇+=已知矢量函数()0jk r E r E e -=其中0E 和k 是常 矢量。
试证明()E r 满足波动方程的条件是22k ωμε=,这里k k =(12分)七、 自由空间中的电磁场表达式为:()()ˆ,1000cos Ez t xt kz V m ω=- ()()ˆ, 2.65cos H z t yt kz A m ω=- 式中,0.42/k rad m ==求解:(1) 瞬时坡印廷矢量;(2) 平均坡印廷矢量;(3)任意时刻流入右图示平行六面体(长1m 横截面积为0.252m )中的净功率(8分)八、 同轴线内导体半径a=1mm ,外导体的内半径b=4mm ,内外导体间为空气,设内外导体间的电场强度为()8100ˆcos 10E t kz V m ρρ=-,(1)利用电场旋度公式计算出磁场H ,(2)确定k 的值 (10分)九、 自由空间的均匀平面波的电场表达式为()()()ˆˆˆ,102cos 3z E r t xy E z t x y z V m ω=+++--式中的z E 为待定量。
《电磁场与电磁波》期末考试参考题

1、一半径为a 的均匀带电圆环,电荷总量为q ,求圆环轴线上离环中心o 点为z 处的电场强度E。
解:设圆环电荷线密度为λ,再在圆环上任取微元dl ,则dl dq λ=∴圆环上点电荷元dq 在p 处产生的电场强度为204RdqE d πε=根据对称性原理可,整个圆环在p 点产生的场强为沿轴线方向分量之和,即()232202044cos za dl z RzR dq E d E d z +===πελπεθ∴ ()⎰+=lz dl za z E 232204πελ又a dl lπ2=⎰ λπa q 2=∴ ()232204za zq E z +=πε2、在介电常数为ε的无限大约均匀介质中,有一半径为a 的带电q 的导体球,求储存在介质中的静电能量。
解:导体在空间各点产生的电场为)(4)0(02a r r q E a r E r w >=<<=πε故静电能量为a q dr r r q dV E dV E D W V V πεππεεε844212121202222=⎪⎭⎫ ⎝⎛==•=⎰⎰⎰∞ 3、一电荷面密度为σ的“无限大”平面,在距离平面a 的一点的场强大小的一半是由平面上的一个半径为R 的圆面积范围内的电荷所产生。
圆半径的大小。
解:电荷面密度为σ的“无限大”平面,在其周围任意点的场强为:2εσ=E 以图中O 点为圆心,取半径为r 的环形圆,其电量为:rdr dq πσ2=它在距离平面为a 的一点处产生的场强为:()2/32202ra ardrdE +=εσ则半径为R 的圆面积内的电荷在该点的场强为:()⎪⎪⎭⎫⎝⎛+-=+=⎰22002/322122R a a r ardra E Rεσεσ 0220412εσεσ=⎪⎪⎭⎫ ⎝⎛+-R a a∴ a R 3=4、已知两半径分别为a 和)(a b b >的同轴圆柱构成的电容器,其电位差为V 。
试证:将半径分别为a 和b ,介电常数为ε的介质管拉进电容器时,拉力为abV F ln )(20εεπ-=证明:内外导体间的电场为ab r V E r ln=插入介质管后的能量变化为a b zV dz dr r a b r B dV E W z b a v ln )(ln 2)(21)(21200222020εεππεεεε-=⎪⎭⎫ ⎝⎛-=-=⎰⎰⎰ 式中z 为介质管拉进电容器内的长度。
浙江大学 春夏学期《电磁场与电磁波》期末考试试卷及答案
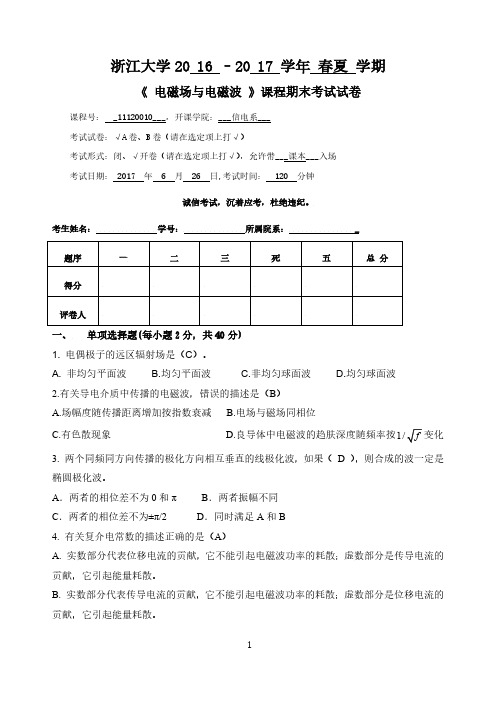
z015.02103 mW / m2
(3)透射波
E2 x0Em2e j2z x01.21510e j1.66z x012.15e j1.66zmV / m
5
H2
1 2
z0
x0 Em2e j2z
1 238.44
y
012.15e
j1.66
z
y0 51103 e j1.66zmA / m
A.都是连续的 B. 不连续的;连续的 C. 连续的;不连续的 D.都不连续
8. z=0 是空气( 0 )与介质( 2 30 )的分界面,若已知空气中的电场强度 E1 3x0 3z0 , 则介质中的电场强度应为(C)。
A. E2 3x0 9z0
B. E2 x0 3z0
D. 实数部分代表传导电流的贡献,它引起电磁波功率的耗散;虚数部分是位移电流的贡献,
它不能引起能量耗散。
5. 有关天线增益和天线方向性的描述,不正确的是(B)
A.天线增益考虑了天线材料中的欧姆损耗,而天线方向性则没有;
B.天线增益是馈入天线电磁信号的放大倍数,方向性是指波束的指向方向;
C.方向图主瓣越窄,副瓣越小,天线方向性就越大,天线增益也越高
浙江大学 20 16 –20 17 学年 春夏 学期
《 电磁场与电磁波 》课程期末考试试卷
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《电磁场与电磁波》期末考试试题A 卷
一:(16分)简答以下各题:
1. 写出均匀、理想介质中,积分形式的无源(电流源、电荷源)麦克斯韦方程组;(4分)
d d d d d 0d 0l S l S S S t t ∂⎧
⋅=⋅⎪∂⎪
∂⎪⋅=-⋅⎪∂⎨
⎪
⋅=⎪⎪
⋅=⎪⎩⎰⎰⎰⎰⎰⎰D H l S B E l S D S B S
2. 假设两种理想介质间带有面密度为S ρ的自由电荷,写出这两种介质间矢量形式的交变电磁场边界条件;(4分)
()()()()12121212000
S ρ⋅-=⎧⎪
⋅-=⎪⎨
⨯-=⎪⎪⨯-=⎩n D D n B B n E E n H H
3. 矩形金属波导中采用TE 10模(波)作为传输模式有什么好处(3点即可);(4分)
4. 均匀平面波从媒质1(ε1,μ1=μ0,σ1=0)垂直入射到与媒质2(ε2,μ2=μ0,
σ2=0)的边界上。
当ε1与ε2的大小关系如何时,边界上的电场振幅大于入射波电场振幅?当ε1与ε2的大小关系如何时,边界上的电场振幅小于入射波电场振幅?(4分)
答:(1)电场在边界上振幅与入射波振幅之比是1+R ,所以问题的关键是判的R 的正负。
第一问答案ε1 < ε2 ,第二问答案 ε1> ε2
二、(16分)自由空间中平面波的电场为:
(
)
120e j t kx z ω+=πE e ,试求:
1. 与之对应的H ;(5分)
2. 相应的坡印廷矢量瞬时值;(5分)
3. 若电场存在于某一均匀的漏电介质中,其参量为(0ε, 0μ,σ),且在频
率为9kHz 时其激发的传导电流与位移电流幅度相等,试求电导率σ。
(6分)
解:
1.容易看出是均匀平面波,因此有
()()()
j j 01120e e 120t kx t kx x x z y ωωπηπ++⎛⎫-=⨯=-⨯⋅= ⎪⎝⎭e H E e e e (A/m )
或者直接利用麦克斯韦方程也可以求解:(
)j 0
e j t kx y ωωμ+∇⨯==-E H e 2.若对复数形式取实部得到瞬时值,则
()120cos z t kx =πω+E e ,()cos y t kx =ω+H e ,
()()()
2
120cos cos 120cos z y x t kx t kx t kx πωωπω⎡⎤=⨯=+⨯+=-+⎡⎤⎣⎦⎣⎦S E H e e e (W/m 2)。
若瞬时值是取虚部,则结果为
()2
120sin x t kx πω=-+S e 。
3.根据条件可知
397
01
29101051036σωεππ--==⨯⨯⨯
⨯=⨯(S/m )
三、(10分)空气中一均匀平面波的电场为
()(1.6 1.2)
34j x y x y z A e --=++E e e e ,问欲使其为左旋圆极化波,
A =?欲使其为右旋圆极化波,A =?
解:(1)左旋圆极化波时,5A j =
(2)右旋圆极化波时,5A j =- 由于
345
x y +=e e ,所以5A =。
在xoy 平面上画出34x y +e e 和43x y
-k =e e ,由
z e 向34x y +e e (相位滞后的方向)旋转,拇指指向k ,符合左手螺旋,因此
左旋圆极化波情况下z e 要超前34x y
+e e ,即5A j =;反之,右旋圆极化波情
况下z e 要滞后
34x y
+e e ,即5A j =-。
四、(16分)自由空间波长为00.3λ=m 的电磁波在导体铜内传播。
已知铜的75.810σ=⨯S/m ,1r
ε=,1r μ=,铜表面处的磁场强
度大小为1
010H -=A/m 。
求:1. 波在铜内的相移常数
β,相速度p ν及波长λ;
(4分)
2. 波在铜内的波阻抗e
η及导体表面处的电场强度大小0E ;
(4分) 3. 波的趋肤深度
δ;(4分)
4. 铜的表面电阻率
S R 。
(4分)
解:(1)频率
8
9
0310100.3c
f λ⨯===(Hz )
损耗角正切7
99
5.810100
12101036σωεππ-⨯=
⨯⨯⨯,故铜可视为良导体。
相移常数
54.78510β===⨯(rad/m ) 相速度9
4
5
2210 1.313104.78510f ωππνββ⨯====⨯⨯(m/s )
波长
5
1.31310f
ν
λ-==⨯(m )
(2)波在铜内的表面阻抗
45450.0117e
j j e η=≈
==(Ω)
因为
0e E H η=,故导体表面处的电场强度
34500 1.1710e j E H e η-==⨯(V/m )
(3)波的趋肤深度
65
1
1
1
2.09104.78510δα
β
-=
=
=
=⨯⨯
(m )
(4)铜的表面电阻率
3
76118.3105.810 2.0910S R ασσδ--=
===⨯⨯⨯⨯(Ω)
五、(16分)一均匀平面波由空气垂直入射到位于x =0的理想介质(μ0,ε)平面上,已知
70410μπ-=⨯(H/m),入射波电场强度为
()jkx
y z E j e
+
+
-=+E e e
试求:1. 若入射波电场幅度30 1.510E +-=⨯V/m ,反射波磁场幅度为
60 1.32610H -
-=⨯A/m ,r ε是多少?(6分)
2. 求反射波的电场强度-
E ;(5分) 3. 求折射波的磁场强度T
H 。
(5分)
解:(1)通过电场的反射系数R 求r ε
反射波电场幅度为
3010000.510/E H H V m ηη--
--=-=-=-⨯
所以电场的反射系数为
3210
3
210.5101/ 1.5103R E E ηηηη--
+--⨯===-=⨯+
所以
210/2/2ηηη==,即
2
10
0000ηεεμεεμ==r r
所以
2=,4
r ε=
(2)求反射波的电场强度
由 2001602ηηπ=
===(Ω)
可得电场的反射系数为
212113R ηηηη-==-+,折射系数为221223T ηηη==
+ 反射波在-x 方向,电场强度的幅度是
++
--==0
0031E RE E
所以 01()3jkx
y z E E a ja e -+
=-+
(3)求折射波的磁场强度
折射波仍在x 方向,电场强度的幅度是
+
+=
=0
032E TE E T ,
相移常数是202k k ===
所以折射波电场强度为
22002()()3jk x T T
j kx
y z y z E E a ja e E a ja e -+-=+=+
所以2021()90T T
j kx
x z y E H a E a ja e ηπ+-=⨯=-
六、(10分)矩形波导传输TE 10波,尺寸为2.5×1.5cm 2,工作频率为
7.5GHz ,波导内部填充2r ε=,1r μ=的理想介质,试求:相移常数β,相速p v ,截止频率c f 及波阻抗Z 的值。
七、(16分)有两个电偶极子,一个水平放于地面上,一个垂直于
地面放置,此两电偶极子与地面无限靠近但不与地面相连,两电偶极子的中心水平相距 d =0.001λ,电偶极子上的电流均为I ,长度为
dl ,试求此二电偶极子在空
间的总辐射功率和总辐射电阻。
辐
射
功
率为:
2
22
d 80πl P I λ⎛⎫
= ⎪
⎝⎭
辐射电阻
为:
2
2d π160⎪
⎭⎫
⎝⎛=λl R r。
