南京邮电大学数字电路书后习题.ppt
合集下载
南京邮电大学 电路分析基础 课后习题解答 第5--11章 (课堂PPT)
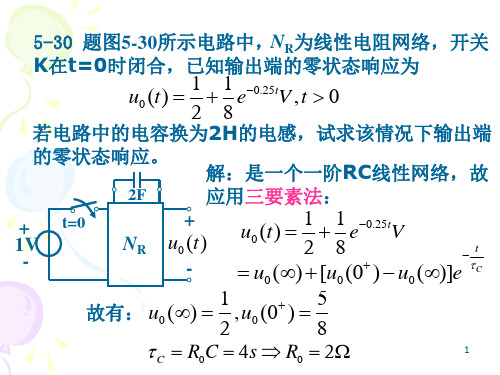
uC (T ) 10(1 et )V
(2)T t 2T时：
uC (T ) uC (T ) 10(1 et )V
uC () US
14
uC (t)
U S
[10(1
e1
)
U
s
]e
t T RC
V
uC (2T ) US [10(1 e1) Us ]e1 0
US 10e1 3.68V
13
5-38 题图5-38中所示脉冲宽度T=RC，施加于RC串联
电路，电路为零状态。试求使uS (t) 在t=2T时仍能回到
零状态所需负脉冲的幅度U
。
S
uS /V
10
U S
T 2T
t/s
+
us
-
+
-uC
解：(1) 0 t T 时：
uC () us 10V
t
uC (t) 10(1 e RC )V
3)求时间常数：
R0C
[(100 //100) 50] C1C2 C1 C2
104 S
5
4) 写出响应表达式： uC1(t) 5(1 e104t )V ,t 0 i1(t) 0.2 0.05e104t A,t 0
6
5-34 电路如图5-34所示，已知 is (t) 10 15 (t) A ，试
50
+
+
40V
-
100
10-V
i1(0 )
用迭加法求 i1(0 )：
i1
(0
)
100
40 100
//
50
50 100
50
10
100
50 100 //100 100 100
南邮数电第5章6序列信号发生器.ppt
Q3 Q2 Q1 状态转移路线 模数 1 01
0 10 1 00 0 00
M=4 ×
0 01
0 10
需增加一个触发器！ 取n=4，重新列状态转移表
Q4 Q3 Q2 Q1 状态转移路线 模数
101 0
010 0 100 0
M=6
000 1
√
001 0
010 1
101 0
(3) 求激励函数
Qn4 Qn3 Qn2 Qn1 Qn4+1 Qn3+1 Qn2+1 Qn+11 D1
解：方法一：用小规模器件实现 （1）设计M=8的计数器，方法同前面的同 步（异步）计数器的设计。 本解取n=3 的异步二进制加法计数器 （2）设计组合电路
组合电路真值表为：
Q3
Q2
Q1 F
0
0
01
0
0
11
0
1
01
0
1
11
1
0
00
1
0
11
1
1
00
1
1
11
用卡诺图化简得到：F=Q3+Q1
逻辑图为：
5
的n位码就是起跳状态。
表 2-4线译码器的真值表
Q2
Q1
Y0
Y1
Y2
Y3
0
0
1
0
0
0
0
1
0
1
0
0
1
0
0
0
1
0
1
1
0
0
0
1
Q2
Q1
1J
1J
C1
C1
1K
1K
南邮课件-数字电路-期末总复习
i0
③任意两个最小项的乘积恒等于0 。
即： mi mj 0 (0 i( j) 2n 1,且i j)
6､ 八进制 → 二进制 转换方法:先将八进制 → 二 — 八进制,
再把二 — 八进制→二进制。 例： （345.1)8=( ? )2
1) 二 — 八进制: (011 100 101.001);
2) 二进制: (11100101.001)2
7､十六 进制→二进制
转换方法:先将十六进制 → 二 — 十六进制, 再把二 — 十六进制 → 二进制。
例： （AF.26)16 =( ? )2
1) 二 — 十六进制: (1010 1111 . 0010 0110)
2) 二 进制: (10101111.0010011)2
8､非十进制之间的互换
不同数制转换时,可采用的转换方法:
1)先转换成十进制数;
2)然后再将十进制数转换成新数制的数。
例： （4321）5=（ ？ ）2 解： 1）先求出（4321）5= （？）10
期末总复习 第一章 数制与码制 一、数制
二､数制转换
1､二､八､十六 进制 → 十进制 将二､八､十六 进制数转换成十进制数，只要
把原数写成按权展开再相加即可。
2､十 进制→ 二､ 八､ 十六进制
十 进制 → 二､ 八､ 十六进制数只需将整数部分 和小数部分分别转换成二､ 八､ 十六进制数,再将转换 结果连接在一起即可。
指出：利用对偶规则，基本定律可只记一半，常用 公式被扩展一倍。如:P18 表2.3所示
四、逻辑函数的表达式 （一）､常用表达式 (五种形式)
五､逻辑函数的标准表达式 1､最小项､最小项表达式 （1）最小项的概念及其表示 最小项的特点：
数字电路习题答案PPT课件
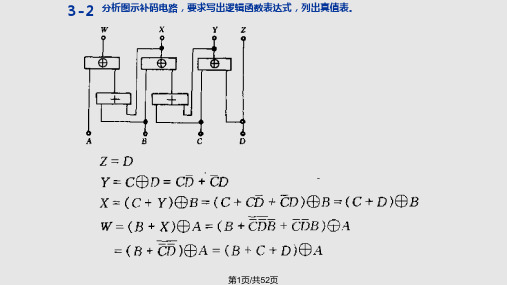
Z2Z1Z0=000时，输出
FD0F00 Z2Z1Z0 000时，输出 F 1
X2X1X0 = Z2Z1Z0时，输出 F=0
X2X1X0 Z2Z1Z0时，输出 F=1
第12页/共52页
3 - 由八线一三线优先编码器74148和与非门构成的电路如下，试说明该电路的 9 逻辑功能。
构成10—4线优先8421BCD编码器。低电平有效，输 出原码。
3-
16 用74LS138三—八线译码器和与非门实现下列逻辑函数。
Y 1AB A C (B C ) m (1,2,3,7) Y1
Y2
Y3 Y4
Y2ABAB m (2,3,4,5)
Y3(AB)A ( C) m (0,1,5,7)
Y 4AB A C BC m(0,7)
Y 0
Y 1
Y 2
Y 3
m (1,2,3,7) Y 2 A B C A B C A B C A B C m (2,3,4,5)
Y 3(A B )A ( C )A B A C A B AC
A B C A B C A B C AB Cm (0,1,5,7) Y 4AB A C BC m(0,7)
第32页/共52页
第37页/共52页
3-20 可控半加/半减器
X=1时；S=A+B，即：S=A-B,CO为借位输出。 X=0时；S=A+B,CO为进位输出。
第38页/共52页
3 - 利用两片74283实现二进制数11001010和11100111的加法运算，要求画出逻辑图。 21
解：实际就是八位二进制数加法运算 计算X-Y可变化为：X+[Y]补码； 求补：Y各位变反加1
F10 CDAB
F30CDAB
2019-2020年人教统编南京邮电大学数据库系统课后习题答案2幻灯片
是编写事务的应用程序员的职责； 由DBMS完整性子系统测试。 保证数据库的完整性。
数据库系统
习题课二
第七章习题
(3) 隔离性(Isolation)： --多个事务并发执行时，系统应保证与这些事务 先后单独执行时的结果一样。 --由DBMS的并发控制子 系统实现。 --提高事务的并发度，又不让错误发生。
第四章（P144-145）
4.24 设有关系模式R(ABCD)，其上的FD集 F={A→B，B→C，D→B}。
参考答案：
①R分解成ρ＝{ACD, BD}，试求F在ACD和BD 上的投影。
解：实际是求F+在ACD和BD上的投影 设：R1(ACD)， R2(BD) 由推理规则： F1 ={A→C，D→C} ←传递性 F2 ={D→B}
解② ：(1)R的关键码 AB、BC (2) ρ中有R1(ACD)， R2(BC)
R1∩R2=C， R1－R2=AD， 由F经合并性推理得： C→AD，ρ无损
(3) F1 ={C→A，C→D} , F2 = φ （F1∪F2）＋ ≠F＋ 分解ρ不保持函数依赖
(4)R1的F1 ={C→A，C→D} Key1: C 按定义4.19 R1 达BCNF
按定义4.19 R1 达BCNF 按定义4.19 R2 达BCNF 按定义4.19 R3 达BCNF
数据库系统
习题课二
第四章习题
4.21设有关系模式R(ABC )，其上的FD集为 F={ B→C，C→A }， 那么分解ρ＝{AB, AC}
相对于F是否是无损分解和保持FD？说明理由
解 (1) ρ中有R1(AB)， R2(AC)
参考答案：
(1)R的基本函数依赖集 F={(职工编号，日期)→日营业额， 职工编号→部门名， 部门名→部门经理} Key: (职工编号，日期)
数据库系统
习题课二
第七章习题
(3) 隔离性(Isolation)： --多个事务并发执行时，系统应保证与这些事务 先后单独执行时的结果一样。 --由DBMS的并发控制子 系统实现。 --提高事务的并发度，又不让错误发生。
第四章（P144-145）
4.24 设有关系模式R(ABCD)，其上的FD集 F={A→B，B→C，D→B}。
参考答案：
①R分解成ρ＝{ACD, BD}，试求F在ACD和BD 上的投影。
解：实际是求F+在ACD和BD上的投影 设：R1(ACD)， R2(BD) 由推理规则： F1 ={A→C，D→C} ←传递性 F2 ={D→B}
解② ：(1)R的关键码 AB、BC (2) ρ中有R1(ACD)， R2(BC)
R1∩R2=C， R1－R2=AD， 由F经合并性推理得： C→AD，ρ无损
(3) F1 ={C→A，C→D} , F2 = φ （F1∪F2）＋ ≠F＋ 分解ρ不保持函数依赖
(4)R1的F1 ={C→A，C→D} Key1: C 按定义4.19 R1 达BCNF
按定义4.19 R1 达BCNF 按定义4.19 R2 达BCNF 按定义4.19 R3 达BCNF
数据库系统
习题课二
第四章习题
4.21设有关系模式R(ABC )，其上的FD集为 F={ B→C，C→A }， 那么分解ρ＝{AB, AC}
相对于F是否是无损分解和保持FD？说明理由
解 (1) ρ中有R1(AB)， R2(AC)
参考答案：
(1)R的基本函数依赖集 F={(职工编号，日期)→日营业额， 职工编号→部门名， 部门名→部门经理} Key: (职工编号，日期)
南邮数字电路与逻辑设计总复习题ppt课件
F = (A + B) ·C + A + B +C
三、（1）若F（ABC）=Σm（0，1，3，6）则其对偶式F’= Σm （ 0, 2, 3, 5
解:
F（ABC）=Σm（0，1，3，6）
F（ABC）=Σm（2，4，5，7） F’（ABC）=Σm（5，3，2，0）
；.
）。
7
四. 填空 (1)F(A,B,C)=AB+BC=∑m(?) 解: F(A,B,C)=AB+BC = AB( C+ C ) + ( A+ A )BC = ABC + ABC +ABC = m7 + m6 +m3 =∑(7,6,3)
即：10000 – 0101 = 1011。
；.
39
9、试用一个四位数值比较器7485和一个四位全加器74283（不允许附加任何 器件）将四位二进制数B3B2B1B0转换成8421BCD码000D10D8D4D2D1（其中 000D10D8D4D2D1 分别表示十进制数的十位、个位数的8421BCD码）。
=AB AC
；.
17
(2)F=(ACD+ABC+ABC+ACD)ABC+ACD+ABC+ACD 求最简“与-或”式。
解:
F=BD
；.
18
(3)、已知
F1（A B C D）=Σm（0，3，4，5，7，9，10，13，14，15） F2（A B C D）=Σm（2，3，5，6，7，9，12，13，15） 试用卡诺图运算的方法求 F3（A B C D）= F1（A B C D）⊙ F2（A B C D）的最简与或表达析这个电路完成什么功能？
南京邮电大学 数字电路 第四章习题.ppt
1 D4 D5 D7 D6
D1 = D2 = D, D4 = D5 = D6 = D7 = 0
2020年3月25日星期三
第四章 组合逻辑电路习题
节目录
23
相应的电路图如下所示：
EN
C
A0
B
A1
C
A
A2
D
D0
D
D1 D2
7 41 5 1
Y
F
D3
D4
D5
D6 D7
2020年3月25日星期三
第四章 组合逻辑电路习题
2020年3月25日星期三
第四章 组合逻辑电路习题
节目录
32
增加冗余项后，相应逻辑电路中应增加一个与 非门，其与非表达式为：
F (A,B,C,D) = ABC ·ACD ·ABC ·A CD ·BD
2020年3月25日星期三
第四章 组合逻辑电路习题
节目录
33
CD
AB
00 01 11 10
00
1
01
节目录
24
(4) 函数有4个输入变量 ，而74151的地址端只有
3个，即A2 、A1 、A0 ，故须对函数的卡诺图进
行降维，即降为3 维。 BC
CD
A 00 01 11 10 0 DD00
AB 00 01 11 10 00 1 1
1 0 0 D1
01
Ø
11 1 1 1
10 Ø
A1A0 A2 00 01 11 10
组合逻辑电路习题
一、组合逻辑电路的基本概念 二、SSI构成的组合逻辑电路的分析和设计 三、MSI组合逻辑电路的工作原理及应用 四、组合逻辑电路中的竞争和冒险 五、习题讲解
D1 = D2 = D, D4 = D5 = D6 = D7 = 0
2020年3月25日星期三
第四章 组合逻辑电路习题
节目录
23
相应的电路图如下所示：
EN
C
A0
B
A1
C
A
A2
D
D0
D
D1 D2
7 41 5 1
Y
F
D3
D4
D5
D6 D7
2020年3月25日星期三
第四章 组合逻辑电路习题
2020年3月25日星期三
第四章 组合逻辑电路习题
节目录
32
增加冗余项后，相应逻辑电路中应增加一个与 非门，其与非表达式为：
F (A,B,C,D) = ABC ·ACD ·ABC ·A CD ·BD
2020年3月25日星期三
第四章 组合逻辑电路习题
节目录
33
CD
AB
00 01 11 10
00
1
01
节目录
24
(4) 函数有4个输入变量 ，而74151的地址端只有
3个，即A2 、A1 、A0 ，故须对函数的卡诺图进
行降维，即降为3 维。 BC
CD
A 00 01 11 10 0 DD00
AB 00 01 11 10 00 1 1
1 0 0 D1
01
Ø
11 1 1 1
10 Ø
A1A0 A2 00 01 11 10
组合逻辑电路习题
一、组合逻辑电路的基本概念 二、SSI构成的组合逻辑电路的分析和设计 三、MSI组合逻辑电路的工作原理及应用 四、组合逻辑电路中的竞争和冒险 五、习题讲解
南京邮电大学 数字电路 第一章-习题
数字电路与系统 第一章习题
节目录
21
数字电路与系统 第一章习题
节目录
10
1.10 已知A=(1011010)2，B=(101111)2，C=(1010100)2，D=(110)2 (1) 按二进制算术运算规律求A+B，A-B，C×D，C÷D;
(2)将A、B、C、D转换成十进制数后，求A+B，A-B，C×D
，C÷D，并将结果与(1)进行比较。 解：(1) A+B = (10001001)2 = (137)10 C×D = (111111000)2 = (504)10 (2) A+B=(90)10+(47)10=(137)10 C×D = (84)10× (6)10 = (504)10 C÷D = (84)10÷ (6)10 = (14)10 两种算法结果相同。 A-B = (101011)2 = (43)10 C÷D = (1110)2 = (14)10 A-B=(90)10-(47)10=(43)10
正”[即减(0011)2]。
2013年9月23日星期一
数字电路与系统 第一章习题
节目录
19
(3) 8+8：
1011 ﹢ 1011 ﹢ 1 0110 0011 0011 0100 1001
所以，8+8 = (0100 1001)余3BCD = 16
相加过程中，产生向高位的进位时，应对产生进 位的代码进行“加33修正”[即加(0011 0011)2]。
(1011.01)2=(11.25)10=(0001 0001.0010 0101)8421BCD
(2) 余3 BCD码：
(123)10 =(0100 0101 0110)余3BCD
南邮数电第3章-(3)PPT课件
在多路数据传送过程中能够根据需要将其中任意一路挑选出来的电路叫做数据选择器也称为多路选择器其作用相当于多路开常见的数据选择器有四选一八选一十六选一电路
3.2.3 数据选择器
在多路数据传送过程中，能够根据需要将 其中任意一路挑选出来的电路，叫做数据选择 器，也称为多路选择器,其作用相当于多路开关。
常见的数据选择器有四选一、八选一、十 六选一电路。
0
01 0 0
1
00 1 0
0
10 0 1
0
01 1 0
1
10 0 1
0
10 0 1
1
00 0 0
1
10 0 1
38
数据比较器的扩展 (1) 串联方式
A0
A0
A1
A 1 7485
A2
A2
F A>B
A3
A3
0
(A>B) i
1
(A=B) i F A=B
0
(A<B) i
B0
B0
B1
B1
F A<B
B2
B2
则可实现三变量多数表决电路，具体电路图 请行画出。
22
例 ：用74151设计函数 F = AB + AC 。
A1A0 A2 00 01 11 10
0 D0 D1 D3 D2
BC A 00 01 11 10
0 0 0 00
1 D4 D5 D7 D6
1 1 0 11
Y
F
比较两卡诺图，若A、B、C分别接A2、A1、A0， 再令D0 =D1= D2 = D3 = D5 ，D4 =D6 =D7 =1，则
① 八选一MUX简化符 ② 八选一MUX的功能表 ③ 八选一MUX的卡诺图 ④ 八选一MUX的逻辑表达式
3.2.3 数据选择器
在多路数据传送过程中，能够根据需要将 其中任意一路挑选出来的电路，叫做数据选择 器，也称为多路选择器,其作用相当于多路开关。
常见的数据选择器有四选一、八选一、十 六选一电路。
0
01 0 0
1
00 1 0
0
10 0 1
0
01 1 0
1
10 0 1
0
10 0 1
1
00 0 0
1
10 0 1
38
数据比较器的扩展 (1) 串联方式
A0
A0
A1
A 1 7485
A2
A2
F A>B
A3
A3
0
(A>B) i
1
(A=B) i F A=B
0
(A<B) i
B0
B0
B1
B1
F A<B
B2
B2
则可实现三变量多数表决电路，具体电路图 请行画出。
22
例 ：用74151设计函数 F = AB + AC 。
A1A0 A2 00 01 11 10
0 D0 D1 D3 D2
BC A 00 01 11 10
0 0 0 00
1 D4 D5 D7 D6
1 1 0 11
Y
F
比较两卡诺图，若A、B、C分别接A2、A1、A0， 再令D0 =D1= D2 = D3 = D5 ，D4 =D6 =D7 =1，则
① 八选一MUX简化符 ② 八选一MUX的功能表 ③ 八选一MUX的卡诺图 ④ 八选一MUX的逻辑表达式
南京邮电大学--编译原理-课后习题答案和讲解PPT课件
Байду номын сангаас
⑥（－，③，⑤）
（2）四元式：
①（＋，a，b，T1）
②（－，a，b，T2）
③（/，T1，T2，T3）
④（*，b，c，T4）
⑤（＋，a，T4，T5）
2021/3/9
⑥（－，T3，T5授，课：TX6X）X
9
刚才的发言，如 有不当之处请多指
正。谢谢大家！
2021/3/9
10
xxx6语法制导翻译是在文法规则中再配上语义动作翻译成后缀表达式并填入到post数组中假设数组元素下标从0开始
1、Chomsky 定义的四种形式语言文法中， 0 型文法又称为（ ）文法； A. 短语结构文法 B. 前后文无关文法 C. 前后文有关文法 D. 正规文法
2、文法：G：S→xSx | y所识别的语言是（ ）。
授课：XXX
1
5、对文法规则Z::=AB|AC|A用扩充的BNF可表示为 Z::=A（B|C|ε）（或是Z::=A[B|C]）
6、语法制导翻译是在文法规则中再配上（ 语义动作 ）。
7、将 if a-b then c:=1 else d:=2 翻译成后缀表达式并填入到POST数组中， 假设数组元素下标从0开始。
2
已知文法G[S]: S->(AS)|(b) A->(SaA)|(a) 试分析句型(A((SaA)(b)))的短语、简单短语、句柄、最左素短语
2021/3/9
授课：XXX
3
画出正规式 (b*abb*)* 对应的DFA状态转换图，并化简
2021/3/9
授课：XXX
4
2021/3/9
授课：XXX
5
试利用算符优先关系，分析句子(a,(a,a))
⑥（－，③，⑤）
（2）四元式：
①（＋，a，b，T1）
②（－，a，b，T2）
③（/，T1，T2，T3）
④（*，b，c，T4）
⑤（＋，a，T4，T5）
2021/3/9
⑥（－，T3，T5授，课：TX6X）X
9
刚才的发言，如 有不当之处请多指
正。谢谢大家！
2021/3/9
10
xxx6语法制导翻译是在文法规则中再配上语义动作翻译成后缀表达式并填入到post数组中假设数组元素下标从0开始
1、Chomsky 定义的四种形式语言文法中， 0 型文法又称为（ ）文法； A. 短语结构文法 B. 前后文无关文法 C. 前后文有关文法 D. 正规文法
2、文法：G：S→xSx | y所识别的语言是（ ）。
授课：XXX
1
5、对文法规则Z::=AB|AC|A用扩充的BNF可表示为 Z::=A（B|C|ε）（或是Z::=A[B|C]）
6、语法制导翻译是在文法规则中再配上（ 语义动作 ）。
7、将 if a-b then c:=1 else d:=2 翻译成后缀表达式并填入到POST数组中， 假设数组元素下标从0开始。
2
已知文法G[S]: S->(AS)|(b) A->(SaA)|(a) 试分析句型(A((SaA)(b)))的短语、简单短语、句柄、最左素短语
2021/3/9
授课：XXX
3
画出正规式 (b*abb*)* 对应的DFA状态转换图，并化简
2021/3/9
授课：XXX
4
2021/3/9
授课：XXX
5
试利用算符优先关系，分析句子(a,(a,a))
南京邮电大学数字电路第二章-习题
第 2章
2.1 (1) (2) (3) 2.4 (1) (2) (3) 2.10 (1) (2)
习题
Evaluation only. 2.11 (1) (2) eated with Aspose.Slides for .NET 3.5 Client Profile 5.2.0 2.12 Copyright (1) (3) (4) 2004-2011 Aspose Pty Ltd.
m(4,11,12,15)
2019年2月6日星期三
数字电路与系统 第二章习题
节目录
7
2.11 试用公式法把下列各表达式 化简为最简与或式。
(1) F A ABC ABC BC B (2) F ( A B)( A B C )( A C )( B C D)
CD AB 00 01 11 10
00 1 1 Ø 01 1 Ø 1 only. Evaluation
eated with Aspose.Slides 3.5 Client Profile 5.2.0 11 Ø for 1 .NET Ø Copyright 10 2004-2011 Aspose Pty Ltd. Ø 1 1
(3) F ( A, B, C ) A B C AB C
Evaluation only. (1) F ( A, B, C, D, E) for [( A .NET B) C D ] E B eated解： with Aspose.Slides 3.5 Client Profile 5.2.0 Copyright Aspose Pty Ltd. ( A, B, C, D2004-2011 F , E) [( A B ) C D] E B
2.1 (1) (2) (3) 2.4 (1) (2) (3) 2.10 (1) (2)
习题
Evaluation only. 2.11 (1) (2) eated with Aspose.Slides for .NET 3.5 Client Profile 5.2.0 2.12 Copyright (1) (3) (4) 2004-2011 Aspose Pty Ltd.
m(4,11,12,15)
2019年2月6日星期三
数字电路与系统 第二章习题
节目录
7
2.11 试用公式法把下列各表达式 化简为最简与或式。
(1) F A ABC ABC BC B (2) F ( A B)( A B C )( A C )( B C D)
CD AB 00 01 11 10
00 1 1 Ø 01 1 Ø 1 only. Evaluation
eated with Aspose.Slides 3.5 Client Profile 5.2.0 11 Ø for 1 .NET Ø Copyright 10 2004-2011 Aspose Pty Ltd. Ø 1 1
(3) F ( A, B, C ) A B C AB C
Evaluation only. (1) F ( A, B, C, D, E) for [( A .NET B) C D ] E B eated解： with Aspose.Slides 3.5 Client Profile 5.2.0 Copyright Aspose Pty Ltd. ( A, B, C, D2004-2011 F , E) [( A B ) C D] E B
南京邮电大学 电路分析基础 课后习题解答 第1---5章 沈元隆
现方式做保护处理对用户上传分享的文档内容本身不做任何修改或编辑并不能对任何下载内容负责
1－1 若流经电路某点的电流i(t)=4e-4tA,t0;(t<0时， i(t)=0)。试求电荷q(t)的表达式。并求t=0.25s时流 经该点的总电荷。 解：
q(t ) i ( )d i ( )d 0 i ( )d
故
4）因为电压、电流为非关联参考
2mA + D 10mV -
ic 1A
3 3
p 10 10 2 10 2 10 5 W
5）因为电压、电流为关联参考，且元件吸收功率为-10w
ie E 10V +
p 10 w 10 ie
故
ie 1A
6）因为电压、电流为非关联参考，且元件吸收功率为10w
p产生＝－p吸收 4mW
1-6 网络A、B由两根导线相连，如图1－6所示，试问i1与i2有何 关系？若电流i1所在支路断开，则i2 支路中有无电流？
i1 A i2 B
解：作题图1－6电路的封闭曲面如图所示， 则有广义KCL 得 i1=i2 即i1与i2大小相等方向相反。显然，若i1 所在支路断开即i1=0，有KCL得i2支路 中电流也为0。
所以戴维南等效电路如图b-3所示
+
-
-8 / 15 Ω
+a
-4/15V -b
b-3
2－27试求题图2－27电路中的电流I2。
I1 2 Ω 2I1 1 I + 2 Ω U2 5 Ω + 2U2
解：列图示回路KVL方程，有
+ 12V -
4 Ω
2 I1 I 3 1 5 I 2 2U 2 12 0
1－1 若流经电路某点的电流i(t)=4e-4tA,t0;(t<0时， i(t)=0)。试求电荷q(t)的表达式。并求t=0.25s时流 经该点的总电荷。 解：
q(t ) i ( )d i ( )d 0 i ( )d
故
4）因为电压、电流为非关联参考
2mA + D 10mV -
ic 1A
3 3
p 10 10 2 10 2 10 5 W
5）因为电压、电流为关联参考，且元件吸收功率为-10w
ie E 10V +
p 10 w 10 ie
故
ie 1A
6）因为电压、电流为非关联参考，且元件吸收功率为10w
p产生＝－p吸收 4mW
1-6 网络A、B由两根导线相连，如图1－6所示，试问i1与i2有何 关系？若电流i1所在支路断开，则i2 支路中有无电流？
i1 A i2 B
解：作题图1－6电路的封闭曲面如图所示， 则有广义KCL 得 i1=i2 即i1与i2大小相等方向相反。显然，若i1 所在支路断开即i1=0，有KCL得i2支路 中电流也为0。
所以戴维南等效电路如图b-3所示
+
-
-8 / 15 Ω
+a
-4/15V -b
b-3
2－27试求题图2－27电路中的电流I2。
I1 2 Ω 2I1 1 I + 2 Ω U2 5 Ω + 2U2
解：列图示回路KVL方程，有
+ 12V -
4 Ω
2 I1 I 3 1 5 I 2 2U 2 12 0
南邮数电-第6章 时序逻辑电路(5)53页PPT
解：7490为异步复0方式，起跳状态为S6， 即：(0110)8421BCD。电路图如下所示：
Q 3 Q 2 Q 1 Q 0 CP 1
7 49 0
R 01 R 02 S 91 S 92 CP 0
CP
图6.5.14 (b)异步复0法
06.01.2020
第六章 时序逻辑电路
14
例3 试用74163用复0法设计M=6的计数器。 解：74163为同步复0方式，起跳状态为S5，
06.01.2020
第六章 时序逻辑电路
8
表6.5.10 图6.5.14(a)电路的状态转移表
Q3 Q2 Q1 000 000 001 001 010 010 0 1/0 1/0
Q0 状态转移路线 0
1
0
1
0
1
0
起跳状态
06.01.2020
第六章 时序逻辑电路
9
1 23 4 56 CP Q0 Q1 Q2 Q3 CR 图6.5.15 图6.5.14(a)电路的工作波形图
即：(0101)2。电路图如下所示：
&
Q CC Q 3 Q 2
Q1 Q0 P
1
CR
7 41 63
T
1
1
LD D3 D2
D 1 D 0 CP
CP
图6.5.14 (c)同步复0法
06.01.2020
第六章 时序逻辑电路
15
(2)置数法（利用置数控制端，并行输入端）
S预 S预+1
S预+(M-1)
S预＋M
①置最小数法
SN-M
SN-(M-1)
SN-2
SN-1
同步置数
06.01.2020
Q 3 Q 2 Q 1 Q 0 CP 1
7 49 0
R 01 R 02 S 91 S 92 CP 0
CP
图6.5.14 (b)异步复0法
06.01.2020
第六章 时序逻辑电路
14
例3 试用74163用复0法设计M=6的计数器。 解：74163为同步复0方式，起跳状态为S5，
06.01.2020
第六章 时序逻辑电路
8
表6.5.10 图6.5.14(a)电路的状态转移表
Q3 Q2 Q1 000 000 001 001 010 010 0 1/0 1/0
Q0 状态转移路线 0
1
0
1
0
1
0
起跳状态
06.01.2020
第六章 时序逻辑电路
9
1 23 4 56 CP Q0 Q1 Q2 Q3 CR 图6.5.15 图6.5.14(a)电路的工作波形图
即：(0101)2。电路图如下所示：
&
Q CC Q 3 Q 2
Q1 Q0 P
1
CR
7 41 63
T
1
1
LD D3 D2
D 1 D 0 CP
CP
图6.5.14 (c)同步复0法
06.01.2020
第六章 时序逻辑电路
15
(2)置数法（利用置数控制端，并行输入端）
S预 S预+1
S预+(M-1)
S预＋M
①置最小数法
SN-M
SN-(M-1)
SN-2
SN-1
同步置数
06.01.2020
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019年3月20日星期三
数字电路与系统 第二章习题
节目录
5
2.10试写出下列各函数表达式F的F和F′的最小项 表达式。
(1) F ABCD ACD BC D (2) F AB A B BC
2019年3月20日星期三
数字电路与系统 第二章习题
节目录
6
解： (1) F ( A, B, C, D) ABCD ACD BC D
m(4,11,12,15)
F ( A, B, C ) m(1,6,7)
F ( A, B, C ) m(0,1,6)
2019年3月20日星期三
数字电路与系统 第二章习题
节目录
7
2.11 试用公式法把下列各表达式 化简为最简与或式。
(1) F A ABC ABC BC B (2) F ( A B)( A B C )( A C )( B C D)
( A B)( A C )
AC A B BC
AC A B
2019年3月20日星期三
数字电路与系统第二章习题
节目录
9
2.12 用卡诺图法把下列函数 化简为最简与或式。 (1) F ( A, B, C ) m(0,1,2,4,5,7)
(3) F ( A, B, C , D) m(0,1,4,7,9,10,13) (2,5,8,12,15)
2019年3月20日星期三
数字电路与系统 第二章习题
节目录
3
2.4试直接写出下列各式的反演式和对偶式。
(1) F ( A, B, C, D, E) [(AB C) D E] B
(2) F ( A, B, C , D, E ) AB C D BC D C E B E
C 0 1 0 1 0 1 0 1
F1 F2 1 1 1 0 1 0 0 1 1 0 0 1 0 1 0 0
F3 0 0 0 1 0 1 1 1
F2 ( A, B, C) m(0,3,5,6) F3 ( A, B, C) m(3,5,6,7)
F1 ( A, B, C) m(0,1,2,4)
(4)F ( A, B, C , D ) m(7,13,15), 且 A B C 0, A BC 0, A B C 0
解： (1) F ( A, B, C ) m(0,1,2,4,5,7)
BC A
0
00 01 11 10
1 1 0 1
F ( A, B, C )
1
1
1
1
0
B AC A C
(3) F ( A, B, C ) A B C
AB C
解： (1) F ( A, B, C, D, E) [( A B) C D ] E B
F ( A, B, C, D, E) [( A B ) C D] E B
(2) F ( A, B, C , D, E ) ( A B )( C D) ( B C ) D(C E ) B E
解： (1) F A ABC ABC BC B
A A( BC BC ) B
A B (2) F ( A B)( A B C )( A C )( B C D) F AB ABC A C BCD AB A C BCD AB A C
F ( A, B, C, D, E) ( A B)(C D ) ( B C ) D (C E) B E
2019年3月20日星期三 数字电路与系统 第二章习题
节目录
4
(3) F ( A, B, C ) A B C
AB C
F ( A, B, C ) ( A B)C A B C F ( A, B, C ) ( A B )C A B C
(2)若A、B、C中出现奇数个0时输出为1，其余 情况下输出为0。 (3)若A、B、C中有两个或两个以上为1时，输出 为1，其余情况下输出为0。
2019年3月20日星期三
数字电路与系统 第二章习题
节目录
2
解：真值表和最小项表达式如下：
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
2019年3月20日星期三 数字电路与系统 第二章习题
节目录
8
F ( F ) ( A B)( A C )
AC A B BC AC A B
(2) F ( A B)( A B C )( A C )( B C D) ( A B)( A C )( B C D)
数电第2章习题
2.1 (1) (2) (3) 2.4 (1) (2) (3) 2.10 (1) (2) 2.11 (1) (2) 2.12 (1) (3) (4) 2.13 (1) 2.14
2019年3月20日星期三
数字电路与系统 第二章习题
节目录
1
2.1有A、B、C三个输入信号，试列出下列问题的 真值表，并写出其最小项表达式m()。 (1)如果A、B、C均为0或其中一个信号为1时， 输出F=1，其余情况下F=0。
F ( A, B, C , D) m(1,2,5,6,7,8,9,10,12,13,14,15)
(2) F ( A, B, C ) AB A B BC m(2,3,4,5,7)
F ( A, B, C , D) m(0,1,2,3,5,6,7,8,9,10,13,14)
2019年3月20日星期三
数字电路与系统 第二章习题
节目录
10
(3) F ( A, B, C , D) m(0,1,4,7,9,10,13) (2,5,8,12,15)
CD AB 00 01 11 10
00 1 11 Ø 10 Ø 1 Ø 01 1 Ø 1 1 Ø 1 1
F ( A, B, C ) C BD B D