最新ansys 优化设计(含几个实例)资料
ANSYS高级分析-优化设计(一)

ANSYS高级分析-优化设计(一)本篇作为ANSYS最常用也是最有用的高级分析技术优化设计技术的开篇,主要从概念上讲述ANSYS优化设计以及在进行ANSYS优化设计分析时通用的基本步骤和考虑方法(本篇所讲述优化分析同样是基于APDL工具,其它优化设计技术具体实现过程随着对优化设计的逐渐深入会逐步描述)。
1 前言优化设计是一种寻找确定最优设计方案的技术。
所谓“最优设计”,指的是一种方案可以满足所有的设计要求,而且所需的支出(如重量,面积,体积,应力,费用等)最小。
也就是说,最优设计方案就是一个最有效率的方案。
设计方案的任何方面都是可以优化的,比如说:尺寸(如厚度),形状(如过渡圆角的大小),支撑位置,制造费用,自然频率,材料特性等。
实际上,因为ANSYS具有专业的和强大的分析能力,具有开放的使用环境,所以所有可以参数化的ANSYS选项都可以作优化设计。
ANSYS参数化设计语言APDL用建立智能分析的手段为用户提供了自动循环的功能,也就是说,程序的输入可设定为根据指定的函数、变量以及选出的分析标准决定输入的形式。
APDL允许复杂的数据输入,使用户实际上对任何设计或分析有控制权。
例如尺寸、材料、载荷、约束位置和网格密度等。
APDL扩展了传统有限元分析之外的能力,并扩展了更高级运算,包括灵敏度研究、零件库参数化建模,设计修改和设计优化。
APDL是一种为ANSYS 二次开发专门设计开发的解释性文本语言,其内容包括参数、数组参数、表达式和函数、分支和循环、重复功能和缩写以及宏和用户程序等。
2 优化设计步骤基于APDL的参数化设计的方法采用ANSYS的批处理方法进行优化的,其主要的优化设计过程通常包括以下几个步骤,这些步骤根据用户所选用优化方法的不同(批处理GUI 方式)而有细微的差别。
生成分析文件:生成分析文件与通常的ANSYS分析并没有很大的不同,唯一的区别就是:优化的分析文件必须是参数化的。
也就是说,必须定义一些参量,至少要把所有的设计变量,状态变量和目标变量定义为参量形式。
ANSYS案例——20例ANSYS经典实例】
→ OK ( 返回到 Plot Results)
(10) 退出系统
ANSYS Utility Menu: File→ Exit … → Save Everything→ OK
工作文件名 ) : beam3→ Run → OK
(2) 设置计算类型 ANSYS Main Menu: Preferences …→ Structural → OK
(3) 选择单元类型 ANSYS Main Menu: Preprocessor → Element Type → Add/Edit/Delete
(7) 模型施加约束和外载 左边加 X 方向的受力 ANSYS Main Menu: Solution → Define Loads → Apply → Structural → Force/Moment → On
Nodes → 选择节点 1→ apply →Direction of force: FX → VALUE : 3000 → OK →
上,完成相应的力学分析。
3-20 。在 ANSYS 平台
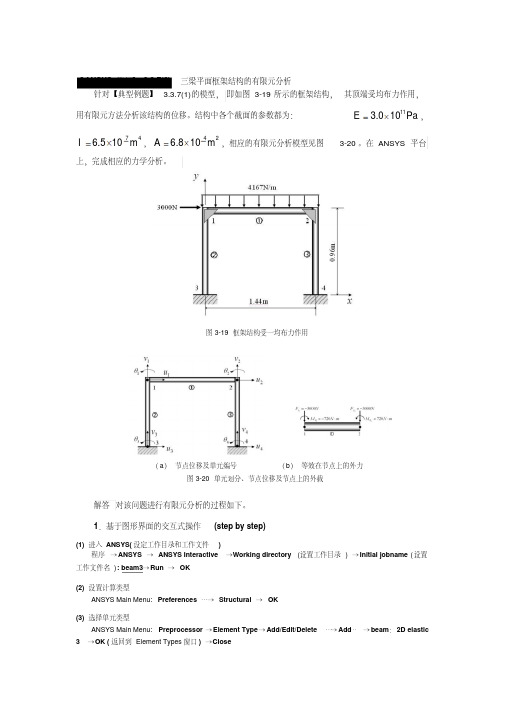
图 3-19 框架结构受一均布力作用
( a) 节点位移及单元编号
(b) 等效在节点上的外力
图 3-20 单元划分、节点位移及节点上的外载
形界面的交互式操作 (step by step)
(1) 进入 ANSYS( 设定工作目录和工作文件 ) 程序 → ANSYS → ANSYS Interactive →Working directory (设置工作目录 ) → Initial jobname ( 设置
ANSYS案例——20例ANSYS经典实例】

ANSYS案例——20例ANSYS经典实例】针对【典型例题】3.3.7(1)的模型,即如图3-19所示的框架结构,其顶端受均布力作用,用有限元方法分析该结构的位移。
结构中各个截面的参数都为:113.010PaE=,746.510mI-=,426.810mA-=,相应的有限元分析模型见图3-20。
在ANSYS平台上,完成相应的力学分析。
图3-19框架结构受一均布力作用图3-20单元划分、节点位移及节点上的外载解答对该问题进行有限元分析的过程如下。
1.基于图形界面的交互式操作(tepbytep)(1)进入ANSYS(设定工作目录和工作文件)程序→ANSYS→ANSYSInteractive→Workingdirectory(设置工作目录)→Initialjobname(设置工作文件名):beam3→Run→OK(2)设置计算类型(3)选择单元类型(4)定义材料参数ANSYSMainMenu:Preproceor→MaterialProp→MaterialModel→Struc tural→Linear→Elatic→Iotropic:E某:3e11(弹性模量)→OK→鼠标点击该窗口右上角的“”来关闭该窗口(5)定义实常数以确定平面问题的厚度ANSYSMainMenu:Preproceor→RealContant…→Add/Edit/Delete→Add→Type1Beam3→OK→RealContantSetNo:1(第1号实常数),Cro-ectionalarea:6.8e-4(梁的横截面积)→OK→Cloe(6)生成几何模型生成节点ANSYSMainMenu:Preproceor→Modeling→Creat→Node→InActiveCS→Nodenumber1→某:0,Y:0.96,Z:0→Apply→Nodenumber2→某:1.44,Y:0.96,Z:0→Apply→Nodenumber3→某:0,Y:0,Z:0→Apply→Nodenumber4→某:1.44,Y:0,Z:0→OK生成单元ANSYSMainMenu:Preproceor→Modeling→Create→Element→AutoNum bered→ThruNode→选择节点1,2(生成单元1)→apply→选择节点1,3(生成单元2)→apply→选择节点2,4(生成单元3)→OK(7)模型施加约束和外载左边加某方向的受力ANSYSMainMenu:Solution→DefineLoad→Apply→Structural→Force/Moment→OnNode→选择节点1→apply→Directionofforce:F某→VALUE:3000→OK→上方施加Y方向的均布载荷ANSYSMainMenu:Solution→DefineLoad→Apply→Structural→Preure→OnBeam→选取单元1(节点1和节点2之间)→apply→VALI:4167→VALJ:4167→OK左、右下角节点加约束(8)分析计算(9)结果显示(10)退出系统(11)计算结果的验证与MATLAB支反力计算结果一致。
运用ANSYSWorkbench快速优化设计

运用ANSYS Workbench快速优化设计SolidWorks是一个优秀的、应用广泛的3D设计软件,尤其在大装配体方面使用了独特的技术来优化系统性能。
本文给出几种改善SolidWorks装配体性能的方法,在相同的系统条件下,能够进步软件的可操纵性,进而进步设计效率。
众所周知,大多数3D设计软件在使用过程中都会出现这样的情况,随着装配零件数目和复杂度增加,软件对系统资源的需求就相对增加,系统的可操纵性就会下降。
造成这种状况的原因有两种:一是计算机系统硬件配置不足,二是没有公道使用装配技术。
本文对这两种情况进行分析并提出相应的解决方案。
一、计算机系统配置不足的解决方案SolidWorks使用过程中,计算机硬件配置不足是导致系统性能下降的直接原因,其中CPU、内存、显卡的影响最大。
假如计算机系统内存不足,Windows就自动启用虚拟内存,由于虚拟内?*挥谟才蹋?斐上低衬诖嬗胗才唐捣苯换皇?荩?贾孪低承阅芗本缦陆担籆 PU性能过低时,延长运算时间,导致系统响应时间过长;显卡性能不佳时引起视图更新慢,移动模型时出现停顿现象,并导致CPU占用率增加。
运行SolidWorks的计算机推荐以下配置方案:CPU:奔腾Ⅱ以上内存:小零件或装配体(少于300个特征或少于1000个零件),内存最少为512M;大零件或装配体(大于1000个特征或2500个零件),内存需要1G或更多;虚拟内存一般设为物理内存的2倍。
显卡:支持OpenGL的独立显卡(避免采用集成显卡),显存最好大于64M。
对于现有的计算机,使用以下方法分析系统瓶颈,有针对性地升级计算机。
(1)在SolidWorks使用过程中启动Windows任务治理器,在性能页,假如CPU的占用率经常在100%,那么系统瓶颈就在CPU或显卡,建议升级CPU或显卡;假如系统内存大部分被占用,虚拟内存使用量又很大,操纵过程中硬盘灯频繁闪烁,这说明系统瓶颈在内存,建议扩大内存。
ansysworkbench优化实例

作业1实验设计Design ExplorationTraining Manual 1•Goal目标–演示Design ExplorationDesign Exploration中进行DOE分析的流程,并且建立响应图;–边界条件如图所示Design Modeler ds_cutout–在Design Modeler中建立模型输入参数:ds_cutout –从中得到的几何参数Bearing load(轴承载荷)输出参数:Mass(质量)Equivalent stress(等效应力)Total deformation(整体变形)Training Manual12Parameter Set 检查所有1. File>Open>Link1.dsdb1. 双击Parameter Set ,检查所有输入和输出参数。
2输入参数输出参数3. 返回到项目中31Training Manual4. 双击“Response Surface”启动DOE分析45. 双击DOEDOE 大纲给出了输入和输出DOE参数51Training Manual6. 在Outline of Design of Experiments中点击选择参数67. 在特性中定义设计变量的类型和上下限。
Ds-cutout,4.5-5-5.5上的连续变量。
78. Bearing load(负载),9-10-1111 上的连续变量8Training Manual19. 选择DOE –默认的DOE 类型是中心组合设计(Central Composite Design )910. 查看和更新设计点1011. 点击Show Progress 展开状态栏11Training Manual1DOE 的表中的给出了9个设计点131312. 选择显示整体变形对应设计点的关系曲线12. 点击Design Points vs Parameter1Training Manual1414. 返回到项目页(ProjectPage)15. 双击ResponseSurface1516. 更新ResponseSurface17. 双击Response17 16Training Manual118. 选择二维模式,如图设置X ,Y 轴1819.选择三维模式,如图设置X ,Y 和Z 轴191Training Manual 20. 点击spider 和local sensitivities 显示图表20Training Manual121. 在响应面上点击鼠标右键选择Insert as Response Point ,将其插入到响应点22. 在需要的响应点上点击鼠标右键选择Insert as Design Point ,将其插入到设计点21其插到设计点22响应点不能和此处给出的一样!Training Manual123. 返回到Project Page2324. 双击Parameter set25. 更新所有设计点242526. 在DP1上点击鼠标右键选择Copy inputs to current 和Updated selected Design Point回到2627. 返回到Project Page271Training Manual28. 双击Solution28检查力学结果作业2What if分析多目标优化设计Training Manual•Goal (目标)–使用参数管理器探索如图所示结构的应力、质量和变形行为因为在垂直载荷的作用下几何参数是在发形行为,因为在垂直载荷的作用下,几何参数是在发生变化的。
ANSYS优化设计

1优化设计什么是优化设计?优化设计是一种寻觅确信最优设计方案的技术。
所谓“最优设计”,指的是一种方案能够知足所有的设计要求,而且所需的支出(如重量,面积,体积,应力,费用等)最小。
也确实是说,最优设计方案确实是一个最有效率的方案。
设计方案的任何方面都是能够优化的,比如说:尺寸(如厚度),形状(如过渡圆角的大小),支撑位置,制造费用,自然频率,材料特性等。
事实上,所有能够参数化的ANSYS选项都能够作优化设计。
(关于ANSYS参数,请参看ANSYS Modeling and Meshing Guide 第十四章。
)ANSYS程序提供了两种优化的方式,这两种方式能够处置绝大多数的优化问题。
零阶方式是一个很完善的处置方式,能够很有效地处置大多数的工程问题。
一阶方式基于目标函数对设计变量的灵敏程度,因此加倍适合于精准的优化分析。
关于这两种方式,ANSYS程序提供了一系列的分析——评估——修正的循环进程。
确实是关于初始设计进行分析,对分析结果就设计要求进行评估,然后修正设计。
这一循环进程重复进行直到所有的设计要求都知足为止。
除这两种优化方式,ANSYS程序还提供了一系列的优化工具以提高优化进程的效率。
例如,随机优化分析的迭代次数是能够指定的。
随机计算结果的初始值能够作为优化进程的起点数值。
大体概念在介绍优化设计进程之前,咱们先给出一些大体的概念:设计变量,状态变量,目标函数,合理和不合理的设计,分析文件,迭代,循环,设计序列等。
咱们看以下一个典型的优化设计问题:在以下的约束条件下找出如下矩形截面梁的最小重量:总应力不超过max [max]梁的变形不超过max [max]梁的高度h不超过hmax [h hmax]图1-1 梁的优化设计例如设计变量(DVs)为自变量,优化结果的取得确实是通过改变设计变量的数值来实现的。
每一个设计变量都有上下限,它概念了设计变量的转变范围。
在以上的问题里,设计变量很显然为梁的宽度b和高度h。
ansys优化方法简介以及实例

拓扑优化理论及在ANSYS软件中的实现一.拓扑优化概论:连续体结构的拓扑优化设计是继结构的尺寸优化设计和形状优化设计之后,在结构优化领域出现的一种富有挑战性的研究方向,它是一种比尺寸优化和形状优化更高层次的优化方法,也是结构优化问题中最为复杂的一类问题。
拓扑优化处于结构的概念设计阶段,其优化结果是一切后续设计的基础。
因而在初始设计阶段需要确定结构的最佳拓扑形式。
拓扑优化的目的是寻求结构的刚度在设计空间最佳的分布形式,或在设计域空间需求结构最佳的传力路线,以优化结构的某些性能或减轻结构的重量。
目前对于拓扑优化的研究主要集中在以下几个方面:结构拓扑描述方式和材料插值模型;拓扑优化中结构拓扑描述方式和材料的插值模型非常重要,是一切后续拓扑优化工作的基础。
常用的拓扑描述方式和材料插值模型有均匀化方法、密度法、变厚度法和拓扑函数描述法等。
拓扑优化求解数值算法,新型优化算法在拓扑优化中的应用;拓扑优化的数值计算方法主要包括有限元法和无网格法,基于成熟的有限元理论的拓扑优化格式简单,便于实现,但在优化过程中常因网格的重分和细化导致计算困难,结构中常出现中间密度材料、棋盘格现象和网格依赖性等问题。
无网格法是今年发展的一种新型数值求解技术,摆脱了有限元繁琐的网格生成过程,从理论上看比有限元法拥有更广阔的应用前景,但目前尚处于发展和完善中。
拓扑优化的特点是:设计变量多,计算规模大,目标函数和约束函数一般为设计变量的非线性、非单调函数。
目前应用于连续体结构拓扑优化计算的优化算法主要包括两类:优化准则法和序列凸规划法。
去除优化过程中数值计算不稳定的方法,优化结果的提取和重构;拓扑优化中经常出现的数值计算问题有:多孔材料、棋盘格现象、网格依赖性和局部极值问题。
优化结果的提取和应用主要考虑的是如何将优化的结果转化为可用的CAD模型问题,实现CAE和CAD之间的数据共享和交流。
随着拓扑优化理论研究的不断深入,拓扑优化在航空和汽车领域已开始得到初步的应用,主要是通过拓扑优化获得结构的最初拓扑形式,并在最初拓扑形式的基础上进行相关的后续优化设计。
ANSYS优化设计

x1 x2 X= . =[x1,x2…x3] T : xn
(7-1)
式(7-1)的意义在于表示了“设计空间”的概念,即以n个设计变量 为坐标轴组成的实空间。这个设计空间成为n纬欧氏空间,用Rn表 示。
2001年6月1日 7-3
当n=2,如例7-2中悬臂梁,则有: x1 d X= = x2 l 此时,设计空间是以x1,x2为坐标轴的平面,平面上任一点的 坐标对应着一个二维设计变量。 X=[x1x2]T代表了一个设计方案。 当n=3时,例如7-1中贮料箱,由三个设计变量组成一个3维设计空 间,空间内任一点的坐标对应着一个三维设计变量X=[x1x2x3]T。同 样,向量X代表了一个设计方案。 依此类推,当n>3时,其n个设计变量x1,x2,…xn组成的空间成为超 越空间。 设计空间是所有设计方案的集合,表示为: XRn
(7-2)
2001年6月1日
7-4
2.目标函数
优化设计是要在多种因素下寻求使人最满意、最 适宜的一组参数。这里的“最满意”是针对某一特定 目标而言的。根据特定目标建立起来的、以设计变量 为自变量的、一个可计算的函数称为目标函数,它是 设计方案评价的标准。 优化设计的过程实际上是寻求目标函数最小值或 最大值的过程。因为求目标函数的最大值可转换为求 负的最小值,故目标函数统一描述为: minF (X)=F (x1,x2,…xn) (7-3)
2001年6月1日
7-9
(2)性能约束 又称性态约束,是由某种设计性能或指标推导出来的一种约 束条件。属于这类设计约束的如零件的工作应力、应变的限制; 对震动频率、震幅的限制;对传动效率、温升、噪声、输出扭矩 波动最大值等的限制;对运动学参数如位移、速度、转速、加速 度的限制等。这类约束条件,一般可以根据设计规范中的设计公 式或通过物理学和力学的基本分析导出的约束函数来表示。如例 7-2中,悬臂梁设计弯曲强度条件Pl/(0.1d3 )<=[б ],扭转强度条件 M/(0.2d³ )<=[τ ] ,刚度条件Pl3 /(3EJ)<=[ƒ]。已知 [б ] = 100N/mm2 ,[τ ] =75/Nmm2 ,[ƒ]=0.1mm,E=7.03*104 N/mm², 可导出性能约束条件为: g5 (X) =g5 (d, l) = (d3/l) -1000>=0 g6 (X) =g6 (d, l) = d3 -6666.6>=0 g7(X) =g7 (d, l) = (d4/l3) –9.65>=0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ANSYS 优化设计1.认识ANSYS优化模块1.1 什么时候我需要它的帮忙?什么是ANSYS优化?我想说明一个例子要比我在这里对你絮叨半天容易理解的多。
注意过普通的水杯吗?底面圆圆的,上面加盖的哪一种。
仔细观察一下,你会发现比较老式的此类水杯有一个共同特点:底面直径=水杯高度。
图1 水杯的简化模型为什么是这样呢?因为只有满足这个条件,才能在原料耗费最少的情况下使杯子的容积最大。
在材料一定的情况下,如果水杯的底面积大,其高度必然就要小;如果高度变大了,底面积又大不了,如何调和这两者之间的矛盾?其实这恰恰就反应了一个完整的优化过程。
在这里,一个水杯的材料是一定的,所要优化的变量就是杯子底面的半径r和杯子的高度h,在ANSYS的优化模块里面把这些需要优化的变量叫做设计变量(DV);优化的目标是要使整个水杯的容积最大,这个目标在ANSYS的优化过程里叫目标函数(OBJ);再者,对设计变量的优化有一定的限制条件,比如说整个杯子的材料不变,这些限制条件在ANSYS 的优化模块中用状态变量(SV)来控制。
下面我们就来看看ANSYS中怎么通过设定DV、SV、OBJ,利用优化模块求解以上问题。
首先参数化的建立一个分析文件(假设叫volu.inp),水杯初始半径为R=1,高度为H =1(DV),由于水杯材料直接喝水杯的表面积有关系,这里假设水杯表面积不能大于100,这样就有S=2πRH+2πR2<100(SV),水杯的容积为V=πR2H(OBJ)。
File:volu.inp (用参数直接定义也可或者在命令栏内直接写)R=1H=1S=2*3.14*R*H+2*3.14*R*RV=10000/(3.14*R*R*H)然后再建一个优化分析文件(假设叫optvolu.inp),设定优化变量,并求解。
/clear,nostart/input,volu,inp/optopanl,volu,inpopvar,R,dv,1,10,1e-2opvar,H,dv,1,10,1e-2opvar,S,sv,,100,1e-2opvar,V,obj,,,1e-2opkeep,onoptype,subpopsave,optvolu,opt0opexec最后,打开Ansys6.1,在命令输入框中键入“/input,optvolu,inp”,整个优化过程就开始了。
图2 ANSYS优化过程图几秒钟的优化过程结束后,让我们来看一下优化的结果:/optoptlist,all图3 优化结果1上图中左右带*的SET 22是最优解,由此可以看出,要想在表面积一定的情况下使水杯容积最大,的确有这样一个规律H=D=2*R。
有兴趣的同志可以用求极值的方法演算一下,一定会得到相同的答案。
ANSYS的优化模块是用来求解工程分析中的优化例子的,但上面一个例子说明即使这样于工程毫无关系纯数学极值问题,也能够轻松求解。
不过在细节处会有一些技巧,后面再仔细分析。
(其实用ANSYS的优化模块完全能解决数学上比较负责的极值问题,不过现在有了Matlab、Mathematica,大概也没有人愿意来用ANSYS献丑了)。
1.2 ANSYS优化设计基础前面写了一个例子,来说明ANSYS的基本优化过程。
在这一节中,我们结合这个例子来说明一下优化模块中的一些概念。
1.2.1 优化模块中的三大变量:设计变量(DV):即自变量。
例子中的opvar,R,dv,1,10,1e-2就是用来定义一个设计变量R,其上限为10,下限为1,公差为10-2(公差和优化过程的收敛有关)。
ANSYS优化模块中允许定义不超过60个设计变量。
状态变量(SV):用来体现优化的边界条件,是设计变量的函数。
例子里面opvar,S,sv,,100,1e-2就是定义了一个状态变量S,它的上限为100,无下限,公差为10-2。
从文件volu.inp中可以看到,S=2*3.14*R*H+2*3.14*R*R。
可见,定义这样一个状态变量,即是限制水杯的表面积(可以认为表示材料的多少)不大于100。
在ANSYS优化模块中用户可以定义不超过100个状态变量。
目标函数(OBJ):最终的优化目的。
它必须是设计变量的函数,而且只能求其最小值。
看到volu.inp里面目标函数的定义了吧V=10000/(3.14*R*R*H),为了把求最大体积转化为求最小值,只好对它求倒数了;如果知道目标函数的上限,还可以用一个大数减目标函数的方法来转换。
例子中opvar,V,obj,,,1e-2就是定义了一个目标函数V,它的公差是10-2。
1.2.2 ANSYS优化模块中的两种求解模式ANSYS优化模块的求解有两种运行模式,一种是在GUI方式下运行,即已经打开ANSYS的分析界面后进行分析;另一种是Batch模式,无需打开ANSYS分析界面,后台运行求解。
前面例子的运行过程其实就是一个典型的GUI方式体现,它涉及到两个重要的文件:一个就是类似volu.inp的ANSYS分析文件,如果是一个工程问题,该文件中应该有参数定义、参数建模、求解、结果提取、目标函数赋值的一个全过程(由于优化求解是一个不断跌代的过程,ANSYS分析文件其实是包涵了一个完整的循环)。
另一个文件是类似optvolu.inp 的优化控制文件,基本语句就那么几条,无非是定义三大变量、优化方式、优化控制等几条,用户拿过去稍稍替换下就可以用在不同的问题上。
(注:细心的读者可能会提问,既然ANSYS分析文件包涵了一个完整的循环,但是整个优化过程中是要求设计变量不断改变的,每次循环都有一个参数重定义的过程,不会使设计变量恢复初始值吗?这一点勿用担心,正是由于有了另一个优化控制文件,优化过程只在第一次进行完全的参数定义工作,在后续循环中,优化控制文件中声明的设计变量定义将被忽略)。
有了这样两个文件,简单的在命令窗口把优化控制文件输入进去(其中的opanl命令会自动调用指定的ANSYS分析文件),就可以完成整个优化过程。
以上说明的是完全使用命令流的GUI方式,至于如何在菜单中进行优化过程的定制,窃以为没有命令流方式快捷,这里就不再赘述了。
另一种方式是后台运行的Batch方式,它只需要一个输入命令流文件(batch文件)。
该文件可以简单的把GUI方式下ANSYS分析文件和优化控制文件合并得到。
不过有几个注意点:1、需要把optanl语句去掉,因为在batch文件中,不需要提供ANSYS分析文件名字,系统默认batch文件中/opt语句以前的所有部分为ANSYS分析文件内容。
2、以前为防止在GUI方式下的重新定义错误而引入的一些语句,如/cle,nostart需要去除。
上述例子经过合并、处理,就可以得到Batch方式下需要的batch文件batch.inp File:batch.inpR=1H=1S=2*3.14*R*H+2*3.14*R*RV=10000/(3.14*R*R*H)/optopvar,R,dv,1,10,1e-2opvar,H,dv,1,10,1e-2opvar,S,sv,,100,1e-2opvar,V,obj,,,1e-2opkeep,onoptype,subpopsave,optvolu,opt0opexec假定batch.inp在目录bvolu下,在cmd命令行方式下,进入bvolu目录,执行命令:ansys61 -b -j bvolu -p ane3flds -i batch.inp –o output.txt命令中-b 参数指定用batch模式求解;-j bvolu参数指定该求解默认工作名字为bvolu (不指定就默认为file)-p ane3flds 参数指定使用ANSYS/Multiphysics/LS-DYNA求解器-i batch.inp 参数指定输入batch文件为batch.inp-o output.txt 参数指定把输出导向到output.txt中,便于查看过程纠错运行结束后,可以从output.txt文件中看到最有解是多少:文件output.txt中的一部分数据:----------SOLUTION HAS CONVERGED TO POSSIBLE OPTIMUM -----------(BASED ON DV TOLERANCES BETWEEN FINAL TWO DESIGNS)FINAL VARIABLES ARESET 22(FEASIBLE)S (SV) 99.997R (DV) 2.2851H (DV) 4.6830V (OBJ) 130.23其结果与用GUI方式求解完全一样,生成的bvolu.opt文件中也有最优解的信息,同时还能看到求解整个参数迭代求解过程。
1.2.3 ANSYS的优化方法和收敛准则例子中优化控制文件里面的优化命令,还有opkeep,on(用来要求保留最优解的DB),opexec(执行优化),剩下重要的命令就只有optype了,这个命令指定ANSYS优化中使用的优化方法。
优化方法发展到今天可说是形形色色,比较完善了。
ANSYS的优化模块中只支持两种优化方法,不能不说是一大遗憾。
但ANSYS的这两种优化方法对绝大多数的工程问题已经足够,更何况ANSYS还留下了用户话优化接口,方便用户写出适合于自己问题的优化方法来使用。
看看例子中的命令”optype,subp”,这里指定的是第一种通用的函数逼进优化方法。
改种方法的本质是采用最小二乘逼进,求取一个函数面来拟和解空间,然后再对该函数面求极值。
无疑这是一种普适的优化方法,不容易陷入局部极值点,但优化精度一般不是很高,因此多用来做粗优化的手段。
另外一种是针对第一种优化方法缺点的改进方法,叫做梯度寻优。
如果说第一种方法是C0阶、大范围普适的粗优化方法;第二种方法就是C1阶、局部寻优的精优化方法。
一般来说,一个比较负责的问题都需要同时采用两种优化方法,先用函数逼进的第一类方法初步求得最优解基本位置,然后再采用梯度寻优的对最优解的位置进行更精确的确定。
(注:但用第二类梯度寻优进行优化,不仅时间消耗长,还可能陷入局部最小点,因此通常的问题都建议使用0阶函数逼进优化subp)前面讨论了ANSYS的两种优化方法,但光了解优化进行的方式是不够的。
ANSYS进行优化计算,都是一个不断迭代的过程。
有时候,了解优化过程什么时候结束比了解优化过程本身更加重要。
下面我们就来谈谈决定优化过程什么时候结束的条件:优化准则。
假设F j、X j和F j-1、X j-1分别为目标函数、设计变量第j次迭代和第j-1次迭代的结果(X j 为矢量),F b和X b分别是当前的最优目标函数和其相应的设计变量值。
如果满足或者,为目标函数的公差,那么认为迭代收敛,于是迭代停止。
