北京理工大学自动化学院自控A习题
北京理工大学2006学年《自动控制原理》期末考试 答案与评分标准(A卷)(缺试题)
自动控制理论（一）答案一. (20分)解：(1) (10分) c r U U U -=2； 22U s C I ⋅=；222I R U R ⋅=；221R R U U U +=；21111I U R I R +=；111I s C U ⋅= ；12U U U R c += 。
消除中间变量得，1)2(1)()()(2122121221++++++=s T T s T T s T T s T T s U s U r c ，其中，，C R T 11=，C R T 22=。
解：(2) (10分)3211G G G P =322121321243G L -=；424213212331G G G H H G G G G ++++=∆；411G +=∆；421G +=∆；4242132124321331)1()2()(G G G H H G G G G G G G G s ++++++=Φ。
(允许使用方框图简化)二. (20分)解：(1) (10分) 22222)5()(nn ns s k s k s k s ωζωωτ++=+++=Φ；7.0%6.4=⇒=ζσp ；588.0=⇒=n p t ω；252==n k ω；08.0=τ；解：(2) (10分) k s k s kG s s GH G G G s e +++-+=++-=Φ)5(511)(2br 2br τ；s k ss G 2.05)(br ==。
三. (15分)解：(1) (6分) 劳斯计算表首列系数变号2次，S 平面右半部有2个闭环极点，系统不稳定。
333206633101234s s s s s -解：(2) (9分))1)(1()1()(312+++=s T s T s T K s G ；1020log 20=⇒=K K ；5002.0/11==T ；05.020/12==T ；05.0200/13==T ；)1005.0)(150()105.0(10)(+++=s s s s G ；2.0=c ω；8.83001.0arctan 10arctan 01.0arctan )(-=--=∠j G ；2.96)(180=∠+=j G γ，闭环系统的稳定。
北京理工大学自动化期末试卷答案07A
（2007~2008学年第一学期）
课程编号：0400003（1）课程名称：自动控制理论（一）
一、控制系统的数学模型（共20分）
1、已知控制系统结构图如下图所示。试通过结构图等效变换求系统的传递函数 。（7分）（要求：有化简过程）。
2、已知控制系统结构图如下图所示。绘制该系统的信号流图，并用梅森增益公式求系统的传递函数 。（8分）
五、线性系统的校正（共15分）
设单位反馈系统的开环传递函数为 ，试采用滞后-超前校正装置进行串联校正，要求：
1、当输入信号为 时，稳态误差
2、截止频率
3、相角裕度
六、非线性控制系统分析（共15分）
非线性控制系统如下图所示。
1、试用描述函数法分析a=1，b=2，k=10时，系统的稳定性。
2、若系统存在自持振荡，计算自持振荡的振幅和频率。
（2）计算输入信号为 时的稳态误差。（5分）
3、复合控制系统的结构图如下图所示，前馈环节的传递函数 ，当输入 为单位加速度信号时（即 ），为使系统的稳态误差为0，试确定前馈环节的参数 和 。（10分）
三、线性系统的根轨迹（共15分）
某系统的结构图如下图所示。要求：
1、绘制系统的根轨迹草图（10分）。
3、求下图有源网络的传递函数 ，并指出该网络属于哪类典型环节？（5分）。
二、线性系统的时域分析（共25分）
1、设系统的特征方程为： 试应用劳斯稳定判据确定欲使系统稳定的 的取值范围。（5分）
2、已知控制系统的结构图如下图所示，单位阶跃响应的超调量 ，峰值时间 s，试求：
（1）根据已知性能确定参数 和 ；（5分）
2、确定使系统稳定的 值范围（2分）。
北京理工大学自动化学院模拟电子技术基础期末考试题
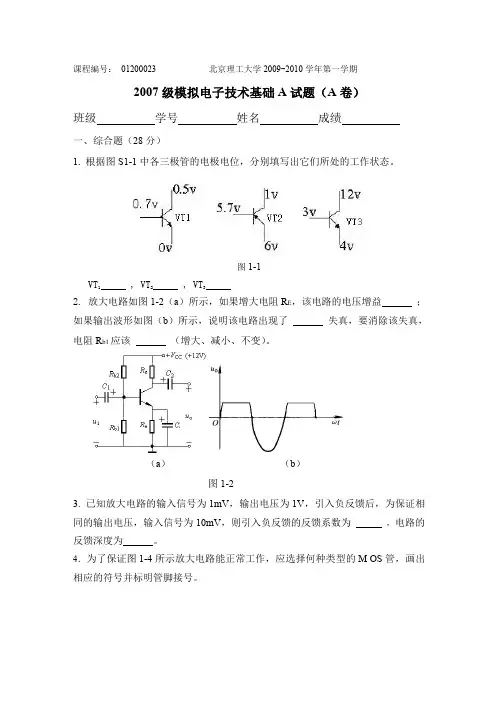
Uo 的表达式并计算其数值。 Ui
3．求输入电阻 Ri 和输出电阻 Ro 。
图2
三、 （12 分）在图 3 所示电路中，各运放均为理想运算放大器，分别计算各电路 的输出电压。
图3
四、 （14 分）电路如图 4 所示，
图4 1． 为了将输入电压 u I 转换为稳定的输出电流 i L ， 说明运放的同相与反相输入端应
图6 七、 （10 分） 在如图 7 所示电路中， 已知三端稳压器 W7812 的输出电压 U23＝12V， 最大输出电流 IOmax＝0.1A； A 为理想运放。 1．设 R1＝R2＝1K, R3＝R4＝2K，求输出电压 UO 的调节范围。 2．计算通过电阻 R2 电流的范围。
图7
失真，要消除该失真，
（a） 图 1-2
（b）
3. 已知放大电路的输入信号为 1mV，输出电压为 1V，引入负反馈后，为保证相 同的输出电压，输入信号为 10mV，则引入负反馈的反馈系数为 反馈深度为 。
，电路的
4．为了保证图 1-4 所示放大电路能正常工作，应选择何种类型的 M OS 管，画出
相应的符号并标明管脚接号。
如何连接。并说明该电路中反馈的组态。 2．如果输入电压 uI 的变化范围为 05V 时，计算电流 i L 的变化范围。 五、 （12 分）判 断 下 列 电 路 是 否 产 生 正 弦 波 ， 并 简 述 理 由 。
（a）
(b)
(c) RC 正弦波振荡电路 图5 六、 （12 分）在图 6 所示三角波发生器中，已知 A1、A2、A3 均为理想运算放大器， 它们输出电压的两个极限值为 12V。 1．说明 A1、A2、A3 组成各电路的功能； 2.求解 u O 的频率 f 和幅值 UOM、 uO1 的峰值 UOM1。 3.画出输出电压 u O 与 u O1 和 u O2 的对应波形。
最新奥鹏北京理工大学北理工《自动控制理论1 》在线作业-参考答案
12. 开环频域性能指标中相角裕度对应时域性能指标 ( ) 。 【选项】： A 超调 B 稳态误差 C 调整时间 D 峰值时间
【答案】：Aபைடு நூலகம்
13. 最小相角系统闭环稳定的充要条件是 （ ） 【选项】： A 奈奎斯特曲线不包围（-1，j0）点 B 奈奎斯特曲线包围（-1，j0）点 C 奈奎斯特曲线顺时针包围（-1，j0）点 D 奈奎斯特曲线逆包围（-1，j0）点
【答案】：A
3. 单位反馈系统的开环传递函数 G(s)=16/(s(s+4*sqrt(2)))，其幅值裕度 h 等于 （ ） 【选项】： A0 B 4sqrt(2)dB C 16dB D 无穷
【答案】：D
4. 系统对输入信号的时域响应中，其调整时间的长短是与（ ）指标密切相关。 【选项】： A 允许的峰值时间 B 允许的超调量 C 允许的上升时间 D 允许的稳态误差
【答案】：A
14. 系统稳定的充分必要条件是其特征方程式的所有根均在根平面的（ ）。 【选项】： A 右半部分 B 左半部分 C 实轴上 D 虚轴上
【答案】：B
15. 放大环节的对数幅频特性曲线是（ ）。 【选项】： A 平行于横轴的直线 B 斜率为 1 的直线 C 逐渐增大至某一值的曲线 D 垂直于横轴的直线
【答案】：A 执行元件的功能是直接带动控制对象 |C 测量元件一般指传感器 |D 计算机属 于补偿元件 |
22. 比例控制的优点是（ ）。 【选项】： A 及时 B 快速 C 控制作用强 D 无稳态偏差
【答案】：A 及时 |B 快速 |C 控制作用强 |
23. 频率特性常用表示方法有（ ）。 【选项】：
D A、B、C 都不是
【答案】：C
10. 二阶系统的调整时间长，则说明（ ）。 【选项】： A 系统响应快 B 系统响应慢 C 系统的稳定性差 D 系统的精度差
北理工《自动控制理论1 》在线作业1答案
北理工《自动控制理论1 》在线作业-0002试卷总分:100 得分:0一、单选题(共20 道试题,共60 分)1.主导极点的特点是（）。
A.距离虚轴很近B.距离实轴很近C.距离虚轴很远D.距离实轴很远正确答案:A2.系统的频率特性（）A.是频率的函数B.与输入幅值有关C.与输出有关D.与时间t有关正确答案:A3.单位反馈系统的开环传递函数G(s)=16/(s(s+4*sqrt(2)))，其幅值裕度h等于（）A.0B.4sqrt(2)dBC.16dBD.无穷正确答案:D4.系统对输入信号的时域响应中，其调整时间的长短是与（）指标密切相关。
A.允许的峰值时间B.允许的超调量C.允许的上升时间D.允许的稳态误差正确答案:D5.系统型次越高，稳态误差越（）。
A.越小B.越大C.不变D.无法确定正确答案:A6.用实验法求取系统的幅频特性时，一般是通过改变输入信号的（）来求得输出信号的幅值。
A.相位B.频率C.稳定裕量D.时间常数正确答案:B7.系统的传递函数在右半S平面上没有零点和极点，则该系统称作（）。
A.非最小相位系统B.最小相位系统C.不稳定系统D.振荡系统正确答案:B8.适合应用传递函数的系统是（）。
A.单输入，单输出的线性定常系统B.单输入，单输出的线性时变系统C.单输入，单输出的定常系统D.非线性系统正确答案:A9.已知串联校正装置的传递函数为0.2(s+5)/(s+10)，则它是（）A.相位迟后校正B.迟后超前校正C.相位超前校正D.A、B、C都不是正确答案:C10.二阶系统的调整时间长，则说明（）。
A.系统响应快B.系统响应慢C.系统的稳定性差D.系统的精度差正确答案:B11.典型二阶系统的超调量越大，反映出系统（）A.频率特性的谐振峰值越小B.阻尼比越大C.闭环增益越大D.相角裕度越小正确答案:D12.开环频域性能指标中相角裕度对应时域性能指标( ) 。
A.超调B.稳态误差C.调整时间D.峰值时间正确答案:A13.最小相角系统闭环稳定的充要条件是（）A.奈奎斯特曲线不包围（-1，j0）点B.奈奎斯特曲线包围（-1，j0）点C.奈奎斯特曲线顺时针包围（-1，j0）点D.奈奎斯特曲线逆包围（-1，j0）点正确答案:A14.系统稳定的充分必要条件是其特征方程式的所有根均在根平面的（）。
北理工《控制与测试》期末考试必备通关指导1
（74） 北京理工大学远程教育学院2021-2021学年第二学期《控制与测试》期末试卷(A 卷)教学站 学号 姓名 成绩（一）控制工程基础部分（共80分）一、单项选择题（在每小题的几个备选答案中，选出一个正确答案，每小题2分，共 10 分）1．与开环控制系统相比较，闭环控制系统的主要缺点是（ ）。
（1）控制精度差 （2）价格便宜（3）具有反馈回路 （4）有稳定性问题2．表征自动控制系统的稳态性能指标是（ ）（1）最大超调量 （2）稳态误差（3）上升时间 （4）调整时间3．设象函数为21()9F s s =+，其原函数()f ∞为（ ） （1）1 （2）0 （3）91 （4）9 4．一阶系统的时间常数T 愈小，其系统（ ）（1）响应愈快；（2）响应愈慢；（3）准确度愈低；（4）稳定性愈差5. 传递函数 ))((b s a s s cs +++ 对应的系统稳态误差为大于零的常数，则其输入可能是（ ）（1）阶跃函数 （2）t 5 （3）2ct （4）23at bt -二、填空题（每空1分，共10分）1．对一阶系统，当过渡过程时间为时间常数T 的三倍时，系统输出稳态误差为 ，当过渡过程时间为时间常数T 的四倍时，系统输出稳态误差为 。
2．欠阻尼二阶系统阻尼比越大，上升时间 ，过渡过程时间 。
3．系统对输出的误差定义为理想输出与 之差，而对扰动的误差来说，其理想输出误差 。
4．系统幅频特性是指系统 随 变化的规律。
5. 串联校正是将 串联在系统 通路上的校正方法。
三、问答题（10分）试说明过渡过程指标与系统无阻尼自由振荡频率的关系。
四．求传递函数（每小题10分，共2021（1）求传递函数()()s R s C （10分）（2）图示为某单位反馈最小相位系统开环对数幅频特性曲线，试求其闭环传递函数。
（10分）ω五．（已知单位反馈控制系统单位阶跃响应的超调量为30％，无阻尼自由振荡频率n ω为1（s rad /），试求（1） 系统阻尼比；（2） 单位阶跃响应的上升时间r t 和调节时间s t六．（15分）已知反馈控制系统开环传递函数为)11.0)(110(100)()(++=s s s s H s G ，试求： （1) 绘制开环对数幅频特性曲线（渐近线）和概略绘制奈魁斯特图；（2)分析系统稳定性并说明理由。
北京理工大学自动化学院810自控2009-2013年真题详细 回忆版
2009年北理810 真题回忆2010年北京理工大学自动控制原理（810）真题（回忆版）2010年试卷总共九道大题，没有选择填空题，除六七题外，每道大题均在3问到5问之间一、二阶系统分析题目给出了一个二阶系统（带框图需要自己求传递函数）的单位阶跃响应的曲线图，让求其峰值，超调量等，这题不难，只需想到其阶跃响应应该是单位阶跃响应的积分，然后在所给曲线上找到与该图像与X轴的交点，这就是峰值时间，积分面积就是峰值，但是给出的数很怪，很影响人的情绪让人一看就不想做的那种，不过总体说来这应该算是试卷上最简单的题之一了，要分析加计算估计20分钟----25分钟。
二、系统框图分析给了一个框图，第一问让化简，它只是让证明，结果已经给了就是用平常的框图化简方法与Mason公式，我之前做了大量的框图化简的题，结果还是没证出来，应该有难度的，大家可以参考一下东北大学09年的那个框图化简题，应该有这个难度，就是知道框图但是很巧妙化Mason图很容易画错的那种，框图化简也不好弄，第二三四问然后赋予了第一问中的G(s)比较麻烦的式子，让你证明这个那个，比如说该系统对所有的某个参数都稳定啦之类，不难，思路你都会，很麻烦，一遍做对很不简单，要完整做完至少至少30分钟（如果你计算能力超强，写字很清晰的话）。
三、状态空间方法第一问还是证明，很麻烦，类似06年第二题，不过T矩阵让你自己取，然后他还给你了一个取矩阵的方法，也是很麻烦，不过如若你线性代数学得好的话，你可以根据给的那个方法一眼抽出该矩阵怎么取，不过计算量超大的，那个变换后的A矩阵，应该是T的逆乘A乘T，这里面T是4*4矩阵，A是含t的约旦标准型，结果可以从试卷这边写到那边，这一问做出来，至少20分钟，后面还有三问，判断可控客观性什么的，这个简单，但通篇做出来，至少30分钟吧。
四、根轨迹方法：用了第一题还是第二个题的框图来着，忘了，让画根轨迹，非最小相位环节的，两个复数零点两个开环零点，光求那个分离点，四个分母通分化简嘛，何况还是复数的，每个通分后都是三项，求出分离点就二十分钟没了，何况还要求什么入射角出射角什么的，第一问保守35分钟，第二问第三问没心情做了，当时一看时间过去一大半了，铁定做不完了，让证明对所有什么都稳定之类，当时脑子糊糊，没啥思路，应该要转个弯的。
北理工06-08年历年真题讲解_自动化
北京理工大学自动化学院自动化专业——2006年真题及解析科目一：代码810 科目名称自动控制理论第 1 页 共 51 页一、真题北京理工大学2006年自动控制理论考试试题一、根轨迹方法 （25分）单位反馈系统如图1，其中()()21+=s s s G 。
为简便起见，图中用R 表示r(t)的Laplace 变换R(s)。
其余的符号和以后的图均采用这种简便记法。
（1）设()K s G c =,画出根轨迹图；（2）确定K 的值，使闭环系统单位阶跃响应的最大超调量为π-=e M p 。
计算相应的上升时间r t ； （3）设计控制器()()11++=Ts Ts K s G c c αα使最大超调量p M 保持不变，上升时间为83π=r t ，并使闭环系统尽可能地简单。
图1：单位反馈系统二、状态空间方法 （30分）第 2 页 共 51 页考虑系统 ⎪⎩⎪⎨⎧+=+=DuCx y BuAx x 。
（1）先设 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=210100100a a a A （ⅰ）证明：若()()()2122101223,λλλλ≠--=+++=其中s s a s a s a s s f ，则可通过状态空间中的线性变换Tx x=ˆ，将状态空间表达式（1）变为⎪⎩⎪⎨⎧+=+=Du xC y u B x A x ˆˆˆˆˆˆ。
（2）其中 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==2211000ˆλλλJ A T 可取为 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=222221112101λλλλλT （ⅱ）设 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=110001000A 求At Jt e e 和。
（ⅲ）A 同（ⅱ）， [][]100,011==C B T第 3 页 共 51 页判断系统的可控性和可观测性。
若系统不可控或不可观测，确定不可控或不可观测的模态；（ⅳ）A,B,C 同（ⅲ），D=0，()[]()t x x T,1110-=是状态方程在初态()0x 下的解，证明()()()0,30≥∀=-t t u e t x x t T ，并解释这个结果。
北京理工大学自动控制理论04-07真题解析
最新整理自动控制原理2004-2007年真题答案 注：本答案仅供参考。
2007年一、1．d 2. b 3. c4 解：单位阶跃输入r(t)=1是单位斜坡输入r(t)=t 的导数， 则单位阶跃响应是单位斜坡响应的导数，即单位阶跃响应为()()41tet y t h --='=对其做拉氏变换得，()()1414111+=+-=s s s s s H传递函数为()()()141+==s s R s H s G5 解：由图可得，开环传递函数()()()102.012++=s s s K s G()()10201lg 201=⇒⎭⎬⎫===K L K L ωω时，则()()()102.01102++=s s s s G速度误差系数()∞==→s sG K s v 0lim加速度误差系数a K ()10lim 20==→s G s s二、解：（1）系统的开环传递函数()()()a s s b s K s G -+=根据分离点、汇合点的计算公式b d a d d +=-+111依题意，得分离点11=d ，汇合点32-=d ，代入上式得 a=3，b=1则开环传递函数()()()310-+=s s s K s G绘制根轨迹的步骤如下:①开环极点01=p ，32=p 数目 n=2；开环零点1-=z ，数目m=1系统有两条根轨迹。
②实轴上根轨迹段为()()301，，，-∞-； ③渐近线与实轴夹角为πϕ±=a ；④分离点11=d ，汇合点32-=d由以上计算得到的参数，得根轨迹如图所示：（2）根轨迹与虚轴的交点 由()010=+s G ，得特征方程为()032=+-+K s K s劳斯阵：Ks k s K s 01231-要与虚轴有交点，则有一行全零，即303=⇒=-K k 辅助方程：js s 3032,12±=⇒=+综上，与虚轴的交点是j 3±，使闭环系统稳定的K 值范围应是K>3。
2004-2007北京理工大学自动控制理论真题及解析
北京理工大学2007年自动控制理论考试试题一、选择填空 （每小题10分，共60分）1 采样系统的特征方程为()()05.275.122=+-+=z K z z D ，使系统稳定的K 是（ ）（a ）63.2≥K （b ）63.20≤<K （c ）所有0>K（d ）不存在这样的K 值。
2 采样系统的输出()()zz z z z z Y z kT y 6.025222323+-++=-变换为的，则前四个采样时刻的输出为（ ）（a ）()()()()05.603,472,27,00====T y T y T y y （b ）()()()()8.168453,4.6742,27,10====T y T y T y y （c ）()()()()05.6603,6472,27,10====T y T y T y y （d ）()()()()273,472,647,10====T y T y T y y3 s-域的传递函数为()()()6210++=s s s s G ，T 为采样周期。
经采样后z-域的脉冲传递函数()z Gˆ是（ ） （a ）()T T e z z e z z z z z G---+---=12545165ˆ6 （b ）()TT e z z e z z z z z G---+---=125165ˆ6 （c ）()T T e z z e z z z z z G6212545165ˆ---+---= （d ）()TT e z z e z z z z z G6265161ˆ---+---= 4 线性系统的单位斜坡响应为()444t et t y -+-=，则该系统的单位阶跃响应为_______，该系统的传递函数为_______。
5 最小相位系统的开环对数幅频特性如图1，则该系统的速度误差系数v K =-_______，加速度误差系数a K =_______。
图1：折线对数幅频特性6 非线性系统的一个平衡态e x 位于不稳定的极限环内，该极限环内没有其它极限环。
北理工《自动控制理论2》在线作业1答案
北理工《自动控制理论2》在线作业 -0001试卷总分:100 得分:0一、单选题(共10 道试题,共30 分)1.基于能量的稳定性理论是由（）构建的。
A.LyapunovB.KalmanC.RouthD.Nyquist正确答案:A2.引入状态反馈的目的是（）。
A.配置系统的极点B.改变系统的能控性C.改变系统的能观性D.使得系统能观正确答案:A3.齐次状态方程就是指状态方程中不考虑（）的作用。
A.输入B.输出C.状态D.系统正确答案:A4.对于单变量系统，特征方程的根就是传递函数的（）。
A.零点B.极点C.拐点D.死点正确答案:B5.齐次状态方程的解就是系统在无外力作用下由初始条件引起的（）。
A.自由运动B.强迫运动C.离心运动D.旋转运动正确答案:A6.线性系统的系数矩阵A如果是非奇异的，则系统存在（）平衡点。
A.一个B.两个C.三个D.无穷多个正确答案:A7.原系统的维数是n，则全维状态观测器的维数是（）。
A.2nB.nC.3nD.n-1正确答案:A8.能够完整的描述系统运动状态的最小个数的一组变量称为（）。
A.状态变量B.状态空间C.状态方程D.输出方程正确答案:A9.由初始状态所引起的自由运动称为状态的（）。
A.零输入响应B.零状态响应C.输入响应D.输出响应正确答案:A10.以状态变量为坐标轴所构成的空间，称为（）。
A.状态变量B.状态空间C.状态方程D.输出方程正确答案:B二、多选题(共10 道试题,共30 分)1.由动态方程导出可约传递函数时，表明系统是（）。
A.可控不可观测B.可观测不可控C.不可控不可观测D.可控可观测正确答案:ABC2.经典控制理论线性系统稳定性判别方法有（）。
A.代数判据B.Nquist稳定判据C.根轨迹判据D.Lyapunov稳定性理论正确答案:ABC3.利用Lyapunov第二法可以分析（）。
A.线性系统响应的快速性B.非线性系统的稳定性C.线性时变系统稳定性D.以上均不正确正确答案:ABC4.任何状态不完全能控的线性定常连续系统，总可以分解成（）两部分。
2021北理自控回忆版
2021北京理工大学自动控制理论回忆版第一题系统建模分析这个题目很简单，题目中给的是LC电路，说白了就是简单的电路分析，电感电量为x1,电容电压为X2,电容电压为输出。
列写状态空间表达式和传递函数〔10分〕第二题动态性能分析了一个冲激函数函数的响应，利用此条件求输入为单位阶跃，单位斜坡的响应〔10分〕刚开始做这道题，还美的，后来发现那个相应的反拉普拉斯竟然以前我没注意到，最后没方法只好用数学公式推出来。
所以大家平时一定要留意下小知识点，细节决定成败。
第三题第一问求状态转移矩阵A为四阶，在输入为零的条件下，了X1〔0〕X2〔0〕X3〔0〕X4〔0〕；X1〔t〕X2〔t〕X3〔t〕X4〔t〕,求eAt及A。
这道题挺简单的，平时也老见的题型第二问：关于可控可观，给了个约当标准形矩阵，B,C矩阵都是字母表示，问b1,b2,b3,b4什么关系能控，c1,c2,c3,c4关系能观第三问问的是在什么条件下基于状态观测器的状态配置使闭环系统稳定第四题根轨迹直接参考08年真题的那道就OK第五题频率特性一个只有一个零点的一型系统，大概是分母(1/3S+1)分子s(1.5s+1)(0.4s^2+as+b)。
让你画奈奎斯特曲线。
其中求与负实轴的交点给了一个提示，用那个提示正好做。
二问要求使闭环系统稳定的K 值范围第六题离散系统第一小问给了一个抽象的结构框图，含有采样开关的，让你直接写闭环传递函数，很根底的。
第二问，题目给的是含有零阶保持器的一阶系统，有点不习惯哈。
但是做题思路根本是一样。
判断系统的稳定性并且在给的r(t)下求稳态误差。
嗯嗯。
都还行吧第七题非线性描述函数法非线性环节为含有死区的继电特性环节，线性环节为常见的一型系统。
让你求自激振荡的幅值和频率第二问是个小证明题，证明通过调节O=b\a使消除自激震荡第八题李雅普诺夫稳定性给了一个非线性空间表达式，让你求平衡状态及选用李亚普诺夫函数判断系统的稳定性那个李雅普诺夫函数有提示第九题最优控制〔20分〕第一问貌似写欧拉公式。