模式识别导论习题参考-齐敏-第6章-句法模式识别
模式识别课后习题答案

• 2.16 证明M ahalanobis距离r符合距离定义三定理,即 – (1) r(a, b) = r(b, a) – (2) 当且仅当a = b时,r(a, b) = 0 – (3) r(a, c) ≤ r(a, b) + r(b, c) 证明: (1) r(a, b) = (a − b)T Σ−1 (a − b) = (b − a)T Σ−1 (b − a) = r(b, a) (2) Σ为半正定矩阵所以r(a, b) = (a − b)T Σ−1 (a − b) ≥ 0,只有当a = b时,才有r(a, b) = 0。 (3) Σ−1 可对角化,Σ−1 = P ΛP T • 2.17 若将Σ−1 矩阵写为:Σ−1 h1d h2d ,证明M ahalanobis距离平方为 . . . hdd
• 2.13 把连续情况的最小错误率贝叶斯决策推广到离散情况,并写出其判别函数。 • 2.14 写出离散情况条件风险R(ai |x)的定义,并指出其决策规则。 解: R(ai |x) = = R(ak |x) = min
c ∑ j =1 c ∑ j =1
λij P (wj |x) λij pቤተ መጻሕፍቲ ባይዱx|wj )P (wj )////omit the same part p(x)
j =1,...,c j =1,...,c
考虑两类问题的分类决策面为:P (w1 |x) = P (w2 |x),与p(x|w1 )P (w1 ) = p(x|w2 )P (w2 ) 是相同的。 • 2.9 写出两类和多类情况下最小风险贝叶斯决策判别函数和决策面方程。 • 2.10 随机变量l(x)定义为l(x) = p(x|w1 ) ,l(x)又称为似然比,试证明 p(x|w2 )
1
模式识别习题及答案

模式识别习题及答案第⼀章绪论1.什么是模式具体事物所具有的信息。
模式所指的不是事物本⾝,⽽是我们从事物中获得的___信息__。
2.模式识别的定义让计算机来判断事物。
3.模式识别系统主要由哪些部分组成数据获取—预处理—特征提取与选择—分类器设计/ 分类决策。
第⼆章贝叶斯决策理论1.最⼩错误率贝叶斯决策过程答:已知先验概率,类条件概率。
利⽤贝叶斯公式得到后验概率。
根据后验概率⼤⼩进⾏决策分析。
2.最⼩错误率贝叶斯分类器设计过程答:根据训练数据求出先验概率类条件概率分布利⽤贝叶斯公式得到后验概率如果输⼊待测样本X ,计算X 的后验概率根据后验概率⼤⼩进⾏分类决策分析。
3.最⼩错误率贝叶斯决策规则有哪⼏种常⽤的表⽰形式答:4.贝叶斯决策为什么称为最⼩错误率贝叶斯决策答:最⼩错误率Bayes 决策使得每个观测值下的条件错误率最⼩因⽽保证了(平均)错误率最⼩。
Bayes 决策是最优决策:即,能使决策错误率最⼩。
5.贝叶斯决策是由先验概率和(类条件概率)概率,推导(后验概率)概率,然后利⽤这个概率进⾏决策。
6.利⽤乘法法则和全概率公式证明贝叶斯公式答:∑====m j Aj p Aj B p B p A p A B p B p B A p AB p 1)()|()()()|()()|()(所以推出贝叶斯公式7.朴素贝叶斯⽅法的条件独⽴假设是(P(x| ωi) =P(x1, x2, …, xn | ωi)= P(x1| ωi) P(x2| ωi)… P(xn| ωi))8.怎样利⽤朴素贝叶斯⽅法获得各个属性的类条件概率分布答:假设各属性独⽴,P(x| ωi) =P(x1, x2, …, xn | ωi) = P(x1| ωi) P(x2| ωi)… P(xn| ωi)后验概率:P(ωi|x) = P(ωi) P(x1| ωi) P(x2| ωi)… P(xn| ωi)类别清晰的直接分类算,如果是数据连续的,假设属性服从正态分布,算出每个类的均值⽅差,最后得到类条件概率分布。
模式识别答案

答:在模式识别学科中,就“模式”与“模式类”而言,模式类是一类事物的代表,概念或典型,而“模式”则是某一事物的具体体现,如“老头”是模式类,而王先生则是“模式”,是“老头”的具体化。
问答第2题答:Mahalanobis距离的平方定义为:其中x,u为两个数据,是一个正定对称矩阵(一般为协方差矩阵)。
根据定义,距某一点的Mahalanobis 距离相等点的轨迹是超椭球,如果是单位矩阵Σ,则Mahalanobis距离就是通常的欧氏距离。
问答第3题答:监督学习方法用来对数据实现分类,分类规则通过训练获得。
该训练集由带分类号的数据集组成,因此监督学习方法的训练过程是离线的。
非监督学习方法不需要单独的离线训练过程,也没有带分类号(标号)的训练数据集,一般用来对数据集进行分析,如聚类,确定其分布的主分量等。
就道路图像的分割而言,监督学习方法则先在训练用图像中获取道路象素与非道路象素集,进行分类器设计,然后用所设计的分类器对道路图像进行分割。
使用非监督学习方法,则依据道路路面象素与非道路象素之间的聚类分析进行聚类运算,以实现道路图像的分割。
问答第4题答:动态聚类是指对当前聚类通过迭代运算改善聚类;分级聚类则是将样本个体,按相似度标准合并,随着相似度要求的降低实现合并。
问答第5题答:在给定观察序列条件下分析它由某个状态序列S产生的概率似后验概率,写成P(S|O),而通过O 求对状态序列的最大似然估计,与贝叶斯决策的最小错误率决策相当。
问答第6题答:协方差矩阵为,则1)对角元素是各分量的方差,非对角元素是各分量之间的协方差。
2)主分量,通过求协方差矩阵的特征值,用得,则,相应的特征向量为:,对应特征向量为,对应。
这两个特征向量即为主分量。
3) K-L变换的最佳准则为:对一组数据进行按一组正交基分解,在只取相同数量分量的条件下,以均方误差计算截尾误差最小。
4)在经主分量分解后,协方差矩阵成为对角矩阵,因而各主分量间相关消除。
模式识别习题参考1-齐敏教材第6章
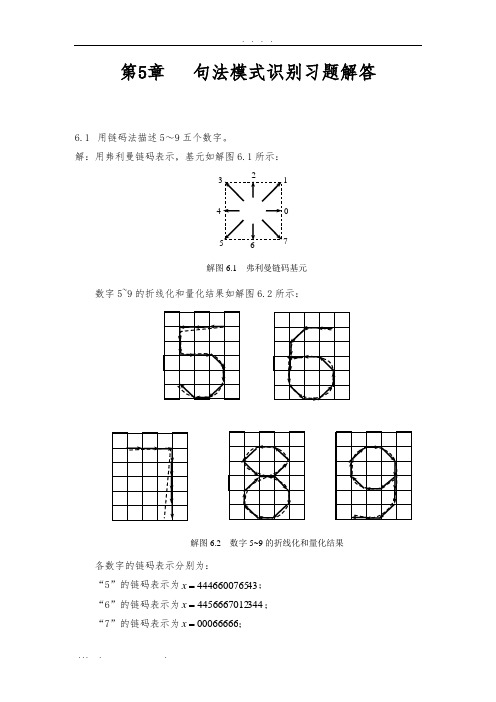
第5章 句法模式识别习题解答6.1 用链码法描述5~9五个数字。
解:用弗利曼链码表示,基元如解图6.1所示:数字5~9的折线化和量化结果如解图6.2所示:各数字的链码表示分别为:“5”的链码表示为434446600765=x ; “6”的链码表示为3444456667012=x ; “7”的链码表示为00066666=x ;0 17解图6.1 弗利曼链码基元解图6.2 数字5~9的折线化和量化结果“8”的链码表示为21013457076543=x ; “9”的链码表示为5445432107666=x 。
6.2 定义所需基本基元,用PDL 法描述印刷体英文大写斜体字母“H ”、“K ”和“Z ”。
解:设基元为:用PDL 法得到“H ”的链描述为)))))(~((((d d c d d x H ⨯+⨯+=;“K ”的链描述为))((b a d d x K ⨯⨯+=; “Z ”的链描述为))((c c g x Z ⨯-=。
6.3 设有文法),,,(S P V V G T N =,N V ,T V 和P 分别为},,{B A S V N =,},{b a V T =:P ①aB S →,②bA S →,③a A →,④aS A →⑤bAA A →,⑥b B →,⑦bS B →,⑧aBB B → 写出三个属于)(G L 的句子。
解:以上句子ab ,abba ,abab ,ba ,baab ,baba 均属于)(G L 。
bcadeabba abbA abS aB S ⇒⇒⇒⇒ ① ⑦ ② ③ab aB S ⇒⇒ ① ⑥ ba bA S ⇒⇒② ③ abab abaB abS aB S ⇒⇒⇒⇒ ① ⑦ ① ⑥baab baaB baS bA S ⇒⇒⇒⇒ ② ④ ① ⑥baba babA baS bA S ⇒⇒⇒⇒② ④ ② ③6.4 设有文法),,,(S P V V G T N =,其中},,,{C B A S V N =,}1,0{=T V ,P 的各生成式为①A S 0→,②B S 1→,③C S 1→ ④A A 0→,⑤B A 1→,⑥1→A ⑦0→B ,⑧B B 0→,⑨C C 0→,⑩1→C问00100=x 是否属于语言)(G L ? 解:由可知00100=x 属于语言)(G L 。
(完整word版)模式识别试题及总结

一、填空与选择填空(本题答案写在此试卷上,30分)1、模式识别系统的基本构成单元包括:模式采集、特征提取与选择和模式分类。
2、统计模式识别中描述模式的方法一般使用特真矢量;句法模式识别中模式描述方法一般有串、树、网。
3、聚类分析算法属于(1);判别域代数界面方程法属于(3)。
(1)无监督分类 (2)有监督分类(3)统计模式识别方法(4)句法模式识别方法4、若描述模式的特征量为0-1二值特征量,则一般采用(4)进行相似性度量。
(1)距离测度(2)模糊测度(3)相似测度(4)匹配测度5、下列函数可以作为聚类分析中的准则函数的有(1)(3)(4)。
(1)(2) (3)(4)6、Fisher线性判别函数的求解过程是将N维特征矢量投影在(2)中进行。
(1)二维空间(2)一维空间(3)N-1维空间7、下列判别域界面方程法中只适用于线性可分情况的算法有(1);线性可分、不可分都适用的有(3)。
(1)感知器算法(2)H-K算法(3)积累位势函数法8、下列四元组中满足文法定义的有(1)(2)(4)。
(1)({A, B}, {0, 1}, {A→01, A→ 0A1 , A→ 1A0 , B→BA , B→ 0}, A)(2)({A}, {0, 1}, {A→0, A→ 0A}, A)(3)({S}, {a, b}, {S → 00S, S → 11S, S → 00, S → 11}, S)(4)({A}, {0, 1}, {A→01, A→ 0A1, A→ 1A0}, A)9、影响层次聚类算法结果的主要因素有(计算模式距离的测度、(聚类准则、类间距离门限、预定的类别数目))。
10、欧式距离具有( 1、2 );马式距离具有(1、2、3、4 )。
(1)平移不变性(2)旋转不变性(3)尺度缩放不变性(4)不受量纲影响的特性11、线性判别函数的正负和数值大小的几何意义是(正(负)表示样本点位于判别界面法向量指向的正(负)半空间中;绝对值正比于样本点到判别界面的距离。
模式识别习题及答案

模式识别习题及答案模式识别习题及答案模式识别是人类智能的重要组成部分,也是机器学习和人工智能领域的核心内容。
通过模式识别,我们可以从大量的数据中发现规律和趋势,进而做出预测和判断。
本文将介绍一些模式识别的习题,并给出相应的答案,帮助读者更好地理解和应用模式识别。
习题一:给定一组数字序列,如何判断其中的模式?答案:判断数字序列中的模式可以通过观察数字之间的关系和规律来实现。
首先,我们可以计算相邻数字之间的差值或比值,看是否存在一定的规律。
其次,我们可以将数字序列进行分组,观察每组数字之间的关系,看是否存在某种模式。
最后,我们还可以利用统计学方法,如频率分析、自相关分析等,来发现数字序列中的模式。
习题二:如何利用模式识别进行图像分类?答案:图像分类是模式识别的一个重要应用领域。
在图像分类中,我们需要将输入的图像分为不同的类别。
为了实现图像分类,我们可以采用以下步骤:首先,将图像转换为数字表示,如灰度图像或彩色图像的像素矩阵。
然后,利用特征提取算法,提取图像中的关键特征。
接下来,选择合适的分类算法,如支持向量机、神经网络等,训练模型并进行分类。
最后,评估分类结果的准确性和性能。
习题三:如何利用模式识别进行语音识别?答案:语音识别是模式识别在语音信号处理中的应用。
为了实现语音识别,我们可以采用以下步骤:首先,将语音信号进行预处理,包括去除噪声、降低维度等。
然后,利用特征提取算法,提取语音信号中的关键特征,如梅尔频率倒谱系数(MFCC)。
接下来,选择合适的分类算法,如隐马尔可夫模型(HMM)、深度神经网络(DNN)等,训练模型并进行语音识别。
最后,评估识别结果的准确性和性能。
习题四:如何利用模式识别进行时间序列预测?答案:时间序列预测是模式识别在时间序列分析中的应用。
为了实现时间序列预测,我们可以采用以下步骤:首先,对时间序列进行平稳性检验,确保序列的均值和方差不随时间变化。
然后,利用滑动窗口或滚动平均等方法,将时间序列划分为训练集和测试集。
模式识别练习题

2013模式识别练习题一. 填空题1、模式识别系统的基本构成单元包括:模式采集、特征的选择和提取和模式分类。
2、统计模式识别中描述模式的方法一般使用特征矢量;句法模式识别中模式描述方法一般有串、树、网。
3、影响层次聚类算法结果的主要因素有计算模式距离的测度、聚类准则、类间距离阈值、预定的类别数目。
4、线性判别函数的正负和数值大小的几何意义是正负表示样本点位于判别界面法向量指向的正负半空间中,绝对值正比于样本点与判别界面的距离。
5、感知器算法1 ,H-K算法 2 。
(1)只适用于线性可分的情况;(2)线性可分、不可分都适用。
6、在统计模式分类问题中,聂曼-皮尔逊判决准则主要用于某一种判别错误较另一种判别错误更为重要的情况;最小最大判别准则主要用于先验概率未知的情况。
7、“特征个数越多越有利于分类”这种说法正确吗?错误。
特征选择的主要目的是从n个特征中选取最有利于分类的m个特征(m<n),以降低特征维数。
一般在和(C n m>>n )的条件下,可以使用分支定界法以减少计算量。
8、散度J ij越大,说明ωi类模式与ωj类模式的分布差别越大;当ωi类模式与ωj类模式的分布相同时,J ij= 0。
二、选择题1、影响聚类算法结果的主要因素有(B、C、D )。
A.已知类别的样本质量;B.分类准则;C.特征选取;D.模式相似性测度2、模式识别中,马式距离较之于欧式距离的优点是(C、D)。
A.平移不变性;B.旋转不变性;C尺度不变性;D.考虑了模式的分布3、影响基本K-均值算法的主要因素有(ABD)。
A.样本输入顺序;B.模式相似性测度;C.聚类准则;D.初始类中心的选取4、位势函数法的积累势函数K(x)的作用相当于Bayes判决中的(B D)。
A. 先验概率;B. 后验概率;C. 类概率密度;D. 类概率密度与先验概率的乘积5、在统计模式分类问题中,当先验概率未知时,可以使用(BD )。
A. 最小损失准则;B. 最小最大损失准则;C. 最小误判概率准则;D. N-P 判决6、散度J D 是根据( C )构造的可分性判据。
模式识别导论习题集

模式识别导论习题集模式识别导论习题集1、设⼀幅256×256⼤⼩的图像,如表⽰成向量,其维数是多少?如按⾏串接成⼀维,则第3⾏第4个象素在向量表⽰中的序号。
解:其维数为2;序号为256×2+4=5162、如标准数字1在5×7的⽅格中表⽰成如图所⽰的⿊⽩图像,⿊为1,⽩为0,现若有⼀数字1在5×7⽹格中向左错了⼀列。
试⽤分别计算要与标准模板之间的欧⽒距离、绝对值偏差、偏差的夹⾓表⽰,异⼰⽤“异或”计算两者差异。
解:把该图像的特征向量为5×7=35维,其中标准模版的特征向量为:x =[0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0]T待测样本的特征向量为:y =[0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0]T,绝对值偏差为351|()|14i i i x y =-=∑,夹⾓余弦为cos 0||||||||T x y x y θ==?,因此夹⾓为90度。
3、哈明距离常⽤来计算⼆进制之间的相似度,如011与010的哈明距离为1,010与100距离为3。
现⽤来计算7位LED 编码表⽰的个数字之间的相似度,试计算3与其它数字中的哪个数字的哈明距离最⼩。
解:是“9”,距离为14、对⼀个染⾊体分别⽤⼀下两种⽅法描述:(1)计算其⾯积、周长、⾯积/周长、⾯积与其外接矩形⾯积之⽐可以得到⼀些特征描述,如何利⽤这四个值?属于特征向量法,还是结构表⽰法?(2)按其轮廓线的形状分成⼏种类型,表⽰成a 、b 、c 等如图表⽰,如何利⽤这些量?属哪种描述⽅法? (3)设想其他结构描述⽅法。
解:(1)这是⼀种特征描述⽅法,其中⾯积周长可以体现染⾊体⼤⼩,⾯积周长⽐值越⼩,说明染⾊体越粗,⾯积占外接矩形的⽐例也体现了染⾊体的粗细。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6章 句法模式识别习题解答6.1 用链码法描述5~9五个数字。
解:用弗利曼链码表示,基元如解图6.1所示:数字5~9的折线化和量化结果如解图6.2所示:各数字的链码表示分别为:“5”的链码表示为434446600765=x ; “6”的链码表示为3444456667012=x ; “7”的链码表示为00066666=x ; “8”的链码表示为21013457076543=x ; “9”的链码表示为5445432107666=x 。
17解图6.1 弗利曼链码基元 解图6.2 数字5~9的折线化和量化结果6.2 定义所需基本基元,用PDL 法描述印刷体英文大写斜体字母“H ”、“K ”和“Z ”。
解:设基元为:用PDL 法得到“H ”的链描述为)))))(~((((d d c d d x H ⨯+⨯+=;“K ”的链描述为))((b a d d x K ⨯⨯+=; “Z ”的链描述为))((c c g x Z ⨯-=。
6.3 设有文法),,,(S P V V G T N =,N V ,T V 和P 分别为},,{B A S V N =,},{b a V T =:P ①aB S →,②bA S →,③a A →,④aS A →⑤bAA A →,⑥b B →,⑦bS B →,⑧aBB B → 写出三个属于)(G L 的句子。
解:以上句子ab ,abba ,abab ,ba ,baab ,baba 均属于)(G L 。
6.4 设有文法),,,(S P V V G T N =,其中},,,{C B A S V N =,}1,0{=T V ,P 的各生成式为①A S 0→,②B S 1→,③C S 1→bcadeabba abbA abS aB S ⇒⇒⇒⇒ ① ⑦ ② ③ab aB S ⇒⇒ ① ⑥ba bA S ⇒⇒② ③ abab abaB abS aB S ⇒⇒⇒⇒ ① ⑦ ① ⑥baab baaB baS bA S ⇒⇒⇒⇒ ② ④ ① ⑥baba babA baS bA S ⇒⇒⇒⇒② ④ ② ③④A A 0→,⑤B A 1→,⑥1→A ⑦0→B ,⑧B B 0→,⑨C C 0→,⑩1→C问00100=x 是否属于语言)(G L ? 解:由可知00100=x 属于语言)(G L 。
6.5 写出能产生图示树的扩展树文法,设基元a ,b 分别为“→”和“↓”,它所描述的模式是什么?解:1. 写出生成树的扩展树文法生成式集:2. 检查非终止符的等价性。
a$babbab001000010001000⇒⇒⇒⇒⇒B B A A S① ④ ⑤ ⑧ ⑦⑴$A →14A 2A 3⑵a A →2⑶a A →3⑸b A →59A 6A 5⑷b A →4⑿a A →12(6)a A →6A 7A 8⑺a A →7⑻a A →8⑼b A →9A 10⑽b A →10A 11⑾a A →11A 12查得1172A A A ≡≡。
删除7A 和11A 及其后代生成式,其余生成式中的7A 和11A 用2A 代替,合并后得到3. 建立起始产生式。
将⑴中的1A 用S 代替得到:设推断的扩展树文法为),,,(S P r V G t =',由以上推断得:T N V V V =,},,,,,,,{10965432A A A A A A A S V N =,},,{b a $V T =2)(=$r ,}0,1{)(=a r ,}1,2{)(=b rP 的各生成式为当基元a ,b 分别为“→”和“↓”时, 它所描述的模式如解图6.3所示:a ab b b ba aa aa$ $S →4A 2⑸b A →59A 6A 5⑷b A →4(6)a A →6A 2⑼b A →9A 10⑽b A →10A 2⑴$A →14A 2A 3⑵a A →2⑶a A →3⑸b A →59A 6A 5⑷b A →4(6)a A →6A 2⑼b A →9A 10⑽b A →10A 2⑴$S →4A 2A 3⑵a A →2⑶a A →3解图6.3 描述的模式6.6 已知)(G L 的正样本集}0010,111,100,01{=+R ,试推断出余码文法c G 。
解:设余码文法为),,,(S P V V G T N c =。
(1) 由+R 得c G 的终止符集}1,0{=T V 。
(2) 求+R 的全部余码,组成非终止符集N V 。
+R 的全部余码为}0010,111,100,01{=+R D λ,}010,1{0=+R D ,}11,00{1=+R D}{01λ=+R D ,}0{10=+R D ,}1{11=+R D ,}10{00=+R D }{100λ=+R D ,}{111λ=+R D , }0{001=+R D ,}{0010λ=+R D等号右边相同的合并,非空余码标以符号组成非终止符集N V :}0010,111,100,01{==+R D S λ,}010,1{01==+R D U ,}11,00{12==+R D U}0{103==+R D U ,}1{114==+R D U ,}10{005==+R D U所以},,,,,{54321U U U U U S V N =。
(3) 建立生成式集P 。
由10}010,1{U S D ==,有生成式10U S →; 由510}10{U U D ==,有生成式510U U →; 由320}0{U U D ==,有生成式320U U →; 由λ=30U D ,有生成式03→U ;由21}11,00{U S D ==,有生成式21U S →; 由λ=11U D ,有生成式11→U ;由421}1{U U D ==,有生成式421U U →; 由λ=41U D ,有生成式14→U ; 由351}0{U U D ==,有生成式351U U →; 所以余码文法),,,(S P V V G T N c =为},,,,,{54321U U U U U S V N =,}1,0{=T V P :10U S →,510U U →,320U U →,03→U 21U S →,11→U ,421U U →,14→U ,351U U →6.7 设文法),,,(S P V V G T N =,其中},,{B A S V N =,}1,0{=T V ,P 的各生成式为①1→S ,②1B S →,③B S →④A B 1→,⑤A B B 1→,⑥0→A ,⑦0A A →设待识别链1000=x ,试用填充树图法的顶下法分析x 是否属于)(G L ? 解:(1) 从S 开始考察P 中的①、②、③式:若选①,则结果为x =1,排除;若选②,导出的x 末位必为1,与题不符,排除; 选③式,如解图6.4(a)所示。
(2) 填充目标为B ,考察④、⑤均可填充,先试④,如解图6.4(b)所示。
若不行,再返回用⑤式。
(3) 此时填充目标为A ,考察⑥、⑦。
若选⑥,导出的x 为 2位,与题不符,排除。
选⑦式,如解图6.4(c)所示。
(4) 类似地,得到图6.4所示各步结果,树叶为1000。
故x 属于)(G L 。
6.8 设上下文无关文法),,,(S P V V G T N =,},{C S V N =,}1,0{=T V ,P 中生成式的乔姆斯基范式为CC S →,CS S →,1→S ,SC C →,CS C →,0→C用CYK 分析法分析链01001=x 是否为该文法的合法句子。
解图6.4 填充树图过程 S1BAAS1BAAS1BAAS1BAS B (a) (b) (c) (d) (e)解:待识别链为5位,构造5行5列的三角形分析表,如解图6.5所示。
求表中元素ij t 的值:(1) 令1=j ,求1i t ,51≤≤i 。
各子链为0,1,0,0,1。
对于01=a ,C t =11; 对于12=a ,S t =21; 对于03=a ,C t =31; 对于04=a ,C t =41。
对于15=a ,S t =41。
(2) 令2=j ,求2i t ,41≤≤i 。
各子链为01,10,00,01。
对于0121=a a ,因有CS S →和CS C →,0→C ,1→S ,故S C t ,12=; 对于1032=a a ,有SC C →,1→S ,0→C ,故C t =22。
对于0043=a a ,有CC S →,0→C ,0→C ,故S t =32。
对于0154=a a ,有CS S →和CS C →,0→C ,1→S ,故S C t ,42=; (3) 令3=j ,求3i t ,31≤≤i 。
各子链为010,100,001。
对于010321=a a a ,因有CC S →,0→C ,10*⇒C ;和SC C →,01*⇒S , 0→C 。
故S C t ,13=。
类似地有S t =23,S C t ,33=,S C t ,14=,S C t ,24=,S C t ,15=。
填表结果如解图6.6所示。
解图6.5 分析表t 14 t 13t 12 t 11t 23t 22 t 21t 32 t 31t 41t 15 t 51t 42 t 33t 24因为S 在15t 中,所以)(G L x ∈。
6.9 已知正则文法),,,(S P V V G T N =,其中},{B S V N =,},{b a V T =,P 的各生成式为aB S →,aB B →,bS B →,a B →构成对应的有限态自动机,画出自动机的状态转换图。
解:设有限态自动机),,,,(0∑=F q Q A δ,由A 与G 的对应关系得∑==},{b a VT},,{F B S F V Q N ==S q =0δ:由aB S →,有B a S =),(δ;由aB B →,a B →有},{),(F B a B =δ;由bS B →,有S b B =),(δ。
故有限态自动机),,,,(0∑=F q Q A δ为∑=},{b a ,},,{F B S Q =,S q=0δ:B a S =),(δ,},{),(F B a B =δ,S b B =),(δ解图6.6 CYK 分析表填表结果 C,S C,S CS C SS CCC,S SC,S C,S C,S C,S 解图 6.7 自动机的状态转换图6.10 已知有限态自动机),,,,(0∑=F q Q A δ,其中∑=}1,0{,},,,{321q q q q Q =,}{3qF =A 的状态转换图如图6.15所示,求A 对应的正则文法G 。
解:设正则文法为),,,(S P V V G T N =,由G 与A 的对应关系得:},,,{3210q q q q Q V N ==;∑==}1,0{T V ;0q S =;根据状态转换图有:P :因}{)0,(20q q =δ,有200q q →; 因}{)1,(10q q =δ,有101q q →;因}{)0,(31q q =δ,有310q q →;而F q ∈3,故01→q ; 因}{)1,(01q q =δ,有011q q →; 因}{)0,(02q q =δ,有020q q →;因}{)1,(32q q =δ,有321q q →;而F q ∈3,故12→q ; 因}{)0,(13q q =δ,有130q q →; 因}{)1,(23q q =δ,有231q q →。
