北京理工大学数学专业微分几何2012级期末试题(MTH17071)
北京理工大学2012-2013学年第一学期工科数学分析期末试题(A卷)试题2012-2(A)
1 北京理工大学2012-2013学年第一学期 工科数学分析期末试题(A 卷)一. 填空题（每小题2分, 共10分）1. 设⎪⎩⎪⎨⎧<≥++=01arctan 01)(x x x x a x f 是连续函数，则=a ___________.2. 曲线θρe 2=上0=θ的点处的切线方程为_______________________________.3. 已知),(cos 4422x o bx ax ex x ++=- 则_,__________=a .______________=b 4. 微分方程1cos2=+y dx dy x 的通解为=y __________________________________. 5. 质量为m 的质点从液面由静止开始在液体中下降, 假定液体的阻力与速度v 成正比, 则质点下降的速度)(t v v =所满足的微分方程为_______________________________.二. (9分) 求极限 210)sin (cos lim xx x x x +→.三. (9分) 求不定积分⎰+dx e xx x x )1arctan (12. 四. (9分) 求322)2()(x x x f -=在区间]3,1[-上的最大值和最小值.五. (8分) 判断212arcsin arctan )(x x x x f ++= )1(≥x 是否恒为常数. 六. (9分) 设)ln(21arctan 22y x x y +=确定函数)(x y y =, 求22,dxy d dx dy . 七. (10分) 求下列反常积分. (1);)1(122⎰--∞+x x dx (2) .1)2(10⎰--x x dx八. (8分) 一垂直立于水中的等腰梯形闸门, 其上底为3m, 下底为2m, 高为2m, 梯形的上底与水面齐平, 求此闸门所受到的水压力. (要求画出带有坐标系的图形)九. (10分) 求微分方程x e x y y y 3)1(96+=+'-''的通解.十. (10分) 设)(x f 可导, 且满足方程a dt t f x x x f xa +=+⎰)())((2 ()0(>a , 求)(x f 的表达式. 又若曲线)(x f y =与直线0,1,0===y x x 所围成的图形绕x 轴旋转一周所得旋转体的体积为,67π 求a 的值. 十一. (8分) 设)(x f 在]2,0[上可导, 且,0)2()0(==f f ,1sin )(121=⎰xdx x f 证明在)2,0(内存在ξ 使.1)(='ξf。
北京理工大学数学专业解析几何期末试题(MTH17014-H0171006)
北京理工大学数学专业解析几何期末试题(MTH17014-H0171006)课程编号：MTH17014 北京理工大学2011-2012学年第一学期2011级本科生解析几何期末试题A 卷姓名--------------，班级------------，学号--------------，题目一 二三四五六总分得分一，单选题(30分)1,已知空间三点A,B,C,下面哪个条件能确定A,B,C 四点共面( ) (a),空间任意一点O,三点满足 (b),空间任意一点O,三点满足(c),空间任意一点O,三点满足(d),空间任意一点O,三点满足2, 已知三向量满足下面哪个条件说明这三向量共面( )(a), , (b),, (c), , (d), .3,在一仿射坐标系中,平面,点A(1,-2,-1)和点B(2,-1,3).则下面说法正确的是( )(a)点A 和点B 在平面π的两侧; (b)点A 和点B 在平面π的同侧;(c)线段AB 平行于平面π; (d)线段AB 垂直于平面π.4, 在仿射坐标系中,已知直线和直线,则下面说法正确的是( ).OA OB OC =+ 11.22OA OB OC =+0.OA OB OC ++= 110.23OA OB OC ++=,,,αβγ()0αβγ⋅=0.αββγγα⨯+⨯+⨯=()0αβγ⨯⨯=()()αβγβγα⨯∙=⨯∙:2430x y z π+++=2103260x z x y ++=⎧⎨+-=⎩2102140x y z x z +--=⎧⎨+-=⎩(a)两直线平行; (b)两直线相交; (c)两直线异面; (d)两直线重合.5, 在仿射坐标系中,已知平面和直线,则下面说法正确的是( )(a)直线和平面平行; (b)直线和平面相交; (c)直线在平面上; (d)直线和平面垂直.6,在平面仿射坐标中,直线与轴相交,则( )(a),(b),(c),(d)7，在空间直角坐标系下，方程的图形是（ ）(a),椭球面；(b),单叶双曲面；(c),双叶双曲面；(d),锥面。
北京理工大学数学专业数理统计期末试题（07000233）
北京理⼯⼤学数学专业数理统计期末试题（07000233）课程编号：07000233 北京理⼯⼤学2011-2012学年第⼆学期2010级数理统计期末试题A 卷⼀、设总体()20,X N σ，12,,,m n X X X +是抽⾃总体X 的简单随机样本，求常数c 使得随机变量2221222212mm m m n X X X Y c X X X ++++++=?+++服从F 分布，指出分布的⾃由度并证明。
⼆、设总体()2,X N µσ，其中220σσ=为已知常数，R µ∈为未知参数。
12,,,nX X X 是抽⾃总体X 的简单随机样本，12,,,n x x x 为相应的样本观测值。
1.求参数µ的矩估计；2.求参数µ和2EX 的极⼤似然估计；3.证明1n i i i X X α='=∑，其中11ni i α==∑和11ni i X X n ==∑都是µ的⽆偏估计；4.⽐较两个⽆偏估计X '和X 的有效性并解释结果。
三、设总体X 服从泊松分布()P λ，123,,X X X 是抽⾃总体X 的简单随机样本，设假设检验问题011:3;:3H H λλ==的否定域为(){}123,,0.5D X X XX =≤。
1.求该检验问题犯第⼀类错误的概率；2.求该检验问题犯第⼆类错误的概率和在1H 下的功效函数。
四、设总体X 的概率密度函数为()32,0,20,0xx e x f x x θθθ-?>?=??≤?，其中0θ>为未知参数，12,,,n X X X 是抽⾃总体X 的简单随机样本。
1.验证样本分布族是指数族，并写出其⾃然形式（标准形式）；2.证明()1nii T X X==∑是充分完全（完备）统计量，并求()ET X ；3.利⽤充分完全统计量法和Cramer-Rao 不等式⽅法证明113n i i X n =∑是1θ的⼀致最⼩⽅差⽆偏估计。
北京理工大学《高等数学》历年期末考试试题及答案解析(精编版)
x = (t − 1)et 八. 设曲线 C 的方程为 y = 1 − t4
求
dy dx
,
d2y dx2
及曲线
C
在参数
t
=
0
对应点处
–2/48–
第 1 部分 北京理工大学试题集
的曲率半径.
九. 设 f ′(x).
f (x)
=
1 x
−
ex
1 −
1,
x
<
0
1
−
1 c2os x
x
,
, x
x= >0
等于
mg k
.
∫1
十一. 设 f (x) 在 [0, 1] 上连续, 在 (0, 1) 内可导, 且满足 f (1) = 2 2 xe1−x f (x)dx, 证明:
0
至少存在一点 ξ, 使得 f ′(ξ) = (1 − ξ−1) f (ξ).
1.2 2011 级秋季学期期末试卷
一. 填空题
1. 极限 lim
x→0
x
− ln(1 x2
+
x)
=
2. 设 y
=
x2 + ln x, 则
dx dy
=
dy =
∫∞
3. 广义积分
e
dx x ln2
x
=
4.
微分方程
y′′
=
1
1 + x2
的通解为
; lim
1
∫
x
(1
+
sin
2t)
1 t
dt
=
.
x→0 x 0
√ ; 设 f 可导,y = f (tan x) + 1 − x2, 则
北京理工大学2011-2012学年第二学期数学物理方程与特殊函数期末试题(A卷)
课程编号： 07000125 北京理工大学2011-2012学年第二学期2010级数学物理方程与特殊函数期末试题（A 卷）班级_______________学号_______________姓名______________成绩_____________一、简答下列各题（直接写出结果，无需推导求解，每题5分，共计15分）1.设正方形薄板上下两面绝热，板的两边(0x =,x a =)始终保持零度,另外两边(0y =,y a =)的温度分别为()f x 和()g x ,请写出板内稳恒状态下的温度分布所满足的定解问题。
2. 长为1的均匀细杆侧表面绝热，0x =端有恒定热流q 进入，1x =端绝热，杆的初始温度为()f x , 试写出杆内温度分布的定解问题。
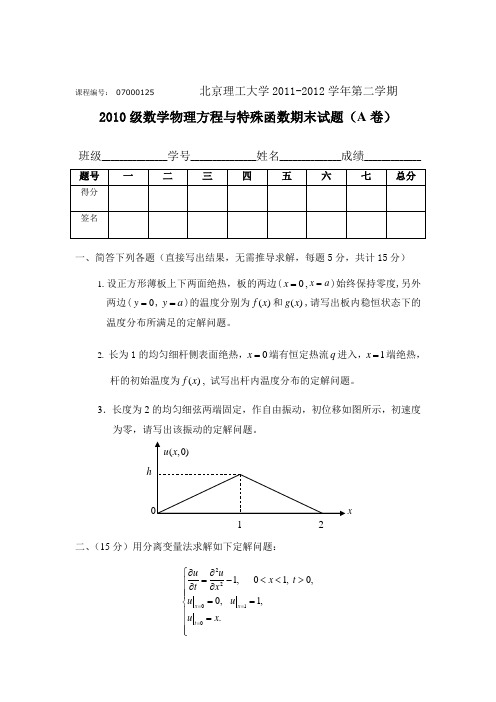
3．长度为2的均匀细弦两端固定，作自由振动，初位移如图所示，初速度为零，请写出该振动的定解问题。
hx1 2二、（15分）用分离变量法求解如下定解问题：220101, 01, 0,0, 1,.x x t u ux t t x u u u x ===⎧∂∂=-<<>⎪∂∂⎪⎪==⎨⎪=⎪⎪⎩三、（15分）用特征线法解下列定解问题：0020, , 0,|sin , |0.tt xt xx t t t u u u x t u x u ==+-=-∞<<+∞>⎧⎨==⎩四、（15分）用积分变换法求解如下定解问题：001,0,0,|1,| 1.xy x y u x y u y u ===>>⎧⎪=+⎨⎪=⎩附：常用的拉普拉斯变换五、（15分）求拉普拉斯方程第一边值问题在半空间1y >-内的格林函数，并求解定解问题：01,(1)().xx yy zz u u u y u x z f x z x z ++=>-⎧⎨-=-∞<<+∞⎩，，，，， ，六、（15分） 设(1,2,)i i α= 是一阶贝塞尔函数1()J x 的正零点，将函数3()(01)f x x x =≤≤ 展开成贝塞尔函数1()i J x α的级数。
（完整word版）北京理工大学数学专业泛函分析期末试题（MTH17060）
（完整word版）北京理⼯⼤学数学专业泛函分析期末试题（MTH17060）北京理⼯⼤学2012-2013学年第⼀学期2010级泛函分析试题（A 卷）⼀、（10分）设T 是赋范线性空间X 到⾃⾝的线性映射。
证明以下三条等价：（1）T 连续；（2）T 在零点连续；（3）T 有界。
⼆、（10分）设H 是Hilbert 空间。
证明：（1）若n x x →，则对于任意固定的y H ∈，()(),,n x y x y →；（2）若n x x →，n y y →，则()(),,n n x y x y →。
三、（10分）设H 是Hilbert 空间，()A B H ∈且存在0m >使得()2,,x H Ax x m x ?∈≥，证明：存在()1A B H -∈。
四、（10分）设H 是Hilbert 空间，M 是H 的线性⼦空间。
证明：M 在H 中稠密的充分必要条件是{}M θ⊥=。
注：M 仅为H 的⼦集时充分性不成⽴，试举反例五、（15分）设[]0,1C 为区间[]0,1上连续函数的全体，对于[]0,1f C ∈，令[]()0,1max x f f x ∈=。
证明：（1）[]0,1C 是完备的赋范线性空间，即Banach 空间；（2）对于[]0,1t ∈，令()()t F f f t =，则t F 是[]0,1C 上线性有界泛函，求t F 。
六、（15分）设[]2,0,1,1,2,k f f L k ∈=L ，且[],..0,1k f f a e →。
证明：lim k k f f →∞=当且仅当lim 0k k f f →∞-=，其中()[][]12220,1,0,1f f x dx f L ?? ?=∈ ?。
七、（15分）设12,f f 是Hilbert 空间H 上的线性⽆关的线性有界泛函，12ker ker M f f =I。
证明：（1）M 是闭的线性⼦空间；（2）存在12,y y H ∈使得对于x H ∈，有01122x x y y λλ=++，其中0x 为x 在M 上的正交投影，12,λλ∈￡。
【数学】北京理工大学数学专业数学析试题MTHMTH
【关键字】数学课程编号：MTH17042 北京理工大学2014-2015学年第一学期2014.11.32013级数学专业数学分析Ⅲ阶段测验（一）试题1.设是中的调和函数，S是中任意的分片光滑闭曲面。
求证：，其中和分别表示函数和沿S 外法线方向的方向导数。
2.叙述正项级数敛散性的比较判别法和D’Alembert比值判别法，并利用前者证明后者。
3.判断下列级数的敛散性：（1）（2）（3）（4）（5）4.设。
又设广义极限存在。
求证：当（含）时，级数收敛；当（含）时，级数发散。
5.研究级数的敛散性，包括绝对收敛性和条件收敛性，其中是实参数。
6.设收敛，其中R>0，求证：对一切，绝对收敛。
7.设，且有极限。
求证：数列收敛，且。
8.设存在，又设绝对收敛。
求证：。
课程编号：MTH17042 北京理工大学2014-2015学年第一学期2014.112013级数学专业数学分析Ⅲ期中试卷一、（15分）（1）设数项级数与均绝对收敛，问：是否一定收敛？为什么？如果收敛，绝对收敛，那么是否一定收敛？为什么？（2）设，绝对收敛，又设的n次部分和序列有界，求证：收敛。
2、（10分）设单调递减，且；又设是任意固定的正整数，求证：收敛当且仅当收敛。
三、（15分）设对每一个自然数n，函数在数集E内有定义，（1）用肯定语气叙述函数项级数在数集E内不满足一致收敛的Cauchy准则的严格含义；（2）设存在数列和，满足，都有，且数项级数与均收敛，试利用一致收敛的Cauchy准则证明函数项级数在数集E内一致收敛。
四、（10分）设，求证：收敛。
五、（15分）研究函数项级数的敛散性，包括绝对收敛和条件收敛，并证明：（1）函数项级数的和函数在其收敛域内连续；（2）函数项级数在其收敛域内不一致收敛。
六、（10分）设。
（1）求证：函数序列在中内闭一致收敛；（2）用两种方法证明在内不一致收敛。
七、（15分）（1）求幂级数的收敛域及和函数；（2）求函数的Maclaurin级数展开式并确定收敛区间。
北京理工大学2012级线性代数(A)A卷及答案
课程编号：A073122 北京理工大学2012-2013学年第一学期线性代数A 试题 A 卷班级 ________ 学号 _________ 姓名 __________ 成绩 ___________一、（10分）已知3阶方阵123035002A ⎛⎫⎪= ⎪ ⎪⎝⎭，计算行列式*123A I+。
二、（10分） 设423110, 2123A AX A X ⎛⎫ ⎪⎪==+ ⎪ ⎪-⎝⎭, 求X 。
三、（10分）已知线性空间4][x F 的自然基为231,,,x x x 。
(1) 证明：2231,12,123,1234x x x x x x ++++++为4][x F 的一个基；(2) 求自然基231,,,x x x 到基2231,12,123,1234x x x x x x ++++++的过渡矩阵，以及23()1h x x x x =--+在后一个基下的坐标。
四、（10分）已知123(1,0,1), (2,2,0), (0,1,1)TTTααα=-==。
(1) 求向量组123,,ααα的一个极大无关组；(2) 求生成子空间123(,,)L ααα的一个标准正交基。
五、（10分）设A 是5阶方阵，且已知存在5阶可逆矩阵P ，使得111112P AP --⎛⎫ ⎪- ⎪= ⎪ ⎪-⎝⎭试写出A 的初等因子，同时判断P 的哪几列是A 的特征向量。
六、（10分）在多项式空间4[]R x 中定义变换σ：233012330201()()a a x a x a x a a a x a a x σ+++=-+++（1）证明：σ是4[]R x 上的线性变换；（2）求σ在4[]R x 的自然基231,,,x x x 下的矩阵，并判断σ是否可逆。
七、（10分）假设A 是m n ⨯的实矩阵，证明：()()TA A A =秩秩八 (10分）已知(1,1,1)T ξ=-是矩阵2125312A a b -⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦的一个特征向量， （1）确定参数a , b 及特征向量ξ所对应的特征值； （2）判断A 是否可以相似对角化，说明理由。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课程编号：MTH17071 北京理工大学2014-2015学年第二学期
2012级微分几何期末试题（回忆复原版）
一、设曲线()r r s =的挠率τ是一非零常数，s 是弧长参数，
求曲线()()()1
r s s s ds βγτ=-⎰ 的曲率和挠率。
二、设在曲线():C r r s =的所有法线上截取长度为λ的一段，它们的端点的轨迹构成曲面
S ，称为围绕曲面C 的管状曲面，其方程是()()()()(),cos sin r
s r s s s θλθβθγ=+⋅+⋅ ，其中s 是曲线的弧长参数，()(),s s βγ分别是曲线C 的主法向量和次法向量，试研究此曲面上各种类型的点的分布。
三、证明：曲面S 的平均曲率12
H b g αβαβ=。
四、求锥面2220x y z +-=上的测地线。
五、写出Gauss-Bonnet 公式，并说明其意义。
六、假定,,x y z 是,,u v w 的光滑函数，证明()()
,,,,x y z dx dy dz du dv dw u v w ∂∧∧=∧∧∂。
附：2012级微分几何考题回忆
1.曲率，挠率
2.椭圆点，双曲点，抛物点
3.练习题第五章第一题
4.测地线
5.写出gauss-bonnet 公式，以及意义
6.第七章倒数第二题。