转动惯量与刚体定轴转动定律
刚体定轴转动的角动量定理和角动量守恒定律

刚体定轴转动的角动量定理和角动量守恒定律
1、刚体定轴转动的角动量
刚体绕定轴转动的角动量等于刚体对该轴的转动惯量与角速度的乘积;方向与角速度的方向相同。
2、刚体定轴转动的角动量定理
(1)微分形式:刚体绕某定轴转动时,作用于刚体的合外力矩,等于刚体绕该定轴的角动量随时间的变化率。
(2)积分形式:当物体绕某定轴转动时,作用在物体上的冲量矩等于角动量的增量。
3、刚体定轴转动的角动量守恒定律
如果物体所受的合外力矩等于零,或者不受外力矩作用,物体的角动量保持不变。
练习:1角动量守恒的条件是 。
0=M 11222
1ωωJ J Mdt t t -=⎰刚体 ) 21J J ==ωJ 恒量
ωJ L =()ωJ dt d dt dL M ==。
一,刚体的定轴转动(运动)二,力矩,刚体定轴转动的转动定律,转动惯量

二、刚体定轴转动的转动定律
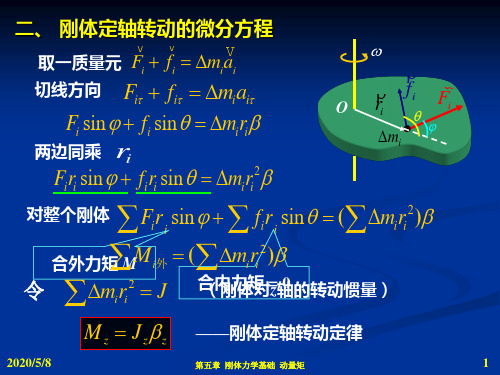
~利用力矩定义+牛顿第二定律,研究刚体作定 轴转动的动力学规律。 设:oz为定轴, 为 P 刚体中任一质点 i ,其 质量为 ∆ m i。质点 iv ur 受外力 F i ,内力 F i ′ 的作用,均在与 O z 轴 相垂直的同一平面内。 ①牛顿第二定律: ur r v F i + Fi ′ = ∆ m i a i 建立自然坐标:切向、法向;
三、转动惯量 J 1.转动惯量的物理意义: 当以相同的力矩分别作用于两个绕定轴转动的不同 刚体时,它们所获得的角加速度一般是不一样的,转 动惯量大的刚体所获得的角加速度小,即角速度改变 得慢,也就是保持原有转动状态的惯性大;反之,转 动惯量小的刚体所获得的角加速度大,即角速度改变 得快,也就是保持原有转动状态的惯性小。因此,转 动惯量是描述刚体在转动中的惯性大小的物理量。 2.与转动惯量有关的因素:①刚体的质量;②转轴的 位置;③刚体的形状。 实质与转动惯量有关的只有前两个因素。形状即质量 分布,与转轴的位置结合决定转轴到每个质元的矢径。
R 3
例3、求长为L、质量为m的均匀细棒对图中不同轴的 转动惯量。 B 解:取如图坐标,dm=λdx A
J
A
=
∫
∫
L
0
x 2 λ dx = mL 2 / 3
A
x λ dx = mL
2 2
JC =
L 2 L − 2
L C L/2 L/2
X B X
/ 12
例4. 求质量 m ,半径 R 的球壳对直径的转动惯量 解:取离轴线距离相等的点的 集合为积分元
F i t ri + F i t′ ri = ∆ m i ri 2 α
外力矩 内力矩
③对所有质元的同样的式子求和:
刚体绕定轴转动定律和角动量定理的表达式

刚体绕定轴转动定律和角动量定理的表达式
刚体绕定轴转动定律:
Mz=Jβ,其中Mz表示对于某定轴的合外力矩,J表示刚体绕给定轴的转动惯量,β表示角加速度。
刚体定轴转动定律是指刚体所受的对于某定轴的合外力矩等于刚体对此定轴的转动惯量与刚体在此合外力矩作用下所获得的角加速度的乘积。
角动量定理的表达式:
角动量守恒定律是物理学的普遍定律之一,反映质点和质点系围绕一点或一轴运动的普遍规律;反映不受外力作用或所受诸外力对某定点(或定轴)的合力矩始终等于零的质点和质点系围绕该点(或轴)运动的普遍规律。
角动量守恒定律是对于质点,角动量定理可表述为质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
角动量L=转动惯量J*角速度ω
所以角动量守恒表达为J1ω1=J2ω2。
刚体绕定轴转动的转动定律

刚体绕定轴转动的转动定律《刚体绕定轴转动的转动定律:一场奇妙的物理之旅》嘿,小伙伴们!今天咱们要来聊一个超级有趣的物理知识,那就是刚体绕定轴转动的转动定律。
你可能会想,这听起来好复杂呀,就像一团乱麻似的。
可是呀,等我给你细细讲来,你就会觉得它像一个好玩的游戏一样。
我记得我第一次听到这个概念的时候,脑袋里就像装了一团浆糊。
我就跑去问我的物理老师。
老师笑着说:“想象一下,刚体就像一个特别结实、不会变形的大圆盘,绕着一个固定的轴在转动,就像咱们教室的门绕着门轴转动一样。
”我听了,眼睛一下子就亮了。
我就说:“那这个转动有啥特殊的规律吗?”老师就开始给我讲这个转动定律。
在这个奇妙的刚体转动世界里,有个很重要的东西叫力矩。
力矩是啥呢?就好比是推动刚体转动的力量。
我当时就想,这和我推东西有啥区别呢?老师就说:“你推一个小盒子在地上走,是让它平动。
可是力矩呢,是让刚体绕着轴转起来的特殊力量。
”我还是有点迷糊,我就拉着我的好朋友小明一起讨论。
我跟小明说:“这个刚体绕定轴转动的转动定律,就像一场神秘的魔法。
”小明说:“啥魔法呀?我都快被这个搞晕了。
”我就学着老师的样子说:“你看啊,力矩就像魔法棒,它越大,刚体转动得就越快,就像魔法棒的力量越大,变出来的魔法就越厉害一样。
”小明眼睛眨巴眨巴的,好像有点懂了。
那这个转动定律到底是怎么回事呢?其实呀,转动定律说的是,刚体所受的合外力矩等于刚体的转动惯量和角加速度的乘积。
这时候我又迷糊了,转动惯量又是啥呢?老师说:“转动惯量就像是刚体自己的一种特性,它决定了刚体有多难被转动起来。
就好比是一个大胖子和一个小瘦子,要让大胖子转起来肯定比小瘦子难,这个大胖子就有更大的转动惯量。
”我和小明就开始做一些小实验。
我们找了一些小物件,试着让它们绕着一个小棍转动。
我们发现,那些重的东西,而且离转动轴远的,真的很难转动起来。
我就说:“哎呀,这个就像大货车的轮子,又大又重,要让它转起来得多费劲呀。
力学10-转动定律,转动惯量,刚体绕定轴转动中的功、能量、功能关系
第五章 刚体力学基础 动量矩
§5-3 绕定轴转动刚体的动能 动能定理
一. 转动动能
设系统包括有 N 个质量元 取 ∆mi,其动能为 其动能为
ω
O
z
1 1 2 2 2 Eki = ∆mivi = ∆miri ω 2 2
刚体的总动能
r ri
r vi
P
• ∆mi
1 1 2 2 2 1 Ek = ∑Eki = ∑ ∆mi ri ω = ∑∆mi ri ω2 = Jω2 2 2 2
第五章 刚体力学基础 动量矩
m1g
m2g
五式联立,可解 五式联立,可解T1,T2,a1,a2,β
2012-4-16 11
总结
力的瞬时作用规律 力矩的瞬时作用规律
v F =0
v v F = ma
静止 匀速直线
M = Jβ
M = 0 静止 匀角速转动
J—转动时惯性大小的量度 转动时惯性大小的量度 力矩的持续作用规律: 力矩的持续作用规律: 空间: 空间: 时间: 时间:
(2) M、J、β必须对同一转轴定义。 必须对同一转轴定义。 、 、 必须对同一转轴定义 (3) M 正比于 β ,力矩越大,刚体的 β 越大 。 力矩相同,若转动惯量不同,产生的角加速度不同。 (4) 力矩相同,若转动惯量不同,产生的角加速度不同。
M (5) 与牛顿定律比较: → F, J → m, β → a 与牛顿定律比较:
14
讨论
(1) 力矩对刚体的功就是力对刚体的功。 力矩对刚体的功就是力对刚体的功。
θ2 θ2
1
(2) 合力矩的功
A= ∫
θ1
∑Midθ = ∑∫θ i i
Midθ = ∑Ai
16定轴转动刚体的角动量转动惯量和定轴转动定律

m
I = I C + md
2
刚体绕质心轴的 转动惯量最小。 转动惯量最小。
12
例5:如图所示刚体对经过棒端且与棒垂直的轴 : 的转动惯量如何计算? 棒长为 棒长为L、圆半径为R) 的转动惯量如何计算?(棒长为 、圆半径为 )
1 2 I L1 = m L L 3 1 I o = mo R 2
1 1 2 I = m LL + moR 3 2
7
.转动惯量的计算 2 .转动惯量的计算
Δm 2 分立质点系 I = ∑( iri ) = ∑ Ii
质量连续分布的刚体
I = ∫ r dm
2
dm为质量元,简称质元。其计算方法如下: 为质量元,简称质元。其计算方法如下:
质量为线分布 质量为面分布
dm = λ dl
dm = σ ds 质量为体分布 dm = ρ dV
Fiτ ri + ∑ f iτ r i = ∑ ∆mi ai ri = ∑ ∆mi ri 2 β ∑
∑ F τ r + ∑ f τ r = ∑ ∆m a r = ∑ ∆m r
i i i
2
⇓ 合外力矩
⇓
i
i i i
i i
β
内力矩之和
刚体定轴 转动定律! 转动定律!
⇓ Iβ
合外力矩) 用M表示∑Fit ri (合外力矩),有: M = Iβ 刚体所受的对于某一固定转动轴的合外力矩等于 刚体所受的对于某一固定转动轴的合外力矩等于 某一固定转动轴 刚体对此转轴的转动惯量与刚体在此合外力矩 对此转轴的转动惯量与刚体在此合外力矩作用 刚体对此转轴的转动惯量与刚体在此合外力矩作用 下所获得的角加速度的乘积。 下所获得的角加速度的乘积。 注意几点: 注意几点: 1. 是矢量式(在定轴转动中力矩只有两个方向)。 是矢量式(在定轴转动中力矩只有两个方向)。 2. M、I、β是对同一轴而言的。 是对同一轴而言的。 3. 具有瞬时性,是力矩的瞬时效应。 具有瞬时性,是力矩的瞬时效应。 4. 转动惯量 是刚体转动惯性大小的量度。 转动惯量I是刚体转动惯性大小的量度 是刚体转动惯性大小的量度。 5.刚体转动定律的地位与牛顿第二定律相当。 刚体转动定律的地位与牛顿第二定律相当。 刚体转动定律的地位与牛顿第二定律相当
刚体定轴转动的转动定律力矩

力矩平衡的条件
静平衡
刚体在转动过程中,如果合力矩 为零,则刚体保持静止状态。
动平衡
刚体在转动过程中,如果合力矩为 零,则刚体保持匀速转动状态。
平衡状态
无论是静平衡还是动平衡,刚体的 平衡状态都满足合力矩为零的条件。
力矩平衡的应用
机械平衡
在机械设计中,通过调整刚体的质量 分布或添加平衡装置,使刚体在转动 过程中满足力矩平衡条件,以保证机 械设备的稳定性和可靠性。
刚体的定轴转动
定轴转动:刚体绕某一固定轴线作旋 转运动。
在定轴转动中,刚体的角速度和角加 速度是矢量,其方向沿固定轴线,而 力矩是改变刚体转动状态的唯一物理 量。
刚体定轴转动的特点
角速度矢量、角加速度矢量和力 矩矢量都与固定轴线平行。
刚体定轴转动时,其上各点的速 度方向与该点到轴线的垂直线段 相垂直,各点的加速度方向与该
实例三:旋转木马的旋转
总结词
旋转木马的旋转是刚体定轴转动的又一实例,通过外力矩的作用,使旋转木马绕轴转动。
详细描述
旋转木马在外力矩的作用下开始转动,当旋转木马转动时,由于摩擦阻力和空气阻力的作用,旋转木 马会逐渐减速并最终停止。
实例四:陀螺的稳定旋转
总结词
陀螺的稳定旋转是刚体定轴转动的最后一个实例,陀螺通过自转保持稳定的旋转状态。
在日常生活和工业生产中,转动 定律也广泛应用于各种旋转运动
的分析和设计。
04
刚体定轴转动的力矩平衡
力矩平衡的概念
力矩平衡
刚体在转动过程中,受到 的力矩之和为零,即合力 矩为零。
力矩
力对转动轴的力矩等于力 和力臂的乘积,其中力臂 是从转动轴到力的垂直距 离。
转动轴
刚体转动的中心轴,可以 是固定的点或线。
10 刚体定轴转动 力矩 转动定律 转动惯量

若棒的质量均匀分布: M 1 mgl sin
2 解:
dMdm gxsin
O
x
2 x d x g x sin 2 g sin x 2 d x
ml
dmg
M 0 l2gsinx2dx2 3gl3sin
例 有一大型水坝高110 m、长1 000 m ,
水深100m,水面与大坝表面垂直,如图所 示. 求作用在大坝上的力,以及这个力对通
i Fji
Fij
M ji
MijMji
一 力矩
用来描述力对刚体
的转动作用.
M Fsrin Fd
d: 力臂
FM 对 转r轴F z的力矩
z
F
O
M r
d
P*
M 方向: 沿转轴,与刚体转动方向 构成右手螺旋关系的方向.
M 方向: 沿转轴, 与刚体转动方向构 成右手螺旋关系的 方向.
其中 Fz对转轴的
力矩为零,故 F对转 轴的力矩
M zrF rF
z
F
k
O
r Fz
F
M zrF sink
(2)合 力矩 等于 各分力矩的矢量和 M M 1 M 2 M 3
M r F r F 1 F 2 . .F n . r F 1 r F 2 . .r . F n
:质量面密度
对质量体分布的刚体:dmdV
:质量体密度
例 一质量为 m、长为 l 的均匀细长棒,求
通过棒中心并与棒垂直的轴的转动惯量 .
Or
Or
l 2 O´ dr l 2
O´ dr l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
转动惯量与刚体定轴转动定律
先阐明几个概念:
刚体:简单的说,即形变可以忽略的物体。
作为理想的物理模型,刚体的特征是有质量、大小和形状,而在处理时我们往往不考虑其形变(但有时会出现断裂、破碎或者磨损的情况)。
力矩:和力类似,并不好直接定义,可以简单的认为是力乘以力臂或者M F r =⨯(关于叉乘,请自行百度)。
转动惯量:度量转动时惯性的量。
详见后文。
下面是准备工作:
定理:无外力系统内各质点相互作用的合力矩为0 证:
①考虑两个质点的系统:
如图,
由牛顿第三定律,
120F F +=,
且1221()F F r r -
而,合力矩=1221121()0F r F r F r r ⨯+⨯=⨯-= 成立。
②假设,含k 个质点的无外力系统其内力的合力矩为0 ③对于含(k+1)个质点的无外力系统,
分为两组,一组含k 个质点,另一组则为第(k+1)个质点。
含k 个质点的一组,其内力的合力矩为
而该组任一质点与第(k+1)个质点的相互作用合力矩也为
0 故含(k+1)个质点的无外力系统其内力的合力矩为
0 因而,无外力系统内各质点相互作用的合力矩为
0 推论:对系统施加M 的外力矩,有i M M =∑ (i M 为系统内第i 个质点所受力矩。
) 证:
将施加外力的质点纳入系统,由上, 则有,0i M M -+=∑ 故,i M M =∑
刚体定轴转动定律:M I β=
(M 为合外力矩,β为角加速度,I 为转动惯量(见下)。
) ①考虑只有一个质点,
由牛顿第二定律:
()r F ma m a a θ==+
(其中,,r
a r a r θ⊥)
则
2
()()[()()]r F r m a a ma m r r
m r r r r mr θθββββ
⨯=+==⨯⨯=-= 『1』
②考虑多个质点时, 对于系统中第i 个质点,
2i i i i F r m r β⨯=
(同一刚体角加速度相同)
有2i i i i i M M F r m r β==⨯=∑∑∑ ③对于连续物体, 则,222i i D
V
m r r dm r dV δρ==∑⎰⎰⎰⎰
(式中dm 表示刚体的某个质元的质量,r 表示该质元到转轴的垂直距离,ρ表示该处的密度,积分遍及整个刚体。
) 式2i i M m r β=∑ 与牛顿第二定律相似,我们称之为刚体定轴转动定律,并视2i i m r ∑为刚体绕轴转动时惯性(回转物体保持
记作I (或J )。
下面是一些关于转动惯量的辅助定理: 平行轴定理:2c I I md =+
(m 为刚体质量,绕通过质心的转轴转动的转动惯量为c I ,I 为绕与该通过质心的转轴距离为d 的转轴转动的转动惯量。
)
『2』 证:
以质心C 为原点,则有0i i m r =∑ (i r 表示i m 到z 轴的垂直距离) 有2c i i I m r =∑
若转轴位于z ’处(方向向量为s r )
则s
r d =
2
2
2
2()2i i s i i s i i s i
c I m r r m r r m r r m
I md =-=++=+∑∑∑∑
垂直轴定理1:z x y I I I =+
(一平面刚体薄板,绕垂直该平面的轴转动的转动惯量z I ,等于绕平面内与该垂直轴相交的任意两相互正交的轴转动的转动惯量之和。
) 证:
注意“薄板”,22,x i i y i i I m y I m x ==∑∑
而,22222()z i i i i i i i i i x y I mr m x y m y m x I I ==+=+=+∑∑∑∑
垂直轴定理2:22x y z D
I I I r dm ++=⎰
(绕交于同一点O 且两两垂直的轴x ,y ,z 的转动惯量分别为,,x y z I I I ,r 为质元dm 到O 的距离。
) 证:
2222222222
(),(),()2()2x y z D
D
D
x y z D
D
I y z dm I x z dm I x y dm
I I I x y z dm r dm
=+=+=+++=++=⎰⎰⎰⎰⎰
伸展定则:
(将物体的任意一点沿转轴方向平移任意大小,该物体绕该轴的转动惯量不变。
) 证: 显然。
应用这些定理,可以简化处理一些问题:
例一:求质量为m ,长为L 的均质细棒绕其端轴转动的转动惯量。
解:
由已知量和量纲知2I kmL = ∵均质 ∴质心C 在棒的中点
又∵绕质心轴转动惯量可视为两段L/2长的细棒绕端轴的转动惯量,即22()22
c m L I k =⋅
由平行轴定理,2()2
c L I m I +=
解得k=1/3 故213
I mL =
例二:求质量为m ,长为a ,宽为b 的均质矩形薄板绕边轴、绕中轴、绕过中心的垂直轴转动的转动惯量。
解: 对边轴:
由伸展定则及例一,绕长轴的转动惯量213
a I m
b = ,
同理,绕短轴,213
b I ma =
对中轴:
由平行轴定理,绕平行于长边的轴,221
()212
x a b I I m mb =-=
同理,21
12
y I ma =
绕过中心的垂直轴: 由垂直轴定理1,221
()12
z x y I I I m a b =+=
+
例三:求质量为m ,半径为R 的均质实心球体绕过球心的轴转动的转动惯量。
解:
由对称性及垂直轴定理2,
2
2
2
5
2
2
86322455
2
5
R D
I r dm r r dr R mR I mR ππρρ∴====⇒=⎰⎰
后记:
我写这篇文章主要是因为在百度上找不到“刚体定轴转动定律”的证明,就在这里给各位读者一个方便。
更加深入的讨论请寻找一些刚体动力学的教材或资料。
这似乎是一个实验定律,但也应能用牛顿定律得出。
文中的证明方法是本人原创(但不一定是独创)。
本人能力有限,如有错误或纰漏,欢迎各位指正。
参考资料:
『1』二重向量积Vector Triple Product https:///wiki/Triple_product#Vector_tri
ple_product
『2』图片来自wikipedia:https:///wiki/Parallel_axis_theorem。
