《结构力学习题集及标准答案》(上)-
《结构力学习题集及标准答案》(下)-2a
第九章 结构的动力计算一、判断题：1、结构计算中，大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变，只有刚度EI 增大到原来的2倍，则周期比原来的周期减小1/2。
4、结构在动力荷载作用下，其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形，图a 刚架的振动自由度为2，图b 刚架的振动自由度也为2。
6、图示组合结构，不计杆件的质量，其动力自由度为5个。
7、忽略直杆的轴向变形，图示结构的动力自由度为4个。
8、由于阻尼的存在，任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率，ω与ωD 的关系为ωω=D 。
二、计算题：10、图示梁自重不计，求自振频率ω。
l l /411、图示梁自重不计，杆件无弯曲变形，弹性支座刚度为k ，求自振频率ω。
l /2l /212、求图示体系的自振频率ω。
l l0.5l 0.513、求图示体系的自振频率ω。
EI = 常数。
ll 0.514、求图示结构的自振频率ω。
l l15、求图示体系的自振频率ω。
EI =常数，杆长均为l 。
16、求图示体系的自振频率ω。
杆长均为l 。
17、求图示结构的自振频率和振型。
l /2l /2l /18、图示梁自重不计，W EI ==⨯⋅2002104kN kN m 2,，求自振圆频率ω。
B2m2m19、图示排架重量W 集中于横梁上，横梁EA =∞，求自振周期ω。
EIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EIEIWEI 221、求图示体系的自振频率ω。
各杆EI = 常数。
a aa22、图示两种支承情况的梁，不计梁的自重。
求图a 与图b 的自振频率之比。
l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ，各杆EA 相同，杆重不计。
求水平自振周期T 。
结构力学习题资料
结构力学复习题一、单选题1、①下图结构的自由度为。
（A）0 （B）-1 （C）-2 （D）1正确答案（B）②下图结构的自由度为。
（A）0 （B）-1 （C）-2 （D）1 正确答案（C）③下图结构的自由度为。
（A）0 （B）-1 （C）-2 （D）1 正确答案（A）④下图结构的自由度为。
（A）0 （B）-1 （C）-2 （D）1 正确答案（D）2、①分析下图所示体系的几何组成为。
（A）几何不变，无多于约束（B）几何可变（C）几何瞬变（D）几何不变，有多于约束正确答案（A）②分析下图所示体系的几何组成为。
（A）几何不变，无多于约束（B）几何可变（C）几何瞬变（D）几何不变，有多于约束正确答案（D）③分析下图所示体系的几何组成为。
（A）几何不变，无多于约束（B）几何可变（C）几何瞬变（D）几何不变，有多于约束正确答案（D）④分析下图所示体系的几何组成为。
（A）几何不变，无多于约束（B）几何可变（C）几何瞬变（D）几何不变，有多于约束正确答案（B）3、①指出下列结构的零杆个数为。
（A）2 （B）3 （C）4 （D）5正确答案（C）②指出下列结构的零杆个数为。
（A）9 （B）10 （C）11 （D）12 正确答案（C）③指出下列桁架的类型。
（A）简单桁架（B）联合桁架（C）组合桁架（D）复杂桁架正确答案（B）④指出下列桁架的类型。
（A）简单桁架（B）联合桁架（C）组合桁架（D）复杂桁架正确答案（A）⑤指出下列结构的单铰个数为。
（A）13 （B）14 （C）15 （D）16正确答案（D）4、①指出下列结构的超静定次数为。
（A）2 （B）3 （C）4 （D）5 正确答案（B）②指出下列结构的超静定次数为。
（A）2 （B）3 （C）4 （D）5 正确答案（C）③指出下列结构的超静定次数为。
（A）2 （B）3 （C）4 （D）5 正确答案（A）④指出下列结构的超静定次数为。
（A）2 （B）3 （C）4 （D）5 正确答案（B）⑤指出下列结构的超静定次数为。
结构力学复习材料(含规范标准答案)
《结构力学》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】：本课程《结构力学》（编号为06014）共有单选题,判断题,计算题1,计算题2,计算题3,计算题4,几何构造分析等多种试题类型，其中，本习题集中有[计算题4]等试题类型未进入。
一、单选题1.弯矩图肯定发生突变的截面是（）。
A.有集中力作用的截面；B.剪力为零的截面；C.荷载为零的截面；D.有集中力偶作用的截面。
2.图示梁中C截面的弯矩是（）。
4m2m4mA.12kN.m(下拉)；B.3kN.m(上拉)；C.8kN.m(下拉)；D.11kN.m(下拉)。
3.静定结构有变温时，（）。
A.无变形，无位移，无内力；B.有变形，有位移，有内力；C.有变形，有位移，无内力；D.无变形，有位移，无内力。
4.图示桁架a杆的内力是（）。
A.2P；B.－2P；C.3P；D.－3P。
5.图示桁架，各杆EA为常数，除支座链杆外，零杆数为（）。
A.四根；B.二根；C.一根；D.零根。
Pal= aP PP66.图示梁A点的竖向位移为（向下为正）（）。
A.)24/(3EIPl； B.)16/(3EIPl； C.)96/(53EIPl； D.)48/(53EIPl。
PEI EIAl/l/2227.静定结构的内力计算与（）。
A.EI无关；B.EI相对值有关；C.EI绝对值有关；D.E无关，I有关。
8.图示桁架，零杆的数目为：（）。
A.5；B.10；C.15；D.20。
9.图示结构的零杆数目为（）。
A.5；B.6；C.7；D.8。
10.图示两结构及其受力状态，它们的内力符合（）。
A.弯矩相同，剪力不同；B.弯矩相同，轴力不同；C.弯矩不同，剪力相同；D.弯矩不同，轴力不同。
PPll11. 刚结点在结构发生变形时的主要特征是（ ）。
A.各杆可以绕结点结心自由转动；B.不变形；C.各杆之间的夹角可任意改变；D.各杆之间的夹角保持不变。
12. 若荷载作用在静定多跨梁的基本部分上，附属部分上无荷载作用，则（ ）。
结构动力学习题答案
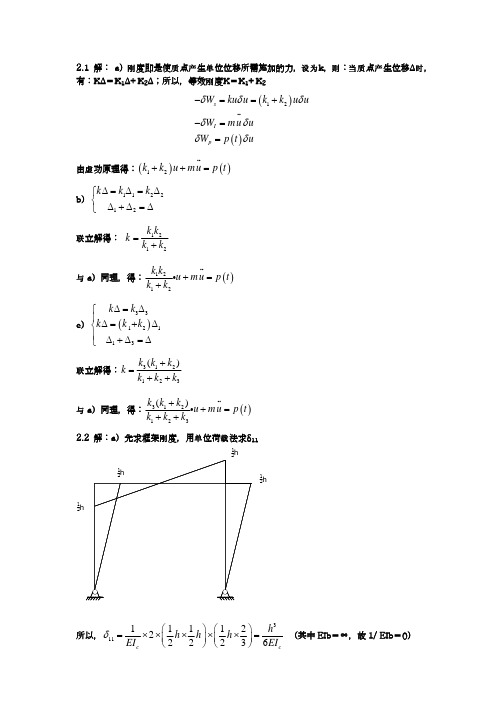
3.4
m2 g k
( m1 + m2 ) u (0) = m2 2 gh
即 u (0) =
i
i
m2 2 gh m1 + m2
动力方程： ( m1 + m2 )( u − ust )′′ + K ( u − ust ) = 0
5 .0 1 = u st 2ξ
(1)
当 w wn = 1 时，发生共振有： Rd 1 =
当 w wn = 1 10 时， Rd 1 =
0 .5 = u st
(1 − 0.1 ) + (2ξ × 0.1)
2 2
1
(2)
2
由式(1),(2)可以解得 ξ = 4.95%
3.6 解：
TR =
[1 − (w w ) ] + [2ξ w w ]
ii
ii
ii
ii
ii
δ Wp = −m2 g sin θ i Lδθ
虚 功原理： δ Ws
+ δ WI + δ W D +δ W p = 0 得：
⎡ m1 + m2 ⎢ mL ⎣ 2
2.6 解：
ii ⎫ ⎧i⎫ m2 L ⎤ ⎧ 0 ⎫ ⎪ u ⎪ ⎡C 0 ⎤ ⎪ u ⎪ ⎡ k 0 ⎤ ⎧ u ⎫ ⎧ +⎢ ⎨ i ⎬+ ⎢ ⎨ ⎬=⎨ ⎬ ⎥ ⎥ 2 ⎥ ⎨ ii ⎬ m2 L ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎩θ ⎭ ⎩−m2 g sin θ i L ⎭ ⎩θ ⎭ ⎩θ ⎭
《结构力学习题集及答案》(上)-
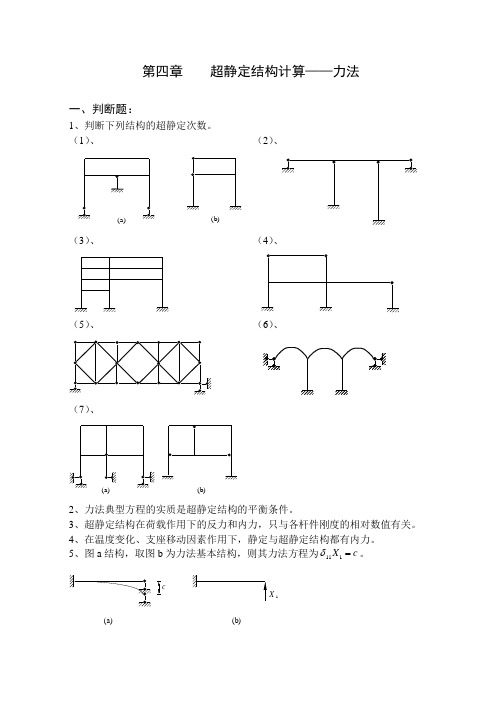
第四章 超静定结构计算——力法一、判断题：1、判断下列结构的超静定次数。
（1）、 （2）、(a )(b)（3）、 （4）、（5）、 （6）、（7）、 (a)(b)2、力法典型方程的实质是超静定结构的平衡条件。
3、超静定结构在荷载作用下的反力和内力，只与各杆件刚度的相对数值有关。
4、在温度变化、支座移动因素作用下，静定与超静定结构都有内力。
5、图a 结构，取图b 为力法基本结构，则其力法方程为δ111X c =。
(a)(b)X 1c6、图a 结构，取图b 为力法基本结构，h 为截面高度，α为线膨胀系数，典型方程中∆12122t a t t l h =--()/()。
t 21t lA h (a)(b)X 17、图a 所示结构，取图b 为力法基本体系，其力法方程为 。
(a)(b)PkPX 1二、计算题：8、用力法作图示结构的M 图。
B EI 3m 4kN A 283kN 3m EI/mC9、用力法作图示排架的M 图。
已知 A = 0.2m 2，I = 0.05m 4，弹性模量为E 0。
q 8m =2kN/m6mI I AMaa aa11、用力法计算并作图示结构的M图。
qll ql/22 EI EI EI12、用力法计算并作图示结构的M图。
q = 2 kN/m 3 m 4 m 4 mA EICEIB13、用力法计算图示结构并作出M图。
E I 常数。
（采用右图基本结构。
）Pl2/3l/3l/3l2/3Pl/3X1X214、用力法计算图示结构并作M图。
EI =常数。
3m 6mq=10kN/m3m2m 4mq =16kN/m2m 2m2m16、用力法计算图示结构并作M 图。
EI =常数。
l l ql l17、用力法计算并作图示结构M 图。
E I =常数。
P Pl lll18、用力法计算图示结构并作弯矩图。
16CD 2EI EI2EI 1A B 100100kNkN m m m 4m19、已知EI = 常数，用力法计算并作图示对称结构的M 图。
结构动力计算课后习题答案
结构动力计算课后习题答案结构动力计算课后习题答案在学习结构动力学这门课程时，我们经常会遇到各种各样的习题。
这些习题旨在帮助我们巩固所学的知识，并提供实践的机会。
在这篇文章中，我将为大家提供一些结构动力计算课后习题的答案，希望能对大家的学习有所帮助。
1. 计算一个简支梁的固有频率。
答案：简支梁的固有频率可以通过以下公式计算：f = (1/2π) * √(k/m)其中，f为固有频率，k为刚度，m为质量。
在简支梁的情况下，刚度k等于弹性模量E乘以截面面积A除以长度L。
质量m等于密度ρ乘以截面面积A除以长度L。
2. 计算一个悬臂梁的固有频率。
答案：悬臂梁的固有频率可以通过以下公式计算：f = (1/2π) * √(3k/m)在悬臂梁的情况下，刚度k等于弹性模量E乘以截面面积A的三次方除以长度L的四次方。
质量m等于密度ρ乘以截面面积A除以长度L。
3. 计算一个简支梁的振动模态。
答案：简支梁的振动模态可以通过以下公式计算：f_n = (n^2 * v) / (2L)其中，f_n为第n个振动模态的频率，v为波速，L为长度。
n为振动模态的序号，从1开始。
4. 计算一个悬臂梁的振动模态。
答案：悬臂梁的振动模态可以通过以下公式计算：f_n = (2n-1) * (v/4L)其中，f_n为第n个振动模态的频率，v为波速，L为长度。
n为振动模态的序号，从1开始。
5. 计算一个简支梁的最大挠度。
答案：简支梁的最大挠度可以通过以下公式计算：δ_max = (5qL^4) / (384EI)其中，δ_max为最大挠度，q为均布载荷，L为长度，E为弹性模量，I为截面惯性矩。
6. 计算一个悬臂梁的最大挠度。
答案：悬臂梁的最大挠度可以通过以下公式计算：δ_max = (qL^4) / (8EI)其中，δ_max为最大挠度，q为均布载荷，L为长度，E为弹性模量，I为截面惯性矩。
以上是一些常见的结构动力计算课后习题的答案。
通过解答这些习题，我们可以更好地理解结构动力学的概念和原理，提高我们的计算能力和问题解决能力。
《结构力学习题集》9-结构动力计算
第九章 结构的动力计算一、是非题1、结构计算中，大小、方向随时间变化的荷载必须按动荷载考虑。
2、忽略直杆的轴向变形，图示结构的动力自由度为4个。
3、仅在恢复力作用下的振动称为自由振动。
4、单自由度体系其它参数不变，只有刚度EI 增大到原来的2倍，则周期比原来的周期减小1/2。
5、图 a 体 系 的 自 振 频 率 比 图 b 的 小 。
l /2l /2l /2l /2(a)(b)6、单 自 由 度 体 系 如 图 ，W =98.kN ，欲 使 顶 端 产 生 水 平位 移 ∆=001.m ，需 加 水 平 力 P =16kN ，则 体 系 的 自振 频 率 ω=-40s 1。
∆7、结构在动力荷载作用下，其动内力与动位移仅与动力荷载的变化规律有关。
8、由于阻尼的存在，任何振动都不会长期继续下去。
9、桁 架 ABC 在 C 结 点 处 有 重 物 W ，杆 重 不 计 ，EA 为 常 数 ，在 C 点 的 竖 向 初 位 移 干 扰 下 ，W 将 作 竖 向 自 由 振 动 。
AC10、不 计 阻 尼 时 ，图 示 体 系 的 运 动 方 程 为 ：m m XX h EI EI EI EI X X P t 00148242424012312⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭+--⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭=⎧⎨⎩⎫⎬⎭()二、选择题1、图 示 体 系 ，质 点 的 运 动 方 程 为 ： A ．()()()y l Ps i n m y EI =-77683θ t /； B ．()()m y EIy l Ps i n /+=19273θ t ； C ．()()m y EIy l Ps i n /+=38473θ t ； D ．()()()y l Ps i n m yEI =-7963θ t / 。
ll0.50.5 2、在 图 示 结 构 中 ，若 要 使 其 自 振 频 率 ω增 大 ，可 以A ．增 大 P ；B ．增 大 m ；C ．增 大 E I ； D ．增 大 l 。
(2021年整理)《建筑力学与结构》课程题库答案
(完整版)《建筑力学与结构》课程题库答案编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)《建筑力学与结构》课程题库答案）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)《建筑力学与结构》课程题库答案的全部内容。
（完整版)《建筑力学与结构》课程题库答案编辑整理：张嬗雒老师尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方,但是我们任然希望 (完整版）《建筑力学与结构》课程题库答案这篇文档能够给您的工作和学习带来便利。
同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉，前进的动力.本文可编辑可修改，如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为〈(完整版）《建筑力学与结构》课程题库答案〉这篇文档的全部内容。
第一章静力学基础一、填空题1、力是物体之间的相互机械作用。
2、力是矢量,力的三要素分别为：大小、方向、作用点3、刚体是在力的作用下不变形的物体4、所谓平衡，就是指物体相对于地球处于静止状态或匀速直线运动状态5、力对物体的作用效果一般分为内（变形）效应和外(运动)效应.6、二力平衡条件是刚体上仅受两力作用而平衡的必要与充分条件是:此两力必须等值、反向、共线。
7、加减平衡力系原理是指对于作用在刚体上的任何一个力系，可以增加或去掉任一个平衡力系，并不改变原力系对于刚体的作用效应。
8、力的可传性是刚体上的力可沿其作用线移动到该刚体上的任一点而不改变此力对刚体的影响。
9、作用于物体上同一点的两个力，可以合成为一个合力，该合力的大小和方向由力的平行四边形法则确定。
郑州大学远程教育结构力学练习题
一、单项选择题1、为了保证结构不致发生过大的变形，并满足使用要求，要计算结构B、刚度2、对结构进行强度计算，是为了保证结构A、既经济又安全3、对结构进行刚度计算，`是为了保证结构A、不致发生过大的变形4、结构的强度是指A、结构抵抗破坏的能力5、结构的刚度是指B、结构抵抗变形的能力力6、杆系结构中的构件的长度D、远远大于截面的高和宽7、结构里学的研究对象是B、杆件结构8、为了保证结构不致发生过大的变形，并满足使用要求，要计算结构B、刚度9、对结构进行强度计算，是为了保证结构A、既经济又安全10、对结构进行刚度计算，是为了保证结构C、不致发生过大的变形11、固定铰支座有几个约束反力分量B、两个12、可动铰支座有几个约束反力分量A、一个13、滑动支座有几个约束反力分量B、两个14、固定端支座有几个约束反力分量C、三个二、多项选择题1、结构的稳定性是指D、结构抵抗失稳的能力E、结构保持原有平衡形式的能力2、下列哪种情况不是平面结构B、所有杆件的轴线都位于同一平面内，荷载与该平面垂直C、所有杆件的轴线都位于同一平面内，荷载与该平面平行D、所有杆件的轴线都不位于同一平面内E、荷载不作用在结构的平面内3、下列哪种情况应按空间结构处理A、所有杆件的轴线都位于同一平面内，荷载与该平面垂直B、所有杆件的轴线都不位于同一平面内D、所有杆件的轴线都位于同一平面内，荷载与该平面平行E、荷载不作用在结构的平面内4、按几何形状，结构可分为A、杆系结构B、板结构C、实体结构D、壳结构5、为了保证结构既经济又安全，要计算结构A、强度C、稳定性6、对结构进行几何组成分析，是为了D、保证结构不发生刚体运动E、寻找恰当的求解方法7、选取结构的计算简图的原则是A、忽略次要因素，便于分析计算C、能反映结构的实际受力特点，使计算结果接近实际情况8、铰结点的约束特点是A、约束的各杆端不能相对移动B、约束的各杆端可相对转动9、铰结点的受力特点是A、可以传递轴力B、可以传递剪力C、不能传递力矩10、刚结点的约束特点是A、约束各杆端不能相对移动C、约束各杆端不能相对转动11、刚结点的受力特点是A、可以传递轴力B、可以传递剪力E、能传递力矩12、如果在一结点处，一些杆端刚结在一起，而另一些杆端铰结一起，这样的结点称为C、组合结点D、不完全铰结点E、半铰结点13、可动铰支座的特点是B、允许杆端沿一个方向移动C、允许杆端转动D、只有一个反力14、定向支座的特点是A、允许杆端沿一定方向自由移动而沿其它方向不能移动B、不允许杆端转动D、有一个反力和一个反力偶15、固定端支座的特点是A、不允许杆端移动B、不允许杆端转动D、有两个反力和一个反力偶三、判断题1、结构是建筑物和构筑物中承受荷载起骨架作用的部分。
结构动力学习题答案
结构动力学习题答案结构动力学学习题答案结构动力学是土木工程中的一个重要分支，它研究结构在受到外部荷载作用下的响应和变形规律。
在学习结构动力学的过程中，我们经常会遇到一些复杂的问题和难题。
下面我将为大家提供一些常见结构动力学学习题的答案，希望能够帮助大家更好地理解和掌握这门学科。
1. 什么是结构的固有频率？结构的固有频率是指结构在没有外部激励作用下，自由振动时的频率。
它是结构的固有特性之一，与结构的质量、刚度和几何形状有关。
固有频率越高，结构的振动越快。
2. 如何计算结构的固有频率？计算结构的固有频率需要先求解结构的固有振型和固有频率。
常用的方法有模态分析法和有限元法。
模态分析法是通过求解结构的特征方程得到结构的固有频率和振型；有限元法则是将结构离散化为有限个单元，通过求解单元的振动特征得到整体结构的固有频率和振型。
3. 结构的固有频率对结构有何影响？结构的固有频率与结构的动态特性密切相关。
当外部激励频率接近结构的固有频率时，会引起共振现象，使结构的振幅急剧增大，从而可能导致结构的破坏。
因此，在结构设计和抗震设计中，需要合理选择结构的固有频率，以避免共振现象的发生。
4. 什么是结构的阻尼？结构的阻尼是指结构在振动过程中能量损耗的程度。
阻尼可以分为线性阻尼和非线性阻尼。
线性阻尼是指结构的阻尼与结构的振幅成正比，非线性阻尼则是指结构的阻尼与结构的振幅不成正比。
5. 如何考虑结构的阻尼？在结构动力学分析中，通常会考虑结构的阻尼对结构响应的影响。
常用的阻尼模型有粘滞阻尼模型和柱塞阻尼模型。
粘滞阻尼模型是指结构的阻尼与结构的速度成正比；柱塞阻尼模型是指结构的阻尼与结构的速度平方成正比。
根据结构的实际情况和要求，可以选择适当的阻尼模型进行分析。
6. 结构的地震反应分析中常用的方法有哪些？在结构的地震反应分析中，常用的方法有等效静力法、响应谱法和时程分析法。
等效静力法是一种简化的方法，将地震作用等效为静力作用进行计算；响应谱法是一种基于地震响应谱的方法，通过将地震作用转化为结构的响应谱进行计算；时程分析法是一种基于地震时程的方法，通过模拟地震过程对结构进行动力响应分析。
工程力学课后习题集答案解析
工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
（a）（b）（c）（d）（e）（f）（g）1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）1-3 画出图中指定物体的受力图。
所有摩擦均不计，各物自重除图中已画出的外均不计。
（a）（b）（c）（d）（e）（f）（g）第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。
梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如图所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。
电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象，三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得：ααα2-4 图示为一拔桩装置。
结构力学习题难？1答案
结构力学习题集答案水利建筑工程学院力学教研室2004.21．图示体系是几何不变体系。
()(X)（2分）2．有多余约束的体系一定是几何不变体系。
() (X)(2分)3．图中链杆1和2的交点O可视为虚铰。
()O(X)(2分)4．三个刚片用三个铰两两相互联结而成的体系是：A．几何不变；B．几何常变；C．几何瞬变；D．几何不变几何常变或几何瞬变。
() (D)（3分）5．联结三个刚片的铰结点，相当的约束个数为：A．2个；B．3个；C．4个；D．5个。
()(C)（3分）6．两个刚片，用三根链杆联结而成的体系是：A．几何常变；B．几何不变；C．几何瞬变；D．几何不变或几何常变或几何瞬变。
() (D)（3分）7．图示体系是：A．几何瞬变有多余约束；B．几何不变；C ．几何常变；D ．几何瞬变无多余约束。
()(A)(3分）8．在不考虑材料 的条件下，体系的位置和形状不能改变的体系称为几何 体系。
()应变(1.5分)，不变(1.5分)9．几何组成分析中，在平面内固定一个点，需要 。
不共线的两根链杆(3分）10．图示体系是 体系，因为 。
几何可变，W =5>0(3分)11．联结两个刚片的任意两根链杆的延线交点称为 ，它的位置是 定的。
瞬(虚)铰(2分)，不(1分)。
12．试对图示体系进行几何组成分析。
ACDBAB 刚片固接于基础(1分)；BC 刚片由铰B 及不过B 的链杆C 联结于几何不变体系上(1分)；BD 刚片与BC 刚片相同(1分)；整个体系为无多余约束的几何不变体系(1分)。
13．三个刚片用三个铰两两相联时的瞬变原因是_________________________。
三铰在一直线上（3分）14．对图示体系进行几何组成分析。
ACD BE刚片AB 固接于基础(1分)；刚片BC 由铰B 及不通过B 的链杆于不变体上(1分)； 又刚片DE 由铰D 及不通过D 的链杆联结于所得的不变体上(1分)； 整个体系为无多余约束的几何不变体系(1分)。
结构动力学试题及答案
结构动力学试题及答案一、选择题（每题2分，共10分）1. 结构动力学中，动力响应分析通常不包括以下哪一项？A. 自振频率分析B. 模态分析C. 静力分析D. 动力放大系数分析答案：C2. 在结构动力学中，下列哪一项不是确定结构动力特性的基本参数？A. 质量B. 刚度C. 阻尼D. 材料强度答案：D3. 单自由度振动系统的动力平衡方程中，下列哪一项是正确的？A. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t)B. m\(\ddot{x}\) + c\(\dot{x}\) + kx = 0C. m\(\ddot{x}\) + c\(\dot{x}\) + kx = FD. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t) - F答案：A4. 对于多自由度振动系统，下列哪一项不是求解动力响应的方法？A. 模态叠加法B. 直接积分法C. 能量守恒法D. 振型分解法答案：C5. 在结构动力学中，阻尼比通常用来描述阻尼的相对大小，其定义为：A. 临界阻尼比B. 阻尼比C. 阻尼比的倒数D. 阻尼比的平方答案：B二、填空题（每题2分，共10分）1. 结构动力学中，当外力作用频率与结构的_________相等时，结构会发生共振。
答案：自振频率2. 多自由度振动系统的振型是指系统在自由振动时的_________。
答案：位移分布模式3. 动力响应分析中，_________是指在给定的外力作用下，结构的响应随时间变化的过程。
答案：动力响应4. 在结构动力学中，_________是指结构在动力作用下，其响应与外力作用的关系。
答案：动力特性5. 阻尼比越大，结构的_________越小，振动衰减越快。
答案：振幅三、简答题（每题5分，共20分）1. 简述结构动力学中模态分析的目的和意义。
答案：模态分析的目的是确定结构的自振频率和振型，意义在于了解结构的动力特性，为结构设计提供依据，以及评估结构在动力作用下的安全性和稳定性。
船舶结构力学课后答案
船舶结构力学课后答案【篇一：结构力学答案部分】t>２.1题设坐标原点在左跨时与在跨中时的挠曲线分别为v(x)与v(x1)１）图2.1? v(x)?m0x2ei2?n?x36ei2?l43p(x?l)?6eil23p(x?l)?6ei3lp(x?3l)6ei3原点在跨中：v1(x1)?v0?m0x12ei?n?x16ei3?l43?v(l)?0v(l)?0p(x?l)12?12，? p6ei?v1(0)?0n1(0)?２）图2.2?v(x)??0x?mx22ei?n?x36eix0?l3p(x?l)6ei3p(x?l)6ei３）图2.3?v(xx)??0xx?n?x36ei??qxdx6ei3?l2２.２题a) v1?vpppl?1131?pl?1131??vp?(3???)??(?2?)? ?6ei?41626ei?164444???? pl333=331?13?pl3?9pl???()??? ?ei96ei1624??? v2??16ei?4?b) v(0)??ml3ei?ml6ei?2pl296ei2(1?2)2=?0.1pl6ei2?5pl3?27ei2pl2?73plei?(l)??ml3ei?ml6ei2?6ei2(1?)30.1pl6ei?4pl3?27ei22??107pl2ei?l??2l?2p???l??3??3???3 vl3eil6ei ??1????1????m2?3?m1??3??????=37pl22430ei445qlc) vl ???2192ei768ei2304ei??ql47qlv(0)??ql324ei??pl216ei??ql26ei?l?ql11?ql3?1????ei8ei?3612??3d)2.1图、2.2图和2.3图的弯矩图与剪力图如图2.1、图2.2和图2.3图2.1图2.2图2.32.3题1）??右??m?ml6ei13q1l?2ql324ei?ml?l?q?q??0?21???45ei?2?3ei2l22）?0??ml3ei3?q1l324ei?ml?l?lq?1??180ei?2?6ei7l2ql?1q1l1713?=1?? ??????ei?18243606?120?80ei2.4 题图2.5 ?v(x)?v0??0x??n0x36ei，v0?a?p?n0??x3??v(x)?ap??0x???a?n0 ?6ei?如图2.4，由v?l??v??l??0得 ??l3?ap??0l???a?n0?0???6ei??2l??0?n0?0?2ei?2?pl?ap????0?l6ei??n?p3?0解出33pl?3xx?3?v(x)??1?9ei?2l2l?? 图2.4 ?图2.6?v?x???1x?由v?l??0,mx2?n0x6ei3v??l???2?n0l3得4ei2ei?m?????201? ?ll??n?6ei?????0122?l?2??0??2ei6ei?2m0ln0l?1????2??ei2ei??1l?m0l2解得?v?x???1x??2?1??2?x2l???1??2?x3l2.5题图2.5：（剪力弯矩图如２．５） ??r1?pl?mll3?p??2p32p3??pl22p39ei33v0?ar?6eimlplpl5pl?l?vv???0????216ei18ei48ei144ei?2?v??0???0?? v0l?ml6ei??pl29ei?pl218ei??pl26eim?pa?bb? ，图2.5 a?1??ka?6l????将a?l,b?0a?l6,ka?16?13?12代入得：m?pl???6312pl2.7图：（剪力弯矩图如２．６） v1?a1r1?v2?a2r2?0.05leil433???ql2ql24??ql440eiql450ei100ei5qlql?11??l?v????????2?384ei2ei?40100? ql?57?293ql?????ei?384400?9600ei44图２．６??0??ql324eiql3?v1?v2l?ql?111?2ql??????ei?2440100?75ei333??l????v1?v2l24ei?ql?111??17ql ??????ei?2440100?300ei3图2.8（剪力弯矩图如２．７） 21?b???m???12a??1???24ka?l?????qa由q?qa,a?l,b?0,?,a?824ka????,代入得 82432m?r1?qlql2224??2?12?ql8?ql3ql4?24?1??ql2,v0?ar1?64ei图２．７5qlqlml5ql?l??v??????384ei?2?384ei128ei16eiql34424ql?111??(0)????????24eil6eiei?246448?3ql?192eiv0ml3?(l)???m??l8ei?ql82??ql364ei2.6题【篇二：《船舶结构力学》b卷参考答案】>2009～2010学年度第一学期《船舶结构力学》参考答案、评分标准专业：船舶与海洋工程使用范围：本科考试时间：2009年11月27日卷型：b卷考试方式：开卷课程性程：必修(学位课程)1. 为什么单跨直梁在几种横向载荷作用下引起的弯曲要素可以采用叠加法求出，而单跨直梁在复杂弯曲时横荷重与轴向力的影响不可分开考虑？ (10分)解答：(1)因为梁的弯曲公式是在小变形与材料符合胡克定律的前提下导出的，因此梁的弯曲要素与梁上的横向载荷成正比，即梁的弯曲要素与外载成线性关系，因此当梁上受到几种不同载荷作用时就可以运用叠加原理计算。
同济大学推荐结构力学习题集含答案
P 3m
2m
(j) 16、图(k)所示结构的零杆有 7 根。 17、图(l)所示结构中，CD 杆的内力 N1 = P 。
P PP
C
a
D 4a
(l)
18、图(m)所示桁架中，杆 1 的轴力为 0。
P
3m
3m
3m (k)
P P/2 P /2
1
4a
(m)
—— 6 ——
《结构力学》习题集 （上册）
二、作图题：作出下列结构的弯矩图（组合结构要计算链杆轴力）。
M =1
A.
B.
C
;
C
M =1
M =1
C.
C
D. ;
C
5、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形 体系。
6、已知 M p 、 M k 图，用图乘法求位移的结果为： (ω 1 y1 + ω 2 y2 ) / ( EI ) 。
ω 1
Mp * ω2*
y 2
y 1
Mk
P =1
A
26、
4m 2m 2m q
2a
28、
a 2a
a
P a
aa
29、
30、
—— 7 ——
《结构力学》习题集 （上册）
m0
a
a
P
P
a
a a/2 a/2
a
a /2 a /2
31、
P
q = P/a
P
B
A
aa
a 1.5 a 1.5 a
33、
m
l
l
l
l
35、
40kN/m
CD
3m
(完整版)结构动力学-习题解答
解
11
5 48
l3 EI
;
3.098
EI ml 3
;
l/2
ml 3 T 2.027 ;
EI
m
EI y1(t)
l
l/2 l/2
l/4
7-1（b)试求图示体系的自振频率与周期。
解: 求柔度系数: 用位移法或力矩分配法 求单位力作用引起的弯矩图（图a); 将其与图b图乘，得
48EI 2k
T 2 ( 1 l3 1 )m
48 EI 2k
m
k EI
k
l/2
l/2
7-3 试求图示体系质点的位移幅值和最大弯矩值。
已知 0.6
l
解:
yst
FPl 3 EI
m
y1(t)
1
1
2
/
2
1.5625
位移幅值
A
yst
1.5625
FPl 3 EI
2l
yst
11
5 3
l3 EI
1 11
l
X11 0.4612 ; X12 4.336
X 21
X 22
12 7.965 EI / ml 3
2 2
65.53EI
/
ml 3
1 2.822 EI / ml3
8-6.试求图示刚架的自振频率和振型。设楼面质量分别为m1=120t和m2=100t,
柱的质量已集中于楼面, 柱的线刚度分别为i1=20MN.m和i2=14MN.m,横梁
m 2 A 0.3375 FP
l/2
EI=常数
FP sin t
2l
FP
FPl
《结构力学习题集及答案》(下)-2a
第九章结构的动力计算一、判断题：1、结构计算中，大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变，只有刚度EI增大到原来的2倍，则周期比原来的周期减小1/2。
4、结构在动力荷载作用下，其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形，图a刚架的振动自由度为2，图b刚架的振动自由度也为2。
(a)(b)6、图示组合结构，不计杆件的质量，其动力自由度为5个。
7、忽略直杆的轴向变形，图示结构的动力自由度为4个。
8、由于阻尼的存在，任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率，ω与ωD的关系为ωω=D。
二、计算题：10、图示梁自重不计，求自振频率ω。
EI lW l/411、图示梁自重不计，杆件无弯曲变形，弹性支座刚度为k，求自振频率ω。
EIWool/2l/2k12、求图示体系的自振频率ω。
m l EI EIl0.5l0.5213、求图示体系的自振频率ω。
EI = 常数。
mll0.514、求图示结构的自振频率ω。
ml l l lEI=常数15、求图示体系的自振频率ω。
E I=常数，杆长均为l 。
m16、求图示体系的自振频率ω。
杆长均为l 。
EA=ooEImEIEI17、求图示结构的自振频率和振型。
mmEI EI EIl /2l /2l /218、图示梁自重不计，WE I ==⨯⋅2002104k N k N m2,，求自振圆频率ω。
EI WABC2m2m19、图示排架重量W 集中于横梁上，横梁E A=∞，求自振周期ω。
hEIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
hEIEIWEI221、求图示体系的自振频率ω。
各杆EI = 常数。
ma aa222、图示两种支承情况的梁，不计梁的自重。
求图a 与图b 的自振频率之比。
ml /2l /2EIEI(a)ml /2l /2EIEI(b)23、图示桁架在结点C 中有集中重量W ，各杆EA 相同，杆重不计。
结构设计原理第一章材料的力学性能习题及答案
第一章材料的力学性能一、填空题1、钢筋混凝土及预应力混凝土中所用的钢筋可分为两类：有明显屈服点的钢筋和无明显屈服点的钢筋，通常分别称它们为_______________和 ____________ 。
2、对无明显屈服点的钢筋，通常取相当于残余应变为_______ 时的应力作为假定的屈服点，即 ______________ o3、碳素钢可分为______ 、_______ 和________ 。
随着含碳量的增加，钢筋的强度 ______ 、塑性。
在低碳钢中加入少量锰、硅、钛、铬等合金元素，变成为 ____________ 。
4、钢筋混凝土结构对钢筋性能的要求主要是_________ 、 ________ 、5、钢筋和混凝土是不同的材料，两者能够共同工作是因为_________________6光面钢筋的粘结力由 _________ 、__________ 、________ 三个部分组成。
7、钢筋在混凝土中应有足够的锚固长度，钢筋的强度越___________ 、直径越 _____ 、混凝土强度越 _________ ，则钢筋的锚固长度就越长。
8、混凝土的极限压应变包括________ 和__________ 两部分。
____________ 部分越大，表明变形能力越 ________ ， _________ 越好。
9、混凝土的延性随强度等级的提高而。
同一强度等级的混凝土，随着加荷速度的减小，延性有所 __________ ，最大压应力值随加荷速度的减小而 ________ 。
10、钢筋混凝土轴心受压构件，混凝土收缩，则混凝土的应力________ ，钢筋的应力 ______ 。
11、混凝土轴心受拉构件，混凝土徐变，则混凝土的应力__________ ，钢筋的应力 ________ 。
12、混凝土轴心受拉构件，混凝土收缩，则混凝土的应力__________ ，钢筋的应力 ________ 。
二、判断题1、混凝土强度等级是由一组立方体试块抗压后的平均强度确定的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《结构力学习题集及答案》(上)-————————————————————————————————作者：————————————————————————————————日期：2第四章超静定结构计算——力法一、判断题：1、判断下列结构的超静定次数。
（1）、（2）、(a)(b)（3）、（4）、（5）、（6）、（7）、(a)(b)2、力法典型方程的实质是超静定结构的平衡条件。
3、超静定结构在荷载作用下的反力和内力，只与各杆件刚度的相对数值有关。
4、在温度变化、支座移动因素作用下，静定与超静定结构都有内力。
5、图a结构，取图b为力法基本结构，则其力法方程为δ111X c=。
(a)(b)X1c—— 0 ———— 1 ——6、图a 结构，取图b 为力法基本结构，h 为截面高度，α为线膨胀系数，典型方程中∆12122t a t t l h =--()/()。
t 21t lA h (a)(b)X 17、图a 所示结构，取图b 为力法基本体系，其力法方程为 。
(a)(b)PkPX 1二、计算题：8、用力法作图示结构的M 图。
B EI 3m 4kN A 283kN 3m EI/mC9、用力法作图示排架的M 图。
已知 A = 0.2m 2，I = 0.05m 4，弹性模量为E 0。
q 8m =2kN/m6mI I AMaa aa11、用力法计算并作图示结构的M图。
qll ql/22 EI EI EI12、用力法计算并作图示结构的M图。
q= 2 kN/m3 m4 m 4 mA EICEIB13、用力法计算图示结构并作出M图。
E I 常数。
（采用右图基本结构。
）Pl2/3l/3l/3l2/3Pl/3X1X214、用力法计算图示结构并作M图。
EI =常数。
3m 6mq=10kN/m3m—— 2 ———— 3 ——2m 4m q =16kN/m2m 2m 2m16、用力法计算图示结构并作M 图。
EI =常数。
l l ql l17、用力法计算并作图示结构M 图。
E I =常数。
P Pl lll18、用力法计算图示结构并作弯矩图。
16CD 2EI EI2EI 1A B 100100kNkN m m m 4m19、已知EI = 常数，用力法计算并作图示对称结构的M 图。
q l l lqEA=q qaa aa21、用力法作图示结构的M 图。
EI = 常数。
q2lql22、用力法作M图。
各杆EI相同，杆长均为l 。
P23、用力法计算图示结构并作M图。
EI = 常数。
44m2kN24m4mmkN.m24、用力法计算并作出图示结构的M图。
E = 常数。
2II II I2I8m 6m 6mP—— 4 ———— 5 ——20kN3m 4m 3m 4m26、用力法计算图示结构并作M 图。
EI =常数。
l l lP P/2l /2l /2l /227、利用对称性简化图示结构，建立力法基本结构(画上基本未知量)。
E =常数。
Pl l l l II III I II II I I 222228、用力法计算图示结构并作M 图。
E =常数。
l l l l l PPP /2/2/2/2P IIII I I 2I—— 6 ——29、已知EA 、EI 均为常数，用力法计算并作图示结构M 图。
l l llAE C B FDm30、求图示结构A 、D 两固定端的固端力矩，不考虑轴力、剪力的影响。
l l P B2EI EICD/2l 2EI A31、选取图示结构的较简便的力法基本结构。
EI =常数。
6m 6m6m240kN6m32、选择图示结构在图示荷载作用下，用力法计算时的最简便的基本结构。
PP I A 2II II II I =∞33、用力法求图示桁架杆AC 的轴力。
各杆EA 相同。
Pa aBCA D—— 7 —— 34、用力法求图示桁架杆BC 的轴力，各杆EA 相同。
P a aAB C D35、用力法计算图示桁架中杆件1、2、3、4的内力，各杆EA =常数。
Pd 1234d d d36、用力法求图示桁架DB 杆的内力。
各杆EA 相同。
PD B4 m4 m 4 m 4 m 4 m37、用力法作图示结构杆AB 的M 图。
各链杆抗拉刚度EA 1相同。
梁式杆抗弯刚度为EI EI a EA ,=21100，不计梁式杆轴向变形。
P a ACBaa38、用力法计算并作出图示结构的M 图。
已知EI =常数，EA =常数。
P PEA EAEA2a a a a EIa39、用力法计算并作图示结构M 图，其中各受弯杆EI=常数，各链杆EA EI l =()42。
P lll40、图示结构支座A 转动θ，EI =常数，用力法计算并作M 图。
llAθ41、图a 所示结构EI =常数，取图b 为力法基本结构列出典型方程并求∆1c 和∆2c 。
llX 21c(a)X c(b)θ42、用力法计算图示超静定梁并作M 图。
E =常数。
l /2=1I 2ϕI l /243、用力法计算并作图示结构由支座移动引起的M 图。
EI =常数。
cclll44、用力法计算并作图示结构由支座移动引起的M 图。
EI =常数。
l l /2/2lcCAB45、用力法作图示结构的M 图。
EI =常数，截面高度h 均为1m ，t = 20℃，+t 为温度升高，-t 为温度降低，线膨胀系数为α。
6m8m-t +t-t46、用力法计算图示结构由于温度改变引起的M 图。
杆件截面为矩形，高为h ，线膨胀系数为α。
l EI+10-10C C47、用力法计算并作图示结构的M 图，已知：α=0.00001及各杆矩形截面高h EI ==⨯⋅0321052.,m kN m 。
6m4m+10EI+30+10CCCEI48、图示连续梁，线膨胀系数为α，矩形截面高度为h ，在图示温度变化时，求M B 的值。
EI 为常数。
lCCl-10+20BC -1049、已知EI =常数，用力法计算，并求解图示结构由于AB 杆的制造误差(短∆)所产生的M 图。
aaa a /2/2ABEA=o o50、求图示单跨梁截面C 的竖向位移∆C V 。
l l ABCEI /2/2∆ϕ51、图示等截面梁AB ，当支座A 转动θA ，求梁的中点挠度f C 。
l θCEIBAf C/2l /2A52、用力法计算并作图示结构M 图。
E I =常数，K EI l ϕ=。
PK ϕl 2l 2l53、图b 为图a 所示结构的M 图，求B 点的竖向位移。
EI 为常数。
qlABql23ql26ql28(a) (b) M 图54、求图示结构中支座E 的反力R E ，弹性支座A 的转动刚度为k 。
q ll lAk CEI EIEI DEB EA=∞55、用力法作图示梁的M 图。
EI =常数，已知B 支座的弹簧刚度为k 。
B Al1k=EI/l 356、用力法计算图示结构并作M 图。
EI =常数，k EIa353。
Pkaaa第四章 超静定结构计算——力法（参考答案）1、（1）、4，3；（2）、3；（3）、21；（4）、6；（5）、1； （6）、7；（7）、5，62、（X ）3、（O ）4、（X ）5、（X ）6、（X ）8、m kN M AB ⋅=31（上侧受拉）；m kN M BC ⋅=15（有侧受拉）。
9、X 12219=. （压力）（水平链杆轴力） 10、1MM M /8M 图7/8X M /8 11、()←=281 ql X （有侧支座水平反力）12、m kN M CB⋅=06.2（上侧受拉）13、PX 1X 215、 17、l2PlPl PlPl PX 1Pl 2Pl 2M 1图M P 图M 图δ1131312315==-=l EI Pl EIX PP ,,.∆18、m kN M CA⋅=7600（右侧受拉） 19、四 角 处 弯 矩 值：202ql M =（外侧受拉）20、21、M P 图M 图M 1图X 1=13ql 2/83ql 2/8ql 2/8ql 2/8ql 2/2l22、P /2P /2X 1/2X 1=1l /2l /2l /2l M 1图P /2P /2M 图P l M 图/4P l /4P l /4P l /4P l /2P23、X 1413431基本体系图 M ()kN .m kN .m4kN .m24、P/2P/2X 1基本体系M 图1.77P 1.77P3P PP3P1.23P 1.23P4.234.2325、10.445基本体系11.82210.44511.82210kNX1图M()kN.m26、29、141411（⨯m28）30、M M PlA D==/3(上侧受拉)33、X N PAC10561==.34、X N PCB10789==-.35、N P N P N N P123422202 ==-==,,,36、N N X PD B DB=+=10086.（拉力）37、M＝0。
38、Pa2Pa239、X 1364Pl 2964Pl M 图40、l图M X 11=()34EI l θ基 本 体 系41、./ , , , 02122221211211111l c c X X X X c c c c -=∆-=∆-=∆++=∆++θδδδδ43、M6EI5l 2c44、/2c 图M X 16EIC7l245、M 1图X 1=1644M ´EI a ()46、X 1基 本 结 构图M 30EI hl α/()48、M EIhB =45α，下 侧 受 拉 50、()∆∆C V l=⋅-⎛⎝ ⎫⎭⎪↓316516ϕ51、()f EI l l EI llC A A =⨯⨯⨯⎛⎝ ⎫⎭⎪=↓1124123316θθ 52、11X 11=M 1图M P 图M 图PPl 21180Pl14580.Pl 2980Plδ1153=l EI ，∆12129482980P Pl EIX Pl=-=, 53、()∆B ql EI=↓424 54、qqqX 11=X 1ql22kkkk2lB A k EI l 136=δ1132834=+l EIl k ，∆14332422Pql EI ql k ql l EI k =-+⎛⎝ ⎫⎭⎪=-+⎛⎝ ⎫⎭⎪，δ111111316X X k l EI X P+=-=-∆，k EI l k EI l ql X 461722 1++=，R X E=12 55、《结构力学》习题集 （上册）—— 18 —— 1X 1基 本 结 构 ∆ δ1111131X X k l EI X +=-==∆∆∆∆,, δ11313==-l EIl ,, ∆∆ ()l EI X l l EI X l X EI31312133131-=-+=, ，X EI l 1234= 34EI l图 M。