工程力学课后习题答案第8章题解g
《工程力学》课后习题与答案全集
由 ，作出速度平行四边形，如图示：
即：
7．图示平行连杆机构中， mm, 。曲柄 以匀角速度 2rad/s绕 轴转动，通过连杆AB上的套筒C带动杆CD沿垂直于 的导轨运动。试示当 时杆CD的速度和加速度。
解：取CD杆上的点C为动点，AB杆为动系。对动点作速度分析和加速度分析，如图（a）、（b）所示。图中：
解：设该力系主矢为 ，其在两坐标轴上的投影分别为 、 。由合力投影定理有：
=-1.5kN
kN
kN
；
由合力矩定理可求出主矩：
合力大小为： kN，方向
位置： m cm，位于O点的右侧。
2．火箭沿与水平面成 角的方向作匀速直线运动，如图所示。火箭的推力 kN与运动方向成 角。如火箭重 kN，求空气动力 和它与飞行方向的交角 。
(d)由于不计杆重，杆AB在A、C两处受绳索作用的拉力 和 ，在B点受到支座反力 。 和 相交于O点，
根据三力平衡汇交定理，
可以判断 必沿通过
B、O两点的连线。
见图(d).
第二章力系的简化与平衡
思考题：1.√;2.×;3.×;4.×;5.√;6.×;7.×;8.×;9.√.
1．平面力系由三个力和两个力偶组成，它们的大小和作用位置如图示，长度单位为cm，求此力系向O点简化的结果，并确定其合力位置。
则
（mm/s）
故 =100（mm/s）
又有： ，因
故：
即：
第四章刚体的平面运动
思考题
1．×；2.√; 3.√;4.√;5.×.
习题四
1．图示自行车的车速 m/s,此瞬时后轮角速度 rad/s,车轮接触点A打滑，试求点A的速度。
材料力学课后答案
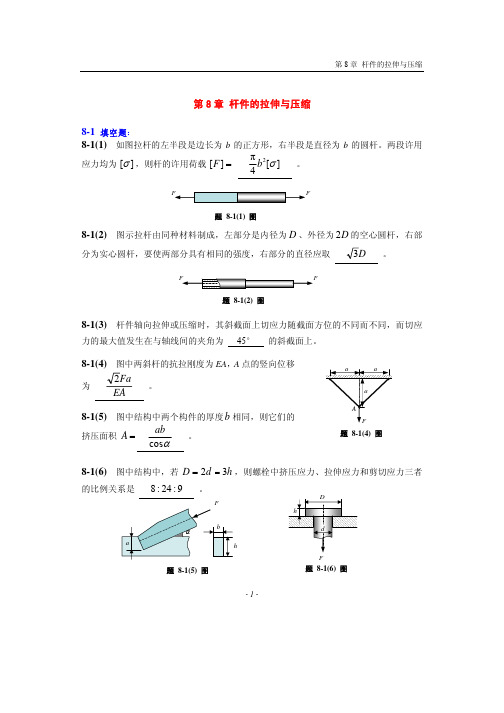
- 1 -第8章 杆件的拉伸与压缩8-1 填空题：8-1(1) 如图拉杆的左半段是边长为b 的正方形，右半段是直径为b 的圆杆。
两段许用应力均为 ][σ，则杆的许用荷载 =][F ][4π2σb 。
8-1(2) 图示拉杆由同种材料制成，左部分是内径为D 、外径为D 2的空心圆杆，右部分为实心圆杆，要使两部分具有相同的强度，右部分的直径应取 D3 。
8-1(3) 杆件轴向拉伸或压缩时，其斜截面上切应力随截面方位的不同而不同，而切应力的最大值发生在与轴线间的夹角为 45° 的斜截面上。
8-1(4) 图中两斜杆的抗拉刚度为EA ，A 点的竖向位移为EAFa 2 。
8-1(5) 图中结构中两个构件的厚度b 相同，则它们的挤压面积 =A αcos ab。
8-1(6) 图中结构中，若 h d D 32==，则螺栓中挤压应力、拉伸应力和剪切应力三者的比例关系是 9:24:8 。
题 8-1(5) 图题 8-1(1) 图题 8-1(2) 图题 8-1(6)图F题 8-1(4) 图- 2 -分析：222bs 3π4)(π4d F d D F =−=σ， 2tπ4d F =σ， 22π3πd F hd F ==τ，故有 9:24:883:1:31::tbs ==τσσ。
8-2 单选题：8-2(1) 图示的等截面杆左端承受集中力，右端承受均布力，杆件处于平衡状态。
1、3两个截面分别靠近两端，2截面则离端部较远。
关于1、2、3这三个截面上的正应力的下列描述中，正确的是 C 。
A ．三个截面上的正应力都是均布的 B ．1、2两个截面上的正应力才是均布的 C ．2、3两个截面上的正应力才是均布的 D ．1、3两个截面上的正应力才是均布的8-2(2) 若图示两杆的材料可以在铸铁和钢中选择，那么，综合强度和经济性两方面的因素， C 更为合理。
A ．两杆均选钢 B ．两杆均选铸铁C ．① 号杆选钢，② 号杆选铸铁D ．① 号杆选铸铁，② 号杆选钢8-2(3) 图示承受轴向荷载的悬臂梁中，在加载前的一条斜直线KK 在加载过程中所发生的变化是 D 。
《工程力学》课后习题答案全集
工程力学习题答案第一章 静力学基础知识思考题：1. ×;2. √;3. √;4. √;5. ×;6. ×;7. √;8. √习题一1．根据三力汇交定理，画出下面各图中A 点的约束反力方向。
解：（a ）杆AB 在A 、B 、C 三处受力作用。
由于力p 和B R的作用线交于点O 。
如图（a ）所示，根据三力平衡汇交定理，可以判断支座A 点的约束反力必沿通过A 、O 两点的连线。
（b ）同上。
由于力p 和B R的作用线交于O 点，根据三力平衡汇交定理，可判断A 点的约束反力方向如下图（b ）所示。
2．不计杆重，画出下列各图中AB 解：（a ）取杆AB 为研究对象，杆除受力p外，在B 处受绳索作用的拉力B T ，在A 和E 两处还受光滑接触面约束。
约束力A N 和E的方向分别沿其接触表面的公法线，并指向杆。
其中力E N与杆垂直，力A N通过半圆槽的圆心O 。
AB 杆受力图见下图（a ）。
(b)由于不计杆重，曲杆BC 只在两端受铰销B 和C 对它作用的约束力B N 和C N ，故曲杆BC 是二力构件或二力体，此两力的作用线必须通过B 、C 两点的连线，且B N =C N 。
研究杆A N 和B N，以及力偶m 的作用而平衡。
根据力偶的性质，A N 和B N必组成一力偶。
(d)由于不计杆重，杆AB 在A 、C 两处受绳索作用的拉力A T 和C T，在B 点受到支座反力B N 。
A T 和C T相交于O 点，根据三力平衡汇交定理，可以判断B N必沿通过B 、O 两点的连线。
见图(d).第二章力系的简化与平衡思考题：1. √;2. ×;3. ×;4. ×;5. √;6. ×;7. ×;8. ×;9. √.1．平面力系由三个力和两个力偶组成，它们的大小和作用位置如图示，长度单位为cm ，求此力系向O 点简化的结果，并确定其合力位置。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第8章 弯曲刚度
课
后 答
案
网
解：由挠度表查得：
FP al 180° × 3 EI π Wal 180° = ⋅ 3 EI π 20000 × 1 × 2 × 64 180° = ⋅ 3 × 200 × 109 × π d 4 π ≤ 0 .5 ° d ≥ 0.1117 m，取 d = 112mm。
θB =
ww w
6 ( 246 + 48) ×10 × 200 ×10 × π × 32 × 10−12
2
co
m
8—3 具有中间铰的梁受力如图所示。试画出挠度曲线的大致形状，并说明需要分几段 建立微分方程，积分常数有几个，确定积分常数的条件是什么？（不要求详细解答）
习题 8－3 图
后 答
案
网
习题 8－4 图
课
习题 8－4a 解图
解： (a)题 1.
wA = wA1 + wA 2
wA1 =
⎛l⎞ q⎜ ⎟ ⎝2⎠
87图示承受集中力的细长简支梁在弯矩最大截面上沿加载方向开一小孔若不考虑应力集中影响时关于小孔对梁强度和刚度的影响有如下论述试判断哪一种是正确的
eBook
工程力学
（静力学与材料力学）
习题详细解答
(第 8 章) 范钦珊 唐静静
课
后 答
案
网
2006-12-18
ww w
1
.k hd
aw .
co
m
（教师用书）
−3 9 4
(
.k hd
解：由挠度表查得 F ba 2 wC = P l − a 2 − b2 6lEI
(
)
习题 8－9 图
8
aw .
)
清华出版社工程力学答案-第8章弯曲强度问题
eBook工程力学习题详细解答教师用书(第8章)2011-10-1范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan ,s Education & Teaching Studio习题8－1 习题8－2 习题8－3 习题8－4 习题8－5 习题8－6 习题8－7 习题8－8 习题8－9 习题8－10 习题8－9 习题8－10习题8－11 习题8－12 习题8－13 习题8－14 习题8－15 习题8－16 习题8－17 习题8－18 习题8－19 习题8－20习题8－21工程力学习题详细解答之八第8章 弯曲强度问题8－1 直径为d 的圆截面梁，两端在对称面内承受力偶矩为M 的力偶作用，如图所示。
若已知变形后中性层的曲率半径为ρ；材料的弹性模量为E 。
根据d 、ρ、E 可以求得梁所承受的力偶矩M 。
现在有4种答案，请判断哪一种是正确的。
(A) ρ64π4d E M ＝(B) 4π64d E M ρ＝(C) ρ32π3d E M ＝(D) 3π32dE M ρ＝正确答案是 A 。
8－2 矩形截面梁在截面B 处铅垂对称轴和水平对称轴方向上分别作用有F P1和F P2，且F P1=F P2，如图所示。
关于最大拉应力和最大压应力发生在危险截面A 的哪些点上，有4种答案，请判断哪一种是正确的。
(A) +max σ发生在a 点，−max σ发生在b 点M习题8－1图A Ba b cd P2z固定端习题8－2图(B) +max σ发生在c 点，−max σ发生在d 点 (C) +max σ发生在b 点，−max σ发生在a 点 (D) +max σ发生在d 点，−max σ发生在b 点正确答案是 D 。
8－3 关于平面弯曲正应力公式的应用条件，有以下4种答案，请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载；(B) 弹性范围内加载、载荷加在对称面或主轴平面内；(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内；(D) 细长梁、载荷加在对称面或主轴平面内。
《工程力学(工程静力学与材料力学)(第3版)》习题解答：第8章 剪应力分析
2．确定梁内横截面上的最大拉应力和最大压应力；
3．确定梁内横截面上的最大切应力；
4．画出横截面上的切应力流。
知识点：弯曲切应力公式的应用、切应力流
难度：难
解答：
1．图（a）：
kN
， kN
剪力与弯矩图如图（b）、（c）；
2．形心C位置
MPa
MPa
3． m3
MPa
4．切应力流如图（e）。
（A）下移且绕点O转动；
（B）下移且绕点C转动；
（C）下移且绕z轴转动；
（D）下移且绕 轴转动。
知识点：弯曲中心、薄壁截面梁产生平面弯曲的加载条件
难度：一般
解答：
正确答案是D。
8－19试判断下列图示的切应力流方向哪一个是正确的。
知识点：横向弯曲时梁横截面上的切应力流、弯曲切应力分析方法
难度：难
解答：
（A）细长梁、横截面保持平面；
（B）弯曲正应力公式成立，切应力沿截面宽度均匀分布；
（C）切应力沿截面宽度均匀分布，横截面保持平面；
（D）弹性范围加载，横截面保持平面。
知识点：弯曲时梁横截面上切应力分析
难度：易
解答：
正确答案是B。
公式 推导时应用了局部截面的正应力合成的轴力，该正应力 则要求弯曲正应力公式成立；另外推导时在 时，应用了 沿截面宽度均匀分布假设。
难度：难
解答：
正确答案是D。
8－21简支梁受力与截面尺寸如图所示。试求N－N截面上a、b两点的铅垂方向的切应力以及腹板与翼缘交界处点c的水平切应力。
知识点：弯曲切应力公式的应用、切应力流
难度：难
解答：
FQ = 120kN，形心C位置。
(完整版)工程力学课后习题答案
工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
（a）（b）（c）2 第一章静力学基础（d）（e）（f）（g）第一章静力学基础 3 1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计，各物自重除图中已画出的外均不计。
（a）第一章静力学基础 5 （b）（c）（d）6 第一章静力学基础（e）第一章静力学基础7 （f）（g）8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。
梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如第二章 平面力系 9图所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。
电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。
工程力学课后习题答案_范钦珊(合订版)
Fw
习题 1—9 图
FT1
F Fw
T2
FN
习题 1—9 解图
7
1 一 10 图示压路机的碾子可以在推力或拉力作用下滚过 100mm 高的台阶。假定力 F 都是沿着杆 AB 的方向，杆与水平面的夹角为 30°，碾子重量为 250 N。试比较这两种情形 下，碾子越过台阶所需力 F 的大小。
习题 1－10 图
即 (d + 3) sinθ = 2(4.5 − d ) sinθ 2 d +3=9−d
d =3
（2）
y
4 G
C
E
θ2
Dθ d −4.5 F O
FR
3
Ax
2
习题 2－2 解图
∴ F 点的坐标为（-3, 0） 合力方向如图所示，作用线过 B、F 点；
tan θ = 4 3
AG = 6 sinθ = 6 × 4 = 4.8 5
nb2返回总目录下一章11ebook工程力学静力学与材料力学习题详细解答教师用书第2章范钦珊唐静静200612181第2章力系的简化21由作用线处于同一平面内的两个力f和2f所组成平行力系如图所示
eBook
工程力学
（静力学与材料力学）
习题详细解答
（教师用书） (第 1 章)
范钦珊 唐静静
2006-12-18
FC C
A FA
习题 1－3e 解 1 图
C
BF
FB
FAx A
FAy
习题 1－3b 解 1 图
A FA
FB
α C
B
D
FD 习题 1－3d 解 1 图
D
F
C
F'c
B
【工程力学 课后习题及答案全解】第8章弹性杆件横截面上的正应力分析习题解
习题 8-9 图
8－10 图示直角三角形截面中，A、B 分别为斜边和直角边中点，y1z1、y2 z2 为两对互 相平行的直角坐标轴。试判断下列结论中，哪一个是正确的。
— 39 —
σa
=
−175Ea Es
= −175 70 200
= −61.25 MPa（压）
8－14 从圆木中锯成的矩形截面梁，受力及尺寸如图所示。试求下列两种情形下 h 与 b 的比值：
（1）横截面上的最大正应力尽可能小； （2）曲率半径尽可能大。 解：（1） σ = M z = M z = 6M z
正确答案是 A 。 解：若用右手系，y 轴坐标朝上为正，则由 h1 = b1 得
Sz
(I)
=
3 2
b1h12
>
0
，
Sz
(II)
=
−2b1h12
<
0
若考虑正负号，则应选 A；若考虑静矩的绝对值，则应选 B。
8－7 图示矩形中 y1、z1 与 y2、z2 为两对互相平行的坐标轴。试判断下列关系式中， 哪一个是正确的。
解：变形谐调：
FNs = FNa Es As Ea Aa FNs + FNa = FP
（1） （2）
⎧ ⎪⎪FNs ⎨ ⎪⎪⎩FNa
= =
Es As Es As + Ea Aa
Ea Aa Es As + Ea Aa
FP FP
（压）
（1）
σs
=
FNs As
工程力学第8章第9章作业答案
6.6 107 m m4
• P228 9-1 试求图示各梁指定横截面上的剪力和弯矩。
F=ql/2 q
解：求得支座约束力 B
(c)
A
l/4
1
2
3 3D l/2 l
1C 2
ql FA FB 2
FA
FB
(c)
ql Fs1 2
1 2 M 1 ql 8 1 M 2 ql 2 8 1 M 3 ql 2 8
FB
Fs x1 56 4 x1
M x1 56x1 2x12
Fs x2 24 4x2
40kN 56kN
2 M x2 56 x2 80 x2 4 2 x2
max 56kN
M max 192kN m
192kN.m
A支座右侧截面 C截面
1 M max 113.125 2.156 80 1.656 20 1.6562 83.994kN m 2 M max 83.994 103 Wz 494.08 106 m 3 选择28a号工字钢 Wz 508cm3 6 170 10
Fs max Szmax 113.125 103 max 54.1MPa 2 3 Izb 24.6 10 8.5 10
故选择28a号工字钢。
F
F
F
F
F
q
A
113kN B
h 360mm, b 96mm d 9.0mm, t 16mm
z
* Sz max 96 16 180 8
6×1m=6m
y
180 16 2 385224 10 9 m 3 180 16 9
工程力学课后习题答案
工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触.（a）（b）（c)2 第一章静力学基础（d）（e）（f)（g）第一章静力学基础 3 1—2 试画出图示各题中AC杆(带销钉）和BC杆的受力图（a）（b）（c)（a)4 第一章静力学基础1—3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计.（a)第一章静力学基础 5 （b）（c）（d）6 第一章静力学基础（e）第一章静力学基础7 （f)（g）8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0.如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上,如图第二章 平面力系 9所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线,下垂距离CD =f =1m ，两电线杆间距离AB =40m.电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力.题2—3图以AC 段电线为研究对象,三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得：ααα2-4 图示为一拔桩装置。
工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析
![工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析](https://img.taocdn.com/s3/m/dda002bed0d233d4b14e696e.png)
解：
1-11：用绳索吊运一重 的重物。设绳索的横截面积 ，许用应力 试问：
（1）当 时，绳索强度是否够用？
（2）如改为 ，再校核绳索的强度。
解：（1）当 ， 强度不够
（2）当 ， 强度够
1-12：图示一板卷夹钳同时吊两个钢卷，已知每个钢卷重100kN,AB与AC两杆夹角为 ，其横截面为 的矩形，
AB段
BC段
比较 得最大剪应力发生在BC段，其数值为
(3)最大相对扭转角因轴内各截面扭矩方向都一致，所以最大相对扭转角 即为整个轴长的总扭转角。在使用扭转角公式 时，注意到该式的使用
条件必须是对应于所算转角 的长度 段内， 、 、T为常数。故分别计算两段轴的扭转角，然后相加即得最大相对扭转角。
+ 0.0213弧度=1.22度
解:
1.59*104,
6.36*104
1-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径
d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧
制压力.压头材料的弹性模量E=200Gpa.
最大应力。
解：
1-23两钢杆如图所示，已知截面面积 =1 ， =2 ；材料的弹性模量E=210Gpa，线膨胀系数 =12.5× l C。当
温度升3 C时，试求两杆内的最大应力。
解：
第二章剪切
2-1一螺栓连接如图所示，已知P=200 kN， =2 cm，螺栓材料的许用切应力[τ]=80Mpa，试求螺栓的直径。
解：
1-15悬臂吊车的尺寸和载荷情况如图所示。斜杆BC由两角钢组成，载荷Q=25 kN。设材料的许用应力[] =140 MPa，试选择
工程力学课后习题答案第8章题解g
2 ∑ M D = 0 ， FA × 3 + FC × 2 = 0 ， FA = − kN (↓ ) 3 2 ∑ Fy = 0 ， F = 1 kN 3
b 解 图（b1）
FD = FC = 25 kN
图（b2）
FA = 75 kN ， M A = −200 kN ⋅ m
c 解 图（c1）见下页。
62
∑ M C = 0 ， FD = 0 ， ∑ Fy = 0 ， FC+ = 0
图（c2）
∑ M A = 0 ， FB × 2l − ql × 3l − q × 2l × l = 0 , F =
∑ F y = 0 ， FA =
d 解 图（d1） 图（d2）
5 ql 2
1 ql 2
FA = FC = ql (↑ ) FC+ = ql (↓ ) ， FB = 2ql , M B = −3ql 2
8-4 已知梁的剪力图和弯矩图，求各自的载荷图。
(a)
(b)
8-5 利用载荷与内力的微积分关系及对称性和反对称性作图示各梁的剪力图和弯矩图。
(a)
(b)
(c)
(d)
61
8-6
作图示各组合梁的剪力图和弯矩图。
(a)
(b)
a 解 图（a1）
∑ M E = 0 ， FC = 1 kN, ∑ Fy = 0 ， FE = 3 kN
c解
∑ M A = 0 ， − q × 2l × l + FB × 2l + ql 2 = 0 ， FB =
∑ Fy = 0 , FA + FB = 2ql ， FA =
3 ql (↑ ) 2
ql (↑) 2
工程力学课后答案第8章
第8章 压杆稳定习题：1.【解】d 图临界力最大，b 图临界力最小。
2.【解】σBC =11.25MPa <[σst ]=16.83MPa ,BC 杆满足稳定性要求3.【解】最合理的情况为AB 、BC 两杆同时失稳，此时F 最大。
()βθ22222cr cos ππcos AC AB AB l EI l EI F F === ()βθ22222cr sin ππsin AC BC BCl EI l EI F F === 两式相除得到βθ2cot tan =即()βθ2cot arctan = 4. 【解】由于杆端的约束在各个方向相同，因此，压杆将在抗弯刚度最小的平面内失稳，即杆件横截面将绕其惯性矩为最小的形心主惯性轴转动。
32123min min b bh hb AI i === 欧拉公式适用于λ≥p λ，即min i l μ≥p2πσE 由此得到 l ≥m 76.1m 10200102105.032π103032π693p =⨯⨯⨯⨯⨯=-σμE b 故此压杆适用于欧拉公式时的最小长度为1.76m 。
5. 【解】（1）F cr =329.64kN（2）n =2.29<[n st ]=2.5，结构不安全6. 【解】（1）求挺杆的柔度挺杆的横截面为圆形，两端可简化为铰支座，μ=1，i=d/4计算柔度λ=μli=4μld=4×1×0.2570.008=128.5λ1=π√EσP =π√210×109240×106=92.9挺杆是细长压杆，使用欧拉公式计算临界压力（2）校核挺杆的稳定性I=πd464=π×0.008464=2.01×10−10m4P cr=π2EI(μl)2=π2×210×109×2.01×10−10(1×0.257)2=6.31kN工作安全系数n=P crP max=6.311.76=3.59所以挺杆满足稳定性要求7. 【解】[F]=53.31kN8. 【解】（1）F cr=355.31kN（2）bℎ=0.525。
《工程力学》课后习题解答
4日1－１试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e) A(a)(b) A(c)A(d)A(e)(c)(a)(b)98 解:1-３ 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解:１-4 试画出以下各题中指定物体的受力图。
（a) 拱ABCD ；（b) 半拱AB 部分；(ｃ) 踏板AB;(d) 杠杆AB ；(e) 方板AB ＣＤ；(f ） 节点B 。
解:(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b) CB(c)BF D2-2 杆A Ｃ、ＢＣ在C 处铰接，另一端均与墙面铰接，如图所示,F 1和F 2作用在销钉C 上,Ｆ１=445 Ｎ，F 2=535 Ｎ,不计杆重,试求两杆所受的力。
解：(１) 取节点Ｃ为研究对象,画受力图，注意AC 、BC 都为二力杆,(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力Ｆ作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
(d) FC(e)WB (f)F F BCF 1F解:(１)取整体ＡBCD为研究对象,受力分析如图,画封闭的力三角形: （2)2111.1222D A DD AF F FF FBC AB ACFF F F F=====∴===2-4 在简支梁ＡB的中点C作用一个倾斜４５ｏ的力Ｆ,力的大小等于２０KN，如图所示。
若梁的自重不计，试求两支座的约束力。
解：(1) 研究ＡB，受力分析并画受力图:（2）画封闭的力三角形:相似关系：B AF FFCDE cdeCD CE ED∆≈∆∴==几何尺寸:1122CE BD CD ED=====求出约束反力：FDFF AF DFF BF A dce12010 22010.4 45arctan 18.4B A o oCE F F kNCDED F F kN CDCECD α=⨯=⨯==⨯===-=２-6 如图所示结构由两弯杆AB Ｃ和DE 构成。
工程力学材料力学第四版习题答案解析
工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。
解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。
解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa 上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。
解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
工程力学(静力学与材料力学)习题及答案 - 剪应力分析
工程力学（静力学与材料力学）习题第8章 剪应力分析8－1 扭转切应力公式p /)(I M x ρρτ=的应用范围有以下几种，试判断哪一种是正确的。
（A ）等截面圆轴，弹性范围内加载；（B ）等截面圆轴；（C ）等截面圆轴与椭圆轴；（D ）等截面圆轴与椭圆轴，弹性范围内加载。
正确答案是 。
8－2 两根长度相等、直径不等的圆轴受扭后，轴表面上母线转过相同的角度。
设直径大的轴和直径小的轴的横截面上的最大切应力分别为max 1τ和max 2τ，切变模量分别为G 1和G 2。
试判断下列结论的正确性。
（A ）max 1τ＞max 2τ；（B ）max 1τ＜max 2τ；（C ）若G 1＞G 2，则有max 1τ＞max 2τ；（D ）若G 1＞G 2，则有max 1τ＜max 2τ。
正确答案是 。
8－3 承受相同扭矩且长度相等的直径为d 1的实心圆轴与内、外径分别为d 2、)/(222D d D =α的空心圆轴，二者横截面上的最大切应力相等。
关于二者重之比（W 1/W 2）有如下结论，试判断哪一种是正确的。
（A ）234)1(α-；（B ）)1()1(2234αα--；（C ）)1)(1(24αα--；（D ）)1/()1(2324αα--。
正确答案是 。
8－4 由两种不同材料组成的圆轴，里层和外层材料的切变模量分别为G 1和G 2，且G 1 = 2G 2。
圆轴尺寸如图所示。
圆轴受扭时，里、外层之间无相对滑动。
关于横截面上的切应力分布，有图中所示的四种结论，试判断哪一种是正确的。
正确答案是 。
8－5 等截面圆轴材料的切应力－切应变关系如图中所示。
圆轴受扭后，已知横截面上点)4/(d a a =ρ的切应变s γγ=a ，若扭转时截面依然保持平面，则根据图示的γτ-关系，可以推知横截面上的切应力分布。
试判断图中所示的四种切应力分布哪一种是正确的。
正确答案是 。
8－6图示实心圆轴承受外扭转力偶，其力偶矩T = 3kN ·m 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(c)
(d)
63
∑ M B = 0 ， FA ⋅ l +
8-3 根据内力与外力的关系作图示各梁的剪力图和弯矩图。
(a)
(b)
59
M −M （↑） ； ∑ Fy = 0 ， FA = （↓） 2l 2l M ， | M |max = 2 M | FS | max = 2l l 1 2 （b） ∑ M A = 0 ， − ql − ql ⋅ + ql ⋅ l + FB ⋅ 2l = 0 ， FB = ql （↑） 2 4 −1 ql （↓） ∑ Fy = 0 ， FA = 4 1 1 2 ， M A = ql M C = FB ⋅ l = ql ⋅ l = ql 2 （＋） 4 4 5 | FS | max = ql , | M |max = ql 2 4
3 1 qlx − qx 2 (0 ≤ x ≤ 2l ) 2 2 FS ( x ) = 0 (2l < x < 3l )
(2l ≤ x ≤ 3l )
解
ql 3l 5 × − ql 2 = 0 ， FA = ql (↑ ) 2 4 8 9 ∑ Fy = 0 ， FB = − ql (↓ ) 8 l⎞ 5 ⎛ FS ( x ) = ql + qx ⎜ 0 < x < ⎟ 8 2⎠ ⎝ 5 1 l⎞ ⎛ M ( x ) = qlx + qx 2 ⎜ 0 ≤ x ≤ ⎟ 8 2 2⎠ ⎝ 5 ql 9 ⎛l ⎞ FS ( x ) = ql + = ql ⎜ < x < l ⎟ 8 2 8 ⎝2 ⎠ 5 ql ⎛ l⎞ ⎛l ⎞ M ( x ) = qlx + ⎜ x − ⎟ ⎜ ≤ x < l ⎟ 8 2⎝ 4⎠ ⎝2 ⎠
图（a2）
2 ∑ M D = 0 ， FA × 3 + FC × 2 = 0 ， FA = − kN (↓ ) 3 2 ∑ Fy = 0 ， F = 1 kN 3
b 解 图（b1）
FD = FC = 25 kN
图（b2）
FA = 75 kN ， M A = −200 kN ⋅ m
c 解 图（c1）见下页。
60
（d） ∑ M B = 0 ， FA ⋅ 2l − q ⋅ 3l ⋅
l 5 − ql ⋅ l = 0 ， FA = ql （↑） 2 4 3 q 2 ；∑MB = 0 ， M B = l ∑ Fy = 0 ， FB = ql （↑） 2 4 25 2 ∑MD = 0 ， MD = ql 32 25 2 5 | FS | max = ql , | M |max = ql 4 32
55
习 题
8-1 求图示各梁指定截面（标有细线者）的剪力和弯矩。
(a1)
(a2)
a 解 图（a1） ∑ Fy = 0 ， FSA = F ； 图（a2）
∑MA = 0，MA = 0 ∑ M A = 0 ， M B = Fl
∑ Fy = 0 ， FSB = F ；
(b1)
b 解 图（b1） ∑ M B = 0 ， FA l + M e = 0 ， FA = − 仿题 a 截面法得
8-4 已知梁的剪力图和弯矩图，求各自的载荷图。
(a)
(b)
8-5 利用载荷与内力的微积分关系及对称性和反对称性作图示各梁的剪力图和弯矩图。
(a)
(b)
(c)
(d)
61
8-6
作图示各组合梁的剪力图和弯矩图。
(a)
(b)
a 解 图（a1）
∑ M E = 0 ， FC = 1 kN, ∑ Fy = 0 ， FE = 3 kN
max
8-2 已知各梁如图，求： （1）剪力方程和弯矩方程； （2）剪力图和弯矩图； （3） FS 和M
max
。
解
设左支座为 A，右支座为 B
∑ M B = 0 ， FA = − F (↓ ) l⎞ ⎛ FS (x ) = − F ⎜0 < x < ⎟ 2⎠ ⎝ l⎞ ⎛ M (x ) = − Fx ⎜ 0 ≤ x ≤ ⎟ 2⎠ ⎝ ⎛l ⎞ FS ( x ) = F ⎜ < x < l⎟ ⎝2 ⎠
Me (↓ ) l
FSA = −
Me M ， M A = M e ； FSB = − e ， M B = 0 l l
c 解 图（c1） ∑ M B = 0 ， FA (a + b ) − Fb = 0 ， FA = 仿题 a 截面法得
b F ↑ a+b
()
56
FSA = FS+ C
b b ba − = F , M A = 0 ； FS− F ， MC F C = a+b a+b a+b a ba A + =− = F ，MC F ； FSB = − F ,MB = 0 a+b a+b a+b
c解
∑ M A = 0 ， − q × 2l × l + FB × 2l + ql 2 = 0 ， FB =
∑ Fy = 0 , FA + FB = 2ql ， FA =
3 ql (↑ ) 2
ql (↑) 2
FS (x ) =
3 ql − qx 2
(0 < x < 2l )
58
M (x ) =
M ( x ) = ql 2
57
l⎞ ⎛ M ( x ) = FA x + FB ⎜ x − ⎟ ， FB = 2 F 2⎠ ⎝ ⎛l ⎞ M ( x ) = Fx − Fl ⎜ ≤ x ≤ l ⎟ ⎝2 ⎠ FS max = F ， M max = Fl
b解
ql (0 < x < l ) − qx 4 ql q M ( x ) = x − x 2 (0 ≤ x ≤ l ) 4 2 3 q FS max = ql ， M max = l 2 4 4 FS ( x ) =
解 （a） ∑ ） ∑ Fy = 0 ， FA = ql （↑） ； ∑ M A = 0 ， M A = ql
2
l 3 ∑ M D = 0 ， ql 2 + ql ⋅ l − ql ⋅ − M D = 0 ， M D = ql 2 2 2 3 | FS | max = ql , | M | max = ql 2 2
62
∑ M C = 0 ， FD = 0 ， ∑ Fy = 0 ， FC+ = 0
图（c2）
∑ M A = 0 ， FB × 2l − ql × 3l − q × 2l × l = 0 , F =
∑ F y = 0 ， FA =
d 解 图（d1） 图（d2）
5 ql 2
1 ql 2
FA = FC = ql (↑ ) FC+ = ql (↓ ) ， FB = 2ql , M B = −3ql 2
d 解 图（d1） ， ∑ Fy = 0 ， F = 仿题 a 截面法得
1 3 ql ， ∑ M A = 0 ， M A = − ql 2 2 8
FSA = FS+ C
1 1 3 1 − ql ， M A = − ql 2 ； FS− ql ， M C = − ql 2 C = 2 2 8 8 1 1 + = ql ， M C = − ql 2 ； FSB = 0 ， M B = 0 2 8
第 8 章 弯曲内力
思考题
8-1 平面弯曲的特点是什么？ 答 变形后，梁的轴挠曲线必定是一条与外载荷作用平面重合或平行的平面曲线。 8-2 若梁上某一段无载荷作用，则该段内的剪力图和弯矩图有什么特点？ 答 剪力图水平直线；弯矩图为斜直线。 8-3 梁上剪力、弯矩可能为零的位置各有哪些？ 答 梁上剪力可能为零的位置有（1）无集中载荷作用的自由端； （2）结构对称，载荷对 称的对称面上； （3）左右剪力图变号的（弯矩图取极值）横截面。 梁上弯矩可能为零的位置有（1）无集中力偶作用的自由端或梁端简支处； （2）结构对 称，载荷反对称的对称面上； （3）中间铰（两边无外力偶作用） 。 8-4 梁上剪力、弯矩可能为最大的位置各有哪些？ 答 梁上剪力可能为最大的位置有集中力（包括约束集中力）作用处； 梁上弯矩可能为最大的位置有（1）集中力偶作用面； （2）剪力图变号的横截面。 8-5 梁上剪力、弯矩可能发生突变的位置各有哪些？ 答 梁上剪力可能发生突变的位置有集中力（包括约束集中力）作用处； 梁上弯矩可能发生突变的位置有集中力偶作用面。 8-6 若在结构对称的梁上作用有对称的载荷，则该梁的剪力图、弯矩图各有什么特点？ 答 剪力图反对称；弯矩图对称。 8-7 若在结构对称的梁上作用有反对称的载荷，则该梁的剪力图、弯矩图各有什么特 点？ 答 剪力图对称；弯矩图反对称。 8-8 同一根梁采用不同的坐标系（如右手坐标系与左手坐标系）所得的剪力方程、弯矩 方程是否相同？由剪力方程、弯矩方程绘制的剪力、弯矩图是否相同？其分布载荷、剪力和 弯矩的微分关系式是否相同？ 答 剪力方程、弯矩方程均不同。