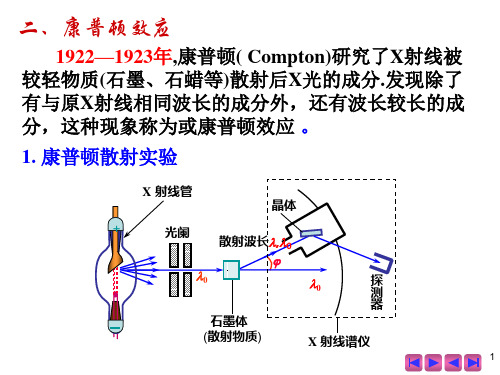
康普顿效应氢原子光谱的规律性。共51页
氢原子光谱的实验规律

原子的光谱线系列,并 得到普遍的实验规律:
普芳德系 布喇开系 m = 5 m= 4
里德伯常量
帕邢系 m= 3
巴耳末系 m=2
赖曼系 m=1
::
1 6
5.0
1 5
4.0 3.0
1
l : 1 2 34
4
n : 3 4 56
2.0 1.0 m m 0.8 0.6 0.4
1 23 2 34
0.2 波长 m m
是
动能 势能
之和
能量量子化
时,
氢原子最低能态
基态
的各个定态,称为 激发态。
欲将电子从基态电离,摆脱氢原子的束缚二变为自由态,外界至少要
供给电子的能量为
称为 电离能
玻尔的氢原子理论导出的 氢氢光原子谱光导谱规出律公公式式
由 及 由n跃迁到m (n m)的频率条件 5
4
3
得
2
波数为
8
(eV)
普芳德系-0.54 -0.85
在原子光谱中,组成每一线系的谱线,一般可表成两项 之差的形式
称为里兹组合原则,
称为光谱项。
可见, 非连续性、稳定性和规律相似性 是原子光谱谱线的普遍特点。
经典理论的困难
1911年卢瑟福根据a粒子散射实验提出了原子有核模型。原子的质量 几乎集中于带正电的原子核,而核的半径只占整个原子半径的万分之一 至十万分之一;带负电的电子散布在核的外围。卢瑟福的原子有核模型 成功地解释了a 粒子散射实验。
电在子定从态某轨一道定上态运向动另的 电一子定,态其跃角迁动时量将只发能射取 h(/ 或(2p吸) 收的)整光数子倍。,即
L 量=若分m初别v态为r 和=E终nn 2和态hp的E=m能n h
氢原子光谱实验规律 波尔理论

二、卢瑟福的原子有核模型
1. 卢瑟福的原子有核模型
1911 年卢瑟福根据 α 粒子散射实验结果建立 了原子的有核模型。
① 所有正电荷和几乎所有的原子 质量都集中在原子中心的一个 非 常 小 ( R≤10-15m ) 的 体 积 内, 这就是“原子核”;
② 原子中的电子围绕原子核转动;
③ 带正电的核和带负电的电子间 的静电引力把整个原子结合在 一起。
解: 赖曼系
1
R(112
1 n2
)
1/[R(1n12)] 其 中 R 1 .0 9 7 1 0 2 n m 1
n = 2 时对应最长波长 max 121.5nm
n = ∞时对应最短波长 min 91.2nm
帕邢系
1/[1.097
104
(
1 32
1 n2
)](nm)
53 1282nm
例题2 :
% R(612n 12) n7,8,9,L
3) 氢原子光谱规律
氢原子光谱有着内在的联系,表现在其波数可用 一普遍公式来表示:
v% 1
R
1 k2
1 n2
(广义巴尔末公式)
式中: k1,2,3L, n k 1 ,k 2 ,k 3 ,L
对应一个 k 就构成一个谱线系。
里兹组合原理:任一条谱线的波数都可以写成两 项之差的形式,即
• 每一谱线的波数都可以表示为二个光谱项之差
% T (k)T (n )
%
1
R
1 k2
1 n2
---广义巴尔末公式
表面上如此繁杂的光谱线竟然由一个式 子简单地表示,这不能不说是一项出色的成 果,但公式是凭经验凑出来的,它为什么与 实验符合得如此好,在公式问世将近三十年 内,一直是个谜。
高二物理竞赛:康普顿效应和波尔的氢原子理论课件
1 e2
2
40 rn2 m rn2
rn n2(m0he22 )
第一玻尔轨道半径
•能量量子化和原子能级
L
mrn
n
h
2
r1
0 h2 me2
0
0.53 A
En
1 2
m
2 n
e2
4 0 rn
rn
n2
(
0 h2 me 2
)
En
1 n2
me4
( 802h2
)
(n 1,2,3,)
11
基态能级 激发态能级
布喇开系(远红外)
~
1 RH (42
1 n2
)
n=5,6, …
7
普芳德系(远红外)
~
1 RH (52
1 n2 )
n=5,6, …
广义巴耳末公式
~
1 RH ( k 2
1 n2
)
k=1,2, … n =k+1, k+2, k+3, …
各谱线的波数 v~ (或频率)都可以用两个正
整数k和n的函数之差来表示:
1
min
1 R 22
1.097 107 / 4
o
min 3464 A
14
例(1)将一个氢原子从基态激发到n=4的激发态需要
多少能量?(2)处于n=4的激发态的氢原子可发出多
少条谱线?其中多少条可见光谱线,其光波波长各多
少?
解:(1)
E
E4
E1
E1 42
E1
13.58 42
(13.58)
12.75eV 2 1018 J
1
实验规律
I
21.3 氢原子光谱的实验规律 玻尔理论

n4 n3 n2
n
E 0
帕邢系 巴耳末系
莱曼系
布拉开系
n 1
E
ห้องสมุดไป่ตู้
4、氢原子玻尔理论的意义和困难
(1)正确地指出原子能级的存在(原子能量量子化);
(2)正确地指出定态和角动量量子化的概念; (3)正确的解释了氢原子及类氢离子光谱; (4)无法解释比氢原子更复杂的原子; (5)把微观粒子的运动视为有确定的轨道是不正确的; (6)是半经典半量子理论,存在逻辑上的缺点,即把 微观粒子看成是遵守经典力学的质点,同时,又
r
h 量子化条件 L mvr n 2π
n 1,2,3,
主量子数
假设三 频率条件假设 当原子从高能量 En 的定态 跃迁到低能量 Em的定态时,要发射频率为 的光子.
频率条件
h En Em
氢原子能级公式
2 vn m 由牛顿定律 2 4π 0 rn rn h 由假设 2 量子化条件 mv n rn n 2π
赋予它们量子化的特征 .
例1:计算赖曼系的最短波长和最长波长 计算帕邢系第二条谱线的波长 解: 赖曼系
1 1 R( 2 2 ) 1 n 1
1 (nm) 1 [1.097 104 (1 2 )] n
n = 2 时对应最长波长 max 121.5nm
n = ∞时对应最短波长 帕邢系
En E1 n
2
基态 n 1
13.6
玻尔理论对氢原子光谱的解释
m e4 1 h En Em En 2 2 2 8 0 h n 1 me4 1 1 ( 2 2 ), n m 2 3 c 8 0 h c m n 4 me 7 1 1 . 097 10 m R (里德伯常量) 2 3 8 0 h c
氢原子光谱的规律性

10
m 第一玻尔半径 ( n 1)
(2)能量量子化
1 2 1 e E n E np E nk mvn 2 40 rn 4 me 1 E1 En 2 2 2 2 8 0 h n n
me 4 E1 13.6ev 2 2 8 0 h
1 1 1 布拉开系: R , n 5 , 6 , 7 , 22 H 4 n
, n 6 ,7 ,8 ,
1 1 1 n 1, 对应莱曼系 f RH n 2 n 2 f i n 2对应巴尔末系 f 怎么解释?必须弄清原子内部结构!
20-1 黑体辐射 普朗克量子假设 一、热辐射现象
1、热辐射:决定于物体温度的电磁辐射. 2、平衡热辐射:辐射与吸收平衡,温度恒定. 3、描述热辐射的物理量 单色辐射强度:在单位时间内从物体表 面单位面积上、单位波长间隔内所辐射 出的能量 M (。 T) 总辐射能:在单位时间内从物体表面单 位面积上辐射的各种波长的能量
量子物理
主要内容:
1、黑体辐射;普朗克量子假设;光电效应 ;康普顿效应. 2、氢原子光谱的规律性;玻尔的氢原子理 论;夫兰赫兹实验. 3、德布罗意波;不确定关系. 4、量子力学简介. 5、激光 重点:黑体辐射、光电效应、康普顿效 应;氢原子光谱的规律性。
教学要求:
1、理解黑体、光电效应、康普顿效应及其实 验规律。 2、理解氢原子光谱的实验规律及玻尔氢原子 理论,并了解此理论的意义及其局限性。
二、实验规律:
三、经典理论的困难
1、饱和电流强度与入射光强度成正比。 2、光电子的初动能随入射光频率线性增 加,与光的强度无关。 3、对给定金属,存在一截止频率。 4、光电子是即时发射的。 1、认为不存在 0,只要光强足够大,即能发生 光电效应.但实验证明:只要 不管光强 0 多大,都不会有光电子逸出。 2、认为电子吸收能量需要一定的时间积累, 但实验发现具有瞬时性。 3、光电子初动能应该与入射光强度成正比.
氢原子光谱的实验规律

氢原子光谱的实验规律氢原子光谱的实验规律是原子光谱学中的重要内容,通过对这些规律的研究,我们可以深入了解氢原子的结构和性质。
以下是氢原子光谱的实验规律:1.光谱线系的规律性:氢原子光谱是由一系列具有特定波长的线组成的线系。
这些线按照波长的顺序排列,形成光谱的各个部分,如赖曼系、巴尔末系等。
这些线系的分布和排列都遵循着一定的规律,反映了氢原子能级的变化规律。
2.波长与能级的关系:氢原子光谱的波长与氢原子的能级有关。
根据玻尔的原子模型,当氢原子从较高能级跃迁到较低能级时,会释放出一定频率的光子,其波长与能级差有关。
因此,通过对光谱线的波长进行测量和分析,可以推导出氢原子的能级结构。
3.谱线强度与能级能量差的关系:氢原子光谱的强度与氢原子的激发态和基态之间的能量差有关。
能量差越大,从激发态跃迁到基态时释放的光子能量越高,谱线的强度越强。
因此,通过对光谱线强度的测量和分析,可以了解氢原子不同能级之间的能量差。
4.跃迁选择定则:根据量子力学原理,氢原子在发生能级跃迁时,只能选择满足选择定则的跃迁方式。
这些选择定则规定了不同能级之间跃迁的条件,包括允许和禁戒跃迁。
通过对谱线的观察和分析,可以了解这些选择定则的具体表现。
5.光谱精细结构:氢原子光谱除了具有主线系外,还有许多细分的结构,称为光谱的精细结构。
这些精细结构是由量子力学中的自旋-轨道耦合作用引起的,它们的观察和分析可以帮助我们深入了解氢原子的内部结构和性质。
6.实验手段的多样性:为了获得更准确和详细的光谱数据,实验上采用了多种手段和技术,如光谱仪的改进、高精度测量技术的运用、激光光谱等。
这些技术和手段的应用,使得我们可以更深入地研究和了解氢原子光谱的规律和机制。
综上所述,氢原子光谱的实验规律是研究原子结构和性质的重要手段之一。
通过对这些规律的研究和分析,我们可以深入了解原子能级结构、能级跃迁类型、跃迁选择定则等方面的问题,为量子力学和原子物理学的发展提供重要的实验依据。
氢原子光谱的规律性
2
(n 1) 4 me E1 2 2 8 0 h (电离能) 13.6eV
基态能量
激发态能量 ( n 1)
自 氢原子能级图 由 态 n E / eV 0 0.85 激 n4 1.51 发 n3 态 3.4 n2
r
h 量子化条件 L mvr n 2π
n 1,2,3,
主量子数
假设三 当原子从高能量 Ei 的定态跃迁到低能量 E f 的定态时,要发射频率为 的光子.
频率条件
h Ei E f
氢原子能级公式
2 vn m 由牛顿定律 2 4π 0 rn rn h 由假设 2 量子化条件 mv n rn n 2π
En E1 n
2
基态 n 1
13.6
m e4 1 1 2 3 ( 2 2 ) , ni n f c 8 0 h c n f ni 4 me 1.097107 m 1 R (里德伯常量) 2 3 8 0 h c n E 0 氢 n4 原 布拉开系 与 n3 帕邢系 子 光 n2 能 1
汤姆孙发现电子1903年汤姆孙提出原子的葡萄干蛋糕模型卢瑟福的原子有核模型行星模型原子中的正电荷和原子的质量均匀地分布在半径1010原子的中心有一带正电的原子核它几乎集中了原子的全部质量电子围绕这个核旋转核的尺寸与整个原子相比是很小的
一
氢原子光谱的规律性
1885 年瑞士数学家巴耳末发现氢原子光谱可见 光部分的规律 2
为1010 m 的球体范围内,电子浸于其中 .
卢瑟福的原子有核模型(行星模型)
原子的中心有一带正电的原子核,它几乎集中了
新16.3 康普顿效应
16.3.2康普顿效应的解释
• 1923年康普顿用光子与静止电子的弹性碰撞解释 了散射光波长的改变,得出了波长移动的公式。
• 他还测量了X射线在石墨中散射后波长的改变, 测量值与理论推测一致
• 于是人们称这个效应为康普顿效应
光子理论对康普顿效应的解释
若光子和外层电子相碰撞,光子有一部分能量 传给电子,散射光子的能量减少,于是散射光的 波长大于入射光的波长。
c
φ
X θ
mv
h
c
0
n 0
X
h 0 m0c2 h mc2
由动量守恒:
(mv)2 (h 0 )2 (h )2 2(h 0 )(h ) cos
c
c
cc
最后得到:
0
2h sin 2 m0c
2
2c
sin 2
2
c
h 2.431012 m m0c
16.3 康普顿效应 16.3.1 康普顿效应的实验规律
光照射在自由带电粒子上,散射光发生波长改 变的现象,在1920年前人们即已发现,用X射线照 射物质,可以观察到散射的X射线波长发生了改变。 据经典电磁理论,散射光波长是不会改变的。
瞄准直缝让散射角 的光子通过
实验测得散射光波长与散射角的关系如图 有两峰值,其一在入射X射线波长处。新的峰对应的 波长即康普顿理论所预言的散射X射线波长。
电子的康普顿波长。
此式说明:波长改变与散射物质无关,仅决定于散
射角;波长改变随散射角增大而增加。
计算的理论值与实验值符合得很好。
若光子和束缚很紧的内层电子相碰撞,光子将 与整个原子交换能量,由于光子质量远小于原子 质量,根据碰撞理论,碰撞前后光子能量几乎不 变,波长不变。
康普顿效应氢原子玻尔理论
3.玻尔理论解释氢原子光谱
h EiE f
En
me4
8
2 0
h2
1 n2
me4
8 02h3c
1
c
8m02eh43c(
1.097107 m1
1
n
2 f
1 ni2
R
) , ni n f
(里德伯常量)
氢
原 子 能 级 跃
与 光 谱 系
n
n4 n3
n2
E 0
帕邢系 布拉开系
巴耳末系
E
迁
n 1
莱曼系
四、玻尔理论的成就与不足
m0c
(2)
Ek
mc2 m0c2
hc hc
0
1
hc
0
0
1
4.72
1017
J =295 eV
(3) p h
1
02
1
2
9.27 1024
kg m s-1
15-4 氢原子的玻尔理论 一、氢原子光谱的实验规律
1.测量原子光谱的实验装置
放电管
摄谱仪
一、氢原子光谱的实验规律
2.氢原子光谱的实验规律
1
11 R(52 n2 ),
n 6,7,
1
1 R( 62
1 n2
),
n 7,8,
一、氢原子光谱的实验规律
2.氢原子光谱的实验规律
每一条光谱线的波数 可1以表示为两项之差;
波数 1 R( 1 1 )
n n 2
2
f
i
里得伯—里兹 合并原则
n f 1,2,3,4, ni n f 1, n f 2, n f 3,
(Auger Electron Spectrometer)
6.1.6康普顿效应
康普顿效应一、康普顿效应的实验及其规律康普顿效应(康普顿散射):波长变长的散射光阑X 射线管探测器光谱仪晶体石墨体(散射物质)j1B2B1)散射光中不仅有原波长λ0的成分,还有 > 0的成分康普顿散射的实验规律2) 随散射角φ的增大而增加,与入射X 射线的波长无关。
4)原子量越小的物质,康普顿效应越显著3)与散射物质无关。
二、对实验结果的分析1、光的波动说解释电子做同频率的受迫振动辐射同一频率的电磁波电磁波通过物体光的波动理论只能说明波长不变的散射,而不能解释康普顿散射不应该出现与入射波波长不同的成分2. 康普顿效应的量子解释1) 波长改变的散射:X射线光子与原子外层电子的弹性碰撞入射光子被原子核束缚较弱的外层电子的束缚能,“X射线光子与静止自由电子的弹性碰撞”2)波长不变的散射是X射线光子与原子内层电子的弹性碰撞相当于与整个原子作弹性碰撞3)为什么原子量越小的物质,康普顿效应越显著?原子量越大的物质,内层束缚电子数相对越多,而外层电子数相对越少。
特别注意:按照康普顿的粒子碰撞模型的解释,似乎在碰撞中,电子吸收了入射光子的一部分能量,使光子能量减小,然后以较小的频率出现在散射方向。
其实这种理解是违反量子理论的基本观点的,爱因斯坦认为:光子不能再分割,而只能整个的被吸收或放出。
辐射电场的量子论也认为:在光子与电子相互作用时,电子是整个地吸收了入射光子,又整个地辐射出散射光子。
2200mc h c m h h h e e m c c 00 202m m 1c 康普顿效应公式001cos )(h m c j 000h p e c h 0三、康普顿散射的定量计算c (1cos ) j h p e ch j 0m 20m c m 2mc 1224310m .c o h m c 电子的康普顿波长处于X 射线波段理论结果与实验结果完全相一致波长的改变量与散射物的种类及入射光的波长无关,c (1cos ) j 1224310m .c o h m c康普顿散射只有在入射光的波长与电子的康普顿波长相比拟时,散射才显著πΔ2000486.c nm j ,波长改变最大电子获得的能量也最大0Δ0j , 增大。
