三角形之旋转问题(北师版)(含答案)
北师版九年级数学上册 第1章 特殊平行四边形中的旋转、最值、动点问题 专题训练 (含答案)

6.解:(1)根据图形的对称性,本来DF和BF相等,但是“在正方形AEFG绕点A旋转的过程中,线段DF与BF始终相等”不正确.例如,当点F旋转到AB上时,BF最短(小于AB),而这时DF大于AD,即DF大于BF
(2)如图②,若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转的过程中,你能否找到一条线段与DG始终相等,并以图为例说明理由.
二、最值问题
7.如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.4
∴BD,EG互相平分,∴BO=OD,
∴点O为正方形的角平分线的交点,
∴直线EG必过正方形角平分线的交点
20.解:(1)BG=DE,BG⊥DE,证明如下:
延长BG交DE于点H,
∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
∴△BCG≌△DCE(SAS),
(2)当点E,F的运动时间t为何值时,四边形BEDF为矩形?
24.已知点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为点E,F,点Q为斜边AB的中点.
(1)如图①,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系式是;
(2)如图②,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
北师大版八年级下册数学3.2图形旋转(有关旋转图形的旋转方向、旋转中心、旋转角)(含解析)

找出旋转图形的旋转方向、旋转中心、旋转角一、选择题1、如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向转动一个角度到A1BC1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )A .120°B .90°C .60°D .30°2、如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P 的坐标为()A.(0,1)B.(1,-1)C.(0,-1)D.(1,0)3、在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△,则其旋转中心可能是( )A .点AB .点BC .点CD .点D4、如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是( )A .(1,1)B .(1,2)C .(1,3)D .(1,4)5、在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是()A.点A B.点B C.点C D.点D6、如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为()A.30°B.45°C.90°D.135°7、如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是()A.点M B.格点N C.格点P D.格点Q8、如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O 按逆时针方向旋转而得,则旋转的角度为( )A .30°B .45°C .90°D .135°二、填空题9、如图,在▱ABCD中,∠A=70°,将▱ABCD绕顶点B顺时针旋转到▱A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1= __________ .10、分别以正方形的各边为直径向其内部作半圆得到的图形如图所示.将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是__________度.11、如图所示,两个全等的正方形ABCD与CDEF,旋转正方形ABCD能和正方形CDEF重合,则可以作为旋转中心的点有__________个.三、解答题12、在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图(1)指出旋转中心,并求出旋转角的度数.(2)求出∠BAE的度数和AE的长.13、如图,在△BDE中,∠BDE=90°,BD=4,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 __________ .14、如图1,有一组平行线l1∥l2∥l3∥l4,正方形ABCD的四个顶点分别在l1,l2,l3,l4上,EG过点D且垂直l1于点E,分别交l2,l4于点F,G,EF=DG=1,DF=2.(1)AE= __________ ,正方形ABCD的边长= __________ ;(2)如图2,将∠AEG绕点A顺时针旋转得到∠AE′D′,旋转角为α(0°<α<90°),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′,C′分别在直线l2,l4上.①写出∠B′AD′与α的数量关系并给出证明;②若α=30°,求菱形AB′C′D′的边长.15、如图,已知:BC与CD重合,∠ABC=∠CDE=90°,△ABC≌△CDE,并且△CDE可由△ABC逆时针旋转而得到.请你利用尺规作出旋转中心O(保留作图痕迹,不写作法,注意最后用墨水笔加黑),并直接写出旋转角度是 __________ .16、如图是两个等边三角形拼成的四边形.(1)这个图形是不是旋转对称图形?是不是中心对称图形?若是,指出对称中心.(2)若△ACD旋转后能与△ABC重合,那么图形所在平面上可以作为旋转中心的点共有几个?请一一指出.17、如图1,△ABC为边长为6的等边三角形,点D为AB边上的点,且AD=2BD;过D作DE∥BC交AC边于E;AH⊥BC于H,AH交于DE于点O.(1)求梯形BDEC的面积;(2)将图1中的△ADE以每秒1个单位长度的速度沿直线AH从上往下平移,直到点A与点H重合为止,设运动时间为t秒,△ADE与四边形BDEC重叠部分的面积为S,请求出S与t的函数关系,并写出相应的t的取值范围;(3)将图1中的△ADE沿直线DE向下翻折得△A′DE,连接CO:将△A′DE绕点O旋转,设直线A′O与直线BC相交于点P.问:是否存在这样的时刻,使得△CPO为等腰三角形?若存在,直接写出△A′DE绕点O旋转的方向(顺时针或逆时针)以及对应的旋转角度α的大小(0°<α<180°);若不存在,请说明理由.找出旋转图形的旋转方向、旋转中心、旋转角的答案和解析一、选择题1、答案:A试题分析:利用旋转的性质计算.解:∵∠ABC=60°,∴旋转角∠CB=180°-60°=120°.∴这个旋转角度等于120°.故选:A.2、答案:B试题分析:根据网格结构,找出对应点连线的垂直平分线的交点即为旋转中心.试题解析:由图形可知,对应点的连线CC′、AA′的垂直平分线的交点是点(1,-1),根据旋转变换的性质,点(1,-1)即为旋转中心.故旋转中心坐标是P(1,-1).故选B.3、答案:B试题分析:连接、、,分别作、、的垂直平分线,看看三线都过哪个点,那个点就是旋转中心.解:∵△MNP绕某点旋转一定的角度,得到△,∴连接、、,作的垂直平分线过B、D、C,作的垂直平分线过B、A,作的垂直平分线过B,∴三条线段的垂直平分线正好都过B,即旋转中心是B.故选:B.4、答案:B试题分析:先根据旋转的性质得到点A的对应点为点A′,点B的对应点为点B′,再根据旋转的性质得到旋转中心在线段AA′的垂直平分线,也在线段BB′的垂直平分线,即两垂直平分线的交点为旋转中心。
北师大版六年级数学下册《三、图形的运动》单元测试3含答案
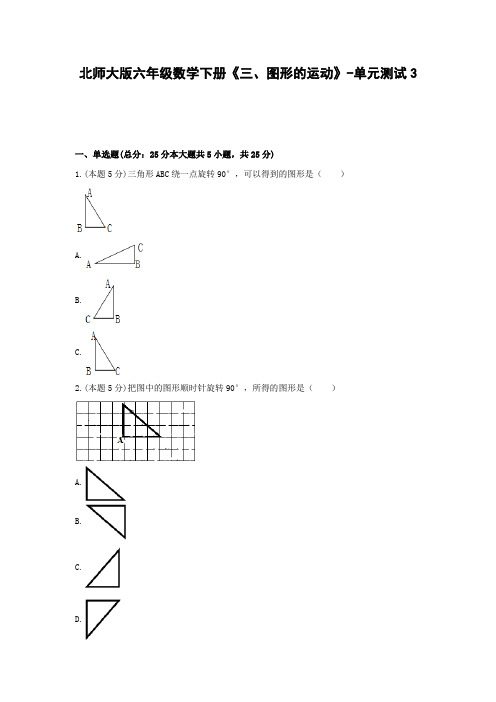
北师大版六年级数学下册《三、图形的运动》-单元测试3一、单选题(总分:25分本大题共5小题,共25分)1.(本题5分)三角形ABC绕一点旋转90°,可以得到的图形是()A.B.C.2.(本题5分)把图中的图形顺时针旋转90°,所得的图形是()A.B.C.D.3.(本题5分)将图形A绕点O逆时针旋转90度,得到图形B的是()A.B.C.4.(本题5分)如图()个图形经过旋转后会形成圆柱.A.B.C.5.(本题5分)如图所示,阀门手柄逆时针旋转了()A.90°B.180°C.270°二、填空题(总分:40分本大题共8小题,共40分)6.(本题5分)如图,三角形绕轴旋转一圈后得到的立体图形的体积是____立方厘米.7.(本题5分)如图,在△ABC中,∠C=90°,AC=2cm,把这个三角形在平面内绕点C顺时针旋转90°,那么点A移动所走过的路线长是____cm.(不取近似值)8.(本题5分)把一个半圆以直径为轴旋转一周得到的空间图形是____.9.(本题5分)观察图形填空.(1)图B可以看作图A绕点O____时针旋转____得到.(2)图D可以看作图B绕点O____时针旋转____得到.(3)图C可以看作图____的轴对称图形.10.(本题5分)如图:三角形A′OB′是三角形AOB绕O顺时针旋转90度后的图形.____11.(本题5分)如图:(1)指针按顺时针方向旋转90゜,从A旋转到____.(2)指针逆时针旋转90゜,从____旋转到C.(3)时针从C到D,是按____方向旋转了90゜.(4)时针从B到A,是按____方向旋转了90゜.12.(本题5分)以长方形的一边为轴旋转一周得到圆柱,以直角三角形的一条直角边为轴旋转一周可得到圆锥.____.(判断对错)13.(本题5分)从上午10:00到10:20,分针旋转了____度.三、解答题(总分:35分本大题共5小题,共35分)14.(本题7分)(1)画出这个三角形绕点O逆时针旋转90度后的图形.(2)按2:1的比画出这个三角形放大后的图形.15.(本题7分)按要求在如图的方格纸上画出图形.(1)将三角形ABC绕C点顺时针方向旋转90度.(2)按2:1的比画出平行四边形放大后的图形.16.(本题7分)动手操作①O点的位置在(____,____).②画出三角形向右平移4格后的图形.③画出三角形按2:1放大后的图形.④画出三角形绕O点顺时针旋转90°后得到的图形.17.(本题7分)转动后会形成什么样的图形?18.(本题7分)操作:画出三角形ABC绕顶点C逆时针旋转90度后的图形.北师大版六年级数学下册《三、图形的运动》-单元测试3参考答案与试题解析1.【答案】:A;【解析】:解:根据题干分析可得:三角形ABC绕一点顺时针旋转90°,可以得到的图形是三角形ABC绕一点逆时针旋转90°,可以得到的图形是.所以符合题意的只有选项A.故选:A.2.【答案】:D;【解析】:解:根据旋转的含义及其方法可知,图中直角三角形绕点A顺时针旋转90°后,会得到图形.故选:D.3.【答案】:B;【解析】:解:将图形A绕点O逆时针旋转90度,得到图形B的是:故选:B.4.【答案】:A;【解析】:解:根据长方形、直角三角形、直角梯形及圆柱的特征,长方形经过旋转后会形成圆柱.故选:A.5.【答案】:A;【解析】:解:如图,阀门手柄逆时针旋转了90°.故选:A.6.【答案】:12.56;【解析】:解:1313×3.14×4×3=12.56(立方厘米),答:这个立体图形的体积是12.56立方厘米.故答案为:12.56.7.【答案】:π;【解析】:解:2π×2×14cm).故答案为:π.8.【答案】:球;【解析】:解:半圆绕它的直径旋转360度形成球.故答案为:球.9.【答案】:顺;90度;顺;180度;B;【解析】:解:根据题干分析可得:(1)图B可以看作图A绕点O顺时针旋转9度得到.(2)图D可以看作图B绕点O顺时针旋转180度得到.(3)图C可以看作图B的轴对称图形.故答案为:顺;90度;顺;180度;B.10.【答案】:√;【解析】:解:由以上分析:上图三角形A′OB′是三角形AOB绕O顺时针旋转90度后的图形.故答案为:√.11.【答案】:D;B;逆时针;顺时针;【解析】:解:根据图和分析可知:(1)指针按顺时针方向旋转90゜,从A旋转到 D.(2)指针逆时针旋转90゜,从 B旋转到C.(3)时针从C到D,是按逆时针方向旋转了90゜.(4)时针从B到A,是按顺时针方向旋转了90゜.故答案为:D,B,逆时针,顺时针.12.【答案】:√;【解析】:解:以长方形的一边为轴旋转一周得到圆柱,以直角三角形的一条直角边为轴旋转一周可得到圆锥.故答案为:√.13.【答案】:120;【解析】:解:如图,从上午10:00到10:20,分针旋转了120°.故答案为:120.14.【答案】:解:(1)根据题干分析,画图如下:(2)原三角形的两条直角边分别是3、2个格,扩大后的三角形的直角边分别是3×2=6个格、2×2=4个格,据此画出两条6格和4格的相交垂线段然后连线,画成三角形;画图如下:;【解析】:(1)点O就是图形旋转后的对应点,把其它两点绕点O逆时针旋转90°后,顺次连接即为所求的图形1.(2)三角形按2:1放大,只要数出两条直角边各自的格数,然后分别乘2画出,连接两边即可.15.【答案】:解:(1)将三角形ABC绕C点顺时针方向旋转90度(下图).(2)按2:1的比画出平行四边形放大后的图形(下图).;【解析】:(1)根据旋转的特征,三角形ABC绕点C顺时针旋转90°后,点C的位置不动,其余各部分均绕此点按相同的方向旋转相同的度数,即可画出旋转后的图形A′B′C′.(2)图上中平移四边形的底是3格,高是2格,根据图形放大或缩小的意义,按2:1的比放大后的平行四边形对应的底是6格,高是4格,对应角大小不变.16.【答案】:24;【解析】:解:①O点的位置在(2,4).②画出三角形向右平移4格后的图形(图中A′)③画出三角形按2:1放大后的图形(图中A″)④画出三角形绕O点顺时针旋转90°后得到的图形(图中A″′):故答案为:2,4.17.【答案】:解:根据题干分析可得,平面图形经过旋转一周可以形成几何体,长方形旋转一周,得到的是圆柱;半圆沿直径旋转一周得到的是球体;直角三角形沿一直角边旋转一周得到的是圆锥;直角梯形沿直角边旋转一周得到的是圆台.;【解析】:根据旋转的性质,长方形沿一边和直角三角形沿直角边旋转得出圆柱和圆锥出发,发展空间观念,即可得出,直角梯形沿直角边旋转一周得到的是圆台(圆柱减去了上面圆锥部分),半圆沿直径旋转一周得到的是球体.18.【答案】:解:画出三角形ABC绕顶点C逆时针旋转90度后的图形:;【解析】:根据旋转的特征,三角形ABC绕点C逆时针旋转90°后,点C的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后的图形A′B′C′.。
七年级数学三角形全等之动点问题(建等式)(北师版)(专题)(含答案)

三角形全等之动点问题(建等式)(北师版)(专题)一、单选题(共8道,每道10分)1.已知:如图,等边△ABC的边长为8,点D是BC上一点,且BD=6.动点P从点C出发,以每秒2个单位的速度沿CA—AB—BC向终点C运动,连接AD,AP,BP.设点P运动的时间为t秒.解答下列问题:(1)当4≤t≤8时,线段AP的长可用含t的式子表示为( )A.2tB.-2t+16C.2t-8D.-2t+8答案:C解题思路:点P速度已知,可判断此题为动点问题,按照动点问题的解决方法解决:1.研究基本图形,标注:2.研究动点运动状态,包括起点、终点、状态转折点、速度、时间范围,如图:3.表达线段长,建等式.由题意,点P在运动过程中有2个状态转折点,需分成3种情况:①点P在CA上,对应的时间范围:0≤t≤4;②点P在AB上,对应的时间范围:4<t≤8;③点P在BC上,对应的时间范围:8<t≤12.由题意,当4≤t≤8时,点P在线段AB上运动,如图:点P已走路程为CA+AP=2t,因此AP=2t-CA=2t-8.故选C.试题难度:三颗星知识点:动点问题2.(上接第1题)(2)当点P在AC上运动时,若某一时刻△ABP≌△BAD,则t的值为( )A.1B.2C.3D.4答案:A解题思路:当点P在CA上时,即0≤t≤4,在等边△ABC中,AB=BA=8,∠BAP=∠ABD=60°,要使△ABP≌△BAD,则需AP=BD,即8-2t=6,解得t=1.故选A.试题难度:三颗星知识点:动点问题3.已知:如图,在长方形ABCD中,AB=4,AD=6.点E是BC上一点,CE=2,连接DE.动点P从点D出发,以每秒2个单位的速度沿DA-AB-BC向终点C运动,设点P的运动时间为t 秒.解答下列问题:(1)请你根据题意画出对应的运动状态分析图,并指出当P在DA,BC上运动时,对应的t 的取值范围分别为( )A.0≤t≤5;5<t≤8B.0≤t≤3;5≤t≤8C.0≤t≤3;3<t≤8D.0≤t≤3;3<t≤5答案:B解题思路:点P速度已知,可判断此题为动点问题,按照动点问题的解决方法解决:1.研究基本图形,标注:2.研究动点运动状态,包括起点、终点、状态转折点、速度、时间范围,如图:3.表达线段长,建等式.由题意,点P在运动过程中有2个状态转折点,需分成3种情况:①点P在DA上,对应的时间范围:0≤t≤3;②点P在AB上,对应的时间范围:3<t≤5;③点P在BC上,对应的时间范围:5<t≤8.故选B.试题难度:三颗星知识点:动点问题4.(上接第3题)(2)当P在BC上运动时,线段BP的长可用含t的式子表示为( )A.2t-10B.2tC.-2t+10D.-2t+16答案:A解题思路:当P在BC上运动时,如图:点P已走路程为DA+AB+BP=2t,则BP=2t-DA-AB=2t-10.故选A.试题难度:三颗星知识点:动点问题5.(上接第3,4题)(3)连接AP,BP.若△ABP和△DEC全等,则此时t的值为( )秒A.2B.1或7C.1或6D.2或6答案:D解题思路:根据点P的运动状态分三种情况分析:①当点P在DA上运动时,0≤t≤3;∵AB=CD且∠A=∠C=90°,∴点A和点C,点P和点E是对应点,∴△ABP≌△CDE,∴AP=CE,即6-2t=2,解得:t=2;②当点P在AB上运动时,3<t≤5,不符合题意,舍去;③当点P在BC上运动时,5<t≤8,∵AB=CD且∠B=∠C=90°,∴点B和点C,点P和点E是对应点,∴△BAP≌△CDE,∴BP=CE,即2t-10=2,解得:t=6.综上,当t=2或6时,△ABP和△DEC全等.故选D.试题难度:三颗星知识点:动点问题6.已知:如图,在△ABC中,AB=AC=18,BC=12,点D为AB的中点.点P在线段BC上以每秒3个单位的速度由B点向C点运动,同时点Q在线段CA上由C点向A点以每秒a个单位的速度匀速运动,连接DP,QP.设点P的运动时间为t秒,解答下列问题:(1)根据点P的运动,对应的t的取值范围为( )A.0≤t≤4B.0≤t≤6C.0≤t≤12D.0≤t≤18答案:A解题思路:点P速度已知,可判断此题为动点问题,按照动点问题的解决方法解决:①研究基本图形,标注:②研究动点运动状态,包括起点、终点、状态转折点、速度、时间范围,如图:③表达线段长,建等式.由点P的运动状态可知,对应的t的取值范围为0≤t≤4.故选A.试题难度:三颗星知识点:动点问题7.(上接第6题)(2)根据点P的运动,线段BP,PC的长可用含t的式子分别表示为( )A.at;3tB.3t;atC.12-3t;3tD.3t;12-3t答案:D解题思路:由题意,线段BP为点P已走路程,∴BP=3t,PC为点P未走路程,∴PC=12-3t.故选D.试题难度:三颗星知识点:动点问题8.(上接第6,7题)(3)若某一时刻△BPD与△CQP全等,则t的值与相应的CQ的长为( )A.t=2,CQ=9B.t=1,CQ=3或t=2,CQ=9C.t=1,CQ=3或t=2,CQ=6D.t=1,CQ=3答案:B解题思路:由题意,△BPD与△CQP全等,对应关系不明确,首先分析其对应情况,∵∠B=∠C,∴B和C是对应点,因此应分为两种情况:①△BPD≌△CQP,此时即解得②△BPD≌△CPQ,此时即解得综上:当t=1,CQ=3或t=2,CQ=9时,△BPD与△CQP全等.故选B.试题难度:三颗星知识点:动点问题。
北师大版八年级数学下册 第三章 图形的平移与旋转 单元复习题 (含答案)

北师版八年级数学下册图形的平移与旋转单元复习题(含答案)一、选择题1.(2019·河南期末)观察下面图案,在(A)(B)(C)(D)四幅图案中,能通过图案(1)平移得到的是(C)A B C D2.(2019·南阳唐河县期末)如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是(D)A.BC∥EF B.AD=BE C.BE∥CF D.AC=EF 3.(2019·驻马店平舆县期末)如图,若图形A经过平移与下方图形拼成一个长方形,则正确的平移方式是(A)A.向右平移4格,再向下平移4格B.向右平移6格,再向下平移5格C.向右平移4格,再向下平移3格D.向右平移5格,再向下平移3格4.(2019·郑州新密市期中)下列四幅图片,是中心对称图形的是(B)A B C D5.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是(A)A.O1 B.O2 C.O3 D.O46.如图,紫荆花图案旋转一定角度后能与自身重合,则旋转的角度可能是(C) A.30°B.60°C.72°D.90°7.(2019·驻马店确山县期末)把点A(3,-4)先向上平移4个单位长度,再向左平移3个单位长度得到点B,则点B的坐标为(D)A.(0,-8) B.(6,-8) C.(-6,0)D.(0,0)8.(2019·邓州市期末)如图,∠1=68°,直线a平移后得到直线b,则∠2-∠3=(D)A.78°B.132°C.118°D.112°9.(2019·南阳社旗县一模)剪纸是我国传统的民间艺术,下列剪纸作品中,既是中心对称图形,又是轴对称图形的是(C)A B C D二、填空题10.(2018·张家界)如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为15°.11.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个相同的格点正方形,并涂上阴影,使这两个格点正方形无重叠部分,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有4种.12如图,在△ABO中,AB⊥OB,OB=3,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A113.如图,在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号是②.14.(2018·株洲)如图,O为坐标原点,△OAB是等腰直角三角形,∠OAB=90°,点B的坐标为(0,22),将该三角形沿x轴向右平移得到Rt△O′A′B′,此时点B′的坐标为(22,22),则线段OA在平移过程中扫过部分的图形面积为4.15.(2019·新疆)如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为三、解答题16.如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°.若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.(不要求尺规作图)解:如图.连接AD.在Rt△ABC中,AB=5,BC=4,∴AC=AB2-BC2=3.由旋转的性质,得CD=AC=3,∠ACD=90°.∴AD=AC2+CD2=3 2.17.(2019·宁夏)已知:在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).(1)画出△ABC关于原点成中心对称的△A1B1C1,并写出点C1的坐标;(2)画出将A1B1C1绕点C1按顺时针旋转90°所得的△A2B2C1.解:(1)如图所示,△A1B1C1即为所求,其中点C1的坐标为(-2,-1).(2)如图所示,△A2B2C1即为所求.18.(2019·邓州市期末)取一副三角板按图1拼接,其中∠ACD=30°,∠ACB=45°.(1)如图2,三角板ACD固定,将三角板ABC绕点A按顺时针方向旋转一定的角度得到△ABC′,当∠CAC′=15°时,请你判断AB与CD的位置关系,并说明理由;(2)如图3,三角板ACD固定,将三角板ABC绕点A按逆时针方向旋转一定的角度(0°<α<180°)得到△ABC′,猜想当∠CAC′为多少度时,能使CD∥BC′?并说明理由.解:(1)AB∥CD.理由如下:∵∠BAC=∠BAC′-∠CAC′=45°-15°=30°,∴∠BAC=∠C=30°.∴AB∥CD.(2)当∠CAC′=75°时,能使CD∥BC′.理由如下:延长BA交CD于点E.∵∠BAC′=45°,∴∠BAC=75°+45°=120°.又∵∠BAC=∠AEC+∠ACD,∴∠AEC=120°-30°=90°.又∵∠B=90°,∴∠B+∠AEC=90°+90°=180°.∴CD∥BC′.。
北师大版七年级下册数学第四章 三角形含答案(综合题)
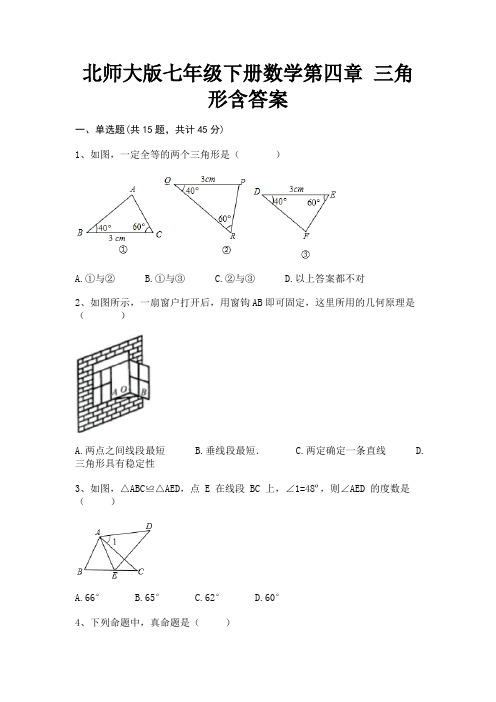
北师大版七年级下册数学第四章三角形含答案一、单选题(共15题,共计45分)1、如图,一定全等的两个三角形是()A.①与②B.①与③C.②与③D.以上答案都不对2、如图所示,一扇窗户打开后,用窗钩AB即可固定,这里所用的几何原理是()A.两点之间线段最短B.垂线段最短.C.两定确定一条直线D.三角形具有稳定性3、如图,△ABC≌△AED,点 E 在线段 BC 上,∠1=48º,则∠AED 的度数是()A.66°B.65°C.62°D.60°4、下列命题中,真命题是()A.周长相等的锐角三角形都全等B.周长相等的直角三角形都全等C.周长相等的钝角三角形都全等D.周长相等的等腰直角三角形都全等5、如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=;②四边形CGMH是矩形;③△EGM≌△MHA;④S△ABC +S△CDE≥S△ACE;⑤图中的相似三角形有10对.正确结论是()A.①②③④B.①②③⑤C.①③④D.①③⑤6、下列条件中,不能判定△ABC是直角三角形的是()A.∠A:∠B:∠C=3:4:5B.∠A ∠B= ∠CC.∠B=50°,∠C=40°D.a=5,b=12,c=137、以下列各组线段长为边,能组成三角形的是( )A.1cm,2cm,3cmB.2cm,3cm,8cmC.5cm,12cm,6cm D.4cm,6cm,9cm8、如图,在等边中,,点在上,且,点是上一动点,连结,将线段绕点逆时针旋转得到线段.要使点恰好落在上,则的长是()A. B. C. D.9、若△ABC∽△A'B'C',∠A=30°,∠C=110°,则∠B'的度数为()A.30°B.50°C.40°D.70°10、如图,中,于D,下列条件中:① ;②;③ ;④ ;⑤,⑥ ,一定能确定为直角三角形的条件的个数是()A.1B.2C.3D.411、如图,,,,,则A.27°B.54°C.30°D.55°12、如图,在△ABC中,∠C=40 ° ,按图中虚线将∠C剪去后,∠1+∠2等于().A.140°B.210°C.220°D.320°13、已知m是整数,以4m+5、2m-1、20-m这三个数作为同一个三角形三边的长,则满足条件的三角形个数有()A.0个B.1个C.2个D.无数个14、如图,矩形ABCD中,AB=3,AD=9,点E在边AD上,AE=1,过E、D两点的圆的圆心O在边AD的上方,直线BO交AD于点F,作DG⊥BO,垂足为G.当△ABF与△DFG全等时,⊙O的半径为()A. B. C. D.15、如图所示,在中,,于,,则线段的长是()A.3B.4C.8D.1二、填空题(共10题,共计30分)16、下列关于两个三角形全等的说法:①面积相等的两个三角形全等;②三条边对应相等的两个三角形全等;③有两角和其中一个角的对边对应相等的两个三角形全等;④有两边和一个角对应相等的两个三角形全等;⑤腰相等的两个等腰三角形一定全等.其中说法正确的是________.(填写序号)17、如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠ADE=________°.18、如图,AB=AC,AD=AE,∠BAC=∠DAE,点D在线段BE上.若,∠2=30°,∠3=55°则∠1=________.19、已知等腰三角形的周长为20,腰长为x,则x的取值范围是________ .20、如图,中有6个条形方格图,图上由实线围成的图形是全等形的有哪几对________21、如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是________.①BE=CD;②∠BOD=60º;③△BOD∽△COE.22、已知,如图,AC=AE,∠1=∠2,AB=AD,若∠D=25°,则∠B的度数为________.23、若等腰三角形的两边长为3cm和7cm,则该等腰三角形的周长为________ cm.24、如图,在△ABC中,已知D,E,F分别为边BC,AD,CE的中点,且,则阴影部分的面积为________ cm2.25、三角形的一边是5,另一边是1,第三边如果是整数,则第三边是________.三、解答题(共5题,共计25分)26、如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并证明你的结论.27、如图,△ABC中,∠ACB=90°,AC=6,BC=8。
北师大版2020八年级数学下册第三章图形的平移与旋转单元综合能力达标测试题(附答案)

又∵∠A′OA=90°,
∴∠AOB+∠BAO=∠AOB+∠A′OC=90°,
∴∠BAO=∠A′OC,
又∵OA′=OA,
∴△A′OC≌△OAB,
∴A′C=OB,OC=AB,
∵点A的坐标为(-4,-3),
∴OB=4,AB=3,
∴OC=3,A′C=4,
又∵点A′在第二象限,
3.B
【解析】试题解析:A.平移不改变图形的形状和大小,而旋转同样不改变图形的形状和大小,故错误;
B.平移和旋转的共同点是改变图形的位置,而图形的形状大小没有变化,故正确;
C.图形可以向某方向平移一定距离,而旋转是围绕中心做圆周运动,故错误;
D.在平移和旋转图形中,对应角相等,平移中对应线段相等且平行,旋转图形对应线段相等但不一定平行,故错误.
(2)请写出第(1)小题平移的过程.
22.如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出A1的坐标;
(2)请画出△ABC关于原点对称的△A2B2C2,并写出A2的坐标;
(3)请画出△ABC以点B为旋转中心,沿逆时针旋转90°后△A3B3C3.
故选B.
4.D
【解析】【分析】该图形被平分成五部分,因而每部分被分成的圆心角是72°,因而旋转72度的整数倍,就可以与自身重合.
【详解】根据旋转对称图形的概念可知:该图形被平分成五部分,旋转72度的整数倍,就可以与自身重合,因而国旗上的每一个正五角星绕着它的中心至少旋转72度能与自身重合,
故选D.
【点睛】本题考查了旋转对称图形的性质,正确识图、理解求解方法是关键.
北师大版八年级数学下册 第三章 :图形的平移与旋转 达标检测卷(含详细解答)

北师大版八年级数学下册第三章达标检测卷(考试时间:120分钟满分:120分)班级:________ 姓名:________ 分数:________第Ⅰ卷(选择题共30分)一、选择题(每小题3分,共30分)1.(崆峒区期末)把如左图所示的海豚吉祥物进行平移,能得到的图形是()A B C D2.观察下列四个图形,中心对称图形是()A B C D3.把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′B′C′的面积大小变化情况是()A.增大 B.减小 C.不变 D.不确定4.图中的两个三角形是经过什么变换得到的()A.旋转 B.旋转与平移C.旋转与轴对称 D.平移与轴对称第4题图第5题图5.如图,四边形OABC绕点O逆时针旋转得到四边形ODEF,∠AOC=50°,∠COD =60°,那么四边形OABC旋转的角度是()A.10° B.40° C.50° D.110°6.(河南期中)在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都减去3,则所得图形与原图形的关系:将原图形()A.向上平移3个单位长度B.向下平移3个单位长度C.向左平移3个单位长度D.向右平移3个单位长度7.如图,将△ABC绕点A按顺时针方向旋转某个角度得到△APQ,使AP平行于CB,CB,AQ的延长线相交于点D.如果∠D=40°,则∠BAC的度数为()A.30° B.40° C.50° D.60°第7题图第8题图8.如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,使点D刚好落在斜边AB上,则n的大小为()A.30 B.45 C.60 D.759.如图,EF∥BC,ED∥AC,FD∥AB,D,E,F为三边中点,图中可以通过平移互相得到的三角形有()A.2 对 B .3 对 C .4 对 D.5对10.在平面直角坐标系中,点A(-1,m)在直线y =2x +3上,连接OA ,将线段OA 绕点O 顺时针旋转90°,点A 的对应点B 恰好落在直线y =-x +b 上,则b的值为( )A .-2B .1C .32D .2 第Ⅱ卷 (非选择题 共90分)二、填空题(每小题3分,共24分)11.(邵阳期末)如图,将Rt △ABC 绕直角顶点A 按顺时针方向旋转180°得△AB 1C 1,则旋转后BC 的对应线段为 .第11题图12.平面直角坐标系中,点P 的坐标是(2,-1),则点P 关于原点对称的点的坐标是 .13.在平面直角坐标系中,点O 为坐标原点,现有一点A(2,5),将点A 向下平移5个单位长度,可以得到对应点的坐标A ′ .14.五角星图形绕它的中心旋转,要与它本身完全重合,旋转角至少为 .15.如图是由两个正三角形和两个等腰三角形组成的图案,图中两个阴影部分的三角形可以通过:①平移;②旋转;③轴对称中的哪些方式得到.在横线上写上答案的序号: .第15题图16.如图,将△ABC沿BC方向平移2 cm得到△DEF.如果四边形ABFD的周长是20 cm,则△ABC周长是 cm.第16题图第17题图17.如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是 .18.★如图,已知直线MN∥PQ,把∠C=30°的直角三角板ABC的直角顶点A放在直线MN上,将直角三角板ABC在平面内绕点A任意转动,若转动的过程中,直线BC与直线PQ的夹角为60°,则∠NAC的度数为.三、解答题(共66分)19.(6分)将已知△ABC的顶点A,B,C在格点上,按下列要求在网格中画图.(1)将△ABC绕点C逆时针旋转90°得到△A1B1C;(2)画△ABC关于点O的中心对称图形△A2B2C2.20.(8分)(南城县期中)如图,在△ABC中,∠BAC=15°,将△ABC绕点A按逆时针方向旋转90°,到△ADE的位置,然后将△ADE以AD为轴翻折到△ADF的位置,连接CF,判断△ACF的形状,并说明理由.21.(8分)如图,等边△ABC与等边△A1B1C1关于某点成中心对称,已知A,A1,B 三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标;(2)写出顶点C,C1的坐标.22.(8分)在平面直角坐标系中,点M的坐标为(a,-2a).(1)当a=-1时,点M在坐标系的第象限;(直接填写答案)(2)将点M向左平移2个单位长度,再向上平移1个单位长度后得到点N,当点N 在第三象限时,求a的取值范围.23.(10分)如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;(2)若点P(a+3b,4a-b)与点Q(2a-9,2b-9)也是通过上述变换得到的对应点,求a,b的值.24.(12分)(鼓楼区期末)如图,在Rt△ABC中,∠C=90°,∠CAB=35°,BC=7.线段AD由线段AC绕点A按逆时针方向旋转125°得到,△EFG由△ABC沿CB 方向平移得到,且直线EF过点 D.(1)求∠DAE的大小;(2)求DE的长.25.(14分)如图,O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.(1)求证:△COD是等边三角形;(2)当α=150°时,试判断△AOD的形状,并说明理由;(3)探究:当α为多少度时,△AOD是等腰三角形?参考答案第Ⅰ卷(选择题共30分)一、选择题(每小题3分,共30分)1.(崆峒区期末)把如左图所示的海豚吉祥物进行平移,能得到的图形是(C)A B C D2.观察下列四个图形,中心对称图形是(C)A B C D3.把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′B′C′的面积大小变化情况是(C)A.增大 B.减小 C.不变 D.不确定4.图中的两个三角形是经过什么变换得到的(D)A.旋转 B.旋转与平移C.旋转与轴对称 D.平移与轴对称第4题图第5题图5.如图,四边形OABC绕点O逆时针旋转得到四边形ODEF,∠AOC=50°,∠COD =60°,那么四边形OABC旋转的角度是(D)A.10° B.40° C.50° D.110°6.(河南期中)在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都减去3,则所得图形与原图形的关系:将原图形(C)A.向上平移3个单位长度B.向下平移3个单位长度C.向左平移3个单位长度D.向右平移3个单位长度7.如图,将△ABC绕点A按顺时针方向旋转某个角度得到△APQ,使AP平行于CB,CB,AQ的延长线相交于点 D.如果∠D=40°,则∠BAC的度数为(B)A.30° B.40° C.50° D.60°第7题图第8题图8.如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,使点D刚好落在斜边AB上,则n的大小为(C)A.30 B.45 C.60 D.759.如图,EF∥BC,ED∥AC,FD∥AB,D,E,F为三边中点,图中可以通过平移互相得到的三角形有 (B )A.2 对 B .3 对 C .4 对 D.5对10.在平面直角坐标系中,点A(-1,m)在直线y =2x +3上,连接OA ,将线段OA 绕点O 顺时针旋转90°,点A 的对应点B 恰好落在直线y =-x +b 上,则b 的值为 (D ) A .-2 B .1 C .32D .2第Ⅱ卷 (非选择题 共90分)二、填空题(每小题3分,共24分)11.(邵阳期末)如图,将Rt △ABC 绕直角顶点A 按顺时针方向旋转180°得△AB 1C 1,则旋转后BC 的对应线段为B 1C 1.第11题图12.平面直角坐标系中,点P 的坐标是(2,-1),则点P 关于原点对称的点的坐标是(-2,1).13.在平面直角坐标系中,点O 为坐标原点,现有一点A(2,5),将点A 向下平移5个单位长度,可以得到对应点的坐标A ′(2,0).14.五角星图形绕它的中心旋转,要与它本身完全重合,旋转角至少为72度. 15.如图是由两个正三角形和两个等腰三角形组成的图案,图中两个阴影部分的三角形可以通过:①平移;②旋转;③轴对称中的哪些方式得到.在横线上写上答案的序号:②③.第15题图16.如图,将△ABC沿BC方向平移2 cm得到△DEF.如果四边形ABFD的周长是20 cm,则△ABC周长是16cm.第16题图第17题图17.如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是2 2 .18.★如图,已知直线MN∥PQ,把∠C=30°的直角三角板ABC的直角顶点A放在直线MN上,将直角三角板ABC在平面内绕点A任意转动,若转动的过程中,直线BC与直线PQ的夹角为60°,则∠NAC的度数为30°或90°或150°.选择、填空题答题卡一、选择题(每小题3分,共30分)题号 1 2 3 4 5 6 7 8 9 10 得分答案 C C C D D C B C B D二、填空题(每小题3分,共24分)得分:________11.__B1C1__ 12.__(-2,1)__13.__(2,0)__ 14.__72度__15.__②③__ 16.__16__17.__2 2 __ 18.__30°或90°或150°__三、解答题(共66分)19.(6分)已知△ABC的顶点A,B,C在格点上,按下列要求在网格中画图.(1)将△ABC绕点C逆时针旋转90°得到△A1B1C;(2)画△ABC关于点O的中心对称图形△A2B2C2.解:(1)如图,△A1B1C即为所求.(2)如图,△A2B2C2即为所求.20.(8分)(南城县期中)如图,在△ABC中,∠BAC=15°,将△ABC绕点A按逆时针方向旋转90°,到△ADE的位置,然后将△ADE以AD为轴翻折到△ADF的位置,连接CF,判断△ACF的形状,并说明理由.解:由旋转的性质可知:∠BAC=∠DAE=15°,AC=AE,∠CAE=90°,由翻折的性质可知:∠FAD=∠EAD=15°,AF=AE.∴AC=AF,∠CAF=60°,∴△ACF为等边三角形.21.(8分)如图,等边△ABC与等边△A1B1C1关于某点成中心对称,已知A,A1,B 三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标;(2)写出顶点C,C1的坐标.解:(1)点A1和点B为对应点,∴对称中心为A1B的中点,∴对称中心的坐标为(0,2.5).(2)在△ABC中,AB=2,C到AB的距离为 3 .即点C到y轴的距离为 3 ,∴点C的坐标为(- 3 ,3),点C1的坐标为( 3 ,2).22.(8分)在平面直角坐标系中,点M的坐标为(a,-2a).(1)当a =-1时,点M 在坐标系的第象限;(直接填写答案)(2)将点M 向左平移2个单位长度,再向上平移1个单位长度后得到点N ,当点N 在第三象限时,求a 的取值范围.解:(1)当a =-1时,点M 的坐标为(-1,2), 所以M 在第二象限,所以应填“二”.(2)将点M 向左平移2个单位长度,再向上平移1个单位长度后得到点N ,点M 的坐标为(a ,-2a),所以N 点的坐标为 (a -2,-2a +1). 因为N 点在第三象限,所以⎩⎪⎨⎪⎧a -2<0,-2a +1<0,解得12<a<2,所以a 的取值范围为12 <a<2.23.(10分)如图,三角形DEF 是三角形ABC 经过某种变换得到的图形,点A 与点D ,点B 与点E ,点C 与点F 分别是对应点,观察点与点的坐标之间的关系,解答下列问题:(1)分别写出点A 与点D ,点B 与点E ,点C 与点F 的坐标,并说说对应点的坐标有哪些特征;(2)若点P(a +3b ,4a -b)与点Q(2a -9,2b -9)也是通过上述变换得到的对应点,求a ,b 的值.解:(1)点A 的坐标为(2,3),点D 的坐标为(-2,-3),点B 的坐标为(1,2),点E 的坐标为(-1,-2),点C 的坐标为(3,1),点F 的坐标为(-3,-1),对应点的横、纵坐标分别互为相反数.(2)由(1),得⎩⎪⎨⎪⎧a +3b +2a -9=0,4a -b +2b -9=0, 解得⎩⎪⎨⎪⎧a =2,b =1,答:a 的值为2,b 的值为1.24.(12分)(鼓楼区期末)如图,在Rt △ABC 中,∠C =90°,∠CAB =35°,BC =7.线段AD 由线段AC 绕点A 按逆时针方向旋转125°得到,△EFG 由△ABC 沿CB 方向平移得到,且直线EF 过点 D. (1)求∠DAE 的大小; (2)求DE 的长.解:(1)∵△EFG 是 由△ABC 沿CB 方向 平移得到,∴AE∥CF,∴∠EAC+∠C=180°.∵∠C=90°,∴∠EAC=90°.又线段AD是由线段AC绕点A按逆时针方向旋转125°得到,即∠DAC=125°,∴∠DAE=35°.(2)∵△EFG是由△ABC沿CB方向平移得到,∴AE∥CF,EF∥AB,∴∠AED=∠F=∠ABC.又∵∠DAE=∠BAC=35°,AD=AC,∴△ADE≌△ACB(AAS),∴DE=BC=7.25.(14分)如图,O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.(1)求证:△COD是等边三角形;(2)当α=150°时,试判断△AOD的形状,并说明理由;(3)探究:当α为多少度时,△AOD是等腰三角形?(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得到△ADC,∴CO=CD,∠OCD=60°,∴△COD 是等边三角形.(2)解:当α=150°时,△AOD 是直角三角形. 理由:∵△BOC ≌△ADC , ∴∠ADC =∠BOC =150°, ∵△COD 是等边三角形, ∴∠ODC =60°,∴∠ADO =∠ADC -∠ODC =90°, 则△AOD 是直角三角形.(3)解:①要使OA =AD ,需∠AOD =∠ADO , ∵∠AOD =360°-110°-60°-α=190°-α, ∠ADO =α-60°, ∴190°-α=α-60°, ∴α=125°;②要使OA =OD ,需∠OAD =∠ADO. ∵∠OAD =180°-(∠AOD +∠ADO) =180°-(190°-α+α-60°) =50°,∴α-60°=50°, ∴α=110°;③要使OD =AD.需∠OAD =∠AOD.∵∠AOD =360°-110°-60°-α=190°-α, ∠OAD =180°-(α-60°)2 =120°-α2,∴190°-α=120°-α2 ,解得α=140°.综上所述,当α的度数为125°,110°或140°时, △AOD 是等腰三角形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形之旋转问题(北师版)
一、单选题(共6道,每道11分)
1.如图,将等腰直角△ABC(∠ACB=90°,AC=BC)绕C点按逆时针方向旋转到的位置,若=170°,则等于( )
A.35°
B.45°
C.55°
D.65°
答案:C
解题思路:
试题难度:三颗星知识点:旋转的的性质
2.如图,等腰直角△ABC绕点A按逆时针方向旋转60°后得到△ADE,且AB=1,那么EC的长为( )
A. B.1
C. D.
答案:B
解题思路:
试题难度:三颗星知识点:旋转的的性质
3.如图,已知Rt△ABC绕直角顶点A按逆时针方向旋转到的位置,点B在上,∠C=25°,则∠AOB=( )
A.65°
B.50°
C.75°
D.40°
答案:C
解题思路:
试题难度:三颗星知识点:旋转的的性质
4.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=6,Rt可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,则线段的长为( )
A.3
B.
C. D.
答案:D
解题思路:
试题难度:三颗星知识点:旋转的的性质
5.如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到,连接,若∥,则的度数为( )
A.45°
B.60°
C.70°
D.90°
答案:D
解题思路:
试题难度:三颗星知识点:旋转的的性质
6.如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转
α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,若△ADF是等腰三角形,则旋转角α的度数为( )
A.30°
B.40°
C.20°或40°
D.40或60°
答案:C
解题思路:
试题难度:三颗星知识点:旋转的的性质
二、填空题(共3道,每道11分)
7.如图,把△ABC绕点C按逆时针方向旋转35°得到,交BC于点D,若
=90°,则∠B=____度.
答案:55
解题思路:
试题难度:知识点:旋转的的性质
8.如图,将△ABC绕点A按逆时针方向旋转得到△ADE,DE交AC于F,交BC于G,
若∠C=35°,∠EFC=60°,则这次旋转了____度.
答案:25
解题思路:
试题难度:知识点:旋转的的性质
9.如图,在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转45°后得到,则阴影部分的面积为____.
答案:
解题思路:
试题难度:知识点:旋转的的性质。
