人教 B 版高中数学必修4第一章导学案
高中数学(人教B版)必修四导学案：1.1.3 弧度制和弧度制与角度制的换算 Word版缺答案
弧度制和弧度制与角度制的换算（自学自测）【学习目标】1 了解角的另一种度量方法——弧度制；2熟练进行角度制和弧度制的换算；3掌握弧度制中扇形的弧长公式和面积公式。
【学习重点】角度制和弧度制的换算。
【学习难点】弧长公式和面积公式的应用。
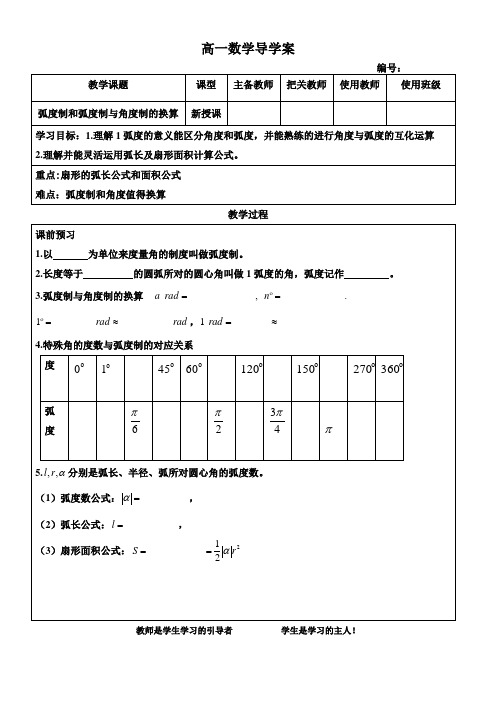
【自主学习】1、把圆周分成360份，其中1份所对的圆心角是 度，这种用度作单位来度量角的制度叫2、我们规定：长度等于 的圆弧所对的 叫做1弧度的角，记作 以 为单位来度量角的制度叫做弧度制。
（1）.在半径为1的圆中，弧长为2的圆弧对的圆心角为 弧度；弧长为1.8的圆弧对的圆心角为 弧度；弧长为π 的圆弧所对的圆心角为 弧度；圆的周长为 弧长为π2的圆弧所对的圆心角为 弧度， 度？（2）.在半径为r 的圆中，弧长为r 2的圆弧对的圆心角为 弧度；弧长为r 8.1的圆弧对的圆心角为 弧度；弧长为πr 的圆弧所对的圆心角为 弧度；圆的周长为 ，弧长为r π2的圆弧所对的圆心角为 弧度， 度？3、弧度数公式α= ;弧长公式: l = ；扇形面积公式：s = = 。
【结论】（1）在半径为r 的圆中，弧长为l 的弧所对的圆心角为α，则（2）=0360 rad =0180 rad所以：01= rad =rad 1 =0n rad 3、常见角度和弧度的转化【自练自提】1、 把下列各角的度化为弧度。
015-= ， 0210= ， 0300= ， 0690= 。
2、 把下列各角的弧度数化为度数。
34π= ， 45π-= ， 611π= ，125π-= 。
23π= ， 8π= 。
3、已知半径为3cm ，圆心角为060的扇形的弧长为 ，面积为 。
3、 扇形面积为4，圆心角弧度数为2，则扇形半径为 ，弧长为 ，周长为 。
弧度制和弧度制与角度制的换算（自研自悟）例1 把下列各角化为0到π2的角加上πk 2（z k ∈）的形式。
并指出他们是哪个象限的角。
（1）623π （2）718π- （3）0225- 2、已知扇形的圆心角为3，周长为20，求扇形的面积3、（选作）弧长等于圆内接正三角形的边长，其所对的圆心角的弧度数为 。
西城学探诊高中数学 1.1相似三角形导学案(无答案)新人教B版选修4-1
§1.1相似三角形 学习目标 1、理解相似三角形的判定定理与性质定理，并会利用定理解决三角形边的比例关系； 2、理解相似三角形的性质定理，并会应用该定理；学习过程【任务一】知识准备相似三角形的判定与性质(1)相似三角形的判定定理：预备定理：_____于三角形一边的直线与其他两边(或两边的延长线)相交，所构成的三角形与原三角形相似．判定定理 1：_____对应相等，两三角形相似．判定定理 2：__________________的两个三角形相似．判定定理 3：_____对应成比例且_____相等，两三角形相似．判定定理 4：两直角三角形有一个______对应相等，则它们相似．判定定理 5：两直角三角形的_________对应成比例，则它们相似．判定定理 6：如果一个直角三角形的_____和___________与另一个直角三角形的_____和____________对应成比例，则它们相似．(2)相似三角形的性质定理：①相似三角形对应高的比、对应中线的比和对应角平分线的比都等于________； ②相似三角形周长的比等于________③相似三角形面积的比等于_______________射影定理的结论在直角三角形 ABC 中，∠BAC 为直角，AD ⊥BC 于 D.则：AB2＝_________，AC2＝_________；AD2＝_________.【任务二】典型例题分析【例1】在梯形ABCD 中，AD ∥BC ，AD ＝2，BC ＝5，点E 、F 分别在AB 、CD 上，且EF ∥AD ，若AE EB ＝34，则EF 的长为________．变式训练1：如图，在△ABC 中，DE ∥BC ，EF ∥CD ，若BC ＝3，DE ＝2，DF ＝1，则AB 的长为________．【例2】已知，如图，在△ABC 中，AB ＝AC ，BD ⊥AC ，点D 是垂足．求证：BC 2＝2CD ·AC .变式训练2：如图，在△ABC 中，DE ∥BC ，DF ∥AC ，AE ∶AC ＝3∶5，DE ＝6，则BF ＝________.【例3】:已知圆的直径AB ＝13，C 为圆上一点，过C 作CD ⊥AB 于D (AD ＞BD )，若CD ＝6，则AD ＝________.变式训练3： 在△ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，AD ∶BD ＝2∶3.则△ACD 与△CBD 的相似比为________．【任务四】课堂达标练习1．如图所示，已知a ∥b ∥c ，直线m 、n 分别与a 、b 、c 交于点A ，B ，C 和A ′，B ′，C ′，如果AB ＝BC ＝1，A ′B ′＝32，则B ′C ′＝________.2．如图所示，BD 、CE 是△ABC 的高，BD 、CE 交于F ，写出图中所有与△ACE 相似的三角形_．3．如图，在△ABC 中，M 、N 分别是AB 、BC 的中点，AN 、CM 交于点O ，那么△MON 与△AOC 面积的比是________．4．如图所示，已知DE ∥BC ，BF ∶EF ＝3∶2，则AC ∶AE ＝______，AD ∶DB ＝________.5．如图，在直角梯形ABCD 中，DC ∥AB ，CB ⊥AB ，AB ＝AD ＝a ，CD ＝a2，点E 、F 分别为线段AB 、AD 的中点，则EF ＝________.。
高中数学 第一章 三角函数 1.4.2 正弦函数、余弦函数的性质(一)导学案 新人教A版必修4-新人
1.4.2 正弦函数、余弦函数的性质(一) 学习目标 1.了解周期函数、周期、最小正周期的定义.2.会求函数y ＝A sin(ωx ＋φ)及y ＝A cos(ωx ＋φ)的周期.3.掌握函数y ＝sin x ，y ＝cos x 的奇偶性，会判断简单三角函数的奇偶性.知识点一 函数的周期性思考1 如果函数f (x )满足f (x ＋3)＝f (x )，那么3是f (x )的周期吗？答案 不一定.必须满足当x 取定义域内的每一个值时，都有f (x ＋3)＝f (x )，才可以说3是f (x )的周期.思考2 所有的函数都具有周期性吗？答案 不是.只有同时符合周期函数定义中的两个条件的函数才具有周期性.思考3 周期函数都有最小正周期吗？答案 周期函数不一定存在最小正周期.例如，对于常数函数f (x )＝c (c 为常数，x ∈R )，所有非零实数T 都是它的周期，而最小正周期是不存在的，所以常数函数没有最小正周期. 梳理 函数的周期性(1)对于函数f (x )，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有f (x ＋T )＝f (x )，那么函数f (x )就叫做周期函数，非零常数T 叫做这个函数的周期.(2)如果在周期函数f (x )的所有周期中存在一个最小的正数，那么这个最小正数叫做f (x )的最小正周期.知识点二 正弦函数、余弦函数的周期性思考1 证明函数y ＝sin x 和y ＝cos x 都是周期函数.答案 ∵sin(x ＋2π)＝sin x ，cos(x ＋2π)＝cos x ，∴y ＝sin x 和y ＝cos x 都是周期函数，且2π就是它们的一个周期.思考2 证明函数f (x )＝A sin(ωx ＋φ)(或f (x )＝A cos(ωx ＋φ))(Aω≠0)是周期函数. 答案 由诱导公式一知，对任意x ∈R ，都有A sin[(ωx ＋φ)＋2π]＝A sin(ωx ＋φ)，所以A sin[ω⎝ ⎛⎭⎪⎫x ＋2πω＋φ]＝A sin(ωx ＋φ)， 即f ⎝ ⎛⎭⎪⎫x ＋2πω＝f (x )，所以f (x )＝A sin(ωx ＋φ)(ω≠0)是周期函数，2πω就是它的一个周期. 同理，函数f (x )＝A cos(ωx ＋φ)(ω≠0)也是周期函数.梳理 由sin(x ＋2k π)＝sin x ，cos(x ＋2k π)＝cos x (k ∈Z )知，y ＝sin x 与y ＝cos x 都是周期函数，2k π (k ∈Z 且k ≠0)都是它们的周期，且它们的最小正周期都是2π. 知识点三 正弦函数、余弦函数的奇偶性思考 对于x ∈R ，sin(－x )＝－sin x ，cos(－x )＝cos x ，这说明正弦函数、余弦函数具备怎样的性质？答案 奇偶性.梳理 (1)对于y ＝sin x ，x ∈R 恒有sin(－x )＝－sin x ，所以正弦函数y ＝sin x 是奇函数，正弦曲线关于原点对称.(2)对于y ＝cos x ，x ∈R 恒有cos(－x )＝cos x ，所以余弦函数y ＝cos x 是偶函数，余弦曲线关于y 轴对称.类型一 三角函数的周期性例1 求下列函数的最小正周期.(1)y ＝sin(2x ＋π3)(x ∈R )； (2)y ＝|sin x |(x ∈R ).解 (1)方法一 令z ＝2x ＋π3，因为x ∈R ，所以z ∈R . 函数f (x )＝sin z 的最小正周期是2π，即变量z 只要且至少要增加到z ＋2π，函数f (x )＝sin z (z ∈R )的值才能重复取得.而z ＋2π＝2x ＋π3＋2π＝2(x ＋π)＋π3，所以自变量x 只要且至少要增加到x ＋π，函数值才能重复取得，所以函数f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π3(x ∈R )的最小正周期是π. 方法二 f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π3的最小正周期为2π2＝π. (2)因为y ＝|sin x |＝⎩⎪⎨⎪⎧ sin x (2k π≤x ≤2k π＋π)，－sin x (2k π＋π<x ≤2k π＋2π)(k ∈Z ).其图象如图所示，所以该函数的最小正周期为π.反思与感悟 对于形如函数y ＝A sin(ωx ＋φ)，Aω≠0时的最小正周期的求法常直接利用T ＝2π|ω|来求解，对于y ＝|A sin ωx |的周期情况常结合图象法来求解. 跟踪训练1 求下列函数的周期.(1)y ＝sin ⎝ ⎛⎭⎪⎫－12x ＋π3；(2)y ＝|cos 2x |. 解 (1)T ＝2π|－12|＝4π. (2)T ＝π2. 类型二 三角函数的奇偶性例2 判断下列函数的奇偶性.(1)f (x )＝sin ⎝ ⎛⎭⎪⎫－12x ＋π2； (2)f (x )＝lg(1－sin x )－lg(1＋sin x )；(3)f (x )＝1＋sin x －cos 2x 1＋sin x. 解 (1)显然x ∈R ，f (x )＝cos 12x ， ∵f (－x )＝cos ⎝ ⎛⎭⎪⎫－12x ＝cos 12x ＝f (x )， ∴f (x )是偶函数.(2)由⎩⎪⎨⎪⎧ 1－sin x >0，1＋sin x >0，得－1<sin x <1.解得定义域为{x |x ∈R 且x ≠k π＋π2，k ∈Z }. ∴f (x )的定义域关于原点对称.又∵f (x )＝lg(1－sin x )－lg(1＋sin x )，∴f (－x )＝lg[1－sin(－x )]－lg[1＋sin(－x )]＝lg(1＋sin x )－lg(1－sin x )＝－f (x ).∴f (x )为奇函数.(3)∵1＋sin x ≠0，∴sin x ≠－1，∴x ∈R 且x ≠2k π－π2，k ∈Z . ∵定义域不关于原点对称，∴该函数是非奇非偶函数.反思与感悟 判断函数奇偶性应把握好两个关键点：关键点一：看函数的定义域是否关于原点对称；关键点二：看f (x )与f (－x )的关系.对于三角函数奇偶性的判断，有时可根据诱导公式先将函数式化简后再判断.跟踪训练2 判断下列函数的奇偶性.(1)f (x )＝cos ⎝ ⎛⎭⎪⎫32π＋2x ＋x 2sin x ； (2)f (x )＝1－2cos x ＋2cos x －1.解 (1)f (x )＝sin 2x ＋x 2sin x ，∵x ∈R ，f (－x )＝sin(－2x )＋(－x )2sin(－x )＝－sin 2x －x 2sin x ＝－f (x )，∴f (x )是奇函数.(2)由⎩⎪⎨⎪⎧ 1－2cos x ≥0，2cos x －1≥0，得cos x ＝12. ∴f (x )＝0，x ＝2k π±π3，k ∈Z . ∴f (x )既是奇函数又是偶函数.类型三 三角函数的奇偶性与周期性的综合应用例3 定义在R 上的函数f (x )既是偶函数又是周期函数，若f (x )的最小正周期是π，且当x ∈⎣⎢⎡⎦⎥⎤0，π2时，f (x )＝sin x ，求f ⎝ ⎛⎭⎪⎫5π3的值. 解 ∵f (x )的最小正周期是π，∴f ⎝ ⎛⎭⎪⎫5π3＝f ⎝ ⎛⎭⎪⎫5π3－2π＝f ⎝ ⎛⎭⎪⎫－π3. ∵f (x )是R 上的偶函数，∴f ⎝ ⎛⎭⎪⎫－π3＝f ⎝ ⎛⎭⎪⎫π3＝sin π3＝32. ∴f ⎝ ⎛⎭⎪⎫5π3＝32. 反思与感悟 解决此类问题的关键是运用函数的周期性和奇偶性，把自变量x 的值转化到可求值区间内.跟踪训练3 若f (x )是以π2为周期的奇函数，且f ⎝ ⎛⎭⎪⎫π3＝1，求f ⎝ ⎛⎭⎪⎫－5π6的值. 解 因为f (x )是以π2为周期的奇函数，所以f ⎝ ⎛⎭⎪⎫－5π6＝f ⎝ ⎛⎭⎪⎫－5π6＋π2＝f ⎝ ⎛⎭⎪⎫－π3＝－f ⎝ ⎛⎭⎪⎫π3＝－1.类型四 函数周期性的综合应用例4 已知函数f (x )＝cos π3x ，求f (1)＋f (2)＋f (3)＋…＋f (2 020)的值. 解 ∵f (1)＝cos π3＝12，f (2)＝cos 2π3＝－12，f (3)＝cos π＝－1，f (4)＝cos 4π3＝－12，f (5)＝cos 5π3＝12，f (6)＝cos 2π＝1， ∴f (1)＋f (2)＋f (3)＋f (4)＋f (5)＋f (6)＝0.同理，可得每连续六项的和均为0.∴f (1)＋f (2)＋f (3)＋…＋f (2 020)＝f (2 017)＋f (2 018)＋f (2 019)＋f (2 020)＝cos 2 017π3＋cos 2 018π3＋cos 2 019π3＋cos 2 020π3＝cos π3＋cos 2π3＋cos π＋cos 4π3＝12＋(－12)＋(－1)＋(－12)＝－32. 反思与感悟 当函数值的出现具有一定的周期性时，可以首先研究它在一个周期内的函数值的变化情况，再给予推广求值.跟踪训练4 设函数f (x )＝sin π3x ，则f (1)＋f (2)＋f (3)＋…＋f (2 015)＝ .解析 ∵f (x )＝sin π3x 的周期T ＝2ππ3＝6， ∴f (1)＋f (2)＋f (3)＋…＋f (2 015)＝335[f (1)＋f (2)＋f (3)＋f (4)＋f (5)＋f (6)]＋f (2 011)＋f (2 012)＋f (2 013)＋f (2 014)＋f (2 015)＝335⎝ ⎛⎭⎪⎫sin π3＋sin 23π＋sin π＋sin 43π＋sin 53π＋sin 2π ＋f (335×6＋1)＋f (335×6＋2)＋f (335×6＋3)＋f (335×6＋4)＋f (335×6＋5)＝335×0＋f (1)＋f (2)＋f (3)＋f (4)＋f (5)＝sin π3＋sin 23π＋sin π＋sin 43π＋sin 53π＝0.1.函数f (x )＝3sin ⎝ ⎛⎭⎪⎫x 2－π4，x ∈R 的最小正周期为( ) A.π2B.πC.2πD.4π 答案 D2.下列函数中最小正周期为π的偶函数是( )A.y ＝sin x 2B.y ＝cos x2 C.y ＝cos xD.y ＝cos 2x 答案 D3.设函数f (x )＝sin ⎝⎛⎭⎪⎫2x －π2，x ∈R ，则f (x )是( ) A.最小正周期为π的奇函数B.最小正周期为π的偶函数C.最小正周期为π2的奇函数 D.最小正周期为π2的偶函数解析 ∵sin ⎝ ⎛⎭⎪⎫2x －π2＝－sin ⎝ ⎛⎭⎪⎫π2－2x ＝－cos 2x ， ∴f (x )＝－cos 2x .又f (－x )＝－cos(－2x )＝－cos 2x ＝f (x )，∴f (x )是最小正周期为π的偶函数.4.函数y ＝sin(ωx ＋π4)的最小正周期为2，则ω的值为 . 答案 ±π解析 ∵T ＝2π|ω|＝2，∴|ω|＝π，∴ω＝±π. 5.若函数f (x )的定义域为R ，最小正周期为3π2，且满足 f (x )＝⎩⎪⎨⎪⎧ cos x ，－π2≤x ＜0，sin x ，0≤x ＜π，则f ⎝⎛⎭⎪⎫－15π4＝ . 答案 22 解析 f ⎝ ⎛⎭⎪⎫－154π＝f ⎝ ⎛⎭⎪⎫－15π4＋3π2×3 ＝f ⎝ ⎛⎭⎪⎫3π4＝sin 3π4＝22.1.求函数的最小正周期的常用方法：(1)定义法，即观察出周期，再用定义来验证；也可由函数所具有的某些性质推出使f (x ＋T )＝f (x )成立的T .(2)图象法，即作出y ＝f (x )的图象，观察图象可求出T ，如y ＝|sin x |.(3)结论法，一般地，函数y ＝A sin(ωx ＋φ)(其中A 、ω、φ为常数，A ≠0，ω>0，x ∈R )的周期T ＝2πω. 2.判断函数的奇偶性，必须坚持“定义域优先”的原则，准确求函数定义域和将式子合理变形是解决此类问题的关键.如果定义域关于原点对称，再看f (－x )与f (x )的关系，从而判断奇偶性.课时作业一、选择题1.下列函数中，周期为π2的是( ) A.y ＝sin x 2B.y ＝sin 2xC.y ＝cos x 4D.y ＝cos(－4x ) 答案 D解析 T ＝2π|－4|＝π2. 2.函数f (x )＝sin ⎝⎛⎭⎪⎫ωx ＋π6的最小正周期为π5，其中ω>0，则ω等于( ) A.5 B.10 C.15 D.20答案 B3.已知a ∈R ，函数f (x )＝sin x －|a |(x ∈R )为奇函数，则a 等于( )A.0B.1C.－1D.±1答案 A解析 因为f (x )为奇函数，所以f (－x )＝sin(－x )－|a |＝－f (x )＝－sin x ＋|a |，所以|a |＝0，从而a ＝0，故选A.4.下列函数中是奇函数，且最小正周期是π的函数是( )A.y ＝cos|2x |B.y ＝|sin x |C.y ＝sin ⎝ ⎛⎭⎪⎫π2＋2x D.y ＝cos ⎝ ⎛⎭⎪⎫3π2－2x 答案 D 解析 y ＝cos|2x |是偶函数，y ＝|sin x |是偶函数，y ＝sin ⎝ ⎛⎭⎪⎫π2＋2x ＝cos 2x 是偶函数，y ＝cos ⎝ ⎛⎭⎪⎫3π2－2x ＝－sin 2x 是奇函数，根据公式求得其最小正周期T ＝π. 5.函数y ＝cos ⎝ ⎛⎭⎪⎫k 4x ＋π3(k ＞0)的最小正周期不大于2，则正整数k 的最小值应是( ) A.10 B.11 C.12 D.13答案 D解析 ∵T ＝2πk 4≤2，即k ≥4π， ∴正整数k 的最小值是13.6.函数y ＝|sin x |(1－sin x )1－sin x的奇偶性为( ) A.奇函数B.既是奇函数也是偶函数C.偶函数D.非奇非偶函数答案 D解析 由题意知，当1－sin x ≠0，即sin x ≠1时，y ＝|sin x |(1－sin x )1－sin x＝|sin x |， 所以函数的定义域为{x |x ≠2k π＋π2，k ∈Z }， 由于定义域不关于原点对称，所以该函数是非奇非偶函数.7.函数f (x )＝3sin(23x ＋15π2)是( ) A.周期为3π的偶函数B.周期为2π的偶函数C.周期为3π的奇函数D.周期为4π3的偶函数 答案 A二、填空题8.若0<α<π2，g (x )＝sin(2x ＋π4＋α)是偶函数，则α的值为 . 答案 π4解析 要使g (x )＝sin(2x ＋π4＋α)为偶函数， 则需π4＋α＝k π＋π2，k ∈Z ，∴α＝k π＋π4，k ∈Z . ∵0<α<π2，∴α＝π4. 9.函数f (x )＝2sin ⎝⎛⎭⎪⎫5π2＋2x ＋1的图象关于 对称.(填“原点”或“y 轴”) 答案 y 轴解析 f (x )＝2sin ⎝ ⎛⎭⎪⎫5π2＋2x ＋1＝2cos 2x ＋1， ∵f (－x )＝f (x )，∴f (x )是偶函数.∵偶函数的图象关于y 轴对称，∴f (x )的图象关于y 轴对称.10.关于x 的函数f (x )＝sin (x ＋φ)有以下说法： ①对任意的φ，f (x )都是非奇非偶函数； ②存在φ，使f (x )是偶函数；③存在φ，使f (x )是奇函数；④对任意的φ，f (x )都不是偶函数.其中错误的是 .(填序号)答案 ①④解析 当φ＝0时，f (x )＝sin x 是奇函数.当φ＝π2时，f (x )＝cos x 是偶函数. 三、解答题11.判断下列函数的奇偶性.(1)f (x )＝cos(π2＋2x )cos(π＋x )； (2)f (x )＝1＋sin x ＋1－sin x ；(3)f (x )＝e sin x ＋e －sin x e sin x －e－sin x . 解 (1)∵x ∈R ，f (x )＝cos(π2＋2x )cos(π＋x ) ＝－sin 2x ·(－cos x )＝sin 2x cos x .∴f (－x )＝sin(－2x )cos(－x )＝－sin 2x cos x＝－f (x )，∴y ＝f (x )是奇函数.(2)∵对任意x ∈R ，－1≤sin x ≤1，∴1＋sin x ≥0，1－sin x ≥0，∴f (x )＝1＋sin x ＋1－sin x 的定义域是R .又∵f (－x )＝1＋sin (－x )＋1－sin (－x )， ＝1－sin x ＋1＋sin x ＝f (x )，∴y ＝f (x )是偶函数.(3)∵e sin x －e －sin x ≠0，∴sin x ≠0，∴x ∈R 且x ≠k π，k ∈Z .∴定义域关于原点对称.又∵f (－x )＝e sin (－x )＋e －sin (－x)e sin (－x )－e－sin (－x ) ＝e －sin x ＋e sin x e －sin x －esin x ＝－f (x )，∴y ＝f (x )是奇函数. 12.已知f (x )是以π为周期的偶函数，且当x ∈⎣⎢⎡⎦⎥⎤0，π2时，f (x )＝1－sin x ，求当x ∈⎣⎢⎡⎦⎥⎤52π，3π时，f (x )的解析式. 解 当x ∈⎣⎢⎡⎦⎥⎤52π，3π时，3π－x ∈⎣⎢⎡⎦⎥⎤0，π2， ∵当x ∈⎣⎢⎡⎦⎥⎤0，π2时，f (x )＝1－sin x ， ∴f (3π－x )＝1－sin(3π－x )＝1－sin x .又∵f (x )是以π为周期的偶函数，∴f (3π－x )＝f (－x )＝f (x )， ∴f (x )的解析式为f (x )＝1－sin x ，x ∈⎣⎢⎡⎦⎥⎤52π，3π. 13.已知函数f (x )满足f (x ＋2)＝－1f (x )，求证：f (x )是周期函数，并求出它的一个周期. 证明 ∵f (x ＋4)＝f (x ＋2＋2)＝－1f (x ＋2)＝f (x )，∴f (x )是周期函数，且4是它的一个周期.四、探究与拓展14.若函数f (x )＝2cos ⎝⎛⎭⎪⎫ωx ＋π3的最小正周期为T ，且T ∈(1，4)，则正整数ω的最大值为 .答案 6解析 ∵T ＝2πω，1＜2πω＜4，则π2＜ω＜2π. ∴ω的最大值是6.15.欲使函数y ＝A sin ωx (A >0，ω>0)在闭区间[0，1]上至少出现50个最小值，求ω的最小值.解 函数y ＝A sin ωx 的最小正周期为2πω，因为在每一个周期内，函数y ＝A sin ωx (A >0，ω>0)都只有一个最小值，要使函数y ＝A sin ωx 在闭区间[0，1]上至少出现50个最小值，则y 在区间[0，1]内至少含4934个周期，即⎩⎪⎨⎪⎧ T ＝2πω，4934T ≤1，解得ω≥199π2，所以ω的最小值为199π2.。
人教B版高一数学(必修4)导学案：1.1.2弧度制和弧度制和角度制的换算(无答案)
2.集合 等于（）
A.ቤተ መጻሕፍቲ ባይዱB. C. D.
3.已知扇形AOB的面积为4，圆心角的弧度数为2，则该扇形的弧长为（）
A. 4 B. 2 C. 1 D. 8
4. 弧度化为角度是，是第象限的角。
B组：
1. 1弧度的圆心角所对的弦长为2，求这个圆心角所对的弧长及圆心角所夹的扇形的面积。
教学反思
落实是成功的保证！
2. 转化为弧度数为（）
A. B. C. D.
3.圆的半径是 ，则 的圆心角与圆弧围成的扇形的面积是（）
A. B. C. D.
4. 7弧度的角是第象限的角，与7弧度的角的终边相同的最小正角为。
积极思考勤于动手天才来自勤奋！
课后巩固作业
A组：
1.在面积不等的圆内，1弧度的圆心角所对的（）
A.弧长相等B.弦长相等
引申（1）把 化成弧度，（2）把 化成度。
探究二把下列各角化成0到 的角加上 的形式，并指出它们是哪个现象的角： 。
引申把下列各角的度数化成弧度数，并写成0到 的角加上 的形式
（1） ；（2） ；（3） 。
认真听讲是学习高效的捷径！
探究三 （1）已知扇形的周长为 ，面积为 ，求扇形圆心角的弧度数；
（2）已知一扇形的圆心角是 ，半径等于 ，求扇形的面积；
2.长度等于的圆弧所对的圆心角叫做1弧度的角，弧度记作。
3.弧度制与角度制的换算
，
4.特殊角的度数与弧度制的对应关系
度
弧度
5. 分别是弧长、半径、弧所对圆心角的弧度数。
（1）弧度数公式： ，
（2）弧长公式： ，
（3）扇形面积公式：
教师是学生学习的引导者学生是学习的主人！
数学人教B版必修4：1.3.2余弦、正切函数的图象与性质 导学案 Word版缺答案
§1.3.2余弦、正切函数的图象与性质（课前预习案）班级：___ 姓名：________ 编写：一、新知导学1.由y=cosx=sin （＿＿＿＿）（x R ∈）可知，余弦函数y=cosx 图象与正弦函数y=sinx 的图象的形状 ，把正弦曲线向 平移个单位就可得余弦函数图象。
2.3.余弦函数y=cosx 的定义域是 ，值域是 ，奇偶性为 ，周期为 ，单调递增区间为 ，单调递减区间为 ，对称中心为 ，对称轴为 。
4. R x xy ∈=tan ，且()z k k x ∈+≠ππ的图象，称“正切曲线”.5.正切函数的性质：（1）定义域：＿＿＿＿＿＿＿＿＿＿＿＿；（2）值域：＿＿＿＿＿ （3）周期性：＿＿＿＿＿＿＿；（4）奇偶性：＿＿＿＿＿＿＿＿；（5）单调性：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.（6）对称中心：4.函数y=-xcosx的部分图象是（ ） A. B. C.D.例3.求函数tan()4y x π=+的定义域．跟进练习3.函数)42tan(π-=x y 的定义域＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿. 例4.不通过求值，比较下列各组中两个正切函数值的大小： （1） 与 ； （2）)411tan(π- 与)513tan(π- ． 四、当堂检测 1.要由y=sin2x 的图象平移后得到y=cos （2x+3π）的图象，只要把y=sin2x 的图象（ ） A.向左平移56π个单位 B.向右平移56π个单位 C.向左平移512π个单位 D.向右平移512π个单位 2.函数y=-xcosx 的部分图象是（ ）A. B. C. D. 3.下列函数中，以π为周期的偶函数是（ ）A.y=sin xB.y=sin xC.y=cos(2x+3π)D.y=sin(x+2π) 4.给出下列命题： ①函数y=sinx 在第一.四象限都是增函数；②函数y=cos(x ωϕ+)的最小正周期 为2πω；③函数y=sin(2732x π+)是偶函数；④函数y=sin2x 的图象向左平移4π个 单位，得到y=sin(2x+4π)的图象。
【西城学探诊】人教B版高中数学选修4-4导学案：1.2.(1、2)极坐标系
§1.2.（1、2）极坐标及其与直角坐标的关系学习目标1.通过具体实例引入确定点的位置的新形式，即极坐标。
2.能够建立极坐标系并描出系中点的位置，在极坐标系中观察一些对称点的坐标关系。
学习过程【任务一】问题分析问题1：一艘军舰在海面上巡逻，发现附近水域里有一片水雷，如何确定它们的位置以便将它们引爆？问题2：思考解决上述问题的关键因素是什么？【任务二】新知理解1.极坐标系：在平面上取一个定点O ，由O 点出发的一条 ，一个 及计算 的正方向（通常 ），合称为一个 。
2.在下图极坐标系中，O 点称为 ，Ox 称为 。
3.图中点M 的位置可以由线段OM 的长度ρ和从Ox 到OM 的角度θ来刻画，这两个数组成的有序数对 称为点M 的极坐标。
其中ρ称为 ，θ称为 。
【任务三】典型例题分析例1：在同一个极坐标系中，画出以下点：)62(π，A )66(π-，B )321(π，C )4(π，D )05(，E )4(π-，F注意：1.一般限定0≥ρ。
特别地：⎩⎨⎧<=,00ρρ， 2.与直角坐标不同，给定点的极坐标),(θρ，唯一确定平面上点，但是平面上点的极坐标并不唯一，比如例1中的 ,如何限定则除极点外一一对应？例2：建立极坐标系描出点)22()63(ππ，，，B A ，分别求点A 关于极轴，直线OB ，极点的对称点的极坐标。
小结：点),(θρ关于极轴的对称点是 ，关于某直线的对称点是 ，关于极点的对称点是 。
思考：极坐标系中，ρ恒为1的点的集合构成什么样的曲线？θ恒为4π的点呢？ 【任务四】探究极坐标与直角坐标的关系如图，在平面上取定一个极坐标系，一极轴作为直角坐标系的x 轴的正半轴，以2πθ=的射线作为y1.用θρ，表示y x ,。
2.用y x ,表示θρtan ，。
例3：把点M 的极坐标)65,3(π化为直角坐标形式。
例4：把点M 的直角坐标)1,1(-化为极坐标形式（限定πθπρ≤<-≥，0）【任务五】课后作业教材P10习题1-2，附纸交。
人教B版高中数学必修1-3.2.2对数函数导学案(2)
对数函数（2）
编者: 学习目标 高小燕 审稿人：全组人员 星期
（10）月（
授课类型：
）日
新授
2.求函数 y log 1 4
2 x log 1 x 5 4
2
2 x 4 的最大值和最小值
会求有关对数函数的复合函数的值域，会判断其奇偶性，求其单调区间
课堂内容展示
单调性 过定点 取值 范围 0<x<1 时，y__________ x>1 时，y__________ 合作探究 题型一 对数函数的值域： 1. 求下列函数的值域: （1） y log2 x 2 4 x 6 0<x<1 时，y________ x>1 时，y________ 题型三 对数函数的奇偶性 4.判断函数的奇偶性： 1 x (1) f x lg （2） f x log2 1 x
规律总结
反馈：求函数 f x log 2
x x log 2 2 4
1 x 16 的最大值和最小值
图 像 定义域 值 域
题型二 对数函数的单调性 3.求下列各函数的单调区间 (1) y ln 4 3x x 2
（2） y log2 x 2 4 x 6
高中数学必修四导学案
高中数学必修四导学案目录第一章 三角函数1.1.1 任意角 ..........................................................................................1 1.1.2 弧度角 ..........................................................................................5 1.2.1 任意角的三角函数(1) ........................................................................8 1.2.1 任意角的三角函数(2) ........................................................................12 1.2.2 同角三角函数的关系(1) .....................................................................15 1.2.2 同角三角函数的关系(2) .....................................................................17 1.2.3 三角函数的诱导公式(1) .....................................................................19 1.2.3 三角函数的诱导公式(2) .....................................................................22 1.2.3 三角函数的诱导公式(3) .....................................................................25 1.3.1 三角函数的周期性 ...........................................................................27 1.3.2 三角函数的图象和性质(1) ..................................................................30 1.3.2 三角函数的图象和性质(2) ..................................................................33 1.3.2 三角函数的图象和性质(3) ..................................................................36 1.3.3 函数)sin(ϕω+=x A y 的图象(1) ......................................................38 1.3.3 函数)sin(ϕω+=x A y 的图象(2) ......................................................41 1.3.4 三角函数的应用.................................................................................44 三角函数复习与小结 (46)第二章 平面的向量2.1 向量的概念及表示..............................................................................49 2.2.1 向量的加法.......................................................................................52 2.2.2 向量的减法.......................................................................................55 2.2.3 向量的数乘(1) .................................................................................58 2.2.3 向量的数乘(2) .................................................................................62 2.3.1 平面向量的基本定理 ........................................................................65 2.3.2 向量的坐标表示(1) ........................................................................68 2.3.2 向量的坐标表示(2) ........................................................................70 2.4.1 向量的数量积(1) ...........................................................................72 2.4.1 向量的数量积(2) (75)第三章 三角恒等变换3.1.1 两角和与差的余弦公式 .....................................................................77 3.1.2 两角和与差的正弦公式 .....................................................................81 3.1.3 两角和与差的正切公式 .....................................................................85 3.2.1 二倍角的三角函数(1) .....................................................................88 3.2.1 二倍角的三角函数(2) (92)第一章 三角函数 1.1.1 任意角【学习目标】1． 了解任意角的概念；正确理解正角、零角、负角的概念2． 正确理解终边相同的角的概念，并能判断其为第几象限角，熟悉掌握终边相同的角的集合表示【学习重点、难点】用集合与符号语言正确表示终边相同的角 【自主学习】 一、复习引入问题1：回忆初中我们是如何定义一个角的？______________________________________________________ 所学的角的范围是什么？______________________________________________________ 问题2：在体操、跳水中，有“转体0720”这样的动作名词，这里的“0720”，怎么刻画？______________________________________________________二、建构数学 1．角的概念角可以看成平面内一条______绕着它的_____从一个位置_____到另一个位置所形成的图形。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课题：角的概念的推广第一章第 1 节第 1 课时【学习目标】1.了解角的概念及推广。
2.掌握终边相同的角及象限角的概念。
【学习重点】角的概念的推广。
【学习难点】1.角的旋转合成。
2.终边相同的角的集合。
【学习方法】阅读，讨论，练习【学习过程】一、预习成果展示（学生以思维导图形式展示预习成果）二、小组探究解疑（小组合作学习新知，讨论解疑）1.角的概念的推广：2.角的加减法运算：3.终边相同的角的集合：4.象限角（轴上角）：GAGGAGAGGAFFFFAFAF三、反馈矫正点拨（将难点问题集中呈现，教师点拨）1.（1）分别写出终边在x正半轴和负半轴，y正半轴和负半轴，x轴和y轴上的角的集合。
（2）分别写出第一象限、第二象限、第三象限和第四象限的角的集合。
2.在直角坐标系中，判断下列语句的真假：（1）第一象限的角一定是锐角。
（2）终边相同的角一定相等。
（3）相等的角终边一定相同。
（4）小于90°的角一定是锐角。
（5）象限角为钝角的终边一定在第二象限。
（6）终边在直线y=3x上的象限角表示为0060⋅，k∈Z。
k+3603.在0°～360°范围内，找出与下列各角终边相同的角，并判断它们是第几象限角：GAGGAGAGGAFFFFAFAF（1）-150°（2）650°（3）-950°15′GAGGAGAGGAFFFFAFAFGAGGAGAGGAFFFFAFAF4.射线OA 绕端点O 逆时针旋转270°到达OB 位置，由OB 位置顺时针旋转一周到达OC 位置，求∠AOC 的大小？四、 强化巩固练习（通过精选习题训练巩固新知）1.若α分别是第一，二，三，四象限的角，那么2α分别是第几象限角？α2的终边又分别在哪呢？（你能总结出一点规律吗）2.小明发现自己的手表走慢了10分钟，他想把时间调准那么时针和分针各旋转了多大的角度呢？3.（1）若︒<<<︒-9090βα ，则βα-的取值范围是_________________.GAGGAGAGGAFFFFAFAF（2）若︒<<<︒-6030βα ，则βα-的取值范围是_________________.五、反思总结提升（绘制完善思维导图总结本课内容）【课后作业】《阳光课堂》对应练习（一）课题：弧度制和弧度制与角度制的换算第一章第 1 节第 2 课时【学习目标】1.了解弧度的意义。
2.掌握弧度与角度的换算方法。
3.加强自身的计算能力。
【学习重点】弧度与角度的换算。
【学习难点】记住一些特殊角度的弧度。
【学习方法】记忆，练习，讨论【学习过程】一、预习成果展示（学生以思维导图形式展示预习成果）二、小组探究解疑（小组合作学习新知，讨论解疑）1. 1弧度的角（弧度制）：2.特殊角度与弧度的换算：GAGGAGAGGAFFFFAFAFGAGGAGAGGAFFFFAFAF3.推导弧长与扇形面积公式（弧度制表示）：三、反馈矫正点拨（将难点问题集中呈现，教师点拨）1．已知扇形的周长为6 cm,面积是2cm ，则扇形的圆心角的弧度数是（ ）A ．1 B.4 C.1或4 D.2或4四、强化巩固练习（通过精选习题训练巩固新知）1.将下列角度化为弧度（1）-240° （2）1080° （3）22°30′ （4）-180°2.将下列弧度化为角度（1）12π （2）23π- （3）35π （4）2 （5）-3GAGGAGAGGAFFFFAFAF3.把下列各角化为0到π2的角加上πk 2（Z k ∈）的形式（1）-64° （2）718π- （3）400° （3）-24.在半径为5cm 的扇形中，圆心角为2rad ，求扇形的面积。
5.已知集合M={x ｜x=2πk +4π ，Z k ∈}，P={x ｜x=4πk +2π ，Z k ∈}，则（ ）A. M=PB. M ⊆PC. M ⊇PD. M ⋂P=Φ6.集合A={x ｜24ππππ+<<+k x k ， Z k ∈}，集合B={x ｜6+x-2x ≥0}，则A ⋂B=？五、反思总结提升（绘制完善思维导图总结本课内容）【课后作业】《阳光课堂》对应练习（二）GAGGAGAGGAFFFFAFAF课题：三角函数的定义第一章第 2 节第 1 课时【学习目标】1.理解并掌握正弦，余弦，正切的定义。
2.了解余切，正割，余割的定义。
3.掌握三角函数在各象限的符号。
【学习重点】1.三角函数的定义。
2.三角函数在各象限的符号。
【学习难点】由定义判断三角函数在各象限的符号。
【学习方法】阅读，记忆，讨论【学习过程】一、预习成果展示（学生以思维导图形式展示预习成果）二、小组探究解疑（小组合作学习新知，讨论解疑）1. 三角函数的定义：GAGGAGAGGAFFFFAFAF2.一些特殊角的各个三角函数值：3.三角函数在各象限的符号：GAGGAGAGGAFFFFAFAFGAGGAGAGGAFFFFAFAF三、反馈矫正点拨（将难点问题集中呈现，教师点拨） 1.已知角α终边经过点P （21-，23），则cos α=＿＿＿＿，sin α=＿＿＿＿，tan α=＿＿＿＿，cot α=＿＿＿＿，sec α=＿＿＿＿，csc α=＿＿＿＿2.求23π的各三角函数值。
3.已知角α的终边在直线y=2x 上，求sin α，cos α，tan α的值。
4.确定下列各三角函数的符号（1）sin156° （2）cos 516π （3）cos （-80°）（4）tan （817π-） （5）sin （3π-） （6）tan556°12′四、强化巩固练习（通过精选习题训练巩固新知）1.填空：（1）若sinα>0，且cosα<0，则α是第＿＿＿＿象限角；（2）若tanα>0，且cosα<0，则α是第＿＿＿＿象限角；（3）若sinα<0，且tanα<0，则α是第＿＿＿＿象限角；（4）若cosα>0，且sinα<0，则α是第＿＿＿＿象限角。
2.设A是三角形的一个内角，那么在sinA，cosA，tanA中，哪些可能是负值？五、反思总结提升（绘制完善思维导图总结本课内容）【课后作业】《阳光课堂》对应练习（三）GAGGAGAGGAFFFFAFAF课题：三角函数的定义第一章第 1 节第 2 课时【学习目标】1.理解并掌握正弦，余弦，正切的定义。
2.了解余切，正割，余割的定义。
3.掌握三角函数在各象限的符号。
【学习重点】1.三角函数的定义。
2.三角函数在各象限的符号。
【学习难点】由定义判断三角函数在各象限的符号。
【学习方法】练习【学习过程】一、预习成果展示（学生以思维导图形式展示预习成果）二、强化巩固练习（通过精选习题训练巩固新知）1.设角α终边上一点P（-4a，3a）（a≠0）则2sinα+cosα=（）。
GAGGAGAGGAFFFFAFAFGAGGAGAGGAFFFFAFAFA. 52 B. 52± C. 52- D. 与α有关但不确定。
2.若角α终边经过点P （2sin30°，-2cos30°）则sin α=（ ）。
A. 21 B. 21- C. 23-D. 33-3.使得代数式αααtan cos sin -有意义的α的取值范围是＿＿＿＿＿＿＿＿。
4.sin 2θ=53 ，542cos -=θ，则θ角的终边在第＿＿＿＿象限。
5. 已知α是第三象限角，且2sin α=2sin α-，则2α是第＿＿＿＿象限角。
GAGGAGAGGAFFFFAFAF6.已知函数f （x ）=xxx x xx xx cot cot tan tan cos cos sin sin +++则函数f （x ）的值域是 。
7. 若sin α·cos α>0 则角α的终边在第 象限。
8.已知∆ABC 中sin cos 0A B ⋅<则∆ABC 为（ ）。
A. 钝角三角形B. 锐角三角形C. 直角三角形D.任意三角形9. 已知α是第三象限角，则下列各式中不成立的是（ ）。
A. sin α+cos α<0B. tan α-sin α<0C. cos α-cot α<0D.cot α⨯csc α<010.已知α是第二象限角，则点P （sin （cos α），cos （sin α））在第＿＿＿＿象限。
三、反馈矫正点拨（将难点问题集中呈现，教师点拨） 1.若)21(α2sin < 1 则α的取值范围是＿＿＿＿。
2.已知点()-+在角α的终边上，且cosα0≤，sinα>0 39,2P a a则α的取值范围是？四、、反思总结提升（绘制完善思维导图总结本课内容）【课后作业】三角函数的定义练习题1~5GAGGAGAGGAFFFFAFAF课题：单位圆与三角函数线第一章第 2 节第 3 课时【学习目标】1.能正确用三角函数线表示任意角的三角函数值。
2.培养数形结合的良好思维习惯。
【学习重点】利用单位圆有关的三角函数线表示三角函数值。
【学习难点】利用单位圆有关的三角函数线表示三角函数值。
【学习方法】阅读，记忆，讨论，练习【学习过程】一、预习成果展示（学生以思维导图形式展示预习成果）二、小组探究解疑（小组合作学习新知，讨论解疑）1.单位圆：2.正弦线：3.余弦线：4.正切线：GAGGAGAGGAFFFFAFAFGAGGAGAGGAFFFFAFAF5.分别作出下列各角的正弦线，余弦线，正切线：（1）3π（2）32π-（3）65π （4）613π-6.已知点P （sin α-cos α,tan α）在第一象限，则在[0,2π）内的角α的取值范围是（ ）。
A.)45,()43,2(ππππ⋃ B.)45,()2,4(ππππ⋃ C.)23,45()43,2(ππππ⋃ D.),43()2,4(ππππ⋃三、反馈矫正点拨（将难点问题集中呈现，教师点拨） 1.（1）设24παπ<<，角α的正弦线，余弦线，正切线的数量分别是a ，b 和c ，试比较a ，b ，c 的大小；（2）若432παπ<<，那么a,b,c 的大小关系又如何？GAGGAGAGGAFFFFAFAF2.证明：若20πα<< ，则sin α+cos α>13.证明：若20πα<<，则sin α<α<tan α4.由三角函数线你能否判断sin α-cos α的正负分界线吗？能否判断sin α+cos α的正负分界线吗？四、强化巩固练习（通过精选习题训练巩固新知） 1.确定1cos 1sin -的符号2.（1）在[0,2π）内满足sin α≥21的角α的取值范围是 。