浙江省宁波市九校2016-2017学年高二下期末联考数学试卷及答案
2016-2017学年浙江省宁波市九校高二下学期期末联考数学试题-解析版

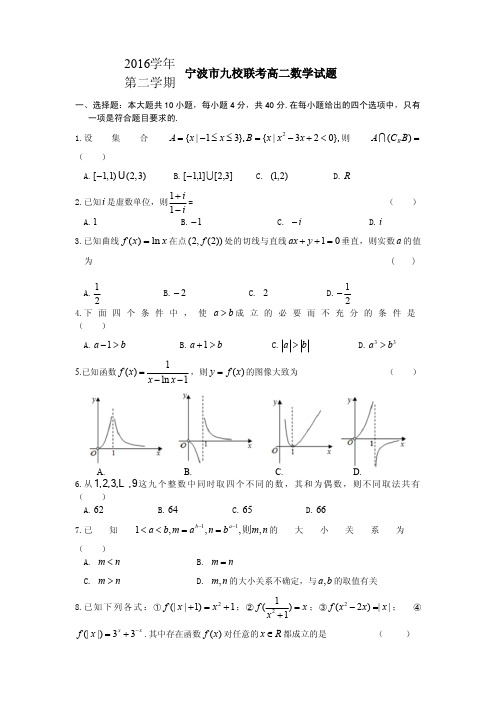
浙江省宁波市九校2016-2017学年高二下学期期末联考数学试题一、选择题 1.设集合2{|13},{|320},A x x B x x x =-≤≤=-+<则()R A C B ⋂=( )A. [)()1,12,3-⋃B. ][1,12,3⎡⎤-⋃⎣⎦C. ()1,2D. R【答案】B【解析】集合A ={x |-1≤x ≤3}=[-1,3],B ={x |x 2-3x +2<0}={x |1<x <2}=[1,2], 则A ∩(∁R B )=[-1,3]∩[2,+∞)∪(-∞,1]=[2,3]∪[-1,1], 本题选择B 选项. 2.已知i 是虚数单位,则11ii+-=( )A. 1B. 1-C. i -D. i 【答案】D【解析】()()()2111121112i i i i i i i ++-+===-+- 本题选择D 选项.3.已知曲线()ln f x x =在点()()2,2f 处的切线与直线10ax y ++=垂直,则实数a 的值为( ) A.12 B. 2- C. 2 D. 12- 【答案】C【解析】f (x )=lnx 的导数为f ′(x )= 1x ,可得曲线f (x )=lnx 在点(2,f (2))处的切线斜率为12, 切线与直线ax +y +1=0垂直,可得−a ⋅12=−1,解得a =2.本题选择C 选项.4.下面四个条件中,使a b >成立的必要而不充分的条件是( )A. 1a b ->B. 1a b +>C. a b >D. 33a b >【答案】B【解析】 “a >b ”不能推出“a -1>b ”,故选项A 不是“a >b ”的必要条件,不满足题意; “a >b ”能推出“a +1>b ”,但“a +1>b ”不能推出“a >b ”,故满足题意;“a >b ”不能推出“|a |>|b |”,故选项C 不是“a >b ”的必要条件,不满足题意; “a >b ”能推出“a 3>b 3”,且“a 3>b 3”能推出“a >b ”,故是充要条件,不满足题意; 本题选择B 选项.点睛:有关探求充要条件的选择题,破题关键是:首先,判断是选项“推”题干,还是题干“推”选项;其次,利用以小推大的技巧,即可得结论. 5.已知函数()1ln 1f x x x =--,则()y f x =的图象大致为( )A.B.C.D.【答案】A【解析】由于()102f e e =>-,排除D .由于10f e e ⎛⎫=> ⎪⎝⎭,排除B .由于()()2213f e f e e =<- ,故函数在()1,+∞为减函数,排除C .所以选A . 点睛:本题主要考查函数图像的判断.一般采用特殊值的方法利用选项中图像的特殊性,对x 进行赋值,然后利用相应函数值来排除错误的选项.本题还可以利用导数来判断,利用导数,可求得原函数的导数为()()21ln 1x f x x x x -'-=-,故当01x <<,函数单调递增,当1x >时,函数单调递减.6.从1,2,3,,9 这九个整数中同时取四个不同的数,其和为偶数,则不同取法共有 ( )A. 62B. 64C. 65D. 66 【答案】D【解析】根据题意,从1,2,3,4,5,6,7,8,9中任取四个数,使其和为偶数需要分3种情况讨论:①当取出的4个数都是奇数,有455C =种情况,②当取出的4个数有2个奇数、2个偶数,有225410660C C ⨯=⨯=种情况, ③当取出的4个数都是偶数,当取出的数字没有奇数有441C =种情况,根据分类计数原理总共有5+60+1=66种取法; 本题选择D 选项.7.已知111,,,,b a a b m a n b m n --<<==则的大小关系为( ) A. m n < B. m n =C.m n > D. ,m n 的大小关系不确定,与,a b 的取值有关【答案】C【解析】∵1<a <b ,∴b −1>a −1>0,∴m =a b −1>a a −1>n =b a −1,则m >n , 本题选择C 选项. 8.已知下列各式:①()211f x x +=+;②211f x x ⎛⎫= ⎪+⎝⎭;③()22f x x x -=; ④()33xx fx -=+.其中存在函数()f x 对任意的x R ∈都成立的是( )A. ①④B. ③④C. ①②D. ①③ 【答案】A【解析】①f (|x |+1)=x 2+1,由t =|x |+1(t ⩾1),可得|x |=t −1,则f (t )=(t −1)2+1, 即有f (x )=(x −1)2+1对x ∈R 均成立; ②22111,(01),111f x t t x x x t ⎛⎫==<=±-⎪++⎝⎭令…, 对0<t ⩽1,y =f (t )不能构成函数,故不成立;③f (x 2−2x )=|x |,令t =x 2−2x ,若t <−1时,x ∈∅; t ⩾−1,可得()111x t t =±+-…,y =f (t )不能构成函数;④f (|x |)=3x +3−x .当x ⩾0时,f (x )=3x +3−x ;当x <0时,f (−x )=3x +3−x ;将x 换为−x 可得f (x )=3x +3−x ;故恒成立。
宁波市高中高二数学下册期末测试卷答案

宁波市高中高二数学下册期末测试卷答案就是二面角的平面角 10分本文导航 1、首页2、高二数学下册期末测试卷答案-23、高二数学下册期末测试卷答案-3中,,.即二面角的余弦值为 .14分解法二:建立如图所示的空间直角坐标系,可知平面的一个法向量为设平面的一个法向量为则,可求得 . 10分所以,所以二面角的余弦值为 . 14分21.解:(Ⅰ)设P(x0,y0)是y=f(x)图象上点,Q(x,y),则,-y=loga(x+a-3a),y=loga (x2a) ----------- 5分新_课_标第_一_网(2)令由得,由题意知,故,从而,故函数在区间上单调递增 ------------------8分( 1)若,则在区间上单调递减,所以在区间上的最大值为 .在区间上不等式恒成立,等价于不等式成立,从而,解得或 .结合得 . ---------------------------------- --11分(2)若,则在区间上单调递增,所以在区间上的最大值为 .在区间上不等式恒成立,等价于不等式成立,本文导航 1、首页2、高二数学下册期末测试卷答案-23、高二数学下册期末测试卷答案-3从而,即,解得 .易知,所以不符合. -----------------------14分综上可知:的取值范围为 . ----------------------------15分22.解:(1 )焦点 -----------------------3分代入,得 -----------------------5分(2)联立,得即-----------------------8分----10分-----------------------12分的面积 -----------------------15分只要大家用心学习,认真复习,就有可能在高中的战场上考取自己理想的成绩。
查字典数学网的编辑为大家带来的2019-2019宁波市高中高二数学下册期末测试卷答案,希望能为大家提供帮助。
最新【word精校版】江省宁波市2017学年第二学期九校联考期末考高二数学试题

解得 或 或 ,………………5分
所以原不等式的解集为 . ………………6分
(Ⅱ) ,
所以 ,解得 . ………………9分
法一:令 ,则 ………………11分
又 ,所以 . ………………14分
法二:因为 ,所以 ,………………11分
则 . ………………14分
19.解:(Ⅰ) , ,
,………………3分
在 上单调递增, ;…………7分
当 时, ,
在 上单调递增,在 上单调递减,在 上单调递增,
所以 , ,
而 ,
当 时, ;
当 时, ;…………10分
当 时, ,
所以 在 上单调递增,在 上单调递减,
此时 ;…………12分
当 时, ,所以 在 上单调递增,
此时 ;…………14分
综上所述,当 时, …………15分
宁波市2017学年第二学期九校联考高二数学试题
一、选择题(每小题4分,共40分)
1.已知集合 , ,则集合 ()
A. B. C. D.
2.下列函数中,在定义域上为增函数的是()
A. B. C. D.
3.已知函数 ,则下列选项错误的是()
A. B. C. D.
4.函数 的零点所在的大致区间是()
A. B. C. D.
(2)求函数 在区间 上的取值范围
21.已知函数 ,
(1)判断函数 的奇偶性;
(2)若 且 ,求函数 在区间 上的最大值
22.已知函数
(1)(ⅰ)讨论函数 的极值点个数;
(ⅱ)若 是函数 的极值点,求证:
(2)若 , 是 的两个零点,证明:
宁波市2017学年期末九校联考高二数学参考答案
一、选择题:本大题共10小题,每小题4分,共40分.
浙江省宁波市高二下学期数学期末统考试卷

浙江省宁波市高二下学期数学期末统考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共3题;共6分)1. (2分)设,则集合= ()A . {i}B . {i,-i}C . {2i}D .2. (2分)火星的半径约是地球半径的一半,则地球的体积是火星的()A . 4倍B . 8倍C . 倍D . 倍3. (2分) (2016高二上·包头期中) 已知直线l,m和平面α,则下列命题正确的是()A . 若l∥m,m⊂α,则l∥αB . 若l∥α,m⊂α,则l∥mC . 若l⊥m,l⊥α,则m⊥αD . 若l⊥α,m⊂α,则l⊥m二、填空题 (共8题;共8分)4. (1分) (2015高二下·和平期中) 已知i为虚数单位,a∈R,(2﹣ai)i的实部与虚部互为相反数,则a 的值为________.5. (1分)在正方体ABCD-A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、B1C1的中点,则异面直线EF与GH所成的角等于________.6. (1分)(2017·海淀模拟) 已知正方体ABCD﹣A1B1C1D1的棱长为2,长度为2的线段MN的一个端点M在棱DD1上运动,另一个端点N在正方形ABCD内运动,则MN中点的轨迹与正方体ABCD﹣A1B1C1D1的表面所围成的较小的几何体的体积等于________.7. (1分) (2016高二上·重庆期中) 若一个圆台的正视图如图所示,则其体积等于________.8. (1分) (2018高二下·重庆期中) 的展开式中的常数项是________9. (1分)正方体ABCD-A1B1C1D1 的棱长为1,在正方体的表面上与点A距离为的点形成一条曲线,这条曲线的长度为________.10. (1分)(2020·桂林模拟) 某校13名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共9种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以2人一-组或者3人一组.如果2人一组,则必须角色相同;如果3人一组,则3人角色相同或者3人为级别连续的3个不同角色.已知这13名学生扮演的角色有3名士兵和3名司令,其余角色各1人,现在新加入1名学生,将这14名学生分成5组进行游戏,则新加入的学生可以扮演的角色的种数为________.11. (1分)(2017·绍兴模拟) 将3个男同学和3个女同学排成一列,若男同学甲与另外两个男同学不相邻,则不同的排法种数为________.(用具体的数字作答)三、解答题 (共4题;共40分)12. (10分)设复数z=,若z2+az+b=1+i,求实数a,b的值.13. (10分)(2018高三上·大连期末) 已知椭圆的一个焦点与抛物线的焦点重合,且点到直线的距离为,与的公共弦长为 .(1)求椭圆的方程及点的坐标;(2)过点的直线与交于两点,与交于两点,求的取值范围.14. (10分)如图所示(单位:cm),四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.15. (10分)(2018·许昌模拟) △ABC中,已知B=2C,AB:AC=2:3.(1)求cosC;(2)若AC=,求BC的长度.参考答案一、单选题 (共3题;共6分)1-1、2-1、3-1、二、填空题 (共8题;共8分)4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、三、解答题 (共4题;共40分)12-1、13-1、13-2、14-1、15-1、15-2、。
宁波市九校2016-2017学年高二下期末联考数学试卷含答案
宁波市九校联考高二数学试题一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有 一项是符合题目要求的. 1.设集合则2{|13}{|320}A x x B x x x =-≤≤=-+<,,=)(B C A R ( )A. B. C. D.[1,1)(2,3)-U ]3,2[]1,1[ -)2,1(R 2.已知是虚数单位,则= ( ) i ii-+11 A. B. C. D.11-i -i 3.已知曲线在点处的切线与直线垂直,则实数的值x x f ln )(=))2(,2(f 01=++y ax a 为 ( )A.B. C. D.212-221-4.下面四个条件中,使成立的必要而不充分的条件是a b >( )A. B.C.D.1a b ->1a b +>a b >33a b >5.已知函数,则的图像大致为()1ln 1)(--=x x x f )(x f y = A. B. C. D.6.从这九个整数中同时取四个不同的数,其和为偶数,则不同取法共有 1,2,3,,9L ( )A. B. C. D. 626465667.已知的大小关系为n m b n a m b a a b ,,,,111则--==<<( )A. B.n m <n m = C. D. 的大小关系不确定,与的取值有关 n m >n m ,b a ,8.已知下列各式:①;②;③; ④1)1|(|2+=+x x f x x f =+)11(2||)2(2x x x f =-.其中存在函数对任意的都成立的是 ( )x x xf -+=33|)(|)(x f R x ∈第二学期学年2016A.①④B.③④C.①②D.①③9.设函数,若存在实数,使得对任意的 )0(log )(2>++=a b ax x x f b [])0(2,>+∈t t t x 都有,则的最小值是a x f +≤1|)(|t ( )A. B. C.D. 21433210.定义在上的可导函数满足,当时R )(x f 32)()(x x f x f =--(]0,∞-∈x ,3)(2x x f <' 实数满足,则的取值范围是 ( ) a 1332)()1(23+-+-≥--a a a a f a f a A. B. C. D.⎪⎭⎫⎢⎣⎡∞+23⎥⎦⎤ ⎝⎛∞-23,⎪⎭⎫⎢⎣⎡∞+21⎥⎦⎤ ⎝⎛∞-21,二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 11.若则 ,用表示为 . ,3log ,2log n m a a ===+n m a 2n m ,6log 412.已知的展开式中二项式系数和为64,则 ,该展开式中常数项 nxx 212(-=n 为 . 13.已知函数.若时方程有两 10,2,122,4)(≠>⎩⎨⎧>++≤+-=a a x a a x x x f x且其中21=a b x f =)( 个不同的实根,则实数的取值范围是 ;若的值域为,则实数b )(x f [)∞+,2a 的取值范围是 . 14.函数的奇偶性为 ,在上的增减性为 (填xxee x x xf --+-=2)(3R “单调递增”、“单调递减”或“有增有减”).15.小明和爸爸妈妈、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小 明的父母至少有一人与小明相邻,则不同的坐法总数为 . 16.已知的最小值为,则实数 . a x a x x a x x x f 22|1||1|)(-+--+-+=)(0>x 23=a 17.已知函数在区间上有零点,则的)R b a b ax x x f ∈++=,()(2(]1,00x )31914(00-+x x ab 最大值是 .三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 18.已知,.*∈N n (1)(2)(),n S n n n n =+++L 213(21)nn T n =⨯⨯⨯⨯-L(Ⅰ)求 ;321321,,,,,T T T S S S (Ⅱ)猜想与的关系,并用数学归纳法证明. n S n T19.(Ⅰ)已知,其中1021001210(21)(1)(1(1)x a a x a x a x -=+-+-++-L ) .(i )求;(ii )求.,1,2,10i a R i ∈=L 01210a a a a ++++L 7a(Ⅱ)2017年5月,北京召开“一带一路”国际合作高峰论坛.组委会将甲、乙、丙、 丁、戊五名志愿者分配到翻译、导游、礼仪、司机四个不同的岗位,每个岗位至 少有一人参加,且五人均能胜任这四个岗位.(i )若每人不准兼职,则不同的分配方案有几种?(ii)若甲乙被抽调去别的地方,剩下三人要求每人必兼两职,则不同的分配方案 有几种? 20.已知,函数满足 R a ∈)(x f .12)2(22-+-=a ax x f x(Ⅰ)求的解析式,并写出的定义域; )(x f )(x f (Ⅱ)若在上的值域为,求实数的取值范围.)(x f ]2,2[2212+--a aa []0,1-a。
2016学年浙江省高二下学期期末考试数学试卷【含答案及解析】

①若 且 ,则 ;
②若 且 ,则 ;
③若方程 在 内恰有四个不同的实根 ,则 或8;
④函数 在 内至少有5个零点,至多有13个零点
其中结论正确的有___________。
A.1个___________ B.2个___________ C.3个___________ D.4个
A.1___________ B. ___________ C. ___________ D.
7.已知点P为双曲线 右支上一点, 分别为双曲线的左右焦点,且 ,I为三角形 的内心,若 成立,则 的值为___________。
A. ___________ B. ___________ C. ___________D.
(Ⅰ)求证: 平面 ;
(Ⅱ)若 ,求二面角 的正切值的大小。
18.已知函数 。
(Ⅰ)若当 时,不等式 恒成立,求实数 的取值范围;
(Ⅱ)求函数 在区间 上的最大值。
19.已知椭圆 ,其长轴长为 ,直线 与 只有一个公共点 ,直线 与 只有一个公共点 。
(I)求椭圆 的方程;
(II)设 是 上(除 外)的动点,连结 交椭圆于另外一点 ,连结 交椭圆于 两点( 在 的下方),直线 分别交直线 于点 ,若 成等差数列,求点<a href=""> 的坐标。
二、填空题
9.若经过点 的直线 与圆 相切,则圆 的圆心坐标是___________;半径为___________;切线在 轴上的截距是___________。
10.若表示 两数中的最大值,若 ,则 的最小值为___________,若 关于 对称,则 ___________。
浙江省宁波市高二数学下学期期末考试试卷(含解析)
2016-2017学年浙江省宁波高二下学期期末考试数学一、选择题:共10题1.设,且,则等于A. B. C. D.【答案】A【解析】本题考查排列组合.解答本题时要注意根据排列数与组合数公式,确定选项.由排列、组合数公式可知,.故选A.2.若,则正整数的值为A.2B.8C.2或6D.2或8【答案】D【解析】本题考查组合数公式的性质.解答本题时要注意利用组合数公式的性质,计算求值.因为,所以有,解得.故选D.3.下列求导运算正确的是A.=B.(3x)′=3x log3eC.(log2x)′=D.(x2cos x)′=-2x sin x【答案】C【解析】本题考查导数的运算.解答本题时要注意根据导数的运算法则,判断选项的准确性.因为,所以选项A错误;因为(3x)′=,所以选项B错误;因为(x2cos x)′=,所以选项D错误;选项C正确.故选C.4.用反证法证明命题:“已知,若可被5整除,则中至少有一个能被5整除”时,反设正确的是A.都不能被5整除B.都能被5整除C.中有一个不能被5整除D.中有一个能被5整除【答案】A【解析】本题考查反证法.解答本题时要注意利用反证法时反证的正确性.由题可得,“中至少有一个能被5整除”的反设为“都不能被5整除”.故选A.5.设是函数的导函数,的图象如图1所示,则的图象最有可能的是【答案】C【解析】本题考查导数的应用.解答本题时要注意根据导函数的图象,确定倒数在给定区间的正负,判断函数的单调性,由此确定函数的图象.由题可得,当时,,当时,,当时,,所以函数在上单调递增,在(0,2)上单调递减,在上单调递增,对比选项.故选C.6.某校三位学生参加省举行的数学团体竞赛,对于其中一题,他们各自解出的概率分别是,则此题能解出的概率是A. B. C. D.【答案】D【解析】本题考查随机事件的概率.解答本题是要注意根据条件利用对立事件的概率求值计算.由题可得,此题能解出的概率为.故选D.7.甲、乙两人练习射击, 命中目标的概率分别为和, 甲、乙两人各射击一次,有下列说法: ①目标恰好被命中一次的概率为+;②目标恰好被命中两次的概率为;③目标被命中的概率为; ④目标被命中的概率为,以上说法正确的序号依次是A.②③B.①②③C.②④D.①③【答案】C【解析】本题考查随机事件的概率.解答本题时要注意根据每种说法,分别推理,确定其准确性,得到正确答案.对于说法①,目标恰好被命中一次的概率为.所以错误,结合选项可知,排除B,D;对于说法③,目标被命中的概率为,所以错误,排除A.故选C.8.随机变量ξ的概率分布列为P(ξ=k)=,k=1,2,3,4,其中c是常数,则P()的值为A. B. C. D.【答案】D【解析】本题考查随机变量的分布列.解答本题时要注意先根据k的值及分布列的特点,确定c的值,再求满足条件的事件的概率.由题可得,,解得.所以P()=.故选D.9.设,则的值是A.17B.18B.19C.20【答案】B【解析】本题考查二项分布.解答本题时要注意利用二项分布的期望方差的求法,计算求值.由题可得,因为是二项分布,所以,所以解得,所以.故选B.10.有下列命题:①若存在导函数,则;②若,则;③若函数y=f(x)满足f′(x)>f(x),则当a>0时,f(a)>e a f(0);④若,则是有极值点的充要条件,其中正确命题的个数为A.1B.2C.3D.4【答案】B【解析】本题考查导数相关性质的真假判断.解答本题时要注意利用导数的相关运算及性质,对每个命题的真假解析判断.对于①,所以错误;对于②,由导数的运算法则可知,正确;对于③当f′(x)>f(x)时,则有函数是增函数,所以当a>0时,>,所以f(a)>e a f(0),正确;对于④,,要使函数存在极值,则需且,所以错误.所以正确命题的个数为2个.故选B.二、填空题:共7题11.若+++,则_____,_____.【答案】6,63【解析】本题考查二项式定理.解答本题时要注意利用二项式展开式特点,化简式子,求值计算.因为+++,解得.因为,所以原式.12.现有5本不同的书,其中有2本数学书,将这5本书排成一排,则数学书不能相邻且又不同时排在两边的排法有_________种;将这5本书分给3个同学,每人至少得1本,则所有不同的分法有_________种.【答案】60,150【解析】本题考查排列组合.解答本题时要注意根据排列组合的及两个计数原理,采用恰当的分法,求值计算.采用插空法,先排其他书,再排数学书,则满足要求的排法有.书可按1+2+2或1+1+3的模式进行分配.所以满足条件的不同的分法由.13.若对于任意实数,恒有成立,则__________,______________.【答案】【解析】本题考查二项式定理.解答本题时要注意先利用换元法,转化二项式,再利用二项式展开式的通项公式,求相应的系数,再通过赋值法,求系数的和.令,则,所以上述二项式展开式可转化为.所以.令,则.所以.14.已知,则在处的切线方程是_____________,若存在使得成立,则实数的取值范围是_____________.【答案】【解析】本题考查导数的应用.解答本题时要注意先利用导数的几何意义,求切线方程;再通过构造函数,利用导数求函数的最值,通过函数的最值,求得实数的取值范围.因为.由导数的几何意义可知,,且.所以在处的切线方程是.令,则,所以可知在上单调递减,在上单调递增.因为存在使得成立,所以只需.所以.15.从装有6个白球和4个红球的口袋中任取一个球,用表示“取到的白球个数”,即则______________.【答案】【解析】本题考查随机变量的分布列及其期望和方差.解答本题时要注意根据条件形成分布列,并计算期望,由此计算方差.由题可得.所以.所以.16.锅中煮有芝麻馅汤圆6个,花生馅汤圆5个,豆沙馅汤圆4个,这三种汤圆的外部特征完全相同. 从中任意舀取4个汤圆,则每种汤圆都至少取到1个的概率为___________.【答案】【解析】本题考查随机事件的概率.解答本题时要注意结合排列组合数公式,利用古典概型,求相应事件的概率.由题可得.17.已知都是定义在上的函数,>=,在有穷数列中,任意取正整数,则前项和大于的概率是__________.【答案】【解析】本题考查等可能事件的概率,数列与函数的综合.解答本题时要注意先根据导数不等式,构造函数,并确定其单调性,再计算得到实数的值,然后构造不等式,确定n的取值范围,再利用等可能事件的概率,求值计算.令,则.所以单调递减,所以.因为,解得.所以其前n项和为.所以有,解得.故所求概率为.三、解答题:共5题18.已知二项式的展开式中第四项为常数项.(1)求的值;(2)求展开式的各项系数绝对值之和;(3)求展开式中系数最大的项.【答案】(1)的展开式中第四项为常数项,,(2)由(1)知,展开式的各项系数绝对值之和为.(3)设展开式的第项系数绝对值为,且为最大值则,或,又时是展开式中第四项,其系数是负值,故的展开式中系数最大的项为:.【解析】本题考查二项式定理.解答本题时要注意(1)利用二项式展开式的通项公式,结合第四项为常数项,建立关于n的方程,解得n的值.(2)利用条件,结合最大项的表示方式,建立不等式组,求解不等式组,确定系数最大的项,并表示之.19.设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内,(1)只有一个盒子空着,共有多少种投放方法?(2)没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?(3)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?【答案】(1)(种);(2)(种);(3)满足的情形:第一类,五个球的编号与盒子编号全同的放法:1种;第二类,四个球的编号与盒子编号相同的放法:0种;第三类,三个球的编号与盒子编号相同的放法:10种;第四类,二个球的编号与盒子编号相同的放法:种;故满足条件的放法数为种.【解析】本题考查排列组合.解答本题时要注意(1)根据条件先确定哪两个球在一起,然后再确定哪四个盒子有球,最后利用分步乘法计数原理求得投放的方法;(2)利用间接法,所有情况去掉球的编号与盒子编号相同的,剩余的就是满足条件的;(3)利用分类加法计数原理,确定满足条件的方法,最后将所得到的方法相加.20.某校为促进学生全面的发展,在高二年级开设了化学研究性学习课程,某班学生在一次研究活动课程中,一个小组进行一种验证性实验,已知该种实验每次实验成功的概率为.(1)求该小组做了5次这种实验至少有2次成功的概率;(2)如果在若干次实验中累计有2次成功就停止实验,否则将继续下次实验,但实验的总次数不超过5次,求该小组所做实验的次数ξ的分布列和数学期望.【答案】(1)记“该小组做了5次试验至少有2次成功”为事件A,“只成功1次”为事件A1,“一次都不成功”为事件A2,则P(A)=1-P(A1+A2)=1-P(A1)-P(A2)=1-()5-()5=,故该小组做了5次这种实验至少有2次成功的概率为.(2)ξ的可能取值为2,3,4,5.则P(ξ=2)=()2=;P(ξ=3)=()3=;P(ξ=4)=()4=;P(ξ=5)=()5+()5+()5=.所以ξ的分布列为所以Eξ=2×+3×+4×+5×=.【解析】本题主要考查概率的计算、分布列、期望等知识,考查考生的数据处理能力、运算求解能力.根据对立事件的概率计算公式可求出(1);对于(2),写出ξ的取值情况,由相互独立事件同时发生的概率计算公式可得出ξ的分布列,进而求出数学期望.【备注】高考对离散型随机变量的考查主要有两个方面:一是求随机变量的概率分布列,二是求随机变量的期望.求概率的过程中要注意分类讨论思想的运用,分类要做到不重不漏,所有变量的概率之和为1,可用来快速检验计算结果或分类是否正确.21.是否存在常数使得对一切均成立,并证明你的结论.【答案】令得:,下面利用数学归纳法加以证明:(1)验证当时,由上面计算知等式成立;(2)假设时等式成立,即=;当时有:===,时等式成立.故由(1)(2)知存在常数使得=对一切均成立.【解析】本题考查数学归纳法.解答本题时要注意先通过赋值法,利用n的前3个值,确定参数a,b,c的值,然后结合数学归纳法,证明等式成立.22.已知,函数,(1)若函数在上递减, 求实数的取值范围;(2)当时,求的最小值的最大值;(3)当时,设,证明:.【答案】(1)函数在(0,2)上递减⇔, 恒有成立, 而⇒,恒有成立, 而, 则 即满足条件的的取值范围是.(2)当时,x 2(0,)a 2a 2(,)a +∞()f x ' - 0 +()f x ↘ 极小值 ↗的最小值= ,a (0,2) 2 (2,)+∞()g a '+ 0 - ()g x ↗ 极大值 ↘ 故的最大值为(3)当时,,所以在上是增函数,故 当时, x a x a x )2(ln 2--+ ==解得或,. 综上所述:.【解析】本题考查导数的应用.解答本题时要注意(1)先对函数进行求导,然后利用导数与函数单调性的关系,利用不等式恒成立问题,求得实数的取值范围;(2)先对函数进行求导,然后利用导数判断函数的极值及单调性,确定函数的最值,再对最值进行求导,利用导数判断函数单调性,由此确定最大值的最大值;(3)构建新函数并求导,利用新函数的单调性,判断其最值,证明不等式成立.。
宁波2017学年第二学期期末九校联考高二数学试题
宁波市2017-2018学年期末九校联考高二数学参考答案一、选择题:本大题共10小题,每小题4分,共40分.题号12345678910答案C B A C D A C B D B二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.10;4312.6;313.240;x x 160-14.1;Z),2,12(∈-k k k 15.3016.9217.),254[+∞三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.解:(Ⅰ)由题意可得⎪⎩⎪⎨⎧≤+---∈≥-,01243)2)((,N ,22*n n n n n ………………3分所以⎪⎩⎪⎨⎧≤+-∈≥,0189,N ,42*n n n n ,即⎪⎩⎪⎨⎧≤--∈≥,0)6)(3(,N ,4*n n n n 解得4=n 或5=n 或6=n ,………………5分所以原不等式的解集为}6,5,4{.………………6分(Ⅱ)n n n n x a x a x a a x x )2()2()2()]2(31[)53(2210-++-+-+=-+=- ,所以1352)1(93222=-==n n C a n ,解得6=n .………………9分法一:令37=x ,则662210663332)5373(a a a a ++++==-⨯ ………………11分又100==n C a ,所以63206621=-=+++a a a a .………………14分法二:因为)6,5,4,3,2,1,0(36==r C a r r r ,所以r r r C a 63=,………………11分则 ++=+++261666221333C C a a a 6312666=-=+C .………………14分19.解:(Ⅰ)8181=⨯⨯=S ,242882=⨯⨯+=S ,4948753825247538222223=⨯⨯+=⨯⨯+=S S ,………………3分由此猜想()()()2*2211N 21n n S n n +-=∈+(Ⅱ)①当1n =时,()()2122118==921S +-+,等式成立,………………7分②假设当k n =时,等式成立,即()()2221121k k S k +-=+,………………8分则当1+=k n 时,()22+18(1)21(23)k k k S S k k +=++=+()()()22222118(1)+211(23)2k k k k k +++++-()()()()222222222[211]8(1)218(1)==212(23)(23)(23)(23)(231)k k k k k k k k k k k +-+++++++-+++++()()22222(23)21=(21)(123)2k k k k k -+++++2222==(23)1[2(1)1)]1(23)[2(1)1]k k k k +-++-+++所以当1+=k n 时,等式也成立,综上,对任意的*N n ∈,()()2221121n n S n +-=+.………………15分20.解:(Ⅰ)x x x x x x x f 333e )3sin 3(cos )1(sin e 3e cos )(′-+=-+⋅=………3分则曲线)(x f y =在))0(,0(f P 处的切线斜率为31)0(′-=f ,…………4分又1)0(-=f ,…………5分则切线方程为)0)(31()1(--=--x y ,即1)31(--=x y .…………7分(Ⅱ)由(Ⅰ)得x x x x x f 33e ]3)πsin(2[e3sin 3(cos )(′-+=-+=,…………8分令0)(′=x f ,得6π=x 或2π=x ,则当6π≤0<x 或π2π≤<x 时,0)(′<x f ,………………6分………………10分………………14分当2π6π<<x 时,0)(′>x f ,所以)(x f 在]6π0[,和π]2π[,单调递减,在)2π6π(,上单调递增,…………12分又1)0(-=f ,6π3e 216π(-=f ,02π(=f ,π3e )π(-=f ,则π3min e )(-=x f ,0)(max =x f ,…………14分所以函数)(x f 在区间]π,0[上的取值范围是]0e [π3,-.…………15分21.解:(Ⅰ)①当0=a 时,()||f x x x bx=+因为)(||)(x f bx x x x f -=--=-,所以函数)(x f 为奇函数.…………3分②当0≠a 时,非奇非偶;…………5分(Ⅱ)⎩⎨⎧<++-≥-+=ax x a x a x x a x x f 2,)22(2,)22()(221︒当01a <≤时,有121a a a -<≤+,()y f x =在[]0,4上单调递增,()()4248M a f a ==-;…………7分2︒当12a <<时,01124a a a <-<+<<,()y f x =在[]0,1a +上单调递增,在[]1,2a a +上单调递减,在[]2,4a 上单调递增,所以()()(){}1,4max M a f f a +=,()()2(81,2441)f a f a a =+=-+,而()()()()222481411023f f a a a a a --=++--+=,①当15a <<时,()()4248M a f a ==-;②当52a -≤<时,()()21(1)M a f a a ==++;…………10分3︒当23a ≤<时,1142a a a -<+<≤,所以()y f x =在[]0,1a +上单调递增,在[]1,4a +上单调递减,此时()()()211M a f a a =+=+;…………12分4︒当3a ≥时,14a +≥,所以()y f x =在[]0,4上单调递增,此时()()848M a f a ==-;…………14分综上所述,当[]0,2x ∈时,⎪⎪⎩⎪⎪⎨⎧≥-<≤-+-<<-=3,883534,)1(5340,824)(2a a a a a a a M …………15分22.解:(Ⅰ)()f x 的定义域为(1,)-+∞(ⅰ)22)1(2)1(111)('x a x x a x x f +-+=+-++=,…………1分①当1≤a 时,012>+≥-+x a x ,所以)(x f 在)1(∞+-,上单调递增,此时无极值点;…………2分②当1>a 时,)21(--∈a x ,时,0)('<x f ,)(x f 在)21(--a ,单调递减,)2(∞+-∈,a x 时,)(x f 在(2,)a -+¥单调递增,所以)(x f 有一个极小值点2-a ,综上所述,1≤a 时,无极值点;1>a 时,有一个极小值点2-a .…………4分(ⅱ)法一:由(ⅰ)得02x a =-,则20+=x a ,所以000)1ln()(x x x f -+=,……5分即证010e ln(1)0x x --+>,令1()e ln(1)x h x x -=-+,…………6分11'()e 1x h x x -=-+,11()e 1x g x x -=-+,121'()e 0(1)x g x x -=+³+,所以)()('x g x h =在)1(∞+-,上为增函数,因为11(0)(1)(1)0e 2g g ×=-<,所以存在)1,0(1∈x 使得111111()'()e 01x g x h x x -==-=+,则)(x h 在)1(1x ,-单调递减,在)(1∞+,x 单调递增,所以11min 11()()e ln(1)x h x h x x -==-+0111112111>+=-++=x x x x ,所以11()e ln(1)()0x h x x h x -=-+³>,从而有0100e )(x x f x -<-.…………9分法二:由(ⅰ)得20-=a x ,则20+=x a ,所以000)1ln()(x x x f -+=,…………5分令x x x h -+=)1ln()(,则1111)('+-=-+=x x x x h ,所以)(x h 在)0,1(-单调递增,在),0(+∞单调递减,所以0)0()()(max ==≤h x h x h ,…………7分令1()e x g x x -=-,则1'()e 1x g x -=-,所以)(x g 在)1,1(-单调递减,在(1,)+¥单调递增,0)1()()(min ==≥g x g x g ,所以()()h x g x <恒成立,即证0100()e x f x x -<-.…………9分(Ⅱ)法一:不妨设21x x <,由(Ⅰ)得)21(1--∈a x ,,)2(2∞+-∈,a x ,1>a 且2≠a ,令)42()()(x a f x f x g ---=))21((--∈a x ,,…………11分=)('x g 2222)32(2)1(2)421(242)1(2x a x a x a x x a a x a x a x ----++-+=--+-+--++-+0)32()1()2()1(4222<--+-+-=x a x a x a 则)(x g 在)21(--a ,上单调递减,…………13分所以0)2()(1=->a g x g 即)42()(11x a f x f -->,所以)42()(12x a f x f -->,因为)2,1(1--∈a x ,所以)32,2(421--∈--a a x a ,由(Ⅰ)得)(x f 在)2(∞+-,a 单调递增,所以1242x a x -->,即4221->+a x x .…………15分法二:不妨设21x x <,由(Ⅰ)得)21(1--∈a x ,,)2(2∞+-∈,a x ,1>a 且2≠a 因为0)0(=f ,…………10分1当00x >时,所以01=x ,要证4221->+a x x ,即证022x x >,因为)(x f 在()0,x +¥上单调递增,故只需证)2()(02x f x f >,即证0)2(0<x f ,因为000002(1)(2)ln(21)21x x f x x x +=+-+,令021(1,)u x =+Î+¥,1()ln 22u h u u u=-+,2222211121(1)'()02222u u u h u u u u u -+-=--=-=-<,所以)(u h 单调递减,则()(1)0h u h <=,从而0)2(0<x f ,即4221->+a x x .…………13分2当010x -<<时,所以20x =,要证4221->+a x x ,即证102x x >,因为)(x f 在0x (-1,)上单调递减,故只需证10()(2)f x f x <,即证0(2)0f x >,因为000002(1)(2)ln(21)21x x f x x +=+-+,令021(1,1)u x =+Î-,1()ln 22u h u u u =-+,2222211121(1)'()02222u u u h u u u u u-+-=--=-=-<,所以)(u h 单调递减,则()(1)0h u h >=,从而0(2)0f x >,即4221->+a x x .…………15分。
2016年宁波市高二数学下期末九校联考试卷(带答案和解释)
2016年宁波市高二数学下期末九校联考试卷(带答案和解释)2015-2016学年浙江省宁波市九校联考高二(下)期末数学试卷一、选择题(本大题共8小题,每小题5分,共40分) 1.已知U=R,集合A={x|x≥0},B={x|2≤x≤4},则A∩(∁UB)=() A.{x|x≤0} B.{x|2≤x≤4} C.{x|0<x≤2或x≥4} D.{x|0≤x<2或x>4} 2.已知a=(),b=(),c=(),则下列关系中正确的是()A.a>b>c B.b>a>c C.a>c>b D.c>a>b 3.函数y=x3和y=log2x在同一坐标系内的大致图象是() A. B. C. D. 4.若(1�2x)5=a0+a1x+…+a5x5(x∈R),则(a0+a2+a4)2�(a1+a3+a5)2=() A.243 B.�243 C.81 D.�81 5.已知离散型随机变量ξ~B(n,p),且E(2ξ+1)=5.8,D(ξ)=1.44,那么n,p的值分别为() A.n=4,p=0.6 B.n=6,p=0.4 C.n=8,p=0.3 D.n=24,p=0.1 6.设函数f(x)= ,记f1(x)=f(f(x)),f2(x)=f(f1(x)),…,fn+1(x)=f(fn(x)),n∈N*,那么下列说法正确的是() A.f(x)的图象关于点(�1,1)对称,f2016(0)=0 B.f (x)的图象关于点(�1,�1)对称,f2016(0)=0 C.f(x)的图象关于点(�1,1)对称,f2016(0)=1 D.f(x)的图象关于点(�1,�1)对称,f2016(0)=1 7.把7个字符1,1,1,A,A,α,β排成一排,要求三个“1”两两不相邻,且两个“A“也不相邻,则这样的排法共有() A.12种 B.30种 C.96种 D.144种 8.已知定义在[1,+∞)上的函数f(x)= 给出下列结论:①函数f(x)的值域为(0,8];②对任意的n∈N,都有f(2n)=23�n;③存在k∈(,),使得直线y=kx与函数y=f(x)的图象有5个公共点;④“函数f(x)在区间(a,b)上单调递减”的充要条件是“存在n∈N,使得(a,b)⊆(2n,2n+1)” 其中正确命题的序号是() A.①②③ B.①③④ C.①②④ D.②③④ 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分9.计算:(1)()�160.25= ;(2)log93+lg3•log310=. 10.若二项式(�)n的展开式共有7项,则n= ;展开式中的第三项的系数为.(用数字作答) 11.已知定义在R上的奇函数f(x)= ,则f(1)= ;不等式f(f(x))≤7的解集为. 12.我省新高考采用“7选3”的选考模式,即从政治、历史、地理、物理、化学、生物、技术这7门科目中选3门作为选考科目,那么所有可能的选考类型共有种;甲、乙两人根据自己的兴趣特长以及职业生涯规划愿景进行选课,甲必选物理和政治,乙不选技术,则两人至少有一门科目相同的选法共有种(用数学作答) 13.掷两颗质地均匀的骰子,在已知它们的点数不同的条件下,有一颗是6点的概率是. 14.已知a 为实数,若函数f(x)=|x2+ax+2|�x2在区间(�∞,�1)和(2,+∞)上单调递减,则实数a的取值范围为. 15.设函数f(x)=ex(x3�3x+2�c)+x(x≥�2),若不等式f(x)≥0恒成立,则实数c的最大值是.三、解答题(本大题共5小题,共74分) 16.已知对任意的n∈N*,存在a,b∈R,使得1×(n2�12)+2×(n2�22)+3×(n2�32)+…+n(n2�n2)= (an2+b)(Ⅰ)求a,b的值;(Ⅱ)用数学归纳法证明上述恒等式. 17.一个口袋装有大小相同的小球9个,其中红球2个、黑球3个、白球4个,现从中抽取2次,每次抽取一个球.(Ⅰ)若有放回地抽取2次,求两次所取的球的颜色不同的概率;(Ⅱ)若不放回地抽取2次,取得红球记2分,取得黑球记1分,取得白球记0分,记两次取球的得分之和为随机变量X,求X的分布列和数学期望. 18.已知函数f(x)=x2�2x�t(t为常数)有两个零点,g(x)= .(Ⅰ)求g(x)的值域(用t表示);(Ⅱ)当t变化时,平行于x轴的一条直线与y=|f(x)|的图象恰有三个交点,该直线与y=g(x)的图象的交点横坐标的取值集合为M,求M. 19.定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1,B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1,B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1.(Ⅰ)(i)求C的方程;(ii)求证:C1与C相似;(Ⅱ)过B1点任作一直线,自下至上依次与C1、x轴的正半轴、C交于不同的四个点P,Q,R,S,求的取值范围. 20.已知函数f(x)=lnx� ax2+(1�a)x,其中a∈R,f(x)的导函数是f′(x).(Ⅰ)求函数f(x)的极值;(Ⅱ)在曲线y=f(x)的图象上是否存在不同的两点A(x1,y1),B(x2,y2)(x1≠x2),使得直线AB的斜率k=f′()?若存在,求出x1与x2的关系;若不存在,请说明理由.2015-2016学年浙江省宁波市九校联考高二(下)期末数学试卷参考答案与试题解析一、选择题(本大题共8小题,每小题5分,共40分) 1.已知U=R,集合A={x|x≥0},B={x|2≤x≤4},则A∩(∁UB)=() A.{x|x≤0} B.{x|2≤x≤4} C.{x|0<x≤2或x≥4} D.{x|0≤x<2或x>4} 【考点】交、并、补集的混合运算.【分析】先求出补集∁UB,再根据并集的定义求出A∪(∁UB).【解答】解:∵B={x|2≤x≤4},∴∁UB={x|x<1或x>4},∵A={x|x≥0},∴A∪(∁UB)={x|0≤x<1或x>4},故选:D. 2.已知a=(),b=(),c=(),则下列关系中正确的是() A.a>b>c B.b >a>c C.a>c>b D.c>a>b 【考点】对数值大小的比较.【分析】利用指数函数与幂函数的单调性即可得出.【解答】解:∵ ,∴b=()>c=(),∵ ,∴a=()>b=(),∴a>b>c.故选:A. 3.函数y=x3和y=log2x在同一坐标系内的大致图象是() A. B. C. D.【考点】函数的图象.【分析】直接根据幂函数和对数函数的单调性即可判断.【解答】解:函数y=x3为单调递增函数,且过定点(1,1),y=log2x为单调递增函数,且过定点(1,0),故选:A. 4.若(1�2x)5=a0+a1x+…+a5x5(x∈R),则(a0+a2+a4)2�(a1+a3+a5)2=() A.243 B.�243 C.81 D.�81 【考点】二项式系数的性质.【分析】可令x=1,求得a0+a1+…+a5=�1,再令x=�1求得a0�a1+…�a5=243,而(a0+a2+a4)2�(a1+a3+a5)2=(a0+a2+a4+a1+a3+a5)(a0+a2+a4�a1�a3�a5),问题得以解决.【解答】解:∵(1�2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,∴令x=1,有a0+a1+…+a5=�1 再令x=�1,有a0�a1+…�a5=35…=243,∴(a0+a2+a4)2�(a1+a3+a5)2=(a0+a2+a4+a1+a3+a5)(a0+a2+a4�a1�a3�a5)=�243.故选:B. 5.已知离散型随机变量ξ~B(n,p),且E(2ξ+1)=5.8,D(ξ)=1.44,那么n,p的值分别为() A.n=4,p=0.6 B.n=6,p=0.4 C.n=8,p=0.3 D.n=24,p=0.1 【考点】离散型随机变量的期望与方差.【分析】由已知求出E(ξ)=2.4,D(ξ)=1.44,利用二项分布的性质列出方程组,能求出n,p的值.【解答】解:∵离散型随机变量ξ~B(n,p),且E(2ξ+1)=5.8,D(ξ)=1.44,∴2E(ξ)+1=5.8,∴E(ξ)=2.4,∴ ,解得n=6,p=0.4.故选:B. 6.设函数f(x)= ,记f1(x)=f(f(x)),f2(x)=f(f1(x)),…,fn+1(x)=f(fn(x)),n∈N*,那么下列说法正确的是() A.f(x)的图象关于点(�1,1)对称,f2016(0)=0 B.f(x)的图象关于点(�1,�1)对称,f2016(0)=0 C.f (x)的图象关于点(�1,1)对称,f2016(0)=1 D.f(x)的图象关于点(�1,�1)对称,f2016(0)=1 【考点】函数的值.【分析】根据函数f(x),求出f1(x)、f2(x),…,fn+1(x)的解析式,即可得出结论.【解答】解:∵函数f(x)= ,∴f1(x)=f (f(x))=x, f2(x)=f(f1(x))= ,…, fn+1(x)=f(fn (x)),n∈N*;又f(x)= =�1+ ,所以f(x)的图象关于点(�1,�1)对称,且f2016(0)= =1.故选:D. 7.把7个字符1,1,1,A,A,α,β排成一排,要求三个“1”两两不相邻,且两个“A“也不相邻,则这样的排法共有() A.12种 B.30种 C.96种 D.144种【考点】排列、组合及简单计数问题.【分析】先求出两个“A“没有限制的排列,再排除若A,A相邻时的排列,问题得以解决.【解答】解:先排列A,A,α,β,若A,B不相邻,有A22C32=6种,若A,B相邻,有A33=6种,共有6+6=12种,从所形成了5个空中选3个插入1,1,1,共有12C53=120,若A,A相邻时,从所形成了4个空中选3个插入1,1,1,共有6C43=24,故三个“1”两两不相邻,且两个“A“也不相邻,则这样的排法共有120�24=96种,故选:C. 8.已知定义在[1,+∞)上的函数f (x)= 给出下列结论:①函数f(x)的值域为(0,8];②对任意的n∈N,都有f(2n)=23�n;③存在k∈(,),使得直线y=kx 与函数y=f(x)的图象有5个公共点;④“函数f(x)在区间(a,b)上单调递减”的充要条件是“存在n∈N,使得(a,b)⊆(2n,2n+1)” 其中正确命题的序号是() A.①②③ B.①③④C.①②④ D.②③④ 【考点】命题的真假判断与应用.【分析】①根据分段函数的表达式结合函数的最值进行求解判断,②利用f (2n)= f(1)进行求解判断,③作出函数f(x)和y=kx的图象,利用数形结合进行判断,④根据分段函数的单调性进行判断.【解答】解:①当1≤x<2时,f(x)=�8x(x�2)=�8(x�1)2+8∈(0,8],②∵f(1)=8,∴f(2n)= f(2n�1)= f(2n�2)= f (2n�3)=…= f(20)= f(1)= ×8=23�n,故②正确,③当x≥2时,f(x)= f()∈0,4],故函数f(x)的值域为(0,8];故①正确,当2≤x<4时,1≤ <2,则f(x)= f()= [�8(�1)2+8]=�4(�1)2+4,当4≤x<8时,2≤ <4,则f(x)= f()= [�4(�1)2+4]=�2(�1)2+2,作出函数f(x)的图象如图:作出y= x和y= x的图象如图,当k∈(,),使得直线y=kx与函数y=f(x)的图象有3个公共点;故③错误,④由分段函数的表达式得当x∈(2n,2n+1)时,函数f(x)在(2n,2n+1)上为单调递减函数,则函数f(x)在区间(a,b)上单调递减”的充要条件是“存在n∈N,使得(a,b)⊆(2n,2n+1)”为真命题.,故④正确,故选:C 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分 9.计算:(1)()�160.25= ;(2)log93+lg3•log310= 3 .【考点】对数的运算性质;有理数指数幂的化简求值.【分析】根据对数和指数幂的运算性质计算即可.【解答】解:(1)()�160.25= �24×0.25= �1= ;(2)log93+lg3•log310= +lg3 =2+1=3 10.若二项式(�)n的展开式共有7项,则n= 6 ;展开式中的第三项的系数为60 .(用数字作答)【考点】二项式系数的性质.【分析】根据展开式中的项数共有7项可求出n的值是6,利用二项展开式的通项公式求出通项,令r的指数为2,将r的值代入通项求出展开式中的第三项的系数.【解答】解:∵二项式(�)n的展开式共有7项,∴n=6 展开式的通项为Tr+1=(�2)rC6r ,展开式中的第三项即r=2时,所以展开式中的第三项的系数为4C62=60 故答案为:6,60 11.已知定义在R上的奇函数f(x)= ,则f(1)= �1 ;不等式f(f (x))≤7的解集为(�∞,2] .【考点】函数奇偶性的性质.【分析】由奇函数关于原点对称的性质,即可求得f(1);不等式f(f (x))≤7的解集等价于f(x)≥�3的解集,即可求得答案.【解答】解:∵R上的奇函数f(x)= ,∴f(1)=�f(�1)=�[()�1�1]=�1,∵不等式f(f(x))≤7,f(�3)=7,∴f(x)≥�3,∵R上的奇函数f(x)= ,∴g(x)=1�2x,∴f(x)≥�3等价于或,可以解得x≤2,即不等式f(f(x))≤7的解集为(�∞,2].故答案为:�1;(�∞,2]. 12.我省新高考采用“7选3”的选考模式,即从政治、历史、地理、物理、化学、生物、技术这7门科目中选3门作为选考科目,那么所有可能的选考类型共有35 种;甲、乙两人根据自己的兴趣特长以及职业生涯规划愿景进行选课,甲必选物理和政治,乙不选技术,则两人至少有一门科目相同的选法共有92 种(用数学作答)【考点】排列、组合及简单计数问题.【分析】①直接根据组合定义即可求出,②利用间接法,先求出甲必选物理和政治,乙不选技术的种数,再排除两人没有科目相同的选法,问题得以解决.【解答】解:①从政治、历史、地理、物理、化学、生物、技术这7门科目中选3门作为选考科目,那么所有可能的选考类型共有C73=35种,②甲必选物理和政治,乙不选技术,则甲乙的选法为C51C63=100种,其中没有相同的科目,若甲选技术,则乙有C43=4种,若甲不选技术,甲有4种,乙只有1种,故有4×1=4种,则其中没有相同的科目的为4+4=8种,故两人至少有一门科目相同的选法共有100�8=92,故答案为:35,92 13.掷两颗质地均匀的骰子,在已知它们的点数不同的条件下,有一颗是6点的概率是.【考点】列举法计算基本事件数及事件发生的概率.【分析】掷两颗质地均匀的骰子,它们的点数不同,列举出所有的基本事件和其中有一颗是6点包含的基本事件个数,由此能求出它们的点数不同的条件下,有一颗是6点的概率.【解答】解:掷两颗质地均匀的骰子,它们的点数不同,所有的基本事件为:(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),共有30个,其中有一颗是6点包含的基本事件个数有10个,∴它们的点数不同的条件下,有一颗是6点的概率p= = .故答案为:. 14.已知a为实数,若函数f(x)=|x2+ax+2|�x2在区间(�∞,�1)和(2,+∞)上单调递减,则实数a的取值范围为[�8,0).【考点】分段函数的应用;函数的单调性及单调区间.【分析】将函数表示为分段函数形式,结合一元二次函数的单调性的性质进行判断即可.【解答】解:f(x)=|x2+ax+2|�x2= ,设x2+ax+2=0的两个根分别为x1,x2,(x1<x2),则f(x)= ,∵当x≥x2时,函数f(x)=ax+2,函数f(x)在(2,+∞)上单调递减,∴a<0,当x1<x<x2时,抛物线的对称轴为x=� =�.若函数f(x)在(2,+∞)上单调递减,则�≤2,得�8≤a<0.若f(x)在区间(�∞,�1)递减,则x1= ≥�1,即�a�≥�2,则≥a�2,∵�8≤a<0,∴ ≥a�2恒成立,综上�8≤a<0,故答案为:[�8,0) 15.设函数f(x)=ex(x3�3x+2�c)+x(x≥�2),若不等式f(x)≥0恒成立,则实数c的最大值是�2e2 .【考点】函数恒成立问题.【分析】问题转化为c≤x3�3x+2+ ,(x≥�2),令h(x)=x3�3x+2+ ,(x≥�2),求出h(x)的最小值,从而求出c的最大值即可.【解答】解:∵函数f(x)=ex(x3�3x+2�c)+x(x≥�2),若不等式f(x)≥0恒成立,则c≤x3�3x+2+ ,(x≥�2),令h(x)=x3�3x+2+ ,(x≥�2),h′(x)=(x�1)[3(x+1)�e�x],令h′(x)>0,解得:x>1或x<x0,(�1<x0<0),令h′(x)<0,解得:x0<x<1,∴h(x)在[�2,x0)递增,在(x0,1)递减,在(1,+∞)递增,∴h(x)的最小值是h(�2)或h (1),而h(�2)=�2e2<h(1)= ,∴c≤�2e2,c的最大值是�2e2;故答案为:�2e2.三、解答题(本大题共5小题,共74分) 16.已知对任意的n∈N*,存在a,b∈R,使得1×(n2�12)+2×(n2�22)+3×(n2�32)+…+n(n2�n2)= (an2+b)(Ⅰ)求a,b的值;(Ⅱ)用数学归纳法证明上述恒等式.【考点】数学归纳法.【分析】(Ⅰ)分别取n=1,2,得到关于a,b的方程组解得即可,(Ⅱ)先根据当n=1时,把n=1代入求值等式成立;再假设n=k时关系成立,利用变形可得n=k+1时关系也成立,综合得到对于任意n∈N*时都成立【解答】解:(Ⅰ)由题意1×(n2�12)+2×(n2�22)+3×(n2�32)+…+n(n2�n2)= (an2+b),上述等式分别取n=1,2得,解得,(Ⅱ)由(Ⅰ)得1×(n2�12)+2×(n2�22)+3×(n2�32)+…+n(n2�n2)= (n2�1),证明:①当n=1时,左边=1×(12�12)=0,右边= ×12(12�1)=0,等式成立,②假设当n=k时,等式成立,即1×(k2�12)+2×(k2�22)+3×(k2�32)+…+k(k2�k2)= k2(k2�1),则当n=k+1时,左边=1×[(k2�12)+(2k+1)]+2×[(k2�22)+(2k+1)]+…+k[(k2�k2)+(2k+1)],=1×(k2�12)+2×(k2�22)+3×(k2�32)+…+k (k2�k2)+(2k+1)(1+2+3+…+k), = k2(k2�1)+(2k+1) k (k+1), = k(k+1)(k2+3k+2), = (k+1)2k(k+2), = (k+1)2[(k+1)2�1],所以当n=k+1时等式成立,综上所述,对任意n∈N*,原等式成立. 17.一个口袋装有大小相同的小球9个,其中红球2个、黑球3个、白球4个,现从中抽取2次,每次抽取一个球.(Ⅰ)若有放回地抽取2次,求两次所取的球的颜色不同的概率;(Ⅱ)若不放回地抽取2次,取得红球记2分,取得黑球记1分,取得白球记0分,记两次取球的得分之和为随机变量X,求X的分布列和数学期望.【考点】离散型随机变量的期望与方差;离散型随机变量及其分布列.【分析】(Ⅰ)设事件A为“两次所取的球颜色不同”,利用对立事件概率计算公式能求出两次所取的球的颜色不同的概率.(Ⅱ)由题意得X的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出X的分布列和数学期望.【解答】解:(Ⅰ)设事件A为“两次所取的球颜色不同”,则P(A)=1�[()2+()2+()2]= .(Ⅱ)由题意得X的可能取值为0,1,2,3,4, P (X=0)= = , P(X=1)= = , P(X=2)= = , P(X=3)= = , P (X=4)= = ,∴X的分布列为: X 0 1 2 3 4 PEX= = . 18.已知函数f(x)=x2�2x�t(t为常数)有两个零点,g(x)= .(Ⅰ)求g(x)的值域(用t表示);(Ⅱ)当t 变化时,平行于x轴的一条直线与y=|f(x)|的图象恰有三个交点,该直线与y=g(x)的图象的交点横坐标的取值集合为M,求M.【考点】二次函数的性质;函数的值域.【分析】(Ⅰ)求出t的范围,根据基本不等式的性质求出g(x)的值域即可;(Ⅱ)求出t= ,得到>�1,解不等式即可.【解答】解:(Ⅰ)∵函数f(x)=x2�2x�t (t为常数)有两个零点,∴△=4(1+t)>0,解得:t>�1, g (x)= =(x�1)+ +2,∵|(x�1)+ |=|x�1|+ ≥2 ,当且仅当x=1± 时取“=”,∴(x�1)+ ≤�2 或(x�1)+ ≥2 ,∴g(x)≤2�2 或g(x)≥2+2 ,即g(x)的值域是(�∞,2�2 ]∪[2�2 ,+∞);(Ⅱ)当x=1时,f(x)取最小值�t�1,由|f(x)|的图象得,平行x轴的直线y=x+1与函数y=|f(x)|的图象恰有三个交点,由 =t+1得,(x�2)t=x2�x+1,显然x≠2,∴t= ,由于t >�1,∴ >�1,即>0,解得:�1<x<1或x>2,∴M=(�1,1)∪(2,+∞). 19.定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1,B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1,B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1.(Ⅰ)(i)求C的方程;(ii)求证:C1与C相似;(Ⅱ)过B1点任作一直线,自下至上依次与C1、x轴的正半轴、C交于不同的四个点P,Q,R,S,求的取值范围.【考点】椭圆的简单性质.【分析】(Ⅰ)(i)设C的方程: + =1(a>b>0),则,求出a,b,即可求C的方程;(ii)求出轨迹C1,可得离心率相等,即可证明C1与C相似;(Ⅱ)设直线方程为y=kx�3(k>0),代入椭圆方程,求出相应线段的长,可得 = 构造函数,利用导数确定函数的单调性,即可确定的取值范围.【解答】(Ⅰ)(i)解:设C的方程: + =1(a>b>0),则,∴a=6,b=3,∴C的方程: =1;(ii)证明:设G(x,y),M(x0,y)(x0≠0),则x0=3x,y0=3y 把点M(3x,3y)的坐标代入C的方程,得轨迹C1的方程为 =1(x≠0),∴轨迹C1也为椭圆(除去(0,�1),(0,1)两点),求得a1=2,c1= ,e1= ,∵C的离心率e= ,∴e1=e,∴C1与C相似;(Ⅱ)解:设直线方程为y=kx�3(k>0),代入C的方程得(1+4k2)x2�24kx=0,∴xS= ,yS= ,∴ = ,代入C1的方程得(1+4k2)x2�24kx+32=0,由k>0,△>0得k>,由韦达定理得xP+xR= ,xPxR= ,∴|PR|2=(1+k2)[ �].∵|AQ|=6�= ,∴ = 令f(k)= (k )则f′(k)= • <0 ∴f(k)在(,+∞)上是减函数,∴ )= ∴0<<. 20.已知函数f(x)=lnx�ax2+(1�a)x,其中a∈R,f(x)的导函数是f′(x).(Ⅰ)求函数f(x)的极值;(Ⅱ)在曲线y=f(x)的图象上是否存在不同的两点A(x1,y1),B(x2,y2)(x1≠x2),使得直线AB的斜率k=f′()?若存在,求出x1与x2的关系;若不存在,请说明理由.【考点】利用导数研究函数的极值;利用导数研究曲线上某点切线方程.【分析】(Ⅰ)求导数,讨论a的符号,这样便可判断导数的符号,从而可判断每种情况是否存在极值,若存在便可求出该极值;(Ⅱ)先根据条件求出斜率,而可得到,这样便可根据条件得出,然后换元,并设x1>x2,t>1,从而得出;求导数并可判断导数符号g′(t)>0,从而g(t)>g(1),而g(1)=0,这即说明g (t)=0无解,从而得出满足条件的两点A,B不存在.【解答】解:(Ⅰ)由已知得,f′(x)= (1)当a≤0时,∵x>0,∴f′(x)>0;∴f(x)在(0,+∞)上是增函数,此时函数f(x)无极值;(2)当a>0时,;∴当x 时,g′(x)>0;当x 时,g′(x)<0;∴函数f(x)在上是增函数,在上是减函数;∴当时,f (x)有极大值,无极小值;综上所述,当a≤0时,函数f(x)无极值,当a>0时,f(x)有极大值,无极小值.(Ⅱ)由题意得, = = = ..由得,;即,即;令,不妨设x1>x2,则t>1,记;,所以g(t)在(1,+∞)上是增函数;所以g(t)>g(1)=0,所以方程g(t)=0无解,则满足条件的两点A,B不存在.2016年8月3日。
宁波市2017学年九校联考高二数学(含答案)2018.6.26
宁波市2017学年期末九校联考 高二数学参考答案二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 11. 10;4312. 6;3 13. 240;x x 160- 14. 1;Z ),2,12(∈-k k k 15. 30 16. 9217. ),254[+∞三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.解:(Ⅰ)由题意可得⎪⎩⎪⎨⎧≤+---∈≥-,01243)2)((,N ,22*n n n n n ………………3分所以⎪⎩⎪⎨⎧≤+-∈≥,0189,N ,42*n n n n ,即⎪⎩⎪⎨⎧≤--∈≥,0)6)(3(,N ,4*n n n n解得4=n 或5=n 或6=n , ………………5分所以原不等式的解集为}6,5,4{. ………………6分(Ⅱ)n n n n x a x a x a a x x )2()2()2()]2(31[)53(2210-++-+-+=-+=- ,所以1352)1(93222=-==n n C a n ,解得6=n . ………………9分 法一:令37=x ,则662210663332)5373(a a a a ++++==-⨯ ………………11分 又100==n C a ,所以6323330666221=-=+++a a a a . ………………14分法二:因为)6,5,4,3,2,1,0(36==r C a r r r ,所以r r rC a 63=, ………………11分则 ++=+++261666221333C C a a a 6312666=-=+C . ………………14分19.解:(Ⅰ)983118221=⨯⨯=S ,2524532898222=⨯⨯+=S , 4948753825247538222223=⨯⨯+=⨯⨯+=S S , ………………3分 由此猜想()()()2*2211N 21n n S n n +-=∈+(Ⅱ)①当1n =时, ()()2122118==921S +-+,等式成立, ………………7分②假设当k n =时,等式成立,即()()2221121k k S k +-=+, ………………8分 则当1+=k n 时,()22+18(1)21(23)k k k S S k k +=++=+()()()22222118(1)+211(23)2k k k k k +++++-()()()()222222222[211]8(1)218(1)==212(23)(23)(23)(23)(231)k k k k k k k k k k k +-+++++++-+++++()()22222(23)21=(21)(123)2k k k k k -+++++2222==(23)1[2(1)1)]1(23)[2(1)1]k k k k +-++-+++ 所以当1+=k n 时,等式也成立,综上,对任意的*N n ∈,()()2221121n n S n +-=+. ………………15分20.解:(Ⅰ)xxxx x x x x f 333e)3sin 3(cos )1(sin e3e cos )(′-+=-+⋅= ………3分则曲线)(x f y =在))0(,0(f P 处的切线斜率为31)0(′-=f , …………4分 又1)0(-=f , …………5分 则切线方程为)0)(31()1(--=--x y ,即1)31(--=x y . …………7分 (Ⅱ)由(Ⅰ)得xxx x x x f 33e]3)6πsin(2[e)3sin 3(cos )(′-+=-+=, …………8分令0)(′=x f ,得6π=x 或2π=x ,则当6π≤0<x 或π2π≤<x 时,0)(′<x f , ………………6分………………10分………………14分当2π6π<<x 时,0)(′>x f , 所以)(x f 在]6π0[,和π]2π[,单调递减,在)2π6π(,上单调递增, …………12分又1)0(-=f ,6π3e21)6π(-=f ,0)2π(=f ,π3e)π(-=f ,则π3min e)(-=x f ,0)(max =x f , …………14分所以函数)(x f 在区间]π,0[上的取值范围是]0e [π3,-. …………15分21. 解:(Ⅰ)①当0=a 时,()||f x x x bx =+因为)(||)(x f bx x x x f -=--=-,所以函数)(x f 为奇函数. …………3分②当0≠a 时,非奇非偶; …………5分(Ⅱ)⎩⎨⎧<++-≥-+=ax x a x ax x a x x f 2,)22(2,)22()(221︒ 当01a <≤时,有121a a a -<≤+,()y f x =在[]0,4上单调递增,()()4248M a f a ==-; …………7分 2︒ 当12a <<时, 01124a a a <-<+<<,()y f x =在[]0,1a +上单调递增,在[]1,2a a +上单调递减,在[]2,4a 上单调递增,所以()()(){}1,4max M a f f a +=,()()2(81,2441)f a f a a =+=-+, 而()()()()222481411023f f a a a a a --=++--+= ,①当15a <<时,()()4248M a f a ==-;②当52a ≤<时,()()21(1)M a f a a ==++; …………10分3︒ 当23a ≤<时, 1142a a a -<+<≤,所以()y f x =在[]0,1a +上单调递增,在[]1,4a +上单调递减,此时()()()211M a f a a =+=+; …………12分4︒ 当3a ≥时, 14a +≥, 所以()y f x =在[]0,4上单调递增,此时()()848M a f a ==-; …………14分综上所述, 当[]0,2x ∈时,⎪⎪⎩⎪⎪⎨⎧≥-<≤-+-<<-=3,883534,)1(5340,824)(2a a a a a a a M …………15分22.解:(Ⅰ)()f x 的定义域为(1,)-+∞(ⅰ)22)1(2)1(111)('x ax x a x x f +-+=+-++=, …………1分 ①当1≤a 时,012>+≥-+x a x ,所以)(x f 在)1(∞+-,上单调递增,此时无极值点; …………2分 ②当1>a 时,)21(--∈a x ,时,0)('<x f ,)(x f 在)21(--a ,单调递减,)2(∞+-∈,a x 时,)(x f 在(2,)a 单调递增,所以)(x f 有一个极小值点2-a ,综上所述,1≤a 时,无极值点;1>a 时,有一个极小值点2-a . …………4分(ⅱ)法一:由(ⅰ)得02x a ,则20+=x a ,所以000)1ln()(x x x f -+=, ……5分即证010e ln(1)0x x ,令1()eln(1)x h x x , …………6分11'()e 1x h x x ,11()e 1xg x x ,121'()e 0(1)xg x x ,所以)()('x g x h =在)1(∞+-,上为增函数,因为11(0)(1)(1)0e 2g g ,所以存在)1,0(1∈x 使得111111()'()e 01x g x h x x ,则)(x h 在)1(1x ,-单调递减,在)(1∞+,x 单调递增, 所以11min 11()()e ln(1)x h x h x x 0111112111>+=-++=x x x x , 所以11()e ln(1)()0xh x x h x ,从而有0100e )(x x f x -<-. …………9分法二:由(ⅰ)得20-=a x ,则20+=x a ,所以000)1ln()(x x x f -+=, …………5分 令x x x h -+=)1ln()(,则1111)('+-=-+=x xx x h , 所以)(x h 在)0,1(-单调递增,在),0(+∞单调递减,所以0)0()()(max ==≤h x h x h , …………7分令1()e xg x x ,则1'()e 1xg x ,所以)(x g 在)1,1(-单调递减,在(1,)单调递增,0)1()()(min ==≥g x g x g ,所以()()h x g x 恒成立,即证0100()e x f x x . …………9分(Ⅱ)法一:不妨设21x x <,由(Ⅰ)得)21(1--∈a x ,,)2(2∞+-∈,a x ,1>a 且2≠a , 令)42()()(x a f x f x g ---=))21((--∈a x ,, …………11分=)('x g 2222)32(2)1(2)421(242)1(2x a xa x a x x a a x a x a x ----++-+=--+-+--++-+ 0)32()1()2()1(4222<--+-+-=x a x a x a则)(x g 在)21(--a ,上单调递减, …………13分 所以0)2()(1=->a g x g即)42()(11x a f x f -->,所以)42()(12x a f x f -->, 因为)2,1(1--∈a x ,所以)32,2(421--∈--a a x a , 由(Ⅰ)得)(x f 在)2(∞+-,a 单调递增,所以1242x a x -->,即4221->+a x x . …………15分法二:不妨设21x x <,由(Ⅰ)得)21(1--∈a x ,,)2(2∞+-∈,a x ,1>a 且2≠a 因为0)0(=f , …………10分 ① 当00x 时,所以01=x ,要证4221->+a x x ,即证022x x >,因为)(x f 在0,x 上单调递增,故只需证)2()(02x f x f >,即证0)2(0<x f ,因为000002(1)(2)ln(21)21x x f x x x ,令021(1,)ux ,1()ln 22u h u uu,2222211121(1)'()02222u u u h u u u u u ,所以)(u h 单调递减,则()(1)0h u h ,从而0)2(0<x f ,即4221->+a x x . …………13分② 当010x 时,所以20x ,要证4221->+a x x ,即证102x x ,因为)(x f 在0x (-1,)上单调递减,故只需证10()(2)f x f x ,即证0(2)0f x ,因为000002(1)(2)ln(21)21x x f x x x ,令021(1,1)ux ,1()ln 22u h u uu,2222211121(1)'()02222u u u h u u u u u ,所以)(u h 单调递减,则()(1)0h u h ,从而0(2)0f x ,即4221->+a x x . …………15分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁波市九校联考高二数学试题一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有 一项是符合题目要求的.1.设集合2{|13}{|320}A x x B x x x =-≤≤=-+<,,则=)(B C A R I( )A.[1,1)(2,3)-UB.]3,2[]1,1[Y -C. )2,1(D.R2.已知i 是虚数单位,则ii-+11= () A.1 B.1- C. i - D.i3.已知曲线x x f ln )(=在点))2(,2(f 处的切线与直线01=++y ax 垂直,则实数a 的值为 ( )A.21 B.2- C. 2 D.21-4.下面四个条件中,使a b >成立的必要而不充分的条件是 ( )A.1a b ->B.1a b +>C.a b >D.33a b > 5.已知函数1ln 1)(--=x x x f ,则)(x f y =的图像大致为 ( )A. B. C. D.6.从1,2,3,,9L 这九个整数中同时取四个不同的数,其和为偶数,则不同取法共有 ( ) A.62 B.64 C.65 D.667.已知n m b n am b a a b ,,,,111则--==<<的大小关系为 ( )A. n m <B. n m =C. n m >D. n m ,的大小关系不确定,与b a ,的取值有关 8.已知下列各式:①1)1|(|2+=+x x f ;②x x f =+)11(2;③||)2(2x x x f =-; ④x x x f -+=33|)(|.其中存在函数)(x f 对任意的R x ∈都成立的是 ( )A.①④B.③④C.①②D.①③9.设函数)0(log )(2>++=a b ax x x f ,若存在实数b ,使得对任意的[])0(2,>+∈t t t x第二学期学年2016都有a x f +≤1|)(|,则t 的最小值是 ( ) A.2 B.1 C.43 D.3210.定义在R 上的可导函数)(x f 满足32)()(x x f x f =--,当(]0,∞-∈x 时,3)(2x x f <'实数a 满足1332)()1(23+-+-≥--a a a a f a f ,则a 的取值范围是 ( ) A.⎪⎭⎫⎢⎣⎡∞+,23 B.⎥⎦⎤⎝⎛∞-23, C. ⎪⎭⎫⎢⎣⎡∞+,21 D.⎥⎦⎤⎝⎛∞-21, 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 11.若,3log ,2log n m a a ==则=+n m a 2 ,用n m ,表示6log 4为 . 12.已知nxx )212(-的展开式中二项式系数和为64,则=n ,该展开式中常数项 为 .13.已知函数10,2,122,4)(≠>⎩⎨⎧>++≤+-=a a x a a x x x f x 且其中.若21=a 时方程b x f =)(有两个不同的实根,则实数b 的取值范围是 ;若)(x f 的值域为[)∞+,2,则实数a 的 取值范围是 . 14.函数xxee x x xf --+-=2)(3的奇偶性为 ,在R 上的增减性为 (填“单调递增”、“单调递减”或“有增有减”).15.小明和爸爸妈妈、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小 明的父母至少有一人与小明相邻,则不同的坐法总数为 . 16.已知ax a x x a x x x f 22|1||1|)(-+--+-+=)(0>x 的最小值为23,则实数=a . 17.已知函数)R b a b ax x x f ∈++=,()(2在区间(]1,0上有零点0x ,则)31914(00-+x x ab 的最大值是 .三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.已知*∈N n ,(1)(2)(),n S n n n n =+++L 213(21)nn T n =⨯⨯⨯⨯-L .(Ⅰ)求 321321,,,,,T T T S S S ;(Ⅱ)猜想n S 与n T 的关系,并用数学归纳法证明.19.(Ⅰ)已知1021001210(21)(1)(1(1)x a a x a x a x -=+-+-++-L ),其中 ,1,2,10i a R i ∈=L .(i )求01210a a a a ++++L ;(ii )求7a .(Ⅱ)2017年5月,北京召开“一带一路”国际合作高峰论坛.组委会将甲、乙、丙、 丁、戊五名志愿者分配到翻译、导游、礼仪、司机四个不同的岗位,每个岗位至 少有一人参加,且五人均能胜任这四个岗位.(i )若每人不准兼职,则不同的分配方案有几种?(ii)若甲乙被抽调去别的地方,剩下三人要求每人必兼两职,则不同的分配方案 有几种? 20.已知R a ∈,函数)(x f 满足.12)2(22-+-=a ax x f x(Ⅰ)求)(x f 的解析式,并写出)(x f 的定义域; (Ⅱ)若)(x f 在]2,2[2212+--a aa 上的值域为[]0,1-,求实数a 的取值范围.21.已知函数()1e1xf x x-=-+. (Ⅰ)证明: 当[]0,3x ∈时,xe x 911+≥-. (Ⅱ)证明: 当[]2,3x ∈时, 0)(72<<-x f .22.已知1-<a ,函数)(|1|)(33R x ax x x x f ∈++-=. (Ⅰ)求函数)(x f 的最小值;(Ⅱ)已知存在实数),1(,≤<n m n m 对任意),,(0n m t ∈总存在两个不同的),,1(,21+∞∈t t 使得)()(2)(210t f t f t f ==-,求证:274≤-m n .2016学年第二学期宁波市九校联考高二数学参考答案一、选择题(本大题共10小题,每小题4分,共40分)BDCBA DCADD二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.12 ,2m n m + 12.6,60 13.)(49,2 ,),1()1,21[+∞⋃ 14.奇,单调递增 15.84 16.45 17.14410)31914()(,170002≥-+=--=x x x g ax x b 题:20000()()()ab g x a x ax g x ⋅=--[])()(000x g a x a x --≤343200000()1()44439x g x x x x ⋅≤=-+求导知其在11220,,,,,13333⎛⎤⎡⎤⎡⎤⎥⎢⎥⎢⎥⎝⎦⎣⎦⎣⎦上分别递增、递减、递增,故 1441)}1(),31(max{=⋅⋅≤g ab g ab 其.)21,21,1(0时等号成立-=-==b a x方法2:三、解答题:本大题共5小题,共74分 18.(本小题满分14分)解:(Ⅰ)120,12,2332211======T S T S T S ; ……(3分)(Ⅱ)猜想:n n S T =(*n N ∈) ……(4分)证明:(1)当1n =时,11S T =; ……(6分) (2)假设当()*1n k k k N=≥∈且时,kk ST =,即(1)(2)()213(21)kk k k k k +++=⨯⨯⨯-L L ,……(8分) 则当1n k =+时200002002222200000011()493113=92()11313131(1)(1)942362362144ax b x x ab x ax b x ax b x x x x x +=-+-+⎡⎤≤=-=-≤⎢⎥⎣⎦g 可得则(-)(-)111)(12)(11)(1)(11)k S k k k k k k k k +=++++++-+++++L ( =(2)(3)(2)(21)(22)k k k k k ++++L=213(21)(21)(22)1k k k k k ⨯⨯⨯-⨯+++L =11213(21)(21)k k k k T ++⨯⨯⨯-+=L . ……(13分)即1+=k n 时也成立,由(1)(2)可知*n N ∈,n n S T =成立 ……(14分) 19.(本小题满分15分)解:(Ⅰ)(i )令,2=x 则10012103(59049)a a a a ++++=L 即.……(3分) (ii)令10210012101,(12),x y y a a y a y a y -=+=+++L 则 得77710215360.a C == …… (7分)(Ⅱ)(i ).2404425=⋅A C……(11分)(ii) ()114)))(((233233424324=-+-C C C CC ……(15分)20.(本小题满分15分)解:(Ⅰ)令20,xt =>则,log 2t x =则,1log 2)(log )(2222-+-=a t a t t f 即.1log 2)(log )(2222-+-=a x a x x f ……(5分) 定义域为()+∞,0 ……(7分) (Ⅱ))(x f 在]2,2[2212+--a aa 上的值域为[]0,1-等价于12)(22-+-=a ax x x g在区间]22,1[2+--a a a 上的值域为].0,1[- ……(9分)101+1y x ay x a x a =-⇒==⇒=-=令或由图可得2221a a a a ≤-+≤+ ……(13分)353512a a -+≤≤≤≤或 ……(15分)21.(本小题满分15分) 解:(Ⅰ)证明: 要证1e19xx-≥+, 也即证e 19xx ≤+. ……(2分) 令()e 91xF x x =--, 则()'e 9xF x =-. 令()'0F x >, 则2ln3x >. 因此, 当02ln3x ≤<时, 有()'0F x <, 故()F x 在[]0,2ln3上单调递减; 当2ln33x <≤时, 有()'0F x >, 故()F x 在[]2ln3,3上单调递增. ……(5分)所以, ()F x 在[]0,3上的最大值为()(){}max 0,3F F .又()00F =,()33e 280F =-<. 故()[]0, 0,3F x x ≤∈成立, 即[]e 19, 0,3xx x ≤+∈成立. 原命题得证. ……(7分) (Ⅱ) 证明: 由 (I) 得: 当[]2,3x ∈时, ()111e1191xf x x x x -=-≥-+++令()11191t x x x=-++, 则 ()()()()()()()()()()()[]22222222222199119'19911191917280, 2,3.191x x t x x x x x x x x x x x --+-+=-+⋅++=-=++++-=≥∈++(9分)所以, ()t x 在[]2,3上单调递增,即()()[]161622, 2,357567t x t x ≥=->-=-∈所以()f x 72->得证. ……(12分) 下证0)(<x f . 即证1+>x e x令),1()(+-=x e x h x则01)(>-='xe x h ,所以)(x h 在[]32,上单调递增, 所以,03)1()(2>-≥+-=e x e x h x ,得证. ……(15分)另证:要证7211911->+-+x x ,即证011892>+-x x , 令8)19(1189)(22--=+-=x x x x m 在[]32,上递增,所以01)2()(>=≥m x m 得证.22.(本小题满分15分)解:(1)⎩⎨⎧≥-+<+=++-=1,121,1|1|)(333x ax x x ax ax x x x f记)1(12)(),1(1)(321≥-+=<+=x ax x x f x ax x f则a x x f +=2'26)( , 因为 1-<a 则由6,0)('2ax x f -±==得 ……(2分) (i )时,即1616-<≤-≤-a a,上递增,在上递减,在),1[)()1,()(21+∞-∞x f x f 所以1)1()]([min +==a f x f ……(4分) (ii )时,即616-<>-a a,上递减,在)1,()(1-∞x f 递增,上递减,在在)6[)6,1[)(2∞+--a a x f , 所以1632)6()(2min --=-=aa a f x f综上,⎪⎩⎪⎨⎧-<≤-+-<--=16,16,1632)(mina a a aa x f……(6分) (2)不妨设,21t t <则由(1)知,若,16-<≤-a 则)(2x f 在),1(+∞上递增, 不满足题意,所以6-<a . ……(7分) 所以),6(),6,1(21+∞-∈-∈a t a t ,且 1632)6()(2min --=-=a a a f x f (i )>-+21a 1632--a a ,即⎩⎨⎧<<--<1)1(2)(22721x f x f a 时,由即 ⎩⎨⎧<+<-+1121x a ax ,解得121<<+x a ,即)1,21(0a t +∈ 所以)1,21(),(a n m +⊆,所以1,21≤+≥n a m ,所以2742<-≤-a m n ……(11分)(ii )≤-+21a 1632--a a ,即⎪⎩⎪⎨⎧->-<--<≤-)6(2)()1(2)(62272121a f x f f x f a 时,由 即⎪⎩⎪⎨⎧-->-++<-+163221121aa ax a ax ,解得63221a x a -<<+, 所以)632,21(),(a a n m -+⊆,所以632,21a n a m -≤+≥ 所以aa m n 21632---≤- 令]23,1(6∈=-u a ,则23113221632uu a a +-=--- 令231132)(u u u +-=ϕ,则0)11(32)(3'>-=u u ϕ 所以 231132)(u u u +-=ϕ在]23,1(∈u 递增,所以 274)23()(=≤ϕϕu ,所以 274)(≤≤-u m n ϕ. ……(15分)。
