浙江省宁波市九校2020-2021学年高二下期末联考数学试卷及答案

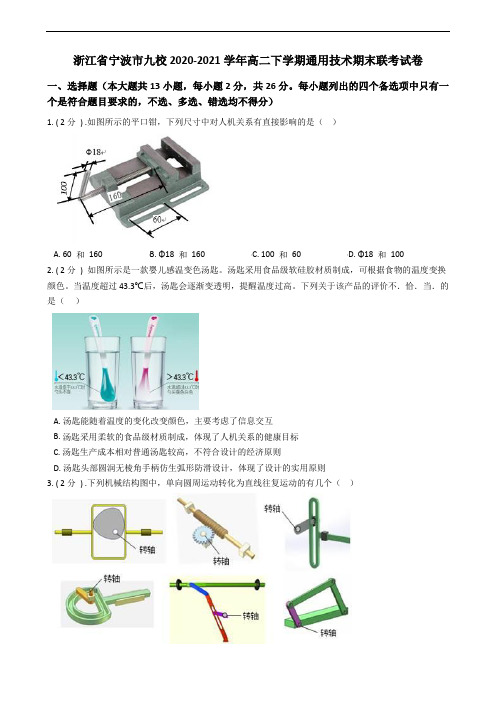
浙江省宁波市九校2020-2021学年高二下期末联考试卷数 学(全卷满分：150分 考试时间：120分钟)班级___________ 姓名___________ 学号____________ 分数____________一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有 一项是符合题目要求的.1.设集合2{|13}{|320}A x x B x x x =-≤≤=-+<,,则=)(B C A R（ ）A.[1,1)(2,3)- B.]3,2[]1,1[ - C. )2,1( D.R2.已知i 是虚数单位，则ii-+11= （ ） A.1 B.1- C. i - D.i3.已知曲线x x f ln )(=在点))2(,2(f 处的切线与直线01=++y ax 垂直，则实数a 的值为 ( )A.21 B.2- C. 2 D.21-4.下面四个条件中，使a b >成立的必要而不充分的条件是 （ ）A.1a b ->B.1a b +>C.a b >D.33a b > 5.已知函数1ln 1)(--=x x x f ，则)(x f y =的图像大致为 （ ）A. B. C. D.6.从1,2,3,,9这九个整数中同时取四个不同的数，其和为偶数，则不同取法共有 （ ） A.62 B.64 C.65 D.667.已知n m b n am b a a b ,,,,111则--==<<的大小关系为 （ ）A. n m <B. n m =C. n m >D. n m ,的大小关系不确定，与b a ,的取值有关 8.已知下列各式：①1)1|(|2+=+x x f ；②x x f =+)11(2；③||)2(2x x x f =-； ④x x x f -+=33|)(|.其中存在函数)(x f 对任意的R x ∈都成立的是 （ ）A.①④B.③④C.①②D.①③9.设函数)0(log )(2>++=a b ax x x f ,若存在实数b ,使得对任意的[])0(2,>+∈t t t x 都有a x f +≤1|)(|，则t 的最小值是 （ ） A.2 B.1 C.43 D.3210.定义在R 上的可导函数)(x f 满足32)()(x x f x f =--,当(]0,∞-∈x 时,3)(2x x f <'实数a 满足1332)()1(23+-+-≥--a a a a f a f ,则a 的取值范围是 （ ） A.⎪⎭⎫⎢⎣⎡∞+，23 B.⎥⎦⎤⎝⎛∞-23, C. ⎪⎭⎫⎢⎣⎡∞+，21 D.⎥⎦⎤⎝⎛∞-21, 二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分. 11.若,3log ,2log n m a a ==则=+n m a 2 ,用n m ,表示6log 4为 . 12.已知nxx )212(-的展开式中二项式系数和为64，则=n ,该展开式中常数项 为 . 13.已知函数10,2,122,4)(≠>⎩⎨⎧>++≤+-=a a x a a x x x f x且其中.若21=a 时方程b x f =)(有两 个不同的实根，则实数b 的取值范围是 ；若)(x f 的值域为[)∞+，2，则实数a 的 取值范围是 . 14.函数xxee x x xf --+-=2)(3的奇偶性为 ,在R 上的增减性为 (填“单调递增”、“单调递减”或“有增有减”）.15.小明和爸爸妈妈、爷爷奶奶一同参加《中国诗词大会》的现场录制，5人坐成一排.若小 明的父母至少有一人与小明相邻，则不同的坐法总数为 . 16.已知ax a x x a x x x f 22|1||1|)(-+--+-+=）（0>x 的最小值为23，则实数=a . 17.已知函数）R b a b ax x x f ∈++=,()(2在区间(]1,0上有零点0x ，则)31914(00-+x x ab 的最大值是 .三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤. 18.已知*∈N n ，(1)(2)(),n S n n n n =+++213(21)nn T n =⨯⨯⨯⨯-.(Ⅰ)求 321321,,,,,T T T S S S ；(Ⅱ)猜想n S 与n T 的关系，并用数学归纳法证明.19.(Ⅰ)已知1021001210(21)(1)(1(1)x a a x a x a x -=+-+-++-），其中,1,2,10i a R i ∈=.（i ）求01210a a a a ++++；（ii ）求7a .(Ⅱ)2017年5月,北京召开“一带一路”国际合作高峰论坛.组委会将甲、乙、丙、 丁、戊五名志愿者分配到翻译、导游、礼仪、司机四个不同的岗位，每个岗位至 少有一人参加，且五人均能胜任这四个岗位.（i ）若每人不准兼职，则不同的分配方案有几种？（ii)若甲乙被抽调去别的地方，剩下三人要求每人必兼两职，则不同的分配方案 有几种？ 20.已知R a ∈,函数)(x f 满足.12)2(22-+-=a ax x f x(Ⅰ)求)(x f 的解析式,并写出)(x f 的定义域； (Ⅱ)若)(x f 在]2,2[2212+--a a a 上的值域为[]0,1-，求实数a 的取值范围.21.已知函数()1e1xf x x-=-+. (Ⅰ)证明: 当[]0,3x ∈时,xe x 911+≥-. (Ⅱ)证明: 当[]2,3x ∈时, 0)(72<<-x f .22.已知1-<a ，函数)(|1|)(33R x ax x x x f ∈++-=. (Ⅰ)求函数)(x f 的最小值；(Ⅱ)已知存在实数),1(,≤<n m n m 对任意),,(0n m t ∈总存在两个不同的),,1(,21+∞∈t t 使得)()(2)(210t f t f t f ==-，求证：274≤-m n .宁波市九校联考第二学期高二数学参考答案一、选择题（本大题共10小题，每小题4分，共40分）BDCBA DCADD二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分.11.12 ，2m n m + 12.6，60 13.）（49,2 ,),1()1,21[+∞⋃ 14.奇，单调递增 15.84 16.45 17.14410)31914()(,170002≥-+=--=x x x g ax x b 题：20000()()()ab g x a x ax g x ⋅=--[])()(000x g a x a x --≤343200000()1()44439x g x x x x ⋅≤=-+求导知其在11220,,,,,13333⎛⎤⎡⎤⎡⎤⎥⎢⎥⎢⎥⎝⎦⎣⎦⎣⎦上分别递增、递减、递增，故 1441)}1(),31(max{=⋅⋅≤g ab g ab 其.)21,21,1(0时等号成立-=-==b a x方法2：三、解答题：本大题共5小题，共74分 18.（本小题满分14分）解：(Ⅰ)120,12,2332211======T S T S T S ； ……（3分）(Ⅱ)猜想：n n S T =（*n N ∈） ……（4分）证明：(1)当1n =时，11S T =； ……（6分） （2）假设当()*1n k k k N =≥∈且时，kk ST =，即(1)(2)()213(21)k k k k k k +++=⨯⨯⨯-，……（8分）则当1n k =+时200002002222200000011()493113=92()11313131(1)(1)942362362144ax b x x ab x ax b x ax b x x x x x +=-+-+⎡⎤≤=-=-≤⎢⎥⎣⎦可得则（-）（-）111)(12)(11)(1)(11)k S k k k k k k k k +=++++++-+++++（=(2)(3)(2)(21)(22)k k k k k ++++=213(21)(21)(22)1k k k k k ⨯⨯⨯-⨯+++ =11213(21)(21)k k k k T ++⨯⨯⨯-+=. ……（13分）即1+=k n 时也成立,由（1）（2）可知*n N ∈，n n S T =成立 ……（14分） 19.（本小题满分15分）解：(Ⅰ)（i ）令,2=x 则10012103(59049)a a a a ++++=即.……（3分)(ii)令10210012101,(12),x y y a a y a y a y -=+=+++则得77710215360.a C == …… （7分）(Ⅱ)（i ）.2404425=⋅A C……（11分）(ii) ()114)))(((233233424324=-+-C C C CC ……（15分）20.（本小题满分15分）解：(Ⅰ)令20,xt =>则,log 2t x =则,1log 2)(log )(2222-+-=a t a t t f 即.1log 2)(log )(2222-+-=a x a x x f ……（5分） 定义域为()+∞,0 ……（7分） (Ⅱ))(x f 在]2,2[2212+--a aa 上的值域为[]0,1-等价于12)(22-+-=a ax x x g在区间]22,1[2+--a a a 上的值域为].0,1[- ……（9分）101+1y x ay x a x a =-⇒==⇒=-=令或由图可得2221a a a a ≤-+≤+ ……（13分）12a a ≤≤≤≤或 ……（15分）21.（本小题满分15分） 解:(Ⅰ)证明: 要证1e19xx-≥+, 也即证e 19xx ≤+. ……（2分） 令()e 91xF x x =--, 则()'e 9xF x =-. 令()'0F x >, 则2ln3x >. 因此, 当02ln3x ≤<时, 有()'0F x <, 故()F x 在[]0,2ln3上单调递减; 当2ln33x <≤时,有()'0F x >, 故()F x 在[]2ln3,3上单调递增. ……（5分） 所以, ()F x 在[]0,3上的最大值为()(){}max 0,3F F .又()00F =,()33e 280F =-<. 故()[]0, 0,3F x x ≤∈成立, 即[]e 19, 0,3xx x ≤+∈成立. 原命题得证. ……（7分） (Ⅱ) 证明: 由 (I) 得: 当[]2,3x ∈时, ()111e1191xf x x x x -=-≥-+++令()11191t x x x=-++, 则 ()()()()()()()()()()()[]22222222222199119'19911191917280, 2,3.191x x t x x x x x x x x x x x --+-+=-+⋅++=-=++++-=≥∈++（9分）所以, ()t x 在[]2,3上单调递增，即()()[]161622, 2,357567t x t x ≥=->-=-∈所以()f x 72->得证. ……（12分） 下证0)(<x f . 即证1+>x e x令),1()(+-=x e x h x则01)(>-='xe x h ，所以)(x h 在[]32，上单调递增, 所以，03)1()(2>-≥+-=e x e x h x ，得证. ……（15分）另证：要证7211911->+-+x x ，即证011892>+-x x ， 令8)19(1189)(22--=+-=x x x x m 在[]32，上递增，所以01)2()(>=≥m x m 得证.22.（本小题满分15分）解：（1）⎩⎨⎧≥-+<+=++-=1,121,1|1|)(333x ax x x ax ax x x x f记)1(12)(),1(1)(321≥-+=<+=x ax x x f x ax x f则a x x f +=2'26)( , 因为 1-<a 则由6,0)('2ax x f -±==得 ……（2分） （i ）时，即1616-<≤-≤-a a，上递增，在上递减，在),1[)()1,()(21+∞-∞x f x f 所以1)1()]([min +==a f x f ……（4分） （ii ）时，即616-<>-a a,上递减，在)1,()(1-∞x f 递增，上递减，在在)6[)6,1[)(2∞+--a a x f , 所以1632)6()(2min --=-=aa a f x f综上，⎪⎩⎪⎨⎧-<≤-+-<--=16,16,1632)(mina a a aa x f……（6分） （2）不妨设,21t t <则由（1）知，若,16-<≤-a 则)(2x f 在),1(+∞上递增，不满足题意，所以6-<a . ……（7分） 所以),6(),6,1(21+∞-∈-∈a t a t ，且 1632)6()(2min --=-=a a a f x f （i ）>-+21a 1632--a a ，即⎩⎨⎧<<--<1)1(2)(22721x f x f a 时，由即 ⎩⎨⎧<+<-+1121x a ax ，解得121<<+x a ，即)1,21(0a t +∈ 所以)1,21(),(a n m +⊆，所以1,21≤+≥n a m ，所以2742<-≤-a m n ……（11分）（ii ）≤-+21a 1632--a a ，即⎪⎩⎪⎨⎧->-<--<≤-)6(2)()1(2)(62272121a f x f f x f a 时，由 即⎪⎩⎪⎨⎧-->-++<-+163221121aa ax a ax ，解得63221a x a -<<+， 所以)632,21(),(a a n m -+⊆，所以632,21a n a m -≤+≥ 所以aa m n 21632---≤- 令]23,1(6∈=-u a ，则23113221632uu a a +-=--- 令231132)(u u u +-=ϕ，则0)11(32)(3'>-=u u ϕ 所以 231132)(u u u +-=ϕ在]23,1(∈u 递增，所以 274)23()(=≤ϕϕu ，所以 274)(≤≤-u m n ϕ. ……（15分）。