特殊四边形精选练习题
特殊四边形难题整理(附答案)
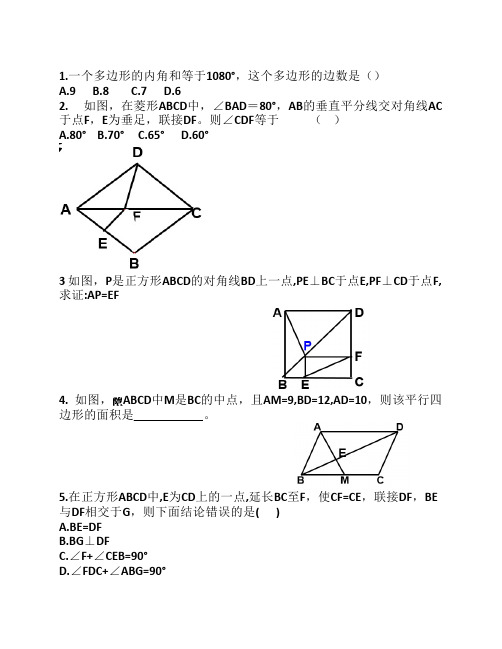
解答：(1)如图①，过A. D分别作AK⊥BC于K，DH⊥BC于H，则四边
形ADHK是矩形。
∴KH=AD=3. 在Rt△ABK中,AK=AB⋅sin45∘=42√⋅2√2=4BK=AB⋅cos45∘=42√⋅2√2=4， 在Rt△CDH中,由勾股定理得,HC=52−42−−−−−−−√=3. ∴BC=BK+KH+HC=4+3+3=10. (2)如图②,过D作DG∥AB交BC于G点，则四边形ADGB是平行四边 形。 ∵MN∥AB， ∴MN∥DG. ∴BG=AD=3. ∴GC=10−3=7. 由题意知，当M、N运动到t秒时，CN=t，CM=10−2t. ∵DG∥MN，∴∠NMC=∠DGC. 又∵∠C=∠C，∴△MNC∽△GDC.∴CNCD=CMCG，即t5=10−2t7.解 得,t=5017.
6.已知，如图,矩形ABCD中，BC=2，AE⊥BD于E，∠BAE=30°，那么 △ECD的面积是( )
7、如图，正方形ABCD的周长为4a，四边形EFGH的四个顶点E、F、G、 H分别在AB、BC、CD、DA上滑动，在滑动过程中，始终有 EH∥BD∥FG，且EH=FG，问:是否可求出四边形EFGH的周长?若能求 出，它的周长是多少?若不能求出，请说明理由.
(3)分三种情况讨论： ①当NC=MC时，如图③，即t=10−2t，∴t=103.
②当MN=NC时，如图④，过N作NE⊥MC于E. 解法一：由等腰三角形三线合一性质得EC=12MC=12(10−2t)=5−t. 在Rt△CEN中,cosC=ECNC=5−tt， 又在Rt△DHC中,cosC=CHCD=35， ∴5−tt=35.解得t=258. 解法二：∵∠C=∠C,∠DHC=∠NEC=90∘，∴△NEC∽△DHC. ∴NCDC=ECHC，即t5=5−t3.∴t=258. ③当MN=MC时,如图⑤,过M作MF⊥CN于F点.FC=12NC=12t. 解法一：(方法同②中解法一)cosC=FCMC=12t10−2t=35,
特殊的四边形培优
特殊的四边形培优1.如图，已知在菱形ABCD中，DE⊥AB，DF⊥BC，垂足分别为E、F，且AE=BE，则∠EDF=______度．1.如图，四边形ABCD是正方形，△BDE是等边三角形，EF⊥DF,则∠BEF=________3.如图，正方形ABCD的面积为256，点F在AD上，点E在AB的延长线上，Rt△CEF的面积为200，则BE 的长为_______FB CA DE4. 如图，在菱形ABCD 中，AB=4a ，E 在BC 上，BE=2a ，∠BAD=120°，P 点在BD 上，则PE+PC 的最小值为（ ）5.如图,矩形AEFG 与矩形APQK 的周长都等于120cm,求△ABC 的周长6.如图，在矩形ABCD 中，M ，N 分别是AD ，DC 边的中点，AN 与MC 交于P 点，若∠MCB=∠NBC+33°，那么∠MPA 的大小是（ ）1. 边长为25cm 的正方形纸片,AD 上有一点P ,且AP=66cm,将这纸片折叠使B 落在P 上,则折痕的长是________2. 已知直角三角形ABCD 中,∠C=90°,AC=3,BC=5,以AB 为边向外作正方形ABEF 求此正方形KGP E BC中心O到C点的距离OC的长________3.如图,已知在矩形ABCD中,E为CB延长线上一点,CE=AC,F是AE的中点.（1）求证BF⊥DF（2）若AB=8,AD=6,求DF的长10.如图，已知三角形ABC中，AB=AC,点M为BC 的中点，MG⊥BA于G,MD⊥AC于D,GF⊥AC于点E，GF与DF相交于点F,（1）求证：四边形HGMD是菱形（2）若∠GMD=120°，求证：从M点向所对的HG 和HD边引出的两条垂线MK和MQ分别平分这两条线段.E FQKDG11．如图,将一矩形的每一内角三等分,连接靠近同一边上的两三等分线所交成4交点组成四边形EFGH,试判断四边形EFGH形状12.在正方形ABCD中,AK和AN是∠A内的两射线,BK⊥AK,BL⊥AN,DM⊥AK,DN⊥AN,试求KL=MN1.在锐角△ABC中,BE是高,CF是中线,若∠ACF=30°则BE:CF=________2.如图，D、E、F分别是△ABC三边的中点，G是AE的中点，BE与DF、DG分别交于P、Q两点，则PQ：BE=______．3.如图，△ABC中，∠BAC=120°,以AB,AC为边分别向形外作正三角形ABD和正三角形ACE,M为AD中点,N为AE中点,P为BC中点,求∠MPN的度数.4.凸五边形ABCDE中,∠ABC=∠AED=90°,∠CAD=30°,∠BAE=70°,F是CD中点,且FB=FE,则∠BAC=_________.5.已知：如图所示，在△ABC中，D、G分别为AB、AC上的点，且BD=CG，M、N分别是BG、CD的中点，过MN的直线交AB于点P，交AC于点Q，求证：AP=AQ。
初二数学特殊四边形练习题
初二数学特殊四边形练习题四边形是初中数学的重要内容之一，其中特殊四边形更是一个关键知识点。
通过练习题的形式，我们可以加深对特殊四边形的理解和应用。
本文将为大家提供一些初二数学特殊四边形练习题，并解析答案，希望对你的学习有所帮助。
练习一：平行四边形性质1. 什么是平行四边形？2. 平行四边形有哪些性质？练习二：矩形和正方形1. 什么是矩形和正方形？2. 矩形和正方形有什么相同点和不同点？3. 在矩形和正方形中，对角线的长度是否相等？为什么？练习三：菱形的性质1. 什么是菱形？2. 菱形有哪些性质？3. 菱形的对角线有什么特点？练习四：平行四边形和菱形的关系1. 平行四边形和菱形有什么关系？2. 如果一个平行四边形的对角线相等，它一定是什么形状？练习五：梯形和等腰梯形1. 什么是梯形和等腰梯形？2. 梯形和等腰梯形有哪些性质？练习六：总结请你总结一下初二数学特殊四边形的性质和关系。
解析：练习一：1. 平行四边形是指两边两边之间互相平行的四边形。
2. 平行四边形的性质有：对边平行，对角线互相平分，相邻角互补，对角线等分。
练习二：1. 矩形是四个角都是直角的四边形，而正方形是四个边都相等且四个角都是直角的特殊矩形。
2. 矩形和正方形的相同点是都拥有对边平行和对角线等分的性质，不同点是正方形的四条边相等。
3. 在矩形和正方形中，对角线的长度相等，因为它们都是菱形的对角线，而菱形的对角线相等。
练习三：1. 菱形是四个边都相等的四边形。
2. 菱形的性质有：对边平行，对角线互相垂直，对角线等分，相邻角互补。
3. 菱形的对角线相等且互相垂直。
练习四：1. 平行四边形是菱形的特殊情况，即四个边都相等的菱形为正方形。
2. 如果一个平行四边形的对角线相等，它一定是正方形。
练习五：1. 梯形是有两条平行边的四边形，其中一对相邻边不平行的梯形叫做等腰梯形。
2. 梯形的性质有：两条底边平行，上底角和下底角互补，两对对角线互相平分。
(完整版)特殊平行四边形练习题(答案已做)
特殊平行四边形专题练习1、练习：①矩形ABCD 的两条对角线相交于O ，∠AOD=120°，AB=4cm ，则矩形对角线AC 长为______cm ．②．四边形ABCD 的对角线AC ，BD 相交于点O ，能判断它为矩形的题设是（ ）A ．AO=CO ，BO=DOB ．AO=BO=CO=DOC ．AB=BC ，AO=COD ．AO=CO ，BO=DO ，AC ⊥BD③．四边形ABCD 中，AD //BC ，则四边形ABCD 是 ___________，又对角线AC ，BD 交于点O ， 若∠1=∠2，则四边形ABCD 是_______________．2、练习：①．如图，BD 是菱形ABCD 的一条对角线，若∠ABD=65°，则∠A=_____．②． 一个菱形的两条对角线分别是6cm ，8cm ，则这个菱形的周长等于 cm,面积= cm 2③．若菱形的周长为8cm,高为1cm,则菱形两邻角的度数比为(三)正方形:3．练习：①正方形的面积为4，则它的边长为____，对角线长为_____．②已知正方形的对角线长是4，则它的边长是 ，面积是 。
③如图所示，在△ABC 中，AB=AC ，点D ，E ，F 分别是边AB ，BC ，AC 的中点，连接DE ，EF ，要使四边形ADEF 是正方形，还需增加条件：_______．二、复习练习： （一）、选择题：1、矩形ABCD 的长AD=15cm ，宽AB=10cm ，∠ABC 的平分线分AD 边为AE 、ED两部分，这AE 、ED 的长分别为（ ）A ．11cm 和4cmB ．10cm 和5cmC ．9cm 和6cmD ．8cm 和7cm2、四边形ABCD 的对角线互相平分，要使它变为矩形，需要添加的条件是（ ） A ．AB=CD B ．AD=BC C ．AB=BC D ．AC=BD3、如图，在正方形ABCD 的外侧，作等边三角形ADE ，则∠AEBO （ ） A. 10° B ．15° C ．20° D ．12.5°4、如图，在菱形ABCD 中，E 、F 分别是AD 、BD 的中点，如果EF=2，那么菱形ABCD 的周长是（ ） A. 4 B ．8 C ．12 D ．16ABDECABCDEEF（二）、填空题5、已知正方形ABCD 对角线AC ，BD 相交于点O ，•且AC=•16cm ，•则DO=•_____cm ， •BO=____cm ，∠OCD=____度．6、在平面直角坐标系中，四边形ABCD 是菱形，∠ABC=60°， 且点A 的坐标为（0，2）,则点B 坐标（ ）， 点C 坐标为（ ），点D 坐标为（ ）。
特殊四边形练习题
特殊四边形练习题一、选择题1. 下列四边形中，哪一个是平行四边形？A. 两组对边分别平行的四边形B. 两组对边分别相等的四边形C. 对角线互相平分的四边形D. 一组对边相等且平行的四边形2. 菱形的对角线具有以下哪个性质？A. 垂直平分B. 互相垂直C. 互相平行D. 相等3. 矩形的四个角都是：A. 锐角B. 直角C. 钝角D. 平角4. 梯形中，上底和下底平行，且两腰相等的梯形是：A. 等腰梯形B. 直角梯形C. 等腰直角梯形D. 普通梯形5. 正方形的对角线具有以下哪个性质？A. 垂直平分B. 互相垂直C. 互相平行D. 相等且垂直二、填空题6. 平行四边形的对角线______，矩形的对角线______。
7. 菱形的四条边都______，且对角线______。
8. 等腰梯形的两腰相等，且上底和下底______。
9. 正方形的四条边都______，且四个角都是______。
10. 如果一个四边形的两组对边分别相等，那么这个四边形可能是______或______。
三、判断题11. 所有平行四边形都是矩形。
（）12. 所有菱形都是平行四边形。
（）13. 所有矩形都是正方形。
（）14. 所有正方形都是菱形。
（）15. 所有等腰梯形都是平行四边形。
（）四、简答题16. 请简述平行四边形、矩形、菱形、正方形和梯形的定义。
17. 请说明为什么矩形的对角线相等，而菱形的对角线垂直。
18. 请解释等腰梯形的判定方法。
五、计算题19. 若一个平行四边形的两组对边分别是10cm和8cm，求其对角线的长度范围。
20. 已知一个矩形的长为15cm，宽为10cm，求其对角线的长度。
21. 如果一个菱形的边长为6cm，求其对角线的长度。
22. 已知一个正方形的边长为8cm，求其对角线的长度。
23. 若一个等腰梯形的上底为4cm，下底为10cm，高为3cm，求其两腰的长度。
六、证明题24. 证明：平行四边形的对角线互相平分。
特殊的四边形练习题
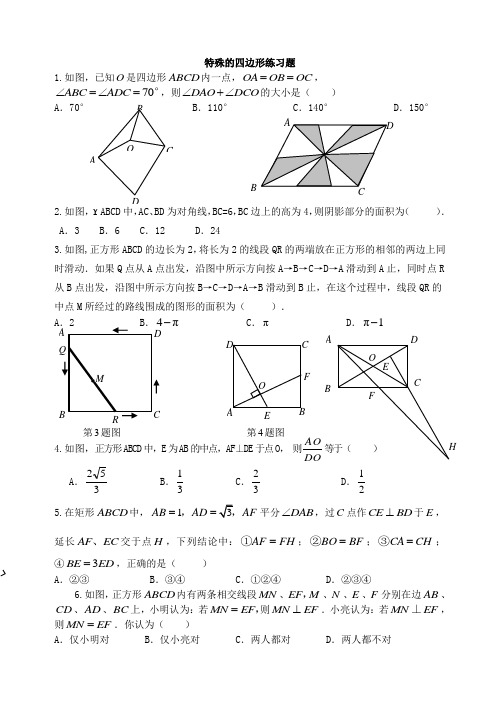
F C D E O 第3题图 第4题图B C O AD特殊的四边形练习题1.如图，已知O 是四边形ABCD 内一点，OA OB OC ==， 70ABC ADC ∠=∠=°，则DAO DCO ∠+∠的大小是（ ） A ．70° B ．110° C ．140° D ．150°2.如图，Y ABCD 中，AC 、BD 为对角线，BC=6，BC 边上的高为4，则阴影部分的面积为（ ）． A ．3 B ．6 C ．12 D ．243.如图,正方形ABCD 的边长为2，将长为2的线段QR 的两端放在正方形的相邻的两边上同时滑动．如果Q 点从A 点出发，沿图中所示方向按A→B→C→D→A 滑动到A 止，同时点R 从B 点出发，沿图中所示方向按B→C→D→A→B 滑动到B 止，在这个过程中，线段QR 的中点M 所经过的路线围成的图形的面积为（ ）．A π- C ．π D ．π1-4.如图，正方形ABCD 中，E 为AB 的中点，AF⊥DE 于点O ， 则DOAO等于（ ）A ．352 B ．31 C ．32D ．215.在矩形ABCD 中，1AB AD AF ==，平分DAB ∠，过C 点作CE BD ⊥于E ，延长AF EC 、交于点H ，下列结论中：AF FH =①；BO BF =②；CA CH =③；④3BE ED =，正确的是（ ）A ．②③B ．③④C ．①②④D ．②③④ 6.如图，正方形ABCD 内有两条相交线段MN 、EF ，M 、N 、E 、F 分别在边AB 、CD 、AD 、BC 上，小明认为：若MN EF =，则MN EF ⊥．小亮认为：若MN EF ⊥，则MN EF =．你认为（ ）A ．仅小明对B ．仅小亮对C ．两人都对D ．两人都不对B DA BCOE F HM A 'D E A B NC7.如图，梯形ABCD 中，AD∥BC，DC⊥BC，将梯形沿对角线BD 折叠，点A 恰好落在DC 边上的点A '处，若20A BC '∠=°，则A BD '∠的度数为（ ）． A ．15° B．20° C ． 25° D ．30°8.如图所示，正方形ABCD 的面积为12，ABE △是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，使PD PE +的和最小，则这个最小值为（ ）A．．C ．3 D9.矩形纸片ABCD 的边长AB =4，AD =2．将矩形纸片沿EF 折叠，使点A 与点C 重合，折叠后在其一面着色（如图），则着色部分的面积为（ ）A ． 8B ．112C ． 4D ．5210.如图，正方形纸片ABCD 的边长为1，M N ，分别是AD BC 、边上的点，将纸片的一角沿过点B 的直线折叠，使点A 落在MN 上，落点记为A '，折痕交AD 于点E ，若M N ，分别是AD BC ，边的中点，则A N '= ；若M N ，分别是AD BC ，边上距DC 最近的n 等分点（2n ≥，且n 为整数），则A N '= （用含有n 式子表示）．11.如图，正方形ABCD 的边长为1cm ，E 、F 分别是BC 、CD 的中点，连接BF 、DE ，则图中阴影部分的面积是 cm 2．A B D CEF MND A C B A ' A DE PBCED FC 1D 1 D 2C 2 DA B12.如图，边长为1的菱形ABCD 中，60DAB ∠=°．连结对角线AC ，以AC 为边作第二个菱形11ACC D ，使160D AC ∠=°；连结1AC ，再以1AC 为边作第三个菱形122AC C D ，使2160D AC ∠=°；……，按此规律所作的第n 个菱形的边长为___________． 13.如图，在边长为2㎝的正方形ABCD 中，点Q 为BC 边的中点，点P 为对角线AC 上一动点，连接PB 、PQ ，则△PBQ 周长的最小值为____________㎝14.如图，在等腰梯形ABCD 中，AD BC ∥，BC =4AD =42B ∠=45°．直角三角板含45°角的顶点E 在边BC 上移动，一直角边始终经过点A ，斜边与CD 交于点F ．若ABE △为等腰三角形，则CF 的长等于 ．15.如图，在梯形ABCD 中，AB CD ∥， 90A B ∠+∠=°， 511CD AB ==，，点M N 、分别为AB CD、的中点，则线段MN = ． 16.已知：如图在ABCD Y中，过对角线BD 的中点O 作直线EF 分别交DA 的延长线、AB DC BC 、、的延长线于点E M N F 、、、．（1）观察图形并找出一对全等三角形：△________≌△____________，请加以证明； （2）在（1）中你所找出的一对全等三角形，其中一个三角形可由另一个三角形经过怎样的变换得到？17.已知正方形ABCD 中，E 为对角线BD 上一点，过E 点作EF⊥BD 交BC 于F ，连接DF ，G 为DF 中点，连接EG ，CG ．（1）求证：EG=CG ；D BCA FA B C D N ME B MO DNF C A（2）将图①中△BEF 绕B 点逆时针旋转45º，如图②所示，取DF 中点G ，连接EG ，CG ．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．（3）将图①中△BEF 绕B 点旋转任意角度，如图③所示，再连接相应的线段，问（1） 中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）18.如图，ABC △中，AB AC =，P 为底边BC 上任意一点，点P到两腰的距离分别为12r r ，，腰上的高为h ，连接AP ，则ABP ACP ABC S S S +=△△△．即：12111222AB r AC r AB h +=g g g 12r r h ∴+=（定值）．（1）理解与应用如图，在边长为3的正方形ABCD 中，点E 为对角线BD 上的一点，且BE BC =，F 为CE 上一点，FM BC ⊥于M ，FN BD ⊥于N ，试利用上述结论求出FM FN +的长． （2）类比与推理如果把“等腰三角形”改成“等边三角形”，那么P 的位置可以由“在底边上任一点”放宽为“在三角形内任一点”，即： 已知等边ABC △内任意一点P 到各边的距离分别为123r r r ，，，等边ABC △的高为h ，试证明123r r r h ++=（定值）． （3）拓展与延伸若正n 边形12n A A A L 内部任意一点P 到各边的距离为12n r r r L ，请问是12n r r r +++L 是否为定值，如果是，请合理猜测出这个定值．F BD 图①B D E 图②B 图③ AC B P r 1 r 2hDCBAE NF MCAB P r 1r 3 r 2h。
特殊四边形测试题
特殊四边形测试题一、选择题1. 下列哪个选项不是特殊四边形的特点？A. 对角线互相平分B. 四边形的对角线垂直C. 四边形的对角线相等D. 四边形的对边相等2. 菱形的对角线具有以下哪个特点？A. 平行B. 垂直C. 相等D. 互相平分3. 矩形的对角线具有以下哪个特点？A. 平行B. 垂直C. 相等D. 互相垂直4. 梯形中，哪两个角相等？A. 相邻角B. 对角C. 同底角D. 没有角相等5. 以下哪个选项是平行四边形的判定条件？A. 对角线相等B. 对边相等C. 对角线互相垂直D. 对角线互相平分二、填空题6. 一个四边形的对角线互相垂直且平分，那么这个四边形是________。
7. 如果一个四边形的对边相等，且对角线互相平分，那么这个四边形是________。
8. 一个四边形的对角线相等，且对边平行，那么这个四边形是________。
9. 梯形中，如果有一个角是直角，那么这个梯形是________。
10. 如果一个四边形的一组对边平行，且另一组对边不平行，那么这个四边形是________。
三、简答题11. 描述矩形和正方形的相似之处和不同之处。
12. 解释为什么菱形的对角线互相垂直。
13. 根据题目给出的条件，如果一个四边形的对角线互相平分，且一边上的两个角都是直角，那么这个四边形是什么形状？四、计算题14. 已知一个平行四边形的两组对边长度分别为6cm和8cm，对角线长度分别为10cm和2x cm。
求x的值。
15. 如果一个梯形的上底长为5cm，下底长为10cm，且两底平行，求这个梯形的高，假设这个梯形是等腰梯形。
五、证明题16. 证明：如果一个四边形的对角线互相垂直且相等，那么这个四边形是正方形。
17. 证明：如果一个四边形的对角线互相平分，且一边上的两个角都是直角，那么这个四边形是矩形。
请注意，以上题目仅为示例，具体内容应根据实际教学大纲和学生水平进行调整。
特殊四边形典型题演练及答案
1、如图，在四边形ABCD中，AB=CD，E、F分别是AD、BC的中点，G、H分别是对角线BD、AC的中点. （1）求证：四边形EGFH是菱形；（2）若AB=1，则当时，求四边形EGFH的面积.2、在△ABC中，借助作图工具可以作出中位线EF，沿着中位线EF一刀剪切后，•用得到的△AEF和四边形EBCF可以拼成平行四边形EBCP，剪切线与拼图如图所示1．仿照上述的方法，按要求完成下列操作设计，并在规定位置画出图示． .（1）在△ABC中，增加条件：_________，沿着_______一刀剪切后可以拼成矩形，剪切线与拼图画在图示2的位置上． .（2）在△ABC中，增加条件：_________，沿着_______一刀剪切后可以拼成菱形，剪切线与拼图画在图示3的位置上． .（3）在△ABC中，增加条件：_________，沿着_______一刀剪切后可以拼成正方形，剪切线与拼图画在图示4的位置上． .（4）在△ABC中（AB≠AC），一刀剪切后也可以拼成等腰梯形，首先要确定剪切线，•其操作过程（剪切线的作法）是：___________，然后，沿着剪切线一刀剪切后可以拼成等腰梯形，剪切线与拼图画在图示5的位置上．（10分）3、如图，已知正方形ABCD的边长为1，G为CD边上的一个动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于点H.求证：①△BCG≌△DCE；②BH⊥DE.（2）当点G运动到什么位置时，BH垂直平分DE？请说明理由.4、如图，在△中，∠，的垂直平分线交于，交于，在上，且． .⑴求证：四边形ACEF是平行四边形；⑵当∠B满足什么条件时，四边形ACEF是菱形，并说明理由． .5、已知：如图，正方形ABCD中，点E是BA延长线上一点，连接DE，点F在DE上且DF=DC，DG⊥CF于G. DH平分∠ADE交CF于点H，连接BH.（1）若DG=2，求DH的长；（2）求证：BH+DH=CH.6、如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C．(1)求证：四边形ABCD是正方形；(2)连接BD分别交AE、AF于点M、N，将△ABM绕点A逆时针旋转，使AB与AD重合，得到△ADH，试判断线段MN、ND、DH之间的数量关系，并说明理由．(3)若EG=4，GF=6，BM=3，求AG、MN的长．7、如图，在正方形ABCD中，E是AB边上任意一点，BG⊥CE，垂足为点O,交AC于点F，交AD于点G。
特殊四边形练习题及答案
特殊四边形练习题及答案一、填空题1、已知正方形ABCD的对角线AC，BD相交于点O，以AB为边向外作等边三角形ABE，CE与BD相交于点F，则的值为1 2 32、如图，在△ABC中，点D是BC的中点，点E、F分别在线段AD及其延长线上，且DE=DF，给出下列条件：①BE⊥EC；②BF∥CE；③AB=AC；从中选择一个条件使四边形BECF是菱形，你认为这个条件是 (只填写序号).3、如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE=3，点Q为对角线AC上的动点，则△BEQ周长的最小值为 .4、我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形。
则矩形的中点四边形是 .5、如图，在正方形中，点，分别在边，上，若，，，则正方形的面积等于．5 6 7 86、如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是．7、如图，菱形ABCD中，E、F分别是BC、CD的中点，过点E作EG⊥AD于G，连接GF．若∠A=80°，则∠DGF的度数为．8、如图，菱形ABCD中，对角线AC=6，BD=8，M、N分别是BC、CD的中点，P是线段BD上的一个动点，则PM+PN的最小值是．二、简答题9、如图，在四边形ABCD中，∠A=∠BCD=90°，BC=CD，CE⊥AD，垂足为E.求证：AE=CE.10、如图，正方形ABCD的边长为4，点E是正方形边上的点，AE=5，BF⊥AE，垂足为点F，求BF的长.11、如图，正方形ABCD中，E、F分别为BC、CD上的点，且AE⊥BF，垂足为G，求证：AE=BF.12、如图，已知△ABC是等腰三角形，顶角∠BAC=α(α<60°)，D是BC边上的一点，连接AD，线段AD绕点A顺时针旋转α到AE，过点E作BC的平行线，交AB于点F,连接DE,BE,DF.(1)求证：BE=CD；(2)若AD⊥BC，试判断四边形BDFE的形状，并给出证明.13、如图，四边形ABCD是正方形，BE⊥BF，BE＝BF，EF与BC交于点G.(1)求证：AE＝CF；(2)若∠ABE＝55°，求∠EGC的大小.14、如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．（1）判断OE与OF的大小关系？并说明理由；（4分）（2）当点O运动到何处时，四边形AECF是矩形？并说出你的理由；（4分）（3）在（2）的条件下，当△ABC满足什么条件时，四边形AECF会是正方形．不要写理由。
中考数学 专题23《特殊四边形》练习题
《特殊四边形》练习题一．选择题1.如图，在正方形ABCD的外侧，作等边三角形ADE. AC，BE相交于点F，则∠BFC为( )A．45° B．55° C．60° D．75°2．下列关于矩形的说法中正确的是（）A．对角线相等的四边形是矩形B．矩形的对角线相等且互相平分C．对角线互相平分的四边形是矩形D．矩形的对角线互相垂直且平分3.下列命题中，真命题是( )A．对角线相等的四边形是矩形B．对角线互相垂直的四边形是菱形C．对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形4．如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平；再一次折叠，使点D落到EF上点G处，并使折痕经过点A，展平纸片后∠DAG的大小为（）A．30°B．45°C．60°D．75°5．（2016·四川泸州）如图，矩形ABCD的边长AD=3，AB=2，E为AB的中点，F在边BC上，且BF=2FC，AF分别与DE、DB相交于点M，N，则MN的长为（）A．B．C．D．6．如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（）A．△AFD≌△DCE B．AF=AD C．AB=AF D．BE=AD﹣DF二．填空题7. （2016·内蒙古包头）如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，则∠BAE=度．8. 如图，在菱形ABCD中，∠ABC=60°，AB=2，点P是这个菱形内部或边上的一点，若以点P、B、C为顶点的三角形是等腰三角形，则P、D（P、D两点不重合）两点间的最短距离为．9. 如图，在菱形ABCD中，点A在x轴上，点B的坐标为（8，2），点D的坐标为（0，2），则点C的坐标为．10. 如图，矩形ABCD中，AD=5，AB=7. 点E为DC上一个动点，把△ADE沿AE折叠，当点D 的对应点D'落在∠ABC的角平分线上时，DE的长为 .11. 如图，正方形ABCD的边长为a，在AB、BC、CD、DA边上分别取点A1、B1、C1、D1，使AA1=BB1=CC1=DD1=13a，在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2，使A1A2=B1B2=C1C2=D1D2=13A1B2，…．依次规律继续下去，则正方形A n B n C n D n的面积为．三．解答题12.已知：如图，在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ于点P．（1）求证：AP=BQ；（2）在不添加任何辅助线的情况下，请直接写出图中四对线段，使每对中较长线段与较短线段长度的差等于PQ的长．13．已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°．（1）如图1，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系；（2）如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE=CF；（3）如图3，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离．14．如图，在Rt△ABC中，∠ABC=90°，点M是AC的中点，以AB为直径作⊙O分别交AC，BM于点D，E．（1）求证：MD=ME；（2）填空：①若AB=6，当AD=2DM时，DE= ；②连接OD，OE，当∠A的度数为时，四边形ODME是菱形．15．（2016·陕西）问题提出（1）如图①，已知△ABC，请画出△ABC关于直线AC对称的三角形．问题探究（2）如图②，在矩形ABCD中，AB=4，AD=6，AE=4，AF=2，是否在边BC、CD上分别存在点G、H，使得四边形EFGH的周长最小？若存在，求出它周长的最小值；若不存在，请说明理由．问题解决（3）如图③，有一矩形板材ABCD，AB=3米，AD=6米，现想从此板材中裁出一个面积尽可能大的四边形EFGH部件，使∠EFG=90°，EF=FG=米，∠EHG=45°，经研究，只有当点E、F、G分别在边AD、AB、BC上，且AF＜BF，并满足点H在矩形ABCD内部或边上时，才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形EFGH部件？若能，求出裁得的四边形EFGH部件的面积；若不能，请说明理由．答案：1.C2.B3.C4.C5.B6.B7. 22.5°8. 2﹣2 9. （4，4）10. 52或53.11. 25()9n a12. 解：（1）∵正方形ABCD∴AD=B A，∠BAD=90°，即∠BAQ+∠DAP=90°∵DP⊥AQ∴∠ADP+∠DAP=90°∴∠BAQ=∠ADP∵AQ⊥BE于点Q，DP⊥AQ于点P∴∠AQB=∠DPA=90°∴△AQB≌△DPA（AAS）∴AP=BQ（2）①AQ﹣AP=PQ②AQ﹣BQ=PQ③DP﹣AP=PQ④DP﹣BQ=PQ13. （1）解：结论AE=EF=AF．理由：如图1中，连接AC，∵四边形ABCD是菱形，∠B=60°，∴AB=BC=CD=AD，∠B=∠D=60°，∴△ABC，△ADC是等边三角形，∴∠BAC=∠DAC=60°∵BE=EC，∴∠BAE=∠CAE=30°，AE⊥BC，∵∠EAF=60°，∴∠CAF=∠DAF=30°，∴AF⊥CD，∴AE=AF（菱形的高相等），∴△AEF是等边三角形，∴AE=EF=AF．（2）证明：如图2中，∵∠BAC=∠EAF=60°，∴∠BAE=∠CAE，在△BAE和△CAF中，，∴△BAE≌△CAF，∴BE=CF．（3）解：过点A作AG⊥BC于点G，过点F作FH⊥EC于点H，∵∠EAB=15°，∠ABC=60°，∴∠AEB=45°，在RT△AGB中，∵∠ABC=60°AB=4，∴BG=2，AG=2，在RT△AEG中，∵∠AEG=∠EAG=45°，∴AG=GE=2，14. （1）证明：∵∠ABC=90°，AM=MC，∴BM=AM=MC，∴∠A=∠ABM，∵四边形ABED是圆内接四边形，∴∠ADE+∠ABE=180°，又∠ADE+∠MDE=180°，∴∠MDE=∠MBA，同理证明：∠MED=∠A，∴∠MDE=∠MED，∴MD=ME．（2）①由（1）可知，∠A=∠MDE，∴DE∥AB，∴=，∵A D=2DM，∴DM：MA=1：3，∴DE=AB=×6=2．故答案为2．②当∠A=60°时，四边形ODME是菱形．理由：连接OD、OE，∵OA=OD，∠A=60°，∴△AOD是等边三角形，∴∠AOD=60°，∵DE∥AB，∴∠ODE=∠AOD=60°，∠MDE=∠MED=∠A=60°，∴△ODE，△DEM都是等边三角形，∴OD=OE=EM=DM，∴四边形OEMD是菱形．故答案为60°．15. 解：（1）如图1，△ADC即为所求；（2）存在，理由：作E关于CD的对称点E′，作F关于BC的对称点F′，连接E′F′，交BC于G，交CD于H，连接FG，EH，则F′G=FG，E′H=EH，则此时四边形EFGH的周长最小，由题意得：BF′=BF=AF=2，DE′=DE=2，∠A=90°，∴AF′=6，AE′=8，∴E′F′=10，EF=2，∴四边形EFGH的周长的最小值=EF+FG+GH+HE=EF+E′F′=2+10，∴在边BC、CD上分别存在点G、H，使得四边形EFGH的周长最小，最小值为2+10；（3）能裁得，理由：∵EF=FG=，∠A=∠B=90°，∠1+∠AFE=∠2+AFE=90°，∴∠1=∠2，在△AEF与△BGF中，，∴△AEF≌△BGF，∴AF=BG，AE=BF，设AF=x，则AE=BF=3﹣x，∴x2+（3﹣x）2=（）2，解得：x=1，x=2（不合题意，舍去），∴AF=BG=1，BF=AE=2，∴DE=4，CG=5，连接EG，作△EFG关于EG的对称△EOG，则四边形EFGO是正方形，∠EOG=90°，以O为圆心，以EG为半径作⊙O，则∠EHG=45°的点在⊙O上，连接FO，并延长交⊙O于H′，则H′在EG的垂直平分线上，连接EH′GH′，则∠EH′G=45°，此时，四边形EFGH′是要想裁得符合要求的面积最大的，∴C在线段EG的垂直平分线设，∴点F，O，H′，C在一条直线上，∵EG=，。
特殊四边形专项训练题
1．下列说法不正确的是( )A ．一组邻边相等的矩形是正方形B ．对角线相等的菱形是正方形C ．对角线互相垂直的矩形是正方形D ．有一个角是直角的平行四边形是正方形2．(2012年天津)如图4－3－25，在边长为2的正方形ABCD 中，M 为边AD 的中点，延长MD 至点E ，使ME ＝MC ，以DE 为边作正方形DEFG ，点G 在边CD 上，则DG 的长为( ) 图4－3－25A. 3－1 B ．3－ 5 C.5＋1 D. 5－13.如图，正方形ABCD 的边长为4，点E 在对角线BD 上，且∠BAE ＝22.5 º，EF ⊥AB ，垂足为F ，则EF 的长为（ ）A ．1B ． 2C ．4－2 2D ．32－44.如图，在矩形ABCD 中，点E ，F 分别在边AB ，BC 上，且AB AE 31 ，将矩形沿直线EF 折叠，点B 恰好落在AD 边上的点P 处，连接BP 交EF 于点Q ．对于下列结论：①EF＝2BE ；②PF＝2PE ；③FQ＝4EQ ；④△PBF 是等边三角形．其中正确的是（ ） A ．①② B ．②③ C ．①③ D ．①④5 如图4－3－26，菱形ABCD 的边长是2 cm ，E 是AB 的中点，且DE⊥AB ，则菱形ABCD 的面积为________cm 2.6．如图4－3－27，▱ABCD 的顶点B 在矩形AEFC 的边EF 上，点B 与点E ，F 不重合，若△ACD 的面积为3，则图中阴影部分两个三角形的面积和为______．7．已知菱形ABCD 的边长为6，∠A ＝60°，如果点P 是菱形内的一点，且PB ＝PD ＝2 3，那么AP 的长为__________．8.如图4－3－28，在正方形ABCD 中，点G 是BC 上任意一点，连接AG ，过B ，D 两点分别作BE ⊥AG ，DF ⊥AG ，垂足分别为E ，F 两点，求证：△ADF ≌△BAE .9. 实际应用：如图，有一块形状为平行四边形的木料，用AB 表示较长的一边，BC 为较短的一边，现有AB=2AD ，现在想用这块木料裁一个直角三角板，并且希望AB 为斜边，直角顶点在CD 上，问此想法可行吗？如果可行的话，请说明应该怎么做？如果不行，说明理由。
特殊的四边形测试题
特殊的四边形测试题一、选择题1. 下列四边形中，哪一个不是特殊的四边形？A. 平行四边形B. 矩形C. 菱形D. 任意四边形2. 特殊四边形中，哪一个的对角线相等？A. 平行四边形B. 矩形C. 菱形D. 梯形3. 以下哪个选项不是矩形的性质？A. 对边相等B. 四个角都是直角C. 对角线相等D. 对角线互相垂直4. 菱形的对角线性质是：A. 互相垂直B. 互相平行C. 相等D. 互相垂直且平分5. 下列哪个不是梯形的特点？A. 一组对边平行B. 另一组对边不平行C. 所有角都是直角D. 一组对边相等二、填空题6. 一个四边形的两组对边分别相等，且对角线相等，这个四边形是________。
7. 如果一个四边形的对角线互相垂直且平分，那么这个四边形是________。
8. 矩形的对角线性质是________。
9. 在特殊四边形中，只有________的对角线是互相垂直的。
10. 如果一个四边形的两组对边分别平行，那么这个四边形可能是________或________。
三、判断题11. 所有平行四边形的对角线都相等。
（对/错）12. 矩形的对角线将矩形分为两个相等的三角形。
（对/错）13. 菱形的对角线将菱形分为四个相等的直角三角形。
（对/错）14. 梯形的两组对边中，至少有一组是相等的。
（对/错）15. 所有特殊四边形的内角和都是360度。
（对/错）四、简答题16. 请简述矩形和正方形的共同性质。
17. 请解释为什么菱形的面积可以通过对角线的长度来计算。
18. 梯形的中位线定理是什么？请简述其内容。
19. 如果一个四边形的对角线互相垂直，那么这个四边形可能是哪种特殊四边形？20. 请描述如何通过已知的一组对边和对角线来确定一个四边形是否是平行四边形。
五、计算题21. 已知一个矩形的长为10厘米，宽为8厘米，求其对角线的长度。
22. 已知一个菱形的对角线长度分别为20厘米和16厘米，求其面积。
23. 如果一个梯形的上底为6厘米，下底为10厘米，高为4厘米，求其面积。
特殊的平行四边形专项练习(含答案)
特殊的平行四边形（含答案）一、选择题（本大题共49小题，共147.0分）1.一个菱形的周长是20cm，两条对角线长的比是4︰3，则这个菱形的面积是()A. 12cm2B. 96cm2C. 48cm2D. 24cm22.若菱形的周长为8，高为1，则菱形两邻角的度数之比是()A. 3:1B. 4:1C. 5:1D. 6:13.如图，在矩形ABCD中，O为AC中点，EF过O点，且EF⊥AC分别交DC于F，交AB于E，点G是AE中点，且∠AOG=30°.①DC=3OG；②OG=12BC；③△OGE是等边三角形；④S△AOE=16S矩形ABCD.则结论正确的个数为()A. 4B. 3C. 2D. 14.如图，ABCD是一张平行四边形纸片，要求利用所学知识作出一个菱形，甲、乙两位同学的作法如下：则关于甲、乙两人的作法，下列判断正确的为()A. 仅甲正确B. 仅乙正确C. 甲、乙均正确D. 甲、乙均错误5.如图，在菱形ABCD中，∠A=130°，连接BD，∠DBC等于()A. 25°B. 35°C. 50°D. 65°6.如图，两张等宽的纸条交叉重叠在一起，重叠的部分为四边形ABCD，若测得A，C之间的距离为6cm，点B，D之间的距离为8cm，则线段AB的长为()A. 5cmB. 4.8cmC. 4.6cmD. 4cm7.如图，矩形ABCD中，DE⊥AC于E，且∠ADE：∠EDC=3：2，则∠BDE的度数为()A. 36°B. 27°C. 18°D. 9°8.如图，四边形ABCD是菱形，AC=12，BD=16，AH⊥BC于H，则AH等于()A. 4B. 5C. 245D. 4859.菱形具有而一般平行四边形不具有的性质是()A. 两组对边分别相等B. 两条对角线相等C. 四个内角都是直角D. 每一条对角线平分一组对角10.如图，在菱形ABCD中，∠BAD=100°，AB的垂直平分线交对角线AC于点F，E为垂足，连接DF，则∠CDF等于()A. 60°B. 50°C. 30°D. 20°11.如图，在矩形ABCD中，F是BC中点，E是AD上一点，且∠ECD=30°，∠BEC=90°，EF=4cm，则矩形的面积为()．A. 16cm2B. 8√3cm2C. 16√3cm2D. 32cm212.如图，正方形ABCD中，BE=FC，CF=2FD，AE，BF交于点G，连接AF，给出下列结论：①AE⊥BF;②AE=BF;③BG=43GE;④S四边形CEGF=S▵ABG．其中正确的个数为()A. 1个B. 2个C. 3个D. 4个13.在△ABC中，点D是边BC上的点(与B，C两点不重合)，过点D作DE//AC，DF//AB，分别交AB，AC于E、F两点，下列说法错误的是()A. 四边形AEDF是平行四边形B. 若AB⊥AC，则四边形AEDF是矩形C. 若BD=CD，则四边形AEDF是正方形D. 若AD平分∠BAC，则四边形AEDF是菱形14.如图，在矩形ABCD中，AB>BC，点E，F，G，H分别是边DA，AB，BC，CD的中点，连接EG，HF，则图中的矩形共有()A. 5个B. 8个C. 9个D. 11个15.如图，将长方形纸片折叠，使A点落BC上的F处，折痕为BE，若沿EF剪下，则折叠部分是一个正方形，其数学原理是()A. 邻边相等的矩形是正方形B. 对角线相等的菱形是正方形C. 两个全等的直角三角形构成正方形D. 轴对称图形是正方形16.平行四边形、矩形、菱形、正方形都具有的性质是()A. 对角线互相平分B. 对角线互相垂直C. 对角线相等D. 对角线互相垂直平分且相等17.如图，在菱形ABCD中，E，F，G，H分别是菱形四条边的中点，连结EG与FH，交点为O，则图中的菱形共有()A. 4个B. 5个C. 6个D. 7个18.如图，已知某广场菱形花坛ABCD的周长是24米，∠BAD=60∘，则花坛对角线AC的长等于()A. 6√3米B. 6米C. 3√3米D. 3米19.如图，在平行四边形ABCD中，AD=2AB，CE⊥AB于点E，点F、G分别是AD、BC的中点，连接CF、EF、FG，下列结论：①CE⊥FG；②四边形ABGF是菱形；③EF=CF；④∠EFC=2∠CFD.其中正确的个数是()A. 1个B. 2个C. 3个D. 4个20.如图①，正方形A的一个顶点与正方形B的对称中心重合，重叠部分面积是正方形A面积的12，如图②，移动正方形A的位置，使正方形B的一个顶点与正方形A 的对称中心重合，则重叠部分面积是正方形B面积的()A. 12B. 14C. 16D. 1821.如图①、图②，在给定的一张矩形纸片上作一个正方形，甲、乙两人的作法如下：甲：以点A为圆心，AD长为半径画弧，交AB于点E，以点D为圆心，AD长为半径画弧，交CD于点F，连接EF，则四边形AEFD即为所求；乙：作∠DAB的平分线，交CD于点M，同理作∠ADC的平分线，交AB于点N，连接MN，则四边形ADMN即为所求．对于以上两种作法，可以做出的判定是()A. 甲正确，乙错误B. 甲、乙均正确C. 乙正确，甲错误D. 甲、乙均错误22.如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点，当AB︰AD的比为()时，四边形MENF是正方形．A. 1︰1B. 1︰2C. 2︰3D. 1︰423.如图，在菱形ABCD中，∠ADC=72∘，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB的度数是()A. 108∘B. 72∘C. 90∘D. 100∘24.在一次数学课上，张老师出示了一个题目：“如图，▱ABCD的对角线相交于点O，过点O作EF垂直于BD交AB，CD分别于点F，E，连接DF，BE.请根据上述条件，写出一个正确结论．”其中四位同学写出的结论如下：小青：OE=OF；小何：四边形DFBE是正方形；小夏：S四边形AFED=S四边形FBCE；小雨：∠ACE=∠CAF．这四位同学写出的结论中不正确的是()A. 小青B. 小何C. 小夏D. 小雨25.如图，将边长为2cm的正方形OABC放在平面直角坐标系中，O是原点，点A的横坐标为1，则点C的坐标为()A. (√3,−1)B. (2,−1)C. (1,−√3)D. (−1,√3)26.七巧板是我国祖先的一项卓越创造，流行于世界各地．由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板，如图1所示．分别用这两副七巧板试拼如图2中的平行四边形或矩形，则这两个图形中，中国七巧板和日本七巧板能拼成的个数分别是()A. 1和1B. 1和2C. 2和1D. 2和227.四边形ABCD的对角线AC，BD，下面给出的三个条件中，选取两个，能使四边形ABCD是矩形，①AC，BD互相平分；②AC⊥BD；③AC=BD，则正确的选法是()A. ①②B. ①③C. ②③D. 以上都可以28.如图，菱形ABCD周长为20，对角线AC、BD相交于点O，E是CD的中点，则OE的长是()A. 2.5B. 3C. 4D. 529.如图，在正方形ABCD中，E是BC边上的一点，BE=2，EC=4，将正方形边AB沿AE折叠到AF，延长EF交DC于G，连接AG.现在有如下四个结论：①∠EAG=45°；②FG=FC；③FC//AG；④S△GFC=3.6.其中结论正确的个数是()A. 1B. 2C. 3D. 430.在菱形ABCD中，AC、BD为对角线，若AC=4，BD=8，则菱形ABCD的面积是()A. 12B. 16C. 24D. 3231.四边形具有不稳定性，对于四条边长确定的四边形．当内角度数发生变化时，其形状也会随之改变．如图，改变正方形ABCD的内角，正方形ABCD变为菱形ABC′D′.若∠D′AB=30°，则菱形ABC′D′的面积与正方形ABCD的面积之比是()A. 1B. 12C. √22D. √3232.一个菱形的边长为6，面积为28，则该菱形的两条对角线的长度之和为()A. 8B. 12C. 16D. 3233.矩形OABC在平面直角坐标系中的位置如图所示，已知B(2√3,2)，点A在x轴上，点C在y轴上，P是对角线OB上一动点(不与原点重合)，连接PC，过点P作PD⊥PC，交x轴于点D.下列结论：①OA=BC=2√3；②当点D运动到OA的中点处时，PC2+PD2=7；③在运动过程中，∠CDP是一个定值；④当△ODP为等腰三角形时，点D的坐标为(2√33,0)．其中正确结论的个数是()A. 1个B. 2个C. 3个D. 4个34.如图，矩形ABCD中，点E在BC边上，DF⊥AE于F，若EF=CE=1，AB=3，则线段AF的长为()A. 2√5B. 4C. √10D. 3√235.如图，在矩形ABCD中，BC=8，CD=6，E为AD上一点，将△ABE沿BE折叠，点A恰好落在对角线BD上的点F处，则折线BE的长为()A. 2√5B. 3√3C. 3√5D. 6√336.如图，菱形ABCD的边长为13，对角线AC=24，点E、F分别是边CD、BC的中点，连接EF并延长与AB的延长线相交于点G，则EG=()A. 13B. 10C. 12D. 537.下列说法正确的是()A. 一组对边平行另一组对边相等的四边形是平行四边形B. 对角线互相垂直平分的四边形是菱形C. 对角线相等的四边形是矩形D. 对角线互相垂直且相等的四边形是正方形38.如图，在菱形ABCD中，∠BCD=60°，BC的垂直平分线交对角线AC于点F，垂足为E，连接BF、DF，则∠DFC的度数是()A. 130°B. 120°C. 110°D. 100°39.若菱形的周长为16，高为2，则菱形两邻角的度数之比为()A. 4：1B. 5：1C. 6：1D. 7：140.已知四边形ABCD是平行四边形，AC，BD相交于点O，下列结论错误的是()A. OA=OC，OB=ODB. 当AB=CD时，四边形ABCD是菱形C. 当∠ABC=90°时，四边形ABCD是矩形D. 当AC=BD且AC⊥BD时，四边形ABCD是正方形41.下列是关于某个四边形的三个结论：①它的对角线相等；②它是一个正方形；③它是一个矩形．下列推理过程正确的是()A. 由②推出③，由③推出①B. 由①推出②，由②推出③C. 由③推出①，由①推出②D. 由①推出③，由③推出②42.菱形不具备的性质是()A. 是轴对称图形B. 是中心对称图形C. 对角线互相垂直D. 对角线一定相等43.如图，矩形ABCD的对角线AC，BD交于点O，AB=6，BC=8，过点O作OE⊥AC，交AD于点E，过点E作EF⊥BD，垂足为F，则OE+EF的值为()A. 485B. 325C. 245D. 12544.下列说法正确的有几个()①对角线互相平分的四边形是平行四边形；②对角线互相垂直的四边形是菱形；③对角线互相垂直且相等的平行四边形是正方形；④对角线相等的平行四边形是矩形．A. 1个B. 2个C. 3个D. 4个45.在矩形ABCD中，AC、BD相交于点O，若△AOB的面积为2，则矩形ABCD的面积为()A. 4B. 6C. 8D. 1046.如图，已知正方形ABCD边长为1，连接AC、BD，CE平分∠ACD交BD于点E，则DE长为()A. 2√2−2B. √3−1C. 2−√2D. √2−147.如图，在菱形ABCD中，对角线AC、BD相交于点O，H为BC中点，AC=6，BD=8.则线段OH的长为()A. 125B. 52C. 3D. 548.如图所示，点O是矩形ABCD对角线AC的中点，OE//AB交AD于点E.若OE=3，BC=8，则OB的长为()A. 4B. 5C. √342D. √3449.菱形的对角线不一定具有的性质是()A. 互相平分B. 互相垂直C. 每一条对角线平分一组对角D. 相等二、填空题（本大题共21小题，共63.0分）50.如图，将两条宽度都为6的纸片重叠在一起，使∠ABC=60°，则四边形ABCD的面积为________．51.如图，在菱形ABCD中，对角线AC、BD相交于点O，H为边AD的中点，菱形ABCD的周长为28，则OH的长等于________．52.已知菱形ABCD中，对角线AC与BD交于点O，∠BAD=120°，AC=4，则该菱形的面积是______．53.在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点(不与端点重合)，对于任意矩形ABCD，下面四个结论中，①存在无数个四边形MNPQ是平行四边形；②存在无数个四边形MNPQ是矩形；③存在无数个四边形MNPQ是菱形；④至少存在一个四边形MNPQ是正方形．所有正确结论的序号是______．54.菱形的面积是24，一条对角线长是6，则菱形的边长是______．55.如图，四边形ABCD为菱形，四边形AOBE为矩形，O，C，D三点的坐标为(0,0)，(2,0)，(0,1)，则点E的坐标为______．56.如图，在菱形ABCD中，AB=18cm，∠A=60°，点E以2cm/s的速度沿AB边由A向B匀速运动，同时点F以4cm/s的速度沿CB边由C向B运动，F到达点B时两点同时停止运动．设运动时间为t秒，当△DEF为等边三角形时，t的值为______．57.如图1，已知四边形ABCD是正方形，将△DAE，△DCF分别沿DE，DF向内折叠得到图2，此时DA与DC重合(A、C都落在G点)，若GF=4，EG=6，则DG的长为______．58.已知矩形ABCD，对角线AC、BD相交于点O，点E为BD上一点，OE=1，连接AE，∠AOB=60°，AB=2，则AE的长为______．59.菱形ABCD中，∠A=60°，AB=9，点P是菱形ABCD内一点，PB=PD=3√3，则AP的长为______．60.如图，在平面直角坐标系中，菱形OABC的一个顶点在原点O处，且∠AOC=60°，A点的坐标是(0,4)，则直线AC的表达式是______．61.如图，将菱形ABCD折叠，使点B落在AD边的点F处，折痕为CE.若∠D=70°，则∠AEF=______．62.如图，已知点P(2,0)，Q(8,0)，A是x轴正半轴上一动点，以OA为一边在第一象限内作正方形OABC，当PB+BQ取最小值时，点B的坐标是______．63.已知正方形ABCD，以∠BAE为顶角，边AB为腰作等腰△ABE，连接DE，则∠DEB=______．64.一个菱形的周长为52cm，一条对角线长为10cm，则其面积为______ cm2．65.菱形有一个内角为60°，较短的对角线长为6，则它的面积为______．66.如图，在菱形ABCD中，对角线AC、BD相交于点O，点E在线段BO上，连接AE，若CD=2BE，∠DAE=∠DEA，EO=1，则线段AE的长为______．67.如图，在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1，先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2019次，点B的落点依次为B1，B2，B3，…，则B2019的坐标为______．68.如图，在Rt△ABC中，∠A=90°，AB=6，BC=10，P是BC边上的一点，作PE垂直AB，PF垂直AC，垂足分别为E、F，求EF的最小值是______．69.如图1，直角三角形纸片的一条直角边长为2，剪四块这样的直角三角形纸片，把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙)，则图2中阴影部分面积为______．70.若顺次连接四边形ABCD四边中点形成的四边形为矩形，则四边形ABCD满足的条件为______．三、解答题（本大题共19小题，共152.0分）71.如图，在▵ABCD中，E，F分别为边AB，CD的中点，BD是对角线．(1)求证：△ADE≌△CBF；(2)若∠ADB是直角，请证明四边形BEDF是菱形．72.如图，在△ABC中，D，E分别是AB，AC的中点，连接DE并延长DE至点F，使EF=DE，连接CF．(1)求证：四边形DBCF是平行四边形；(2)探究：当△ABC满足什么条件时，四边形ADCF是矩形，并说明理由．73.如图1，直角梯形ABCD中，AD//BC，∠ADC=90°，AD=8，BC=6，点M从点D出发，以每秒2个单位长度的速度向点A运动，同时，点N从点B出发，以每秒1个单位长度的速度向点C运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点N作NP⊥AD于点P，连接AC交NP于点Q，连接MQ.设运动时间为t秒．(1)AM=______，AP=______.(用含t的代数式表示)(2)当四边形ANCP为平行四边形时，求t的值；(3)如图2，将△AQM沿AD翻折，得△AKM，是否存在某时刻t，①使四边形AQMK为为菱形，若存在，求出t的值；若不存在，请说明理由②使四边形AQMK为正方形，则AC=______．74.如图，在长方形纸片ABCD中，AD//BC，将长方形纸片折叠，使点D与点B重合，点C落在点C′处，折痕为EF．(1)求证：BE=BF．(2)若∠ABE=18°，求∠BFE的度数．(3)若AB=4，AD=8，求AE的长．75.如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于点D，交AB于点E，点F在DE的延长线上，且AF=CE．(1)四边形ACEF是平行四边形吗？说明理由．(2)当∠B的大小满足什么条件时，四边形ACEF为菱形？请说明你的结论．(3)四边形ACEF有可能是正方形吗？为什么？76.如图，P是正方形ABCD对角线BD上一点，PE⊥DC，PF⊥BC，E、F分别为垂足，若CF=3，CE=4，求AP的长．77.如图，长方形纸片ABCD中，AB=8cm，把长方形纸片沿直线AC折叠，点B落在点E处，AE交cm，求AD．DC于点F，AF=25478.如图，在▱ABCD中，AE⊥BC，AF⊥CD，垂足分别为点E、F，且BE=DF．求证：▱ABCD是菱形．CE．79.如图，AE=AC，点B是CE的中点，且AD//CE，AD=12(1)若AE=25，CE=14，求△ACE的面积；(2)求证：四边形ABCD是矩形．80.如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点，点M是AB边上一动点(不与点A重合)，延长ME交射线CD于点N，连接MD、AN．(1)求证：四边形AMDN是平行四边形；(2)在点M移动过程中：①当四边形AMDN成矩形时，求此时AM的长；②当四边形AMDN成菱形时，求此时AM的长．81.如图，点P是正方形ABCD内的一点，连接CP，将线段CP绕点C顺时旋转90°，得到线段CQ，连接BP，DQ．(1)如图1，求证：△BCP≌△DCQ；(2)如图，延长BP交直线DQ于点E．①如图2，求证：BE⊥DQ；②如图3，若△BCP为等边三角形，判断△DEP的形状，并说明理由．82.如图，在四边形ABCD中，BC=CD，∠C=2∠BAD.O是四边形ABCD内一点，且OA=OB=OD.求证：(1)∠BOD=∠C；(2)四边形OBCD是菱形．83.如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使CF=BE，连接DF．(1)求证：四边形AEFD是矩形；(2)连接OE，若AD=10，EC=4，求OE的长度．84.如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别在BD和DB的延长线上，且DE=BF，连接AE，CF．(1)求证：△ADE≌△CBF；(2)连接AF，CE.当BD平分∠ABC时，四边形AFCE是什么特殊四边形？请说明理由．85.如图，以矩形OABC的顶点O为坐标原点，OA所在直线为x轴，OC所在直线为y轴建立平面直角坐标系．已知，OA=2，OC=4，点D为x轴上一动点，以BD为一边在BD右侧作正方形BDEF．(1)若点D与点A重合，请直接写出点E的坐标；(2)若点D在OA的延长线上，且EA=EB，求点E的坐标；(3)若OE=2√17，求点E的坐标．86.如图，BD是△ABC的角平分线，过点D作DE//BC交AB于点E，DF//AB交BC于点F．(1)求证：四边形BEDF为菱形；(2)如果∠A=90°，∠C=30°，BD=6，求菱形BEDF的面积．87.已知抛物线y=ax2+bx+c(a≠0)过点A(1,0)，B(3,0)两点，与y轴交于点C，OC=3．(1)求抛物线的解析式及顶点D的坐标；(2)过点A作AM⊥BC，垂足为M，求证：四边形ADBM为正方形；(3)点P为抛物线在直线BC下方图形上的一动点，当△PBC面积最大时，求点P的坐标；QC是否存在最小值？若存在，求岀(4)若点Q为线段OC上的一动点，问：AQ+12这个最小值；若不存在，请说明理由．88.如图所示，顺次延长正方形ABCD的各边AB，BC，CD，DA至E，F，G，H，且使BE=CF=DG=AH．求证：四边形EFGH是正方形．89.已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE//AC，AE//BD．(1)求证：四边形AODE是矩形；(2)若AB=2，DE=1，求四边形AODE的面积．答案和解析1.【答案】D【解析】【分析】此题主要考查菱形的性质，根据菱形的对角线互相垂直平分，利用勾股定理求解．【解答】解：设菱形的对角线长分别为8x cm和6x cm，已知菱形的周长为20cm，故菱形的边长为5cm，根据菱形的性质可知，菱形的对角线互相垂直平分，即可知(4x)2+(3x)2=25，解得x=1，故菱形的对角线长分别为8cm和6cm，×8×6=24(cm2).所以菱形的面积为122.【答案】C【解析】【分析】本题考查了菱形的性质、含30°角的直角三角形的判定；熟练掌握菱形的性质和含30°角的直角三角形的判定是解决问题的关键．先根据菱形的性质求出边长AB=2，再根据直角三角形的性质求出∠B=30°，得出∠DAB=150°，即可得出结论．【解答】解：如图所示：∵四边形ABCD是菱形，菱形的周长为8，∴AB=BC=CD=DA=2，∠DAB+∠B=180°，∵AE=1，AE⊥BC，∴AE=1AB，2∴∠B=30°，∴∠DAB=150°，∴∠DAB：∠B=5：1；故选C．3.【答案】B【解析】【分析】本题考查了矩形的性质，直角三角形斜边上的中线等于斜边的一半的性质，等边三角形的判定与性质，等腰三角形的判定与性质，三角形的面积，设出AE、OG，然后用a表示出相关的边更容易理解，根据直角三角形斜边上的中线等于斜边的一半可得OG= AG=GE=12AE，再根据等边对等角可得∠OAG=30°，根据直角三角形两锐角互余求出∠GOE=60°，从而判断出△OGE是等边三角形，判断出③正确；设AE=2a，根据等边三角形的性质表示出OE，利用勾股定理列式求出AO，从而得到AC，再求出BC，然后利用勾股定理列式求出AB=3a，从而判断出①正确，②错误；再根据三角形的面积和矩形的面积列式求出判断出④正确．【解答】解：∵EF⊥AC，点G是AE中点，∴OG=AG=GE=12AE，∵∠AOG=30°，∴∠OAG=∠AOG=30°，∠GOE=90°−∠AOG=90°−30°=60°，∴△OGE是等边三角形，故③正确；设AE=2a，则OE=OG=a，由勾股定理得，AO=√AE2−OE2=√(2a)2−a2=√3a，∵O为AC中点，∴AC=2AO=2√3a，∴BC=12AC=12×2√3a=√3a，在Rt△ABC中，由勾股定理得，AB=√(2√3a)2−(√3a)2=3a，∵四边形ABCD是矩形，∴CD=AB=3a，∴DC=3OG，故①正确；∵OG=a,12BC=√32a，∴OG≠12BC，故②错误；∵S△AOE=12a⋅√3a=√32a2，S ABCD=3a⋅√3a=3√3a2，∴S△AOE=16S ABCD，故④正确；综上所述，结论正确是①③④共3个．故选B．4.【答案】C【解析】【分析】此题主要考查了菱形的判定，关键是掌握菱形的判定方法：①菱形定义：一组邻边相等的平行四边形是菱形(平行四边形+一组邻边相等=菱形)；②四条边都相等的四边形是菱形．③对角线互相垂直的平行四边形是菱形(或“对角线互相垂直平分的四边形是菱形”)．【解答】解：甲的作法正确；∵四边形ABCD是平行四边形，∴AD//BC，∴∠DAC=∠ACB，∵EF是AC的垂直平分线，∴AO=CO，在△AOE和△COF中，{∠EAO =∠FCO AO =CO ∠AOE =∠COF, ∴△AOE≌△COF(ASA)，∴AE =CF ，又∵AE//CF ，∴四边形AECF 是平行四边形，∵EF ⊥AC ，∴四边形AECF 是菱形；乙的作法正确；∵AD//BC ，∴∠1=∠2，∠6=∠7，∵BF 平分∠ABC ，AE 平分∠BAD ，∴∠2=∠3，∠5=∠6，∴∠1=∠3，∠5=∠7，∴AB =AF ，AB =BE ，∴AF =BE∵AF//BE ，且AF =BE ，∴四边形ABEF 是平行四边形，∵AB =AF ，∴平行四边形ABEF 是菱形；故选C ．5.【答案】A【解析】【试题解析】【分析】此题主要考查了菱形的性质，正确应用菱形的性质是解题关键．直接利用菱形的性质得出∠ABC 的度数，进而得出∠DBC 的度数．【解答】解：∵在菱形ABCD中，∠A=130°，∴∠ABC=180°−130°=50°，∴∠DBC=12∠ABC=25°．故选：A．6.【答案】A【解析】【分析】本题主要考查菱形的判定和性质，证得四边形ABCD是菱形是解题的关键．作AR⊥BC于R，AS⊥CD于S，根据题意先证出四边形ABCD是平行四边形，再由AR= AS得平行四边形ABCD是菱形，再根据根据勾股定理求出AB即可．【解答】解：如图，作AR⊥BC于R，AS⊥CD于S，连接AC，BD交于点O，由题意知，AD//BC，AB//CD，∴四边形ABCD是平行四边形．∵两张纸条等宽，∴AR=AS．∵AR⋅BC=AS⋅CD，∴BC=CD，∴平行四边形ABCD是菱形，∴AC⊥BD．在Rt△AOB中，OA=12AC=3cm，OB=12BD=4cm，∴AB=√OA2+OB2=√32+42=5cm．故选A．7.【答案】C【解析】【分析】本题考查了矩形的性质、等腰三角形的判定与性质、角的互余关系，熟练掌握矩形的性质，并能进行推理计算是解决问题的关键，解答此题由矩形的性质得出OC=OD，得出∠ODC=∠OCD，求出∠EDC=36°，再由角的互余关系求出∠ODC，即可得出∠BDE的度数．【解答】解：∵四边形ABCD是矩形，∴∠ADC=90°，OC=12AC，OD=12BD，AC=BD，∴OC=OD，∴∠ODC=∠OCD，∵∠ADE：∠EDC=3：2，∴∠EDC=25×90°=36°，∵DE⊥AC，∴∠DEC=90°，∴∠ODC=∠OCD=90°−36°=54°，∴∠BDE=∠ODC−∠EDC=54°−36°=18°．故选C．8.【答案】D【解析】【分析】本题考查了菱形的性质，也涉及了勾股定理，要求我们掌握菱形的面积的两种表示方法，及菱形的对角线互相垂直且平分．根据菱形的性质得出BO、CO的长，在Rt△BOC中求出BC，利用菱形面积等于对角线乘积的一半，也等于BC×AH，即可得出AH的长度．【解答】解：∵四边形ABCD是菱形，AC=12，BD=16，∴CO=12AC=6，BO=12BD=8，CO⊥BO，∴BC=√BO2+CO2=√62+82=10，∴S菱形ABCD =12AC⋅BD=12×16×12=96，∵S菱形ABCD=BC×AH，∴BC×AH=96，∴AH=9610=485．故选D．9.【答案】D【解析】【分析】此题主要考查了菱形的性质和平行四边形的性质，关键是根据菱形对角线垂直及平行四边形对角线平分的性质的理解．根据菱形的特殊性质可知对角线互相垂直．【解答】解：A.两组对角分别相等，两者均有此性质，故此选项不正确；B.两条对角线相等，两者均没有此性质，故此选项不正确；C.四个内角都是直角，两者均不具有此性质，故此选项不正确；D.每一条对角线平分一组对角，菱形具有而一般平行四边形不具有此性质，故此选项正确．故选D．10.【答案】C【解析】【分析】本题考查了三角形外角的性质，全等三角形性质和判定，线段垂直平分线性质，菱形的性质的应用，注意：菱形的四条边相等，菱形的对角线互相平分、垂直，且每一条对角线平分一组对角．连接BF，根据菱形性质得出AD=AB，∠DCB=100°，∠DCA= 50°，∠DAC=∠BAC=50°，根据线段垂直平分线得出AF=BF，求出∠FAB=∠FBA= 50°，求出∠AFB=80°，证△DAF≌△BAF，求出∠DFA=∠BFA=80°，根据三角形外角性质求出即可．【解答】解：如图，连接BF．∵在菱形ABCD中，∠BAD=100°，∴∠DAC=∠BAC=50°，∠ADC=∠ABC=180°−100°=80°．∵EF是线段AB的垂直平分线，∴AF=BF．∴∠ABF=∠CAB=50°．在△ADF与△ABF中，∵{AD=AB,∠DAF=∠BAF, AF=AF,∴△ADF≌△ABF(SAS)，∴∠ADF=∠ABF=50°，∴∠CDF=∠ADC−∠ADF=80°−50°=30°．11.【答案】C【解析】【分析】本题考查了矩形的性质，直角三角形斜边上的中线等于斜边的一半的性质，等边三角形的判定及性质，求出矩形的宽是解题的关键．根据直角三角形斜边上的中线等于斜边的一半求出BC，然后判断出△CEF是等边三角形，过点E作EG⊥CF于G，根据等边三角形的性质及勾股定理求出EG，然后根据矩形的面积公式列式进行计算即可得解．【解答】解：作EG⊥BC于G．∵F是BC中点，∠BEC=90°，∴EF=BF=FC，BC=2EF=2×4=8(cm)，∵∠ECD=30°，∴∠BCE=60°，∴△CEF是等边三角形，∴CE=EF=4cm，∠CEG=30°，∴CG=12CE=2cm，则EG=√CE2−CG2=2√3(cm)，∴矩形的面积=8×2√3=16√3(cm2).故选C．12.【答案】C【解析】【分析】此题考查三角形全等的判定和性质、正方形的性质和勾股定理。
初二数学特殊四边形练习题(含答案)
初二数学特殊四边形练习题一．选择题（共5小题）1．如图，在平行四边形ABCD中，AB ACAB=，12AC=，则BD的长是()⊥，若8A．22B．16C．18D．202．如图，正方形ABCD的对角线BD是菱形BEFD的一边，菱形BEFD的对角线交正方形ABCD的一边CD于点P，FPC∠的度数是()A．135︒B．120︒C．112.5︒D．67.5︒3．已知四边形ABCD是平行四边形，则下列结论中正确的是()A．当AB BD⊥时，它是菱形B．当AC BD=时，它是正方形C．当90=时，它是矩形∠=︒时，它是矩形D．当AB BCABC4．如图，在ABCBC=，点P为斜边AB上一动点，过点P作PE AC⊥于AC=，8C∠=︒，6∆中，90点E，PF BC⊥于点F，连结EF，则线段EF的最小值为()A．1.2B．2.4C．2.5D．4.85．如图，在ABC∠=︒，BD为AC的中线，过点C作ABC∆中，90⊥于点E，过点A作BD的平行线，交CE的延长线于点CE BDF，在AF的延长线上截取FG BD=，连接BG、DF．若AC AF=+，则四边形BDFG的周长为()CF=，26A．9.5B．10C．12.5D．20二．填空题（共5小题）6．已知平行四边形ABCD 中，50A B ∠-∠=︒，则C ∠= ．7．已知：如图，平行四边形ABCD 中，BE 平分ABC ∠交AD 于E ，CF 平分BCD ∠交AD 于F ，若3AB =，5BC =，则EF = ．8．如图，菱形ABCD 的边长是4cm ，E 是AB 的中点，且DE AB ⊥，则菱形ABCD 的面积为 2cm ．9．如图，矩形ABCD 中，8AB =，15BC =，P 是边AD 上的动点，PE AC ⊥于点E ，PF BD ⊥于点F ，则PE PF +的值为 ．10．已知正方形ABCD 的边长为4，点E ，F 分别在AD ，DC 上，1AE DF ==，BE 与AF 相交于点G ，点H 为BF 的中点，连接GH ，则GH 的长为 ．三．解答题（共4小题）11．已知：如图，在ABC ∆中，AB AC =，AD 是BAC ∠的平分线，AN 是ABC ∆外角CAM ∠的平分线，CE AN ⊥，垂足为点E ．求证：四边形ADCE 为矩形；12．如图，在四边形ABCD中，//cm s的速度BC cm=，点P自点A向D以1/AD BC，12AD cm=，15运动，到D点即停止．点Q自点C向B以2/cm s的速度运动，到B点即停止，点P，Q同时出发，设运动时间为()t s．（1）用含t的代数式表示：AP=；DP=；BQ=．（2）当t为何值时，四边形APQB是平行四边形？13．如图，菱形ABCD对角线交于点O，//AE BD，EO与AB交于点F．BE AC，//（1）试判断四边形AEBO的形状，并说明你的理由；（2）求证：EO DC=．14．如图，四边形ABCD为正方形，点G是BC上的任意一点，分别过点B，D作BF AG⊥于点F，⊥于点E于点E，猜想DE，EF，BF三条线段存在怎样的数最关系，并证明你的结论．DE AG答案与解析一．选择题（共5小题）1．如图，在平行四边形ABCD 中，AB AC ⊥，若8AB =，12AC =，则BD 的长是( )A ．22B ．16C ．18D ．20【分析】由四边形ABCD 是平行四边形，根据平行四边形的对角线互相平分，可得OA 的长，然后由AB AC ⊥，8AB =，12AC =，根据勾股定理可求得OB 的长，继而求得答案． 【解答】解：四边形ABCD 是平行四边形，12AC =， 162OA AC ∴==，2BD OB =， AB AC ⊥，8AB =，228610OB ∴=+=，220BD OB ∴==． 故选：D ．2．如图，正方形ABCD 的对角线BD 是菱形BEFD 的一边，菱形BEFD 的对角线交正方形ABCD 的一边CD 于点P ，FPC ∠的度数是( )A ．135︒B ．120︒C ．112.5︒D ．67.5︒【分析】先根据正方形的性质求出45DBC ∠=︒，再根据角平分线的定义得出EBF ∠，然后由外角的性质即可得出结果．【解答】解：四边形ABCD 是正方形，90ABC BCD ∴∠=∠=︒，45DBC ABD ∠=∠=︒， 四边形BEFD 是菱形， 122.52EBF DBC ∴∠=∠=︒，9022.5112.5FPC BCD EBF ∴∠=∠+∠=︒+∠︒=︒； 故选：C ．3．已知四边形ABCD 是平行四边形，则下列结论中正确的是( )A ．当AB BD ⊥时，它是菱形 B ．当AC BD =时，它是正方形 C ．当90ABC ∠=︒时，它是矩形 D ．当AB BC =时，它是矩形 【分析】依据矩形和菱形的判定定理进行判断即可．【解答】解：A 、当AB BD ⊥时，90ABD ∠=︒，则90ABC ∠>︒，当AC BD ⊥，四边形ABCD 是菱形，故A 错误；B 、由四边形ABCD 是平行四边形，AC BD =，则四边形ABCD 为矩形，故B 错误；C 、当90ABC ∠=︒时，四边形ABCD 是矩形，故C 正确；D 、由四边形ABCD 是平行四边形，AB BC =，则四边形ABCD 为菱形，故D 错误． 故选：C ．4．如图，在ABC ∆中，90C ∠=︒，6AC =，8BC =，点P 为斜边AB 上一动点，过点P 作PE AC ⊥于点E ，PF BC ⊥于点F ，连结EF ，则线段EF 的最小值为( )A ．1.2B ．2.4C ．2.5D ．4.8 【分析】连接PC ，当CP AB ⊥时，PC 最小，利用三角形面积解答即可． 【解答】解：连接PC ， PE AC ⊥，PF BC ⊥，90PEC PFC C ∴∠=∠=∠=︒， ∴四边形ECFP 是矩形， EF PC ∴=，∴当PC 最小时，EF 也最小，根据垂线段最短，当CP AB ⊥时，PC 最小， 6AC =，8BC =， 10AB ∴=，PC ∴的最小值为：684.810AC BC AB ⨯==． ∴线段EF 长的最小值为4.8． 故选：D ．5．如图，在ABC ∆中，90ABC ∠=︒，BD 为AC 的中线，过点C 作CE BD ⊥于点E ，过点A 作BD 的平行线，交CE 的延长线于点F ，在AF 的延长线上截取FG BD =，连接BG 、DF ．若6CF =，2AC AF =+，则四边形BDFG 的周长为( )A ．9.5B ．10C ．12.5D ．20【分析】首先可判断四边形BGFD 是平行四边形，再由直角三角形斜边中线等于斜边一半，可得BD FD =，则可判断四边形BGFD 是菱形，设AF x =，则2AC x =+，6FC =，在Rt ACF ∆中利用勾股定理可求出x 的值，进而得出答案． 【解答】解：//AG BD ，BD FG =， ∴四边形BGFD 是平行四边形， CF BD ⊥， CF AG ∴⊥，又点D 是AC 中点，12BD DF AC ∴==， ∴四边形BGFD 是菱形，设AF x =，则2AC x =+，6FC =， 在Rt ACF ∆中，90CFA ∠=︒， 222AF CF AC ∴+=，即2226(2)x x +=+，解得：8x =， 故10AC =，故四边形BDFG 的周长421020BD ==⨯=． 故选：D ．二．填空题（共5小题）6．已知平行四边形ABCD 中，50A B ∠-∠=︒，则C ∠= 115︒ ．【分析】利用平行四边形的邻角互补， 和50A B ∠-∠=︒，就可建立方程求出两角 ． 【解答】解： 在平行四边形ABCD 中，180A B ∠+∠=︒， 又有50A B ∠-∠=︒，把这两个式子相加即可求出2∠A=230°，∴115A C ∠=∠=︒， 故答案为：115︒． 7．已知：如图，平行四边形ABCD 中，BE 平分ABC ∠交AD 于E ，CF 平分BCD ∠交AD 于F ，若3AB =，5BC =，则EF = 1 ．【分析】先证明3AB AE ==，3DC DF ==，再根据EF AE DF AD =+-即可计算． 【解答】解：四边形ABCD 是平行四边形， 3AB CD ∴==，5BC AD ==，//AD BC ，BE 平分ABC ∠交AD 于E ，CF 平分BCD ∠交AD 于F ， ABF CBE AEB ∴∠=∠=∠，BCF DCF CFD ∠=∠=∠， 3AB AE ∴==，3DC DF ==，3351EF AE DF AD ∴=+-=+-=． 故答案为1．8．如图，菱形ABCD 的边长是4cm ，E 是AB 的中点，且DE AB ⊥，则菱形ABCD 的面积为 83 2cm ．【分析】利用勾股定理求出DE ，根据菱形ABCD 的面积AB DE =计算即可． 【解答】解：四边形ABCD 是菱形， 4AD AB ∴==， ∵E 是AB 的中点， 2AE EB ∴==， DE AB ⊥， ∴在Rt ADE ∆中，2223DE AD AE -∴菱形ABCD 的面积42383AB DE ===，故答案为839．如图，矩形ABCD 中，8AB =，15BC =，P 是边AD 上的动点，PE AC ⊥于点E ，PF BD ⊥于点F ，则PE PF +的值为12017．【分析】连接PO ，由勾股定理求出AC ，得出OA 、OD 的长，根据三角形面积和矩形面积关系求出PE PF +即可．【解答】解：连接PO ，如图所示： 四边形ABCD 是矩形，90ADC ∴∠=︒，8AB CD ==，15AD BC ==，OA OC =，OB OD =，AC BD =， OA OD ∴=，由勾股定理得：222281517AC AB BC =+=+=， 11722OA OD AC ∴===， 111158224AOD S OA PE OD PF ∆=⨯+⨯=⨯⨯，∴1171()158224PE PF ⨯⨯+=⨯⨯， 12017PE PF ∴+=； 故答案为：12017． 10．已知正方形ABCD 的边长为4，点E ，F 分别在AD ，DC 上，1AE DF ==，BE 与AF 相交于点G ，点H 为BF 的中点，连接GH ，则GH 的长为52． 【分析】根据正方形的四条边都相等可得AB AD =，每一个角都是直角可得90BAE D ∠=∠=︒，然后利用“边角边”证明ABE DAF ∆≅∆得ABE DAF ∠=∠，进一步得90AGE BGF ∠=∠=︒，从而知12GH BF =，利用勾股定理求出BF 的长即可得出答案． 【解答】解：四边形ABCD 为正方形， 90BAE D ∴∠=∠=︒，AB AD =， 在ABE ∆和DAF ∆中，AB AD BAE D AE DF =⎧⎪∠=∠⎨⎪=⎩，()ABE DAF SAS ∴∆≅∆，ABE DAF ∴∠=∠，90ABE BEA ∠+∠=︒， 90DAF BEA ∴∠+∠=︒， 90AGE BGF ∴∠=∠=︒， 点H 为BF 的中点，12GH BF ∴=，4BC =，413CF CD DF =-=-=，225BF BC CF ∴=+=， 1522GH BF ∴==，故答案为：52．三．解答题（共4小题）11．已知：如图，在ABC ∆中，AB AC =，AD 是BAC ∠的平分线，AN 是ABC ∆外角CAM ∠的平分线，CE AN ⊥，垂足为点E ．求证：四边形ADCE 为矩形； 【分析】根据三个角是直角是四边形是矩形即可证明； 【解答】证明：AB AC =，AD 是BAC ∠的平分线， AD BC ∴⊥，BAD CAD ∠=∠． 90ADC ∴∠=︒，AN 为ABC ∆的外角CAM ∠的平分线， MAN CAN ∴∠=∠． 90DAE ∴∠=︒， CE AN ⊥， 90AEC ∴∠=︒．∴∠ADC=∠DAE=∠AEC=90°， ∴四边形ADCE 为矩形．12．如图，在四边形ABCD 中，//AD BC ，12AD cm =，15BC cm =，点P 自点A 向D 以1/cm s 的速度运动，到D 点即停止．点Q 自点C 向B 以2/cm s 的速度运动，到B 点即停止，点P ，Q 同时出发，设运动时间为()t s ．（1）用含t 的代数式表示：AP = t ；DP = ；BQ = ． （2）当t 为何值时，四边形APQB 是平行四边形？【分析】（1）直接利用P ，Q 点的运动速度和运动方法进而表示出各部分的长； （2）利用平行四边形的判定方法得出t 的值． 【解答】解：（1）由题意可得：AP t =，CQ=2t ，故12DP t =-，152BQ t =-， 故答案为：t ，12t -，152t -； （2）//AD BC ，∴当AP BQ =时，四边形APQB 是平行四边形， 152t t ∴=-， 解得：5t =．13．如图，菱形ABCD 对角线交于点O ，//BE AC ，//AE BD ，EO 与AB 交于点F ． （1）试判断四边形AEBO 的形状，并说明你的理由； （2）求证：EO DC =． 【分析】（1）由菱形的性质可证明90BOA ∠=︒，然后证明四边形AEBO 为平行四边形，从而可证明四边形AEBO 是矩形；（2）依据矩形的性质可得到EO BA =，然后依据菱形的性质可得到AB CD =． 【解答】解：（1）四边形AEBO 是矩形． 证明：//BE AC ，//AE BD ∴四边形AEBO 是平行四边形． 又菱形ABCD 对角线交于点O AC BD ∴⊥，即90AOB ∠=︒． ∴四边形AEBO 是矩形．（2）四边形AEBO 是矩形 EO AB ∴=，∵在菱形ABCD 中，AB DC =． EO DC ∴=．14．如图，四边形ABCD 为正方形，点G 是BC 上的任意一点，分别过点B ，D 作BF AG ⊥于点F ，DE AG ⊥于点E 于点E ，猜想DE ，EF ，BF 三条线段存在怎样的数最关系，并证明你的结论． 【分析】通过证明ABF ADE ∆≅∆得到BF AE =，AF DE =，从而得到DE EF BF =+． 【解答】解：DE EF BF =+．理由如下：四边形ABCD 为正方形， AB AD ∴=，90ABG DAB ∠=∠=︒， BF AG ⊥，DE AG ⊥， 90AED BFA ∴∠=∠=︒，90DAE BAF ∠+∠=︒，90ABF BAF ∠+∠=︒， DAE ABF ∴∠=∠，在ABF ∆和ADE ∆中，AFB DEA ABF DAE AB DA ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ABF ADE AAS ∴∆≅∆，BF AE ∴=，AF DE =， 又∵AF AE EF =+， DE BF EF ∴=+．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
特殊平行四边形专题练习
一、基础知识点复习：
（一）矩形：
1、矩形的定义：__________________________的平行四边形叫矩形．
2、矩形的性质：①．矩形的四个角都是______；矩形的对角线_________________________ ②.矩形既是对称图形,又是图形,它有条对称轴.
3、矩形的判定：①．有_____个是直角的四边形是矩形．②．对角线____________________________的平行四边形是矩形．③．对角线________________________________的四边形是矩形．
4、练习：①矩形ABCD的两条对角线相交于O，∠AOD=120°，AB=4cm，
则矩形对角线AC长为______cm．
②．四边形ABCD的对角线AC，BD相交于点O，能判断它为矩形的题设是（） A．AO=CO，BO=DO B．AO=BO=CO=DO C．AB=BC，AO=CO D．AO=CO，BO=DO，AC⊥BD ③．四边形ABCD中，AD//BC，则四边形ABCD是 ___________，又对角线AC，BD交于点O，若∠DAB=∠ABC，则四边形ABCD是_______________．（二）菱形：
1、菱形的定义：有一组_____________________相等的平行四边形叫菱形．
2、菱形的性质：①．菱形的四条边______；菱形的对角线_____________，且每条对角线______________．②.菱形既是对称图形,又是图形,它有条对称轴.
3、菱形的判定：①．_____边都相等的四边形菱形．②．对角线______的平行四边形是菱形．③．对角线___________ 的四边形是菱形．
4、菱形的面积与两对角线的关系是________________________
5、练习：①．如图，BD是菱形ABCD的一条对角线，若∠ABD=65°，则∠A=_____．②．一个菱形的两条对角线分别是6cm，8cm，则这个菱形的周长等于cm,面积= cm2③．若菱形的周长为8cm,高为1cm,则菱形两邻角的度数比为
(三)正方形:
1、正方形的定义：的平行四边形叫正方形。
2、正方形的性质：①．正方形的四个角是_____角，四条边_____，对角线_______________________．②．正方形是______对称图形，又是对称图形,它有______条对称轴．
3．正方形的判定：先判定这个四边形是矩形，•再判定这个矩形还是_____形；或者先判定四边形是菱形，再判定这个菱形也是_____形．
4．练习：①正方形的面积为4，则它的边长为____，对角线长为_____．
②已知正方形的对角线长是4，则它的边长是，面积是。
③如图所示，在△ABC中，AB=AC，点D，E，F分别是边AB，BC，AC的中
点，连接DE，EF，要使四边形ADEF是正方形，还需增加条件：_______．
一、选择题
1、在下列命题中，正确的是（ ） A ．一组对边平行的四边形是平行四边形 B ．有一个角是直角的四边形是矩形C ．有一组邻边相等的平行四边形是菱形 D ．对角线互相垂直平分的四边形是正方形
2、如图，在矩形ABCD 中，对角线AC 、BD 相交于点O ，若OA ＝2，则BD 的长为（ ）
A ．4
B ．3
C ．2
D ．1
3、如图，在菱形ABCD 中，
对角线AC BD ，相交于点O E ，为AB 的中点，且OE a ，则菱形ABCD 的周长为（ ） A ．16a B ．12a C ．8a D ．4a 4、顺次连接菱形各边中点所得的四边形一定是（ ） A .等腰梯形 B .正方形 C .平行四边形 D .矩形
5、如图，已知菱形ABCD 的对角线AC 、BD 的长分别为6cm 、8cm ，AE ⊥BC 于点E ，则AE 的长是（ ） A ．53cm B ．25cm C ．
48
5
cm D ．
245
6、如图，将一个长为10cm ，宽为8cm 的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到的菱形的面积为（ ） A ．10 B ．20 C ．40 D ．80 二、填空题
7、如图所示，菱形ABCD 中，对角线AC BD ，相交于点O ，若再补充
一个条件能使菱形ABCD 成为正方形，则这个条件是 （只填一个条件即可）．
8、如图，已知P 是正方形ABCD 对角线BD 上一点，且BP = BC ，则∠ACP 度数是 ．
9、如图，在矩形ABCD 中，AB=2，BC=4，对角线AC 的垂直平分线分别交AD 、AC 于点E 、O ，连接CE ，则CE 的长为
10、如图，正方形ABCD 中，AB=4，E 是BC 的中点，点P 是对角线AC 上一动点，则PE+PB 的最小值为 。
11．已知菱形两条对角线的长分别为5cm 和8cm ，则这个菱形的面积是______cm ．12、菱形ABCD 的周长为36，其相邻两内角的度数比为1:5，则 此菱形的面积为_________。
13、对角线长为22的正方形的周长为
___________，面积为__________。
三、解答题
13（12分）已知：如图 ，AD 是 ∠BAC 的角平分线，
DE ∥AC ，DF ∥AB 。
求证：四边形AEDF 是菱形。
14、如图，在△ABC 中，AB=AC ，D 为BC 中点，四边形ABDE 是平行四边形．求证：四边形ADCE 是矩形．
15、（9分）E 是正方形ABCD 的对角线BD 上一点，EF ⊥BC ，EG ⊥CD ，•垂足分别是F 、G ，求证：AE=FG ．
A P G
F
E
D
C
B
16、如图，点E 、F 在正方形ABCD 的边BC 、CD 上，AE 、BF 相交于点G ，BE=CF
猜想AE 与BF 的关系并证明。
17、如图，四边形ABCD 是菱形 ，∠ACD=30°,BD=6,求: （1）∠BAD,∠ABC 的度数； （2）边AB 及对角线AC 的长。
18、在Rt △ABC 中，∠ACB=90°CD ⊥AB 于点D ，∠BCD=3∠ACD ，点E 是斜边AB 的中点，求∠ECD 的度数。
19、如图，E 、F 、M 、N 分别是正方形ABCD 四条边上的点，且AE=BF=CM=DN ，
求证，四边形EFMN 是正方形 。
A
B
C
D
E
G F A
B
C
D
E。