数阵图形
第4讲 数阵图
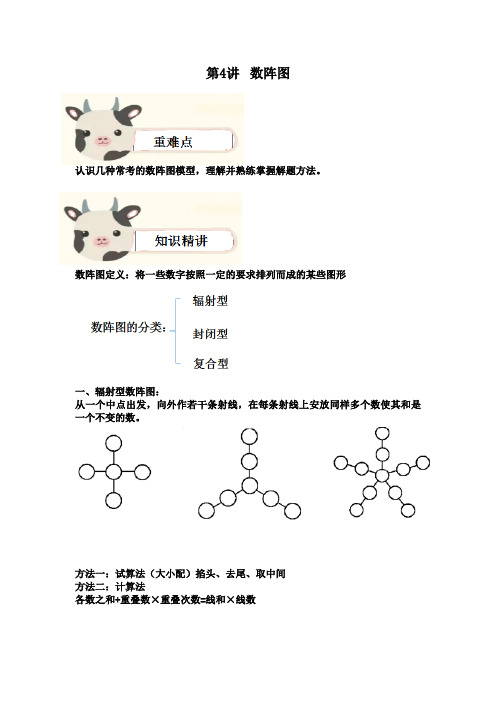
第4讲数阵图认识几种常考的数阵图模型,理解并熟练掌握解题方法。
数阵图定义:将一些数字按照一定的要求排列而成的某些图形一、辐射型数阵图:从一个中点出发,向外作若干条射线,在每条射线上安放同样多个数使其和是一个不变的数。
方法一:试算法(大小配)掐头、去尾、取中间方法二:计算法各数之和+重叠数×重叠次数=线和×线数二、封闭的数阵图:计算法各数之和+重叠数×重叠次数=线和×线数三、复合型数阵图即是辐射型数阵图,又是封闭型数阵图。
将1-7这7个数字分别填入图中各个○内,使每条线段上的三个○内的数之和等于14将1-11填入下图的各个圆圈内,使每条线段上的三个圆圈内的数之和相等。
1、将1-5分别填入圆圈内,使每条线上3个圆圈的数字之和都等于92.将1-9分别填入圆圈内,是每条线上的三个数之和相等将1-6六个数字分别填入下图6个圆圈内,使每条边上的和都等于11.把1-12这十二个数,分别填在如右图中正方形四条边上的十二个圆圈内,使每条边上四个圆圈内数的和都等于22,试求出一个基本解。
1.把1-9个数分别填入○中,使每条边上四个数的和相等于17.2.把1-8个数分别填入○中,使每条边上三个数的和相等12.(1)将1-7七个数字填入下图的七个圆圈内,使每个大圆圈和每条直线上的三个数字之和相等。
(2)将1-6这6个数字分别填入下图的6个圆圈内,使得三条线段上的数字之和都相等。
下图中,是有三个正三角形,将1-9分别填入9个圆圈内,使得三个正三角形三个顶点之和都相等,通过四个圆的每条线段之和也相等1.将1-5这五个数分别填入如果中的圆圈内,使每条线段上三个圆圈内的和相等。
2.将1-10这十个数分别填入下图中的十个○内,使每条线段上四个○内数的和相等,3.将1-9这九个数分别填入图中○内,使每条线段三个数相等.。
第29讲数阵图

第29讲、数阵图----初级版数阵是比较常见的填数问题,是一种老少都为之着迷的数学游戏。
无论数阵怎么变化,也都有规律可循,解题的关键就是求出重叠数。
只要你细心观察、分析,相信你一定能够解决更复杂的数阵问题。
一、数阵图的分类:1、数阵图分辐射型数阵图2、封闭型数阵图3、复合型数阵图。
二、解题方法1、去头、去尾、去中间。
2、求已知数总和,3、求数阵图中的总和,也就是图和-数和=“公用数”的总和。
1、1、将1、2、3、4、5填入下图的方格中,使横行、竖列的和都是10。
2、将1、3、5、7、9、11填入下图的圈内,使得对两个正方形,各自顶点上的数的和都等于22。
知识导引金典例题3、将1~7这七个数填入下图的圈内,使每一个正方形的四个数的和相等。
4、将1~9这九个数填在下图的圈中,使得横行的5个数,和是24.竖列的5个数,和也是24。
5、将1~8填入图中的圈内,使每条线上3个数的和都是12。
6、将3—9这七个数分别填入右图中的○里(其中9已填好),使每条直线上的三个数之和都相等。
9基础入门1、将1到9这九个数填入下图,使得从中心出发的每条线段上的三个数的和相等。
2、将1—7这7个自然数填入下图的7个○内,使得每条边上的3个数之和都等于10。
4623、将1—6这6个自然数分别填入右图的6个○内,使每条边上的3个数之和都等于10。
4、将2—9这8个数分别填入下图的○里,使每条边上的3个数之和等于18。
5、 右图中三个圆圈两两相交形成七个部分,分别填上自然数1~7,在一些部分中,自然数2、4、6三个数已经填好,请填上其余各数,使每个圆圈中四个数的和都是14.6、请将1、2、3、4、5、6、7、8、9九个数分别填入下图的九个小圆圈里,使每个三角形上三个数的和都等于15。
10658714102030每列、每条对角线上各数和都等于27。
2、在有图中的空格内填入适当的数,使每行、每列、每条对角线上各数的和都等于33。
3、在空格中填入不同的数,使每一横行、竖行、斜行三个数的和等于75。
数阵图

数阵图
一、数阵图定义及分类:
定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.
数阵:是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.
二、解题方法:
解决数阵类问题可以采取从局部到整体再到局部的方法入手:
第一步:区分数阵图中的普通点(或方格)和关键点(或方格);
第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;
第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.
简单数阵图
一、辐射型数阵图
从一个中心出发,向外作若干条射线,在每条射线上安放同样多个数,使其和是一个不变的数。
突破关键:确定中心数,多算的次数,公共的和
数和+中心数×重复次数=公共的和×线数
数和:指所有要填的数字加起来的和
中心数:指中间那数字,即重复计算那数字
重复次数:中心数多算的次数,一般比线数少1
公共的和:指每条直线上几个数的和
线数:指算公共和的线条数
二、封闭型数阵图
多边形的每条边放同样多的数,使它们的和都等于一个不变的数。
突破关键:确定顶点上的数字,公共的和
数和+重叠数的和=公共的和×边数
数和、公共的和跟辐射型数阵图一样的意思
重叠数的和:指数阵图顶角重复算的数全加起来的和
边数:指封闭图形的边数。
第五讲有趣的数阵图

例2 把1~7填入下图中,使每条线段上三个 内的数的和相等.
分析: 中心圆填入的数是公共数,它参与3条线的连加, 这意味着每一条线的另外两数相加的和相等即可,将1-7 这7个自然数分组组合便可得到如下的结果: (1)1、(2,7)、(3,6)、(4,5)由此可得中心 圆是1。 (2)4、(1,7)、(2,6)、(3,5)由此可得中心 圆是4。 (3)7、(1,6)、(2,5)、(3,4)由此可得中心 圆是7。
分析:每个面上4个数之和为18, 把这几个数前后配对(1,8)、 (2,7)、(3,6)、(4,5)。
小数学家们,接下来是你们大 展身手的时候咯!加油!
ห้องสมุดไป่ตู้
小朋友们,周六晚上见 ~~
例(3)在下图各圆空余部分填上1、2、4、 6,使每个圆中4个数的和都是15。
3 7
5
分析:由于每个圆中4个数的和为15, 求出上圆的和为15-3-5=7,易知1+6=7; 左圆另外两个圆的和为15-3-7=5,易知1+4=5; 右圆另外两个圆的和为15-5-7=3,易知1+2=3。 则中间数一定为1。
有趣的数阵图
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形,通常叫做数阵图。 数阵图的种类繁多,绚丽多彩,这里只 向大家介绍三种数阵图: 封闭型数阵图 辐射型数阵图 复合型数阵图
例1 将1~6分别填在图中,使每条边上的三个 内的数的和都等于9.
分析: 因为 1+2+3+4+5+6 = 21 ,而 每条边上的三个数的和为9,则三条边上的和 为 9×3 = 27 , 27-21 = 6 , 这个 6 就是由于 三个顶点都被重复算了一次。所以三个顶点的 和为 6 ,在 1-----6中,只能选1、2、3 填入三 个顶点中,再将4、5、6填入另外的三个圈即可。
9.数阵图

第八讲有趣的数阵图把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,常见的有三种数阵图:封闭型数阵图—数阵中只有一个重叠数辐射型数阵图—数阵中至少有两个重叠数复合型数阵图—数阵中同时含有辐射型和封闭型两种数阵;解决数阵图的问题,基本思路如下:确定公共部分可能填的数确定每条边上可能的和总观全局调试出正确的结果【例1】将1~6六个自然数字分别填入下左图的圆圈内,使三角形每边上的三数之和都等于9。
【练习1】把4—9填入上右图中,使每条直线上三个数的和相等,都是18。
【例2】将1—6这六个数字填入下左图的的六个小圆圈中,使得大圆圈上相邻的两个小圆圈中的数之和都是质数。
【练习2】如上右图,将2—7分别填入圈内,使图中相邻两数之和都是质数。
【例3】请你把1~7这七个自然数,分别填在下图(1)的圆圈内,使每条直线上的三个数的和都相等.应怎样填?【练习3】把1—8填入下图中,使每条直线上三个圆圈内的数的和相等。
【例4】将1~8这八个自然数分别填入下左图中的八个○内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?【练习4】将1—8个数分别填入图中,使每个圆圈上五个数的和为21。
1.在右上图的空白的区域内分别填上1、2、4、6四个数,使每个圆中的四个数的和都是15.2.将0.01、0.02、…、0.09这九个数分别填入右图九个圆圈内,使每条边上的四个圆圈内的数之和都等于0.23.将2~9这八个自然数分别填入上右图中的八个○内,使四边形每条边上的三个数之和都等于15。
4.把3—10填入下图中,使每条直线上三个圆圈内的数的和相等。
数阵图(二)(含详细解析)

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.复合型数阵图【例 1】 由数字1、2、3组成的不同的两位数共有9个,老师将这9个数写在一个九宫格上,让同学选数,每个同学可以从中选5个数来求和.小刚选的5个数的和是120,小明选的5个数的和是111.如果两人选的数中只有一个是相同的,那么这个数是_____________.313233212223131211【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】迎春杯,中年级,决赛,3题【分析】 这9个数的和:111213212223313233++++++++10203031233198=++⨯+++⨯=()()例题精讲知识点拨教学目标5-1-3-2.数阵图由小刚和小明选的数中只有一个是相同的,可知他们正好把这9个数全部都取到了,且有一个数取了两遍.所以他们取的数的总和比这9个数的和多出来的部分就是所求的数.那么,这个数是12011119833+-=.【答案】33【例 2】 如图1,圆圈内分别填有1,2,……,7这7个数。
如果6个三角形的顶点处圆圈内的数字的和是64,那么,中间圆圈内填入的数是 。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】希望杯,五年级,复赛,第5题,5分【解析】 2 【答案】2【例 3】 如下图(1)所示,在每个小圆圈内填上一个数,使得每一条直线上的三个数的和都等于大圆圈上三个数的和.(1)17894【考点】复合型数阵图 【难度】3星 【题型】填空 【解析】 为叙述方便,先在每个圆圈内标上字母,如图(2),(2)a cb49817则有a+4+9=a+b+c (1)b+8+9=a+b+c (2)c+17+9=a+b+c (3)(1)+(2)+(3):(a+b+c )+56=3(a+b+c ),a+b+c=28,则 a=28-(4+9)=15,b=28-(8+9)=11,c=28-(17+9)=2解:见图.1789411215【答案】17 89411215【例 4】请你将数字1、2、3、4、5、6、7填在下面图(1)所示的圆圈内,使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填?【考点】复合型数阵图【难度】3星【题型】填空【解析】为了叙述方便,将各圆圈内先填上字母,如图(2)所示.设A+B+C=A+F+G=A+D+E=B+D+F=C+E+G=k (A+B+C)+(A+F+G)+(A+D+E)+(B+D+F)+(C+E+G)=5k,3A+2B+2C+2D+2E+2F+2G=5k,2(A+B+C+D+E+F+G)+A=5k,2(1+2+3+4+5+6+7)+A=5k,56+A=5k.,因为56+A为5的倍数,得A=4,进而推出k=12,因为在1、2、3、5、6、7中,1+5+6=7+3+2=12,不妨设B=1,F=5,D=6,则C=12-(4+1)=7,G=12-(4+5)=3,E=12-(4+6)=2.,解:得到一个基本解为:(见图)7654321【答案】7654321【例 5】在左下图的每个圆圈中填上一个数,各数互不相等,每个圆圈有3个相邻(即有线段相连的圆圈)的圆圈。
(完整)小学三年级奥数--数阵图

数阵图(一)在神奇的数学王国中,有一类非常有趣的数学问题,它变化多端,引人入胜,奇妙无穷。
它就是数阵,一座真正的数字迷宫,它对喜欢探究数字规律的人有着极大的吸引力,以至有些人留连其中,用毕生的精力来研究它的变化,就连大数学家欧拉对它都有着浓厚的兴趣。
那么,到底什么是数阵呢?我们先观察下面两个图:左上图中有3个大圆,每个圆周上都有四个数字,有意思的是,每个圆周上的四个数字之和都等于13。
右上图就更有意思了,1~9九个数字被排成三行三列,每行的三个数字之和与每列的三个数字之和,以及每条对角线上的三个数字之和都等于15,不信你就算算。
上面两个图就是数阵图。
准确地说,数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵。
要排出这样巧妙的数阵图,可不是一件容易的事情。
我们还是先从几个简单的例子开始。
例1把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了,七拼八凑就写出了右上图的答案,可是却搞不清其中的道理。
下面我们就一起来分析其中的道理,只有弄懂其中的道理,才可能解出复杂巧妙的数阵问题。
分析与解:中间方格中的数很特殊,横行的三个数有它,竖列的三个数也有它,我们把它叫做“重叠数”。
也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次,即重叠了一次,其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9,所以(1+2+3+4+5)+重叠数=9+9,重叠数=(9+9)-(1+2+3+4+5)=3。
重叠数求出来了,其余各数就好填了(见右上图)。
试一试:练习与思考第1题。
例2把1~5这五个数填入下页左上图中的○里(已填入5),使两条直线上的三个数之和相等。
分析与解:与例1不同之处是已知“重叠数”为5,而不知道两条直线上的三个数之和都等于什么数。
所以,必须先求出这个“和”。
根据例1的分析知,两条直线上的三个数相加,只有重叠数被加了两遍,其余各数均被加了一遍,所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5]÷2=10。
(完整版)小学三年级奥数--数阵图

数阵图(一)在神奇的数学王国中,有一类非常有趣的数学问题,它变化多端,引人入胜,奇妙无穷。
它就是数阵,一座真正的数字迷宫,它对喜欢探究数字规律的人有着极大的吸引力,以至有些人留连其中,用毕生的精力来研究它的变化,就连大数学家欧拉对它都有着浓厚的兴趣。
那么,到底什么是数阵呢?我们先观察下面两个图:左上图中有3个大圆,每个圆周上都有四个数字,有意思的是,每个圆周上的四个数字之和都等于13。
右上图就更有意思了,1~9 九个数字被排成三行三列,每行的三个数字之和与每列的三个数字之和,以及每条对角线上的三个数字之和都等于15,不信你就算算。
上面两个图就是数阵图。
准确地说,数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵。
要排出这样巧妙的数阵图,可不是一件容易的事情。
我们还是先从几个简单的例子开始。
例1 把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了,七拼八凑就写出了右上图的答案,可是却搞不清其中的道理。
下面我们就一起来分析其中的道理,只有弄懂其中的道理,才可能解出复杂巧妙的数阵问题。
分析与解:中间方格中的数很特殊,横行的三个数有它,竖列的三个数也有它,我们把它叫做“重叠数”。
也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次,即重叠了一次,其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9,所以(1+2+3+4+5)+重叠数=9+9,重叠数=(9+9)-(1+2+3+4+5)=3 。
重叠数求出来了,其余各数就好填了(见右上图)。
试一试:练习与思考第1 题。
例2 把1~5 这五个数填入下页左上图中的○里(已填入5),使两条直线上的三个数之和相等。
分析与解:与例1 不同之处是已知“重叠数”为5,而不知道两条直线上的三个数之和都等于什么数。
所以,必须先求出这个“和”。
根据例1 的分析知,两条直线上的三个数相加,只有重叠数被加了两遍,其余各数均被加了一遍,所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5] ÷2=10。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数阵图形
1、教会学生找到解决问题的“钥匙”。
2、教会学生如何研读、观察,寻求切入点。
3、教会学生解题要有明确的目的和步骤。
4、培养学生的逻辑思维能力和推理能力。
5、培养学生的联想、试探归纳等思维能力。
勇闯数学迷宫
蓝天教育的数学迷宫里有这样一个迷宫图:如右图,将1—7分 别填入右图中的○内,使每条线段上三个○内数的和相等。
只有这样 才能进入下一关。
在座的各位同学能否闯过此关,就要发挥你们的聪 明才智啦!我们开始吧……
将1—7这七个数分别填进下图的○里,使每条线上3个○内的数之和都为12。
观察上面的图
形,你能发现
这个数阵图有
哪些特征?
中间的数是三条直线公有的,三条直线上的和相等。
将三条直线上
的和再加恰来
一定是3的倍
数。
中间的数出现了3次,是不是应该先确定它的值呢?
1. 将1—9填入下图(如图1)的○中,使横、竖行五个数相加的和都相
等。
图1 图2
2、将1—11这十一个数分别填进上图(如图2)的○里,使每条线上3个○内的数的和相等。
将1—6这六个数分别填入图中的○内,使每条边上三个○内数的和都等于9。
中心○中的数多用了两次,可以用每条线上的数之和×3-7个数的和,所得的差不就是中心
我知道,我们应该先确定关键位置上的数——中心○。
但怎么求出中心○上的数
想得真好!本题属于辐射型数阵图,填辐射型数阵图的关键在于确定中心数,然后把其余的数进行配对,采用试验配对法就能确定其它各位置上的数。
如果只告诉每条线上3○内的数之和相等,应该怎样填数呢?
对!我们就从这里着手,假设三
角形的三个顶点上的数为:a、
b、c,这样我们就可以求出a、
b、c三个数的和。
每条边上三个数的和都
为9,而三角形三个顶点
上3个数不是重复算了
一遍吗?
你们想得真棒!封闭型数阵,
先要确定各边顶点所应填的
数,一般来说,数阵图中各边
数之和-所填入数的和=重复
多加的各顶点之和,这样再来
填图就不会太困难了。
1、将1-9这九个数分别填入下面数阵(图1)的9个○内,使三角形每条边上4个○内数的和相等。
(图1)(图2)
2、在图2中填入1—9,使每边4个数的和等于17。
(想一想,有没有其他填法?)
把1-8这八个数字,分别填入下图的圆圈内,使每一个圆上五个数的和都等于21。
1、将3—10填入下图中的圆圈内,使每个大圆圈上的5个数的和为31。
2、把1—10的10个数填入下图中的10个○内,使每个正方形4个顶点上各数的和都是24。
将5—14这十个自然数填入下图中的○中,使每个大圆上六个数的和都相等且最小。
封闭型数阵图,关键是先确定数阵中两个重复数之和。
如果在没有告诉每个大圆圈中的数之和的情况下,可以进行分别讨论,得出重复数的不同的和及与它对应的大圆圈中数的和。
这样数阵图还可以产生许多不同的填法。
我们就从这里着手,要确定这两个数,就要先确定这两个数的和。
然后就可以找到符合条件的两
这是一道封闭型数阵图,要先确定中心○位置上的数。
题目已经告诉了每个大圆中5个数的和,那么我们怎么确定中心
如果要使每个圆圈的
和都相等且最小,只
需要中间a与b的和
最小,就可以求出结
果了。
没有告诉大圆中数之和哦,我们假设重复数为a、b,
那么每个圆圈中六个数的和为(5+6+7+…+14+a
+b)÷2=(95+a+b)÷2,那么a与b的和可能是
11、13、15、…、27共9种。
本题如果要使每个大圆
的和相等且最大,应怎
么填呢?
1、把1—8填入下图○内,使每边上三个数的和最大,求最大和是多少?如果和最小,最小是多少?
和最大:_________ 和最小:_________
2、把1—10这十个数填入下图中,使每个正方形顶点圆圈内四个数之和都相等,而且最大。
这个和是多少?
在下图各圆空余部分分别填上3、5、7、8,使每个圆内的4个数之和都是21。
10
86
这题的关键是找出中间部分填什么,因为已填的3个数都是偶数,恰好每个
圆内有两个偶数,它们的和也是偶数,再填入两个数后,使每个圆的4个数的和是21,21是奇数,也就是每个圆内要填入的两个数之和应为奇数,而3、5、7、8中3、5、7都是单数,要使和为单数,则_____这个数一定要填入中间部分。
1、在图中各圆空余部分分别填上4、5、7、9,使每个圆中4个数的和是
27。
2、在图中各圆空余部分分别填上6、8、10、11,使每个圆中4个数的和是33。
1—10这十个自然数分别填入图中的十个○内,使各条线段上四个○内数的和相等,
每个三角形三个顶点上○内数的和也相等。
2
6
4
9
7
5
这幅数阵图与前面的例题相比,数阵比较复杂。
这是一幅复合型的数阵图,题目第一个要求:“使各条线段上四个○内数的和相等”,这是在辐射型数阵中填数。
第二个要求:“使每个三角形三个顶点上○内数的和相等”,这是在封闭型数阵图中填数。
在辐射型数阵图中填数,先确定中心数,假设中心数为a,则1+2+3+…+9+10+2a=55+2a 55+2a应能被3整除,则a可取1、4、7、10。
如果取a=1时,每条线段上另外三个数的和为:(55-1)÷3=18 这样其余9个数可分成三组:(3、7、8)、(2、6、10)、(4、5、9),这样就容易填图(如右图)。
在辐射型部分填好后再考虑封闭型部分的填法。
当a取4、7、10时,在复
合数阵图中还会有不同种填
法,我们可以试一试、填一
填。
1、把1—9,填入下图中,使每条线段三个数和及四个顶点的和也相等.
2、把1—16填入下图中,使每条边上4个数的和相等,两个八边形上8个数的和也相等.
1、辐射型方法:关键是找出中心数
数阵图 2、封闭型方法:关键是找出重复计算的顶点上的数,从“和相等”入手
3、复合型方法:辐射型部分填好后再考虑封闭型部分的填法
1、将1—7七个数分别填入下图中的七个圆圈里,使每条直线上三个圆圈内各数之和相等。
2、把1—10各数填入“六一”的10个空格里,使在同一直线上的各数的和都是12。
3、把1—8填入下图○中,使每边上三个数的和都等于13。
4、将1、2、3、4、
5、
6、
7、8这几个数字分别填入方格里,使每个五边形的数字和都等于21。
