第十二讲巧填数阵图教师
一年级下册数学试题-奥数思维讲练:第十二讲 巧填数阵图 (含答案)全国通用
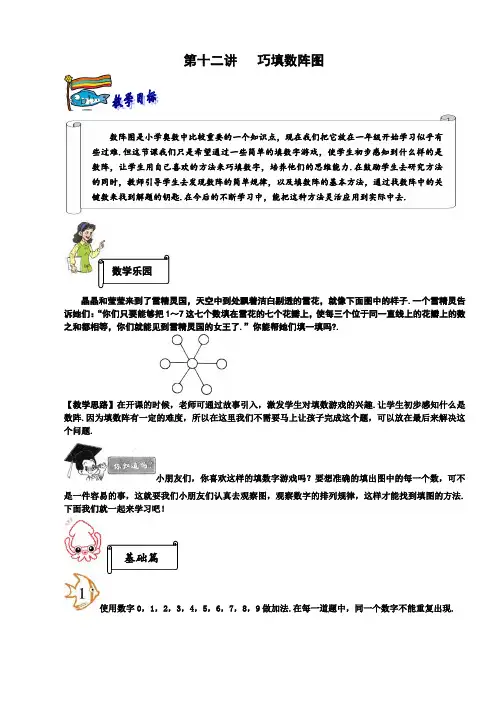
第十二讲巧填数阵图数学乐园晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子.一个雪精灵告诉她们:“你们只要能够把1~7这七个数填在雪花的七个花瓣上,使每三个位于同一直线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.【教学思路】在开课的时候,老师可通过故事引入,激发学生对填数游戏的兴趣.让学生初步感知什么是数阵.因为填数阵有一定的难度,所以在这里我们不需要马上让孩子完成这个题,可以放在最后来解决这个问题.小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数,可不是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法.下面我们就一起来学习吧!基础篇使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现.数阵图是小学奥数中比较重要的一个知识点,现在我们把它放在一年级开始学习似乎有些过难.但这节课我们只是希望通过一些简单的填数字游戏,使学生初步感知到什么样的是数阵,让学生用自己喜欢的方法来巧填数字,培养他们的思维能力.在鼓励学生去研究方法的同时,教师引导学生去发现数阵的简单规律,以及填数阵的基本方法,通过找数阵中的关键数来找到解题的钥匙.在今后的不断学习中,能把这种方法灵活应用到实际中去.【教学思路】一般在解答这类填数问题时,把同一条边上出现两个数字的空格先填.之前我们已经有过这样的练习,学生有了一定的基础.这道题的答案不止一个,我们只要求学生能找到其中的一种就达到要求了.(1)右边两个圆的和应该是9,所以里可填(0,9)(2,7)(3,6).(2)告诉我们中间的数字是2,剩下两边上两个数字的和应该是9-2=7.0+7=1+6=3+4,所以剩下两边上两个数可以填(0,7),(1,6),(3,4)(3)7+6=13,15-13=2,所以第2条线中间填2.左边第一条线:15-7=8,0+8=3+5,数字不重复共两种填法.第三条线15-6=9,0+9=4+5,数字不重复共两种填法(4)6+4=10,13-10=3,所以第2条线最下是3,.左边第一条线:13-6=7,0+7=2+5,数字不重复共两种解法.第三条线:13-3=10,1+9=2+8,数字不重复共两种解法.拓展练习(1)填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.【答案】【答案】在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.【教学思路】方法一:填数时,首先要看哪一行已经有了两个数,然后用18减去这两个数,就得出这一行的第三个数.填数的顺序如下:方法二:从斜行来考虑:要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?【教学思路】首先我们要找到填这个表格的突破口,一般情况下我们先找每行、每列以及每条对角线上已知两个数的来先填.找到这个突破口,后面就容易多了.方法一:从竖行入手.方法二:分别从两条对角线入手.拓展练习在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.【答案】【答案】把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.【教学思路】比较三个已知数1,2,3,和1比2大1,3大2.还剩下三个数4,5,6要我们来填,5+6=11 6+4=10 5+4=9 ,要使每边和相等,5+6+1=6+4+2=5+4+3=12,答案如下:提高篇把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.【教学思路】方法一:观察法.要使横行、竖行的三个数相加都得15,我们就要考虑中间填什么数.观察这五个数3,4,5,6,7,我们发现4和6,3和7可以组成10,它们分别再加上多出来的5都得15,所以中间这个数应该填5,上下,左右可以分别填4和6,3和7,如图:方法二:观察这些图,容易发现,中间方框中的数比较特殊,它既在横行上,又在竖列中,在数阵中这样的数称为“重叠数”.只要我们确定了中间的“重叠数”填几,别的空格就简单了.那么横行3个数的和加上竖列3个数之和就等于所要填入的5个数的和与重叠数的和.于是(3+4+5+6+7)+重叠数=15+15,重叠数=30-25=5,所以中间的这个数应该填5,在剩下的4个数3,4,6,7中,只有3+7=4+6=10,填法如图.建议:在这两种方法中,学生习惯用第一种方法来观察出答案,但是这种方法对于以后数字大的题就很难把握,因此老师在学生掌握了第一种方法的前提下,要介绍第二种解答数阵图的一般方法,不要求学生马上掌握,但是要让学生明确解答这样的题要从重叠数开始入手分析,以后练得多了就能融会贯通了.如果老师觉得这几个数太大学生不容易接受,还可以改成更小的数.拓展练习把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.【答案分析】中间○即为特殊的重叠数,因为它既是横线上的数,又是竖线上的数.中间的数填什么呢?横行加上竖行之和应为 12+12=24,而2+3+4+5+6=20,中间的要多加一次,所以应为4.把1,2,3,4,5,7分别填入○里,使每一个大椭圆上的四个数之和等于13.【教学思路】方法一:观察法,在这6个数中,有两个数是公共的,那么剩下的四个数两两相加应该相等,观察1,2,3,4,5,7中1是公共数,这时我们发现2+7和4+5都等于9,因此剩下的3也应该是公共数,2和7,4和5应该分别填在这两个圆的左边和右边.经检验每个大椭圆上的四个数这和等于13.方法二:每个椭圆里的四个数之和等于13,那么两个椭圆里的四个数之和就是13+13=26,另外这6个数相加的和是1+2+3+4+5+7=22,26和22之间相差的是什么呢?只有中间的这两个重叠数被多加了1次,这相差的4应该是两个重叠数的和,1+3=4,所以中间的这两个重叠数应该是1和3.剩下的数2+7=4+5=9.把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.【教学思路】方法一:观察法,在1,2,3,4,5,6,7这七个数中,除去中间的重叠数,剩下的六个数两两相加应该相等,经验算,当重叠数是4时,1+7=2+6=3+5=8,8+4=12,如图:方法二:因为图中共有3条直线,所以中心的重叠数重叠了2次,于是(1+2+3+4+5+6+7)+重叠数×2=12+12+12.重叠数=(36-28)÷2=8.那么中间的数应该填14剩下的6个数1,2,3,5,6,7,中,2个数的和等于12-4=8的有1+7=2+6=3+5,如图:拓展练习把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.把2,3,4,5,6,7,8这七个数分别填入圆圈中,使两个正方形中四个数之和相等19.【教学思路】先考虑求两个正方形公共的中间数.2+3+4+5+6+7+8+重叠数=19+19.重叠数=3,那么中间圆圈里面应该填3.剩下的数中2+6+8=4+5+7=19-3=16,所以每个正方形中,剩下的三个数应该填:2,6,8或4,5,7.具体填法如下:拓展:如果使两个正方形中四个数之和相等21,又应该怎样填?我会做一做把1,2,3,4,5,6,7这7个数分别填入右图中,使得每条直线上的3个数的和相等.【教学思路】这道题的答案不唯一.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)在空格内填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.【答案】【教学思路】如果有充足的时间,建议这题可放在例3的后面做一个加深,这道题也主要是利用加减法之间的关系来解答的.这个题我们要从已知三个加数的第二列入手开始填,先计算出这三个加数的和,再用64减去这三个加数的和就得到了这第四个加数.用图中已有的三个数填满其余的空格,每个数字必须使用三次.使得每行、每列和两条对角线上的三个数之和相等.【答案】【答案】把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.【答案】【教学思路】这道题可参考放在例6的后面,做一个拓展.在例6的基础上,我们只需要调动四条边上各数的位置就可以验证出结果.使用数字0,1,2,3,4,5,6,7,8, 9求和.而且同一个数在一幅图中不能重复出现.【答案】【答案】把1~11这十一个数分别填入图中的圆圈里,使每条直线上的三个数的和都等于18.【答案】练习十二1.在下面的○里填上适当的数,使每条线上的三个数之和都是12.【答案】2.把3~8这6个数,填在下图中使得每行、每列和两条对角线上的三个数的和都为18.【答案】3. 把1,2,3,4,5这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.【答案】4.把3,4,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为20.【答案】5. 将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.【答案】6.把数字1,2,3,5,6,7,9填在下面的○里,使每边上的和为15.【答案】小朋友,你在少年宫里走过“勇敢者的道路”吗?道路崎岖,充满艰难险阻.但是,它能培养小朋友的勇敢精神和不怕困难的毅力.这里有两幅图,也叫“勇敢者的道路”.图中的道路狭窄、曲折,不易通过,需要小朋友细心和有耐心.现在请小朋友用一枝铅笔,按照图中箭头的方向画出通行路线,而且线条不能碰到两边的“围墙”.小朋友,这可真不容易哦!。
巧填数阵图
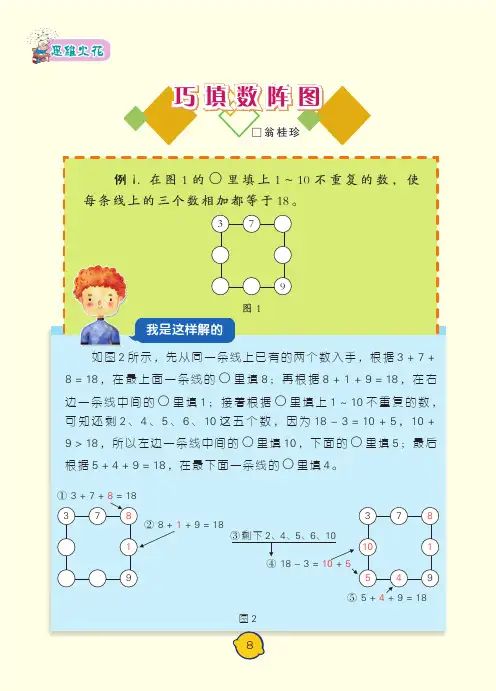
我是这样解的□翁桂珍巧填阵数图例1.在图1的○里填上1~10不重复的数,使每条线上的三个数相加都等于18。
图1379如图2所示,先从同一条线上已有的两个数入手,根据3+7+8=18,在最上面一条线的○里填8;再根据8+1+9=18,在右边一条线中间的○里填1;接着根据○里填上1~10不重复的数,可知还剩2、4、5、6、10这五个数,因为18-3=10+5,10+9>18,所以左边一条线中间的○里填10,下面的○里填5;最后根据5+4+9=18,在最下面一条线的○里填4。
91873①3+7+8=18②8+1+9=18918734510⑤5+4+9=18④18-3=10+5③剩下2、4、5、6、10图2我是这样解的例2.把1、2、3、4、5、6、7七个数分别填入图3的圆圈里,使每条线上三个数的和相等。
不难看出,我们只要填好公用的中心数,再将剩下的六个数分成和相等的三组,就能找到符合条件的填法。
如果公用的中心数填1,那么剩下的六个数通过大小搭配,可以得到:7+2=6+3=5+4=9(如图4),圆圈里每条线上三个数的和是9+1=10。
如果公用的中心数填4,那么剩下的六个数通过大小搭配,可以得到:7+1=6+2=5+3=8(如图5),圆圈里每条线上三个数的和是8+4=12。
如果公用的中心数填7,那么剩下的六个数通过大小搭配,可以得到:6+1=5+2=4+3=7(如图6),圆圈里每条线上三个数的和是7+7=14。
图4图5图6617342572145367143526【提示:公用的中心数除了填入的是1、4和7外,能不能填入其他数呢?如果公用的中心数填入的是2,因为剩下的1、3、4、5、6、7不能分成和相等的三组,所以公用的中心数不能填2。
同样,公用的中心数也不能填3、5和6。
因此,公用的中心数只能填最小的1、最中间的4和最大的7。
】(作者单位:江苏省兴化市垛田中心小学)图3。
《巧填算符数阵图》课件

数阵图填法需要遵循一定的 逻辑关系,如加减乘除等,
不能随意组合。
填法的技巧和方法
观察数阵图:找出规律和特点 利用数字的性质:如奇偶性、质数、合数等 利用数学公式:如加法、乘法、平方等 利用逻辑推理:如排除法、假设法等 利用数阵图的对称性:如中心对称、轴对称等 利用数阵图的周期性:如循环周期、重复周期等
除法算符优先级: 高于乘法和加法, 低于减法和乘法
除法算符应用: 在数学、物理、 化学等学科中广 泛应用
04
数阵图填法
填法的基本原则
数阵图填法需要根据给定的 数字和符号进行填充,不能 随意更改。
数阵图填法需要遵循一定的 规则和顺序,如从左到右、 从上到下等。
数阵图填法需要保证每个数 字和符号在图中的唯一性,
复杂数阵图实例
实例一:九宫数阵图 实例二:十六宫数阵图 实例三:二十四宫数阵图
实例四:三十六宫数阵图 实例五:四十九宫数阵图 实例六:六十四宫数阵图
数阵图填法的规律总结
数阵图由数字 和符号组成, 每个数字和符 号都有其特定 的含义和作用。
数阵图的填法 需要遵循一定 的规律和规则, 如数字的排列、 符号的使用等。
减法算符
含义:表示两个 数相减的运算
符号:“-”
运算规则:ab=a+(-b)
应用:在数学、 物理、化学等领 域广泛应用
乘法算符
乘法算符表示两个数相乘 乘法算符的符号是"*" 乘法算符的运算规则是:两个数相乘,结果等于这两个数的积 乘法算符的逆运算是除法算符
除法算符
除法算符表示: ÷
除法算符作用: 用于计算两个数 相除的结果
数阵图的分类
按照数字排列方式分类:横排、竖排、斜排、环形等 按照数字大小分类:从小到大、从大到小、随机等 按照数字类型分类:整数、小数、分数、负数等 按照数字位置分类:中心、边缘、角点等
二年级奥数学练习试卷思维培训资料 巧填数阵图 教师
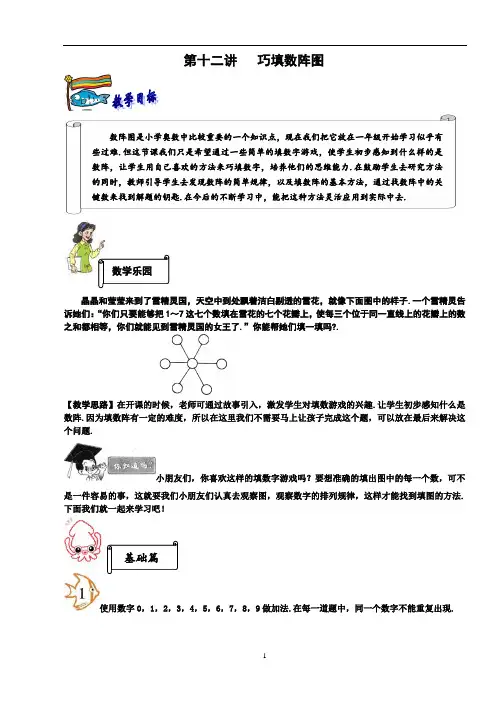
第十二讲巧填数阵图数学乐园晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子.一个雪精灵告诉她们:“你们只要能够把1~7这七个数填在雪花的七个花瓣上,使每三个位于同一直线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.【教学思路】在开课的时候,老师可通过故事引入,激发学生对填数游戏的兴趣.让学生初步感知什么是数阵.因为填数阵有一定的难度,所以在这里我们不需要马上让孩子完成这个题,可以放在最后来解决这个问题.小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数,可不是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法.下面我们就一起来学习吧!基础篇使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现.数阵图是小学奥数中比较重要的一个知识点,现在我们把它放在一年级开始学习似乎有些过难.但这节课我们只是希望通过一些简单的填数字游戏,使学生初步感知到什么样的是数阵,让学生用自己喜欢的方法来巧填数字,培养他们的思维能力.在鼓励学生去研究方法的同时,教师引导学生去发现数阵的简单规律,以及填数阵的基本方法,通过找数阵中的关键数来找到解题的钥匙.在今后的不断学习中,能把这种方法灵活应用到实际中去.【教学思路】一般在解答这类填数问题时,把同一条边上出现两个数字的空格先填.之前我们已经有过这样的练习,学生有了一定的基础.这道题的答案不止一个,我们只要求学生能找到其中的一种就达到要求了.(1)右边两个圆的和应该是9,所以里可填(0,9)(2,7)(3,6).(2)告诉我们中间的数字是2,剩下两边上两个数字的和应该是9-2=7.0+7=1+6=3+4,所以剩下两边上两个数可以填(0,7),(1,6),(3,4)(3)7+6=13,15-13=2,所以第2条线中间填2.左边第一条线:15-7=8,0+8=3+5,数字不重复共两种填法.第三条线15-6=9,0+9=4+5,数字不重复共两种填法(4)6+4=10,13-10=3,所以第2条线最下是3,.左边第一条线:13-6=7,0+7=2+5,数字不重复共两种解法.第三条线:13-3=10,1+9=2+8,数字不重复共两种解法.拓展练习(1)填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.【答案】【答案】在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.【教学思路】方法一:填数时,首先要看哪一行已经有了两个数,然后用18减去这两个数,就得出这一行的第三个数.填数的顺序如下:方法二:从斜行来考虑:要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?【教学思路】首先我们要找到填这个表格的突破口,一般情况下我们先找每行、每列以及每条对角线上已知两个数的来先填.找到这个突破口,后面就容易多了.方法一:从竖行入手.方法二:分别从两条对角线入手.拓展练习在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.【答案】【答案】把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.【教学思路】比较三个已知数1,2,3,和1比2大1,3大2.还剩下三个数4,5,6要我们来填,5+6=11 6+4=10 5+4=9 ,要使每边和相等,5+6+1=6+4+2=5+4+3=12,答案如下:提高篇把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.【教学思路】方法一:观察法.要使横行、竖行的三个数相加都得15,我们就要考虑中间填什么数.观察这五个数3,4,5,6,7,我们发现4和6,3和7可以组成10,它们分别再加上多出来的5都得15,所以中间这个数应该填5,上下,左右可以分别填4和6,3和7,如图:方法二:观察这些图,容易发现,中间方框中的数比较特殊,它既在横行上,又在竖列中,在数阵中这样的数称为“重叠数”.只要我们确定了中间的“重叠数”填几,别的空格就简单了.那么横行3个数的和加上竖列3个数之和就等于所要填入的5个数的和与重叠数的和.于是(3+4+5+6+7)+重叠数=15+15,重叠数=30-25=5,所以中间的这个数应该填5,在剩下的4个数3,4,6,7中,只有3+7=4+6=10,填法如图.建议:在这两种方法中,学生习惯用第一种方法来观察出答案,但是这种方法对于以后数字大的题就很难把握,因此老师在学生掌握了第一种方法的前提下,要介绍第二种解答数阵图的一般方法,不要求学生马上掌握,但是要让学生明确解答这样的题要从重叠数开始入手分析,以后练得多了就能融会贯通了.如果老师觉得这几个数太大学生不容易接受,还可以改成更小的数.拓展练习把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.【答案分析】中间○即为特殊的重叠数,因为它既是横线上的数,又是竖线上的数.中间的数填什么呢?横行加上竖行之和应为 12+12=24,而2+3+4+5+6=20,中间的要多加一次,所以应为4.把1,2,3,4,5,7分别填入○里,使每一个大椭圆上的四个数之和等于13.【教学思路】方法一:观察法,在这6个数中,有两个数是公共的,那么剩下的四个数两两相加应该相等,观察1,2,3,4,5,7中1是公共数,这时我们发现2+7和4+5都等于9,因此剩下的3也应该是公共数,2和7,4和5应该分别填在这两个圆的左边和右边.经检验每个大椭圆上的四个数这和等于13.方法二:每个椭圆里的四个数之和等于13,那么两个椭圆里的四个数之和就是13+13=26,另外这6个数相加的和是1+2+3+4+5+7=22,26和22之间相差的是什么呢?只有中间的这两个重叠数被多加了1次,这相差的4应该是两个重叠数的和,1+3=4,所以中间的这两个重叠数应该是1和3.剩下的数2+7=4+5=9.把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.【教学思路】方法一:观察法,在1,2,3,4,5,6,7这七个数中,除去中间的重叠数,剩下的六个数两两相加应该相等,经验算,当重叠数是4时,1+7=2+6=3+5=8,8+4=12,如图:方法二:因为图中共有3条直线,所以中心的重叠数重叠了2次,于是(1+2+3+4+5+6+7)+重叠数×2=12+12+12.重叠数=(36-28)÷2=8.那么中间的数应该填14剩下的6个数1,2,3,5,6,7,中,2个数的和等于12-4=8的有1+7=2+6=3+5,如图:拓展练习把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.把2,3,4,5,6,7,8这七个数分别填入圆圈中,使两个正方形中四个数之和相等19.【教学思路】先考虑求两个正方形公共的中间数.2+3+4+5+6+7+8+重叠数=19+19.重叠数=3,那么中间圆圈里面应该填3.剩下的数中2+6+8=4+5+7=19-3=16,所以每个正方形中,剩下的三个数应该填:2,6,8或4,5,7.具体填法如下:拓展:如果使两个正方形中四个数之和相等21,又应该怎样填?我会做一做把1,2,3,4,5,6,7这7个数分别填入右图中,使得每条直线上的3个数的和相等.【教学思路】这道题的答案不唯一.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)在空格内填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.【答案】【教学思路】如果有充足的时间,建议这题可放在例3的后面做一个加深,这道题也主要是利用加减法之间的关系来解答的.这个题我们要从已知三个加数的第二列入手开始填,先计算出这三个加数的和,再用64减去这三个加数的和就得到了这第四个加数.用图中已有的三个数填满其余的空格,每个数字必须使用三次.使得每行、每列和两条对角线上的三个数之和相等.【答案】【答案】把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.【答案】【教学思路】这道题可参考放在例6的后面,做一个拓展.在例6的基础上,我们只需要调动四条边上各数的位置就可以验证出结果.使用数字0,1,2,3,4,5,6,7,8, 9求和.而且同一个数在一幅图中不能重复出现.【答案】【答案】把1~11这十一个数分别填入图中的圆圈里,使每条直线上的三个数的和都等于18.【答案】练习十二1.在下面的○里填上适当的数,使每条线上的三个数之和都是12.【答案】2.把3~8这6个数,填在下图中使得每行、每列和两条对角线上的三个数的和都为18.【答案】3. 把1,2,3,4,5这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.【答案】4.把3,4,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为20.【答案】5. 将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.【答案】6.把数字1,2,3,5,6,7,9填在下面的○里,使每边上的和为15.【答案】小朋友,你在少年宫里走过“勇敢者的道路”吗?道路崎岖,充满艰难险阻.但是,它能培养小朋友的勇敢精神和不怕困难的毅力.这里有两幅图,也叫“勇敢者的道路”.图中的道路狭窄、曲折,不易通过,需要小朋友细心和有耐心.现在请小朋友用一枝铅笔,按照图中箭头的方向画出通行路线,而且线条不能碰到两边的“围墙”.小朋友,这可真不容易哦!。
2013.08.21巧填数阵图 (罗嘉淇)
个性化教案
2
这四个数填在四个空格里,是横行、竖行三个填数,使横行、竖行的三个数相加都得
3
例4.在下面的空格里填上合适的数,使每一横行,每一竖行,每一斜行上的三个数相加都等于15。
)填数,是横、竖行三个数相加的和等于16。
4
4、5、6这六个数填入下面的○里,使每一条线上三个数相加的和都等于9。
这六个数填入下面的○里,使每条线上的三个数5
在正方形的空格里填上适当的数,使每一行横行、竖行、斜行上的三个数相加的和都等于指定的数
4.填数,使每条线上的三个数相加都等于指定的数。
6
把1、2、3、4四个数分别填在下图的圆圈里,使每条边上的三个数的。
,1,2,3,4,5,6,7,8,
一个数字不能重复出现.
7
这五个数分别填入圆圈中,使每条线上三个数相加8
2.(1)把3、4、7四个数填在下图的空格里,使横行、竖行三个数相加的和都等于15
、6这四个数填入空格,使横行、竖行三个数相加的和
、12五个数分别填在下面各图的圆圈里,使每条线上9
4.在下面的○里填上适当的数,使每条线上的三个数之和都是12.
5.把数字1,2,3,5,6,7,9填在下面的○里,使每边上的和为10。
(完整word版)奥数一年级教案第十二讲巧填数阵图教师
巧填数阵图数学乐园晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子.一个雪精灵告诉她们:“你们只要能够把1~7这七个数填在雪花的七个花瓣上,使每三个位于同一直线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.【教学思路】在开课的时候,老师可通过故事引入,激发学生对填数游戏的兴趣.让学生初步感知什么是数阵.因为填数阵有一定的难度,所以在这里我们不需要马上让孩子完成这个题,可以放在最后来解决这个问题.小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数,可不是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法.下面我们就一起来学习吧!基础篇数阵图是小学奥数中比较重要的一个知识点,现在我们把它放在一年级开始学习似乎有些过难.但这节课我们只是希望通过一些简单的填数字游戏,使学生初步感知到什么样的是数阵,让学生用自己喜欢的方法来巧填数字,培养他们的思维能力.在鼓励学生去研究方法的同时,教师引导学生去发现数阵的简单规律,以及填数阵的基本方法,通过找数阵中的关键数来找到解题的钥匙.在今后的不断学习中,能把这种方法灵活应用到实际中去.使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现.【教学思路】一般在解答这类填数问题时,把同一条边上出现两个数字的空格先填.之前我们已经有过这样的练习,学生有了一定的基础.这道题的答案不止一个,我们只要求学生能找到其中的一种就达到要求了.(1)右边两个圆的和应该是9,所以里可填(0,9)(2,7)(3,6).(2)告诉我们中间的数字是2,剩下两边上两个数字的和应该是9-2=7.0+7=1+6=3+4,所以剩下两边上两个数可以填(0,7),(1,6),(3,4)(3)7+6=13,15-13=2,所以第2条线中间填2.左边第一条线:15-7=8,0+8=3+5,数字不重复共两种填法.第三条线15-6=9,0+9=4+5,数字不重复共两种填法(4)6+4=10,13-10=3,所以第2条线最下是3,.左边第一条线:13-6=7,0+7=2+5,数字不重复共两种解法.第三条线:13-3=10,1+9=2+8,数字不重复共两种解法.拓展练习(1)填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.【答案】【答案】在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.【教学思路】方法一:填数时,首先要看哪一行已经有了两个数,然后用18减去这两个数,就得出这一行的第三个数.填数的顺序如下:方法二:从斜行来考虑:要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?【教学思路】首先我们要找到填这个表格的突破口,一般情况下我们先找每行、每列以及每条对角线上已知两个数的来先填.找到这个突破口,后面就容易多了.方法一:从竖行入手.方法二:分别从两条对角线入手.拓展练习在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.【答案】【答案】把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.【教学思路】比较三个已知数1,2,3,和1比2大1,3大2.还剩下三个数4,5,6要我们来填,5+6=11 6+4=10 5+4=9 ,要使每边和相等,5+6+1=6+4+2=5+4+3=12,答案如下:提高篇把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.【教学思路】方法一:观察法.要使横行、竖行的三个数相加都得15,我们就要考虑中间填什么数.观察这五个数3,4,5,6,7,我们发现4和6,3和7可以组成10,它们分别再加上多出来的5都得15,所以中间这个数应该填5,上下,左右可以分别填4和6,3和7,如图:方法二:观察这些图,容易发现,中间方框中的数比较特殊,它既在横行上,又在竖列中,在数阵中这样的数称为“重叠数”.只要我们确定了中间的“重叠数”填几,别的空格就简单了.那么横行3个数的和加上竖列3个数之和就等于所要填入的5个数的和与重叠数的和.于是(3+4+5+6+7)+重叠数=15+15,重叠数=30-25=5,所以中间的这个数应该填5,在剩下的4个数3,4,6,7中,只有3+7=4+6=10,填法如图.建议:在这两种方法中,学生习惯用第一种方法来观察出答案,但是这种方法对于以后数字大的题就很难把握,因此老师在学生掌握了第一种方法的前提下,要介绍第二种解答数阵图的一般方法,不要求学生马上掌握,但是要让学生明确解答这样的题要从重叠数开始入手分析,以后练得多了就能融会贯通了.如果老师觉得这几个数太大学生不容易接受,还可以改成更小的数.拓展练习把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.【答案分析】中间○即为特殊的重叠数,因为它既是横线上的数,又是竖线上的数.中间的数填什么呢?横行加上竖行之和应为 12+12=24,而2+3+4+5+6=20,中间的要多加一次,所以应为4.把1,2,3,4,5,7分别填入○里,使每一个大椭圆上的四个数之和等于13.【教学思路】方法一:观察法,在这6个数中,有两个数是公共的,那么剩下的四个数两两相加应该相等,观察1,2,3,4,5,7中1是公共数,这时我们发现2+7和4+5都等于9,因此剩下的3也应该是公共数,2和7,4和5应该分别填在这两个圆的左边和右边.经检验每个大椭圆上的四个数这和等于13.方法二:每个椭圆里的四个数之和等于13,那么两个椭圆里的四个数之和就是13+13=26,另外这6个数相加的和是1+2+3+4+5+7=22,26和22之间相差的是什么呢?只有中间的这两个重叠数被多加了1次,这相差的4应该是两个重叠数的和,1+3=4,所以中间的这两个重叠数应该是1和3.剩下的数2+7=4+5=9.把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.【教学思路】方法一:观察法,在1,2,3,4,5,6,7这七个数中,除去中间的重叠数,剩下的六个数两两相加应该相等,经验算,当重叠数是4时,1+7=2+6=3+5=8,8+4=12,如图:方法二:因为图中共有3条直线,所以中心的重叠数重叠了2次,于是(1+2+3+4+5+6+7)+重叠数×2=12+12+12.重叠数=(36-28)÷2=8.那么中间的数应该填14剩下的6个数1,2,3,5,6,7,中,2个数的和等于12-4=8的有1+7=2+6=3+5,如图:拓展练习把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.把2,3,4,5,6,7,8这七个数分别填入圆圈中,使两个正方形中四个数之和相等19.【教学思路】先考虑求两个正方形公共的中间数.2+3+4+5+6+7+8+重叠数=19+19.重叠数=3,那么中间圆圈里面应该填3.剩下的数中2+6+8=4+5+7=19-3=16,所以每个正方形中,剩下的三个数应该填:2,6,8或4,5,7.具体填法如下:拓展:如果使两个正方形中四个数之和相等21,又应该怎样填?我会做一做把1,2,3,4,5,6,7这7个数分别填入右图中,使得每条直线上的3个数的和相等.【教学思路】这道题的答案不唯一.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)在空格内填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.【答案】【教学思路】如果有充足的时间,建议这题可放在例3的后面做一个加深,这道题也主要是利用加减法之间的关系来解答的.这个题我们要从已知三个加数的第二列入手开始填,先计算出这三个加数的和,再用64减去这三个加数的和就得到了这第四个加数.用图中已有的三个数填满其余的空格,每个数字必须使用三次.使得每行、每列和两条对角线上的三个数之和相等.【答案】【答案】把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.【答案】【教学思路】这道题可参考放在例6的后面,做一个拓展.在例6的基础上,我们只需要调动四条边上各数的位置就可以验证出结果.使用数字0,1,2,3,4,5,6,7,8, 9求和.而且同一个数在一幅图中不能重复出现.【答案】【答案】把1~11这十一个数分别填入图中的圆圈里,使每条直线上的三个数的和都等于18.【答案】练习十二1.在下面的○里填上适当的数,使每条线上的三个数之和都是12.【答案】2.把3~8这6个数,填在下图中使得每行、每列和两条对角线上的三个数的和都为18.【答案】3. 把1,2,3,4,5这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.【答案】4.把3,4,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为20.【答案】5. 将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.【答案】6.把数字1,2,3,5,6,7,9填在下面的○里,使每边上的和为15.【答案】小朋友,你在少年宫里走过“勇敢者的道路”吗?道路崎岖,充满艰难险阻.但是,它能培养小朋友的勇敢精神和不怕困难的毅力.这里有两幅图,也叫“勇敢者的道路”.图中的道路狭窄、曲折,不易通过,需要小朋友细心和有耐心.现在请小朋友用一枝铅笔,按照图中箭头的方向画出通行路线,而且线条不能碰到两边的“围墙”.小朋友,这可真不容易哦!。
第十二讲 巧填数阵图 教师
第十二讲巧填数阵图数学乐园晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子.一个雪精灵告诉她们:“你们只要能够把1~7这七个数填在雪花的七个花瓣上,使每三个位于同一直线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.【教学思路】在开课的时候,老师可通过故事引入,激发学生对填数游戏的兴趣.让学生初步感知什么是数阵.因为填数阵有一定的难度,所以在这里我们不需要马上让孩子完成这个题,可以放在最后来解决这个问题.小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数,可不是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法.下面我们就一起来学习吧!基础篇使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现.数阵图是小学奥数中比较重要的一个知识点,现在我们把它放在一年级开始学习似乎有些过难.但这节课我们只是希望通过一些简单的填数字游戏,使学生初步感知到什么样的是数阵,让学生用自己喜欢的方法来巧填数字,培养他们的思维能力.在鼓励学生去研究方法的同时,教师引导学生去发现数阵的简单规律,以及填数阵的基本方法,通过找数阵中的关键数来找到解题的钥匙.在今后的不断学习中,能把这种方法灵活应用到实际中去.【教学思路】一般在解答这类填数问题时,把同一条边上出现两个数字的空格先填.之前我们已经有过这样的练习,学生有了一定的基础.这道题的答案不止一个,我们只要求学生能找到其中的一种就达到要求了.(1)右边两个圆的和应该是9,所以里可填(0,9)(2,7)(3,6).(2)告诉我们中间的数字是2,剩下两边上两个数字的和应该是9-2=7.0+7=1+6=3+4,所以剩下两边上两个数可以填(0,7),(1,6),(3,4)(3)7+6=13,15-13=2,所以第2条线中间填2.左边第一条线:15-7=8,0+8=3+5,数字不重复共两种填法.第三条线15-6=9,0+9=4+5,数字不重复共两种填法(4)6+4=10,13-10=3,所以第2条线最下是3,.左边第一条线:13-6=7,0+7=2+5,数字不重复共两种解法.第三条线:13-3=10,1+9=2+8,数字不重复共两种解法.拓展练习(1)填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.【答案】【答案】在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.【教学思路】方法一:填数时,首先要看哪一行已经有了两个数,然后用18减去这两个数,就得出这一行的第三个数.填数的顺序如下:方法二:从斜行来考虑:要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?【教学思路】首先我们要找到填这个表格的突破口,一般情况下我们先找每行、每列以及每条对角线上已知两个数的来先填.找到这个突破口,后面就容易多了.方法一:从竖行入手.方法二:分别从两条对角线入手.拓展练习在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.【答案】【答案】把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.【教学思路】比较三个已知数1,2,3,和1比2大1,3大2.还剩下三个数4,5,6要我们来填,5+6=11 6+4=10 5+4=9 ,要使每边和相等,5+6+1=6+4+2=5+4+3=12,答案如下:提高篇把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.【教学思路】方法一:观察法.要使横行、竖行的三个数相加都得15,我们就要考虑中间填什么数.观察这五个数3,4,5,6,7,我们发现4和6,3和7可以组成10,它们分别再加上多出来的5都得15,所以中间这个数应该填5,上下,左右可以分别填4和6,3和7,如图:方法二:观察这些图,容易发现,中间方框中的数比较特殊,它既在横行上,又在竖列中,在数阵中这样的数称为“重叠数”.只要我们确定了中间的“重叠数”填几,别的空格就简单了.那么横行3个数的和加上竖列3个数之和就等于所要填入的5个数的和与重叠数的和.于是(3+4+5+6+7)+重叠数=15+15,重叠数=30-25=5,所以中间的这个数应该填5,在剩下的4个数3,4,6,7中,只有3+7=4+6=10,填法如图.建议:在这两种方法中,学生习惯用第一种方法来观察出答案,但是这种方法对于以后数字大的题就很难把握,因此老师在学生掌握了第一种方法的前提下,要介绍第二种解答数阵图的一般方法,不要求学生马上掌握,但是要让学生明确解答这样的题要从重叠数开始入手分析,以后练得多了就能融会贯通了.如果老师觉得这几个数太大学生不容易接受,还可以改成更小的数.拓展练习把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.【答案分析】中间○即为特殊的重叠数,因为它既是横线上的数,又是竖线上的数.中间的数填什么呢?横行加上竖行之和应为 12+12=24,而2+3+4+5+6=20,中间的要多加一次,所以应为4.把1,2,3,4,5,7分别填入○里,使每一个大椭圆上的四个数之和等于13.【教学思路】方法一:观察法,在这6个数中,有两个数是公共的,那么剩下的四个数两两相加应该相等,观察1,2,3,4,5,7中1是公共数,这时我们发现2+7和4+5都等于9,因此剩下的3也应该是公共数,2和7,4和5应该分别填在这两个圆的左边和右边.经检验每个大椭圆上的四个数这和等于13.方法二:每个椭圆里的四个数之和等于13,那么两个椭圆里的四个数之和就是13+13=26,另外这6个数相加的和是1+2+3+4+5+7=22,26和22之间相差的是什么呢?只有中间的这两个重叠数被多加了1次,这相差的4应该是两个重叠数的和,1+3=4,所以中间的这两个重叠数应该是1和3.剩下的数2+7=4+5=9.把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.【教学思路】方法一:观察法,在1,2,3,4,5,6,7这七个数中,除去中间的重叠数,剩下的六个数两两相加应该相等,经验算,当重叠数是4时,1+7=2+6=3+5=8,8+4=12,如图:方法二:因为图中共有3条直线,所以中心的重叠数重叠了2次,于是(1+2+3+4+5+6+7)+重叠数×2=12+12+12.重叠数=(36-28)÷2=8.那么中间的数应该填14剩下的6个数1,2,3,5,6,7,中,2个数的和等于12-4=8的有1+7=2+6=3+5,如图:拓展练习把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.把2,3,4,5,6,7,8这七个数分别填入圆圈中,使两个正方形中四个数之和相等19.【教学思路】先考虑求两个正方形公共的中间数.2+3+4+5+6+7+8+重叠数=19+19.重叠数=3,那么中间圆圈里面应该填3.剩下的数中2+6+8=4+5+7=19-3=16,所以每个正方形中,剩下的三个数应该填:2,6,8或4,5,7.具体填法如下:拓展:如果使两个正方形中四个数之和相等21,又应该怎样填?我会做一做把1,2,3,4,5,6,7这7个数分别填入右图中,使得每条直线上的3个数的和相等.【教学思路】这道题的答案不唯一.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)在空格内填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.【答案】【教学思路】如果有充足的时间,建议这题可放在例3的后面做一个加深,这道题也主要是利用加减法之间的关系来解答的.这个题我们要从已知三个加数的第二列入手开始填,先计算出这三个加数的和,再用64减去这三个加数的和就得到了这第四个加数.用图中已有的三个数填满其余的空格,每个数字必须使用三次.使得每行、每列和两条对角线上的三个数之和相等.【答案】【答案】把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.【答案】【教学思路】这道题可参考放在例6的后面,做一个拓展.在例6的基础上,我们只需要调动四条边上各数的位置就可以验证出结果.使用数字0,1,2,3,4,5,6,7,8, 9求和.而且同一个数在一幅图中不能重复出现.【答案】【答案】把1~11这十一个数分别填入图中的圆圈里,使每条直线上的三个数的和都等于18.【答案】练习十二1.在下面的○里填上适当的数,使每条线上的三个数之和都是12.【答案】2.把3~8这6个数,填在下图中使得每行、每列和两条对角线上的三个数的和都为18.【答案】3. 把1,2,3,4,5这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.【答案】4.把3,4,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为20.【答案】5. 将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.【答案】6.把数字1,2,3,5,6,7,9填在下面的○里,使每边上的和为15.【答案】学而思教育 07年春季班讲义一年级 实验班 第十二讲 教师版 Page 11 of 12小朋友,你在少年宫里走过“勇敢者的道路”吗?道路崎岖,充满艰难险阻.但是,它能培养小朋友的勇敢精神和不怕困难的毅力.这里有两幅图,也叫“勇敢者的道路”.图中的道路狭窄、曲折,不易通过,需要小朋友细心和有耐心.现在请小朋友用一枝铅笔,按照图中箭头的方向画出通行路线,而且线条不能碰到两边的“围墙”.小朋友,这可真不容易哦!学而思教育07年春季班讲义一年级实验班第十二讲教师版Page 12 of 12。
巧填数阵PPT课件
.
6
例5、把1、2、3、4、5这5个数填入下图的空格中 (每个数只能用一次),使横行、竖行3个数相等。
3 2 15
3 45 1Βιβλιοθήκη 42中间填1时,剩下的也可以分 中间填5时,剩下的也可以分 成两组和一样的组。3+4=2+5。 成两组和一样的组。1+4=2+3。
.
7
小朋友们学会了吗? 有趣的数阵等着你们来 挑战,快点打开练习本 来挑战吧!
.
8
15 15
例2、在下图的空格中填上合适的数,使得横行、 竖行的3个数相加都得8。
我们可以先算横 行的数,也就是 4+2+( )=8。
2
3
然后我们再算竖 行的数,也就是 3+2+( )=8。
.
3
例3、在 填上合适的数,使三角形每条边上3个 数的和都是12.
4
32
5 16
每条边上的和都是12,也就是4+( )+5=12、
4+( )+6=12、5+( )+6=12。用12减去已
知的数,就可以得出 里的数了。
.
4
例4、把3、4、6、7这4个数填入下图的空格中 (每个数只能用一次),使横行、竖行3个数相加 都得15。
4
3
7
6
要想使横行、竖行的3个数 相加得到15。也就是 ( )+5+( )=15; 则( )+( )=10。我们发 现横竖都一样,那就相当于 把这四个数组成两组,每组 得数都是10。3+7=10、
4+6=10
.
5
是3。
例5、把1、2、3、4、5这5个数填入下图的空格中 (每个数只能用一次),使横行、竖行3个数相等。
巧填数阵
巧填数阵
例1:在下图圆圈内分别填入数字1~9,使两条直线上五个数的和相等,和是多少?
例2:将1、2、3、4、5、6六个数字填入图中的小圆圈内,使每个大圆上四个数字的和是16。
例3:将26、27、28、36、37、38、46、47、48九个数分别填入下图中的圆圈里,使每条直线上三个数的和是111。
例4:将1、2、3、4、5、6、7、8、9九个数字分别填入图中的小圆圈中,使三角形每边上四个数的和是17.
例5:将1、2、3、4、5、6、7、8、9、10这十个数字分别填入图中的小圆圈中,使每条线上四个数的和是21,每个三角形顶点上三个数的和都等于17。
例6:将1、2、3、4、5、6、7、8、9九个数字恰当地填入小圆圈里,使每个大圆圈上的四个数相加的和等于17。
.。
二年级巧妙数阵图教案
二年级巧妙数阵图教案
教学要求:
1、使学生掌握解答有趣的数阵图的方法。
2、培养学生的逻辑思维能力和推理能力,以及联想、试探归纳
等思维能力。
教学过程:
一、导入新课语:
如果把一些数按照一定的规律填在特定的图形里,那么这种图形,我们就称
它为数阵图。
它是一种趣味性很强的游戏,它的形式很多,大概分为三种:封闭型数阵、辐射型数阵、复合型数阵。
我们这节课还要
归纳解答数阵图的方法C0m
二、探索新知:
1、教学例5:
把2~9填入O中,使得正方形每条边的和是15解题思路:每边和为15,所以四边总和为15×4=60,由于2+3+4+5+6+7+8+9=44而:60—44=16,所以四个顶点的和为16。
从2~9中选出四个和为16的数是
教学总结:
1、使学生掌握正确数据图。
2、培养学生活跃的思维能力,提高学习的兴趣。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二讲巧填数阵图
数学乐园
晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子.一个雪精灵告诉她们:“你们只要能够把1~7这七个数填在雪花的七个花瓣上,使每三个位于同一直线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.
【教学思路】在开课的时候,老师可通过故事引入,激发学生对填数游戏的兴趣.让学生初步感知什么是数阵.因为填数阵有一定的难度,所以在这里我们不需要马上让孩子完成这个题,可以放在最后来解决这个问题.
小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数,可不
是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法.下面我们就一起来学习吧!
基础篇
使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现.
数阵图是小学奥数中比较重要的一个知识点,现在我们把它放在一年级开始学习似乎有些过难.但这节课我们只是希望通过一些简单的填数字游戏,使学生初步感知到什么样的是
数阵,让学生用自己喜欢的方法来巧填数字,培养他们的思维能力.在鼓励学生去研究方法
的同时,教师引导学生去发现数阵的简单规律,以及填数阵的基本方法,通过找数阵中的关
键数来找到解题的钥匙.在今后的不断学习中,能把这种方法灵活应用到实际中去.
【教学思路】一般在解答这类填数问题时,把同一条边上出现两个数字的空格先填.之前我们已经有过这样的练习,学生有了一定的基础.这道题的答案不止一个,我们只要求学生能找到其中的一种就达到要求了.
(1)右边两个圆的和应该是9,所以里可填(0,9)(2,7)(3,6).
(2)告诉我们中间的数字是2,剩下两边上两个数字的和应该是9-2=7.0+7=1+6=3+4,所以剩下两边上两个数可以填(0,7),(1,6),(3,4)
(3)7+6=13,15-13=2,所以第2条线中间填2.左边第一条线:15-7=8,0+8=3+5,数字不重复共两种填法.第三条线15-6=9,0+9=4+5,数字不重复共两种填法
(4)6+4=10,13-10=3,所以第2条线最下是3,.左边第一条线:13-6=7,0+7=2+5,数字不重复共两种解法.第三条线:13-3=10,1+9=2+8,数字不重复共两种解法.
拓展练习
(1)填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.
【答案】【答案】
在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.
【教学思路】方法一:填数时,首先要看哪一行已经有了两个数,然后用18减去这两个数,就得出这一行的第三个数.填数的顺序如下:
方法二:从斜行来考虑:
要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?
【教学思路】首先我们要找到填这个表格的突破口,一般情况下我们先找每行、每列以及每条对角线上已知两个数的来先填.找到这个突破口,后面就容易多了.方法一:从竖行入手.方法二:分别从两条对角线入手.
拓展练习
在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.
【答案】
【答案】
把1,2,3,4,5,6六个数,分别填入○,使每条线上3个数的和相等.
【教学思路】比较三个已知数1,2,3,和1比2大1,3大2.还剩下三个数4,5,6要我们来填,5+6=11 6+4=10 5+4=9 ,要使每边和相等,5+6+1=6+4+2=5+4+3=12,答案如下:
提高篇
把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.
【教学思路】方法一:观察法.要使横行、竖行的三个数相加都得15,我们就要考虑中间填什么数.观察这五个数3,4,5,6,7,我们发现4和6,3和7可以组成10,它们分别再加上多出来的5都得15,所以中间这个数应该填5,上下,左右可以分别填4和6,3和7,如图:
方法二:观察这些图,容易发现,中间方框中的数比较特殊,它既在横行上,又在竖列中,在数阵中这样的数称为“重叠数”.只要我们确定了中间的“重叠数”填几,别的空格就简单了.那么横行3个数的和加上竖列3个数之和就等于所要填入的5个数的和与重叠数的和.于是(3+4+5+6+7)+重叠数=15+15,重叠数=30-25=5,所以中间的这个数应该填5,在剩下的4个数3,4,6,7中,只有3+7=4+6=10,填法如图.
建议:在这两种方法中,学生习惯用第一种方法来观察出答案,但是这种方法对于以后数字大的题就很难把握,因此老师在学生掌握了第一种方法的前提下,要介绍第二种解答数阵图的一般方法,不要求学生马上掌握,但是要让学生明确解答这样的题要从重叠数开始入手分析,以后练得多了就能融会贯通了.如果老师觉得这几个数太大学生不容易接受,还可以改成更小的数.
拓展练习
把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.
【答案分析】中间○即为特殊的重叠数,因为它既是横线上的数,又是竖线上的数.中间的数填什么呢?横行加上竖行之和应为12+12=24,而2+3+4+5+6=20,中间的要多加一次,所以应为4.
把1,2,3,4,5,7分别填入○里,使每一个大椭圆上的四个数之和等于13.
【教学思路】方法一:观察法,在这6个数中,有两个数是公共的,那么剩下的四个数两两相加应该相等,观察1,2,3,4,5,7中1是公共数,这时我们发现2+7和4+5都等于9,因此剩下的3也应该是公共数,2和7,4和5应该分别填在这两个圆的左边和右边.经检验每个大椭圆上的四个数这和等于13.
方法二:每个椭圆里的四个数之和等于13,那么两个椭圆里的四个数之和就是13+13=26,另外这6个数相加的和是1+2+3+4+5+7=22,26和22之间相差的是什么呢?只有中间的这两个重叠数被多加了1次,这相差的4应该是两个重叠数的和,1+3=4,所以中间的这两个重叠数应该是1和3.剩下的数2+7=4+5=9.
把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.
【教学思路】方法一:观察法,在1,2,3,4,5,6,7这七个数中,除去中间的重叠数,剩下的六个数两两相加应该相等,经验算,当重叠数是4时,1+7=2+6=3+5=8,8+4=12,如图:
方法二:因为图中共有3条直线,所以中心的重叠数重叠了2次,于是(1+2+3+4+5+6+7)+重叠数×2=12+12+12.重叠数=(36-28)÷2=8.那么中间的数应该填14剩下的6个数1,2,3,5,6,7,中,2个数的和等于12-4=8的有1+7=2+6=3+5,如图:
拓展练习
把1~9这九个数字填入下列圆圈,使每条横线、竖线、斜线连接起来的三个圆圈的数之和都等于15.
把2,3,4,5,6,7,8这七个数分别填入圆圈中,使两个形中四个数之和相等19.
【教学思路】先考虑求两个形公共的中间数.2+3+4+5+6+7+8+重叠数=19+19.重叠数=3,那么中间圆圈里面应该填3.剩下的数中2+6+8=4+5+7=19-3=16,所以每个形中,剩下的三个数应该填:2,6,8或4,5,7.具体填法如下:
拓展:如果使两个形中四个数之和相等21,又应该怎样填?
我会做一做
把1,2,3,4,5,6,7这7个数分别填入右图中,使得每条直线上的3个数的和相等.
【教学思路】这道题的答案不唯一.
附加题
(老师可根据自己的课堂进度灵活处理讲义容,附加题仅供老师参考使用.)
在空格填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.
【答案】
【教学思路】如果有充足的时间,建议这题可放在例3的后面做一个加深,这道题也主要是利用加减法之间的关系来解答的.这个题我们要从已知三个加数的第二列入手开始填,先计算出这三个加数的和,再用64减去这三个加数的和就得到了这第四个加数.
用图中已有的三个数填满其余的空格,每个数字必须使用三次.使得每行、每列和两条对角线上的三个数之和相等.
【答案】【答案】
把1~9这九个数字填入下列圆圈,使每条横线、竖线、斜线连接起来的三个圆圈的数之和都等于15.
【答案】
【教学思路】这道题可参考放在例6的后面,做一个拓展.在例6的基础上,我们只需要调动四条边上各数的位置就可以验证出结果.
使用数字0,1,2,3,4,5,6,7,8,9求和.而且同一个数在一幅图中不能重复出现.
【答案】【答案】
把1~11这十一个数分别填入图中的圆圈里,使每条直线上的三个数的和都等于18.
【答案】
练习十二
1.在下面的○里填上适当的数,使每条线上的三个数之和都是1
2.
【答案】
2.把3~8这6个数,填在下图中使得每行、每列和两条对角线上的三个数的和都为18.
【答案】
3. 把1,2,3,4,5这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.
【答案】
4. 把3,4,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为20.
【答案】
5. 将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.
【答案】
6.把数字1,2,3,5,6,7,9填在下面的○里,使每边上的和为15.
【答案】
小朋友,你在少年宫里走过“勇敢者的道路”吗?道路崎岖,充满艰难险阻.但是,它能培养小朋友的勇敢精神和不怕困难的毅力.
这里有两幅图,也叫“勇敢者的道路”.图中的道路狭窄、曲折,不易通过,需要小朋友细
心和有耐心.
现在请小朋友用一枝铅笔,按照图中箭头的方向画出通行路线,而且线条不能碰到两边的“围墙”.小朋友,这可真不容易哦!。
