6 逻辑代数(上):命题演算 习题答案
离散数学-第六章集合代数课后练习习题及答案

第六章作业评分要求:1. 合计57分2. 给出每小题得分(注意: 写出扣分理由).3. 总得分在采分点1处正确设置.一有限集合计数问题(合计20分: 每小题10分, 正确定义集合得4分, 方法与过程4分, 结果2分)要求: 掌握集合的定义方法以及处理有限集合计数问题的基本方法1 对60个人的调查表明, 有25人阅读《每周新闻》杂志, 26人阅读《时代》杂志, 26人阅读《财富》杂志, 9人阅读《每周新闻》和《财富》杂志, 11人阅读《每周新闻》和《时代》杂志, 8人阅读《时代》和《财富》杂志, 还有8人什么杂志也不读.(1) 求阅读全部3种杂志的人数;(2) 分别求只阅读《每周新闻》、《时代》和《财富》杂志的人数.解定义集合: 设E={x|x是调查对象},A={x|x阅读《每周新闻》}, B={x|x阅读《时代》}, C={x|x阅读《财富》}由条件得|E|=60, |A|=25, |B|=26, |C|=26, |A∩C|=9, |A∩B|=11, |B∩C|=8, |E-A∪B∪C|=8 (1) 阅读全部3种杂志的人数=|A∩B∩C|=|A∪B∪C|-(|A|+|B|+|C|)+(|A∩B|+|A∩C|+|B∩C|)=(60-8)-(25+26+26)+(11+9+8)=3(2) 只阅读《每周新闻》的人数=|A-B∪C|=|A-A∩(B∪C)|=|A-(A∩B)∪(A∩C)|=|A|-(|A∩B|+|A∩C|-|A∩B∩C|)=25-(11+9-3)=8同理可得只阅读《时代》的人数为10, 只阅读《财富》的人数为12.2 使用容斥原理求不超过120的素数个数.分析:本题有一定难度, 难在如何定义集合. 考虑到素数只有1和其自身两个素因子, 而不超过120的合数的最小素因子一定是2,3,5或7(比120开方小的素数), 也就是说, 不超过120的合数一定是2,3,5或7的倍数. 因此, 可定义4条性质分别为2,3,5或7的倍数, 先求出不超过120的所有的合数, 再得出素数的个数.解定义集合: 设全集E={x|x∈Z∧1≤x∧x≤120}A={2k|k∈Z∧k≥1∧2k≤120},B={3k|k∈Z∧k≥1∧3k≤120},C={5k|k∈Z∧k≥1∧5k≤120},D={7k|k∈Z∧k≥1∧7k≤120}.则不超过120的合数的个数=|A∪B∪C∪D|-4 (因为2,3,5,7不是合数)=(|A|+|B|+|C|+|D|)-(|A∩B|+|A∩C|+|A∩D|+|B∩C|+|B∩D|+|C∩D|)+(|A∩B∩C|+|A∩B∩D|+|A∩C∩D|+|B∩C∩D|)-|A∩B∩C∩D|-4=(60+40+24+17)-(20+12+8+8+5+3)+(4+2+1+1)-0-4 (理由见说明部分)=89因此不超过120的素数个数=120-1-89=30 (因为1不是素数)说明: |A|=int(120/2); |A⋂B|=int(120/lcd(2,3));|A⋂B⋂C|=int(120/lcd(2,3,5)); |A⋂B⋂C⋂D|=int(120/lcd(2,3,5,7)).二集合关系证明1 设A,B,C是任意集合, 证明(1) (A-B)-C=A-(B∪C)(2) A∩C⊆B∩C ∧A-C⊆B-C ⇒A⊆B(合计12分: 每小题6分; 格式3分, 过程每错一步扣1分)证明(1) 逻辑演算法: ∀x,x∈(A-B)-C⇔x∈(A-B)∧¬x∈C (-定义)⇔(x∈A∧¬x∈B)∧¬x∈C (-定义)⇔x∈A∧(¬x∈B∧¬x∈C) (∧的结合律)⇔x∈A∧¬(x∈B∨x∈C) (德摩根律)⇔x∈A∧¬x∈B∪C (∪定义)⇔x∈A-B∪C (-定义)所以(A-B)-C=A-(B∪C).集合演算法(A-B)-C=(A∩~B)∩~C (补交转换律)=A∩(~B∩~C) (∩的结合律)=A∩~(B∪C) (德摩根律)=A-(B∪C) (补交转换律)得证.(2) 逻辑演算法: ∀x,x∈A⇔x∈A∩(C∪~C) (排中律, 同一律)⇔x∈(A∩C)∪(A∩~C) (∪对∩的分配率)⇔x∈A∩C∨x∈A-C (∪的定义, 补交转换律)⇒x∈B∩C∨x∈B-C (已知条件A∩C⊆B∩C与A-C⊆B-C) ⇔x∈(B∩C)∪(B-C) (∪的定义)⇔x∈(B∩C)∪(B∩~C) (补交转换律)⇔x∈B∩(C∪~C) (∩对∪的分配率)⇔x∈B (排中律, 同一律)所以A⊆B.集合演算法A=A∩(C∪~C) (同一律, 排中律)=(A∩C)∪(A∩~C) (∩对∪的分配率)=(A∩C)∪(A-C) (补交转换律)⊆(B∩C)∪(B-C) (已知条件A∩C⊆B∩C与A-C⊆B-C)=(B∩C)∪(B∩~C) (补交转换律)=B∩(C∪~C) (∩对∪的分配率)=B (排中律, 同一律)得证.方法三因为A∩C⊆B∩C, A-C⊆B-C, 所以(A∩C)∪(A-C)⊆(B∩C)∪(B-C)|, 整理即得A⊆B, 得证.2 求下列等式成立的充分必要条件(1) A-B=B-A(2) (A-B)∩(A-C)=∅(合计10分: 每小题5分; 正确给出充分必要条件2分, 理由3分)解(1) A-B=B-A方法一两边同时∪A得: A=(B-A)∪A=B∪A ⇒B⊆A; 同理可得A⊆B, 综合可得A=B.另一方面, 当A=B时显然有A-B=B-A. 因此所求充要条件为A=B.方法二∀x,x∈A-B∧x∈B-A⇔x∈(A-B)∩(B-A)⇔x∈∅所以A-B=B-A⇔A-B=∅∧B-A=∅⇔A⊆B ∧B⊆A⇔A=B因此A=B即为所求.(2) (A-B)∩(A-C)=∅⇔(A∩~B)∩(A∩~C)=∅⇔A∩(~B∩~C)=∅⇔A∩~(B∪C)=∅⇔A-(B∪C)=∅⇔A⊆B∪C所以A⊆B∪C即为所求充要条件.说明: 这类题型一般先求出必要条件, 再验证其充分性.三设全集为n元集, 按照某种给定顺序排列为E={x1,x2,…,x n}. 在计算机中可以用长为n的0,1串表示E的子集. 令m元子集A={x i1,x i2,…,x im}, 则A所对应的0,1串为j1j2…j n, 其中当k=i1,i2,…,i m时j k=1, 其它情况下j k=0.例如, E={1,2,…,8}, 则A={1,2,5,6}和B={3,7}对应的0,1串分别为11001100和00100010.(1)设A对应的0,1串为10110010, 则~A对应的0,1串是什么?(2) 设A与B对应的0,1串分别为i1i2…i n和j1j2…j n, 且A∪B, A∩B, A-B, A⊕B对应的0,1串分别为a1a2…a n, b1b2…b n, c1c2…c n, d1d2…d n, 求a k,b k,c k,d k, k=1,2,…,n.(合计15分: (1)3分; (2)12分, 每个结果正确2分, 求解过程4分)解下述运算是二进制数的位运算(1) 01001101(2) a k=i k∨j k, b k=i k∧j k, c k=i k∧¬j k, d k=(i k∧¬j k)∨(¬i k∧j k).说明: 这里c k和d k的求解可以使用主范式求解.c k,d k的真值表如下k kc k⇔m2=i k∧¬j kd k⇔m1∨m2=(¬i k∧j k)∨(i k∧¬j k).。
第2章-逻辑门与逻辑代数基础-习题与参考答案3-12
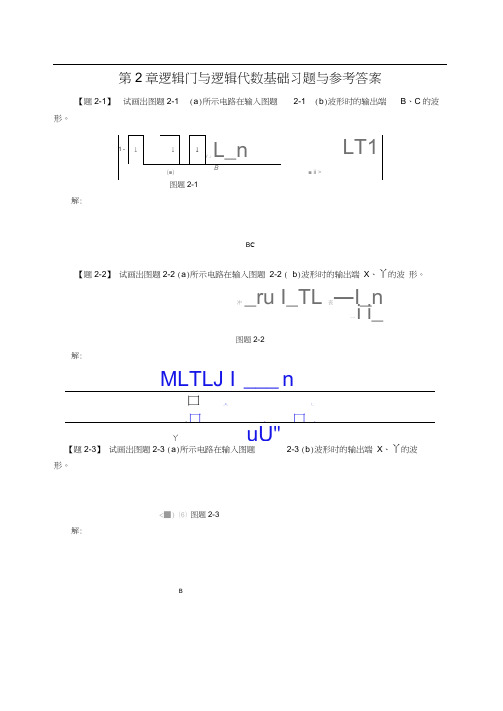
第2章逻辑门与逻辑代数基础习题与参考答案【题2-1】试画岀图题2-1 (a)所示电路在输入图题2-1 (b)波形时的输岀端B、C的波形。
解:B C【题2-2】试画岀图题2-2 (a)所示电路在输入图题2-2 ( b)波形时的输岀端X、丫的波形。
冲_ru I_TL 丧―I_n 一i i_图题2-2解:MLTLJ I ___ n口_n_ i_..x 口n 口n丫uU"【题2-3】试画岀图题2-3 (a)所示电路在输入图题2-3 (b)波形时的输岀端X、丫的波形。
<■) ⑹ 图题2-3解:B【题2-9】 如果如下乘积项的值为 1,试写岀该乘积项中每个逻辑变量的取值。
【题2-4】 试画岀图题2-4 (a )所示电路在输入图题 2-4 ( b )波形时的输岀端 X 、丫的波 形。
解:A J ~I _n ___ rvLB X.丫【题2-5】 试设计一逻辑电路,其信号 A 可以控制信号 B ,使输岀丫根据需要为 Y=B 或Y= B 。
解:可采用异或门实现,Y AB AB ,逻辑电路如下:【题2-6】某温度与压力检测装置在压力信号 A 或温度信号B 中有一个岀现高电平时, 输岀低电平的报警信号,试用门电路实现该检测装置。
解:压力信号、温度信号与报警信号之间的关系为: Y 「B ,有如下逻辑图。
【题2-7】某印刷裁纸机,只有操作工人的左右手同时按下开关 A 与B 时,才能进行裁纸操作,试用逻辑门实现该控制。
解:开关A 、B 与裁纸操作之间的关系为 丫 A B ,逻辑图如下:【题2-8】 某生产设备上有水压信号 A 与重量信号B ,当两信号同时为低电平时,检测电 路输出高电平信号报警,试用逻辑门实现该报警装置。
解:水压信号A 、重量信号B 与报警信号之间的关系为 Y 厂B ,逻辑图如下:A 「> 1(1) AB ; (2) ABC ; (3) ABC ; (4) ABC解:(1) A=1 , B=1(2)A=1、B=1、C=0(3)A=0, B=1, C=0(4)A=1, B=0 或C=1【题2-10】如果如下和项的值为0,试写岀该和项中每个逻辑变量的取值。
第三章 逻辑代数基础 作业题(参考答案)

第三章逻辑代数基础(Basis of Logic Algebra)1.知识要点逻辑代数(Logic Algebra)的公理、定理及其在逻辑代数化简时的作用;逻辑函数的表达形式及相互转换;最小项(Minterm)和最大项(Maxterm)的基本概念和性质;利用卡诺图(Karnaugh Maps)化简逻辑函数的方法。
重点:1.逻辑代数的公理(Axioms)、定理(Theorems),正负逻辑(Positive Logic, Negative Logic)的概念与对偶关系(Duality Theorems)、反演关系(Complement Theorems)、香农展开定理,及其在逻辑代数化简时的作用;2.逻辑函数的表达形式:积之和与和之积标准型、真值表(Truth Table)、卡诺图(Karnaugh Maps)、最小逻辑表达式之间的关系及相互转换;3.最小项(Minterm)和最大项(Maxterm)的基本概念和性质;4.利用卡诺图化简逻辑函数的方法。
难点:利用卡诺图对逻辑函数进行化简与运算的方法(1)正逻辑(Positive Logic)、负逻辑(Negative Logic)的概念以及两者之间的关系。
数字电路中用电压的高低表示逻辑值1和0,将代数中低电压(一般为参考地0V)附近的信号称为低电平,将代数中高电压(一般为电源电压)附近的信号称为高电平。
以高电平表示1,低电平表示0,实现的逻辑关系称为正逻辑(Positive Logic),相反,以高电平表示0,低电平表示1,实现的逻辑关系称为负逻辑(Negative Logic),两者之间的逻辑关系为对偶关系。
(2)逻辑函数的标准表达式积之和标准形式(又称为标准和、最小项和式):每个与项都是最小项的与或表达式。
和之积标准形式(又称为标准积、最大项积式):每个或项都是最大项的或与表达式。
逻辑函数的表达形式具有多样性,但标准形式是唯一的,它们和真值表之间有严格的对应关系。
数理逻辑部分参考答案

4.下面的推理是否正确,请给予说明. (1) (x)A(x) B(x) (2) A(y) B(y) 前提引入 US (1)
错误。 因为(1)中(x)的辖域仅是 A(x),而不是 A(x) B(x)
四.计算题 1. 求 PQR 的析取范式,合取范式、主析取范式,主合取范式.
解:由于 P Q R P Q R 析取范式: P Q R 合取范式: P Q R 主析取范式 P Q R P Q R (P 1 1) (1 Q 1) (1 1 R) (P (Q Q) (R R)) (( P P) Q (R R)) (( P P) (Q Q) R) (P Q R) (P Q R) (P Q R) (P Q R) ( P Q R) ( P Q R) ( P Q R)
( A(a) A(b)) (B(a) B(b))
.
6.设个体域 D={1, 2, 3},A(x)为“x 大于 3”,则谓词公式(x)A(x) 的真值 为 0 . 7.谓词命题公式(x)((A(x)B(x)) C(y))中的自由变元为 8. 谓词命题公式(x)(P(x) Q(x) R(x, y))中的约束变元为 y x . .
三、公式翻译题 1.请将语句“今天是天晴”翻译成命题公式. 设 P:今天是天晴 则该语句符号化为 P 2.请将语句“小王去旅游,小李也去旅游.”翻译成命题公式. 设 P:小王去旅游,Q:小李也去旅游 则该语句符号化为 P∧Q
3.请将语句“他去旅游,仅当他有时间.”翻译成命题公式. 设: P:他去旅游 Q:他有时间 则该语句符号化为 P->Q 4.将语句“41 次列车下午五点开或者六点开.”翻译成命题公式. 设:
第三章 逻辑代数基础 作业题(参考答案)

第三章逻辑代数基础(Basis of Logic Algebra)1.知识要点逻辑代数(Logic Algebra)得公理、定理及其在逻辑代数化简时得作用;逻辑函数得表达形式及相互转换;最小项(Minterm)与最大项(Maxterm)得基本概念与性质;利用卡诺图(Karnaugh Maps)化简逻辑函数得方法。
重点:1.逻辑代数得公理(Axioms)、定理(Theorems),正负逻辑(Positive Logic, Negative Logic)得概念与对偶关系(Duality Theorems)、反演关系(plement Theorems)、香农展开定理,及其在逻辑代数化简时得作用;2.逻辑函数得表达形式:积之与与与之积标准型、真值表(Truth Table)、卡诺图(Karnaugh Maps)、最小逻辑表达式之间得关系及相互转换;3.最小项(Minterm)与最大项(Maxterm)得基本概念与性质;4.利用卡诺图化简逻辑函数得方法。
难点:利用卡诺图对逻辑函数进行化简与运算得方法(1)正逻辑(Positive Logic)、负逻辑(Negative Logic)得概念以及两者之间得关系。
数字电路中用电压得高低表示逻辑值1与0,将代数中低电压(一般为参考地0V)附近得信号称为低电平,将代数中高电压(一般为电源电压)附近得信号称为高电平。
以高电平表示1,低电平表示0,实现得逻辑关系称为正逻辑(Positive Logic),相反,以高电平表示0,低电平表示1,实现得逻辑关系称为负逻辑(Negative Logic),两者之间得逻辑关系为对偶关系。
(2)逻辑函数得标准表达式积之与标准形式(又称为标准与、最小项与式):每个与项都就是最小项得与或表达式。
与之积标准形式(又称为标准积、最大项积式):每个或项都就是最大项得或与表达式。
逻辑函数得表达形式具有多样性,但标准形式就是唯一得,它们与真值表之间有严格得对应关系。
第1章-逻辑代数基础习题解答

复习思考题1-1 离散信号就是数字信号吗?答:离散信号不一定是数字信号,如对连续信号在时间上进行采样,成为时间上离散、幅度上连续的信号就不是数字信号。
1-2 模拟信号转换成数字信号有哪些基本环节?数字系统比模拟系统有哪些优越性?答:模拟信号转换成数字信号包括采样、保持、量化、编码等基本环节。
与模拟电路相比,数字电路具有以下显著的优点:1)数字电路的基本工作信号是用1和0表示的二进制的数字信号,反映在电路上就是高电平和低电平,运算简单。
2)结构简单、设计技术成熟、容易制造,便于集成及系列化生产,通用性强,价格便宜。
3)数字电路能对输入的数字信号进行各种算术运算和逻辑运算、逻辑判断,具有“逻辑思维”能力。
4)可编程数字系统,使用更灵活。
5)速度快,抗干扰性强,可靠性高。
6)易于存储、加密、压缩、传输和再现,便于和计算机连接。
1-3 为什么数字电路采用二进制作为其基本工作信号?答:数字电路采用二进制作为其基本工作信号,主要原因是:1)技术实现容易。
二进制信号只有1和0两种信号,反映在电路上就是高电平和低电平,在电路上很容易由电子器件的开关特性实现。
2)运算规则简单。
二进制的数值运算规则简单,在实现上可以简化电路结构、提高系统的运行速度。
3)与逻辑运算吻合。
数字电路中采用1和0表示高低电平的方式和逻辑运算的数学方法—布尔代数,采用1和0表示不同的逻辑状态不谋而合,一方面可以将布尔代数广泛应用于开关电路和数字电路的设计中,设计方法简单;另一方面,可以由数字电路实现逻辑运算,而采用其它进制是很难实现的。
1-4 逻辑函数有哪两种标准表达式?答:逻辑函数有与-或表达式(最小项和的形式)和或-与表达式(最大项积的形式)两种标准表达式。
1-5 何为最小项?简述其编号方法。
答:设m为包含n个变量的乘积项,且这n个变量以原变量形式或者反变量形式在m中出现且只出现一次,称m为n变量的一个最小项。
最小项的编号规则:把最小项m中的原变量取值为1 ,反变量取值为0,所构成二进制数对应的十进制数即为该最小项的编号i,记作m i。
数理逻辑考试题及答案

数理逻辑考试题及答案一、单项选择题(每题2分,共20分)1. 以下哪个选项不是命题逻辑中的联结词?A. 与B. 或C. 非D. 存在答案:D2. 在布尔代数中,以下哪个表达式是正确的?A. ¬(A∧B) = ¬A∨¬ BB. A∧¬ A = AC. A∨¬ A = 1D. A∧(A∨B) = A答案:C3. 以下哪个命题是真命题?A. 如果今天是星期一,那么明天是星期二。
B. 所有的鸟都会飞。
C. 所有的人都是哲学家。
D. 2+2=5答案:A4. 在命题逻辑中,以下哪个命题的否定是正确的?A. 如果A,则B。
B. A且B。
C. A或B。
D. A当且仅当B。
答案:A5. 以下哪个选项是谓词逻辑中的量词?A. 与B. 或C. 存在D. 非答案:C6. 在谓词逻辑中,以下哪个表达式表示“存在一个x,使得x是学生”?A. ∀x (x 是学生)B. ∃x (x 是学生)C. ¬∃x (x 是学生)D. ¬∀x (x 是学生)答案:B7. 以下哪个选项是模态逻辑中的模态词?A. 与B. 或C. 可能D. 非答案:C8. 在模态逻辑中,以下哪个命题表示“必然P”?A. PB. ¬PC. ◊PD. □P答案:D9. 以下哪个命题是逻辑等价的?A. A∧BB. A∨BC. ¬A∧¬ BD. ¬(A∧¬B)答案:C10. 在逻辑推理中,以下哪个选项是演绎推理?A. 归纳推理B. 演绎推理C. 溯因推理D. 类比推理答案:B二、多项选择题(每题3分,共15分)1. 以下哪些选项是命题逻辑中的有效推理形式?A. 从A∧B,可以推出A。
B. 从A∨B,可以推出A。
C. 从A,可以推出A∨B。
D. 从A∧B,可以推出B。
答案:A, C, D2. 在布尔代数中,以下哪些表达式是等价的?A. A∧(B∨¬A)B. A∨(B∧¬A)C. A∧¬ BD. A∨¬ B答案:A, C3. 以下哪些命题是真命题?A. 如果A则B,且A为真,那么B也为真。
离散数学复习题答案

离散数学复习题答案一、逻辑与证明1. 命题逻辑的真值表:- 对于命题P和Q,给出所有可能的真值组合,并确定复合命题的真值。
2. 命题逻辑的等价性:- 证明两个命题逻辑表达式是等价的,即它们在所有可能的真值组合下都具有相同的真值。
3. 直接证明:- 给出一个逻辑命题,并使用直接证明方法证明其正确性。
4. 反证法:- 描述如何使用反证法证明一个命题的否定。
二、集合论1. 集合的基本运算:- 给出两个集合A和B,计算它们的并集、交集、差集和补集。
2. 子集和幂集:- 确定一个集合的所有子集,并构造它的幂集。
3. 集合的表示法:- 使用描述法和列举法表示集合。
三、关系与函数1. 关系的表示:- 给出一个关系R,并使用有序对集合的形式表示它。
2. 关系的性质:- 确定一个关系是否是自反的、对称的、传递的或反对称的。
3. 函数的定义:- 给出一个函数f的定义域和值域,并描述其性质。
4. 函数的复合:- 给出两个函数f和g,并计算它们的复合。
四、图论1. 图的基本概念:- 定义图的顶点、边、路径、回路等基本概念。
2. 图的分类:- 区分有向图、无向图、加权图和平面图。
3. 图的遍历:- 描述深度优先搜索(DFS)和广度优先搜索(BFS)算法。
4. 最短路径问题:- 使用Dijkstra算法或Floyd-Warshall算法求解图中的最短路径。
五、代数结构1. 群的定义:- 给出一个代数结构,并判断它是否构成一个群。
2. 子群和陪集:- 确定一个群的子群,并计算它的左陪集和右陪集。
3. 环和域:- 描述环和域的定义,并给出它们的性质。
六、布尔代数1. 布尔代数的基本运算:- 给出布尔代数中的逻辑运算:AND、OR、NOT。
2. 布尔表达式的简化:- 使用代数恒等式简化布尔表达式。
3. 布尔函数的真值表:- 为一个布尔函数构造真值表,并确定其等价的最小形式。
七、组合数学1. 排列组合:- 计算给定条件下的排列数和组合数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
---------------------------------------------------------------最新资料推荐------------------------------------------------------6 逻辑代数(上):命题演算习题答案练习 6.1 1. 判断下列语句哪些是命题,若是命题其真值是什么?(1) a+b+c。
(2) x 0 。
(3)请进!(4)离散数学是计算机科学与技术专业的基础课程。
(5) 2009 年 7 月我们去意大利的米兰旅游。
(6)啊!这里真漂亮。
(7)今天是星期四吗?(8)我明天或者后天去天津。
(9)如果买不到飞机票,我就去不了海南。
(10)除非你陪我,否则我不去。
(11)本命题是假的。
(12)如果雪是黑的,太阳从北边升起。
解:(1)不是命题。
(2)不是命题。
(3)不是命题。
(4)是命题。
真值是 1。
(5)是命题。
真值是 0。
1 / 17(6)不是命题。
(7)不是命题。
(8)是命题。
真值是 0。
(9)是命题。
真值是 1。
(10)是命题。
真值是 1。
(11)不是命题,是悖论。
(12)是命题。
真值是 1。
2. 指出下列语句哪些是原子命题,哪些是复合命题?并将复合命题形式化。
(1)他去了教室,也去了机房。
(2)今晚我去书店或者去图书馆。
(3)我昨天没有去超市。
(4)我们不能既看电视又看电影。
(5)如果买不到飞机票,我就去不了海南。
(6)小王不是坐飞机去上海,就是坐高铁去上海。
(7)喜羊羊和懒羊羊是好朋友。
(8)除非小李生病,否则他每天都会练习书法。
(9)侈而惰者贫,而力而俭者富。
---------------------------------------------------------------最新资料推荐------------------------------------------------------ (韩非:《韩非子显学》)解:(1) P:他去了教室。
Q:他去了机房。
PQ (2) P:今晚我去书店。
Q:今晚我去图书馆。
PQ (3) P:我昨天去超市。
(4) P:我们看电视。
Q:我们看电影。
(5) P:我买到飞机票。
Q:我去海南。
(6) P:3 / 17小王坐飞机去上海。
Q:小王坐高铁去上海。
(PQ)或者(7)原子命题(8) P:小李生病。
Q:小李每天都会练习书法。
(9) P:侈。
Q:惰。
R:贫。
()() 3. 判定下列符号串是否为命题公式。
(1)(2) (PQR)S (3) (PQ)P (4) P(PQ (5)(6)()(7)()(PQ)解:(1)不是(2)不是(3)是(4)不是(5)是(6)是(7)是 4. 请给出下列命题公式的真值表。
(1)(2)()()()() 0 0 1 1 0 1 0 1 1 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 0 1---------------------------------------------------------------最新资料推荐------------------------------------------------------5 / 171 0 (3) (PQ )(PQ )(PQ )1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 (4)() ()() ()0 0 1 1 0 1 0 1 1 1 0 1 0 0 1 0 0 0 0 0(5)()() P1 1 0 1 1 11 1 练习 6.2 1. 试判定下列各式是重言式、 可满足式还是矛盾式。
(1) (PQ)(QP) P Q PQ QP (PQ)(QP) 0 0 1 0 1 1 1 0 0 1 1 1 由表中最后一列可以看出, 原式为可满足式。
1 0 1 1 1 0 1 1 (2) ┐ P(PQ) P 0 0 1 1 由表中最后一列可以看出, 原式为重言式。
Q 0 1 0 1 ┐ P PQ ┐ P(PQ)1 1 1 1 0 0 0 1 1 1 1 1 (3) Q┐ (PQ) P Q PQ ┐ (PQ) Q┐ (PQ) 0 0 1 0 0 0 1 1 1 0 1 1 0 1 0 1 0 0 0 0由表中最后一列可以看出, 原式为矛盾式。
(4)1 1 1 1 1 0 0 1由表中最后一列可以看出,原式为重言式。
(5)0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 由表中最后一列可以看出, 原式为可满足式。
1 1 1 1 0 0 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 0 1 1 0 1 0 1 1 1 1 1 1 0 1 1 0 0 1 1 1 0 1 1 0 1 1 1 2.证明下列逻辑等价式:(1)证明:方法一方法二:0 0 1 0 0 1 1 1 1 1 0 0 0 1 1 由此真值表可见(┐ A┐ B)) 是永真式,所以成立。
方法三假设为一指派。
若,则 (A)= (B)。
(i)若 (A)= (B)=0。
则(┐ A)= (┐ B)=1,从而(┐ A┐ B)=1,进而(AB)(┐ A┐ B)=1. (ii)若 (A)= (B)=1。
则 (AB)=1,进而((AB)(┐ A┐ B)) =1。
若,则 (A)和 (B)不相等。
从而(┐ A)和(┐ B)也不相等。
则 (AB)=0且(┐ A┐ B)=0,从而((AB)(┐ A┐ B)) =0。
所以(2)证明:方法一方法二:---------------------------------------------------------------最新资料推荐------------------------------------------------------7 / 171 1 1 1 1 1 0 1 0 0 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 1 由此真值表可见是永真式, 所以成立。
方法三: 假设 为一指派。
若 (A(BC))=1,分以下二种情况:(i ) (A)=1, 则 (BC)=1. 若 (B)=0, 则 (B(AC))=1.若 (B)=1, 则 (C)=1,从而 (B(AC))=1. (ii) (A)=0, 则 (AC)=1。
从而 (B(AC))=1。
若 (A(BC))=0,则 (A)=1, (B)=1, (C)=0,从而 (B(AC))=0。
所以:(3)证明:)(4) 证明:证明下列逻辑蕴涵式:(1)证明:(方法一) 假设任一指派, 使得, 要证。
由于, 于是从而得到。
故得证。
(方法二)(方法三)由于 A 0 0 1 1 所以是永真式,所以。
(2)证明:假设任一指派,使得,要证。
由于,于是无论 B 为真还是为假,都有。
从而。
故得证。
(3)证明:(方法一)假设任一指派,使得要证(1)若于是,此时(2)若且于是,此时(3)若且于是,此时(4)若且于是,此时故得证。
(方法二)假设任一指派,使得要证。
由于所以且且。
由得到或者。
---------------------------------------------------------------最新资料推荐------------------------------------------------------9 / 17(1) 若 , 则由 得到。
(2) 若, 则由 得到故得证。
(方法三化简下列各式:(1) (A┐ B)(AB)(┐ A┐ B) 解:(2)(┐ QP)(PQ) 解:(3) 解:(4) B┐ ((┐ AB)A) 解:(5)(Q(P┐ Q)P)┐ (QP) 解:练习 6.3 1. 把下列各式化为析取范式:(1) (PQ)R 解:(2)(┐ PQ)R 解:(3)┐ (PQ)(PQ) 解:(4)(┐ QP)(P┐ Q) 解:Q┐ P)┐ P┐ Q 2. 把下列各式化为合取范式:(1) (PQ)R 解:(2)┐ B┐ ((┐ AB)A) 解:(3)解:(4)解:---------------------------------------------------------------最新资料推荐------------------------------------------------------11 / 17Q)(PR┐ R)S 3. 求下列公式的主析取范式、 主合取范式, 并据主析取范式直接确定使该公式为真指派,据主合取范式直接确定使该公式为假指派。
(1) (PQ) (┐ PQR) 解:求主析取范式(PQ┐ R) (┐ PQR) 使公式为真的指派有:(1,1,1)、(1,1,0)、(0,1,1) 求主合取范式 (PQ) (┐ PQR)R)(P┐ QR)(┐ PQR)(┐ PQ┐ R) 使公式为假的指派有:(0,0,0)、 (0,0,1)、 (0,1,0)、 (1,0,0)、 (1,0,1) (2) ┐解:求主析取范式Q)(┐ PQ) 使公式为真的指派有:(1,1)、 (1,0) 、(0,1) 求主合取范式使公式为假的指派有:(0,0) (3) P (┐ P(Q(┐ QR))) 解:求主析取范式((P┐ P) (Q┐ Q) R)PQR)(PQ┐ R)(┐ PQ┐ R)(PQR)(┐ PQR)(P┐ QR)(┐ P┐ QR)PQR) (┐ PQ┐ R) (┐ P┐ QR) 使公式为真的指派有:(1,1,1)、 (1,0,1)、 (1,1,0)、 (1,0,0)、 (0,1,1)、 (0,1,0)、(0,0,1) 求主合取范式使公式为假的指派有:(0,0,0) (4)解:求主合取范式PQ┐S)(P┐ QRS)(P┐ QR┐ S)(PQRS)(PQ┐ RS)(P┐ QRS)(P┐ Q┐ RS)(┐R┐ S)(P┐ QRS)(P┐ QR┐ S)(PQRS)(P┐ Q┐ RS)(┐ P┐ Q┐ RS)(┐ P┐ QRS)(┐ PQ┐ RS)(┐ PQRS) 使公式为假的指派有:(0,0,0,0)、 (0,0,1,0)、 (0,0,1,1)、 (0,1,0,0)、 (0,1,0,1)、(0,1,1,0) 、 (1,0,0,0)、 (1,0,1,0)、 (1,1,0,0)、 (1,1,1,0) 使公式为真的指派有:(0,0,0,1)、 (0,1,1,1)、 (1,0,0,1)、 (1,0,1,1)、 (1,1,0,1)、(1,1,1,1) 主析取范式为(┐ P┐ Q┐ RS)(┐ PQRS)(P┐ Q┐ RS)(P┐ QRS)(PQ┐ RS)(PQRS) 4. A、 B、 C、 D 四个人中要派---------------------------------------------------------------最新资料推荐------------------------------------------------------13 / 17两个人出差, 按下述三个条件有几种派法? 如何派? (1) 若去则 C 和 D 中要去一个人; (2) B 和 C 不能都去; (3) C 去则 D 要留下。
