经典力学与量子力学中的一维谐振子
2.7 一维谐振子问题
一
经典简谐运动 弹簧振子的振动
l0
k
x0 F 0
m
A
o
A
x
一维谐振子问题
在经典力学中,一维经典谐振子问题是个基本 的问题 在经典力学中,简谐振动的定义: 任何物理量 x 的变化规律若满足方程式
1 V0 k ( x a )2 2
xa
V(x) a 0
V0
x
取新坐标原点为(a, V0),则势可表示为 标准谐振子势的形式:
V(x)
a
x
1 2 V ( x ) kx 2
0
V0
可见,一些复杂的势场下粒子的运动往往 可以用线性谐振动来近似描述。
在微观领域中,一维量子谐振子问题也是个基 本的问题,甚至更为基本。因为它不仅是微观粒 子在稳定平衡位置附近作小振动一类常见问题的 普遍概括,而且更是将来场量子化的基础。
经典力学中,一维谐振子的哈密顿
p p 1 2 2 H V m x 2m 2m 2
上式用相应算符代入,得
2
2
d 1 2 2 ˆ H m x 2 2m dx 2
是一维谐振子的哈密顿算符,是能量算符。
2
2
————一维谐振子的定态薛定谔方程
2 d2 1 2 2 x ( x ) E ( x ) 2 2 2 dx
x a
V (a) V0
V x
V 0 0 x a x x a
1 2V V0 2! x 2
量子力学课件(7)( 一维线性谐振子)

(2)本征方程及其能量本征值
y z
第二章 薛定谔方程
如果系统 Hamilton 量可以写成
x
则必有: 则必有:
E = E x + E y + Ez Ψ = ψ ( x )ψ ( y )ψ ( z )
因此,设能量本征方程的解为: 因此,设能量本征方程的解为:
E
第二章 薛定谔方程 §8 一维线性谐振子 (ξ)是 项厄密多项式, Hn(ξ)是n项厄密多项式,前4个项厄密多项式分别是
H 0 (ξ ) = 1, H 1 (ξ ) = 2ξ , H 2 (ξ ) = 4ξ − 2,
2
H 3 (ξ ) = 8ξ − 12ξ .
3
ϕ n (ξ ) = (
α π 2 n!
则schrodinger方程可写为第二章薛定谔方程一维线性谐振子取能量单位长度单位取能量单位长度单位此式是一变系数二阶常微分方程设定边界条件束缚态条件意思是谐振设定边界条件束缚态条件意思是谐振子出现在无穷处的概率为零
9.1 坐标空间线性谐振子的哈密顿
(1)何谓谐振子
§8 一维线性谐振子
第二章 薛定谔方程
§8 一维线性谐振子
第二章 薛定谔方程
厄密多项式和谐振子波函数的递推关系: 厄密多项式和谐振子波函数的递推关系:
应 用 实 例
=2ξ, 例:已知 H0 = 1, H1=2ξ, 则根据上述递推关系得出: 则根据上述递推关系得出: H2 = 2ξH1-2nH0 = 4ξ2-2
从上式出发, 从上式出发,可导出 厄密多项式的递推关系: 厄密多项式的递推关系: dH n = 2nH n −1 (ξ ) dξ H n +1 − 2ξ H n + 2nH n −1 = 0
量子力学周世勋习题解答第三章

第三章习题解答3.1 一维谐振子处在基态t i x e x ωαπαψ2222)(--=,求:(1)势能的平均值2221x U μω=; (2)动能的平均值μ22p T =;(3)动量的几率分布函数。
解:(1) ⎰∞∞--==dx e x x U x 2222222121απαμωμωμωμωππαμω ⋅==⋅=2222221111221ω 41= (2) ⎰∞∞-==dx x p x p T )(ˆ)(2122*2ψψμμ ⎰∞∞----=dx e dx d e x x 22222122221)(21ααμπα ⎰∞∞---=dx e x x 22)1(22222αααμπα][222222222⎰⎰∞∞--∞∞---=dx e x dx e x x ααααμπα]2[23222απααπαμπα⋅-=μωμαμαπαμπα⋅===442222222 ω 41=或 ωωω 414121=-=-=U E T (3) ⎰=dx x x p c p )()()(*ψψ 212221⎰∞∞---=dx ee Px i xαπαπ⎰∞∞---=dx eePx i x222121απαπ⎰∞∞--+-=dx ep ip x 2222222)(21 21αααπαπ ⎰∞∞-+--=dx ee ip x p 222222)(212 21αααπαπ παπαπα2212222p e -=22221απαp e-=动量几率分布函数为 2221)()(2απαωp ep c p -==#3.2.氢原子处在基态0/301),,(a r e a r -=πϕθψ,求:(1)r 的平均值;(2)势能re 2-的平均值;(3)最可几半径; (4)动能的平均值;(5)动量的几率分布函数。
解:(1)ϕθθπτϕθψππd rd d r re a d r r r a r sin 1),,(0220/23020⎰⎰⎰⎰∞-==⎰∞-=0/233004dr ar a a r04030232!34a a a =⎪⎪⎭⎫⎝⎛=2203020/232020/232202/2322214 4 sin sin 1)()2(000a e a a e drr ea e d drd r e a e d drd r e ra e r e U a r a r a r -=⎪⎪⎭⎫ ⎝⎛-=-=-=-=-=⎰⎰⎰⎰⎰⎰⎰∞-∞-∞-ππππϕθθπϕθθπ(3)电子出现在r+dr 球壳内出现的几率为 ⎰⎰=ππϕθθϕθψω02022 sin )],,([)(d drd r r dr r dr r e a a r 2/23004-=2/23004)(r e a r a r -=ω 0/2030)22(4)(a r re r a a dr r d --=ω 令 0321 , ,0 0)(a r r r drr d =∞==⇒=,ω当0)( ,0 21=∞==r r r ω时,为几率最小位置/22203022)482(4)(a r e r a r a a dr r d -+-=ω08)(230220<-=-=e a dr r d a r ω ∴ 0a r =是最可几半径。
一维量子谐振子的概率分布.

一维量子谐振子的概率分布摘要:线性谐振子问题作为一种普遍的模型,所以在经典力学中和量子力学中都受到很大关注。
并且谐振子包括很多类型,我们就先研究量子谐振子的问题。
量子谐振子是很多复杂物理模型的基础,量子谐振子在前几个量子态时,概率密度与经典情况相差较多,随着量子数的增加,随之相似性也会增加。
可以通过使用数学软件将量子谐振子的概率分布绘制成图像,从而得出一维量子谐振子的概率分布。
关键词:经典谐振子一维量子谐振子波函数量子谐振子概率分布1.引言:谐振子的振动是一种很常见的物理模型,它在很多方面得到应用。
谐振子大体可分为经典力学和量子力学两部分,谐振在运动学就是简谐振动,这样的振动是物体在某一位置附近往复偏离该振动中心位置,在这样的振动方式下,物体所受到的力的大小总是与它偏离平衡位置的大小成正比关系,并且物体总是受到指向平衡位置的力。
谐振子具有周期运动的物理特征,一些复杂的物理基础可以运用谐振子运动来解决。
通过对经典谐振子的研究,得到经典谐振子的函数关系式。
再利用量子力学中的不确定关系得到量子谐振子的能量最低点,即平衡位置,最后得到谐振子的波函数,从而得到了谐振子的概率。
随着量子数的增加,利用软件Mathematica绘制一维量子谐振子的概率分布。
再和经典的线性谐振子来作比较,得到经典谐振子的关系。
2.经典一维谐振子:首先让我们谐振子在物理中是非常常见的模型,我们很早就已经接触过,并且有了一定的了解。
下面来讨论一维弹性力的一维简谐振子。
例如:质量为m的物体放在光滑的桌面上,在其水平的方向上受到一个弹簧作用,在某一位置处质点所受力的大小为零,则把这一点叫做平衡位置。
弹簧的劲度系数为k,物体m在弹簧弹性力的作用下沿弹簧方向运动,作用于质点的力和质点距离平衡位置的位移成正比,这样受力的质点就是一个典型的一维简谐振子。
大家都知道,质量为m的质点在做简谐振动的过程中用x来表示质点便偏移平衡位置的距离,也就是质点的位置,也是弹簧的伸长或压缩的量。
一维谐振子与量子力学的简正模

一维谐振子与量子力学的简正模一维谐振子是量子力学中经典物理中的一个重要模型。
它的简正模是量子力学中研究谐振子性质的基本工具之一。
首先,让我们先来回顾一下经典物理中的一维谐振子。
在经典物理中,一维谐振子可以用一个均匀弹性棒和一个固定在一端的质点构成。
弹性棒的弹性系数和质点的质量决定了谐振子的固有频率。
当弹性棒偏离平衡位置时,会受到回复力的作用,使谐振子回到平衡位置,形成周期性的振动。
谐振子的运动可以用振幅、频率和相位等参数来描述。
在量子力学中,一维谐振子的简正模类似于经典物理中的固有频率。
但是,由于量子力学的存在,量子力学中的一维谐振子并不像经典物理中那样,可以处于任意能量状态。
相反,在量子力学中,一维谐振子只能处于一个离散的能量状态,称为简正模。
这些简正模对应于不同的能级,而能级之间的能量差是固定的。
量子力学中的一维谐振子的简正模可以用算符来描述。
算符是量子力学中非常重要的工具,它们用来描述物理量的变换和性质。
对于一维谐振子,位置和动量是两个非常重要的物理量。
对应于位置和动量的算符分别是位置算符和动量算符。
这两个算符满足一些特定的对易关系,这些对易关系决定了一维谐振子的简正模的性质。
例如,位置算符和动量算符之间的对易关系可以写为[x, p] = iħ,其中x表示位置算符,p表示动量算符,[x, p]表示它们的对易子,ħ是普朗克常量除以2π。
这个对易关系表明,位置和动量不能同时精确确定,而是存在一定的不确定性。
这也是著名的海森堡不确定性原理的一个具体体现。
通过求解一维谐振子的定态薛定谔方程,我们可以得到一维谐振子的简正模的波函数形式。
一维谐振子的波函数是一个关于位置的函数,它描述了粒子在不同位置的概率分布。
一维谐振子的简正模的波函数是驻波形式的,也就是说,它在空间中有固定的振动模式。
简正模的波函数是离散的,而且对应的能量也是离散的。
这些简正模的波函数的形式和特性可以用波函数的正交性和归一化条件来求解。
量子力学3.3一维谐振子

量子隧道效应实验
总结词
量子隧道效应实验是用来验证量子力学中隧 道效应的实验方法,通过观察粒子穿越障碍 物的现象,可以证明粒子具有穿越障碍物的 能力。
详细描述
在量子隧道效应实验中,粒子在一定能量下 可以穿越高于其自身能量的势垒,这种现象 被称为量子隧道效应。实验中可以通过测量 穿越势垒的粒子数量和能量分布,来验证量 子力学中隧道效应的预测。
子不同。
干涉实验
总结词
干涉实验是用来验证量子力学中波动性 质的另一种实验方法,通过观察粒子在 通过两个相距较近的障碍物后产生的干 涉现象,可以进一步验证量子力学的正 确性。
VS
详细描述
在干涉实验中,粒子通过两个相距较近的 障碍物后,会在屏幕上产生类似于水波通 过两个相距较近的小孔后产生的干涉条纹 。这进一步证明了粒子具有波动性质,并 且其行为方式与经典物理中的粒子不同。
05
CATALOGUE
一维谐振子的实验验证
双缝实验
总结词
双缝实验是用来验证量子力学中波动性质的经典实验,通过观察电子通过双缝后的干涉 现象,可以证明电子具有波动性。
详细描述
在双缝实验中,电子通过双缝后会在屏幕上产生干涉条纹,类似于水波通过两个相距较 近的小孔后产生的干涉现象。这表明电子具有波动性质,其行为方式与经典物理中的粒
经典力学中的一维谐振子
1
在经典力学中,一维谐振子通常由弹簧和质点组 成,其运动方程为 Hooke定律。
2
一维谐振子的能量与其振幅的平方成正比,当能 量增加时,振幅也会增加,导致系统的不稳定性 。
3
在经典力学中,一维谐振子的运动轨迹是确定的 ,可以用经典力学方程进行描述。
02
CATALOGUE
一维谐振子基态和激发态的波函数

标题:深度探讨一维谐振子基态和激发态的波函数一、引言一维谐振子是量子力学中的经典问题之一,它的波函数描述了粒子在谐振势场中的运动状态。
在本文中,我们将深入探讨一维谐振子的基态和激发态的波函数,分析其数学形式和物理意义,以帮助读者更好地理解这一重要概念。
二、基态的波函数让我们来分析一维谐振子的基态波函数。
基态对应能量最低的状态,其波函数通常用Ψ₁(x)来表示。
在一维谐振子中,基态波函数可以用简单的数学形式进行描述:Ψ₁(x) = (mω/πħ)^(1/4) * e^(-mωx²/2ħ)其中,m是粒子的质量,ω是振子的角频率,ħ是约化普朗克常数。
这个波函数描述了基态下粒子在空间中的分布情况,通过对波函数的形式和特性进行分析,我们可以了解到粒子在基态下的基本运动状态和概率分布规律。
在基态下,粒子处于能量最低的状态,波函数的峰值对应着粒子最有可能出现的位置。
基态波函数的特性还可以通过数学手段进行分析,例如计算平均位置、动量期望值等,这些都能帮助我们更好地理解基态下粒子的运动规律和物理性质。
三、激发态的波函数接下来,我们将讨论一维谐振子的激发态波函数。
激发态对应能量高于基态的状态,其波函数通常用Ψ₂(x)来表示。
在一维谐振子中,激发态波函数的数学形式相对复杂一些,但通过分析和理解其特性,我们同样可以获得丰富的物理信息。
激发态波函数通常包含更多的波峰和波谷,描述了粒子在激发状态下的空间分布情况。
通过比较基态和激发态波函数的形式和特性,我们可以发现它们之间的微妙差别,并据此推断粒子在不同能级状态下的运动规律和行为。
激发态波函数的数学性质也具有重要意义,例如其振幅、波长、频率等特征参数都可以提供宝贵的信息。
通过对激发态波函数进行分析,我们可以更全面地理解粒子在谐振势场中的非基态运动状态,为进一步研究和应用提供重要的参考依据。
四、总结与展望通过本文的深度探讨,我们对一维谐振子的基态和激发态波函数有了全面的理解。
经典力学与量子力学中的一维谐振子

经典力学与量子力学中的一维谐振子物理与电子信息工程学院物理学[摘要]一维谐振动是一种最简单的振动形式,许多复杂的运动都可分析为一维谐振动。
本文以一维谐振子为研究对象,首先讨论经典力学与量子力学中的一维谐振子的运动方程和能量特征,然后分析坐标表象以及粒子数表象下的一维谐振子,最后讨论经典力学与量子力学中的一维谐振子的区别与联系。
[关键词]谐振子经典力学量子力学运动方程能量分布1 前言所谓谐振,在运动学中就是简谐振动。
一个劲度系数为k的轻质弹簧的一端固定,另一端固结一个可以自由运动的质量为m的物体,就构成一个弹簧振子[1]。
该振子是在一个位置(即平衡位置)附近做往复运动。
在这种振动形式下,物体受力的大小总是和它偏离平衡位置的距离成正比,并且受力方向总是指向平衡位置。
这种情况即为一维谐振子。
一维谐振子在应用上有很大价值,因为经典力学告诉我们只要选择适当的坐标,任意粒子体系的微小振动都可以认为是一些相互独立的振子的运动的集合。
普朗克在他的辐射理论中将辐射物质的中心当作一些谐振子,从而得到和实验相符合的结果。
在分子光谱中,我们可以把分子的振动近似地当作谐振子的波函数。
另外在量子场论中电磁场的问题也能归结成谐振子的形式。
因此在量子力学中,谐振子问题的地位较经典物理中来得重要。
应用线性谐振子模型可以解决许多量子力学中的实际问题。
本文将以一维谐振子为研究对象,首先分别讨论经典力学与量子力学中一维谐振子的运动方程和能量特征,然后讨论坐标表象以及粒子数表象下的一维谐振子,最后分析经典力学与量子力学中的一维谐振子的区别与联系并简要讨论经典力学与量子力学的过渡问题。
从而帮助我们更加深入的理解一维谐振子的物理实质,充分认识微观粒子的波粒二象性。
2 经典力学中的一维谐振子在经典力学中基本方程以牛顿定律为基础,研究质点位移随时间变化的规律,反映质点特征的是运动方程和能量。
因此我们可以从运动方程和能量这两方面出发讨论一维谐振子的运动特征。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经典力学与量子力学中的一维谐振子物理与电子信息工程学院物理学[摘要]一维谐振动是一种最简单的振动形式,许多复杂的运动都可分析为一维谐振动。
本文以一维谐振子为研究对象,首先讨论经典力学与量子力学中的一维谐振子的运动方程和能量特征,然后分析坐标表象以及粒子数表象下的一维谐振子,最后讨论经典力学与量子力学中的一维谐振子的区别与联系。
[关键词]谐振子经典力学量子力学运动方程能量分布1 前言所谓谐振,在运动学中就是简谐振动。
一个劲度系数为k的轻质弹簧的一端固定,另一端固结一个可以自由运动的质量为m的物体,就构成一个弹簧振子[1]。
该振子是在一个位置(即平衡位置)附近做往复运动。
在这种振动形式下,物体受力的大小总是和它偏离平衡位置的距离成正比,并且受力方向总是指向平衡位置。
这种情况即为一维谐振子。
一维谐振子在应用上有很大价值,因为经典力学告诉我们只要选择适当的坐标,任意粒子体系的微小振动都可以认为是一些相互独立的振子的运动的集合。
普朗克在他的辐射理论中将辐射物质的中心当作一些谐振子,从而得到和实验相符合的结果。
在分子光谱中,我们可以把分子的振动近似地当作谐振子的波函数。
另外在量子场论中电磁场的问题也能归结成谐振子的形式。
因此在量子力学中,谐振子问题的地位较经典物理中来得重要。
应用线性谐振子模型可以解决许多量子力学中的实际问题。
本文将以一维谐振子为研究对象,首先分别讨论经典力学与量子力学中一维谐振子的运动方程和能量特征,然后讨论坐标表象以及粒子数表象下的一维谐振子,最后分析经典力学与量子力学中的一维谐振子的区别与联系并简要讨论经典力学与量子力学的过渡问题。
从而帮助我们更加深入的理解一维谐振子的物理实质,充分认识微观粒子的波粒二象性。
2 经典力学中的一维谐振子在经典力学中基本方程以牛顿定律为基础,研究质点位移随时间变化的规律,反映质点特征的是运动方程和能量。
因此我们可以从运动方程和能量这两方面出发讨论一维谐振子的运动特征。
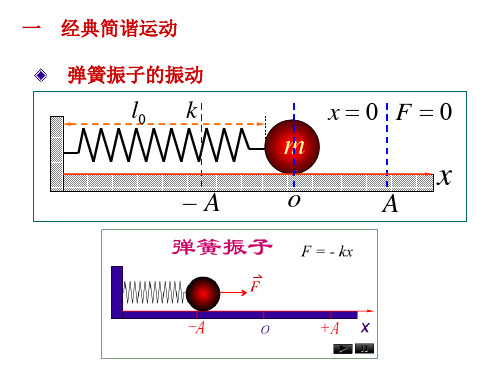
一个劲度系数为k 的轻质弹簧的一端固定,另一端固结一个可以自由运动的质量为m 的物体,就构成一个弹簧振子[1],如图2.1。
当弹簧处于自然长度时,物体处于平衡位置,取作坐标原点,以O 表示。
沿弹簧长度方向(取作x 轴方向)拉动物体然后释放,则物体将在O 点两侧作往复运动。
图2.1 弹簧振子2.1 一维谐振子的运动方程图2.1中的物体可视为一个质点。
设x 代表质点相对于平衡位置的位移,则质点所受的力kx F -=,其中k 为劲度系数。
负号表示F 与位移方向相反,因而总是指向平衡位置。
由牛顿第二定律,谐振子的运动微分方程为:kx xm -= 即 02=+x x ω (2.1.1)这是一个二阶的常系数线性微分方程。
令mk =ω (2.1.2) ω即简谐运动的角频率,由振动系统本身的性质嗦决定。
将(2.1.2)式代入(2.1.1)式,则可求出(2.1.1)式的通解:iwt iwt Ne Me t x -+=)( (2.1.3))sin(ϕω+=t A这就是谐振子的运动方程[2]。
其中M 和N 是任意常数,由质点的初位置和初速度确定。
A 是振幅,ϕ是初相位。
(2.1.3)式表明质点应作简谐振动[2]。
2.2 一维谐振子的能量在谐振子问题中,振子的总能量可以反映出振子的运动特征。
因此我们可以从谐振子的动能和势能出发,求解谐振子的总能量,进而帮助我们分析振子的运动特征。
由(2.1.3)式可知,振子的速度为:)cos(ϕωω+==t A dtdx v 振子的动能为:)(cos 21)(212122222ϕωω+===t C m dt dx m mv E k 由(2.1.2)式,有: )(cos 2122ϕω+=t kA E k (2.2.1) 由(2.2.1)式可知,振子的动能变化频率为ω2。
振子的势能(以平衡位置的势能为零)为:2021kx Fdx E xp =-=⎰ 即为:)(sin 2121222ϕω+==t kA kx E p (2.2.2) 由(2.2.2)式可知,振子的势能变化频率也为ω2。
因此,由(2.2.1)式和(2.2.3)式可得,振子的总能量为:221kA E E E p k =+= (2.2.3) 由(2.2.3)式可知:谐振子的总能量不随时间改变,即其机械能守恒[3]。
(2.2.3)式还说明:对于一定的振子(m 和k 给定,因而ω给定),总能量与振幅的平方成正比[3]。
振幅不仅给出了简谐运动的运动范围,而且还反映了振动系统总能量的大小,或者说反映了振动的强度。
3 量子力学中的一维谐振子在量子力学中,粒子状态用波函数表示,为了描述微观粒子状态随时间变化的规律,就需要找出波函数所满足的运动方程,即薛定谔方程。
因此下面将从谐振子的哈密顿算符出发,求解振子的定态薛定谔方程,进而分析量子力学中一维谐振子的运动特征。
3.1 用运动方程求解的一维谐振子我们可以从谐振子的势能函数出发,写出谐振子的哈密顿算符及薛定谔方程,并求谐振子的能量和定态波函数的解,进而讨论能量分布特点。
取谐振子的平衡位置0r 为坐标原点,并选原点为势能的零点,则有0)(0=r E p 。
仅考虑一维情况。
由于kz j y i x r ˆˆˆ+-= 在x 轴方向分振动的谐振子在x 处的势能可以表示为:221)(kx x E p = (3.1.1) 势能曲线是一条定点在原点的抛物线,如图3.1所示:图3.1 一维谐振子的势能一维谐振子的经典哈密顿函数为:22212kx m p H += 设振子的原子质量为μ,则振子的频率为:mk =ω 振子的哈密顿算符可以写为: 22222ˆ212x m dx d m H ω+-= 相应的定态薛定谔方程)(ψψE H = 为:)()()212(22222x E x x m dx d m ψψω=+- (3.1.1) 这是一个二阶线性微分方程。
如果振子的运动不受限制,x 的变化范围为+∞<<∞-x 。
当∞→x 时,(3.1.1)式的解一般为无穷大,表示振子在无穷远处的几率为无穷大。
这不符合物理要求。
但若振子的能量E 取下列特殊值[4]:ω )21(+=n E )2,1,0( =n (3.1.2) 其中 为普朗克常数,ω为经典力学中谐振子的频率。
则对每一个n 值,方程(3.1.1)都有一个在全区间+∞<<∞-x 中有界的解。
而且当∞→x 时,这个解趋于零。
这显然符合对谐振子问题的物理要求。
与(3.1.2)式的能量值相应的关于定态波函数的解为: )()(2x H Ae x n x αψα-= (3.1.3) 其中0>=hkm α,)(ξn H 是E 的一个n 次多项式,称为厄米多项式[4]。
其前四项为:1)(0=ξH ξξ2)(1=H24)(22-=ξξHξξξ128)(33-=H 由于)(x H n α是x 的n 次多项式,且0>α。
因此,当∞→x 时,(3.1.3)式趋于零。
由(3.1.2)式知,在量子力学中谐振子的能量是分立的,与振幅无关,只依赖于振子的固有特性---振子的本征频率ω。
(3.1.2)式还表明[5],频率为ω的振子其能量的改变只能是能量单元ω 的整数倍。
这一点同普朗克的能量子假设是一致的。
但量子力学中振子的最低能级(基态能量)不再是零而是ω 21,称为零点能[5]。
它充分体现了粒子具有波粒二象性。
3.2 坐标表象中的一维谐振子粒子系统的状态用以空间坐标为自变量,以时间为参量的波函数),(t r 来描述,这种表示形式称为坐标表象[6]。
下面从谐振子的哈密顿算符出发,求解谐振子的能量本征值和定态波函数,并对谐振子在量子力学与经典力学中的几率密度进行比较,给出量子谐振子向经典谐振子过渡的条件。
一维谐振子的哈密顿算符为:22222212x m dx d m H ω+-= 坐标表象中,振子的定态薛定谔方程为:)()()212(22222x E x x m dx d m ψψω=+- 引入没有量纲的变量ξ代替x ,它们的关系是x x m αωξ≡≡ ωαm =ωλ E 2=(3.2.1) 以ω2乘以式(3.1.1),利用式(3.1.2)和式(3.1.3),薛定谔方程可改写为 0)(222=-+ψξλψξd d (3.2.2) 这是一个变系数的二阶常微分方程。
当ξ很大时,λ与2ξ相比可以略去,因而在±∞→ξ时,(3.2.2)式可以写为:ψξξψ222=d d 它的解是ψ~22ξ±e 。
因为波函数的标准条件要求当±∞→ξ时,ψ应为有限,所以对波函数只取指数上的负号:ψ~22ξ-e 。
根据上面的讨论,我们把ψ写成如下形式来求(3.2.2)式的解:)()(22ξξψξH e -= (3.2.3)(3.2.3)式代入(3.2.2)式可得)(ψH 满足方程:0)1(222=-+-H d dH d H d λξξξ(3.2.3) 用级数解法,把H 展开成ξ的幂级数,来求着方程的解。
这个级数必须只含有限项,才能在±∞→ξ时使)(ξψ为有限;而级数只含有限项的条件是λ为奇数:12+=n λ, 2,1,0=n代入(3.2.1)式即可得谐振子的能级为:)21(+=n E n ω , 2,1,0=n (3.2.4) 可见,谐振子的能量只能取分立值,两相邻能级间隔均为ω ,即:ω =-+n n E E 1在坐标表象中可以明显看出:是描述粒子波动性的波函数)(x ψ受到势能场的约束使能谱分立。
与(3.2.4)式定态能量对应的定态波函数:)()(222x H eN x n x n n αψα-= 式中2121)!2(n N n n πα=是归一化常数,它由归一化条件1)()(*=⎰∞∞-dx x x n n ψψ确定。
图3.2中画出了3,2,1,0=n 的几率密度2n ψ(图中实线),图中虚线是经典谐振子的平均位置密度。
从图3.2可见,经典谐振子不能进入A x >的区域。
而量子谐振子能进入这种区域,但进入以后指数衰减。
可见,量子振子和经典振子完全不同,但当n 增大时,n E E ∆减小,量子振子向经典振子过渡。
图3.2 一维谐振子的位置几率密度分布 3.3 粒子数表象中的谐振子以粒子数算符的本征矢|n 〉为基矢的表象称为占有数表象[7],又叫粒子数表象。
我们可以通过引入升降算符求解谐振子,求出谐振子的能量本征值以及坐标算符xˆ和动量算符p ˆ的矩阵元。
一维谐振子的经典哈密顿函数为:22212kx p H +=μ (3.3.1) 在量子力学里,谐振子的哈密顿算符具有同一形式:222ˆ21ˆ21x p H μωμ+-= (3.3.2) 将经典泊松括号换成量子泊松括号:[]1ˆ,ˆ-=PB p x → []1ˆ,ˆ-=p x i由xˆ与p ˆ的对易关系: [] i x p p x p x =-=ˆˆˆˆˆ,ˆ (3.3.3)定义两个非厄米算符aˆ和+a ˆ: )ˆ1ˆ(2ˆx pi xa μωμω+=)ˆ1ˆ(2ˆx pi x a μωμω-=+ (3.3.4) 这两个非厄米算符满足如下基本对易关系:][1ˆ,ˆ=+a a (3.3.5) 则(3.3.4)式的逆变换关系为: )ˆˆ(2ˆa a x +=+μω(3.3.6) )ˆˆ(2ˆa ap -=+μω 利用(3.3.6)式,代入(3.3.2)式,并考虑对易关系(3.3.5),哈密顿算符又可表示为:)21ˆˆ(ˆ+=+a a H ω (3.3.7) 由于Hˆ与算符a a ˆˆ+仅仅相差一个常数矩阵,所以只需求解a a ˆˆ+得本征值问题。
