平面二级倒立摆系统仿真
平面两级倒立摆的建模
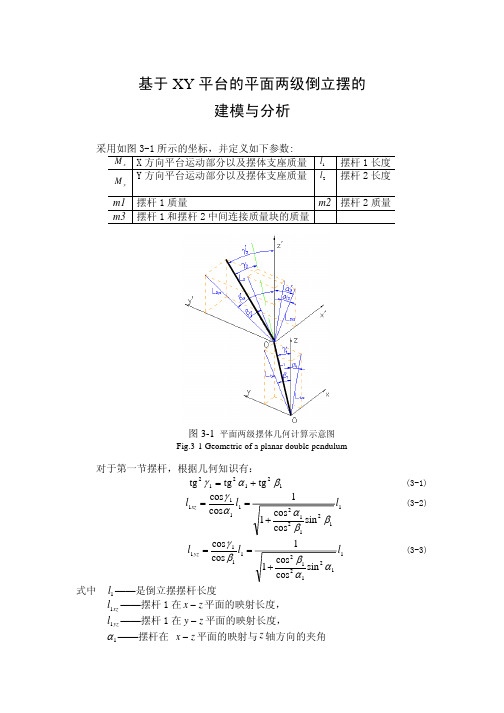
采用如图 3-1 所示的坐标,并定义如下参数:
M x X 方向平台运动部分以及摆体支座质量 l1 摆杆 1 长度
Y 方向平台运动部分以及摆体支座质量
My
l2
摆杆 2 长度
m1 摆杆 1 质量
m2 摆杆 2 质量
m3 摆杆 1 和摆杆 2 中间连接质量块的质量
(3-1) (3-2)
(3-3)
β1 ——摆杆在 y − z 平面的映射与 z 轴方向的夹角 γ 1 ——摆杆与 z 轴方向的夹角 γ 2 ——摆杆与 z 轴方向的夹角 在摆杆垂直向上的方向上,如果偏角α1, β1 << 1 ,则可以近似的认为
l1xz ≈ l1yz ≈ l1
因此,摆杆绕 X 轴和 Y 轴的转动惯量可以表示为:
⋅2
y1
⋅
⋅ y2
+
1 2
m1
⋅
2
+
1 2
m2
⋅2
z1 +
⋅2
⋅ z2
1 2
+
⋅2 ⋅2
J1 ⋅ (α1 + β1 )
1 2
J2
⋅
⋅
(α 2
2
+
⋅
β2
2
)
⎪ ⎪⎪⎩Tm3
=
1 2
m3
⋅
⋅2
x3 +
1 2
m3
⋅
⋅2
y3 +
1 2
m3
⋅
⋅2
z3
式中 x1 ——摆杆 1 中心点的 X 坐标;
y1 ——摆杆 1 中心点的 Y 坐标;
由拉各朗日方程:
二级倒立摆的建模与MATLAB仿真

二级倒立摆的建模与 MATLAB 仿真 刘文斌,等
二级倒立摆的建模与MATLAB仿真
刘文斌,干树川 (四川理工学院电子与信息工程系 四川自贡,643000)
取为最小值。设控制输入函数形式为: U(t)= -Kx(t) (11) 状态反馈矩阵: K = R -1B T P ( 12) 其中,P 可由 Riccati 微分方程: (13) 其中, 性能指标函数: (14)
[J].计算机测量与控制,2006,14(12):1641 - 1642 5 张 春,江 明,陈其工等.平行单级双倒立摆系统的建模与滑
模变结构控制[J].2008.1
23
图1 二级倒立摆模型
(1)
(2)
(3) 经过线性化如下: (4)
(上接第 7 页) 0; 0; 0; 0]; p=eig(A) [num,den]=ss2tf(A,B,C,D,1); printsys(num,den) Q=[1000 0 0 0 0 0; 0 0 0 0 0 0; 0 0 10 0 0 0; 0 0 0 0 0 0; 0 0 0 0 10 0; 0 0 0 0 0 0]; Tc=ctrb(A,B); rank(Tc) To=obsv(A,C); rank(To) R=1; K=lqr(A,B,Q,R); Ac=[(A-B*K)]; Bc=[B]; Cc=[C]; Dc=[D]; T=0:0.005:20; U=0.2*ones(size(T)); [Y,X]=lsim(Ac,Bc,Cc,Dc,U,T); plot(T,Y(:,1),':',T,Y(:,2),' -',T,Y(:,3),'
二级直线倒立摆系统建模、仿真与实物控制的开题报告

二级直线倒立摆系统建模、仿真与实物控制的开题报告一、选题背景及意义直线倒立摆系统是一种应用广泛的控制系统,它具有复杂的非线性特性,因此对其建模、控制和仿真都具有一定的挑战性。
直线倒立摆系统广泛应用于自动驾驶、飞行器、医疗器械等领域。
本文将研究二级直线倒立摆系统的建模、仿真与实物控制,以提高对该系统的理解和掌握。
通过实验控制实际系统,验证仿真模型的正确性并提高控制策略的可靠性与性能。
二、研究内容1.二级直线倒立摆系统的建模研究系统的动力学特性,建立数学模型,包括机械、电子等方面的模型,并给出系统的描述方程。
2.仿真系统的设计与实现通过MATLAB或Simulink等工具,根据系统的动力学模型进行仿真,分析系统的动态特性,验证模型的正确性。
3.实物系统的设计与实现根据建模结果,设计实物系统,包括硬件和软件,搭建实验环境,并选取合适的控制器,使用反馈控制算法对实验数据进行处理。
4.实物控制系统的测试与优化将实验得到的数据进行分析、处理和优化,比较实物系统和仿真系统的差异并给出改进方案,从而提高系统的动态响应特性和控制性能。
三、研究方法及预期结果本文将采用系统分析、数学建模、仿真分析、控制器设计和优化等方法,通过建模、仿真、实物控制等多个方面去了解直线倒立摆系统。
预期结果是建立二级直线倒立摆系统的模型,完成仿真和实验的设计与实现,控制系统实现稳定的控制策略,并得出实物系统和仿真系统的控制性能优化方案。
四、进度安排第一阶段:文献综述和理论研究,研究直线倒立摆控制系统的基本原理和方法。
(2周)第二阶段:根据文献进行仿真研究,建立稳定的仿真模型。
(2周)第三阶段:设计实物控制系统,搭建实验环境。
(2周)第四阶段:实现控制系统与优化,得出实验数据并进行分析和优化,提高系统的控制性能。
(2周)第五阶段:撰写论文和答辩。
(4周)五、预期成果本文通过对二级直线倒立摆系统的建模、仿真和实物控制的研究,完成了对系统的深入理解和掌握,得出了系统的优化控制方案。
二级倒立摆系统的控制与仿真剖析

二级倒立摆系统的控制与仿真一、LQR控制器设计(1) 二级倒立摆系统的状态空间模型设线性定常系统为x’=A*x(t)+B*u(t),y=C*x(t)其初始条件为x(t)=x0;其中:A=[0,1,0,0;40,0,0,0;0,0,0,1;-6,0,0,0];B=[0;-2;0;0.8];C=[1,0,0,0;0,0,1,0](2) 系统的能控性判定n=size(A); Tc=ctrb(A,B); nc=rank(Tc)n=6 6 nc=6从运行结果可知,系统的阶次为6,能控性矩阵的秩也为6,因此系统是能控的。
(3) 系统的能观性判定To=obsv(A,C);no=rank(To)no=6从运行结果可知,能观性矩阵的秩为6,与系统的阶次相等,因此系统是能观测的。
(4) LQR控制设计基于一级倒立摆系统具有能控性和能观性,因此可采用LQR进行控制,经大量反复试验和仿真,选取R=0.2,Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];F=lqr(A,B,Q,R)得到:F =2.2361 106.6465 -155.4620 5.1719 4.9639 -24.5330三、仿真曲线采用LQR控制方式,设初始状态为x(0)=[1,-1,0,0]’,在相同采样周期T下应用数字再设计方法对一级倒立摆系统进行仿真,其中F(T)分别取为:1. F(T)=F1(T)=F2. F(T)=F2(T)=F[I+(A+BF)T/2]3. F(T)=F3(T)=F[I-(A+BF)/2]-1(1) T=0.013s,øc=e(A+BF)T时系统的极点、状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0,0;0,-38.5321,37.8186,0,0,0];B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;[G,H]=c2d(A-B*F,B,T); %%离散一的函数p0=eig(G),x0=[1 -1 0.5 0 0 0]';[y,x t]=dinitial(G,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%响应曲线plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')p0 =0.8647 + 0.0473i0.8647 - 0.0473i0.9224 + 0.0618i0.9224 - 0.0618i0.9932 + 0.0066i0.9932 - 0.0066i图1 øc=e(A+BF)T(2) T=0.013s,øc=ø +ΓF1(T)时系统的极点、状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0,0;0,-38.5321,37.8186,0,0,0]; B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;[Ad,B]=c2d(A,B,T); %%离散二的函数Ad=Ad-B*F;p1=eig(Ad)x0=[1 -1 0.5 0 0 0]';[y,x t]=dinitial(Ad,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%显示程序plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')p1 =0.8349 + 0.0388i0.8349 - 0.0388i0.9247 + 0.0561i0.9247 - 0.0561i0.9932 + 0.0066i0.9932 - 0.0066i图2 øc=ø +ΓF1(T)(3) T=0.013s,øc=ø+ΓF2(T)时系统的极点、F(T)值和状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0,0;0,-38.5321,37.8186,0,0,0]; B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;P2=(A-B*F)*T/2; %%离散3的函数F2=F*(eye(size(P2))+P2)[Add,B]=c2d(A,B,T);Ad=[Add-B*F2];p2=eig(Ad)x0=[1 -1 0.5 0 0 0]';[y,x,t]=dinitial(Ad,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%显示程序plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')F2 =1.7236 90.8365 -126.5481 4.0012 4.5195 -19.9211p2 =0.8676 + 0.0465i0.8676 - 0.0465i0.9224 + 0.0627i0.9224 - 0.0627i0.9932 + 0.0066i0.9932 - 0.0066i图3 øc=ø+ΓF2(T)(4) T=0.013s,øc=ø+ΓF3(T)时系统的极点、F(T)值和状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0,0;0,-38.5321,37.8186,0,0,0]; B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;P3=(A-B*F)*T/2; %%离散4的函数F3=F*(eye(size(P3))-P3)^-1[Add,B]=c2d(A,B,T);Ad=[Add-B*F3];p3=eig(Ad),[y,x,t]=dinitial(Ad,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%显示程序plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')F3 =1.7779 92.1683 -129.2365 4.1238 4.5459 -20.3464p3 =0.8655 + 0.0476i0.8655 - 0.0476i0.9222 + 0.0622i0.9222 - 0.0622i0.9932 + 0.0066i0.9932 - 0.0066i图4 øc=ø+ΓF3(T)由上面的1-4图我们可以知道:F(T)分别取F1(T),F2(T),F3(T)构成的闭环离散系统时仿真曲线基本一致,相应情况的闭环极点也基本相同,而取F(T)=F3(T)时,从系统的极点看,用øc=ø+ΓF3(T)代替øc=e(A+BF)T 构成闭环系统的精确度相当好。
毕业设计 二级倒立摆建模

四川理工学院毕业设计(论文)二级倒立摆系统建模与仿真学生:学号:专业:自动化班级:自动化指导教师:四川理工学院自动化与电子信息学院二O一一年六月摘要常规的PID控制从理论上可以控制二级倒立摆,但在实际中对PID控制器参数的整定为一难点。
本文针对二级倒立摆系统单输入三输出的不稳定系统,通过三回路PID 控制方案,来完成对倒立摆的控制。
利用状态反馈极点配置的方法来对参数进行整定,解决PID参数整定的难点。
然后借助于MATLAB中的Simulink模块对所得的参数进行仿真,结果表明三回路PID控制是成功的,参数的有效性,也证实了这种参数整定方法简单实用。
并通过配置不同位置的极点,对其结果进行分析得到极点配置的最佳配置方案。
关键词:倒立摆;PID;状态反馈; MATLABABSTRACTDouble Inverted Pendulum System Modeling and SimulationConventional PID control theory to control the inverted pendulum, but in practice the parameters of PID controller tuning is a difficult. In this paper, double inverted pendulum system, the instability of single-input three-output system, through the three-loop PID control program to complete the inverted pendulum control.Pole placement using state feedback approach to setting the parameters to resolve the difficulties PID parameter tuning. With MATLAB and Simulink in the module parameters obtained from simulation results show that the three-loop PID control is successful, the effectiveness of the parameters, but also confirms this tuning method is simple and practical.Different locations through the pole configuration, the results were too extreme configuration of the best configuration.Key words:pendulum;PID control ;state feedback;MATLAB目录摘要............................................................... ABSTRACT (I)第1章引言 01.1 倒立摆研究的目的及意义 01.2 倒立摆的发展史和研究现状 01.3本文的主要工作 (3)第2章倒立摆的建模 (3)2.1 二级倒立摆的简介及物理模型 (3)2.2 二级倒立摆计算机控制系统结构 (4)2.3 二级倒立摆的数学模型 (5)2.4根据牛顿力学、刚体动力学列写二级倒立摆的数学模型 (6)第3章控制策略的选择 (11)3.1 MATLAB简介 (11)3.2该系统的能控、能观及稳定性的分析 (14)3.2.1系统的能控性 (14)3.2.2系统能观性 (16)3.2.3系统的稳定性 (16)3.3 确定控制策略 (17)3.4 控制器参数整定方法 (17)3.5 通过状态反馈极点配置法来整定参数 (19)第4章计算机仿真及结果分析 (22)4.1 Matlab下Simulink模块简介 (22)4.2 在Simulink下的仿真 (23)4.3对仿真结果的分析 (31)第5章结束语 (32)致谢 (33)参考文献 (34)第1章引言1.1 倒立摆研究的目的及意义在控制理论发展的过程中, 一种理论的正确性及在实际应用中的可行性,往往需要一个典型对象来验证, 并比较各种控制理论之间的优劣, 倒立摆系统就是这样的一个可以将理论应用于实际的理想实验平台。
二级倒立摆系统的控制与仿真

二级倒立摆系统的控制与仿真一、引言在计算机参与的具有联系受控对象的控制系统中,有必要对联系控制系统设计数字控制器的必要,一般对于联系的控制对象设计数字控制器的方法有:第一种是应用联系系统理论得到的联系控制规律,再将控制规律离散化,用控制器实现,第二种是将联系的控制对象离散化,用离散控制理论设计控制器参数,数字再设计就是根据连续系统及相应的控制规律如何重新设计对应的离散系统与相应的离散控制规律。
我们采用的是最优等价准则、双线性变换法、平均增益法进行数字再设计。
二、LQR控制器设计(1) 二级倒立摆系统的状态空间模型设线性定常系统为x’=A*x(t)+B*u(t),y=C*x(t)其初始条件为x(t)=x0;其中:A=[0,1,0,0;40,0,0,0;0,0,0,1;-6,0,0,0];B=[0;-2;0;0.8];C=[1,0,0,0;0,0,1,0](2) 系统的能控性判定n=size(A); Tc=ctrb(A,B); nc=rank(Tc)n=6 6 nc=6从运行结果可知,系统的阶次为6,能控性矩阵的秩也为6,因此系统是能控的。
(3) 系统的能观性判定To=obsv(A,C);no=rank(To)no=6从运行结果可知,能观性矩阵的秩为6,与系统的阶次相等,因此系统是能观测的。
(4) LQR控制设计基于一级倒立摆系统具有能控性和能观性,因此可采用LQR进行控制,经大量反复试验和仿真,选取R=0.2,Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];F=lqr(A,B,Q,R)得到:F =2.2361 106.6465 -155.4620 5.1719 4.9639 -24.5330三、仿真曲线采用LQR控制方式,设初始状态为x(0)=[1,-1,0,0]’,在相同采样周期T下应用数字再设计方法对一级倒立摆系统进行仿真,其中F(T)分别取为:1. F(T)=F1(T)=F2. F(T)=F2(T)=F[I+(A+BF)T/2]3. F(T)=F3(T)=F[I-(A+BF)/2]-1(1) T=0.013s,øc=e(A+BF)T时系统的极点、状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0, 0;0,-38.5321,37.8186,0,0,0];B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;[G,H]=c2d(A-B*F,B,T); %%离散一的函数p0=eig(G),x0=[1 -1 0.5 0 0 0]';[y,x t]=dinitial(G,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%响应曲线plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')p0 =0.8647 + 0.0473i0.8647 - 0.0473i0.9224 + 0.0618i0.9224 - 0.0618i0.9932 + 0.0066i0.9932 - 0.0066i图1 øc=e(A+BF)T(2) T=0.013s,øc=ø +ΓF1(T)时系统的极点、状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0,0;0,-38.5321,37.8186,0,0,0];B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;[Ad,B]=c2d(A,B,T); %%离散二的函数Ad=Ad-B*F;p1=eig(Ad)x0=[1 -1 0.5 0 0 0]';[y,x t]=dinitial(Ad,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%显示程序plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')p1 =0.8349 + 0.0388i0.8349 - 0.0388i0.9247 + 0.0561i0.9247 - 0.0561i0.9932 + 0.0066i0.9932 - 0.0066i图2 øc=ø +ΓF1(T)(3) T=0.013s,øc=ø+ΓF2(T)时系统的极点、F(T)值和状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0, 0;0,-38.5321,37.8186,0,0,0];B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;P2=(A-B*F)*T/2; %%离散3的函数F2=F*(eye(size(P2))+P2)[Add,B]=c2d(A,B,T);Ad=[Add-B*F2];p2=eig(Ad)x0=[1 -1 0.5 0 0 0]';[y,x,t]=dinitial(Ad,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%显示程序plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')F2 =1.7236 90.8365 -126.5481 4.0012 4.5195 -19.9211 p2 =0.8676 + 0.0465i0.8676 - 0.0465i0.9224 + 0.0627i0.9224 - 0.0627i0.9932 + 0.0066i0.9932 - 0.0066i图3 øc=ø+ΓF2(T)(4) T=0.013s,øc=ø+ΓF3(T)时系统的极点、F(T)值和状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0, 0;0,-38.5321,37.8186,0,0,0];B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;P3=(A-B*F)*T/2; %%离散4的函数F3=F*(eye(size(P3))-P3)^-1[Add,B]=c2d(A,B,T);Ad=[Add-B*F3];p3=eig(Ad),[y,x,t]=dinitial(Ad,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%显示程序plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')F3 =1.7779 92.1683 -129.2365 4.1238 4.5459 -20.3464 p3 =0.8655 + 0.0476i0.8655 - 0.0476i0.9222 + 0.0622i0.9222 - 0.0622i0.9932 + 0.0066i0.9932 - 0.0066i图4 øc=ø+ΓF3(T)由上面的1-4图我们可以知道:F(T)分别取F1(T),F2(T),F3(T)构成的闭环离散系统时仿真曲线基本一致,相应情况的闭环极点也基本相同,而取F(T)=F3(T)时,从系统的极点看,用øc=ø+ΓF3(T)代替øc=e(A+BF)T 构成闭环系统的精确度相当好。
哈工大倒立摆实验报告

研究生自动控制专业实验地点:A区主楼518房间平面二级倒立摆系统实验报告主编:钱玉恒,杨亚非哈工大航天学院控制科学实验室平面二级倒立摆控制系统实验报告一、实验内容1、熟悉平面二级倒立摆控制系统的结构和原理;2、了解平面二级倒立摆物理模型建模与控制器设计;3、掌握LQR控制器仿真与实验;二、实验设备1、平面二级倒立摆控制系统一套平面二级倒立摆控制系统包括平面二级倒立摆控制器、平面二级倒立摆本体实验装置等组成。
在平面二级倒立摆本体上有起动/停止电源开关,螺旋浆起动/停止开关。
2、平面二级倒立摆控制系统计算机部分平面二级倒立摆控制系统计算机部分主要有计算机、SV-400控制卡等;三、实验步骤1、系统实验的线路连接平面二级倒立摆本体与计算机全部采用标准线连接,电源部分有标准电源线,在试验前,实验装置的线路已经连接完毕。
2、启动实验装置通电之前,请详细检察电源等连线是否正确,确认无误后,可接平面二级倒立摆本体电源,随后起动计算机和控制器。
3、系统实验的参数调试根据仿真的数据及控制规则进行参数调试,直到获得较理想参数为止。
四、实验要求1、学生上机前要求学生在实际上机调试之前,必须用自己的计算机,对系统的仿真全部做完,并且经过老师的检查许可后,才能申请上机调试。
2、学生上机要求上机的同学要按照要求进行实验,不得有违反操作规程的现象,严格遵守实验室的有关规定。
五、实验结果与分析 经过实际调试,实验结果如下:当LQR 控制参数为:14.142x K =, 15.722a K =, 74.93b K = ,29.49x K =, ,196.29a K =, ,34.83b K =系统的时间运行曲线如图1、图2所示。
图1 第一组参数X 方向实际运动曲线图2 第二组参数Y 方向实际运动曲线从图1、图2中可以看出,X 方向控制较好,但Y 方向控制的波动幅度比较大,为此,需要进一步调整LQR 控制参数。
经过多次试验,得到如下一组比较好的控制参数:14.142x K =, 15.892a K =, 77.71b K = ,30.018x K =, ,193.73a K =, ,33.355b K =该组参数下,系统的实际运行曲线如下图3、图4所示。
二级倒立摆数学模型的建立与仿真培训资料

二级倒立摆数学模型的建立与仿真二级倒立摆数学模型的建立与仿真专业:控制工程姓名:淡丹学号:1406073摘要本文用分析力学中牛顿力学法及拉格朗日方程建立了二级倒立摆的数学模型。
根据已经建立的倒立摆数学模型,对其进行了可控性,可观测性及稳定性的分析与研究,并对状态反馈及状态观测器进行了仿真模拟,分析研究。
并通过分析比较得出,加状态观测器并不影响系统的输出的结论。
关键词:倒立摆状态空间极点配置状态反馈ABSTRACTNewtonian mechanics analysis method and the Lagrange equation of a mathematical model of double inverted pendulum has been used in this paper. According to the established mathematical model of inverted pendulum on the controllability, observability and stability of the analysis and research, and the state observer and state feedback is carried on the simulation ,analysis and research. And through the analysis and comparison of results, plus state observer does not affect the conclusions of the output of the system.KEY WORDS: inverted pendulum state space pole allocation state feedback一、二级倒立摆系统的组成二级倒立摆主要由以下四部分组成:1.在有限长的轨道L上作直线运动的小车;2.与小车铰接在一起,并能在竖直平面内分别绕q,q点转动的下、上摆;3.驱动小车的直流力矩电机和转轮、钢丝等传动部分;4.使上、下摆稳定在垂直向上的平衡位置,且使小车稳定在轨道中心位置附近的控制器。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考虑本仿真系统,X 和Y 向具有类同性,以X 向作为代表性分析,Y 向类似。
X 向初始条件:1120x=x ααα====
20.05α=
001000
000100000010
00000050.223514.7272000050.890849.4875000A ⎛⎫
⎪
⎪ ⎪
=
⎪ ⎪ ⎪
- ⎪
⎪-⎝
⎭
00015.12485.19294B ⎛⎫ ⎪
⎪ ⎪= ⎪ ⎪ ⎪- ⎪ ⎪⎝⎭
100000010000001000C ⎛⎫
⎪= ⎪ ⎪⎝⎭
000D ⎛⎫ ⎪= ⎪ ⎪⎝⎭
仿真系统程序图
1. 状态控制器设计
(1) 取矩阵(111111)1r r Q diag R == 阶跃输入(X=0.1)
得[1.0000 13.4672 95.6968 2.3975 10.7845 15.9971]r K =
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
12250%70.450.70.62s t s x u σαα==≤≤≤≤
结果:指标不理想
(2) 取矩阵(20011111)1r r Q diag R == 阶跃输入(X=0.1) 得[14.1421 64.9555 166.3031 14.7223 25.4912 28.8348]r K =
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
1260%20.4 1.00.8 2.8s t s x u σαα==≤≤≤≤
结果:指标有改善,需要细致调整。
(3) 取矩阵(111111)10r r Q diag R == 阶跃输入(X=0.1) 得[0.3162 6.1247 81.2826 1.0619 8.3252 13.4153]r K =
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
12460%100.450.70.62s t s x u σαα=≥≤≤≤≤
结果:指标变差,调整r R 破坏了性能指标。
(4) 取矩阵(200250100111)1r r Q diag R == 阶跃输入(X=0.1)
得[14.1421 73.6187 184.4947 15.5483 28.5259 31.9498]r K =
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
1255% 2.30.45 1.2 1.04s t s x u σαα≤=≤≤≤≤
结果:指标有改善,基本达到要求。
(5) 取矩阵(200400100111)1r r Q diag R == 阶跃输入(X=0.1)
得[14.1421 76.0376 191.5354 15.7712 29.5323 33.0307]r K =
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
1255%20.41 1.0 3.2s t s x u σαα≤=≤≤≤≤
结果:指标与前次指标相当,改善不大。
(6) 取矩阵(400400100111)1r r Q diag R == 阶跃输入(X=0.1)
[20.0000 95.8247 214.6783 20.7871 34.8475 37.4409]r K =
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
1242% 1.90.410.95 3.4
s t s x u σαα==≤≤≤≤
结果:指标有改善
(7) 取矩阵(6006001111)1r r Q diag R == 阶跃输入(X=0.1)
[24.4948 113.4059 238.2895 24.8370 39.8287 41.7688]r K =
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
1234% 1.80.37 1.051 3.6s t s x u σαα==≤≤≤≤
结果:指标有改善
(8) 取矩阵(60011111)1r r Q diag R == 阶跃输入(X=0.1)
[24.4948 97.2381 206.9393 23.1529 34.3831 36.2975]r K =
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
1240% 1.50.410.9 3.2s t s x u σαα==≤≤≤≤
结果:指标与前次指标相比,超调量增加,调节时间变小,基本达到要求。
2. 输出控制器设计
(1)取矩阵(111)1Q diag R ==yy 阶跃输入(X=0.1)
[1.0000 11.1225 88.9294 2.0663 9.8267 14.7859]K =y
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
12270%90.450.70.62s t s x u σαα==≤≤≤≤
结果:指标不理想
(2)取矩阵(20011)1Q diag R ==yy 阶跃输入(X=0.1)
[14.1421 63.1246 160.5615 14.5073 24.7031 27.8219]K =y
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
1260% 2.50.4 1.10.93s t s x u σαα==≤≤≤≤
结果:指标有改善,需要细致调整。
(3)取矩阵(111)10Q diag R ==yy 阶跃输入(X=0.1)
[0.3162 5.7215 80.2957 1.0008 8.1743 13.2384]K =y
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
12480%100.450.70.62s t s x u σαα=≥≤≤≤≤
结果:指标变差,调整R y破坏了性能指标。
(4)取矩阵(200400100)1Q diag R ==yy 阶跃输入(X=0.1)
[14.1421 76.4105 188.1828 15.7736 29.3333 32.5804]K =y
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
1250% 2.50.4 1.00.9 3.2s t s x u σαα==≤≤≤≤
结果:指标明显改善,基本达到要求。
(5)取矩阵(400400100)1Q diag R ==yy 阶跃输入(X=0.1)
[19.9999 94.4117 209.9881 20.6237 34.2177 36.6144]K =y
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
1240% 1.90.4 1.00.95 3.4s t s x u σαα==≤≤≤≤
结果:指标有改善
(6)取矩阵(4004001)1Q diag R ==yy 阶跃输入(X=0.1)
[19.9999 94.0005 208.4758 20.5829 34.0190 36.3947]K =y
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
1240% 1.90.4 1.00.95 3.4s t s x u σαα==≤≤≤≤ 结果:指标与前次指标相同
(7)取矩阵(40011)1Q diag R ==yy 阶跃输入(X=0.1) [20.0000 81.6329 184.0645 19.3178 29.8179 32.1367]K =y
状态曲线图(黄色代表X ,紫色代表1α,绿色代表2α)
状态的一阶导数曲线(黄色代表X ,紫色代表1α,绿色代表2α)
u 的曲线
1246% 1.60.40.950.93s t s x u σαα==≤≤≤≤
结果:指标与前次指标对比,超调量增加,调节时间变小,基本达到要求。
