针对二级倒立摆的LQR控制系统设计
环型二级倒立摆LQR控制
环型二级倒立摆LQR控制作者：系别：专业：学号：指导教师：日期：二零零六年五月二十日摘要控制理论发展过程中，某一理论的正确性以及实际应用中可行性，往往需要一个按其理论所设计的控制器去控制一个典型对象来验证其控制策略的效果。
倒立摆就是这样一个较为理想的实验装置。
倒立摆本身是一个自然不稳定体，在控制过程中能有效地反映控制中的许多问题。
倒立摆的典型性在于:作为一个装置，其成本低廉，结构简单，便于模拟，数字实现不同方式控制;作为被控对象，又相当复杂，是高阶次、不稳定、非线性、强耦合系统，只有采取行之有效的控制方法方能使之稳定。
本文在环型二级倒立摆系统进行数学建模的基础上得出系统的状态方程, 应用线性二次型最优控制策略, 对环型二级倒立摆进行ＬＱＲ控制器的设计与ＭＡＴＬＡＢ仿真实验，并给出了相应的实验结果。
关键词: 倒立摆；ＬＱＲ；最优控制；状态方程AbstractThe inverted pendulum is an ideal equipment, which enables the possibility to validate the validity and the feasibility of some control theories, The inverted pendulum is a natural unstable equipment and can effectively reflects many matters in the control process. The model of the inverted pendulum is: as an equipment, low cost, simple machinery, easy to perform all kinds of controls in simulation and digital; as a controlled object, quite complex, high orders, instability, non-linearity, strong coupling system. We can keep it stable through some control method. Inverted pendulum system is a complicated , nonlinear , unstable system of high order. In the paper, it is discussed how to model the system of double inverted pendulums by using dynamics equation and then to t transform into a control problem of linearitied system. The optimized cont rolling policy with LQR cont roller is established on the MATLAB platform. The relevant experiment is also provided.Keywords: LQR; inverted pendulum; optimal control目录１概述………………………………………………………………………………………………………………４１.１当前国内外控制理论发展概述………………………………………………………………………５１.２倒立摆系统的历史…………………………………………………………………………………………６１.３倒立摆控制系统的发展动向………………………………………………………………………………７１.４现代控制在倒立摆系统稳定控制中的应用………………………………………………………………９１.５对倒立摆系统研究的意义…………………………………………………………………………………１０１.６本文的主要工作………………………………………………………………………………………………１１２环型倒立摆系统数学模型的建立……………………………………………………………………………１２２.１环型倒立摆的特点………………………………………………………………………………………１２２.２Lagrange方程的特点……………………………………………………………………………………１２２.３状态空间模型……………………………………………………………………………………………１３２.４环型二级倒立摆系统数学模型的建立…………………………………………………………………１４３线性二次型最优控制器（LQR）的设计……………………………………………………………………２１３.１线性二次型最优控制理论………………………………………………………………………………２１３.１.１二次型最优控制理论…………………………………………………………………………………２１３.１.２加权矩阵的选取………………………………………………………………………………………２３３.２系统的可控性与可观测性………………………………………………………………………………２４３.３环型二级倒立摆LQR调节器的设计……………………………………………………………………２４３.３.１设计要求………………………………………………………………………………………………２５３.３.２理论分析………………………………………………………………………………………………２５３.３.３实例分析………………………………………………………………………………………………２６３.３.４Matlab实现……………………………………………………………………………………………３０４结束语…………………………………………………………………………………………………………３３致谢…………………………………………………………………………………………………………………３４参考文献……………………………………………………………………………………………………………３５附录…………………………………………………………………………………………………………………３６1 概述在现代科学技术的许多领域中，自动控制技术起着越来越重要的作用。
二级倒立摆模糊控制设计
目录绪论 (4)1 倒立摆系统的建模 (5)1.1 倒立摆系统的特性分析 (5)1.2 二级倒立摆系统的数学建模 (5)1.2.1 基于牛顿力学的二级倒立摆系统数学模型建立 (7)1.3 二级倒立摆系统数学模型的线性化处理 (7)2 线性二次型最优控制（LQR）的方案设计 (9)2.1 二级倒立摆性能分析 (9)2.1.1 稳定性分析 (9)2.1.2 能控性能观性分析 (9)2.2 线性二次型最优调节器原理 (10)2.3 加权阵Q和R的选择 (12)3 模糊控制的基本原理 (13)3.1 模糊理论的基本知识 (13)3.1.1 模糊控制概述 (13)3.1.2 模糊集合 (13)3.1.3 模糊规则和模糊推理 (14)3.1.4 反模糊化 (15)3.2 模糊控制系统的设计 (15)3.2.1 模糊控制系统的组成及原理 (15)3.2.2 模糊控制器设计的基本方法与步骤 (17)3.3 二级倒立摆模糊控制器的设计 (18)4 二级倒立摆模糊控制系统的MATLAB仿真 (21)4.1 基于最优调节器的二级倒立摆控制系统的MATLAB仿真 (21)4.2 基于模糊控制器的二级倒立摆控制系统的MATLAB仿真 (24)4.2.1 二级倒立摆模糊控制系统的仿真波形 (24)4.2.2 量化因子和比例因子对模糊控制器性能的影响 (25)4.3 两种控制系统的MATLAB仿真对比研究 (26)结束语 (27)致谢 (28)参考文献 (29)附录 (30)摘要本文以二级倒立摆模型为控制对象，首先阐述了倒立摆系统控制算法的研究发展过程和现状，介绍了倒立摆系统的结构和数学模型，并详细推导了二级倒立摆的数学模型。
其次，本文主要研究倒立摆系统的现代控制方法以及智能控制方法，用LQR 最优控制方法、模糊控制理论设计了控制器，通过MATLAB及SIMULINK仿真两个控制器，分析指出两方法的优缺点，结果表明：智能控制策略不仅能满足非线性系统的控制要求，而且能明显改善控制指标，整个系统具有更好的动态特性。
二阶倒立摆的稳定性控制
二阶倒立摆的稳定性控制
二阶倒立摆的稳定性控制
摘要:本文研究了二阶倒立摆系统的控制方法,采用极点配置、LQR最优控制设计了控制器,通过仿真,分析指出各种方法的优缺点。
在极点配置法中,通过仿真实验寻优,得到具有较好稳定性的初始值。
在LQR最优控制器的设计中,采用仿真结果表明:该控制策略能满足系统的控制要求,系统具有良好的动态性能。
关键词:二阶倒立摆极点配置 LQR最优控制
倒立摆系统是应用于自动控制理论的经典实验装置,是一个复杂的多变量、高度非线性、强耦合和快速运动的绝对不稳定系统,对于倒立摆的稳定性控制,不仅有重要的理论意义,而且还有很重要的工程意义。
一方面倒立摆系统成本低廉,结构简单,物理参数和结构容易调整的优点,在实验条件下容易实现。
对于倒立摆的控制会涉及控制中的许多关键问题,如镇定问题、跟踪问题、随动问题、非线性问题、及鲁棒性问题。
另一方面,任何重心在上,支点在下的控制问题都可以近似于倒立摆系统,如机器人行走的平衡问题,火箭发射的垂直控制和卫星飞行中的姿态控制等。
1 二阶倒立摆系统
二阶倒立摆系统的机械部分主要由小车、摆杆1,2、导轨、皮带轮、传动皮带等组成,电气部分由电机、功率放大器、PWM、传感器、驱动电路以及保护电路组成。
感谢您的阅读，祝您生活愉快。
直线二级倒立摆建模与matlab仿真LQR
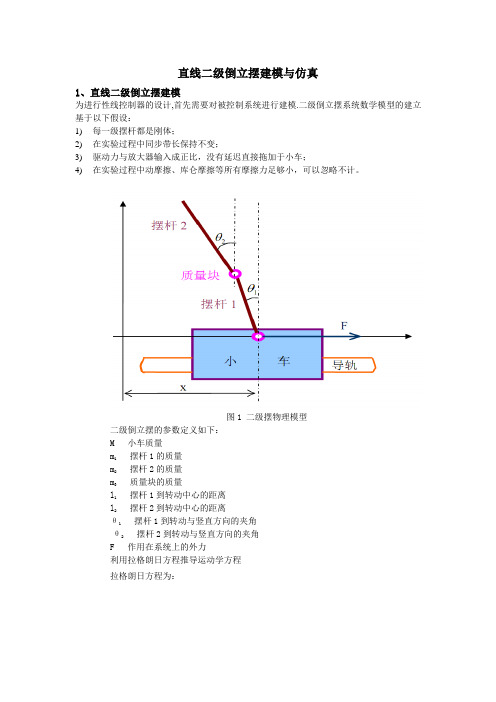
直线二级倒立摆建模与仿真1、直线二级倒立摆建模为进行性线控制器的设计,首先需要对被控制系统进行建模.二级倒立摆系统数学模型的建立基于以下假设：1)每一级摆杆都是刚体；2)在实验过程中同步带长保持不变；3)驱动力与放大器输入成正比，没有延迟直接拖加于小车；4)在实验过程中动摩擦、库仑摩擦等所有摩擦力足够小，可以忽略不计。
图1 二级摆物理模型二级倒立摆的参数定义如下：M 小车质量m1摆杆1的质量m2摆杆2的质量m3质量块的质量l1摆杆1到转动中心的距离l2摆杆2到转动中心的距离θ1摆杆1到转动与竖直方向的夹角θ2摆杆2到转动与竖直方向的夹角F 作用在系统上的外力利用拉格朗日方程推导运动学方程拉格朗日方程为：其中L 为拉格朗日算子，q 为系统的广义坐标，T 为系统的动能，V 为系统的势能其中错误!未找到引用源。
,错误!未找到引用源。
为系统在第i 个广义坐标上的外力，在二级倒立摆系统中，系统有三个广义坐标，分别为x,θ1,θ2,θ3。
首先计算系统的动能：其中错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
分别为小车的动能，摆杆1的动能，摆杆2的动能和质量块的动能。
小车的动能：错误!未找到引用源。
,其中错误!未找到引用源。
，错误!未找到引用源。
分别为摆杆1的平动动能和转动动能。
错误!未找到引用源。
，其中错误!未找到引用源。
，错误!未找到引用源。
分别为摆杆2的平动动能和转动动能。
对于系统，设以下变量： xpend1摆杆1质心横坐标 xpend2摆杆2质心横坐标 yangle1摆杆1质心纵坐标 yangle2摆杆2质心纵坐标 xmass 质量块质心横坐标 ymass 质量块质心纵坐标 又有：(,)(,)(,)L q q T q q V q q =-则有：系统总动能：系统总势能：则有：求解状态方程：可解得：使用MATLAB对得到的系统进行阶跃响应分析，执行命令：A=[0 0 0 1 0 0;0 0 0 0 1 0;0 0 0 0 1 01;0 0 0 0 0 0;0 86.69 -21.62 0 0 0;0 -40.31 39.45 0 0 0];B=[0;0;0;1;6.64;-0.808];C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];D=[0;0;0];sys=ss(A,B,C,D);t=0:0.001:5;step(sys,t)求取系统的单位阶跃响应曲线：图2 二级摆阶跃响应曲线由图示可知系统小车位置、摆杆1角度和摆杆2角度均发散，需要设计控制器以满足期望要求。
倒立摆的LQR稳定控制器设计
——现代控制理论实验
一、实验目的和要求
• 熟悉倒立摆的系统组成 • 学习利用MATLAB软件进行控制器的设计与仿真 • 运用LQR理论设计倒立摆的稳定控制器 • 设计的控制器能够成功进行倒立摆实时控制
二、倒立摆系统原理
计算机
运动控制卡
伺服驱动器
伺服电机
倒立摆
光电码盘1 光电码盘2
• 倒立摆系统原理图
三、理论分析
•二次型最优调节器问题 ：
已知状态完全能控的线性连续定常系统，其状态方 程为：
x(t) Ax(t) Bu(t) x(0) x0
确定下列最优控制向量：
u*(t) Kx(t)
使得下列二次型性能指标达到最小值:
J (u) 1 [xT (t)Qx(t) uT (t)Ru(t)]dt 20
0 27.83
0x 0
0 1
x
0.8832u 0
0
2.357
x
x 1
y
0
0 0
0 1
0 0
x
0 0u
LQR控制器的设计
• 开环仿真
LQR控制器的设计
• 使用完全状态反馈设计控制器
• 系统在阶跃输入R作用下会偏离平衡状态，需要设计控 制器使得摆杆在控制器的作用下仍然回到垂直位置， 小车可以到达新的指定位置。
LQR控制器的设计
可以通过改变Q阵的非零元素来调节控制器以得到期望 的响应。
(2)取Q=diag（3000 0 1000 0），R=1时：
K=[-54.772，-34.419，117.17，21.918]
此时的目标泛函:
J 2
1 2ห้องสมุดไป่ตู้
基于LQR最优调节器的二级倒立摆控制系统
基于LQR最优调节器的二级倒立摆控制系统
吴文进;葛锁良
【期刊名称】《安庆师范学院学报（自然科学版）》
【年(卷),期】2007(013)002
【摘要】倒立摆是一个典型的快速、多变量、非线性、绝对不稳定系统,对倒立摆系统的稳定性研究在理论上和方法上具有深远的意义.本文建立了二级倒立摆的数学模型,并推导出模型的状态空间表达式,分析了系统的稳定性,能控性和能观性,利用了线性二次型最优调节器(LQR)方法实现对二级倒立摆的最优控制,MATLAB仿真结果表明了该方法的有效性.
【总页数】4页(P32-34,41)
【作者】吴文进;葛锁良
【作者单位】安庆师范学院,物理与电气工程学院,安徽,安庆,246011;合肥工业大学,电气与自动化工程学院,安徽,合肥,230009
【正文语种】中文
【中图分类】TP13
【相关文献】
1.基于LQR的直线二级倒立摆最优控制系统研究 [J], 赵文龙;陈能祥;杜浩藩;李海燕
2.基于LQR最优调节器的平面二级倒立摆的建模与仿真 [J], 姜岩蕾;史增芳
3.基于混合算法的二级倒立摆LQR最优控制器设计 [J], 孔德帅
4.基于LQR最优调节器的三自由度直升机控制系统 [J], 赵笑笑;董秀成
5.基于LQR最优调节器的倒立摆控制系统 [J], 黄丹; 周少武; 吴新开; 张志飞因版权原因，仅展示原文概要，查看原文内容请购买。
基于PSO的二级倒立摆LQR最优控制器设计
倒 立摆 作 为 控 制 系 统 的被 控 对 象 ，许 多 抽 象 的控 制 概 念 都 可 以 通 过它 直 观 的表 现 出 来 ， 因此 成 为 检 验 各 种 新 型 控 制 理 论 和 方 法 有效 性 的典 型 装 置 。 年 来 ， 多 学 者 对 倒 立摆 系统 进 行 近 许 广 泛 地 研 究 。 文 献 ［— ］ 出 了 基 于 模 糊 神 经 网 络 的 倒 立 摆 控 １２提 制 系 统 ， 方 法 由 于模 糊 神 经 网 络 系 统 的 自适 应 能 力 ， 效 地 克 该 有 服 了 系 统存 在 的非 线 性 和 不 确 定 性 ，但 该 方 法 过 分 依 赖 人 类 直 接 控 制 被 控 对 象 的 经 验 。文 献 ［ — ］ 出 了倒 立 摆 拟 人 控 制 方 ３４提
优 控 制 器 比 较 ， 真 结 果表 明 ： 方 法 所 设 计 的 最 优 控 制 器 能 使 系统 的 响 应 时 间更 快 ， 调 量 更 小 ， 二 级 倒 立 摆 的 控 制 效 仿 该 超 对
果更理想。
关 键 词 ： 级 倒 立摆 ，ＱＲ Ｐ ０， 二 Ｌ ，Ｓ 最优 控 制 器
基 于 Ｐ Ｏ 的 二级 倒 立 摆 Ｌ Ｓ ＱＲ最 优 控 制器 设 计
基于 Ｐ Ｏ的二级倒立摆 Ｌ Ｓ ＱＲ最优控制器设计
Ｐ Ｏ ａ ｅ Ｌ Ｓ ｂ ｓ ｄ ＱＲ Ｏｐ ｉ ｌＣｏ ｔ ｌ ｒ Ｄｅ ｉ ｎ ｆ ｒ ｔ ｍａ ｎ ｒ ｌ ｓｇ ｏ Ｄｏ ｂｌ ｎ ｅ ｔ ｄ Ｐ ｎ ｕｕ ｏｅ ｕ ｅ Ｉｖ ｒ ｅ ｄ ｌｍ ｅ
，
Ｌ ＱＲ ｔｍａｌ ｏ ｒ ｌ ｏｐ ｉ ｃ ｎｔ ｅｒｄｅｓｇｎ ｏｌ ｉ ｍｅｔｏｄ ｈ ｂａ ｅｄ ｎ ｓ ｏ ＰＳ Ｏ ｉ ｓｕ ｅ ｗｈｉ ｏ ｅｒ ｍ ｅ ｔｅ ｈｏｃ ｂｌ ｄｎ ｓ ｆ ｓ ｔｄｉｄ ｃｈ ｖ ｃｏ ｓ ｈ ｃ ｉｅ ｉ ｅｓ ｏ ｗｅｉ ｉｇ ｎ ｇｈｔ ｍ ａｒ ｎ ｔｉ ｘ ｏｆ ＱＲ ｉ ｔ ｅ Ｌ ｎ ｈ ｄｅ ｉ ｐｒｃｅ ｓ． ｉ ｍ ｅ ｈ ｄ ｓｇｎ ｏ ｓ Ｔｈｓ ｔ ｏ ｍａｋ ｓ ｓ ｏ ＰＳ ｅ ｕ ｅ ｆ Ｏ ａｌ ｉ ｍ ｗｉ ｈ ｒ ｔ ｇｌ ｌ ｔ ｉａｔ ｎ ｏ ｇｏｒｈ ｔ ｔ ｅｕ ｉ ｉ ｈ ｓ ｃ ｏｂａ ｏｐ ｉ ｚ ｉ ｔ ｇｅ Ｑ 、 ｍ ｏ ｔ Ｒ ａ ｎｄ ｓ ａｅ ｅ ｔ ｔ ｆｅｄｂ ｋ ｃｏ ｔｏｌ ａｗ Ｋ． ｕｂｌ ｉｖｅｔ ｄ ａｃ ｎ ｒ ｌ Ｄｏ ｅ ｎ ｒｅ ｐｅｎ ｌｍ ｏ ｉ ｃ ｔｏｌ ａ ｄｕｕ ｐｔ ｍａｌ ｏｎｒ ｌ ｅｒ ｐｐｌ ａ ｉｎ ｈ ｍｅｔｏｄ ｓ ｉ ｔｏ ｏｆｔ ｅ ｃ ｈ ｉ ｄｅ ｉ ｅ ｗｈｉ ｏ ｅｒ ｓｇｎ ｄ ｃｈ ｖ ．
二级直线型倒立摆系统的LQR控制探析
统 的控 制器 ， 并 进行 了数值 仿 真 ， 结 果表 明 了该 方法 的有效 性 。
关 键词 ： 倒 立摆 ； Ｌ ＱＲ ； 数值仿 真
０ 引 言
字母符号
表 １ 二 级 直 线 型 倒 立 摆 系统 的 结 构 参 数
对应参数 字母符 号 对应参数
倒立摆 系统是一种多变量 、 强耦 合 、 严 重非线性 、 自然不稳
现 了 四级 倒 立 摆 控 制 仿 真 实 验 。线 性 二 次 型 调 节 器 （ Ｌ Ｑ Ｒ） 的
０ ３ × １ ０ ３ ×１ ０３ × １
０ ０ ０
Ｌ× ３
０ １ ｘ ３
０ ３ ｘ １
１
最优控制＿ 】 是基 于现代控 制理论 发展 起来 的 ， 通过对 倒立 摆 系统 的分析建立其动力学模型 ， 应用 状态反馈 控制器使得 目标
１ ４ ３
２ ０ １ ３ 第 ９期 总第 ３ ６ ３期
ｓ ｎ ｅ Ｊ — ｕ Ｆ ｅ ｎ × 量 坌 堑 鍪
２ ． ３ 计算风 阻， 并 确 定 风 机 的 工 作点
根据风机形成 的实际风速 １ ３ ． ５ ｍ／ ｓ ， 则雷诺数为 ：
Ｒ 一ｌ ０ Ｖ ／ 一１ ． １ １ ×１ ３ ． ５ ×６ ． ６ ９ ×１ ０ ～／ （ １ ９ ． ４ ×１ ０ 一 ） 一５ １ ６ ７
ｓ ｎ ｅ ｊ — ｕ Ｆ ｅ ｎ × ！ 量 坌 羹
二 级直 线 型 倒 立 摆 系 统 的 Ｌ ＱＲ控 制 探 析
王春平
（ 杭州佐 帕斯 工 业有 限公 司 ， 浙 江 杭州 ３ １ ０ ０ １ ８ ）
摘
要： 以二级 直线 型倒立 摆 系统 为研究 对象 ， 基 于线 性二 次 型调 节 器 （ Ｌ ｉ ｎ ｅ ａ ｒ Ｑ ｕ ａ ｄ ｒ ａ ｔ ｉ ｃ Ｒ ｅ ｇ ｕ ｌ ａ ｔ ｏ ｒ ， Ｌ Ｑ Ｒ ） 理 论 设 计 了二 级倒 立 摆 系
二级倒立摆系统的LQR
本科毕业设计(论文)题目：二级倒立摆系统的LQR控制算法研究1.毕业设计（论文）题目：二级倒立摆系统的LQR控制算法研究2.题目背景和意义：本课题来源于西安工业大学机器人实验室的倒立摆实验台。
倒立摆系统是一个多变量、快速、非线性和自然不稳定系统。
在控制过程中能有效地反映控制中的许多关键问题如非线性问题、系统的鲁棒性问题、随动问题、镇定问题及跟踪问题等。
倒立摆在控制理论研究中是一种较为理想的实验装置。
从日常生活中所见到的各种重心在上，支点在下的控制问题，到空间飞行器和各类伺服机构的稳定，都和倒立摆的控制有很大的相似性，故对其的稳定控制在实际生产和生活中有很多用场。
3.设计(论文)的主要内容（理工科含技术指标）：本题目是以倒立摆为研究对象，设计一个LQR控制器。
借助Matlab语言编程，得出直线二级倒立摆LQR控制器、仿真图。
修改Simulink 的LQR模块中的参数，观察仿真；通过试验对系统进行仿真分析，从而得出对系统的最佳控制方案。
4.设计的基本要求及进度安排（含起始时间、设计地点）：按毕业设计题目的要求在毕业设计时间内完成设计内容并。
1-5周；开题，针对原理及应用、主要技术难点的收集资料，熟悉课题方案。
6-10周；完成方案论证，确定设计方案。
10-15周；利用Matlab对系统做进一步的仿真分析，完善控制器的设计和算法，得到系统的最优控制器。
16—18周；完成所有的设计工作，整理资料，完成毕业论文，准备答辩。
5.毕业设计（论文）的工作量要求：*或实习（天数）：350小时①实验（时数）*：A4一张②图纸（幅面和张数）③其他要求：外文翻译3000字指导教师签名：年月日学生签名：年月日系（教研室）主任审批：年月日说明：1本表一式二份，一份由学生装订入附件册，一份教师自留。
2 带*项可根据学科特点选填。
西安工业大学北方信息工程学院本科毕业设计(论文)题目：二级倒立摆系统的LQR控制算法研究系别电子信息工程系专业电气工程及其自动化班级B070307姓名龙仕学号B07030711导师张荷芳焦灵侠2011年 6 月二级倒立摆系统的LQR控制算法研究摘要倒立摆系统是一个非线性自然不稳定系统，是验证各种控制理论和方法有效性的典型理想模型，许多抽象的控制概念如控制系统的稳定性、系统收敛速度等，都可以通过倒立摆系统直观的表现出来。
基于卡尔曼滤波的二级倒立摆LQR控制方法
收 稿 日期 ：２ ０ １ ５—０ １—１ ９ ；修 回 日期 ：２ ０ １ ５— ０ ３—２ ０ 基 金 项 目 ：国 家 自然 科 学 基 金 资 助 项 目（ ６ １ １ ０ ４ ０ ０ １ ） 作 者 简 介 ：王 莹 莹 （ １ ９ ８ ９一 ） ， 女， 山东肥城人 ， 硕士研究生 ， 主 要 从 事 系 统 辨 识 及 自适 应 控 制 。
火箭 等飞行 器飞行 姿态 的调 整等 。因此 ， 对倒 立摆 系统 的研 究 ＿ １ 具 有重 要意 义 。近 年来 ， 针对倒 立摆 的研 究 成果 已有许 多 ， 刘金琨 研究 了 Ｐ Ｉ Ｄ控 制 ； 宋 君 烈等 人ｌ ＿ ４ 研究 了模 糊控 制 ； Ｇ ． Ｗ． Ｌ ｉ ｎ ｄ ｅ ｎ等人 ［ ６ 研 究 了 Ｈ。 。 状
第 ３ Ｏ卷 第 ３期
２ ０ １ ５年 ９月
青 岛大学 学报 （ 工 程技术版 ）
Ｊ ＯＵＲＮＡＬ ＯＦ ＱＩ ＮＧＤＡＯ ＵＮＩ ＶＥＲＳ Ｉ ＴＹ （ Ｅ＆Ｔ）
Ｖｏｌ ＿ ３ Ｏ Ｎｏ ． ３
Ｓｅ ｐ ．２ ０ １ ５
文 章 编 号 ：１ ０ ０ ６ —９ ７ ９ ８ （ ２ ０ １ ５ ） ０ ３ —０ ０ ２ １ —０ ６ ；Ｄ ＯＩ ：１ ０ ． １ ３ ３ ０ ６ ／ ｊ ． １ ０ ０ ６—９ ７ ９ ８ ． ２ ０ １ ５ ． ０ ３ ． ０ ０ ５
二级倒立摆的LQR和LQY控制
二级倒立摆的LQR 和LQY 控制摘要：本文首先采用小扰动原理将二级倒立摆的非线性模型在其平衡点附近线性化，然后基于该线性化模型，分别采用线性二次状态调节器和输出调节器设计最优性能指标和反馈控制率，最后进行了仿真，并对两者的仿真结果进行了分析和比较。
一． 二级倒立摆非线性数学模型的建立及线性化图1给出了一个二级倒立摆系统的物理结构示意图。
其中r 表示小车在水平位置的位移，1θ表示下摆杆与垂直位置的角度，2θ表示上摆杆与垂直位置的角度。
图 1 二级倒立摆的物理结构示意图为了设计上述二级倒立摆系统的线性控制器，必须先对被控系统进行建模。
另外，为了减小建模的难度，对系统有如下假设：① 每一级摆杆都是刚体。
② 在实验过程中同步带长度保持不变。
③ 驱动力与放大器输入成正比，没有延迟直接施加于小车。
④ 实验过程中的库仑摩擦、动摩擦等所有摩擦力足够小，在建模过程中可忽略不计。
在上述假设的条件下，根据动力学理论，其动力学方程如下：Gu N rF r M ++⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡),(),,,(),(212121212121θθθθθθθθθθθθ （1）其中)cos( cos )cos( cos )( cos cos )( ),(2222122122221221221221111121222112132121⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--++++++=l M J l L M l M l L M L M l M J l M M l M l M M M M M M θθθθθθθθθθ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+∙--+∙-+-∙∙+-=12112212221221221222211121102121 )sin( 0 )sin( )( 0 sin sin )( ),,,(F F l L M F l L M F F l M L M l M F F θθθθθθθθθθθθθθ()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=2221121121sinsin 0 ),(θθθθg l M g L M l M N ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡= 0 0 0G G式中个参量的意义及参数值如下表1所示。
基于LQR最优调节器的平面二级倒立摆的建模与仿真
基于1QR最优调节器的平面二级倒立摆的建模与仿真第一章绪论11研究背景1.2研究目的1.3论文结构第二章平面二级倒立摆建模与仿真2.1动力学分析2.2时间域仿真2.31QR最优调节器第三章非线性系统仿真3.1平面二级倒立摆参数识别3.2平面二级倒立摆非线性特性仿真第四章强化学习控制技术4.1强化学习控制技术原理4.2平面二级倒立摆强化学习仿真第五章改进P1D控制技术5.1P1D控制器参数确定5.2平面二级倒立摆改进PID控制仿真第六章结论6.1总结6.2展望第一章绪论当今社会，智能化机械系统的使用日渐普及，为了使其更好地实现所求的功能，对控制策略的设计和研究发挥了重要作用。
倒立摆系统是很常见的控制问题，具有时变不可知的结构，因而其调节过程十分复杂。
考虑到倒立摆的重要性，本文以平面二级倒立摆为研究对象，建立了基于1QR最优调节器的平面二级倒立摆的建模与仿真。
本文通过对平面二级倒立摆的动力学分析、时间域仿真、1QR最优调节器、平面二级倒立摆非线性特性仿真、强化学习控制和改进PID控制的实验性研究,研究了最优调节系统的建模与仿真方法。
本文的研究目的是建立平面二级倒立摆系统的动力学模型，并以此模型为基础进行研究，研究和比较1QR最优调节器和强化学习技术在此系统中的控制效果，同时提出改进P1D控制技术。
研究希望能够有效地控制平面二级倒立摆系统，针对实际工程情况应用。
本文框架如下：第一章绪论，阐述研究的背景、研究的目的以及本文的结构；第二章介绍了平面二级倒立摆系统的建模与仿真，包括动力学分析、时间域仿真和1QR最优调节器；第三章介绍了平面二级倒立摆参数识别和非线性特性仿真；第四章介绍了强化学习控制；第五章介绍了改进P1D控制；最后，第六章总结出本文的研究结果，并对未来的工作进行展望。
第二章平面二级倒立摆建模与仿真本章首先介绍了平面二级倒立摆系统的动力学分析，然后进行仿真，在此基础上利用1QR最优调节技术进行控制。
基于LQR的倒立摆最优控制系统设计
基于LQR的平面二级倒立摆控制策略研究
s
io
n
f
c o rr e
la te d
u a n
s
t ie s
is
a
dde d
tO s im
p l if y
c t o c
a s
ll
a s
iz
．
the c o n tro
a
in
o
v
ir t
u e
y te
u
c
h n o lo g y
n
T h e in fe
c t io n
f th e q
s c a
tif i
系统 的复 杂 化 模 糊 规 则 的 总 数都 会 随 着 输 入 变 量 的 个
，
对 于 平 面 倒 立 摆 系统
，
．
，
量 化 因 子 对控 制效 果 的 影 响 应 用 所设 计 两 种控制 器 进 行 系统 仿真 与 实 时 控 制实验 其 结 果 证 明 两 种控 制 器都 能保 证 良好 的控
．
，
制精 度 响 应速 度快 有 良好 的 稳 定 性 和 鲁 棒 性
， ，
。
关 键词 ：平面 二 级 例立 摆 t L Q R ；模 糊控 制 ；量 化因子 中图 分类号 ：T
e n
ify t h e
f f i c ie
f the
gg
d
tra te g y
u
．
K
e
y
w o r
ds
： p la n a r
do
b le in
v e r te
d pe
n
d u lu
m ；L
基于LQR的倒立摆最优控制系统设计
基于LQR的倒立摆最优控制系统设计基于LQR的倒立摆最优控制系统设计[摘要]倒立摆系统是一个典型的多变量、非线性、强耦合和快速运动的高阶不稳定系统，它是检验各种新的控制理论和方法有效性的典型理想模型。
在其控制过程中，能有效地反映诸如镇定性、鲁棒性、随动性以及跟踪等许多关键问题。
本文主要研究二级倒立摆LQR控制方法。
本文以二级直线倒立摆为研究对象，对直线二级倒立摆系统进行分析，然后运用Matlab实时控制软件对模型进行控制算法的模拟仿真，最后得出相应结论。
本文先对二级直线倒立摆的模型进行分析，然后通过拉格朗日方程建立倒立摆的数学模型，然后再二级倒立摆的状态方程、系统的稳定性及能控性和能控性做了详细的分析，再以最优控制理论为原理，设计出LQR控制器，通过对倒立摆系统的LQR 控制算法的研究，探讨了加权矩阵Q和R的选取方法，最后利用Matlab建立倒立摆系统模型，进行了二级倒立摆的LQR控制器的仿真，模拟出相应参数下的阶跃响应曲线，通过对响应曲线的稳定性，快速性的观察，选取最合适的加权矩阵Q和R。
[关键词]二级直线倒立摆；LQR控制；仿真Research on Double Inverted Pendulum Control SystemBased on LQR[Abstract]The inverted pendulum is a typical high order system, with multi- variable, non-linear, strong-coupling, fleet and absolutely instable. It is representative as an ideal model to prove new control theory and techniques. During the control process, pendulum can effectively reflect many key problems such as equanimity, robust, follow-up and track, therefore. This paper studies a control method of double inverted pendulum LQR.In this paper, two linear inverted pendulum as the researchobject, linear inverted pendulum system for analysis, then the use of real-time control software Matlab model control algorithm simulation, finally draw the appropriate conclusions.This article first for two straight inverted pendulum model analysis, and then through Lagrange equation established mathematical model of inverted pendulum, and then inverted pendulum equation of state, system stability and controllability and controllability do a detailed analysis, then the theory of optimal control theory to design a LQR controller, through the inverted pendulum system LQR control algorithm, discusses the weighting matrices Q and R, selection methods, and finally the use of Matlab established inverted pendulum system model for the two inverted pendulum LQR controller simulation, simulation of the corresponding parameters of the step response curve, through the response curve of stability, speed observation, select the most appropriate weighting matrices Q and R.[Key Words]Double linear inverted pendulum; LQR control; Simulation前言倒立摆系统是进行控制理论研究的典型实验平台。
直线二级倒立摆系统控制策略研究设计
毕业设计（论文）题目直线二级倒立摆控制策略研究毕业论文（设计）原创性声明本人所呈交的毕业论文（设计）是我在导师的指导下进行的研究工作及取得的研究成果。
据我所知，除文中已经注明引用的内容外，本论文（设计）不包含其他个人已经发表或撰写过的研究成果。
对本论文（设计）的研究做出重要贡献的个人和集体，均已在文中作了明确说明并表示谢意。
作者签名：日期：毕业论文（设计）授权使用说明本论文（设计）作者完全了解**学院有关保留、使用毕业论文（设计）的规定，学校有权保留论文（设计）并向相关部门送交论文（设计）的电子版和纸质版。
有权将论文（设计）用于非赢利目的的少量复制并允许论文（设计）进入学校图书馆被查阅。
学校可以公布论文（设计）的全部或部分内容。
保密的论文（设计）在解密后适用本规定。
作者签名：指导教师签名：日期：日期：注意事项1.设计（论文）的内容包括：1）封面（按教务处制定的标准封面格式制作）2）原创性声明3）中文摘要（300字左右）、关键词4）外文摘要、关键词5）目次页（附件不统一编入）6）论文主体部分：引言（或绪论）、正文、结论7）参考文献8）致谢9）附录（对论文支持必要时）2.论文字数要求：理工类设计（论文）正文字数不少于1万字（不包括图纸、程序清单等），文科类论文正文字数不少于1.2万字。
3.附件包括：任务书、开题报告、外文译文、译文原文（复印件）。
4.文字、图表要求：1）文字通顺，语言流畅，书写字迹工整，打印字体及大小符合要求，无错别字，不准请他人代写2）工程设计类题目的图纸，要求部分用尺规绘制，部分用计算机绘制，所有图纸应符合国家技术标准规范。
图表整洁，布局合理，文字注释必须使用工程字书写，不准用徒手画3）毕业论文须用A4单面打印，论文50页以上的双面打印4）图表应绘制于无格子的页面上5）软件工程类课题应有程序清单，并提供电子文档5.装订顺序1）设计（论文）2）附件：按照任务书、开题报告、外文译文、译文原文（复印件）次序装订3）其它摘要倒立摆是一个复杂的多变量强耦合不稳定非线性的系统，借助于这样一个系统可以有效的检测各种控制理论的好坏。
倒立摆的LQR控制器算法的设计与仿真
Fig 4.1 Conventional LQR control system structure对于状态方程式所表示的连续时间的线性被控对象有：(4-1)0)0(),()()(x x t Bu t Ax t x =+=上式中，x(t)为n 维状态向量；u(t)为m 维控制向量；A ，B 分别为n×n 及n×m 阶的常数矩阵。
在进行线性二次最优控制系统设计时，比较令人感兴趣的是如何选择控制向量u(t)，使得给定的性能指标达到最小，线性二次最优调节器( LQR) 是针对系统状态方程，寻找最优控制，使得控制性能指标 J 达到最小，其中 Q 、R 分别表示了对状态变量和输入变量的加权值。
二次型性能指标函数：(4-2)dt RU U QX X J T T )(+=⎰+∞∞-则有如下状态反馈控制律：(4-3))()(t Kx t U -=式中，K 为最优反馈矩阵：(4-4)P B R K T 1-=在式(4-4)中，P 为Riccati 方程非负定对称解。
而Riccati 方程为：(4-5)01=+-+-Q P B PBR P A PA T T 如此，可得到状态反馈增益向量K ：(4-6)P B R K T 1-= 由此可见最优控制器的设计的关键是选择合适的加权矩阵Q 和R ，并根据式(4-6)可以算出P ，这样就能求出反馈增益K 了。
而加权矩阵Q 和R 的具体作用为：Q 中某元素相对增加时，其对应的状态变量的响应速度增加，其他状态变量的响应速度相对减慢；R 增加时，控制力减小，角度变化变小，跟随速度变慢。
改变矩阵Q 的值，可以得到不同的响应效果，Q 主对角线元素的值在一定范围之内越大，系统调整时间越短，而且抵抗干扰的能力越强，但是Q 不能过大，不然将对实验结果有一定的影响[16]。
上述推导过程即为线性二次最优控制的控制原理。
而当今现在，随着计算机技术的飞速发展，已经可以不使用上述公式进行繁琐的计算，而利用 MATLAB 的lqr 命令轻松的得到反馈矩阵K 的值：(,,,)K lqr A B Q R = 4.3 二次最优控制器的参数调整二次最优控制器的参数调整关键在于选择好合适的加权矩阵Q 和R ，这样就能得出反馈增益K [17]。
基于PSO的二级倒立摆LQR最优控制器设计
基于PSO的二级倒立摆LQR最优控制器设计
何俊强;任开春;武明亮;甘剑锋;高传平
【期刊名称】《工业控制计算机》
【年(卷),期】2010(023)006
【摘要】根据微粒群算法的随机性、快速性、易于实现性等优点,针对LQR在二级倒立摆最优控制设计过程中对加权矩阵Q、R选择的盲目性,研究了基于PSO的LQR最优控制器的设计方法,该方法利用PSO算法的启发式全局优化特点对Q、R 阵进行寻优,然后得到状态反馈控制律K.并设计了基于该方法的二级倒立摆的最优控制器,通过和基于遗传算法的LQR最优控制器比较,仿真结果表明:该方法所设计的最优控制器能使系统的响应时间更快,超调量更小,对二级倒立摆的控制效果更理想.
【总页数】3页(P56-58)
【作者】何俊强;任开春;武明亮;甘剑锋;高传平
【作者单位】重庆通信学院控制工程重点实验室,重庆,400035;重庆通信学院控制工程重点实验室,重庆,400035;重庆通信学院控制工程重点实验室,重庆,400035;重庆通信学院控制工程重点实验室,重庆,400035;重庆通信学院控制工程重点实验室,重庆,400035
【正文语种】中文
【相关文献】
1.基于GA的二级倒立摆LQR最优控制器设计 [J], 王昱;李勇
2.基于LQR的直线一阶单倒立摆最优控制器的设计 [J], 张娓娓;陈乐瑞;赵志远
3.基于混合算法的二级倒立摆LQR最优控制器设计 [J], 孔德帅
4.基于GA的两轮自平衡小车LQR最优控制器设计 [J], 杨凌霄;李晓阳
5.基于极点配置的二级倒立摆最优控制器设计 [J], 李新飞;朱齐丹;邢卓异;蔡成涛因版权原因，仅展示原文概要，查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
目录0. 前言 (1)1. 倒立摆 (2)1.1倒立摆的结构和工作原理 (2)1.2 倒立摆的特性 (3)1.3控制方法 (3)1.4课设目的 (4)2. 直线二级倒立摆的数学模型的建立与分析 (4)2.1建立数学模型 (4)2.2 系统的能控能观测性分析 (8)3. LQR控制器的设计 (9)3.1关于二次型最优控制（LQR） (9)3.2 LQR的基本原理 (10)3.3加权阵Q和R的选择 (11)4. LQR控制器参数的调试与仿真 (12)5. 总结与体会 (17)参考文献 (18).课设题目针对直线二级倒立摆的LQR控制系统设计金万福沈阳航空航天大学自动化学院摘要：倒立摆系统是一个典型的多变量、非线性、强耦合和快速运动的高阶不稳定系统，它是检验各种新的控制理论和方法有效性的典型理想模型。
在其控制过程中，能有效地反映诸如镇定性、鲁棒性、随动性以及跟踪等许多关键问题。
本文主要研究二级倒立摆LQR控制方法。
首先建立了二级倒立摆的数学模型，然后对二级倒立摆的数学模型进行控制设计，应用遗传算法确定系统性能指标函数中的加权阵Q，R得到系统状态反馈控制矩阵。
最后，用MATLAB进行了系统仿真。
在几次凑试Q矩阵值后系统的响应结果都不尽如人意，于是采用遗传算法对Q矩阵优化。
仿真结果证明：经过遗传算法优化后的系统响应能更加满足设计要求。
关键词：二级倒立摆；LQR控制；遗传算法0. 前言随着现代科学技术的快速发展，控制工程所面临的问题越来越复杂。
许多系统具有严重非线性、模型不确定、大滞后等特点。
倒立摆就是这样的复杂系统，对它的研究具有一般性。
倒立摆源于火箭发射器，最初的研究开始于二十世纪50 年代，由美国麻省理工学院的控制理论专家根据火箭发射助推器原理设计出一级倒立摆实验设备。
倒立摆的控制技巧同杂技运动员倒立平衡表演有异曲同工之处，这表明一个不稳定的被控对象，通过人的直觉、采取定性的手段，可以使之具有良好的稳定性。
在控制理论的发展过程中，某一理论的正确性及其在实际应用中的可行性需要一个按其理论设计的控制器去控制一个典型对象来验证。
倒立摆系统作为一个实验装置，形象直观，结构简单，成本低廉；作为一个控制对象，他又相当复杂，同时就其本身而言，是一个高阶次、不稳定、多变量、非线性、强耦合系统，只有采取行之有效的控制方法才能使之稳定，因此倒立摆装置被公认为是自动控制理论中的典型实验设备[1]。
通过对倒立摆系统的研究，不仅可以解决控制中的理论问题，还能将控制理论所涉及的三个基础学科：力学、数学和电学有机的结合起来，在倒立摆系统中进行综合应用。
对倒立摆系统进行控制，其稳定效果非常明了，可以通过角度、位移和稳定时间直接度量，控制好坏一目了然。
理论是工程的先导，对倒立摆的研究不仅有其深远的理论意义，还有重要的工程背景。
从日常生活中所见到的任何重心在上，支点在下的控制问题，到空间飞行器和各类伺服云台的稳定，都和倒立摆的控制有很大的相似性，故对其的稳定控制在实际中有很多用场，如海上钻井平台的稳定控制、卫星发射架的稳定控制、火箭姿态控制、飞机安全着陆化工过程控制等都属于这类问题。
针对上面的实际问题，启发了人们采用智能控制方法对倒立摆进行控制。
因此对倒立摆机理的研究具有重要的理论和实际意义，成为控制理论中经久不衰的研究课题。
1.倒立摆1.1倒立摆的结构和工作原理倒立摆系统是一个多变量、快速非线性和自然不稳定系统。
在控制过程中能有效地反映控制中的许多关键问题，如非线性问题系统的鲁棒性问题、随动问题、镇定问题及跟踪问题等。
倒立摆系统作为一个实验装置形象直观结构简单构件组成参数和形状易于改变成本低廉。
倒立摆系统的控制效果可以通过其稳定性直观地体现，也可以通过摆杆角度小车位移和稳定时间直接度量。
如图1.1，系统包括计算机、运动控制卡、伺服机构、倒立摆本体（小车，上摆，下摆，皮带轮等）和光电码盘几大部分，组成了一个闭环系统。
光电码盘1将小车的位移、速度信号反馈给伺服驱动器和运动控制卡，下面一节摆杆（和小车相连）的角度、角速度信号由光电码盘2反馈回控制卡和伺服驱动器，上面一节摆杆的角度和角速度信号则由光电码盘3反馈。
计算机从运动控制卡中读取实时数据，确定控制决策（小车向哪个方向移动、移动速度、加速度等），并由运动控制卡来实现该控制决策，产生相应的控制量，使电机转动，带动小车运动，保持两节摆杆的平衡。
图1.1 系统结构和工作原理图1.2 倒立摆的特性a.非线性倒立摆是一个典型的非线性复杂系统，实际中可以通过线性化得到系统的近似模型，线性化处理后再进行控制。
也可以利用非线性控制理论对其进行控制。
倒立摆的非线性控制正成为一个研究的热点。
b.不确定性主要是模型误差以及机械传动间隙，各种阻力等，实际控制中一般通过减少各种误差来降低不确定性，如通过施加预紧力减少皮带或齿轮的传动误差，利用滚珠轴承减少摩擦阻力等不确定因素。
c.耦合性倒立摆的各级摆杆之间，以及和运动模块之间都有很强的耦合关系，在倒立摆的控制中一般都在平衡点附近进行解耦计算，忽略一些次要的耦合量。
d.开环不稳定性倒立摆的平衡状态只有两个，即在垂直向上的状态和垂直向下的状态，其中垂直向上为绝对不稳定的平衡点，垂直向下为稳定的平衡点。
e.约束限制由于机构的限制，如运动模块行程限制，电机力矩限制等。
为了制造方便和降低成本，倒立摆的结构尺寸和电机功率都尽量要求最小，行程限制对倒立摆的摆起影响尤为突出，容易出现小车的撞边现象。
1.3 控制方法当前，倒立摆的控制方法可分为以下几类：a.线性理论控制方法将倒立摆系统的非线性模型进行近似线性化处理，获得系统在平衡点附近的线性化模型然后再利用各种线性系统控制器设计方法，得到期望的控制器PID控制、状态反馈控制、LQR控制法是其典型代表这类方法对一、二级的倒立摆(线性化后误差较小模型较简单)控制时，可以解决常规倒立摆的稳定控制问题但对于像非线性较强模型较复杂的多变量系统(三四级以及多级倒立摆)线性系统设计方法的局限性就十分明显，这就要求采用更有效的方法来进行合理的设计。
b.预测控制和变结构控制方法由于线性控制理论与倒立摆系统多变量、非线性之间的矛盾，使人们意识到，针对多变量、非线性对象，采用具有非线性特性的多变量控制。
解决多变量非线性系统的必由之路。
人们先后开展了预测控制、变结构控制和自适应控制的研究。
预测控制是一种优化控制方法，强调的是模型的功能而不是结构。
变结构控制是一种非连续控制，可将控制对象从任意位置控制到滑动曲面上仍然保持系统的稳定性和鲁棒性，但是系统存在颤抖。
预测控制、变结构控制和自适应控制在理论上有较好的控制效果，但由于控制方法复杂成本也高不易在快速变化的系统上实时实现。
c.智能控制方法在倒立摆系统中用到的智能控制方法主要有神经网络控制、模糊控制、仿人智能控制、拟人智能控制和云模型控制等。
(1)神经网络控制神经网络能够任意充分地逼近复杂的非线性关系，能够学习与适应严重不确定性系统的动态特性，所有定量或定性的信息都等势分布贮存于网络内的各种神经元，有很强的鲁棒性、容错性也可将学习算法和神经网络有效结合，实现状态未离散化的倒立摆的无模型学习控制。
但是神经网络控制方法存在的主要问题是缺乏一种专门适合于控制问题的动态神经网络，而且多层网络的层数、隐层神经元的数量、激发函数类型的选择缺乏指导性原则等。
(2)模糊控制经典的模糊控制器利用模糊集合理论将专家知识或操作人员经验形成的语言规则直接转化为自动控制策略，它的设计不依靠对象精确的数学模型，而是利用其语言知识模型进行设计和修正控制算法。
常规的模糊控制器的设计方法有很大的局限性。
首先，难以建立一组比较完善的多维模糊控制规则，即使能凑成这样一组不完整的粗糙的模糊控制规则，其控制效果也是难以保证的。
(3)云模型控制利用云模型实现对倒立摆的控制，用云模型构成语言值用语言值，构成规则，形成一种定性的推理机制。
这种拟人控制不要求给出被控对象精确的数学模型，仅仅依据人的经验、感受和逻辑判断，将人用自然语言表达的控制经验，通过语言原子和云模型转换到语言控制规则器中，就能解决非线性问题和不确定性问题。
1.4 课设目的本次课程设计通过线性二次型最优控制（LQR）方案令二级倒立摆达到稳定状态，用MATLAB和Simulink对控制方案进行了仿真，并实现了二级倒立摆实物系统的稳定控制。
a.建立二级倒立摆系统的数学建模。
b.研究倒立摆系统稳定控制方法，用线性二次型最优控制（LQR）方案配置控制对二级倒立摆系统进行稳定性控制。
c.学习Simulink仿真系统的方法。
d.进行调试，对结果进行分析。
达到预定的稳定精度要求。
2.直线二级倒立摆数学模型的建立与分析2.1 建立数学模型系统建模可以分为两种：机理建模和实验建模。
实验建模就是通过在研究对象上加上一系列的研究者事先确定的输入信号，激励研究对象并通过传感器检测其可观测的输出，应用数学手段建立起系统的输入－输出关系。
这里面包括输入信号的设计选取，输出信号的精确检测，数学算法的研究等等内容。
机理建模就是在了解研究对象的运动规律基础上，通过物理、化学的知识和数学手段建立起系统内部的输入状态关系。
为简化系统，我们在建模时忽略了空气阻力和各种摩擦，并认为摆杆为刚体。
二级倒立摆的组成如图2.1所示：图2.1 直线两级倒立摆物理模型倒立摆参数定义如下：M 小车质量m 1摆杆 1的质量m 2摆杆 2 的质量m 3质量块的质量l1摆杆1 中心到转动中心的距离l2摆杆2 中心到转动中心的距离θ1 摆杆1 与竖直方向的夹角θ2 摆杆 2 与竖直方向的夹角F 作用在系统上的外力利用拉格朗日方程推导运动学方程：拉格朗日方程为：),(),(),(),(q q V q q T q q T qq L -== (2.1) 其中L 为拉格朗日算子，q 为系统的广义坐标，T 为系统的动能，V 为系统的势能。
i i i f q L qL dt d =∂∂-∂∂ (2.2)其中i f n i ,......3,2,1=，i f 为系统在第i 个广义坐标上的外力，在二级倒立摆 系统中，系统的广义坐标有三个广义坐标，分别为21,,θθx 。
首先计算系统的动能：321m m m M T T T T T +++= (2.3) 其中321,,,m m m M T T T T 分别为小车的动能，摆杆1的动能，摆杆2的动能和 量块的动能。
小车的动能：2M Mx 21T =(2.4) 211m m m T T T ''+'=，其中21,m m T T '''分别为摆杆1的平动动能和转动动能。
222m m m T T T ''+'=，其中22,m m T T '''分别为摆杆2的平动动能和转动动能。