二级倒立摆系统的LQR控制算法研究
环型二级倒立摆LQR控制

环型二级倒立摆LQR控制作者:系别:专业:学号:指导教师:日期:二零零六年五月二十日摘要控制理论发展过程中,某一理论的正确性以及实际应用中可行性,往往需要一个按其理论所设计的控制器去控制一个典型对象来验证其控制策略的效果。
倒立摆就是这样一个较为理想的实验装置。
倒立摆本身是一个自然不稳定体,在控制过程中能有效地反映控制中的许多问题。
倒立摆的典型性在于:作为一个装置,其成本低廉,结构简单,便于模拟,数字实现不同方式控制;作为被控对象,又相当复杂,是高阶次、不稳定、非线性、强耦合系统,只有采取行之有效的控制方法方能使之稳定。
本文在环型二级倒立摆系统进行数学建模的基础上得出系统的状态方程, 应用线性二次型最优控制策略, 对环型二级倒立摆进行LQR控制器的设计与MATLAB仿真实验,并给出了相应的实验结果。
关键词: 倒立摆;LQR;最优控制;状态方程AbstractThe inverted pendulum is an ideal equipment, which enables the possibility to validate the validity and the feasibility of some control theories, The inverted pendulum is a natural unstable equipment and can effectively reflects many matters in the control process. The model of the inverted pendulum is: as an equipment, low cost, simple machinery, easy to perform all kinds of controls in simulation and digital; as a controlled object, quite complex, high orders, instability, non-linearity, strong coupling system. We can keep it stable through some control method. Inverted pendulum system is a complicated , nonlinear , unstable system of high order. In the paper, it is discussed how to model the system of double inverted pendulums by using dynamics equation and then to t transform into a control problem of linearitied system. The optimized cont rolling policy with LQR cont roller is established on the MATLAB platform. The relevant experiment is also provided.Keywords: LQR; inverted pendulum; optimal control目录1概述………………………………………………………………………………………………………………41.1当前国内外控制理论发展概述………………………………………………………………………51.2倒立摆系统的历史…………………………………………………………………………………………61.3倒立摆控制系统的发展动向………………………………………………………………………………71.4现代控制在倒立摆系统稳定控制中的应用………………………………………………………………91.5对倒立摆系统研究的意义…………………………………………………………………………………101.6本文的主要工作………………………………………………………………………………………………112环型倒立摆系统数学模型的建立……………………………………………………………………………122.1环型倒立摆的特点………………………………………………………………………………………122.2Lagrange方程的特点……………………………………………………………………………………122.3状态空间模型……………………………………………………………………………………………132.4环型二级倒立摆系统数学模型的建立…………………………………………………………………143线性二次型最优控制器(LQR)的设计……………………………………………………………………213.1线性二次型最优控制理论………………………………………………………………………………213.1.1二次型最优控制理论…………………………………………………………………………………213.1.2加权矩阵的选取………………………………………………………………………………………233.2系统的可控性与可观测性………………………………………………………………………………243.3环型二级倒立摆LQR调节器的设计……………………………………………………………………243.3.1设计要求………………………………………………………………………………………………253.3.2理论分析………………………………………………………………………………………………253.3.3实例分析………………………………………………………………………………………………263.3.4Matlab实现……………………………………………………………………………………………304结束语…………………………………………………………………………………………………………33致谢…………………………………………………………………………………………………………………34参考文献……………………………………………………………………………………………………………35附录…………………………………………………………………………………………………………………361 概述在现代科学技术的许多领域中,自动控制技术起着越来越重要的作用。
基于LQR的二级倒立摆的模糊控制

Ab ta t T e u z c n r l t o y s n r d c d o t d t e o t o l n p o l m o t e o b n i e t d e d l m i t i a e . n r e s r c : h f z y o t o he r i i t o u e t s u y h c n r li g r b e f h d u i nv r e p n u u n h s p p r I o d r
Ke W od Do be i v re p nd l m; J y rs: u l n e td e u u I QR; uz y o t o ; u in un to qu ntfc t0 f co s F z c n rl f so f ci n; a ii ai n a tr
倒立摆系统的模糊控制和LQR控制

摘要提出了一种利用模糊控制器进行倒立摆控制的方法,建立了倒立摆的数学模型,并进行了计算机仿真,仿真结果表明,该方案可以得到较为满意的结果。
关键词倒立摆模糊控制器计算机仿真1引言倒立摆小车系统如图1所示。
它由质量为 M的小车,长为2 L 的倒立摆构成。
倒立摆质量为m,铰链在小车上。
小车在控制函数f =u(t)的作用下,沿滑轨在x方向运动,使倒立摆在垂直平面内稳定。
x=0.05 m, 倒立摆的角度=0.08 rad。
我们通常用状态空间法来解决多输入、输出的问题。
对这个倒立摆问题我们尝试控制倒立摆的角度theta和小车的位置x。
要求小车应在5 s内到达期望位置,并且上升时间在5 s之内,同时限制倒立摆的最大角度为2°(0.35弧度),在5 s内稳定。
其中:M—小车的质量(M=1 kg);m—倒立摆的质量(m=0.1 kg);F—加给小车的外力;b—小车的摩擦系数(50 N/s);2 L —倒立摆的长度(2 L=2 m);x —小车的位置。
2系统分析与建模经分析,系统的动力学方程组为:由于φ较小,系统的动力学方程组可线性化为:计算A的极点为0,-5.1188,-2.6013,2.7476,有一个极点在右半平面,原系统是不稳定的。
而根据原系统的可控性,rank([B AB A2B A3B])=4,因而是可控的,可以任意配置系统的极点。
在matlab中,命令lqr (A,B,Q,R)可解连续时间的线性二次型调节器问题,并可解与其有关的黎卡提方程。
该命令可计算最佳反馈增益矩阵K,并且产生性能指标:在约束方程条件下达到极小的反馈控制律:u=-Kx。
可求得:K=[-22.3607,-30.1549,-142.8290,-52.2546 ],此时系统的极点分别为-4.33082.1985i,-2 56330.4834i,都处于s左半平面,系统是稳定的。
系统对应的响应曲线为图2所示。
由图2知线性化的系统达到了二次型最佳控制条件下的设计要求。
直线二级倒立摆建模与matlab仿真LQR
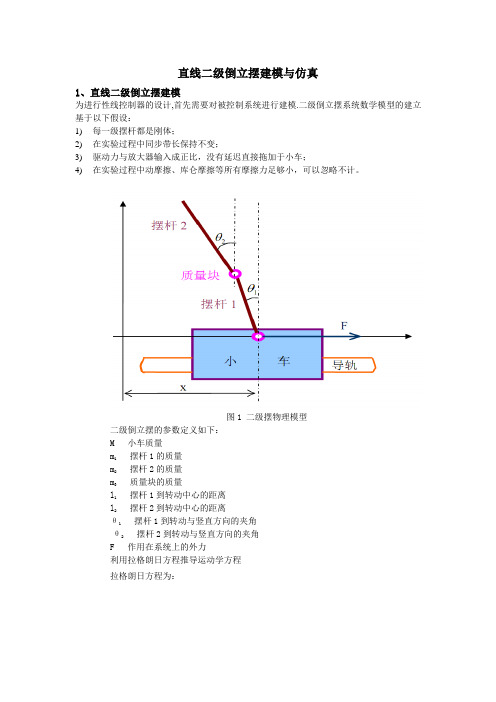
直线二级倒立摆建模与仿真1、直线二级倒立摆建模为进行性线控制器的设计,首先需要对被控制系统进行建模.二级倒立摆系统数学模型的建立基于以下假设:1)每一级摆杆都是刚体;2)在实验过程中同步带长保持不变;3)驱动力与放大器输入成正比,没有延迟直接拖加于小车;4)在实验过程中动摩擦、库仑摩擦等所有摩擦力足够小,可以忽略不计。
图1 二级摆物理模型二级倒立摆的参数定义如下:M 小车质量m1摆杆1的质量m2摆杆2的质量m3质量块的质量l1摆杆1到转动中心的距离l2摆杆2到转动中心的距离θ1摆杆1到转动与竖直方向的夹角θ2摆杆2到转动与竖直方向的夹角F 作用在系统上的外力利用拉格朗日方程推导运动学方程拉格朗日方程为:其中L 为拉格朗日算子,q 为系统的广义坐标,T 为系统的动能,V 为系统的势能其中错误!未找到引用源。
,错误!未找到引用源。
为系统在第i 个广义坐标上的外力,在二级倒立摆系统中,系统有三个广义坐标,分别为x,θ1,θ2,θ3。
首先计算系统的动能:其中错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
分别为小车的动能,摆杆1的动能,摆杆2的动能和质量块的动能。
小车的动能:错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆1的平动动能和转动动能。
错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆2的平动动能和转动动能。
对于系统,设以下变量: xpend1摆杆1质心横坐标 xpend2摆杆2质心横坐标 yangle1摆杆1质心纵坐标 yangle2摆杆2质心纵坐标 xmass 质量块质心横坐标 ymass 质量块质心纵坐标 又有:(,)(,)(,)L q q T q q V q q =-则有:系统总动能:系统总势能:则有:求解状态方程:可解得:使用MATLAB对得到的系统进行阶跃响应分析,执行命令:A=[0 0 0 1 0 0;0 0 0 0 1 0;0 0 0 0 1 01;0 0 0 0 0 0;0 86.69 -21.62 0 0 0;0 -40.31 39.45 0 0 0];B=[0;0;0;1;6.64;-0.808];C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];D=[0;0;0];sys=ss(A,B,C,D);t=0:0.001:5;step(sys,t)求取系统的单位阶跃响应曲线:图2 二级摆阶跃响应曲线由图示可知系统小车位置、摆杆1角度和摆杆2角度均发散,需要设计控制器以满足期望要求。
二级倒立摆系统稳定控制方法研究_论文

西安工业大学北方信息工程学院本科毕业设计(论文)题目:二级倒立摆系统稳定控制方法研究系别:电子信息系专业:自动化班级:姓名:学号:导师:年月毕业设计(论文)任务书系(部)电子信息系专业自动化班姓名学号1.毕业设计(论文)题目:二级倒立摆系统稳定控制方法研究2.题目背景和意义:本课题是个理论研究课题,对控制理论的研究有较高的应用价值,也对实际生产过程有广泛的应用价值。
课题内容紧密结合自动化专业教学要求。
通过本课题,学生可以深入了解分析问题和解决问题的方法,能够把所学理论知识应用于实际问题中,学会Matlabhe和Simulink的软件编程及系统的仿真分析方法。
3.设计(论文)的主要内容(理工科含技术指标):(1)查阅资料深入了解倒立摆系统的结构和特点,以及目前的发展情况。
(2)研究倒立摆系统的建模方法,并进行方案的选择和比较,建立倒立摆系统的模型(3)研究倒立摆系统稳定控制方法,并进行方案的选择和比较,进行算法分析和研究,选择合适的方法对倒立摆系统进行稳定控制(4)研究软件编程的方法,编写代码,完成整个系统的设计;学习Simulink仿真系统的方法,对各种方案进行仿真比较。
(5)系统调试及结果分析。
(6)与题目有关的英文资料翻译(要求:汉字3000以上)(7)撰写毕业设计论文,字数在一万五千左右。
4.设计的基本要求及进度安排(含起始时间、设计地点):起止时间2011.11—2012.5设计地点:西安工业大学金花校区。
完成任务书规定的设计内容,提交相应的设计成果。
1—3周:查阅有关资料,对课题有清楚的了解认知,准备开题答辩。
4—7周:倒立摆建模,认真研究其特点。
对开环系统进行仿真。
8-12周:研究倒立摆系统稳定控制方法,并进行方案的选择和比较,进行算法分析和研究,选择合适的方法对倒立摆系统进行稳定控制;准备中期答辩,完成外文资料翻译。
13—15周:研究软件编程的方法,编写代码,学习Simulink 仿真系统的方法,调试系统,进行实验;16—17周:编写毕业论文。
基于PSO的二级倒立摆LQR最优控制器设计

倒 立摆 作 为 控 制 系 统 的被 控 对 象 ,许 多 抽 象 的控 制 概 念 都 可 以 通 过它 直 观 的表 现 出 来 , 因此 成 为 检 验 各 种 新 型 控 制 理 论 和 方 法 有效 性 的典 型 装 置 。 年 来 , 多 学 者 对 倒 立摆 系统 进 行 近 许 广 泛 地 研 究 。 文 献 [— ] 出 了 基 于 模 糊 神 经 网 络 的 倒 立 摆 控 12提 制 系 统 , 方 法 由 于模 糊 神 经 网 络 系 统 的 自适 应 能 力 , 效 地 克 该 有 服 了 系 统存 在 的非 线 性 和 不 确 定 性 ,但 该 方 法 过 分 依 赖 人 类 直 接 控 制 被 控 对 象 的 经 验 。文 献 [ — ] 出 了倒 立 摆 拟 人 控 制 方 34提
优 控 制 器 比 较 , 真 结 果表 明 : 方 法 所 设 计 的 最 优 控 制 器 能 使 系统 的 响 应 时 间更 快 , 调 量 更 小 , 二 级 倒 立 摆 的 控 制 效 仿 该 超 对
果更理想。
关 键 词 : 级 倒 立摆 ,QR P 0, 二 L ,S 最优 控 制 器
基 于 P O 的 二级 倒 立 摆 L S QR最 优 控 制器 设 计
基于 P O的二级倒立摆 L S QR最优控制器设计
P O a e L S b s d QR Op i lCo t l r De i n f r t ma n r l sg o Do bl n e t d P n uu oe u e Iv r e d lm e
,
L QR tmal o r l op i c nt erdesgn ol i metod h ba ed n s o PS O i su e whi o er m e te hoc bl dn s f s tdid ch v co s h c ie i es o wei ig n ght m ar n ti x of QR i t e L n h de i prce s. i m e h d sgn o s Ths t o mak s s o PS e u e f O al i m wi h r t gl l t iat n o gorh t t eu i i h s c oba op i z i t ge Q 、 m o t R a nd s ae e t t fedb k co tol aw K. ubl ivet d ac n r l Do e n re pen lm o i c tol a duu pt mal onr l er ppl a in h metod s i to oft e c h i de i e whi o er sgn d ch v .
二级直线型倒立摆系统的LQR控制探析

统 的控 制器 , 并 进行 了数值 仿 真 , 结 果表 明 了该 方法 的有效 性 。
关 键词 : 倒 立摆 ; L QR ; 数值仿 真
0 引 言
字母符号
表 1 二 级 直 线 型 倒 立 摆 系统 的 结 构 参 数
对应参数 字母符 号 对应参数
倒立摆 系统是一种多变量 、 强耦 合 、 严 重非线性 、 自然不稳
现 了 四级 倒 立 摆 控 制 仿 真 实 验 。线 性 二 次 型 调 节 器 ( L Q R) 的
0 3 × 1 0 3 ×1 03 × 1
0 0 0
L× 3
0 1 x 3
0 3 x 1
1
最优控制_ 】 是基 于现代控 制理论 发展 起来 的 , 通过对 倒立 摆 系统 的分析建立其动力学模型 , 应用 状态反馈 控制器使得 目标
1 4 3
2 0 1 3 第 9期 总第 3 6 3期
s n e J — u F e n × 量 坌 堑 鍪
2 . 3 计算风 阻, 并 确 定 风 机 的 工 作点
根据风机形成 的实际风速 1 3 . 5 m/ s , 则雷诺数为 :
R 一l 0 V / 一1 . 1 1 ×1 3 . 5 ×6 . 6 9 ×1 0 ~/ ( 1 9 . 4 ×1 0 一 ) 一5 1 6 7
s n e j — u F e n × ! 量 坌 羹
二 级直 线 型 倒 立 摆 系 统 的 L QR控 制 探 析
王春平
( 杭州佐 帕斯 工 业有 限公 司 , 浙 江 杭州 3 1 0 0 1 8 )
摘
要: 以二级 直线 型倒立 摆 系统 为研究 对象 , 基 于线 性二 次 型调 节 器 ( L i n e a r Q u a d r a t i c R e g u l a t o r , L Q R ) 理 论 设 计 了二 级倒 立 摆 系
二级倒立摆基于融合函数的模糊控制

收稿日期:-年-月-日;修回日期:-年-月-日. 基金项目:安徽工程科技学院青年科研基金(2008YQ047).作者简介:邢景虎(1980--),男,汉(安徽、芜湖市),讲师,硕士,从事电力电子技术及现代电力传动控制、智 能控制的研究。
二级倒立摆基于融合函数的模糊控制邢景虎(安徽工程科技学院 电气传动与控制安徽省高校重点实验室,安徽 芜湖241000)摘 要:采用模糊控制理论研究了二级倒立摆的控制问题。
考虑到二级倒立摆为多变量系统,为了解决模糊控制器规则组合爆炸问题,利用LQR 控制方法设计了融合函数以降低模糊控制器的输入变量维数,大大减少模糊控制的规则数,并研究了量化因子对控制效果的影响,通过设置阈值使量化因子可自动调节,进而提高模糊控制器的性能品质。
仿真和实验结果表明,这种模糊控制算法规则数少,响应速度快,有良好的稳定性和鲁棒性。
关键词:二级倒立摆;LQR ;模糊控制;融合函数;量化因子 中图分类号:TP273 文件标识码:AFusion Function Based Fuzzy Control for a Double InvertedPendulumXING Jing-hu(Anhui University of Technology And Science, Anhui Provincial key Laboratory of Electric and Control, Wuhu 241000, China. Correspondent:XING Jing-hu,E-mail:xingjinghu@ )Abstract: The fuzzy control theory is introduced to study the controlling problem of the double inverted pendulum in this paper. In order to solve the fuzzy rule number ’sexplosion in multi-variable system,the dimensions of input varieties of a fuzzy controller are depressed by designing a fusion function using the LQR theory, and it can reduce the rules of fuzzy greatly. The infection of quantification factors to the effect of control is studied. The quality of the fuzzy controller is improved by adding auto turning quantification factors. Simulation and experiment prove that this fuzzy control arithmetic has the advantages of few rules, fast speed, good stability and good robustness. Keywords:Double inverted pendulum; LQR;Fuzzy control; fusion function; quantification factors1 引言倒立摆系统是一个非线性、强耦合、多变量和自然不稳定的系统,倒立摆系统通常用来检验控制策略的效果,是控制理论研究中较为理想的实验装置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.毕业设计(论文)题目:二级倒立摆系统的LQR控制算法研究2.题目背景和意义:本课题来源于西安工业大学机器人实验室的倒立摆实验台。
倒立摆系统是一个多变量、快速、非线性和自然不稳定系统。
在控制过程中能有效地反映控制中的许多关键问题如非线性问题、系统的鲁棒性问题、随动问题、镇定问题及跟踪问题等。
倒立摆在控制理论研究中是一种较为理想的实验装置。
从日常生活中所见到的各种重心在上,支点在下的控制问题,到空间飞行器和各类伺服机构的稳定,都和倒立摆的控制有很大的相似性,故对其的稳定控制在实际生产和生活中有很多用场。
3.设计(论文)的主要内容(理工科含技术指标):本题目是以倒立摆为研究对象,设计一个LQR控制器。
借助Matlab语言编程,得出直线二级倒立摆LQR控制器、仿真图。
修改Simulink 的LQR模块中的参数,观察仿真;通过试验对系统进行仿真分析,从而得出对系统的最佳控制方案。
4.设计的基本要求及进度安排(含起始时间、设计地点):按毕业设计题目的要求在毕业设计时间内完成设计内容并。
1-5周;开题,针对原理及应用、主要技术难点的收集资料,熟悉课题方案。
6-10周;完成方案论证,确定设计方案。
10-15周;利用Matlab对系统做进一步的仿真分析,完善控制器的设计和算法,得到系统的最优控制器。
16—18周;完成所有的设计工作,整理资料,完成毕业论文,准备答辩。
5.毕业设计(论文)的工作量要求:*或实习(天数):350小时①实验(时数)*:A4一张②图纸(幅面和张数)③其他要求:外文翻译3000字指导教师签名:年月日学生签名:年月日系(教研室)主任审批:年月日说明:1本表一式二份,一份由学生装订入附件册,一份教师自留。
2 带*项可根据学科特点选填。
西安工业大学北方信息工程学院本科毕业设计(论文)题目:二级倒立摆系统的LQR控制算法研究系别电子信息工程系专业电气工程及其自动化班级B070307姓名龙仕学号B********导师张荷芳焦灵侠2011年 6 月二级倒立摆系统的LQR控制算法研究摘要倒立摆系统是一个非线性自然不稳定系统,是验证各种控制理论和方法有效性的典型理想模型,许多抽象的控制概念如控制系统的稳定性、系统收敛速度等,都可以通过倒立摆系统直观的表现出来。
最近几年一直是控制领域研究的热点。
对倒立摆系统的研究不仅具有很重要的理论意义,而且在航天科技和机器人学等领域中也有现实指导性意义。
本文以固高公司直线倒立摆为研究对象,对直线二级倒立摆系统进行分析,运用Matlab实时控制软件对模型进行控制算法的仿真,得出相应结论。
本文以最优控制理论为原理,设计出LQR控制器,进行了倒立摆系统的LQR 控制算法的研究。
对二级倒立摆的状态方程、系统的稳定性及可控性做了详细的分析,运用最优控制理论,探讨了加权矩阵Q和R的选取方法。
介绍了如何利用Matlab建立倒立摆系统模型,进行了二级倒立摆的LQR控制器的设计与仿真,通过改变Simulink的LQR中态空间模块的参数,得出最好的控制效果。
关键词:直线倒立摆;LQR算法;控制;仿真Research on LQR Control Algorithm of the Double InvertedPendulum SystemAbstractThe inverted Pendulum systerm is a nonlinear unstable natural system, in the controlling process, it can effectively reflect many key problems such as stability and tracking in control and so on . In resent years, always is a study hotspot in control field. Studying on inverted Pendulum not only has a very important theory significance, but also has a realistic directory mean in aerospace science and technology and robotics.This dissertation, based on the linear inverted Pendulum of Googol ComPany, has analysised the double inverted Pendulum system, with the help of Googol Matlab real-time control software experiment platform, simulated control algorithm of the model, finally, reach the corresponding conclusion.By using optimization control theory, designing and emulated the double inverted Pendulum LQR controller, discussing the simulation of LQR control of the inverted Pendulum system. then analysised the inverted Pendulum state equation, system stability and controllability, the selection of matrix Q and R is dicussed. It is introduced how to realize the simulation of the inverted Pendulum system by the Matlab, the double inverted Pendulum LQR controller is designed and emulated, the LQR control simulation figure of the liner the double inverted Pendulum system has been obtained. And by altering the Parameters of Simulink LQR state space model, the best control result has been achieved.Key words: linear inverted Pendulum; LQR algorithm; control; simulation目录1绪论 (1)1.1 研究倒立摆的背景及意义 (1)1.1.2 倒立摆的特性 (2)1.1.3 倒立摆的控制目标 (3)1.1.4 倒立摆的控制方法 (3)1.2倒立摆的发展及现状 (3)1.3 倒立摆的主要控制算法 (4)1.4 本文的主要工作 (5)2 倒立摆的模型及定性分析 (6)2.1二级倒立摆系统数学模型 (6)2.1.1倒立摆的系统结构 (6)2.1.2 倒立摆的数学模型 (7)2.1.3 倒立摆的空间状态方 (11)2.2二级倒立摆系统定性分析 (12)2.2.1倒立摆系统的稳定性分析 (13)2.2.2倒立摆系统的可控性分析 (13)2.3 本章小结 (14)3 最优控制理论的简介 (15)3.1最优控制理论的发展历程 (15)3.2 LQR最优控制器原理 (16)3.3最优控制理论加权矩阵的选取 (17)3.4本章小结 (19)4 LQR控制器的设计与仿真 (20)4.1倒立摆LQR控制器的设计 (20)4.2二级倒立摆LQR控制仿真 (21)4.3倒立摆系统的硬件结构及工作原理 (25)4.3.1倒立摆系统设备简介 (25)4.3.2直线二级倒立摆系统工作原理 (26)4.3.3 倒立摆系统的硬件连接 (27)4.4本章小结 (27)5总结 (29)5.1总结 (29)5.2展望 (29)参考文献 (31)致谢 (34)毕业设计(论文)知识产权声明 (35)毕业设计(论文)独创性声明 (36)1 绪论1绪论本章介绍了倒立摆产生的背景和研究意义、倒立摆系统的分类、特性、控制方法以及倒立摆系统的发展及现状,最后简要论述了本文所做的工作。
1.1研究倒立摆的背景及意义上世纪五十年代为解决火箭、卫星飞行过程中对姿态修正,双足机器人的行走,直升机飞行时平衡控制,麻省理工大学设计出一级倒立摆实验设备,而后人们参照双足机器人的控制设备设计出二级摆,后来又出现了三级摆、多级摆,柔性连接直线倒立摆、平面倒立摆、环形倒立摆和环形并联多级倒立摆,由于倒立摆系统是研究变结构控制、非线性控制、目标定位控制、智能控制的系统,故在控制中能反映很多关键的工程问题,诸如镇定问题、非线性问题、鲁棒性问题、随动问题和跟踪问题。
研究倒立摆系统不仅具有很强的理论意义,而且还能解决很多实际问题。
凡是重心在上、支点在下的控制问题,都可抽象为一种倒立摆模型;由于倒立摆系统本身就是一个静态的、不稳定的诸如高阶次、多变量、强耦合的非线性系统,其作为控制理论研究中一种比较理想的实验手段,为处理多变量、非线性、绝对不稳定系统提供了最优的控制方法。
倒立摆主要有两个方面的用途。
第一,作为一个非线性自然不稳定系统,倒立摆系统是进行控制理论教学及开展各种控制实验的理想实验平台。
对倒立摆系统的研究能有效直观地反映控制中的许多典型问题:如非线性问题、鲁棒性问题、镇定问题、随动问题以及跟踪问题等。
第二,由于倒立摆系统具有高阶次、不稳定、多变量、非线性和强耦合等特性,其作为控制理论研究中的一个严格的控制对象,通过对倒立摆的控制,用来检验新的控制方法是否有较强的处理非线性和不稳定性问题的能力。
对倒立摆的控制涉及到控制科学中处理非线性、高阶次、强耦合对象的关键技术,许多现代控制理论的研究人员一直将它视为研究对象。
因而倒立摆被誉为“控制领域中的一颗明珠”[1]。
通过对倒立摆的研究不仅可以解决控制中的理论问题,还能将控制理论涉及的三个主要基础学科—力学、数学和电学进行有机合应用[2]。
同时,其控制方法在军工、航天、机器人和一般工业过程领域中都有着广泛的用途,如机器人行走过程中的平衡控制、海上钻井平台的稳定控制、火箭发射中的垂直度控制和卫星飞行中的姿态控制、太空探测器着陆控制和测量仪器展开稳定控制等[3]。
因此,倒立摆提供了一个从控制理论通往实践的桥梁。
