第4章部分习题参考解答
无机及分析化学第4章习题答案

第四章配位化合物习题参考解答1. 试举例说明复盐与配合物,配位剂与螯合剂的区别。
解复盐(如KCl·MgCl2·6H2O)在晶体或在溶液中均无配离子,在溶液中各种离子均以自由离子存在;配合物K2[HgI4]在晶体与溶液中均存在[HgI4]2-配离子,在溶液中主要以[HgI4]2-存在,独立的自由Hg2+很少。
配位剂有单基配位剂与多基配位剂:单基配位剂只有一个配位原子,如NH3(配位原子是N);多基配位剂(如乙二胺H2N-CH2-CH2-NH2)含有两个或两个以上配位原子,这种多基配位体能和中心原子M形成环状结构的化合物,故称螯合剂。
2. 哪些元素的原子或离子可以作为配合物的形成体哪些分子和离子常作为配位体它们形成配合物时需具备什么条件解配合物的中心原子一般为带正电的阳离子,也有电中性的原子甚至还有极少数的阴离子,以过渡金属离子最为常见,少数高氧化态的非金属元素原子也能作中心离子,如Si(Ⅳ)、P(Ⅴ)等。
配位体可以是阴离子,如X-、OH-、SCN-、CN-、C2O4-等;也可以是中性分子,如H2O、CO、乙二胺、醚等。
它们形成配合物时需具备的条件是中心离子(或原子)的价层上有空轨道,配体有可提供孤对电子的配位原子。
3. 指出下列配合物中心离子的氧化数、配位数、配体数及配离子电荷。
[CoCl2(NH3)(H2O)(en)]Cl Na3[AlF6] K4[Fe(CN)6] Na2[CaY] [PtCl4(NH3)2]K2[PtCl6] [Ag(NH3)2]Cl [Cu(NH3)4]SO4K2Na[Co(ONO)6] Ni(CO)4[Co(NH2)(NO2)(NH3)(H2O)(en)]Cl K2[ZnY] K3[Fe(CN)6]二硫代硫酸合银(I)酸钠四硫氰酸根⋅二氨合铬(III)酸铵;四氯合铂(II)酸六氨合铂(II) 二氯⋅一草酸根⋅一乙二胺合铁(III)离子硫酸一氯⋅一氨⋅二乙二胺合铬(III)解Na3[Ag(S2O3)2] NH4[Cr(SCN)4(NH3)2] [Pt(NH3)6][PtCl4][FeCl2(C2O4)(en)]-[CrCl(NH3)(en)2]SO46. 下列配离子具有平面正方形或者八面体构型,试判断哪种配离子中的CO32-为螯合剂[Co(CO3)(NH3)5]+[Co(CO3)(NH3)4]+[Pt(CO3)(en)] [Pt(CO3)(NH3)(en)]解[Co(CO3)(NH3)4]+、[Pt(CO3)(en)]中CO32-为螯合剂。
电工技术第四章正弦交流电路习题解答

tωAi /A222032πtAi /A 2032π6πA102i 1i 第四章 正弦交流电路[练习与思考]4—1-1 在某电路中,()A t i 60 314sin 2220-=⑴指出它的幅值、有效值、周期、频率、角频率及初相位,并画出波形图。
⑵如果i 的参考方向选的相反,写出它的三角函数式,画出波形图,并问⑴中各项有无改变? 解:⑴ 幅值 A I m 2220有效值 A I 220=频率 3145022f Hz ωππ===周期 10.02T s f==角频率 314/rad s ω=题解图4。
01初相位 s rad /3πψ-=波形图如题解图4.01所示 (2) 如果i 的参考方向选的相反, 则At i ⎪⎭⎫ ⎝⎛+=32 314sin 2220π,初相位改变了,s rad /32πψ=其他项不变。
波形图如题解图 4.02所示。
题解图4。
024—1-2已知A)120314sin(101 -=t i ,A )30314sin(202+=t i⑴它们的相位差等于多少?⑵画出1i 和2i 的波形。
并在相位上比较1i 和2i 谁超前,谁滞后。
解:⑴ 二者频率相同,它们的相位差︒-=︒-︒-=-=1503012021i i ψψϕ+1+1(2)在相位上2i 超前,1i 滞后。
波形图如题解图4.03所示。
题解图4。
03 4—2—1 写出下列正弦电压的相量V )45(sin 2201 -=t u ω,)V 45314(sin 1002 +=t u 解:V U ︒-∠=•4521101 V U ︒∠=•4525024-2-2 已知正弦电流)A60(sin 81 +=t i ω和)A 30(sin 62 -=t i ω,试用复数计算电流21i i i +=,并画出相量图.解:由题目得到A j j j j I I I m m m ︒∠=+=-++=︒-︒+︒+︒=︒-∠+︒∠=+=•••1.231093.32.9)32.5()93.64()30sin 630cos 6()60sin 860cos 8(30660821 所以正弦电流为)A 1.23(sin 101 +=t i ω题解图4.04 相量图如题解图4.04所示。
第4章 习题及参考解答

(2)用跳转表实现。
MOV BL,NUMB
MOV CHARS[BX],'$'
MOV DX,OFFSET CHARS
MOV AH,9
INT21H
MOV AH,4CH
INT21H
CODEENDS
ENDSTART
13.某软件共可接收10个键盘命令(分别为A,B,C,…,J),完成这10个命令的程序分别为过程P0,P1,…,P9。编一程序从键盘接收命令,并转到相应的过程去执行。要求用两种方法:
(5)MOV[BX],1000错。两操作数类型不匹配,[BX]只定义了一字节单元,而1000是16位数据。
11.8086汇编语言程序中段的类型有几种?各段如何定义?段定义语句中,定位类型、组合类型、类别各起什么作用?各有什么含义?
解8086汇编语言中,段的类型有三种,即代码段、堆栈段、数据段(附加数据段可归属于数据段)。各段可用段定义语句(SEGMENT与ENDS)和段名赋给段寄存器语句(ASSUME)来定义。段定义语句中,定位类型表示此段的起始边界要求,可允许4种段的起始边界,即PAGE、PARA、WORD或BYTE。它们分别表示段的起始值为以页、节、字、字节为边界,若此项省略,则默认值为PARA。组合类型用来告诉连接程序本段与其他段的关系,分别为NONE、PUBLIC、COMMON、AT表达式、STACK或MEMORY。每一种的含义请参看主教材。类别是连接程序(LINK)需要的。它可以是任何合法的名称,必须用单引号括起来,连接程序只使同类别的段发生关联。典型类别如‘CODE’、'STACK'。
DATASEGMENT
ORG 100H
BUF1DB 00H,01H.02H,…,0FEH,0FFH;共256个数据
大学物理第4章 狭义相对论时空观习题解答改

习 题4-1 一辆高速车以0.8c 的速率运动。
地上有一系列的同步钟,当经过地面上的一台钟时,驾驶员注意到它的指针在0=t ,她即刻把自己的钟拨到0'=t 。
行驶了一段距离后,她自己的钟指到6 us 时,驾驶员瞧地面上另一台钟。
问这个钟的读数就是多少? 【解】s)(10)/8.0(16/12220μ=-μ=-∆=∆c c s cu t t所以地面上第二个钟的读数为)(10's t t t μ=∆+=4-2 在某惯性参考系S 中,两事件发生在同一地点而时间间隔为4 s,另一惯性参考系S′ 以速度c u 6.0=相对于S 系运动,问在S′ 系中测得的两个事件的时间间隔与空间间隔各就是多少?【解】已知原时(s)4=∆t ,则测时(s)56.014/1'222=-=-∆=∆s cu t t由洛伦兹坐标变换22/1'c u ut x x --=,得:)(100.9/1/1/1'''8222220221012m c u t u c u ut x c u ut x x x x ⨯=-∆=-----=-=∆4-3 S 系中测得两个事件的时空坐标就是x 1=6×104 m,y 1=z 1=0,t 1=2×10-4 s 与x 2=12×104 m,y 2=z 2=0,t 2=1×10-4 s 。
如果S′ 系测得这两个事件同时发生,则S′ 系相对于S 系的速度u 就是多少?S′ 系测得这两个事件的空间间隔就是多少? 【解】(m)1064⨯=∆x ,0=∆=∆z y ,(s)1014-⨯-=∆t ,0'=∆t0)('2=∆-∆γ=∆cxu t t 2cxu t ∆=∆⇒ (m/s)105.182⨯-=∆∆=⇒x t c u (m )102.5)('4⨯=∆-∆γ=∆t u x x4-4 一列车与山底隧道静止时等长。
计量经济学(庞浩主编)第四章练习题参考解答
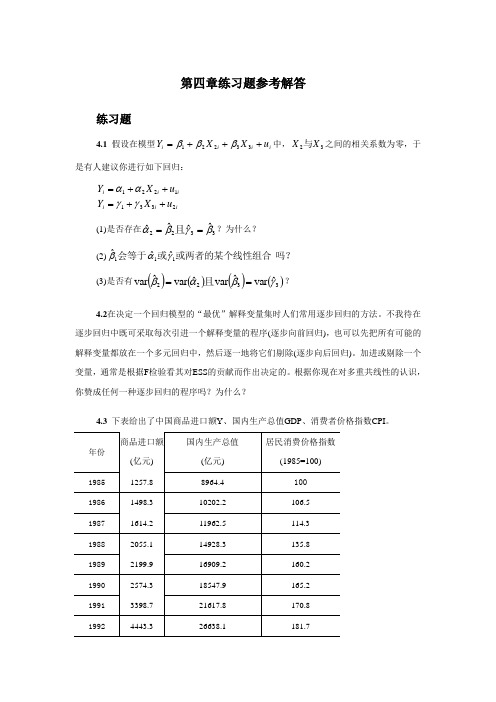
第四章练习题参考解答练习题4.1 假设在模型i i i i u X X Y +++=33221βββ中,32X X 与之间的相关系数为零,于是有人建议你进行如下回归:ii i i i i u X Y u X Y 23311221++=++=γγαα(1)是否存在3322ˆˆˆˆβγβα==且?为什么? (2)吗?或两者的某个线性组合或会等于111ˆˆˆγαβ (3)是否有()()()()3322ˆvar ˆvar ˆvar ˆvar γβαβ==且? 4.2在决定一个回归模型的“最优”解释变量集时人们常用逐步回归的方法。
不我待在逐步回归中既可采取每次引进一个解释变量的程序(逐步向前回归),也可以先把所有可能的解释变量都放在一个多元回归中,然后逐一地将它们剔除(逐步向后回归)。
加进或剔除一个变量,通常是根据F 检验看其对ESS 的贡献而作出决定的。
根据你现在对多重共线性的认识,你赞成任何一种逐步回归的程序吗?为什么?4.3 下表给出了中国商品进口额Y 、国内生产总值GDP 、消费者价格指数CPI 。
资料来源:《中国统计年鉴》,中国统计出版社2000年、20XX 年。
请考虑下列模型:i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗? (3)进行以下回归:it t i t t i t t v CPI C C GDP v CPI B B Y v GDP A A Y 321221121ln ln ln ln ln ln ++=+=+=++根据这些回归你能对数据中多重共线性的性质说些什么?(4)假设数据有多重共线性,但32ˆˆββ和在5%水平上个别地显著,并且总的F 检验也是显著的。
对这样的情形,我们是否应考虑共线性的问题?4.4 自己找一个经济问题来建立多元线性回归模型,怎样选择变量和构造解释变量数据矩阵X 才可能避免多重共线性的出现?4.5 克莱因与戈德伯格曾用1921-1950年(1942-1944年战争期间略去)美国国内消费Y 和工资收入X1、非工资—非农业收入X2、农业收入X3的时间序列资料,利用OLSE 估计得出了下列回归方程:37.107 95.0 (1.09) (0.66) (0.17) (8.92) 3121.02452.01059.1133.8ˆ2==+++=F R X X X Y (括号中的数据为相应参数估计量的标准误)。
高分子化学-高化第四章答案

第四章离子聚合习题参考答案1.与自由基聚合相比,离子聚合活性中心有些什么特点?解答:离子聚合和自由基聚合的根本不同就是生长链末端所带活性中心不同。
离子聚合活性中心的特征在于:离子聚合生长链的活性中心带电荷,为了抵消其电荷,在活性中心近旁就要有一个带相反电荷的离子存在,称之为反离子,当活性中心与反离子之间得距离小于某一个临界值时被称作离子对。
活性中心和反离子的结合,可以是极性共价键、离子键、乃至自由离子等多种形式,彼此处于平衡状态:BA B+A B+A B AⅠ为极性共价物种,它通常是非活性的,一般可以忽略。
Ⅱ和Ⅲ为离子对,引发剂绝大多数以这种形式存在。
其中,Ⅱ称作紧密离子对,即反离子在整个时间里紧靠着活性中心。
Ⅲ称作松散离子对,即活性中心与反离子之间被溶剂分子隔开,或者说是被溶剂化。
Ⅳ为自由离子。
通常在一个聚合体系中,增长物种包括以上两种或两种以上的形式,它们彼此之间处于热力学平衡状态。
反离子及离子对的存在对整个链增长都有影响。
不仅影响单体的的聚合速度,聚合物的立体构型有时也受影响,条件适当时可以得到立体规整的聚合物。
2.适合阴离子聚合的单体主要有哪些,与适合自由基聚合的单体相比的些什么特点?解答:对能进行阴离子聚合的单体有一个基本要求:①适合阴离子聚合的单体主要有:(1)有较强吸电子取代基的烯类化合物主要有丙烯酸酯类、丙烯腈、偏二腈基乙烯、硝基乙烯等。
(2)有π-π共轭结构的化合物主要有苯乙烯、丁二烯、异戊二烯等。
这类单体由于共轭作用而使活性中心稳定。
(3)杂环化合物②与适合自由基聚合的单体相比的特点:(1)有足够的亲电结构,可以为亲核的引发剂引发形成活性中心,即要求有较强吸电子取代基的化合物。
如V Ac,由于电效应弱,不利于阴离子聚合。
(2)形成的阴离子活性中心应有足够的活性,以进行增长反应。
如二乙烯基苯,由于空间位阻大,可形成阴离子活性中心,但无法增长。
(3)不含易受阴离子进攻的结构,如甲基丙烯酸,其活泼氢可使活性中心失活。
第4章习题参考解答

p3()
{
P(s);
…
}
参考解答:
因p1和p2进程是p3进程开始执行的先决条件,即当p1和p2进程均执行完毕时,p3才能执行,则p3需有两个信号量,分别表示p1进程执行完毕的信号量s1,以及p2进程执行完毕的信号量s2。则同步算法描述如下:
main()
{
int s1=0,s2=0;
cobegin
p1();
p4();
coend
}
p1()
{
p1 execute;
V(s12);
V(s13);
V(s14);
}
p2()
{
P(s12);
p2 execute;
}
p3()
{
P(s13);
p3 execute;
}
p4()
{
P(s14);
p4 execute;
}
4-15
解:
main()
{
int sa=1,sb=0;// sa表示缓冲区S是否为空,sb表示是否为满。
(3)设a、b两并发进程,它们共享一临界资源。其执行临界区的算法框图如下图,
进程A和进程B为互斥进程,则需一个互斥信号量s,初值为1,表示临界资源初始情况下无进程使用。
main()
{
int s=1;
cobegin
pa();
pb();
coend
}
pa()
{
P(s);
进入csa…
V(s);
}
pb()
{
P(s);
进入csb…
V(s);
}
4-21
答:线程有时也称为轻量级进程,它是比进程更小的活动单位,它是进程中的一个执行路径。一个进程可以有多个执行路径即线程。
数电习题解答_杨志忠_第四章练习题_部分

教材:数字电子技术基础(“十五”国家级规划教材) 杨志忠 卫桦林 郭顺华 编著高等教育出版社2009年7月第2版; 2010年1月 北京 第2次印刷;第四章 组合逻辑电路(部分练习题答案)练习题P172【4.1】、试分析图P4.1所示电路的逻辑功能。
解题思路:根据逻辑图依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(b )、Y AB AB A B =+=:;(同或功能) 真值表略; 【4.2】、试分析图P4.2所示电路的逻辑功能。
解题思路:根据逻辑图依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(a )、Y AB AB AB AB A B =⋅=+=⊕;(异或功能) 真值表略; 【4.3】、试分析图P4.3所示电路的逻辑功能。
解题思路:根据逻辑图从输入到输出逐级依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(a )、()Y ABC A ABC B ABC C ABC A B C ABC ABC =⋅+⋅+⋅=⋅++=+; 真值表略; 【4.4】、试分析图P4.4所示电路的逻辑功能。
解题思路:根据逻辑图从输入到输出逐级依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
解:12 Y A B C Y AB A B C AB A B C =⊕⊕=⋅⊕⋅=+⊕⋅;该逻辑电路实现一位全加运算。
Y1表示本位和数,Y2是进位输出。
mi A B C Y1 Y2 0 0 0 0 0 0 1 0 0 1 1 02 0 1 0 1 03 0 1 1 0 14 1 0 0 1 05 1 0 1 0 16 1 1 0 0 17 1 1 1 1 1【4.6】、写出图P4.6所示电路的逻辑函数表达式,并且把它化成最简与或表达式。
解题思路:变量译码器实现逻辑函数是把逻辑变量输入译码器地址码,译码器输出i i m Y =,再用与非门(输出低电平有效)变换就可以得到所需的逻辑函数,输出函数具有下列的表达形式:(,,)0356m(0,3,5,6)A B C F Y Y Y Y ==∑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.1 证明以下矢量函数满足真空中的无源波动方程222210EE c t∂∇−∂G =G ,其中2001c με=,为常数。
(1) 0E 0cos()x E e E t z c ωω=−G G ;(2) 0sin()cos()x E e E z t c ωω=G G ; (3) 0cos()y E e E t z cωω=+G G 。
证:(1) 222002cos()cos()x x E e E t z e E t z cz c ωωωω∂∇=∇−=−∂G G G20()cos()x e E t c cz ωωω=−−G2220022cos()cos()x x E e E t z e E t z t t c cωωωωω∂∂=−=−∂∂GG G − 22220022211()cos()cos()0x x E E e E t z e E t z c t c c c c ωωωωωω∂⎡⎤∇−=−−−−−=⎢⎥∂⎣⎦G G G G即矢量函数0cos()x E e E t z cωω=−G G 满足波动方程222210EE c t ∂∇−=∂G G 。
(2) 222002sin()cos()sin()cos()x x E e E z t e E z t c z c ωωωω∂⎡⎤⎡⎤∇=∇=⎢⎥⎢⎥∂⎣⎦⎣⎦G G G 20()sin()cos()x e E z c ct ωωω=−G2220022sin()cos()sin()cos()x x E e E z t e E z t t t c c ωωωωω∂∂⎡⎤⎡⎤==−⎢⎥⎢⎥∂∂⎣⎦⎣⎦GG G 22220022211()sin()cos()sin()cos()0x x E E e E z t e E z t c t c c c c ωωωωωω∂⎡⎤∇−=−−−=⎢⎥∂⎣⎦G G G G即矢量函数0sin()cos()x E e E z t cωω=G G 满足波动方程222210EE c t ∂∇−=∂G G 。
(3) 222002cos()cos()y y E e E t z e E t z cz c ωωωω∂∇=∇+=+∂G G G20()cos()y e E t c cz ωωω=−+G2220022cos()cos()y y E e E t z e E t z t t c cωωωωω∂∂=+=−∂∂GG G + 22220022211()cos()cos()0y y E E e E t z e E t z c t c c c c ωωωωωω∂⎡⎤∇−=−+−−+=⎢⎥∂⎣⎦G G G G即矢量函数0cos()y E e E t z cωω=+G G 满足波动方程222210EE c t ∂∇−=∂G G 。
4.2 在无损耗的线性、各向同性媒质中,电场强度()E r G G的波动方程为22()()0E r E r ωμε∇+=G G G G已知矢量函数j 0()e k r E r E −⋅=G G G G G ,其中0E G和k G 是常矢量。
试证明()E r G G 满足波动方程的条件是22k ωμε=,这里k k =G 。
证:在直角坐标系中x y z r e x e y e z =++G G G G设x x y y z k e k e k e k =++G G G G z则()()x x y y z z x y z x y z k r e k e k e k e x e y e z k x k y k z ⋅=++⋅++=++G G G G G G G G故j()j 00()e e x y z k x k y k z k r E r E E −++−⋅==G G G G G G j()22j 200222j()0222j()22220()e ee ()e x y z x y z x y z k x k y k z k r k x k y k z k x k y k z x y z E r E E E x y z k k k E k E r −++−⋅−++−++∇=∇=∇⎛⎞∂∂∂=++⎜⎟∂∂∂⎝⎠=−−−=−G G G G G G G G G ()G代入方程,得22()()0E r E r ωμε∇+=G G G G 220k E E ωμε−+=G G故22k ωμε=4.3 已知无源的空气中的磁场强度为90.1sin(10π)cos(6π10) A/m y H e x t kz =×G G− 利用波动方程求常数k 的值。
解:在无源的空气中的磁场强度满足波动方程22002(,)(,)0H r t H r t t με∂∇−=∂G G G G而229229(,)[0.1sin(10π)cos(6π10)][(10π)]0.1sin(10π)cos(6π10)]y y H r t e x t kz e k x t ∇=∇×−=−−×−G kz G GG 22922929(,)0.1sin(10π)cos(6π10)(6π10)0.1sin(10π)cos(6π10)]y y H r t e x t kz t te x ∂∂=×−∂∂=−××−G GG Gt kz代入方程22002(,)(,)0H r t H r t tμε∂∇−∂=G G G G,得 {}2292900[(10π)](6π10)0.1sin(10π)cos(6π10)0y e k x t k με−−+××−=Gz 于是有 229200[(10π)](6π10)0k με−−+×=故得k ==4.4 证明:矢量函数0cos()x E e E t x cωω=−G G 满足真空中的无源波动方程222210EE c t ∂∇−=∂G G但不满足麦克斯韦方程。
证:22220002(,)cos()cos()()cos()x x x E r t e E t x e E t x e E t x c x c c cωωωωω∂∇=∇−=−=−−∂G G G G G ωω22220022(,)cos()cos()x x E r t e E t x e E t x t t c c ωωωωω∂∂=−=−∂∂G G G G − 所以22220022211()cos()cos()0x x E E e E t x e E t x c t c c cc ωωωωωω∂⎡⎤∇−=−−−−−=⎢⎥∂⎣⎦G G G G 即矢量函数0cos()x E e E t x c ωω=−G G 满足波动方程222210EE c t ∂∇−=∂G G 。
另一方面,00cos()sin()0E E t x E t x x c c c ωωωωω∂∇⋅=−=−≠∂G而在无源的真空中,应满足麦克斯韦方程为E G0E ∇⋅=G故矢量函数0cos()x E e E t x cωω=−G G 不满足麦克斯韦方程组。
以上结果表明,波动方程的解不一定满足麦克斯韦方程。
4.5 证明:在有电荷密度ρ和电流密度J G的均匀无损耗媒质中,电场强度E G 和磁场强度的波动方程为H G222()E J E t t ρμεμε∂∂∇−=+∇∂∂G G G ,222H H J t με∂∇−=−∇∂×G G G证:在有电荷密度ρ和电流密度J G的均匀无损耗媒质中,麦克斯韦方程组为E H J t ε∂∇×=+∂GG G (1)H E t μ∂∇×=−∂GG (2)0H ∇⋅=G(3) E ρε∇⋅=G (4)对式(1)两边取旋度,得()H J tεE ∂∇×∇×=∇×+∇×∂G G G而2()H H ∇×∇×=∇∇⋅−∇H G G G故2()(H H J tε)E ∂∇∇⋅−∇=∇×+∇×∂G G G G (5)将式(2)和式(3)代入式(5),得222H H J tμε∂∇−=−∇×∂G G G这就是的波动方程,是二阶非齐次方程。
H G同样,对式(2)两边取旋度,得()E H tμ∂∇×∇×=−∇×∂G G即2()(E E H tμ)∂∇∇⋅−∇=−∇×∂G G G将式(1)和式(4)代入式(6),得2221E J E t t μεμε∂∂∇−=+∇∂∂ρG G G此即满足的波动方程。
E G4.6 在应用电磁位时,如果不采用洛伦兹条件,而采用库仑条件0A ∇⋅=G,导出A G 和ϕ所满足的微分方程。
解:将电磁矢量位A G的关系式B A =∇×G G和电磁标量位ϕ的关系式A E t ϕ∂=−∇−∂GG代入麦克斯韦第一方程EH J t ε∂∇×=+∂GG G得1()A A J t t εϕμ⎛⎞∂∂∇×∇×=+−∇−⎜⎟∂∂⎝⎠GG G利用矢量恒等式2()A A ∇×∇×=∇∇⋅−∇A G G G得2()A A A J t t μμεϕ⎛⎞∂∂∇∇⋅−∇=+−∇−⎜⎟∂∂⎝⎠GG G G (1)又由D ρ∇⋅=G得A t ρϕε⎛⎞∂∇⋅−∇−=⎜⎟∂⎝⎠G即2()A t ρϕε∂∇+∇⋅=−∂G (2)按库仑条件,令0A ∇⋅=G,将其代入式(1)和式(2),得222A A J t t ϕμεμμε∂∂⎛∇−=−+∇⎜⎞⎟∂∂⎝⎠G G G (3)2ρϕε∇=−(4) 式(3)和式(4)就是采用库仑条件时,电磁位函数A G和ϕ所满足的微分方程。
4.7 证明在无源空间(0ρ=、0J =G)中,可以引入矢量位m A G 和标量位m ϕ,定义为m D A =−∇×G G ,m m AH tϕ∂=−∇−∂GG并推导和m A Gm ϕ的微分方程。
证:无源空间的麦克斯韦方程组为D H J t ∂∇×=+∂GG G (1)B E t ∂∇×=−∂G G (2)0B ∇⋅=G(3) 0D ∇⋅=G(4)根据矢量恒等式0A ∇⋅∇×=G 和式(4),知D G可表示为一个矢量的旋度,故令m D A =−∇×G G(5) 将式(5)代入式(1),得m ()H A t∂∇×=−∇×∂G G即m 0A H t ⎛⎞∂∇×+=⎜⎟∂⎝⎠G G (6) 根据矢量恒等式0ϕ∇×∇=和式(6),知mA H t∂+∂G G 可表示为一个标量函数的梯度,故令m m A H tϕ∂+=−∇∂G G即m m AH tϕ∂=−∇−∂GG (7)将式(5)和式(7)代入式(2),得m m m 1A A t tμϕε⎛⎞∂∂−∇×∇×=−−∇−⎜⎟∂∂⎝⎠GG (8) 而2m m ()m A A A ∇×∇×=∇∇⋅−∇G G G故式(8)变为22mm m 2()A A A tt ϕμεμε∂∂⎛⎞∇∇⋅−∇=−∇−⎜⎟m ∂∂⎝⎠G G G (9) 又将式(7)代入式(3),得m m 0A t ϕ⎛⎞∂∇⋅−∇−=⎜⎟∂⎝⎠G即2m m ()A tϕ0∂∇+∇⋅=∂G (10)令m m A tϕμε∂∇⋅=−∂G将它代入式(9)和式(10),即得m A G和m ϕ的微分方程22mm 20A A tμε∂∇−=∂G G 22mm 20tϕϕμε∂∇−=∂解:(1) ()x A t x x c c∇⋅==−==∂∂ ()x ct c t t ϕ∂∂=−=−=∂∂ 故 0000(t ϕμεμε∂−=−=∂ 则 00A tϕμε∂∇⋅=−∂G(2) 0x z yz A A B A e e z y∂∂=∇×=−=∂∂G GG G 00B H μ==G G而 ()x x A xE e e t x t cϕϕ∂∂∂=−∇−=−−−∂∂∂GG t G G()x x e x ct e x∂=−−+=∂G G00D E ε==G G解:(1) 瞬时坡印廷矢量222650cos () W/m z S E H e t kz ω=×=−G G G G(2) 平均坡印廷矢量2π/22av 02650cos ()d 1325 W/m 2πz z S e t kz t e ωωω=−=∫G G G (3) 任一时刻流入如图题4.9所示的平行六面体中的净功率为n 0122d ()26500.25[cos ()cos (0.42)]270.2sin(20.42) Wz z S z z P S e S S e S e t t t ωωω==⎡⎤=−⋅=−⋅−+⋅×⎣⎦=×−−=−−∫G G G G G G v 0.25解:(1) 和的瞬时矢量为E G H Gj 0000(,)Re j sin()e sin()sin() V/m t x x E z t e E k z e E k z t ωω⎡⎤==−⎣⎦G G Gj 0000(,)Re cos()e cos()cos() A/m tH z t e k z e k z t ωω⎡⎤==⎢⎥⎣⎦G G G则瞬时坡印廷矢量为020020(,)(,)(,)sin()cos()sin()cos())sin(2) W/m z S z t E z t H z t e k z k z t t e k z t ωωω=×=−=−G G G G G故2(0,)0 W/m S t =G20(/8,))W/m zS t e t λω=−G G 20(/4,)0 W/m S t λ=G(2) *2av 1()Re[()()]0 W/m 2S z E z H z =×=G G G4.11 在横截面积为的矩形金属波导中,电磁场的复矢量为a b ×j 0j 00πj sin()e V/mπππj sin()cos()e A πz y z x z a x E e H aa x x H e H e H a a ββωμβ−−=−⎡⎤=+⎢⎥⎣⎦/m G GG G G式中、0H ω、μ和β都是实常数。
