迎春杯六年级复赛试题与解析
六年级迎春杯试题及答案

六年级迎春杯试题及答案一、选择题(每题2分,共20分)1. 下列哪个选项不是迎春花的特点?A. 花色鲜艳B. 花期在春季C. 叶子宽大D. 花朵小巧答案:C2. 迎春杯是以下哪个学科的竞赛?A. 数学B. 物理C. 化学D. 生物答案:A3. 下列哪个不是迎春杯的参赛条件?A. 必须是六年级学生B. 必须通过学校推荐C. 可以个人报名D. 必须有家长陪同答案:D4. 迎春杯的举办时间通常是在每年的:A. 春季B. 夏季C. 秋季D. 冬季答案:A5. 迎春杯的试题难度属于:A. 基础题B. 提高题C. 竞赛题D. 趣味题答案:C6. 迎春杯的试题通常包括哪些题型?A. 选择题B. 填空题C. 解答题D. 所有以上答案:D7. 迎春杯的考试时间一般为:A. 1小时B. 2小时C. 3小时D. 4小时答案:B8. 下列哪个不是迎春杯的奖项设置?A. 一等奖B. 二等奖C. 三等奖D. 优秀奖答案:D9. 迎春杯的参赛者需要准备哪些物品?A. 身份证B. 学生证C. 准考证D. 所有以上答案:D10. 迎春杯的试题通常由哪些人员出题?A. 教师B. 专家C. 学生D. 所有以上答案:B二、填空题(每题2分,共20分)1. 迎春杯的试题通常由______出题,以确保试题的科学性和严谨性。
答案:专家2. 迎春杯的试题内容通常包括______、______和______。
答案:数学、物理、化学3. 迎春杯的参赛者需要在______分钟内完成所有试题。
答案:1204. 迎春杯的试题答案需要写在______上。
答案:答题卡5. 迎春杯的试题答案需要用______笔填写。
答案:2B铅笔6. 迎春杯的试题答案需要按照______的顺序填写。
答案:试题7. 迎春杯的试题答案需要在______内填写。
答案:指定区域8. 迎春杯的试题答案需要用______的方式填写。
答案:涂黑9. 迎春杯的试题答案需要在______时间内完成。
迎春杯2020六年级数学学科试题

实验学校“迎春杯”竞赛 六年级数学学科试题 【 拟卷人: 】 2020.12 一、填空。
(每题4分,共40分) 1.已知a 、b 、c 都不为0,且a ×45=b ÷76=c ×109,那么a 、b 、c 中最小的数是( )。
2.一位同学把(x+94)×5错当成x+94×5进行计算,这样算出的结果与正确的结果相差( )。
3.一种大豆的出油率是25%~35%,80千克这样的大豆最少可以出油( )千克。
如果要榨出105千克油,最少需要( )千克大豆。
4.小明和小芳都喜爱集邮,小明把自己邮票的71送给小芳后,两人的邮票数同样多,已知小明原来的邮票比小芳多6张,小明原有( )枚邮票。
5.李明刚工作第一个月的工资为6000元,国家规定个人工资超过5000元不到8000元的部分需要缴纳3%的个人所得税。
李明实际拿到的工资是( )元。
6.六(3)班有54人,其中32喜欢画画,95喜欢唱歌,没有人既不喜欢画画又不喜欢唱歌。
既喜欢画画又喜欢唱歌的有( )人。
7.有一块长12厘米,宽8厘米的长方形铁皮,要从它的四个角各剪去一个边长是整厘米数的正方形,然后做成一个容积最大的无盖长方体铁盒,这个铁盒容积最大是( )毫升。
8.(如下图)李老师用几个2立方厘米的正方体木块摆了一个物体,下图是从不同方向看到的图形。
这个物体的体积最少是( )立方厘米。
9.下图是由同样大小的小方块堆积起来的,已知每个小方块棱长是2厘米,它的体积是( )立方厘米,表面积是( )平方厘米。
10.(如下图)两个长方形重叠部分的面积相当于大长方形面积的61,相当于小长方形面积的83。
小长方形与大长方形的面积比是( )。
第8题图 第9题图 第10题图二、简便计算。
(每题5分,共 15分。
)班级姓名学号。
…………………………………………装………………………………订……………………………线…………………………………………23×83+85÷32 61+121+201+301+…+721+901 2019÷201920202019三.解决实际问题。
最新迎春杯六年级复赛试题与解析
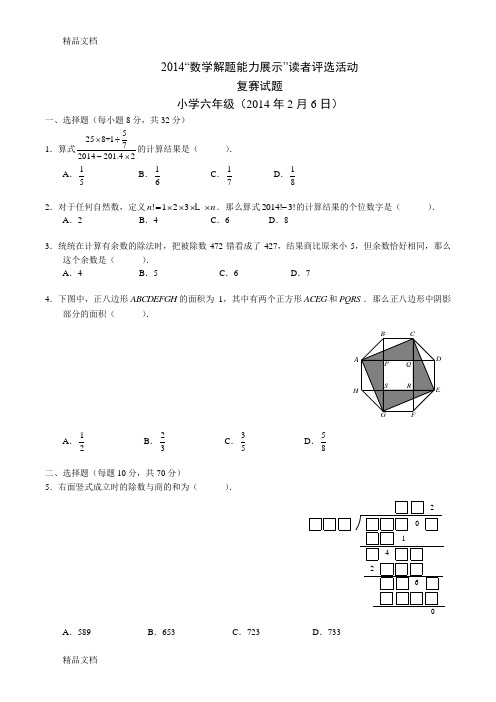
2014“数学解题能力展示”读者评选活动复赛试题小学六年级(2014年2月6日)一、选择题(每小题8分,共32分)1.算式5258+172014201.42⨯÷-⨯的计算结果是( ).A .15B .16C .17D .182.对于任何自然数,定义!123n n =⨯⨯⨯⨯L .那么算式2014!3!-的计算结果的个位数字是( ). A .2 B .4 C .6 D .83.统统在计算有余数的除法时,把被除数472错看成了427,结果商比原来小5,但余数恰好相同,那么这个余数是( ).A .4B .5C .6D .74.下图中,正八边形ABCDEFGH 的面积为1,其中有两个正方形ACEG 和PQRS .那么正八边形中阴影部分的面积( ).H AA .12 B .23 C .35 D .58二、选择题(每题10分,共70分)5.右面竖式成立时的除数与商的和为( ).12642A .589B .653C .723D .7336.甲乙丙三人进行一场特殊的真人CS 比赛,规定:第一枪由乙射出,射击甲或者丙,以后的射击过程中,若甲被击中一次,则甲可以有6发子弹射击乙或丙,若乙被击中一次,则乙可以有5发子弹射击甲或丙,若丙被击中一次,则丙可以有4发子弹射击甲或乙,比赛结束后,共有16发子弹没有击中任何人?则甲乙丙三人被击中的次数有( )种不同的情况.A .1B .2C .3D .47.甲乙二人进行下面的游戏.二人先约定一个整数N ,然后由甲开始,轮流把1,2,3,4,5,6,7,8,9这九个数字之一填入下面任一方格中:□□□□□□,每一方格只填入一个数字,形成一个数字可以重复的六位数.若这个六位数能被N 整除,乙胜;否则甲胜.当N 小于15时,使得乙有必胜策略的N 有( ).A .5B .6C .7D .88.在纸上任意写一个自然数,把这张纸旋转180度,数值不变,如0、11、96、888等,我们把这样的数称为“神马数”.在所有五位数中共有( )个不同的“神马数”.A .12B .36C .48D .609.如图,第(1)个多边形由正三角形“扩展”而来,边数记为3a ,第(2)个多边形由正方形“扩展”而来,边数记为4a ,……,依此类推,由正n 边形“扩展”而来的多边形的边数记为n a (3n ≥ ),则34511112014++++6051n a a a a =L ,那么n =( ).(4)(3)(2)(1)A .2014B .2015C .2016D .201710.如右图所示,五边形ABCDEF 面积是2014平方厘米,BC 与CE 垂直于C 点,EF 与CE 垂直于E 点,四边形ABDF 是正方形,:3:2CD DE =.那么,三角形ACE 的面积是 ( )平方厘米.FEDCB AA .1325B .1400C .1475D .150011.甲乙两车分别从A、B两地同时出发,相向而行,甲车的速度大于乙车.甲行驶了60千米后和乙车在C点相遇.此后甲车继续向前行驶,乙车掉头与甲车同向行驶.那么当甲车到达B地时,甲乙两车最远相距()千米.A.10 B.15 C.25 D.30三、选择题(每题12分,共48分)12.在“爸爸去哪儿”的节目中有一个任务,五个参加任务的孩子(天天、石头、Kimi、Cindy、Angela)需要换爸爸(每个小朋友可以选择除了自己爸爸之外其他四位父亲中的任何一位),那么最终五人有()种不同的选择结果.A.40 B.44 C.48 D.5213.老师在黑板上从1开始将奇数连续地写下去,写了一长串数后,擦去了其中的两个数,将这些奇数隔成了3串,已知第二串比第一串多1个数,第三串比第二串多1个数,且第三串奇数和为4147,那么被划去的两个奇数的和是().A.188 B.178 C.168 D.15814.从一张大方格纸上剪下5个相连的方格(只有一个公共顶点的两个方格不算相连),要使剪下的图形可折叠为一个无盖的正方体,则共可以剪出()种不同的图形(经过旋转或翻转相同的图形市委同一种).A.8 B.9 C.10 D.1115.老师把某个两位数的六个不同约数分别告诉了A F:六个聪明诚实的同学.A和B同时说:“我知道这个数是多少了.”C和D同时说:“听了他们两人的话,我也知道这个两位数是多少了.”E:“听了他们的话,我知道我的数一定比F的大.”F:“我拿的数的大小在C和D之间.”那么六个人拿的数之和是()A.141 B.152 C.171 D.1752014“数学解题能力展示”读者评选活动复赛试题小学六年级参考答案部分解析一、选择题(每小题8分,共32分)1.算式5258+172014201.42⨯÷-⨯的计算结果是().A.15B.16C.17D.18【考点】计算【难度】☆☆【答案】D【解析】5258+1200 1.4201.41 72014201.42201.410201.42201.488⨯÷+=== -⨯⨯-⨯⨯2.对于任何自然数,定义!123n n=⨯⨯⨯⨯L.那么算式2014!3!-的计算结果的个位数字是().A.2 B.4 C.6 D.8【考点】定义新运算【难度】☆☆【答案】B【解析】2014!个位数字是0,3!1236=⨯⨯=,所以2014!3!-个位是4.3.童童在计算有余数的除法时,把被除数472错看成了427,结果商比原来小5,但余数恰好相同,那么这个余数是().A.4 B.5 C.6 D.7【考点】整除同余【难度】☆☆【答案】A【解析】除数=(472427)59-÷=,4724(mod9)≡,所以余数是4.4.下图中,正八边形ABCDEFGH的面积为1,其中有两个正方形ACEG和PQRS.那么正八边形中阴影部分的面积().H AA .12B .23C .35D .58【考点】几何【难度】☆☆☆ 【答案】A【解析】等积变形.H AAH H A所以刚好各占一半.二、选择题(每题10分,共70分)5.右面竖式成立时的除数与商的和为( ).12642A .589B .653C .723D .733 【考点】数字谜 【难度】☆☆☆ 【答案】C【解析】首先根据倒数第三行可以确定0A =,4B =;241ECB A 60D22112611322440854815252824160120再根据顺数第三行最后一位为1可以确定,第一行D 和C 的取值为(1,1)或(3,7)或(9,9)或(7,3),根据尝试只有(1,1)符合题意.再依次进行推理,可得商和除数分别为:142和581.6.甲乙丙三人进行一场特殊的真人CS 比赛,规定:第一枪由乙射出,射击甲或者丙,以后的射击过程中,若甲被击中一次,则甲可以有6发子弹射击乙或丙,若乙被击中一次,则乙可以有5发子弹射击甲或丙,若丙被击中一次,则丙可以有4发子弹射击甲或乙,比赛结束后,共有16发子弹没有击中任何人?则甲乙丙三人被击中的次数有( )种不同的情况. A .1 B .2 C .3 D .4 【考点】不定方程 【难度】☆☆☆ 【答案】B【解析】设甲乙丙分别被击中x 、y 、z 次则三人分别发射6x 、51y +,4z 次[6(51)4]()16x y z x y z +++-++=化简得54315x y z ++=7.甲乙二人进行下面的游戏.二人先约定一个整数N ,然后由甲开始,轮流把1,2,3,4,5,6,7,8,9这九个数字之一填入下面任一方格中:□□□□□□,每一方格只填入一个数字,形成一个数字可以重复的六位数.若这个六位数能被N 整除,乙胜;否则甲胜.当N 小于15时,使得乙有必胜策略的N 有( ).A .5B .6C .7D .8 【考点】数论 【难度】☆☆☆ 【答案】B【解析】若N 是偶数,甲只需第一次在个位填个奇数,乙必败只需考虑N 是奇数.1N =,显然乙必胜.39N =,,乙只需配数字和1-8,2-7,3-6,4-5,9-9即可.5N =,甲在个位填不是5的数,乙必败.71113N =,,,乙只需配成100171113abcabc abc abc =⨯=⨯⨯⨯.8.在纸上任意写一个自然数,把这张纸旋转180度,数值不变,如0、11、96、888等,我们把这样的数称为“神马数”.在所有五位数中共有( )个不同的“神马数”. A .12 B .36 C .48 D .60 【考点】数论 【难度】☆☆☆ 【答案】D【解析】设这个数为ABCBA ,A 位可以填11,88,69,96,4种情况,B 位可以填00,11,88,69,96,5种情况,C 位可以填0,1,8,3种情况,453=60⨯⨯(个).9.如图,第(1)个多边形由正三角形“扩展”而来,边数记为3a ,第(2)个多边形由正方形“扩展”而来,边数记为4a ,……,依此类推,由正n 边形“扩展”而来的多边形的边数记为n a (3n ≥ ),则34511112014++++6051n a a a a =L ,那么n =( ).(4)(3)(2)(1)A .2014B .2015C .2016D .2017 【考点】找规律 【难度】☆☆☆ 【答案】C【解析】33(22)34a =⨯+=⨯,44(23)45a =⨯+=⨯,55(24)56a =⨯+=⨯,……(21)(1)n a n n n n =⨯+-=+ ,34511111111120143445(1)316051n a a a a n n n ++++=+++=-=⨯⨯⨯++L L ,12017n +=,2016n = .10.如右图所示,五边形ABCDEF 面积是2014平方厘米,BC 与CE 垂直于C 点,EF 与CE 垂直于E 点,四边形ABDF 是正方形,:3:2CD DE =.那么,三角形ACE 的面积是 ( )平方厘米.FECB AA .1325B .1400C .1475D .1500 【考点】几何 【难度】☆☆☆ 【答案】A【解析】作正方形ABCD 的“弦图”,如右图所示,IH GFEDCBA假设CD 的长度为3a ,DE 的长度为2a ,那么3BG a =,2DG a =,根据勾股定理可得2222229413BD BG DG a a a =+=+=,所以,正方形ABDF 的面积为213a ;因为CD EF =,BC DE =,所以三角形BCD 和三角形DEF 的面积相等为23a ;又因为五边形ABCEF 面积是2014平方厘米,所以222136192014a a a +==,解得2106a =, 三角形ACE 的面积为:2255522a a a ⨯÷=,即2510613252⨯=.11.甲乙两车分别从A 、B 两地同时出发,相向而行,甲车的速度大于乙车.甲行驶了60千米后和乙车在C 点相遇.此后甲车继续向前行驶,乙车掉头与甲车同向行驶.那么当甲车到达B 地时,甲乙两车最远相距( )千米.A .10B .15C .25D .30 【考点】行程问题 【难度】☆☆☆【答案】A【解析】假设甲走60千米时,乙走了a 千米,甲到达B 地时,乙车应走26060a a a ⨯=千米,此时甲、乙相差最远为1(60)6060a a a a -=⨯-⨯,和一定,差小积大,60a a -=,30a =.甲、乙最远相差900301560-=(千米).三、选择题(每题12分,共48分)12.在“爸爸去哪儿”的节目中有一个任务,五个参加任务的孩子(天天、石头、Kimi 、Cindy 、Angela )需要换爸爸(每个小朋友可以选择除了自己爸爸之外其他四位父亲中的任何一位),那么最终五人有( )种不同的选择结果.A .40B .44C .48D .52【考点】排列组合 【难度】☆☆☆【解析】设五个爸爸分别是A B C D E 、、、、,五个孩子分别是a b c d e 、、、、,a 有4种选择,假设a 选择B , 接着让b 选择,有两种可能,选择A 和不选择A ,(1)选择A ,c d e 、、 选择三个人错排,(2)不选择A ,则b c d e 、、、 选择情况同4人错排.所以5434()S S S =⨯+ 同理4323()S S S =⨯+ ,3212()S S S =⨯+,而10S =(不可能排错),21S =,所以32S =,49S =,544S =.13.老师在黑板上从1开始将奇数连续地写下去,写了一长串数后,擦去了其中的两个数,将这些奇数隔成了3串,已知第二串比第一串多1个数,第三串比第二串多1个数,且第三串奇数和为4147,那么被划去的两个奇数的和是( ).A .188B .178C .168D .158【考点】数论【难度】☆☆☆ 【答案】C【解析】设第一段有n 个,则第2段有1n +个,第一个擦的奇数是21n +,第二个擦的奇数是45n +,和为66n +,是6的倍数.只有168符合.14.从一张大方格纸上剪下5个相连的方格(只有一个公共顶点的两个方格不算相连),要使剪下的图形可折叠为一个无盖的正方体,则共可以剪出( )种不同的图形(经过旋转或翻转相同的图形视为同一种).A .8B .9C .10D .11 【考点】立体几何 【难度】☆☆☆ 【答案】A 【解析】如下图15.老师把某个两位数的六个不同约数分别告诉了A F :六个聪明诚实的同学.A 和B 同时说:“我知道这个数是多少了.” C 和D 同时说:“听了他们两人的话,我也知道这个两位数是多少了.” E :“听了他们的话,我知道我的数一定比F 的大.” F :“我拿的数的大小在C 和D 之间.” 那么六个人拿的数之和是( )A .141B .152C .171D .175 【考点】数论 【难度】☆☆☆☆【解析】(1)这个数的因数个数肯定不低于6个(假定这个数为N,且拿到的6个数从大到小分别是、、、、、)A B C D E F(2)有两个人同时第一时间知道结果,这说明以下几个问题:第一种情况:有一个人知道了最后的结果,这个结果是怎么知道的呢?很简单,他拿到的因数在:之间(也就是说A的2倍是3位数,所以A其实就是N)5099第二种情况:有一个人拿到的不是最后结果,但是具备以下条件:1)这个数的约数少于6个,比如:有人拿到36,单他不能断定N究竟是36还是72.2)这个数小于50,不然这个数就只能也是N了.3)这个数大于33,比如:有人拿到29,那么他不能断定N是58还是87;这里有个特例是27,因为272=54⨯,因数个数少于6个,所以如果拿到27可以⨯,因数个数不少于6个;273=81判断N只能为54)4)这个数还不能是是质数,不然不存在含有这个因数的两位数.最关键的是,这两人的数是2倍关系但是上述内容并不完全正确,需要注意还有一些“奇葩”数:17、19、23也能顺利通过第一轮.因此,这两个人拿到的数有如下可能:(54,27)(68,34)(70,35)(76,38)(78,39)(92,46)(98,49)(3)为了对比清晰,我们再来把上面所有的情况的因数都列举出来:(54,27,18,9,6,3,2,1)(68,34,17,4,2,1)(×)(70,35,14,10,7,5,2,1)(76,38,19,4,2,1)(×)(78,39,26,13,6,3,2,1)(92,46,23,4,2,1)(×)(98,49,14,7,2,1)对于第一轮通过的数,我们用红色标注,所以N不能是68、76、92中的任意一个.之后在考虑第二轮需要通过的两个数.用紫色标注的6、3、2、1,因为重复使用,如果出现了也不能判断N是多少,所以不能作为第二轮通过的数.用绿色标注的14和7也不能作为第二轮通过的数,这样N也不是98.那么通过第二轮的数只有黑色的数.所以N只能是54、70、78中的一个.我们再来观察可能满足E和F所说的内容:(54,27,18,9,6,3,2,1)(70,35,14,10,7,5,2,1)(78,39,26,13,6,3,2,1)因为F说他的数在C和D之间,我们发现上面的数据只有当70F=,在C D、(10N=的时候,7和5)之间,是唯一满足条件的一种情况.又因为E确定自己比F的大,那么他拿到的数一定是该组中剩余数里最大的.所以E拿到的是14(70N=).所以70N=,六个人拿的数之和为:70+35+14+10+7+5=141.。
2014迎春杯复赛五六年级试卷答案以及分析

五年级试卷分析答案:1C、2A、3B、4D、5D、6B、7C、8B、9A、10A、11C、12B、13C、14D、15A试卷分析:第一题:计算。
计算与简单的最值结合,此题保留的是2.5,那么学生只要想到保留2.5最大是几就可以,就是2.55,那运用最基本的除法就可以得到正确答案了。
考察学生的计算功底。
第二题:几何图形的分割。
此题如果出现在填空题就完全是图形分割了,只要把原图分割成相同的小三角形或者三角形和四边形,那么就可以轻易的数出结果。
不过此题出现在选择题中,观察一下,发现阴影部分要比白色部分略少,也就是说阴影部分占总体应该小于一半,选项中只有1个小于一半,就可以轻易得出答案。
考察图形分割。
第三题:分数应用题。
对于分数百分的一系列问题,一定要找准单位1,对于单位1,我们可以设为1也可以设为N,此题将单位1设为4份会变得特别容易。
考察分数应用题和基本解法。
第四题:计算。
此题是课本教材内会涉及到的知识点,但是大多数都只说被除数和除数同时扩大或缩小,商会如何变化,但很少提及余数问题。
在整数范围内,余数是会随被除数和除数一起变化的,只要知道这个知识点,此题就会非常容易。
考察除法的性质。
第五题:计算。
此题有2种解法,第一种是利用同余,就是利用9的余数和11的余数来判断答案,比较简单;第二种解法是直接算,直接算也是比较容易得出答案的,因为数不大,而且和两个11相乘,只要连续写2次,错位相加就可以得到答案。
考察学生的计算能力、数论知识。
第六题:概念题。
此题是考察学生对分数概念的理解,分数中有真分数、假分数,还有真分数化简后的最简真分数,学生很容易弄混,此题也是基础知识的延伸,难度较小。
考察学生基础知识。
第七题:数字谜。
此题与六年级试题重复。
对于大多数的数字谜问题,都需要学生分类讨论,需要用代数的思想帮助解题,整体难度不大,但是有一些做题小技巧,平时数学基本功比较好的学生比较容易解决。
比如此题只问末尾和,很容易就从题中看出除数的末尾为1,这样就可以直接得到答案。
“迎春杯”数学解题能力展示复赛试卷(六年级)

2014年“迎春杯”数学解题能力展示复赛试卷(六年级)一、选择题(每小题8分,共32分)1.(8分)算式的计算结果是()A.B.C.D.2.(8分)对于任何自然数,定义ni=1×2×3×…×n.那么算式2014i﹣3i的计算结果的个位数字是()A.2 B.4 C.6 D.83.(8分)童童在计算有余数的除法时,把被除数472错看成了427,结果商比原来小5,但余数恰好相同,那么这个余数是()A.4 B.5 C.6 D.74.(8分)如图中,正八边形ABCDEFGH的面积为1,其中有两个正方形ACEG 和PQRS.那么正八边形中阴影部分的面积()A.B.C.D.二、选择题(每题10分,共70分)5.(10分)如图所示竖式成立时的除数与商的和为()A.589 B.653 C.723 D.7336.(10分)甲乙丙三人进行一场特殊的真人CS比赛,规定:第一枪由乙射出,射击甲或者丙,以后的射击过程中,若甲被击中一次,则甲可以有6发子弹射击乙或丙,若乙被击中一次,则乙可以有5发子弹射击甲或丙,若丙被击中一次,则丙可以有4发子弹射击甲或乙,比赛结束后,共有16发子弹没有击中任何人?则甲乙丙三人被击中的次数有()种不同的情况.A.1 B.2 C.3 D.47.(10分)甲乙二人进行下面的游戏.二人先约定一个整数N,然后由甲开始,轮流把1,2,3,4,5,6,7,8,9这九个数字之一填入下面任一方格中:□□□□□□,每一方格只填入一个数字,形成一个数字可以重复的六位数.若这个六位数能被N整除,乙胜;否则甲胜.当N小于15时,使得乙有必胜策略的N有()A.5 B.6 C.7 D.88.(10分)在纸上任意写一个自然数,把这张纸旋转180度,数值不变,如0、11、96、888等,我们把这样的数称为“神马数”.在所有五位数中共有()个不同的“神马数”.A.12 B.36 C.48 D.609.(10分)如图,第(1)个多边形由正三角形“扩展”而来,边数记为a3,第(2)个多边形由正方形“扩展”而来,边数记为a4,…,依此类推,由正n边形“扩展”而来的多边形的边数记为a n(n≥3 ),则+++…+=,那么n=()A.2014 B.2015 C.2016 D.201710.(10分)如图所示,五边形ABCEF面积是2014平方厘米,BC与CE垂直于C点,EF与CE垂直于E点,四边形ABDF是正方形,CD:ED=3:2,那么,三角形ACE的面积是()平方厘米.A.1325 B.1400 C.1475 D.150011.(10分)甲乙两车分别从A、B两地同时出发,相向而行,甲车的速度大于乙车.甲行驶了60千米后和乙车在C点相遇.此后甲车继续向前行驶,乙车掉头与甲车同向行驶.那么当甲车到达B地时,甲乙两车最远相距()千米.A.10 B.15 C.25 D.30三、选择题(每题12分,共48分)12.(12分)在“爸爸去哪儿”的节目中有一个任务,五个参加任务的孩子(天天、石头、Kimi、Cindy、Angela)需要换爸爸(每个小朋友可以选择除了自己爸爸之外其他四位父亲中的任何一位),那么最终五人有()种不同的选择结果.A.40 B.44 C.48 D.5213.(12分)老师在黑板上从1开始将奇数连续地写下去,写了一长串数后,擦去了其中的两个数,将这些奇数隔成了3串,已知第二串比第一串多1个数,第三串比第二串多1个数,且第三串奇数和为4147,那么被划去的两个奇数的和是()A.188 B.178 C.168 D.15814.(12分)从一张大方格纸上剪下5个相连的方格(只有一个公共顶点的两个方格不算相连),要使剪下的图形可折叠为一个无盖的正方体,则共可以剪出()种不同的图形(经过旋转或翻转相同的图形视为同一种).A.8 B.9 C.10 D.1115.(12分)老师把某两位数的六个不同因数分别告诉了A~F六个聪明诚实的同学.A和B同时说:我知道这个数是多少了.C和D同时说:听了他们的话,我也知道这个数是多少了.E:听了他们的话,我知道我的数一定比F的大.F:我拿的数的大小在C和D之间.那么六个人拿的数之和是()A.141 B.152 C.171 D.1752014年“迎春杯”数学解题能力展示复赛试卷(六年级)参考答案与试题解析一、选择题(每小题8分,共32分)1.(8分)算式的计算结果是()A.B.C.D.【解答】解:===故选:D.2.(8分)对于任何自然数,定义ni=1×2×3×…×n.那么算式2014i﹣3i的计算结果的个位数字是()A.2 B.4 C.6 D.8【解答】解:由新定义:ni=1×2×3×…×n得:2014i=1×2×3×4×5×…×2013×2014=1×3×4×6×7×8×…×2013×2014×10所以1×3×4×6×7×8×…×2013×2014×10是10的倍数,所以2014i的个位数为0;3i=1×2×3=6所以2014i﹣3i的个位数也就为:10﹣6=4故选:B.3.(8分)童童在计算有余数的除法时,把被除数472错看成了427,结果商比原来小5,但余数恰好相同,那么这个余数是()A.4 B.5 C.6 D.7【解答】解:(472﹣427)÷5=45÷5=9472÷9=52 (4)答:这个余数是4.故选:A.4.(8分)如图中,正八边形ABCDEFGH的面积为1,其中有两个正方形ACEG 和PQRS.那么正八边形中阴影部分的面积()A.B.C.D.【解答】解:根据分析,将图中阴影部分进行等积变形,由图不难发现,阴影部分和空白部分的面积刚好相等,正八边形中阴影部分的面积占:故选:A.二、选择题(每题10分,共70分)5.(10分)如图所示竖式成立时的除数与商的和为()A.589 B.653 C.723 D.733【解答】解:依题意可知用字母表示如图:S首先判断A=0,B=4.再根据除数的2倍是四位数,那么E是大于4的.除数与D 的积是三位数,那么D就是小于2的非零数字,即D=1.再根据顺数第三行最后一位为1可以确定D和C的取值为(1,1).根据C=1,B=4,那么商的十位数字就是4,根据有余数推理E=5.再根据除数的2倍的数字中有6.那么除数的十位数字可能是3或者8.枚举得知除数是581商是142.581+142=723.故选:C.6.(10分)甲乙丙三人进行一场特殊的真人CS比赛,规定:第一枪由乙射出,射击甲或者丙,以后的射击过程中,若甲被击中一次,则甲可以有6发子弹射击乙或丙,若乙被击中一次,则乙可以有5发子弹射击甲或丙,若丙被击中一次,则丙可以有4发子弹射击甲或乙,比赛结束后,共有16发子弹没有击中任何人?则甲乙丙三人被击中的次数有()种不同的情况.A.1 B.2 C.3 D.4【解答】设甲乙丙分别被击中x、y、z次,则三人分别发射6x、5y+1,4z 次依题意有方程:6x+5y+1+4z﹣(x+y+z)=16化简得:5x+4y+3z=15,先考虑x的取值,x=3,1,01)当x=3时,y=z=0;不合题意,舍去;2)当x=1时,y=1,z=2;3)当x=0时,y=3,z=1;或4)x=0,y=0,z=5(不合题意,舍去)甲乙丙三人被击中的次数有2种不同的情况,故选B.7.(10分)甲乙二人进行下面的游戏.二人先约定一个整数N,然后由甲开始,轮流把1,2,3,4,5,6,7,8,9这九个数字之一填入下面任一方格中:□□□□□□,每一方格只填入一个数字,形成一个数字可以重复的六位数.若这个六位数能被N整除,乙胜;否则甲胜.当N小于15时,使得乙有必胜策略的N有()A.5 B.6 C.7 D.8【解答】解:若N是偶数,甲只需第一次在个位填个奇数,乙必败只需考虑N是奇数.N=1,显然乙必胜.N=3,9,乙只需配数字和1﹣8,2﹣7,3﹣6,4﹣5,9﹣9即可.N=5,甲在个位填不是5的数,乙必败.N=7,11,13,乙只需配成=×1001=×7×11×13,故选:B.8.(10分)在纸上任意写一个自然数,把这张纸旋转180度,数值不变,如0、11、96、888等,我们把这样的数称为“神马数”.在所有五位数中共有()个不同的“神马数”.A.12 B.36 C.48 D.60【解答】解:设这个数为,A位可以填11,88,69,96,4种情况,B位可以填00,11,88,69,96,5种情况,C位可以填0,1,8,3种情况,根据分步计数原理,可得在所有五位数中共有4×5×3=60(个),故选:D.9.(10分)如图,第(1)个多边形由正三角形“扩展”而来,边数记为a3,第(2)个多边形由正方形“扩展”而来,边数记为a4,…,依此类推,由正n边形“扩展”而来的多边形的边数记为a n(n≥3 ),则+++…+=,那么n=()A.2014 B.2015 C.2016 D.2017【解答】解:a3=3(2+2)=3×4,a4=4(2+3)=4×5,a5=5(2+4)=5×6,…a n=n(n+1),∴+++…+=,∴﹣+﹣+﹣+…+﹣=,∴﹣=,∴n+1=2017,∴n=2016.10.(10分)如图所示,五边形ABCEF面积是2014平方厘米,BC与CE垂直于C点,EF与CE垂直于E点,四边形ABDF是正方形,CD:ED=3:2,那么,三角形ACE的面积是()平方厘米.A.1325 B.1400 C.1475 D.1500【解答】解:作正方形ABCD的“弦图”,如右图所示,假设CD的长度为3a,DE的长度为2a,那么BG=3a,DG=2a,根据勾股定理可得BD2=BG2+DG2=9a2+4a2=13a2,所以,正方形ABDF的面积为13a2;因为CD=EF,BC=DE,所以三角形BCD和三角形DEF的面积相等为3a2;又因为五边形ABCEF面积是2014平方厘米,所以13a2+6a2=2014,解得a2=106,三角形ACE的面积为:5a×5a÷=a2,即×106=1325.11.(10分)甲乙两车分别从A、B两地同时出发,相向而行,甲车的速度大于乙车.甲行驶了60千米后和乙车在C点相遇.此后甲车继续向前行驶,乙车掉头与甲车同向行驶.那么当甲车到达B地时,甲乙两车最远相距()千米.A.10 B.15 C.25 D.30【解答】解:依题意可知:假设甲走60千米时,乙走了a千米,甲到达B地时,乙车应走千米.此时甲、乙相差最远为a﹣=×(60﹣a).和一定,差小积大,60﹣a=a,a=30.甲、乙最远相差30﹣=15(千米)故选:B.三、选择题(每题12分,共48分)12.(12分)在“爸爸去哪儿”的节目中有一个任务,五个参加任务的孩子(天天、石头、Kimi、Cindy、Angela)需要换爸爸(每个小朋友可以选择除了自己爸爸之外其他四位父亲中的任何一位),那么最终五人有()种不同的选择结果.A.40 B.44 C.48 D.52【解答】解:设五个爸爸分别是A,B,C,D,E,五个孩子分别是a,b,c,d,e,a有4种选择,假设a选择B,接着让b选择,有两种可能,选择A和不选择A,(1)选择A,c,d,e 选择三个人错排,(2)不选择A,则b,c,d,e,选择情况同4人错排.所以S5=4(S4+S3).同理S4=3(S3+S2),S3=2(S2+S1),而S1=0(不可能排错),S2=0,所以S3=2,S4=9,S5=44,故选:B.13.(12分)老师在黑板上从1开始将奇数连续地写下去,写了一长串数后,擦去了其中的两个数,将这些奇数隔成了3串,已知第二串比第一串多1个数,第三串比第二串多1个数,且第三串奇数和为4147,那么被划去的两个奇数的和是()A.188 B.178 C.168 D.158【解答】解:设第一段有n个,则第2段有n+1个,那么第一个擦的奇数是2n+1,第二个擦的奇数是4n+5,被划去的两个奇数的和为:2n+1+4n+5=6n+6,6n+6是6的倍数,在四个选项中只有168是6的倍数,符合要求.故选:C.14.(12分)从一张大方格纸上剪下5个相连的方格(只有一个公共顶点的两个方格不算相连),要使剪下的图形可折叠为一个无盖的正方体,则共可以剪出()种不同的图形(经过旋转或翻转相同的图形视为同一种).A.8 B.9 C.10 D.11【解答】解:依题意可知:剪下来的图形如图所示:共8种.故选:A.15.(12分)老师把某两位数的六个不同因数分别告诉了A~F六个聪明诚实的同学.A和B同时说:我知道这个数是多少了.C和D同时说:听了他们的话,我也知道这个数是多少了.E:听了他们的话,我知道我的数一定比F的大.F:我拿的数的大小在C和D之间.那么六个人拿的数之和是()A.141 B.152 C.171 D.175【解答】解:70+35+14+10+7+5=141【答案】A声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/5 17:59:51;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
六年级迎春杯试题及答案

六年级迎春杯试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项是正确的?A. 地球是平的B. 地球是圆的C. 地球是方的D. 地球是三角形的2. 以下哪个数学公式是正确的?A. 圆的面积 = 半径× 半径B. 圆的面积 = 半径× π × 半径C. 圆的周长 = 直径× 2D. 圆的周长 = 半径× 2π3. 根据题目所给信息,以下哪个选项是错误的?A. 春天是一年四季之一B. 迎春杯是冬季举行的竞赛C. 迎春杯是为了庆祝春天的到来D. 迎春杯通常在春季举行4. 以下哪个成语与“春天”有关?A. 春暖花开B. 秋高气爽C. 夏日炎炎D. 冬日暖阳5. 以下哪个选项是迎春杯试题的类型?A. 选择题B. 填空题C. 判断题D. 论述题二、填空题(每题2分,共10分)6. 春天是_________、_________、_________和_________四个季节之一。
7. 迎春杯试题的类型包括选择题、填空题、_________和_________。
8. 地球的形状是_________,因为它在自转和公转时表现出的离心力和引力的平衡。
9. 圆的周长公式是_________,其中C代表周长,d代表直径。
10. 成语“春暖花开”常用来形容_________。
三、判断题(每题1分,共5分)11. 迎春杯试题及答案的标题是“六年级迎春杯试题及答案”。
()12. 地球的形状是平的。
()13. 迎春杯试题通常在冬季举行。
()14. 成语“秋高气爽”与春天有关。
()15. 圆的面积公式是πr²,其中r代表半径。
()四、简答题(每题5分,共10分)16. 请简述迎春杯试题的特点。
17. 请解释为什么地球的形状是圆的。
五、论述题(15分)18. 论述春天对人们生活的影响。
参考答案:1. B2. B3. B4. A5. A6. 春、夏、秋、冬7. 判断题、论述题8. 圆的9. C = πd10. 春天的气候温暖,百花盛开的景象11. √12. ×13. ×14. ×15. √16. 迎春杯试题通常包括选择题、填空题、判断题和论述题,旨在考查学生的综合能力。
迎春杯六年级试题及答案
迎春杯六年级试题及答案一、选择题(每题3分,共30分)1. 以下哪个数是质数?A. 15B. 23C. 48D. 66答案:B2. 一个长方体的长、宽、高分别是10cm、8cm和6cm,那么它的体积是多少立方厘米?A. 480B. 400C. 320D. 240答案:A3. 一个数的3倍是48,这个数是多少?A. 16B. 12C. 8D. 6答案:A4. 以下哪个分数是最简分数?A. 3/6B. 4/8C. 5/10D. 7/14答案:A5. 一个圆的直径是14cm,那么它的半径是多少?B. 14cmC. 21cmD. 28cm答案:A6. 一个数除以5余3,除以7余1,这个数最小是多少?A. 36B. 37C. 38D. 39答案:B7. 一个等腰三角形的底边长为10cm,两腰长为8cm,那么它的周长是多少?A. 26cmB. 28cmD. 32cm答案:A8. 一个数的5倍加上3等于这个数的7倍减去5,这个数是多少?A. 4B. 5C. 6D. 7答案:A9. 一个长方形的长是宽的两倍,如果宽增加2cm,长减少2cm,那么它的面积不变,原来的长方形的长和宽分别是多少?A. 长8cm,宽4cmB. 长10cm,宽5cmC. 长12cm,宽6cmD. 长14cm,宽7cm答案:B10. 一个数的1/4加上这个数的1/3等于9,这个数是多少?A. 12B. 18C. 24D. 36答案:C二、填空题(每题4分,共40分)11. 一个数的倒数是1/5,这个数是______。
答案:512. 一个数的1/2加上这个数的1/3等于7,这个数是______。
答案:1213. 一个数的3倍减去2等于这个数的2倍加上3,这个数是______。
答案:514. 一个长方体的长、宽、高分别是a、b、c,那么它的表面积是______。
答案:2(ab + ac + bc)15. 一个数的1/4加上这个数的1/6等于1/2,这个数是______。
数学花园探秘(迎春杯)六年级决赛试卷及详解
超 出作答范围不得分.)
102
1.答案:64
2017 数学花园探秘科普活动小高决赛 A 解析 解析:原式=(632-613 )+(1-613 )=63+1=64
2.答案:2384
解析:500+15 ×2×π ×(100+200+300+400+500)=2384
3.答案:94 解析:注意到前三局比前两局多 25 分,后三局比后两局多 25 分,所以中国队得
12.答案:2 解析:注意到如下操作:
所以每次可以将一个“L”形的四个棋子中去掉 3 个,另一个回到原格。所以将 36 枚棋子按图中 的分组依次去掉,最后剩下右下的 1×3 的棋子,再操作一次即可剩下 2 枚。
下面证明最少剩下 2 枚棋子
104
如下图对期盼进行三染色,则每次操作时,有两种颜色格内的棋子数减 1,第三种颜色格内的棋 子数加 1,而开始时三种颜格内的棋子数均相等,所以每次操作后三种颜色格内的棋子数奇偶 性相同,而最后棋子不可能一枚不剩,所以最少剩下 2 枚棋子。
A
B
11. 有一列正整数,其中第 1 个数是 1,第 2 个数是 1、2 的最小公倍数,第 3 个数是 1、2、 3 的最小 公倍数,„„,第 n 个数是 1、2、„„、n 的最小公倍数.那么这列数的前 100 个数 中共_______个不同的值.
“迎春杯”六年级数学花园探秘科普活动总决赛试卷
第 1 页 共 3 页
2018年“迎春杯”六年级数学花园探秘科普活动总决赛试卷解
析版
一、填空题。
(每小题10分,共30分)
1.(10分)如图,在每个空格内填入1~4中的一个,使每行、每列以及每个由粗线所围成
的区域中的四个数都不重复,且任意相邻两个空格所填数的和都是质数.那么四位数ABCD = 2143 .
【解答】解:由题意,C 在1的上方,只能填偶数,但是同一列已经有2,所以C =4, 则B 和D 只能是奇数,在同一区域中已经有1,所以D =3,则B =1,
剩下A =2,四位数ABCD =2143.
故答案为:2143.
2.(10分)一个半径为5厘米的轮子放置在如图的阴影弓形中,它能沿着弓形的弦AB 滚动,
如果弓形的半径OA 、OB 为25厘米,AB 长为48厘米.那么轮子在AB 上滚动时能扫过区域的面积为 395 平方厘米.(π取3)
【解答】解:
先作OC ⊥AB ,过E 点作EF ∥AB ,并与OC 的延长线相交于F 点.
在直角三角形OCB 中,OB =25(厘米),BC =48÷2=24(厘米)
,根据勾股定理求出。
2011年“迎春杯”数学解题能力展示初赛试卷(六年级)-含答案解析
2021年“迎春杯〞数学解题能力展示初赛试卷〔六年级〕一、填空题〔每题8分,共40分〕1.〔8分〕今天是2021年12月19日,欢送同学们参加北京第27届“数学解题能力展示〞活动.那么,计算结果的整数局部是.2.〔8分〕某校有2400名学生,每名学生每天上5节课,每位教师每天教4节课,每节课是一位教师给30名学生讲授.那么该校共有教师位.3.〔8分〕张老师带着一些钱去买签字笔,到商店后发现这种笔降价了25%,结果他带的钱恰好可以比原来多买25支.那么降价前这些钱可以买签字笔支.4.〔8分〕如图为某婴幼儿商品的商标,由两颗心组成,每颗心都是由一个正方形和两个半圆拼成.假设两个正方形的边长分别为40mm,20mm,那么,阴影图形的面积是mm2.〔π取3.14〕5.〔8分〕用4.02乘以一个两位整数,得到的乘积是一个整数,那么这个乘积的10倍是.二、填空题〔每题10分,共50分〕6.〔10分〕某支球队现在的胜率为45%,接下来的8场比赛中假设有6场获胜,那么胜率将提高到50%.那么现在这支球队共取得了场比赛的胜利.7.〔10分〕定义运算:a♥b=,算式的计算结果是.8.〔10分〕在△ABC中,BD=DE=EC,CF:AC=1:3.假设△ADH的面积比△HEF的面积多24平方厘米,求三角形ABC的面积是多少平方厘米?9.〔10分〕一个正整数,它的2倍的约数恰好比它自己的约数多2个,它的3倍的约数恰好比它自己的约数多3个.那么,这个正整数是.10.〔10分〕如图,一个6×6的方格表,现将数字1~6填入空白方格中,使得每一行、每一列数字1~6都恰好出现一次;图中已经填了一些数字.那么剩余空格满足要求的填写方法一共有种.三、填空题〔每题12分,共60分〕11.〔12分〕有一个圆柱体,高是底面半径的3倍.将它如图分成大、小两个圆柱体,大圆柱体的外表积是小圆柱体的3倍.那么,大圆柱体的体积是小圆柱体的倍.12.〔12分〕某岛国的一家银行每天9:00~17:00营业.正常情况下,每天9:00准备现金50万元,假设每小时的提款量都一样,每小时的存款量也一都一样,到17:00下班时有现金60万元.如果每小时提款量是正常情况的4倍的话,14:00银行就没现金了.如果每小时提款量是正常情况的10倍,而存款量减少到正常情况的一半的话,要使17:00下班时银行还有现金50万元,那么9:00开始营业时需要准备现金多少万元?13.〔12分〕40根长度相同的火柴棍摆成如图,如果将每根火柴棍看作长度为1的线段,那么其中可以数出30个正方形来.拿走5根火柴棍后,A,B,C,D,E五人分别作了如下的判断:A:“1×1的正方形还剩下5个.〞B:“2×2的正方形还剩下3个.〞C:“3×3的正方形全部保存下来了.〞D:“拿走的火柴棍所在直线各不相同.〞E:“拿走的火柴棍中有4根在同一直线上.〞这5人中恰有2人的判断错了,那么剩下的图形中还能数出个正方形.14.〔12分〕甲、乙、丙三人同时从A出发去B,甲、乙到B后调头回A,并且调头后速度减少到各自原来速度的一半.甲最先调头,调头后与乙在C迎面相遇,此时丙已行2021米;甲又行一段后与丙在AB中点D迎面相遇;乙调头后也在C与丙迎面相遇.那么,AB间路程是米.15.〔12分〕算式﹣+﹣A,B,C,D,E,F,G,H,I表示1~9中各不相同的数字.那么,五位数=.2021年“迎春杯〞数学解题能力展示初赛试卷〔六年级〕参考答案与试题解析一、填空题〔每题8分,共40分〕1.〔8分〕今天是2021年12月19日,欢送同学们参加北京第27届“数学解题能力展示〞活动.那么,计算结果的整数局部是16.【解答】解:答:整数局部为16.2.〔8分〕某校有2400名学生,每名学生每天上5节课,每位教师每天教4节课,每节课是一位教师给30名学生讲授.那么该校共有教师100位.【解答】解:〔2400×5〕÷〔4×30〕=12000÷120=100〔位〕答:该校共有教师100位.故答案为:100.3.〔8分〕张老师带着一些钱去买签字笔,到商店后发现这种笔降价了25%,结果他带的钱恰好可以比原来多买25支.那么降价前这些钱可以买签字笔75支.【解答】解:设原来可以买x支笔,由题意得:1×x=〔x+25〕×〔1﹣25%〕,x=〔x+25〕×0.75,xx+18.75,x=18.75,x=75;答:降价前这些钱可以买签字笔75支.故答案为:75.4.〔8分〕如图为某婴幼儿商品的商标,由两颗心组成,每颗心都是由一个正方形和两个半圆拼成.假设两个正方形的边长分别为40mm,20mm,那么,阴影图形的面积是2142mm2.〔π取3.14〕【解答】解:如下图:〔402+π×202〕﹣〔202+π×102〕=1600+400π﹣400﹣100π=1200+300π=1200+300×=1200+942=2142〔平方毫米〕.答:阴影局部的面积是2142平方毫米.故答案为:2142.5.〔8分〕用4.02乘以一个两位整数,得到的乘积是一个整数,那么这个乘积的10倍是2021.【解答】解:4.02乘以一个两位整数,得到的乘积是一个整数,这个两位数是50,×50×10=2021.答:这个乘积的10倍是2021.故答案为:2021.二、填空题〔每题10分,共50分〕6.〔10分〕某支球队现在的胜率为45%,接下来的8场比赛中假设有6场获胜,那么胜率将提高到50%.那么现在这支球队共取得了18场比赛的胜利.【解答】解:假设已进行了x场比赛,那么〔x+8〕×50%=45%x+6xx+6x=2x=40;45%x=40×45%=18〔场〕答:现在该队取得18场比赛胜利.故答案为:18.7.〔10分〕定义运算:a♥b=,算式的计算结果是201.【解答】解:a♥b==,♥2021==,♥2021==,找到了规律:有n个2021,就得现在有9颗♥就有10个2021,所以结果是=201;故答案为:201.8.〔10分〕在△ABC中,BD=DE=EC,CF:AC=1:3.假设△ADH的面积比△HEF的面积多24平方厘米,求三角形ABC的面积是多少平方厘米?【解答】解:△ADH的面积比△HEF的面积多24平方厘米,那么三角形ADE的面积比三角形FDE的面积多24平方厘米,又因三角形FDE和三角形FEC的面积相等,也就是说三角形AEC比三角形FEC的面积多24平方厘米,又因多出的24平方厘米,是三角形AEC的面积的,所以三角形AEC的面积是24÷=36平方厘米,那么三角形ABC的面积是36÷=108〔平方厘米〕,答:三角形ABC的面积是108平方厘米.9.〔10分〕一个正整数,它的2倍的约数恰好比它自己的约数多2个,它的3倍的约数恰好比它自己的约数多3个.那么,这个正整数是12.【解答】解:这个数只能含2和3两种质因数,因为如果它还有别的质因数,那么最后增加的个数要比给定的数字大.设x=2a3b,它的约数〔a+1〕〔b+1〕个,它的2倍为2a+13b,它的约数有〔a+1+1〕〔b+1〕个,那么:〔a+1+1〕〔b+1〕﹣〔a+1〕〔b+1〕=b+1=2,求出b=1;同理,它的3倍为2a,它的约数为〔a+1〕〔b+1+1〕个,比原数多3个,即〔a+1〕〔b+1+1〕﹣〔a+1〕〔b+1〕=a+1=3,求出a=2,所以这个数的形式是223=12;答:这个正整数是12.故答案为:12.10.〔10分〕如图,一个6×6的方格表,现将数字1~6填入空白方格中,使得每一行、每一列数字1~6都恰好出现一次;图中已经填了一些数字.那么剩余空格满足要求的填写方法一共有16种.【解答】解:如下列图,四个“□〞格中只能填入2或5,共2种填法;四个“△〞中只能填入3或4.2种填法.√1,√2,√3,√4中,1的填法有2种,那么6的位置确定.四个“○〞和四个“√〞相同,有2种填法.由乘法原理,共2×2×2×2=16种填法.故答案为:16.三、填空题〔每题12分,共60分〕11.〔12分〕有一个圆柱体,高是底面半径的3倍.将它如图分成大、小两个圆柱体,大圆柱体的外表积是小圆柱体的3倍.那么,大圆柱体的体积是小圆柱体的11倍.【解答】解:设这个圆柱体底面半径为r,那么高为3r,小圆柱体高为h,那么大圆柱体高为〔3r﹣h〕;因为大圆柱体的外表积是小圆柱体的3倍,所以h=,那么大圆柱体高为r;又由于两圆柱体底面积相同,r÷=11,所以大圆柱体体积也是小圆柱体体积的11倍.故答案为:11.12.〔12分〕某岛国的一家银行每天9:00~17:00营业.正常情况下,每天9:00准备现金50万元,假设每小时的提款量都一样,每小时的存款量也一都一样,到17:00下班时有现金60万元.如果每小时提款量是正常情况的4倍的话,14:00银行就没现金了.如果每小时提款量是正常情况的10倍,而存款量减少到正常情况的一半的话,要使17:00下班时银行还有现金50万元,那么9:00开始营业时需要准备现金多少万元?【解答】解:9:00~17:00是8个小时,9:00~14:00是5个小时,〔60﹣50〕÷8=1.25〔元万/时〕,50÷5=10〔万元/时〕,提款速度为:〔10+1.25〕÷〔4﹣1〕,÷3,=3.75〔万元/时〕,存款速度为:3.75+1.25=5〔万元/时〕,×10﹣5÷2〕×8+50,﹣2.5〕×8+50,=35×8+50,=280+50,=330〔万元〕.答:需要准备现金330万元.13.〔12分〕40根长度相同的火柴棍摆成如图,如果将每根火柴棍看作长度为1的线段,那么其中可以数出30个正方形来.拿走5根火柴棍后,A,B,C,D,E五人分别作了如下的判断:A:“1×1的正方形还剩下5个.〞B:“2×2的正方形还剩下3个.〞C:“3×3的正方形全部保存下来了.〞D:“拿走的火柴棍所在直线各不相同.〞E:“拿走的火柴棍中有4根在同一直线上.〞这5人中恰有2人的判断错了,那么剩下的图形中还能数出14个正方形.【解答】解:〔1〕每拿走1根火柴棍,最多减少2个1×1小正方形,拿5根最多减少10个1×1正方形,所以1×1的正方形至少还有6个,A必错;〔2〕显然D、E矛盾,必有1错,故B、C都对;〔3〕由于C正确,画出组成3×3的火柴,发现只可去掉第三行和第三列的所有火柴,因此D错误;〔4〕拿走同一直线的4根火柴〔如图〕,还需要在第三列取走一根.由于2×2的正方形有三个,因此只能取走第三列的第一根.〔5〕正方形:1×1的6个,2×2的3个.3×3的4个,4×4的1个,共14个.答:剩下的图形中还能数出14个正方形.故答案为:14.14.〔12分〕甲、乙、丙三人同时从A出发去B,甲、乙到B后调头回A,并且调头后速度减少到各自原来速度的一半.甲最先调头,调头后与乙在C迎面相遇,此时丙已行2021米;甲又行一段后与丙在AB中点D迎面相遇;乙调头后也在C与丙迎面相遇.那么,AB间路程是5360米.【解答】解:设全程为S,甲、丙在D点相遇所需时间为t,∵由于甲折返后与丙在中点相遇,∴甲共走了个全程,丙走了个全程,∵甲折返后的速度减半,∴甲执返前后所需时间一样,∴S甲=S=tV甲+t•V甲=V甲t,∵S丙=S=V丙t,∴S:S=V甲:V丙∴V甲:V丙=4:1,AC:BC=3:1AB的距离=2021×4=8040,那么AB距离为:8040÷1.5=5360〔米〕.答:AB间路程是5360米.故答案为:5360.15.〔12分〕算式﹣+﹣A,B,C,D,E,F,G,H,I表示1~9中各不相同的数字.那么,五位数=34179.【解答】解:由于差12.19=12,即差出现了,所以所以通分后的分母等于100,也就是说GH是25的倍数,由于2021中的约数中已含有一个2,那么I是8的倍数.〔GH 和I互质,故不能是100和1、20和5、10和10〕.所以所以I=8,12.19+=263.44.〔1〕如果GH=75,的小数局部为0.44,说明F一定是3的倍数即3、6、9.经讨论,不存在这样的F,故GH=75不成立.〔2〕如果GH=25,那么的小数局部为0.44,F2除以25余11,所以F﹣=262.用剩余的1,3,4,7,9凑成差为262的两个数:341﹣79=262.所以这个五个数是:34179.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014“数学解题能力展示”读者评选活动复赛试题小学六年级(2014年2月6日)一、选择题(每小题8分,共32分)1.算式5258+172014201.42⨯÷-⨯的计算结果是( ). A.15 B .16 C.17 D.182.对于任何自然数,定义!123n n =⨯⨯⨯⨯.那么算式2014!3!-的计算结果的个位数字是( ). A.2 B.4 C.6 D .83.统统在计算有余数的除法时,把被除数472错看成了427,结果商比原来小5,但余数恰好相同,那么这个余数是( ).A .4B .5 C.6 D.74.下图中,正八边形ABCDEFGH 的面积为1,其中有两个正方形ACEG 和PQRS .那么正八边形中阴影部分的面积().H AA.12 B .23 C .35 D .58二、选择题(每题10分,共70分)5.右面竖式成立时的除数与商的和为( ).12642A.589B.653C.723D.7336.甲乙丙三人进行一场特殊的真人C S比赛,规定:第一枪由乙射出,射击甲或者丙,以后的射击过程中,若甲被击中一次,则甲可以有6发子弹射击乙或丙,若乙被击中一次,则乙可以有5发子弹射击甲或丙,若丙被击中一次,则丙可以有4发子弹射击甲或乙,比赛结束后,共有16发子弹没有击中任何人?则甲乙丙三人被击中的次数有( )种不同的情况.A .1 B.2 C.3 D .47.甲乙二人进行下面的游戏.二人先约定一个整数N ,然后由甲开始,轮流把1,2,3,4,5,6,7,8,9这九个数字之一填入下面任一方格中:□□□□□□,每一方格只填入一个数字,形成一个数字可以重复的六位数.若这个六位数能被N 整除,乙胜;否则甲胜.当N 小于15时,使得乙有必胜策略的N 有( ). A.5 B.6 C .7 D.88.在纸上任意写一个自然数,把这张纸旋转180度,数值不变,如0、11、96、888等,我们把这样的数称为“神马数”.在所有五位数中共有( )个不同的“神马数”.A.12B.36C.48 D.609.如图,第(1)个多边形由正三角形“扩展”而来,边数记为3a ,第(2)个多边形由正方形“扩展”而来,边数记为4a ,……,依此类推,由正n 边形“扩展”而来的多边形的边数记为n a (3n ≥ ),则34511112014++++6051n a a a a =,那么n =(). (4)(3)(2)(1)A .2014B .2015 C.2016 D .201710.如右图所示,五边形ABCDEF 面积是2014平方厘米,BC 与CE 垂直于C 点,EF 与CE 垂直于E 点,四边形ABDF 是正方形,:3:2CD DE =.那么,三角形ACE 的面积是 ( )平方厘米.FECB AA.1325 B .1400 C.1475 D .150011.甲乙两车分别从A、B两地同时出发,相向而行,甲车的速度大于乙车.甲行驶了60千米后和乙车在C点相遇.此后甲车继续向前行驶,乙车掉头与甲车同向行驶.那么当甲车到达B地时,甲乙两车最远相距()千米.A.10B.15 C.25 D.30三、选择题(每题12分,共48分)12.在“爸爸去哪儿”的节目中有一个任务,五个参加任务的孩子(天天、石头、Kimi、Cindy、Ange la)需要换爸爸(每个小朋友可以选择除了自己爸爸之外其他四位父亲中的任何一位),那么最终五人有( )种不同的选择结果.A.40 B.44 C.48 D.5213.老师在黑板上从1开始将奇数连续地写下去,写了一长串数后,擦去了其中的两个数,将这些奇数隔成了3串,已知第二串比第一串多1个数,第三串比第二串多1个数,且第三串奇数和为4147,那么被划去的两个奇数的和是().A.188B.178C.168D.15814.从一张大方格纸上剪下5个相连的方格(只有一个公共顶点的两个方格不算相连),要使剪下的图形可折叠为一个无盖的正方体,则共可以剪出()种不同的图形(经过旋转或翻转相同的图形市委同一种).A.8B.9 C.10 D.1115.老师把某个两位数的六个不同约数分别告诉了A F六个聪明诚实的同学.A和B同时说:“我知道这个数是多少了.”C和D同时说:“听了他们两人的话,我也知道这个两位数是多少了.”E:“听了他们的话,我知道我的数一定比F的大.”F:“我拿的数的大小在C和D之间.”那么六个人拿的数之和是( )A.141 B.152 C.171 D.175ﻬ2014“数学解题能力展示”读者评选活动复赛试题小学六年级参考答案部分解析一、选择题(每小题8分,共32分)1.算式5258+172014201.42⨯÷-⨯的计算结果是( ).A.15B.16C.17D.18【考点】计算【难度】☆☆【答案】D【解析】5258+1200 1.4201.41 72014201.42201.410201.42201.488⨯÷+=== -⨯⨯-⨯⨯2.对于任何自然数,定义!123n n=⨯⨯⨯⨯.那么算式2014!3!-的计算结果的个位数字是( ).A.2B.4 C.6D.8【考点】定义新运算【难度】☆☆【答案】B【解析】2014!个位数字是0,3!1236=⨯⨯=,所以2014!3!-个位是4.3.童童在计算有余数的除法时,把被除数472错看成了427,结果商比原来小5,但余数恰好相同,那么这个余数是().A.4 B.5 C.6 D.7【考点】整除同余【难度】☆☆【答案】A【解析】除数=(472427)59-÷=,4724(mod9)≡,所以余数是4.4.下图中,正八边形ABCDEFGH的面积为1,其中有两个正方形ACEG和PQRS.那么正八边形中阴影部分的面积().HAA.12B.23C.35D.58【考点】几何【难度】☆☆☆【答案】A【解析】等积变形.H AAH H A所以刚好各占一半. 二、选择题(每题10分,共70分)5.右面竖式成立时的除数与商的和为().12642A.589 B .653 C .723 D .733 【考点】数字谜 【难度】☆☆☆ 【答案】C【解析】首先根据倒数第三行可以确定0A =,4B =;241ECB A 60D22112611322440854815252824160120再根据顺数第三行最后一位为1可以确定,第一行D 和C 的取值为(1,1)或(3,7)或(9,9)或(7,3),根据尝试只有(1,1)符合题意.再依次进行推理,可得商和除数分别为:142和581.6.甲乙丙三人进行一场特殊的真人CS 比赛,规定:第一枪由乙射出,射击甲或者丙,以后的射击过程中,若甲被击中一次,则甲可以有6发子弹射击乙或丙,若乙被击中一次,则乙可以有5发子弹射击甲或丙,若丙被击中一次,则丙可以有4发子弹射击甲或乙,比赛结束后,共有16发子弹没有击中任何人?则甲乙丙三人被击中的次数有( )种不同的情况.A.1 B .2 C.3 D.4 【考点】不定方程 【难度】☆☆☆ 【答案】B【解析】设甲乙丙分别被击中x 、y 、z 次则三人分别发射6x 、51y +,4z 次[6(51)4]()16x y z x y z +++-++=化简得54315x y z ++=7.甲乙二人进行下面的游戏.二人先约定一个整数N ,然后由甲开始,轮流把1,2,3,4,5,6,7,8,9这九个数字之一填入下面任一方格中:□□□□□□,每一方格只填入一个数字,形成一个数字可以重复的六位数.若这个六位数能被N 整除,乙胜;否则甲胜.当N 小于15时,使得乙有必胜策略的N 有( ). A.5 B .6 C.7 D.8 【考点】数论 【难度】☆☆☆ 【答案】B【解析】若N 是偶数,甲只需第一次在个位填个奇数,乙必败只需考虑N 是奇数.1N =,显然乙必胜.39N =,,乙只需配数字和1-8,2-7,3-6,4-5,9-9即可.5N =,甲在个位填不是5的数,乙必败.71113N =,,,乙只需配成100171113abcabc abc abc =⨯=⨯⨯⨯.8.在纸上任意写一个自然数,把这张纸旋转180度,数值不变,如0、11、96、888等,我们把这样的数称为“神马数”.在所有五位数中共有( )个不同的“神马数”.A.12 B .36 C.48 D .60 【考点】数论 【难度】☆☆☆ 【答案】D【解析】设这个数为ABCBA ,A 位可以填11,88,69,96,4种情况,B 位可以填00,11,88,69,96,5种情况,C位可以填0,1,8,3种情况,453=60⨯⨯(个).9.如图,第(1)个多边形由正三角形“扩展”而来,边数记为3a ,第(2)个多边形由正方形“扩展”而来,边数记为4a ,……,依此类推,由正n 边形“扩展”而来的多边形的边数记为n a (3n ≥ ),则34511112014++++6051n a a a a =,那么n =( ).(4)(3)(2)(1)A.2014B.2015C.2016D.2017【考点】找规律【难度】☆☆☆【答案】C【解析】33(22)34a=⨯+=⨯,44(23)45a=⨯+=⨯,55(24)56a=⨯+=⨯,……(21)(1)na n n n n=⨯+-=+,34511111111120143445(1)316051na a a a n n n++++=+++=-=⨯⨯⨯++,12017n+=,2016n=.10.如右图所示,五边形ABCDEF面积是2014平方厘米,BC与CE垂直于C点,EF与CE垂直于E点,四边形ABDF是正方形,:3:2CD DE=.那么,三角形ACE的面积是()平方厘米.FECBAA.1325B.1400C.1475D.1500【考点】几何【难度】☆☆☆【答案】A【解析】作正方形ABCD的“弦图”,如右图所示,IHGFEDCBA假设CD的长度为3a,DE的长度为2a,那么3BG a=,2DG a=,根据勾股定理可得2222229413BD BG DG a a a=+=+=,所以,正方形ABDF的面积为213a;因为CD EF=,BC DE=,所以三角形BCD和三角形DEF的面积相等为23a;又因为五边形ABCEF面积是2014平方厘米,所以222136192014a a a+==,解得2106a=, 三角形ACE的面积为:2255522a a a⨯÷=,即2510613252⨯=.11.甲乙两车分别从A 、B 两地同时出发,相向而行,甲车的速度大于乙车.甲行驶了60千米后和乙车在C点相遇.此后甲车继续向前行驶,乙车掉头与甲车同向行驶.那么当甲车到达B 地时,甲乙两车最远相距( )千米.A .10 B.15 C.25 D .30 【考点】行程问题 【难度】☆☆☆ 【答案】A【解析】假设甲走60千米时,乙走了a 千米,甲到达B 地时,乙车应走26060a a a ⨯=千米,此时甲、乙相差最远为1(60)6060a a a a -=⨯-⨯,和一定,差小积大,60a a -=,30a =.甲、乙最远相差900301560-=(千米).三、选择题(每题12分,共48分)12.在“爸爸去哪儿”的节目中有一个任务,五个参加任务的孩子(天天、石头、K imi 、Cin dy、Angela )需要换爸爸(每个小朋友可以选择除了自己爸爸之外其他四位父亲中的任何一位),那么最终五人有( )种不同的选择结果.A .40 B.44 C.48 D.52 【考点】排列组合 【难度】☆☆☆ 【答案】B【解析】设五个爸爸分别是A B C D E 、、、、,五个孩子分别是a b c d e 、、、、,a 有4种选择,假设a 选择B ,接着让b 选择,有两种可能,选择A 和不选择A ,(1)选择A ,c d e 、、 选择三个人错排,(2)不选择A ,则b c d e 、、、 选择情况同4人错排.所以5434()S S S =⨯+ 同理4323()S S S =⨯+ ,3212()S S S =⨯+,而10S =(不可能排错),21S =,所以32S =,49S =,544S =.13.老师在黑板上从1开始将奇数连续地写下去,写了一长串数后,擦去了其中的两个数,将这些奇数隔成了3串,已知第二串比第一串多1个数,第三串比第二串多1个数,且第三串奇数和为4147,那么被划去的两个奇数的和是( ).A.188 B .178 C.168 D.158 【考点】数论 【难度】☆☆☆ 【答案】C【解析】设第一段有n 个,则第2段有1n +个,第一个擦的奇数是21n +,第二个擦的奇数是45n +,和为66n +,是6的倍数.只有168符合.14.从一张大方格纸上剪下5个相连的方格(只有一个公共顶点的两个方格不算相连),要使剪下的图形可折叠为一个无盖的正方体,则共可以剪出( )种不同的图形(经过旋转或翻转相同的图形视为同一种).A.8 B .9 C .10 D .11 【考点】立体几何 【难度】☆☆☆ 【答案】A【解析】如下图15.老师把某个两位数的六个不同约数分别告诉了A F六个聪明诚实的同学.A和B同时说:“我知道这个数是多少了.”C和D同时说:“听了他们两人的话,我也知道这个两位数是多少了.”E:“听了他们的话,我知道我的数一定比F的大.”F:“我拿的数的大小在C和D之间.”那么六个人拿的数之和是()A.141 B.152 C.171D.175【考点】数论【难度】☆☆☆☆【答案】A【解析】(1)这个数的因数个数肯定不低于6个(假定这个数为N,且拿到的6个数从大到小分别是、、、、、)A B C D E F(2)有两个人同时第一时间知道结果,这说明以下几个问题:第一种情况:有一个人知道了最后的结果,这个结果是怎么知道的呢?很简单,他拿到的因数在5099之间(也就是说A的2倍是3位数,所以A其实就是N)第二种情况:有一个人拿到的不是最后结果,但是具备以下条件:1)这个数的约数少于6个,比如:有人拿到36,单他不能断定N究竟是36还是72.2)这个数小于50,不然这个数就只能也是N了.3)这个数大于33,比如:有人拿到29,那么他不能断定N是58还是87;这里有个特例是27,因为272=54⨯,因数个数少于6个,所以如果拿到27可以判断⨯,因数个数不少于6个;273=81N只能为54)4)这个数还不能是是质数,不然不存在含有这个因数的两位数.最关键的是,这两人的数是2倍关系但是上述内容并不完全正确,需要注意还有一些“奇葩”数:17、19、23也能顺利通过第一轮.因此,这两个人拿到的数有如下可能:(54,27)(68,34)(70,35)(76,38)(78,39)(92,46)(98,49)(3)为了对比清晰,我们再来把上面所有的情况的因数都列举出来:(54,27,18,9,6,3,2,1)(68,34,17,4,2,1)(×)(70,35,14,10,7,5,2,1)(76,38,19,4,2,1)(×)(78,39,26,13,6,3,2,1)(92,46,23,4,2,1)(×)(98,49,14,7,2,1)对于第一轮通过的数,我们用红色标注,所以N不能是68、76、92中的任意一个.之后在考虑第二轮需要通过的两个数.用紫色标注的6、3、2、1,因为重复使用,如果出现了也不能判断N是多少,所以不能作为第二轮通过的数.用绿色标注的14和7也不能作为第二轮通过的数,这样N也不是98.那么通过第二轮的数只有黑色的数.所以N只能是54、70、78中的一个.我们再来观察可能满足E和F所说的内容:(54,27,18,9,6,3,2,1)(70,35,14,10,7,5,2,1)(78,39,26,13,6,3,2,1)因为F说他的数在C和D之间,我们发现上面的数据只有当70、(10和N=的时候,7F=,在C D5)之间,是唯一满足条件的一种情况.又因为E确定自己比F的大,那么他拿到的数一定是该组中剩余数里最大的.所以E拿到的是14(70N=).所以70N=,六个人拿的数之和为:70+35+14+10+7+5=141.。
