东华大学自动控制原理实验一
自动控制原理实验资料

自动控制原理实验实验1 控制系统典型环节的模拟利用运算放大器的基本特性,如:开环增益高,输入阻抗大、输出阻抗小等,通过设置不同的反馈网络,可以模拟各种典型环节。
一.实验目的● 掌握用运算放大器组成控制系统典型环节的电子电路原理。
● 观察几种典型环节的阶跃响应曲线。
● 了解参数变化对典型环节输出动态性能(即阶跃响应)的影响。
二.实验仪器● THSCC-1实验箱一台。
● 示波器一台。
三.实验内容 1.比例环节比例(P )环节的方框图如图1-1所示。
图1-1比例环节方框图K Z Z S u S u S G i o ==-=12)()()(当输入为单位阶跃信号,即u i =-1V 时,u i (s )=s 1,则u o (s )=K s1,所以输出响应为:u o (t )=K (t ≥0)。
比例环节实验原理图如图1-2所示。
选择:K=R2/R1=2,例如选择R2=820k ,R1=410k ,或选择R2=100k ,R1=51k 。
R2图1-2 比例环节实验原理图和输出波形实验步骤:(1)调整示波器:● 选择输入通道CH1或CH2。
● 逆时针调节示波器的时间旋钮“TIME/DIV ”到底,使光标为一点,并调节上下“位移”旋钮使光标位于0线上。
● 调整示波器的输入幅度档位选择开关,选择合适的档位使信号幅度便于观察,例如选择档位为1V 档。
● 将输入幅度档位选择开关中心的微调旋钮顺时针旋到底。
● 将信号选择开关打到DC 档。
(2)顺时针调节实验箱的旋钮,使阶跃信号为负(绿灯亮)。
(3)阶跃信号接到示波器上,调节实验箱的幅度旋钮。
使负跳变幅度为一格(即Ui=-1V )。
(4)接好实验线路,按下阶跃信号按钮,观察示波器的波形。
预习思考:输出幅度跳变应为……? 2.惯性环节惯性环节实验原理图如图1-3所示。
其传递函数为:11)()()(+==TS Ks u s u S G i o , K= R2/R1,T=R2*C 当输入为单位阶跃信号,即u i (t )=-1V 时,u i (s )=S 1,则u o (s )=S11TS 1⋅+ 所以输出响应为u o (t )=)e1(K Tt--。
自动控制原理实验一

KTδ(t)+K
实测:μo(t)=
+
e-t/R3C
Ro=
100K R2=
100K
C=1uF
R3=
10K
R1=
100K
R1=
200K
典型
环节
传递函数参数与模拟电路参数
关 系
单位阶跃响应
理想阶跃响应曲线
实测阶跃响应曲线
PID
KP=
TI=Ro C1
TD=
理想:μo(t)= TDδ(t)+Kp+
答:传递函数的相角始终大于零,a>1。
3.你能解释校正后系统的瞬态响应变快的原因吗?
答:由于实际控制系统具有惯性、摩擦、阻尼等原因。
表3-1
参数
项目
Mp(%)
Ts(s)
阶 跃 响 应 曲 线
未校正
0.6
4
校正后
0.125
0.42
实验四 控制系统的频率特性
一、被测系统的方块图及原理:
图4—1 被测系统方块图
关 系
单位阶跃响应
理想阶跃响应曲线
实测阶跃响应曲线
惯性
K=
T=R1C
μo(t)=
K(1-e-t/T)
R1=
250K
Ro=
250K
C=
1μF
C=
2μF
I
T=RoC
μo(t)=
Ro=
200K
C=
1μF
C=
2μF
PI
K=
T=RoC
μo(t)=K+
R1=
100K
Ro=
200K
C=
自动控制原理实验报告(一、二阶系统的电子模拟及时域响应的动态测试等三个实验)

自动控制原理实验报告作者姓名学科专业机械工程及自动化班级学号X X年10月27日实验一一、二阶系统的电子模拟及时域响应的动态测试一、实验目的1、了解一、二阶系统阶跃响应及其性能指标与系统参数之间的关系。
2、学习在电子模拟机上建立典型环节系统模型的方法。
3、学习阶跃响应的测试方法。
二、实验内容1、建立一阶系统的电子模型,观测并记录在不同时间常数T时的跃响应曲线,并测定其过渡过程时间TS。
2、建立二阶系统的电子模型,观测并记录在不同阻尼比ζ时的跃响应曲线,并测定其超调量σ%及过渡过程时间TS。
三、实验原理1、一阶系统阶跃响应性能指标的测试系统的传递函数为:()s()1C s KR s Ts φ=+()=模拟运算电路如下图:其中21R K R =,2T R C =;在实验中,始终保持21,R R =即1K =,通过调节2R 和C 的不同取值,使得T 的值分别为0.25,0.5,1。
记录实验数据,测量过度过程的性能指标,其中按照经验公式取3s t T=2、二阶系统阶跃响应性能指标的测试系统传递函数为:令ωn=1弧度/秒,则系统结构如下图:二阶系统的模拟电路图如下:在实验过程中,取22321,1R C R C ==,则442312R R C R ζ==,即4212R C ζ=;在实验当中取123121,1R R R M C C F μ===Ω==,通过调整4R 取不同的值,使得ζ分别为0.25,0.5,1;记录所测得的实验数据以及其性能指标,其中经验公式为3.5%100%,s net σζω=⨯=.四、试验设备:1、HHMN-1型电子模拟机一台。
2、PC机一台。
3、数字万用表一块。
4、导线若干。
五、实验步骤:1、熟悉电子模拟机的使用,将各运算放大器接成比例器,通电调零。
2、断开电源,按照实验说明书上的条件和要求,计算电阻和电容的取值,按照模拟线路图搭接线路,不用的运算放大器接成比例器。
3、将D/A输出端与系统输入端Ui连接,将A/D1与系统输出端UO连接(此处连接必须谨慎,不可接错)。
自动控制原理实验实验指导书

自动控制原理实验目录实验一二阶系统阶跃响应(验证性实验) (1)实验三控制系统的稳定性分析(验证性实验) (9)实验三系统稳态误差分析(综合性实验) (15)预备实验典型环节及其阶跃响应一、实验目的1.学习构成典型环节的模拟电路,了解电路参数对环节特性的影响。
2.学习典型环节阶跃响应测量方法,并学会由阶跃响应曲线计算典型环节传递函数。
二、实验内容搭建下述典型环节的模拟电路,并测量其阶跃响应。
1.比例(P)环节的模拟电路及其传递函数示于图1-1。
2.惯性(T)环节的模拟电路及其传递函数示于图1-2。
3.积分(I)环节的模拟电路及其传递函数示于图1-3。
4. 比例积分(PI)环节的模拟电路及其传递函数示于图1-4。
5.比例微分(PD)环节的模拟电路及其传递函数示于图1-5。
6.比例积分微分(PID)环节的模拟电路及其传递函数示于图1-6。
三、实验报告1.画出惯性环节、积分环节、比例积分环节、比例微分环节、比例积分微分环节的模拟电路图,用坐标纸画出所记录的各环节的阶跃响应曲线。
2.由阶跃响应曲线计算出惯性环节、积分环节的传递函数,并与由模拟电路计算的结果相比较。
附1:预备实验典型环节及其阶跃响应效果参考图比例环节阶跃响应惯性环节阶跃响应积分环节阶跃响应比例积分环节阶跃响应比例微分环节阶跃响应比例积分微分环节阶跃响应附2:由模拟电路推导传递函数的参考方法1. 惯性环节令输入信号为U 1(s) 输出信号为U 2(s) 根据模电中虚短和虚断的概念列出公式:整理得进一步简化可以得到如果令R 2/R 1=K ,R 2C=T ,则系统的传递函数可写成下面的形式:()1KG s TS =-+当输入r(t)为单位脉冲函数时 则有输入U 1(s)=1输出U 2(s)=G(s)U 1(s)= 1KTS-+由拉氏反变换可得到单位脉冲响应如下:/(),0t TK k t e t T-=-≥ 当输入r(t)为单位阶跃函数时 则有输入U 1(s)=1/s输出U 2(s)=G(s)U 1(s)= 11K TS s-+由拉氏反变换可得到单位阶跃响应如下:/()(1),0t T h t K e t -=--≥当输入r(t)为单位斜坡函数时 则有输入U 1(s)=21s输出U 2(s)=G(s)U 1(s)=2323R R C T R R =+2Cs12Cs-(s)U R10-(s)U 21R R +-=12212)Cs (Cs 1(s)U (s)U )(G R R R s +-==12212)Cs 1((s)U (s)U )(G R R R s +-==由拉氏反变换可得到单位斜坡响应如下:/()(1),0t T c t Kt KT e t -=--≥2. 比例微分环节令输入信号为U 1(s) 输出信号为U 2(s) 根据模电中虚短和虚断的概念列出公式:(s)(s)(s)(s)(s)U100-U U 0U 2=1R1R23(4)CSU R R '''---=++由前一个等式得到 ()1()2/1U s U s R R '=- 带入方程组中消去()U s '可得1()1()2/11()2/12()1134U s U s R R U s R R U s R R R CS+=--+由于14R C〈〈,则可将R4忽略,则可将两边化简得到传递函数如下: 2()23232323()(1)1()11123U s R R R R R R R R G s CS CS U s R R R R R ++==--=-++如果令K=231R R R +, T=2323R R C R R +,则系统的传递函数可写成下面的形式:()(1)G s K TS =-+当输入r(t)为单位脉冲函数时,单位脉冲响应不稳定,讨论起来无意义 当输入r(t)为单位阶跃函数时 则有输入U 1(s)=1/s输出U 2(s)=G(s)U 1(s)=(1)K TS S-+由拉氏反变换可得到单位阶跃响应如下:()(),0h t KT t K t δ=+≥当输入r(t)为单位斜坡函数时 则有输入U 1(s)=21s输出U 2(s)=G(s)U 1(s)=2(1)K TS S -+由拉氏反变换可得到单位斜坡响应如下:(),0c t Kt KT t =+≥实验一 二阶系统阶跃响应(验证性实验)一、实验目的研究二阶系统的两个重要参数阻尼比ξ和无阻尼自然频率n ω对系统动态性能的影响。
自动控制原理实验报告集典型环节的电路模拟与软件仿真研究

验证性实验实验一典型环节的电路模拟与软件仿真研究一、实验目的1.通过实验熟悉并掌握实验装置和上位机软件的使用方法。
2.通过实验熟悉各种典型环节的传递函数及其特性,掌握电路模拟和软件仿真研究方法。
二、实验内容1.设计各种典型环节的模拟电路。
2.完成各种典型环节模拟电路的阶跃特性测试,并研究参数变化对典型环节阶跃特性的影响。
3.利用上位机界面上的软件仿真功能,完成各典型环节阶跃特性的软件仿真研究,并与电路模拟测试的结果作比较。
三、实验步骤1.熟悉实验箱,利用实验箱上的模拟电路单元,参考本实验附录设计并连接各种典型环节(包括比例、积分、比例积分、比例微分、比例积分微分以及惯性环节)的模拟电路。
注意实验前必须先将实验箱断电,再接线。
接线时要注意不同环节、不同测试信号对运放锁零的要求。
在输入阶跃信号时,除比例环节运放可不锁零(G可接-15V)也可锁零外,其余环节都需要考虑运放锁零。
2.利用实验设备完成各典型环节模拟电路的阶跃特性测试,并研究参数变化对典型环节阶跃特性的影响。
在熟悉上位机界面操作的基础上,充分利用上位机提供的虚拟示波器与信号发生器功能。
为了利用上位机提供的虚拟示波器与信号发生器功能,接线方式将不同于上述无上位机情况。
仍以比例环节为例,此时将Ui连到实验箱 U3单元的O1(D/A通道的输出端),将Uo连到实验箱 U3单元的I1(A/D通道的输入端),将运放的锁零G连到实验箱 U3单元的G1(与O1同步),并连好U3单元至上位机的并口通信线。
接线完成,经检查无误,再给实验箱上电后,启动上位机程序,进入主界面。
界面上的操作步骤如下:①按通道接线情况完成“通道设置”:在界面左下方“通道设置”框内,“信号发生通道”选择“通道O1#”,“采样通道X”选择“通道I1#”,“采样通道Y”选择“不采集”。
②进行“系统连接”(见界面左下角),如连接正常即可按动态状态框内的提示(在界面正下方)“进入实验模式”;如连接失败,检查并口连线和实验箱电源后再连接,如再失败则请求指导教师帮助。
自动控制原理(实验指导书)

⾃动控制原理(实验指导书)⽬录实验⼀典型环节的模拟研究(验证型)(2)实验⼆典型系统的瞬态响应和稳定性(设计型)(9)实验三动态系统的数值模拟(验证型)(15)实验三动态系统的频率特性研究(综合型)(16)实验四动态系统的校正研究(设计型)(18)附录XMN—2学习机使⽤⽅法简介(20)实验⼀典型环节的模拟研究⼀、实验⽬的:1、了解并掌握XMN-2型《⾃动控制原理》学习机的使⽤⽅法,掌握典型环节模拟电路的构成⽅法,培养学⽣实验技能。
2、熟悉各种典型线性环节的阶跃响应曲线。
3、了解参数变化对典型环节动态特性的影响。
⼆、实验设备Uo(S)=(K+TS 1)S1?)1()()(21210210CS R R RR R R R S U S U i +++≈(1-19)⽐较式(1-17)和(1-19)得K=21R R R +T=C R R R R ?+2121 (1-20)当输⼊为单位阶跃信号,即Ui(t)=1(t)时,Ui(S)=1/S 。
则由式(1-17)得到111)()(23111022100210++?+++=S C R S C R C R C R S C R R R R S U S U i (1-24) 考虑到R 1》R 2》R 3,则式(1-24)可近似为S C R R R S C R R R S U S U i 2021100101)()(++≈(1-25)⽐较式(1-23)和(1-25)得K P =1R R , T 1=R 0C 1T D =2021C R R R ? (1-26)当输⼊为单位阶跃信号,即Ui(t)=1(t)时,Ui(S)=1/S 。
则由式(1-23)得到U o (S)=(K P +ST 11+T D S )S 1?五、实验报告要求:1、实验前计算确定典型环节模拟电路的元件参数各⼀组,并推导环节传递函数参数与模拟电路电阻、电容值的关系以及画出理想阶跃响应曲线。
2、实验观测记录。
自动控制原理实验报告

《自动控制原理实验》实验报告班级:自动化0901姓名:***学号:*********东华大学信息学院实验一 MATLAB 中数学模型的表示MP2.1考虑两个多项式2()21p s s s =++ ,()1q s s =+使用 MATLAB 计算下列各式:程序: (a )>> A=[1 2 1];B=[1 1]; >> C=conv(A,B)运行结果: C =1 3 3 1 (b)>> num=[1 1]; >> den=[1 2 1]; >> z=roots(num); >> p=roots(den); >> z,p运行结果: z =-1 p =-1 -1 (c)>> value=polyval(p,-1) 运行结果: value = 0程序:(a)>> num1=[1];num2=[1 2];den1=[1 1];den2=[1 3];[num,den]=series(num1,den1,num2,den2);[num,den]=cloop(num,den,-1);printsys(num,den)运行结果:num/den =s + 2----------------s^2 + 5 s + 5(b)step(num,den)运行结果:(a)>> num1=[1]; den1=[1 1];num2=[1]; den2=[1 0 2];[num3,den3]=series(num1,den1,num2,den2);num4=[4 2]; den4=[1 2 1];[num5,den5]=feedback(num3,den3,num4,den4,-1);num6=[1]; den6=[1 0 0];num7=[50]; den7=[1];[num8,den8]=feedback(num6,den6,num7,den7,1);[num9,den9]=series(num5,den5,num8,den8);num10=[1 0 2]; den10=[1 0 0 14];[num11,den11]=feedback(num9,den9,num10,den10,-1);num12=[4]; den12=[1];[num13,den13]=series(num11,den11,num12,den12)F=tf(num13,den13)运行结果:Transfer function:4 s^5 + 8 s^4 + 4 s^3 + 56 s^2 + 112 s + 56 ----------------------------------------------------------------------------------------------------s^10 + 3 s^9 - 45 s^8 - 129 s^7 - 198 s^6 - 976 s^5 - 2501 s^4 - 3558 s^3 - 4841 s^2 - 6996 s – 2798(b)[p,z]=pzmap(num13,den13); pzmap(num13,den13);grid on运行结果:p =7.0710-7.07101.2047 +2.0871i1.2047 -2.0871i0.2984 + 1.4750i0.2984 - 1.4750i-2.4108-1.5219 + 0.9395i-1.5219 - 0.9395i-0.5517>> zz =1.2051 +2.0872i1.2051 -2.0872i-2.4101-1.0000 + 0.0000i-1.0000 - 0.0000i(c)>> Z=roots(num13)Z =1.2051 +2.0872i1.2051 -2.0872i-2.4101-1.0000 + 0.0000i-1.0000 - 0.0000i>> P=roots(den13)P =7.0710-7.07101.2047 +2.0871i1.2047 -2.0871i0.2984 + 1.4750i0.2984 - 1.4750i-2.4108-1.5219 + 0.9395i-1.5219 - 0.9395i-0.5517绘制系统的单位阶跃响应,参数Z=3,6和12。
自动控制原理实验报告
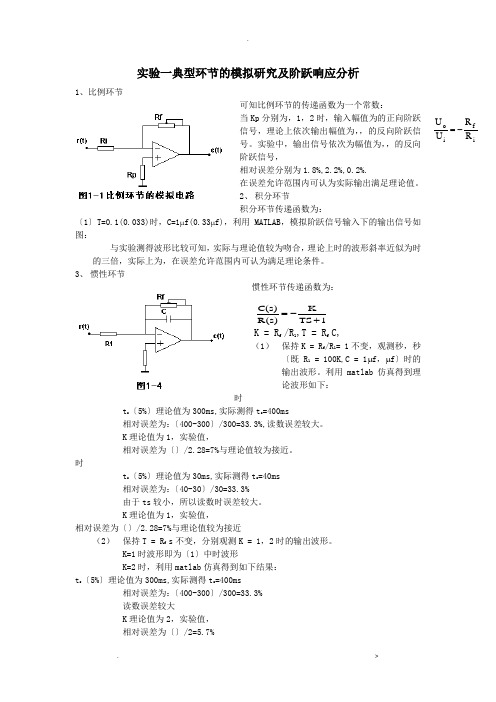
实验一典型环节的模拟研究及阶跃响应分析1、比例环节可知比例环节的传递函数为一个常数:当Kp 分别为,1,2时,输入幅值为的正向阶跃信号,理论上依次输出幅值为,,的反向阶跃信号。
实验中,输出信号依次为幅值为,,的反向阶跃信号,相对误差分别为1.8%,2.2%,0.2%.在误差允许范围内可认为实际输出满足理论值。
2、 积分环节积分环节传递函数为:〔1〕T=0.1(0.033)时,C=1μf(0.33μf),利用MATLAB ,模拟阶跃信号输入下的输出信号如图:与实验测得波形比较可知,实际与理论值较为吻合,理论上时的波形斜率近似为时的三倍,实际上为,在误差允许范围内可认为满足理论条件。
3、 惯性环节惯性环节传递函数为:K = R f /R 1,T = R f C,(1) 保持K = R f /R 1= 1不变,观测秒,秒〔既R 1 = 100K,C = 1μf ,μf 〕时的输出波形。
利用matlab 仿真得到理论波形如下:时t s 〔5%〕理论值为300ms,实际测得t s =400ms 相对误差为:〔400-300〕/300=33.3%,读数误差较大。
K 理论值为1,实验值,相对误差为〔〕/2.28=7%与理论值较为接近。
时t s 〔5%〕理论值为30ms,实际测得t s =40ms 相对误差为:〔40-30〕/30=33.3% 由于ts 较小,所以读数时误差较大。
K 理论值为1,实验值,相对误差为〔〕/2.28=7%与理论值较为接近(2) 保持T = R f s 不变,分别观测K = 1,2时的输出波形。
K=1时波形即为〔1〕中时波形K=2时,利用matlab 仿真得到如下结果:t s 〔5%〕理论值为300ms,实际测得t s =400ms相对误差为:〔400-300〕/300=33.3% 读数误差较大K 理论值为2,实验值, 相对误差为〔〕/2=5.7%if i o R RU U -=1TS K)s (R )s (C +-=与理论值较为接近。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
各位同学请注意:
1.上机实验为1-8周,每次上机请按照第一次的座位坐。
2.请先自习上机内容,实验内容可参考指导书。
3.9号机房座位安排见后面的名单,请按机位号入座,要点名哦。
实验一典型环节的MATLAB仿真
一、实验目的
1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK的使用
MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB软件,在命令窗口栏“>>”提示符下键入simulink命令,按Enter 键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK仿真环境下。
2.选择File菜单下New下的Model命令,新建一个simulink仿真环境常规模板。
3.在simulink仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:
1)进入线性系统模块库,构建传递函数。
点击simulink 下的“Continuous ”,再将右边窗口中“Transfer Fen ”的图标用左键拖至新建的“untitled ”窗口。
2)改变模块参数。
在simulink 仿真环境“untitled ”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK ,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的simulink 的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math ”右边窗口“Gain ”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink 下的“Source ”,将右边窗口中“Step ”图标用左键拖至新建的“untitled ”窗口,形成一个阶跃函数输入模块。
5)选择输出方式。
用鼠标点击simulink 下的“Sinks ”,就进入输出方式模块库,通常选用“Scope ”的示波器图标,将其用左键拖至新建的“untitled ”窗口。
6)选择反馈形式。
为了形成闭环反馈系统,需选择“Math ” 模块库右边窗口“Sum ”图标,并用鼠标双击,将其设置为需要的反馈形式(改变正负号)。
7)连接各元件,用鼠标划线,构成闭环传递函数。
8)运行并观察响应曲线。
用鼠标单击工具栏中的“”按钮,便能自动运行仿真环境下的系统框图模型。
运行完之后用鼠标双击“Scope ”元件,即可看到响应曲线。
三、实验原理
1.比例环节的传递函数为 221211()2100,200Z R G s R K R K Z R =-=-=-==
图1-3所示左侧为其对应的模拟电路右侧即为SIMULINK 的图形。
2.惯性环节的传递函数为
2
21
121
121
2
()100,200,1
10.21
R
Z R
G s R K R K C uf
Z R C s
=-=-=-===
++
图1-4所示左侧为其对应的模拟电路、右侧为SIMULINK图形。
图1-4 惯性环节的模拟电路及SIMULINK图形
图1-3 比例环节的模拟电路及SIMULINK图形
3
.积分环节(I)的传递函数为
uf
C
K
R
s
s
C
R
Z
Z
s
G1
,
100
1.0
1
1
)
(
1
1
1
1
1
2=
=
-
=
-
=
-
=
其对应的模拟电路及SIMULINK图形如图1-5所示。
4.微分环节(D)的传递函数为
uf
C
K
R
s
s
C
R
Z
Z
s
G10
,
100
)
(
1
1
1
1
1
2=
=
-
=
-
=
-
=uf
C
C01
.0
1
2
=
<<
其对应的模拟电路及SIMULINK图形如图1-6所示。
图1-5 积分环节的模拟电路及及SIMULINK图形
5.比例+微分环节(PD )的传递函数为
)11.0()1(
)(111
212
+-=+-=-=s s C R R R Z Z s G uf C C uf C K R R 01.010,10012121=<<===
其对应的模拟电路及SIMULINK 图形如图1-7所示。
图1-7 比例+微分环节的模拟电路及SIMULINK 图形
6.比例+积分环节(PI)的传递函数为
)
1
1(
1
)
(
1
1
2
1
2
s
R
s
C
R
Z
Z
s
G+
-
=
+
-
=
-
=uf
C
K
R
R10
,
100
1
2
1
=
=
=
其对应的模拟电路及SIMULINK图形如图1-8所示。
7.PID环节
图1-8 比例+积分环节的模拟电路及SIMULINK图形
在SIMULINK 环境下建立以上图例右侧的模型,通过仿真即可了解各类输入作用下的输出响应曲线。
四、实验内容
1 系统结构如下图,按下列各典型环节的传递函数,建立相应的SIMULINK 仿真模型,观察并记录其单位阶跃响应波形。
① 比例环节1)(1=s G
② 惯性环节11)(1+=s s G ③ 积分环节s
s G 1)(1= ④ 微分环节s s G =)(1
⑤ 比例+微分环节(PD )2)(1+=s s G
⑥ 比例+积分环节(PI )s
s G 11)(1+=
2 建立如下的系统结构,选取若干个PID 的参数,说明比例积分微分对输出响应的影响。
(PID 控制器在Simulink Extras\Additional Linear\PID controller ) 以下二选一做
A .
使用Simulink 搭建控制系统,被控对象传递函数为1331
)(23+++=s s s s G ,
(1) 使用纯比例控制器P Controller (0,0==D I K K ),分别求出当p K =0.5,1.0,2.0
时系统单位阶越响应的超调量P.O.%,峰值时间p T ,调整时间s T 和稳态误差;分析p K 对系统性能的影响。
(2) 使用比例积分控制器 PI Controller (1=P K ,0=D K ),分别求出当I K =0.5,
1.0,1.5时系统单位阶越响应的超调量P.O.%,峰值时间p T ,调整时间s T 和稳态误差;分析I K 对系统性能的影响。
2、 使用Simulink 搭建如下控制系统,
(1)使用纯比例控制器P Controller (0,0==D I K K ),分别求出当p K =10,20,30时系统单位阶越响应的超调量P.O.%,峰值时间p T ,调整时间s T ,稳态误差;分析p K 对系统性能的影响。
(2)使用比例微分控制器 PD Controller (30=P K 0=I K ),分别求出当D K =1,2,5时系统单位阶越响应的超调量P.O.%,峰值时间p T ,调整时间s T ,稳态误差;分析D K 对系统性能的影响。
B .
B .
五、实验报告
1.画出各典型环节的SIMULINK 仿真模型。
2. 记录各环节的单位阶跃响应波形,并分析参数对响应曲线的影响。
3. 写出实验的心得与体会。
六、预习要求
1.熟悉各种控制器的原理和结构,画好将创建的SIMULINK 图形。
2.预习MATLAB 中SIMULINK 的基本使用方法。
上机座位安排: 9号机房
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
