金融工程讲义古典classical投资组合理论
金融市场中的投资组合理论

金融市场中的投资组合理论在金融市场中,投资组合理论是一个重要而又复杂的概念。
它涉及到投资者如何选择和分配他们的资金,以实现最大的利润和风险管理。
投资组合理论是现代金融学的基石之一,可以帮助投资者做出明智的投资决策。
投资组合理论的核心概念是通过分散投资来降低风险,同时提高收益。
这可以通过将资金分配到不同的资产类别,如股票、债券、房地产等,来实现。
通过将资金分散到不同的资产类别,投资者可以在一个资产表现不好时在其他资产中得到补偿,从而降低整个投资组合的风险。
在投资组合理论中,一个重要的概念是资本资产定价模型(CAPM)。
它是一种衡量资产风险和预期回报之间关系的模型。
根据这个模型,投资者可以评估一个资产的预期回报和风险,并将其与其他资产进行比较。
这可以帮助投资者选择合适的资产来构建他们的投资组合。
除了资本资产定价模型,投资组合理论还涉及到投资者的风险偏好和投资目标。
不同的人有不同的风险承受能力和投资目标。
有些人更愿意承担更高的风险以追求更高的收益,而其他人则更注重资本的保值。
投资组合理论可以帮助投资者根据他们的风险偏好和投资目标来选择合适的投资策略。
在实践中,投资组合理论可以通过建立投资组合优化模型来帮助投资者做出决策。
这个模型将投资者的目标、风险承受能力和预期回报的假设输入,然后计算出最优的投资组合。
这个模型可以帮助投资者优化他们的投资组合,使之在给定的风险水平下获得最大的预期回报。
然而,投资组合理论并不是完美的。
它有一些限制和假设,可能无法完全适应不同的市场环境和投资者需求。
例如,它假设市场是有效的,投资者可以获得完全信息并做出理性决策。
然而,在现实中,市场往往是不完全有效的,投资者的决策也往往受到情绪和非理性因素的影响。
此外,投资组合理论也没有考虑到市场风险的周期性。
在不同的市场周期中,不同的资产类别表现出不同的特点。
例如,在经济萧条时期,债券可能表现得更好,而在经济增长时期,股票可能更具吸引力。
金融工程知识讲座

但员工对这一持股计划非常冷淡,在政府决定对员 工提供10%的折扣后,仍仅有20% 的员工愿意购买公 司的股票。
这无疑使该化工公司的管理层对员工未来的努力 程度和人力资源状况深表忧虑,而政府又不愿提供更 多的折扣来吸引员工购股。
外汇期权
Garman
and
Kohlhagen(1983)
期货期权
Lieu(1的几个阶段
发展阶段: 描述性金融
应用特点:
开创性理论:
偏重于描述 缺乏数量分析
不多
分析性金融 金融工程
以数量分析为 1952 年 , Markowitz 的 资 产 组 合
(5)价格波动的巨大性
150 140 130 120 110 100
90 80
1992.6-2001.6的日元汇率走势
3 0 -J u n - 92 3 1 -O c t - 92 2 8 -F e b - 93 3 0 -J u n - 93 3 1 -O c t - 93 2 8 -F e b - 94 3 0 -J u n - 94 3 1 -O c t - 94 2 8 -F e b - 95 3 0 -J u n - 95 3 1 -O c t - 95 2 9 -F e b - 96 3 0 -J u n - 96 3 1 -O c t - 96 2 8 -F e b - 97 3 0 -J u n - 97 3 1 -O c t - 97 2 8 -F e b - 98 3 0 -J u n - 98 3 1 -O c t - 98 2 8 -F e b - 99 3 0 -J u n - 99 3 1 -O c t - 99 2 9 -F e b - 00 3 0 -J u n - 00 3 1 -O c t - 00 2 8 -F e b - 01 3 0 -J u n - 01
《组合投资理论》课件

xx年xx月xx日
• 组合投资理论概述 • 组合投资策略 • 组合投资的数学模型 • 组合投资的实证研究 • 组合投资理论的未来发展
目录
01
组合投资理论概述
组合投资理论的基本概念
组合投资理论是一种投资策略,旨在通过将资金分散投资于多个不同的资产类别, 以降低投资风险并实现长期稳03
定期调整投资组合的资产配置比例,以维持风险和收益的平衡
。
收益优化策略
Alpha策略
通过选股或择时获取超额收益。
Beta策略
通过跟踪市场指数获取收益。
套利策略
通过寻找不同市场或产品间的价格差异,进行低买高卖获取收益。
03
组合投资的数学模型
马科维茨投资组合模型
总结词
马科维茨投资组合模型是现代投资组合理论的基石,它通过数学方法优化投资组合,以最小风险获得最大收益。
核心-卫星策略
将投资组合分为核心部分和卫星部分,核心部分 追求稳定收益,卫星部分追求高收益。
杠铃策略
同时持有高风险和低风险资产,以寻求在市场波 动中获得更好的收益。
风险控制策略
止损策略
01
设定投资组合的最大亏损限额,一旦达到该限额,即进行减仓
或清仓操作。
止盈策略
02
设定投资组合的目标收益率,达到目标后进行减仓或清仓操作
1 2
股票市场投资组合
选取某只股票作为研究对象,分析其历史价格数 据,构建投资组合并进行实证分析。
债券市场投资组合
选取一组债券作为研究对象,根据其信用评级、 到期日等因素构建投资组合,并进行实证分析。
3
商品期货市场投资组合
选取一组商品期货作为研究对象,根据其价格波 动、市场走势等因素构建投资组合,并进行实证 分析。
金融工程讲义古典classical投资组合理论

第四讲 古典(classical )投资组合理论一.马尔科维茨资产组合理论的基本假设 马尔科维茨的资产组合理论有很多假设,但是这些假设基本上可以归为两大类:一类是关于投资者的假设;另一类是关于资本市场的假设。
㈠关于投资者的假设⑴投资者在投资决策中只关注投资收益这个随机变量的两个数字特征:投资的期望收益和方差。
期望收益率反映了投资者对未来收益水平的衡量,而收益的方差则反映了投资者对风险的估计。
⑵投资者是理性的,也是风险厌恶的。
即在任一给定的风险程度下,投资者愿意选择期望收益高的有价证券;或者在期望收益一定时,投资者愿意选择风险程度较低的有价证券。
⑶投资者的目标是使其期望效用)),(()(2σr E f U E =最大化,其中)(r E 和2σ分别为投资的期望收益和方差。
对于一个风险厌恶的投资者来说,其期望效用函数)(U E 是单调凸函数。
㈡关于资本市场的假设⑴资本市场是有效的。
证券的价格反映了其内在价值,证券的任何信息都能够迅速地被市场上每个投资者所了解,不存在税收和交易成本。
⑵资本市场上的证券是有风险的,也就是说收益具有不确定性,证券的收益都服从正态分布,不同证券的收益之间有一定的相关关系。
⑶资本市场上的每种证券都是无限可分的,这就意味着只要投资者愿意,他可以购买少于一股的股票。
⑷资本市场的供给具有无限弹性,也就是说资产组合中任何证券的购买和销售都不会影响到市场的价格。
⑸市场允许卖空(sell short )(市场不允许卖空的情况在此不做讨论)。
在所有的这些假设中,最值得我们注意的是马尔科维茨独创性地用期望效用(expected utility )最大化准则代替了期望收益最大化准则。
在现代资产组合理论诞生之前,人们在研究不确定条件下的投资时,关于投资者的目标是假定他追求期望收益的最大化,但是这种假设却存在这样的问题:如果资本市场上仅存在一种具有最高收益的资产,投资者只需要将全部资金投资于该种资产即可实现期望收益最大化;如果同时有几种资产具有相同的最大收益,那么对投资者而言,在这些资产中进行组合投资与只投资于一种资产将毫无区别。
古典利率理论:投资学习教材PPT课件

3. 在发达市场经济国家,它已经是货币市场的 主要交易品种之一。 美国和日本都曾在不同阶段选取了可转让 大额存单,作为利率市场化的一个突破口。 1973年,美联储准许所有大额CD不受“Q条 例”(美国在1929年至1933年大萧条之后开始 实施的对利率的管制条例,上世纪80年代才 得以逐步取消)的利率上限限制;日本在货币 市场发育程度较低、交易品种不丰富的情况下, 也是允许CD利率不受临时利率调整法限制, 使其迅速成为货币市场的主要交易工具,为利 率市场化找到了最佳途径。 。
在一年以内的短期资金交易的市场; 长期的资金市场(资本市场):指期限 在一年以上的债券和股票等交易的市场。
四、按照交易后是否立即成交来划分
现货市场:指当天成交,当天或三天之
内进行交割的金融市场; 期货市场:指款项或证券的交割在约定 后的某一时间来进行的金融市场。
五、按融资方式来划分 直接融资市场:没有金融中介机构参与的直 接融资的市场; 间接融资市场:通过金融中介机构来进行融 资的市场。 六、按照金融交易所涉及的地区范围来划分 地方性的金融市场; 全国性的金融市场; 区域性的金融市场; 国际性的金融市场。
票据市场
1. 票据交易的市场称票据市场。
2. 交易品种有二:商业票据和银行承兑票据。 3. 有真实交易背景的商业票据称“真实票据”;无 真实交易背景的商业票据称“融通票据” 。 融通票据又可称为金融票据或空票据,它是在 当事人双方没有发生真实商业交易的情况下直接达 成协定后产生的,一方作为债权人签发票据,另一 方则作为债务人表示承兑,发票人要在票据到期前 把款项交给付款人,以备付款人清偿之用 我国现行立法强调票据应有真实交易背景;发 达市场经济国家的票据主要是融通票据。
第5章 古典经济学

P LRAS1 LRAS2
YN
’ YN
Y
劳动或自然失业率变动引起的移动
移民
生于婴儿潮时期的人的退休
政府降低自然失业率的政策
物质资本或人力资本变动引起的移动
工厂,设备投资
更多人获得大学文凭
飓风损坏工厂
自然资源变动引起的移动
义变量,但不影响真实变量
如果中央银行使货币供给翻一番,休谟和古典
经济学家会认为:
所有名义变量(包括价格)会翻一番 所有真实变量(包括相对价格)保持不变
三、货币中性
货币中性:货币供给变动并不影响真实变量
货币供给翻一番使所有名义价格都翻一番;
那相对价格呢?
名义价格变动之前,CD相对于皮萨的价格:
金融体系如何使储蓄与投资相匹配政府政策和其他因素会如何影响储蓄投资和利率所有存款者都把钱存在这个市场所有借款者都从这个市场借贷只有一个利率这个利率既是储蓄的收益也是借贷的成本利率上升会鼓励储蓄并增加可贷资金的供给利率可贷资金十亿美元供给603806利率可贷资金十亿美元需求利率降低会减少借贷的成本增加可贷资金的需求量507480利率可贷资金十亿美元需求利率调整使可贷资金供求平衡供给可贷资金的均衡数量等于均衡投资也等于均衡储蓄560利率可贷资金十亿美元储蓄的税收激励增加了可贷资金的供给这导致均衡利率下降并增加可贷资金的均衡数量政策1
新矿藏资源的发现
国内石油供给的减少 影响农业生产的气候模式变化
技术知识变动引起的移动
技术进步提高生产率
第4节 储蓄、投资理论与萨伊定律
问题:消费者的现期收入一般不会全部用于现
期消费,收入的一部分被储蓄起来,用于将来 消费。那么,这样会不会造成总需求不足?
《古典投资理论》课件

的期望收益与风险之间的关系。
CML和SML的斜率(即风险溢价的量)由无风险利率和风险厌恶系数决定。
资本资产定价模型的假设条件
01
假设投资者都是理性的,他们会在给定的风险水平下追求最大的期望 收益,并在给定的期望收益水平下追求最小的风险。
有效市场假说的理论基础
有效市场假说的理论基础主要包括随机漫步理论、资本资产定价模型( CAPM)和套利定价理论(APT)。
随机漫步理论认为,证券价格的变动是随机的,无法预测,因此,投资 者无法通过分析过去的价格变动来预测未来的价格走势。
资本资产定价模型和套利定价理论则从风险和回报的角度出发,认为在 有效的市场中,投资者无法通过承担更高的风险或利用套利机会来获得 超额收益。
05
古典投资理论的实践应用
基于古典投资理论的股票选择策略
基本面分析
通过研究公司的财务报表、行业地位、管理层质量等因素,评估公司的内在价 值,从而选择具有低估价值的股票。
价值投资
寻找被低估的股票,注重股票的内在价值与市场价格的差异,以长期持有等待 价值实现为主要策略。
基于古典投资理论的资产配置策略
03
有效市场假说
有效市场假说的基本概念
有效市场假说(EMH)认为,市场中的证券价格能够充分反映所有可获得的信息, 因此,市场是有效的。
在有效市场中,投资者无法通过分析信息或采用特定的交易策略来获得超额收益。
有效市场假说将市场中的投资者视为理性人,他们能够快速、准确地评估证券价值 ,并据此做出投资决策。
《古典投资理论》ppt 课件
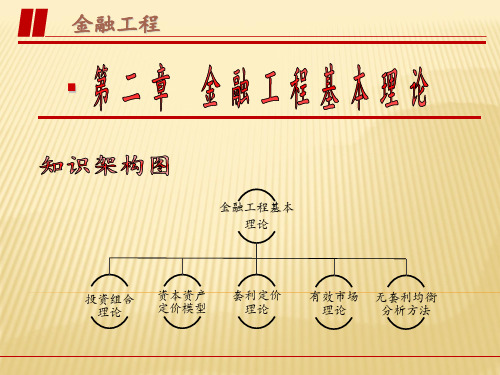
第二章 金融工程基本理论 《金融工程》ppt课件
二、有效市场假说的定义
法玛基于价格与信息的关系,对资本市场有效 性给出了一个颇有影响的描述性定义:如果证券价 格充分反映了可得信息,每种证券的价格都永远等 于其投资价值,则该证券市场是有效的。
金融工程
金融工程基本 理论
投资组合 资本资产
理论
定价模型
套利定价 理论
有效市场 无套利均衡
理论
分析方法
一、投资组合理论的起源
1952年,美国经济学家哈里·马柯维茨发表的 《投资组合选择》(Portfolio Selection)的论文标 志着现代投资组合理论的开端。
投资者在寻求预期收益最大化的同时,也在寻求收 益不确定性的最小化。在此基础上,马柯维茨建立了著 名的“均值—方差模型”来分析投资者的资产选择行为。 这一模型后来成为现代投资组合理论的核心与基石。
APT模型是CAPM模型的一个推广。但与 CAPM模型不同的是,该模型表明资产的期望收益 率受一组公共风险因子影响,市场组合可能只是其 中的一个风险因子,其他风险因子(诸如利率、通 货膨胀率、GDP增长率等)也可能包括在内。简单 地说,市场组合在套利定价理论中并没有特殊作用, 它只是可能影响资产收益的因素之一。
二、多因素套利定价模型
设市场上风险资产的收益一共受到k个风险因 素的影响,可表示如下:
k
ri Eri ij Fj ei j 1
其中,ri是任意一种风险资产的收益,E(ri)是该风险 资产的预期收益,Fj(j=1,2,…,k)是影响风险资产收 益的公共风险因子,βij (j=1,2,…,k)是第i个风险资 产的收益与第j个影响因素之间的协方差,表示风险资产对 不同公共风险因子的敏感度,ei是残差项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四讲 古典(classical )投资组合理论一.马尔科维茨资产组合理论的基本假设 马尔科维茨的资产组合理论有很多假设,但是这些假设基本上可以归为两大类:一类是关于投资者的假设;另一类是关于资本市场的假设。
㈠关于投资者的假设⑴投资者在投资决策中只关注投资收益这个随机变量的两个数字特征:投资的期望收益和方差。
期望收益率反映了投资者对未来收益水平的衡量,而收益的方差则反映了投资者对风险的估计。
⑵投资者是理性的,也是风险厌恶的。
即在任一给定的风险程度下,投资者愿意选择期望收益高的有价证券;或者在期望收益一定时,投资者愿意选择风险程度较低的有价证券。
⑶投资者的目标是使其期望效用)),(()(2σr E f U E =最大化,其中)(r E 和2σ分别为投资的期望收益和方差。
对于一个风险厌恶的投资者来说,其期望效用函数)(U E 是单调凸函数。
㈡关于资本市场的假设⑴资本市场是有效的。
证券的价格反映了其内在价值,证券的任何信息都能够迅速地被市场上每个投资者所了解,不存在税收和交易成本。
⑵资本市场上的证券是有风险的,也就是说收益具有不确定性,证券的收益都服从正态分布,不同证券的收益之间有一定的相关关系。
⑶资本市场上的每种证券都是无限可分的,这就意味着只要投资者愿意,他可以购买少于一股的股票。
⑷资本市场的供给具有无限弹性,也就是说资产组合中任何证券的购买和销售都不会影响到市场的价格。
⑸市场允许卖空(sell short )(市场不允许卖空的情况在此不做讨论)。
在所有的这些假设中,最值得我们注意的是马尔科维茨独创性地用期望效用(expected utility )最大化准则代替了期望收益最大化准则。
在现代资产组合理论诞生之前,人们在研究不确定条件下的投资时,关于投资者的目标是假定他追求期望收益的最大化,但是这种假设却存在这样的问题:如果资本市场上仅存在一种具有最高收益的资产,投资者只需要将全部资金投资于该种资产即可实现期望收益最大化;如果同时有几种资产具有相同的最大收益,那么对投资者而言,在这些资产中进行组合投资与只投资于一种资产将毫无区别。
因此,在资本市场上存在大量的资产时,期望收益最大化准则就无法解释为什么要进行多元化的投资,也无法解释组合投资的效应。
针对这一问题,马尔科维茨假定投资者是追求期望效用最大化的。
也就是说,理性的投资者不光追求高的期望收益,同时还要考虑风险问题,要在风险和收益之间做出权衡,选择能带来最大效用的风险和收益组合。
因此,用期望效用最大化原则代替期望收益最大化原则是更符合实际的。
二.无差异曲线根据投资者对资产的风险和收益的偏好不同,可以将投资者划分为三类:风险规避(risk-awesome )者、风险偏好(risk-loving )者和风险中立(risk-neutral )者。
在资产组合理论中,我们假定投资者是风险规避者,因此,其无差异曲线(indifference curve)就如图4.2所示:沿着无差异曲线移动,投资者或者承担较多的风险并获得较高的收益,或者承担较少的风险同时获得较低的收益,这也正体现了风险规避者的特点。
无差异曲线的基本特征是:第一, 位于无差异曲线上的所有组合(δ),(R E )都向投资者提供了相同的期望效用。
第二, 当无差异曲线向左上移动时,投资者的期望效用增加。
第三, 无差异曲线代表单个投资者对期望收益和风险的均衡点的个人评估,也就是说,无差异趋势是主观确定的,曲线的形状因投资者的不同而不同。
三.最小方差投资组合由前面关于投资者的假设2,我们知道马尔科维茨资产组合理论中的最优资产组合必须符合以下两个条件之一:⑴在预期收益水平确定的情况下,即a ='μω,求ω使风险达到最小,即∑'='ωωω)var(x 最小;⑵在风险水平确定的情况下,即∑='σωω(已知),求ω使收益最大,即x ω'达到最大。
将这两个条件写成数学表达式,分别为: ⑴∑'ωωmin ,它满足约束条件:a ='='μωω,11⑵μω'max ,它满足约束条件:∑='='0,11σωωω实际上,这两个条件是等价的。
下面,我们用拉格朗日(Lagrange )乘数法对∑'ωωmin 式进行求解。
令)(2)11(221a L -'--'-'=∑μωλωλωω则0212221=--=∂∂∑μλλωωL解得:)1(211μλλω-=∑-对)1(211μλλω-=∑-式两边同乘1',得)1(11211μλλω-'='∑-由约束条件可得μλλ∑∑--'+'=12111111对)1(211μλλω-=∑-)两边同乘以μ',得μμλμλμλλμωμ∑∑∑---'+'=+'='12112111)1(由约束条件可知μμλμλ∑∑--'+'=12111a令111∑-'=A μ∑-'=11B μμ∑-'=1C由μλλ∑∑--'+'=12111111式和μμλμλ∑∑--'+'=12111a 式可得方程组:⎩⎨⎧=+=+aC B B A 21211λλλλ 解得∆-=∆=aBC C a B 11λ∆-=∆=BaA A B A 12λ 其中2B AC -=∆将1λ,2λ的值代入)1(211μλλω-=∑-式,得μμω∑∑∑∑----∆-+∆-=∆-+⎪⎭⎫⎝⎛∆-=111111B aA aB C B aA aB C a即μλλω∑∑--+=12111a此证券组合预期收益x a 'ω的方差为:AB a A AC A B a Aa a BaA aB C B aA aB C B aA aB C x a a a a 1)2()2(111)(22112+-∆=+-∆=∆-+∆-='∆-+'∆-=⎪⎭⎫⎝⎛∆-+∆-'='∑∑∑--μωωμωωσ说明1:最小方差资产组合是由给定的期望收益a 确定的,故用a ω表示。
对应不同的a ,有不同的a ω,它满足11='ω,a ='μω,并使得风险∑'ωω达到最小,相应的风险记为)(2x a 'ωσ。
对于给定的收益(如a ),我们将所有大于最小方差)(2x a 'ωσ的资产组合ω称为“可行组合”。
说明2:由AB a A x a 1)2()(22+-∆='ωσ式可得 22)(1AB A A -∆=-μσ故A12≥σ 式中,μ是任意的一个数(与a 含义相同),表示资产组合的预期收益水平,而2σ则表示与μ相对应的证券组合的方差。
对22)(1A B A A -∆=-μσ式两边同乘以A ∆,可得 AA AB 1()(22-∆=-σμ两边开平方并移项,得)1(2AA AB -∆±=σμ 在),(2μσ平面上AA AB 1()(22-∆=-σμ式表示了一条抛物线,该抛物线的顶点为),1(ABA 。
现在我们要确定的是抛物线的开口方向。
因为 0111>'=∑-A (正定),01>'=∑-μμC 由柯西-席瓦尔兹不等式(Cauchy Schwarz inequality)可得:2121212121212121211()11(11BA =''≤'='∑∑∑∑∑∑∑-------μμμ故AC B ≤2,从而0>∆,所以0>∆A,抛物线开口向右。
经过上面的分析,我们知道最小方差资产组合的图形在),(2μσ平面上是一条抛物线,其图形如图4-1所示:说明3:在),(2μσ平面上,由22)(1ABA A -∆=-μσ式得: AA B A 1)(22+-∆=μσ 其图形如图4-2所示:对AA B A 1)(22+-∆=μσ式移项得 1)(111)(11)(2222222=∆--=∆*--=-∆-A A B AA A AB AAA B A μσμσμσ 在),(μσ平面上,1)(1222=∆--A AB Aμσ式为双曲线的标准型,中心在),0(A B ,对称轴为0=σ和BA=μ。
由于0>σ,故只取双曲线在第一象限那一支。
双曲线的图形如图4-3所示:说明4:在图4-3中的g 点是一个特殊的点,它是双曲线在第一象限中图形的顶点。
由图可知,g 所代表的组合是所有可行组合中方差最小的,我们将其称为“全局最小方差组合”。
由图4-3可知,g 点的组合是:A B g =μ Ag 12=σ 以g μ的值代替∆-=∆=aBC C a B11λ式和∆-=∆=BaA A B A 12λ式中a 得: A11=λ 02=λ 再将1λ和2λ的值代人)1(211μλλω-=∑-式得:1111111∑∑∑---'==Agω关于g 点就是全局最小方差组合的严格证明如下:命题4—1 A g 1)(2≥ωσ,且A g 1)(2=ωσ的充分必要条件是AB a g ==μ。
证明:由于0>A ,0>∆,由AB a A x a 1)2()(22+-∆='ωσ 式知:Ag 1)(2≥ωσ必要性:设A g 1)(2=ωσ 由A B a A x a 1)2()(22+-∆='ωσ式可知:0)(2=-A B a AB a =充分性:反之,当A B a =,由AB a A x a 1)2()(22+-∆='ωσ式可得 Ag 1)(2=ωσ g 点以下的前沿是所有可行组合中方差相同而期望收益较小的组合,任何一个理性的投资者都不会选择这样的组合。
g 点以上的边缘是所有可行组合中方差相同而期望收益较大的组合,我们将这些组合称为有效组合,也就是投资者实际上可以选择的组合。
所有有效组合的总和称为有效前沿(efficient frontier )。
投资者在有效前沿上具体选择哪个投资组合,取决于他的期望效用函数)),(()(2σr E f U E =。
期望效用函数在图形上表示为一系列无差异曲线。
同一条无差异曲线上的每一个组合对该投资者来说效用都是一样的,但是不同无差异曲线所代表的效用是有差别的,位置越靠近左上的曲线代表的效用水平越高。
—邑确定了投资者的无差异曲线,则投资者的最优投资组合就是无差异曲线和有效前沿的切点,这一切点是所有的可行组合中能给投资者带来最大效用的组合,图4-4中的点M 就是这样一个最优组合。
说明:pσ表示证券组合P 收益的标准差,p R 表示证券组合的收益,1IDC 、2IDC 分别表示两条无差异曲线。
说明5:前面我们已经假设了n 种资产,其收益为),,2,1(n i x i =,i x 随机变量,且⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n n x E x E x E x E μμμμ 2121)()()()( 毫无疑问,0>i μ;否则,若0≤i μ,则此种证券无人投资。
