《导数及其应用》单元测试题详细答案
高中数学选修第三章《导数及其应用》知识点归纳及单元测试
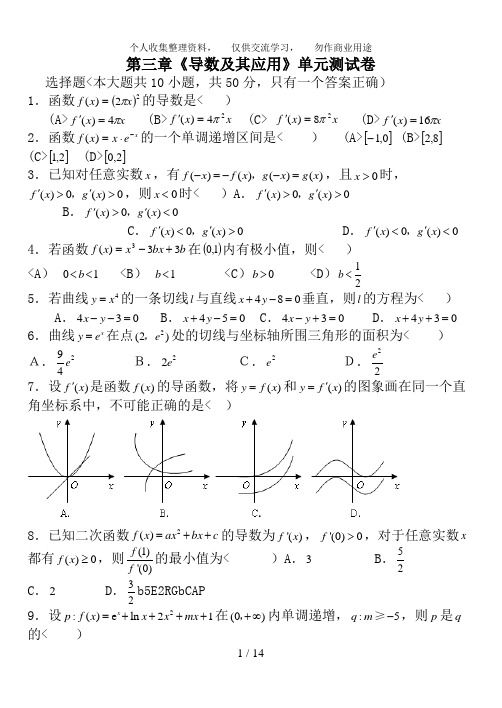
不合要求;综上, 为所求。
20.<1)解法1:∵ ,其定义域为 ,
∴ .
∵ 是函数 的极值点,∴ ,即 .
∵ ,∴ .
经检验当 时, 是函数 的极值点,
∴ .
解法2:∵ ,其定义域为 ,
∴ .
令 ,即 ,整理,得 .
∵ ,
∴ 的两个实根 <舍去), ,
当 变化时, , 的变化情况如下表:
<A) <B) <C) <D)
5.若曲线 的一条切线 与直线 垂直,则 的方程为< )
A. B. C. D.
6.曲线 在点 处的切线与坐标轴所围三角形的面积为< )
A. B. C. D.
7.设 是函数 的导函数,将 和 的图象画在同一个直角坐标系中,不可能正确的是< )
8.已知二次函数 的导数为 , ,对于任意实数 都有 ,则 的最小值为< )A. B. C. D. b5E2RGbCAP
A
如图所示,切线BQ的倾斜角小于
直线AB的倾斜角小于 Q
切线AT的倾斜角
O 1 2 3 4 x
所以选B
11.
12.32
13.
14. (1>
三、解答题
15. 解:设长方体的宽为x<m),则长为2x(m>,高为
.
故长方体的体积为
从而
令V′<x)=0,解得x=0<舍去)或x=1,因此x=1.
当0<x<1时,V′<x)>0;当1<x< 时,V′<x)<0,
17.设函数 分别在 处取得极小值、极大值. 平面上点 的坐标分别为 、 ,该平面上动点 满足 ,点 是点 关于直线 的对称点,.求(Ⅰ>求点 的坐标; (Ⅱ>求动点 的轨迹方程. RTCrpUDGiT
人教A版高中数学选修1-1第三章《导数及其应用》单元检测题(含答案).docx

第三章《导数及其应用》检测题一、选择题(每小题只有一个正确答案)1.已知曲线y = |x2-2上一点P(屈一$,则过点P切线的倾斜角为()乙乙A.30°B. 45°C. 60°D. 120°2.设P为曲线C: y = F+2x + 3上的点,且曲线c在点P处切线倾斜角的取值范围7T 7T为则点P横坐标的取值范围为()4 2( JiA. —co,—B. [—1,0]1D. , + 823.定义在(0, +8)上的函数f(x)的导函数为广(无),且对VxG (0,+oo)都有c. [0,1]/z(x)lnx<^/'(x),则(A. 4/(e) > e3/(e4) > 2e/(e2) C. e3/(e4) > 4/(e) > 2e/(e2) )(其中e«2. 7)B.e3/(e4) > 2e/(e2) > 4/(e) D. 4/(e) > 2e/(e2) > e3/(e4)4.曲线/(x) = (x + l)e x在点(0, f(0))处的切线方程为()A. y = % 4- 1B. y = 2x 4- 1C. y = + 1D.y 弓x+15.对于函数/(x)=—,下列说法正确的有()①f(兀)在x = €处取得极大值》②f(x)有两个不同的零点;③门4) < f (兀)< /(3); @7T4 < 4兀.A.4个B.3个C.2个D. 1个6.定义在R上的奇函数f (x)满足f (・1)=0,且当x>0时,f (x) >xf (x),则下列关系式中成立的是()A. 4f (i) >f (2)B. 4f (2) <f (2)C. f (i) >4f (2)D. f (i) f (2) > 2 2 2 27.定义在[0, +oo)的函数fO)的导函数为f(x),对于任意的%>0,恒有/Xx) </(%),m = n = 则m, zi的大小关系是()・e e zA. m > nB. m < nC. m = nD.无法确定&函数/(x) = e x + x3 - 2在区间(0,1)内的零点个数是().A. 0B. 1C. 2D. 39 .在平面直角坐标系xOy中,已知好一In%! - = 0 , x2 - y2 ~ 2 = 0 ,则(%i -x2)2 +(7i -y2)2的最小值为()A. 1B. 2C. 3D. 410.已知直线2是曲线y = e x与曲线y = e2x-2的一条公切线,2与曲线y =/x 一2切于点(a,b),且a是函数£仗)的零点,贝”仗)的解析式可能为()A. /(%) = e2x(2x + 21n2 -1)-1B. f(x) = e2x(2x + 21n2 -1)-2C.f(x) = e2x(2x一21n2 -1)-1D. /(x) = e2x(2x一21n2 -1)-2二、填空题设函数fd)的导数为f f (x),且f(x)=f‘(^sinx + cosx,则f' (? = _____________________ 12.如图,函数y = f(x)的图象在点P处的切线方程是y = -兀+ 5,则/'⑶+厂⑶=_. Array13._____ 函数y=f (x)的导函数y = f(jc)的图象如图所示,则函数y=f (x)的图象可能是_________ (填序号).(D ②③④14.已知函数/(x)=xlnx + i%2, %是函数f(x)的极值点,给出以下几个命题:乙@0 < %0 < -;②尢o>2;+ X o < 0;④fOo) + Xo>0;e e其中正确的命题是______________ •(填出所有正确命题的序号)、215 .已知函数/(X)= X3 +OT2 +/?JC+C在X =——与兀=1时都取得极值,若对xe[-l,2],不等式f(x)<c2恒成立,则c的取值范围为___________________________ o三、解答题16.求下列函数的导函数®y = X4—3x2—5x + 6 ③y = x2cos x ②y二x+古@y = tan x17.已知函数/'(兀)=|%2一(a + l)x + a\nx.(1)当a VI时,讨论函数f(x)的单调性;(2)若不等式f(X) + (a + l)x n牛+対+ 1 一对于任意x G [e~1,e]成立,求正实数a 的取值范围.18.已知函数f (尤)=^x3— ax1 2 + l(a 6 /?).(1)若曲线y = /(%)在(l,f(l))处的切线与直线x-y + l = 0垂直,求a的值.(2)若a>0,函数y = /(%)在区间(a,a2 - 3)±存在极值,求a的取值范圉.(3)若a >2,求证:函数y = f(x)在(0,2)上恰有一个零点.19.已知函数f^x) = a x^-x2-x\na (a>0,且aHl).(I )求函数/(兀)的单调区间;(II)求函数/(兀)在[-2,2]上的最大值.20.现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P~A\B\G从, 下部的形状是正四棱柱ABCD-A限Cd (如图所示),并要求正四棱柱的高"0是正以棱锥的高%的4倍.1 若AB=6 m, n =2 m,则仓库的容积是多少?2 若正四棱锥的侧棱长为6 m,则当〃为多少时,仓库的容积最大?参考答案I.C2. D3. D4・ B5. C6. A7. B8. B9. B10・ BII.- A/212. 113.④14.①③15.(-00,-1) U(2,4-oo)16.解析:(l)y z = 4x3— 6x — 5(2)y‘ = % 4- x~2(3)y‘ = (x2ycosx + x2(cosx)f = 2xcosx-x2sinx, sinx , (sinx),cosx — sinx(cosx)' cos2% + sin2% 1(4)-------------- y =( ----------------- )= ----- = = :—cos2%cosx cos2%cos2% cos2%17.(1)当a<0时,函数门切在(1,+8)上单调递增,在(0,1)上单调递减;当ova VI时, 函数f(x)在@,1)上单调递减,在(0卫)和(1,+8)上单调递增.(2) (0,1]解析:(1)函数/'仗)的定义域为(0,+s),广(%)=兀 _ @ + 1)+ 兰=*一@+1央+。
导数及其应用测试题(有详细答案)

12.已知函数f{x)=x3+ax2+bx+a2在ul处有极值为10,则犬2)等于.JT13.函数y=尤+2cosx在区间[0,—]±的最大值是14.已知函数fM=x3+ax在R上有两个极值点,则实数。
的取值范围是15.已知函数八尤)是定义在R上的奇函数,/(1)=0,二⑴;'3)>0危>0),则不等式%x2f(x)>0的解集是三、解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)16.设函数/(x)=2x3+3破2+3笊+8c在x=1刚好工=2取得极值.(1)求。
、b的值;(2)若对于随意的xg[0,3],都有/(x)<c2成立,求c的取值范围.17.已知函数f(x)=2x3-3x2+3.(1)求曲线y=f(x)在点工=2处的切线方程;(2)若关于工的方程/(x)+m=0有三个不同的实根,求实数m的取值范围.18.设函S/W=x3-6x+5,x e R.(1)求f(x)的单调区间和极值;《导数及其应用》一、选择题1.r(x0)=o是函数y(尤)在点气处取极值的:A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件2、设曲线y=x2+l在点(x,/(x))处的切线的斜率为g(x),WI函数>=g(x)cosx的部分图象可以4.若曲线y=x2+ax+b在点(0,方)处的切线方程是x-j+l=0,贝!|()A.q=L b=lB.a=—1,b=lC.g=L b=—1D.a=—1,b=—15.函数/(x)=x3+ttx2+3x—9,已知处)在x=—3时取得极值,则0等于()A.2B.3C.4D.56.设函数f⑴的导函数为扩(x),且/(x)=x2+2x-r(l),则广(0)等于()A、0B>-4C、-2D、27.直线y=x是曲线y=a+lnx的一条切线,则实数。
的值为()A.-1B.eC.In2D.18.若函数f(x)=x3-12x^区间以-盘+1)上不是单调函数,则实数k的取值范围()A.kJ—3^4—1■ k<23B.—3<上<—l^(il<k<3C.-2<k<2D.不存在这样的实数k9.函数f(x)的定义域为(m),导函数/(%)在(。
选修1-1《第三章导数及其应用》单元质量评估试卷含答案

单元质量评估(三)第三章(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2019·台州高二检测)函数y=lgx的导数为( )A. B.ln10C. D.【解析】选C.因为(log a x)′=,所以(lgx)′=.2.(2019·泉州高二检测)已知f(x)=sinx+lnx,则f′(1)的值为( )A.1-cos1B.1+cos1C.-1+cos1D.-1-cos1【解析】选B.f′(x)=cosx+,f′(1)=cos1+1.3.设f(x)=x2(2-x),则f(x)的单调递增区间是( )A. B.C.(-∞,0)D.(-∞,0)∪【解析】选A.f(x)=2x2-x3,f′(x)=4x-3x2,由f′(x)>0得0<x<.4.已知物体的运动方程是s=t3-4t2+12t(t表示时间,s表示位移),则瞬时速度为0的时刻是( )A.0秒、2秒或6秒B.2秒或16秒C.2秒、8秒或16秒D.2秒或6秒【解析】选D.s′=t2-8t+12=0,解得t=2或t=6.5.函数y=2x3-2x2在[-1,2]上的最大值为( )A.-5B.0C.-1D.8【解析】选D.y′=6x2-4x=2x(3x-2),列表:-所以y max=8.6.(2019·临沂高二检测)曲线y=3lnx+x+2在点P0处的切线方程为4x-y-1=0,则点P0的坐标是( )A.(0,1)B.(1,-1)C.(1,3)D.(1,0)【解析】选C.f′(x)=+1.设P0(x0,y0),则+1=4,解得x0=1.因为(x0,y0)在直线4x-y-1=0上,所以y0=3.所以点P0的坐标为(1,3).7.若x=1是函数f(x)=(ax-2)·e x的一个极值点,则a的值为( )A.1B.2C.eD.5【解析】选A.因为f′(x)=ae x+(ax-2)e x,所以f′(1)=ae+(a-2)e=0,解得:a=1,把a=1代入函数得:f(x)=(x-2)·e x,所以f′(x)=e x+(x-2)e x=e x(x-1),所以f′(1)=0,且x<1时,f′(x)<0,x>1时,f′(x)>0.故a=1符合题意.8.做一个无盖的圆柱形水桶,若要使其体积是27π且用料最省,则圆柱的底面半径为( )A.5B.6C.3D.2【解析】选C.设圆柱的底面半径为R,母线长为l,则V=πR2l=27π,所以l=.要使用料最省,只需使水桶的表面积最小,而S表=πR2+2πR l=πR2+,令S表′=2πR-=0,解得R=3,即当R=3时,S表最小.9.(2019·菏泽高二检测)函数f(x)=x3-6bx+3b在(0,1)内有极小值,则实数b的取值范围是( )A.(0,1)B.(-∞,1)C.(0,+∞)D.【解析】选D.f′(x)=3x2-6b,因为f(x)在(0,1)内有极小值,所以f′(x)=0在x∈(0,1)有解.所以所以0<b<.10.(2019·合肥高二检测)设a<b,函数y=(x-a)2(x-b)的图象可能是( )【解析】选C.y′=2(x-a)(x-b)+(x-a)2=(x-a)·(3x-a-2b),由y′=0得x=a或x=.因为a<b,所以a<,所以当x=a时,y取极大值0;当x=时,y取极小值且极小值为负.11.(2019·烟台高二检测)已知a<0,函数f(x)=ax3+lnx,且f′(1)的最小值是-12,则实数a的值为( )A.2B.-2C.4D.-4【解析】选B.f′(x)=3ax2+,所以f′(1)=3a+≥-12,即a+≥-4,又a<0,有a+≤-4.故a+=-4,此时a=-2.12.(2019·全国卷Ⅰ)若函数f(x)=x-sin2x+asinx在(-∞,+∞)上单调递增,则a的取值范围是( )A.[-1,1]B.C. D.【解析】选C.方法一:用特殊值法:取a=-1,f(x)=x-sin2x-sinx,f′(x)=1-cos2x-cosx,但f′(0)=1--1=-<0,不具备在(-∞,+∞)上单调递增,排除A,B,D.方法二:f′(x)=1-cos2x+acosx≥0对x∈R恒成立,故1-(2cos2x-1)+acosx≥0,即acosx-cos2x+≥0恒成立,令t=cosx,所以-t2+at+≥0对t∈[-1,1]恒成立,构造函数f(t)=-t2+at+, 开口向下的二次函数f(t)的最小值的可能值为端点值,故只需解得-≤a≤.二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.(2019·中山高二检测)曲线y=x(3lnx+1)在点(1,1)处的切线方程为.【解析】y′=3lnx+1+x·=3lnx+4,所以y′|x=1=3ln1+4=4.又f(1)=1×(3ln1+1)=1,所以所求的切线方程为y-1=4(x-1),即4x-y-3=0.答案:4x-y-3=014.(2019·郑州高二检测)已知函数f(x)=+,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0,则a= ,b= .【解析】f′(x)=-.由于直线x+2y-3=0的斜率为-,且过点(1,1).故即解得a=1,b=1.答案:1 115.函数y=x+2cosx-在区间上的最大值是.【解析】y′=1-2sinx=0,在区间上解得x=,故y=x+2cosx-在区间上是增函数,在区间上是减函数,所以x=时,y=,而x=0时,y=2-,x=时y=-,且>2->-,故函数y=x+2cosx-在区间上的最大值是.答案:【补偿训练】曲线y=x3-2以点为切点的切线的倾斜角为. 【解析】y′=x2,当x=1时,y′=1,从而切线的倾斜角为45°.答案:45°16.设f(x)=x3-x2-2x+5,当x∈[-1,2]时,f(x)<m恒成立,则实数m的取值范围是.【解析】f′(x)=3x2-x-2=(x-1)(3x+2),令f′(x)=0,得x=1或x=-.f(x)极小值=f(1)=1--2+5=,f(x)极大值=f=--++5=5.又f(-1)=-1-+2+5=,f(2)=8-2-4+5=7,比较可得f(x)max=f(2)=7.因为f(x)<m对x∈[-1,2]恒成立.所以m>7.答案:(7,+∞)三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)(2019·南昌高二检测)设函数f(x)=6x3+3(a+2)x2+2ax.(1)若f(x)的两个极值点为x1,x2,且x1x2=1,求实数a的值.(2)是否存在实数a,使得f(x)是(-∞,+∞)上的单调函数?若存在,求出a的值;若不存在,说明理由.【解析】f′(x)=18x2+6(a+2)x+2a.(1)由已知有f′(x1)=f′(x2)=0,从而x1x2==1,所以a=9.(2)由于Δ=36(a+2)2-4×18×2a=36(a2+4)>0,所以不存在实数a,使得f(x)是(-∞,+∞)上的单调函数.【补偿训练】已知函数f(x)=ax2+2x-lnx.(1)当a=0时,求f(x)的极值.(2)若f(x)在区间上是增函数,求实数a的取值范围.【解析】(1)函数的定义域为(0,+∞).因为f(x)=ax2+2x-lnx,当a=0时,f(x)=2x-lnx,则f′(x)=2-,令f′(x)=0得x=,所以当x变化时,f′(x),f(x)的变化情况如表所以当x=时,f(x)的极小值为1+ln2,无极大值.(2)由已知,得f(x)=ax2+2x-lnx,且x>0,则f′(x)=ax+2-=.若a=0,由f′(x)>0得x>,显然不合题意;若a≠0,因为函数f(x)在区间上是增函数,所以f′(x)≥0对x∈恒成立,即不等式ax2+2x-1≥0对x∈恒成立,即a≥=-=-1恒成立,故a≥.而当x=时,函数-1的最大值为3,所以实数a的取值范围为a≥3. 18.(12分)已知函数f(x)=x3+x-16.(1)求曲线y=f(x)在点(2,-6)处的切线的方程.(2)如果曲线y=f(x)的某一切线与直线y=-x+3垂直,求切点坐标与切线的方程. 【解析】(1)因为f′(x)=(x3+x-16)′=3x2+1,所以f(x)在点(2,-6)处的切线的斜率为k=f′(2)=13.所以切线的方程为y=13(x-2)+(-6),即y=13x-32.(2)因为切线与直线y=-+3垂直,所以切线的斜率k=4.设切点的坐标为(x0,y0),则f′(x0)=3+1=4,所以x0=±1,所以或即切点坐标为(1,-14)或(-1,-18).切线方程为y=4(x-1)-14或y=4(x+1)-18.即y=4x-18或y=4x-14.19.(12分)(2019·临沂高二检测)已知函数f(x)=lnx-ax2-2x.(1)若函数f(x)在x=2处取得极值,求实数a的值.(2)若函数f(x)在定义域内单调递增,求a的取值范围.【解析】(1)f′(x)=-(x>0),因为x=2时,f(x)取得极值,所以f′(2)=0,解之得a=-,经检验符合题意.(2)由题意知f′(x)≥0在x>0时恒成立,即ax2+2x-1≤0在x>0时恒成立,则a≤=-1在x>0时恒成立,即a≤(x>0),当x=1时,-1取得最小值-1.所以a的取值范围是(-∞,-1].20.(12分)某5A级景区为提高经济效益,现对某景点进行改造升级,提高旅游增加值,经过市场调查,旅游增加值y万元与投入x(x≥10)万元之间满足:y=f(x)=ax2+x-bln,a,b为常数,当x=10万元时,y=19.2万元;当x=50万元时,y=74.4万元.(参考数据:ln2=0.7,ln3=1.1,ln5=1.6)(1)求f(x)的解析式.(2)求该景点改造升级后旅游利润T(x)的最大值.(利润=旅游增加值-投入) 【解析】(1)由条件可得解得a=-,b=1.则f(x)=-+x-ln(x≥10).(2)由T(x)=f(x)-x=-+x-ln(x≥10),则T′(x)=-+-=-,令T′(x)=0,则x=1(舍)或x=50,当x∈(10,50)时,T′(x)>0,因此T(x)在(10,50)上是增函数;当x>50时,T′(x)<0,因此T(x)在(50,+∞)上是减函数,故x=50为T(x)的极大值点,也是最大值点,且最大值为24.4万元.即该景点改造升级后旅游利润T(x)的最大值为24.4万元.21.(12分)(2019·绍兴高二检测)已知函数f(x)=x3-3ax2-9a2x+a3.(1)设a=1,求函数f(x)的极值.(2)若a>,且当x∈[1,4a]时,f(x)≥a3-12a恒成立,试确定a的取值范围. 【解析】(1)当a=1时,f(x)=x3-3x2-9x+1且f′(x)=3x2-6x-9,由f′(x)=0得x=-1或x=3.当x<-1时,f′(x)>0,当-1<x<3时,f′(x)<0,因此x=-1是函数f(x)的极大值点,极大值为f(-1)=6;当-1<x<3时f′(x)<0,当x>3时f′(x)>0,因此x=3是函数的极小值点,极小值为f(3)=-26.(2)因为f′(x)=3x2-6ax-9a2=3(x+a)(x-3a),a>,所以当1≤x<3a时,f′(x)<0;当3a<x≤4a时,f′(x)>0.所以x∈[1,4a]时,f(x)的最小值为f(3a)=-26a3.由f(x)≥a3-12a在[1,4a]上恒成立得-26a3≥a3-12a.解得a≤-或0≤a≤.又a>,所以<a≤.即a的取值范围为.22.(12分)奇函数f(x)=ax3+bx2+cx的图象过点A(-,),B(2,10).(1)求f(x)的表达式.(2)求f(x)的单调区间.(3)若方程f(x)+m=0有三个不同的实数根,求m的取值范围.【解析】(1)因为f(x)=ax3+bx2+cx为奇函数,所以f(-x)=-f(x)(x∈R).所以b=0.所以f(x)=ax3+cx.因为图象过点A(-,),B(2,10),所以即所以所以f(x)=x3-3x.(2)因为f(x)=x3-3x,所以f′(x)=3x2-3=3(x-1)(x+1),所以当-1<x<1时,f′(x)<0;当x<-1或x>1时,f′(x)>0,所以f(x)的递增区间是(-∞,-1)和(1,+∞),递减区间是(-1,1).(3)因为f(-1)=2,f(1)=-2,为使方程f(x)+m=0,即f(x)=-m有三个不等实数根,则-2<-m<2,即-2<m<2,所以m的取值范围是(-2,2).。
高中数学选修2-2第一章《导数及其应用》单元测试(一)

A. y 2x 1
B. y 3x 2
C. y 2x 3
D. y x 2
7.函数 f (x) e ln x x 在 (0, 2e] 上的最大值为
A.1 e C. e
B. 1 D. 0
8.若函数 f (x) x(x c) 2 在 x 2 处取得极大值,则常数 c
A. 2 C. 2 或 6
数学选修 2-2 第一章《导数及其应用》单元测试
一、选择题(本题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项
是符合题目要求的)
1.定积分 2 (ex 2x)dx 的值为 0
A.1
B. e2
C. e2 3
D. e2 4
2.某物体的位移 s (米)与时间 t (秒)的关系式为 s t 2 t ,则该物体在 t 2 时的瞬时速度为
A. 2 米/秒 C. 5 米/秒
B. 3 米/秒 D. 6 米/秒
3.已知曲线 y x2 上一点 P 处的切线与直线 2x y 1 0 平行,则点 P 的坐标为
A. (1,1)
B. (1,1)
C. (2, 4)
D. (3, 9)
4.已知 f (x) x2 2x f (1) ,则 f (3)
11.若函数 f (x) lnx ax 1 在[1, ) 上是单调函数,则实数 a 的取值范围为 x
A. (, 0] [1 , ) 4
B. (, 1 ] [0, ) 4
C.[ 1 , 0] 4
D. (,1]
12.已知函数 f (x) ax 1 (a 1) ln x 1 在 (0,1] 上的最大值为 3 ,则实数 a x
即 2x y 1 0 .(6 分)
新课标人教A版选修1-1《导数及其应用》单元测试(含答案)
《导数及其应用》单元检测题(文科)一、选择题(本题共12题,每题4分,共48分)1. 一个物体的运动方程为S=1+t+t 2其中s 的单位是米,t 的单位是秒,那么物体在3秒末的瞬时速度是( A )A 7米/秒B 6米/秒C 5米/秒D 8米/秒 2 若()sin cos f x x α=-,则'()f α等于( A ) A sin α B cos α C sin cos αα+D 2sin α3.曲线3()2f x x x在0p 处的切线平行于直线41y x ,则0p 点的坐标为( C )A (1,0)B (2,8)C (1,0)和(1,4)--D (2,8)和(1,4)-- 4。
函数2()2ln f x x x =-的递增区间是( C )A.1(0,)2 B 。
11(,0)(,)22-+∞及 C 。
1(,)2+∞ D 。
11(,)(0,)22-∞-及5。
'()0((,))f x x a b ≥∈是可导函数y =f(x )在区间(,)a b 内单调递增的 ( B )A .充分不必要条件B .必要不充分条件C .充要条件D .非充分非必要条件 6. 函数323922yxxx x 有( C )A 极大值5,极小值27-B 极大值5,极小值11-C 极大值5,无极小值D 极小值27-,无极大值 7。
函数y=2x 3—3x 2-12x+5在区间[0,3]上最大值与最小值分别是(a )A 。
5,-15B . 5,—4C . —4,-15D . 5,-168。
设函数()f x 的导函数为()f x ',且()()221f x x x f '=+⋅,则()0f '等于 ( B )A 、0B 、4-C 、2-D 、29. 已知函数1)(23--+-=x ax x x f 在),(+∞-∞上是单调函数,则实数的取值范围是( B )A ),3[]3,(+∞--∞B ]3,3[-C ),3()3,(+∞--∞D )3,3(-10.已知函数)(x f y =的导函数)(x f y '=的图像如下,则 ( A )A .函数)(x f 有1个极大值点,1个极小值点B .函数)(x f 有2个极大值点,2个极小值点C .函数)(x f 有3个极大值点,1个极小值点D .函数)(x f 有1个极大值点,3个极小值点11.函数223)(a bx ax x x f +--=在1=x 处有极值10, 则点为 ( B )A .)3,3(-B .)11,4(-C .)3,3(-或)11,4(-D .不存在12.以下四图,都是同一坐标系中三次函数及其导函数的图像,其中一定不正确的序号是 (C )A .①、②B .①、③C .③、④D .①、④二、填空题(本题共4个题,每题4分,共16分) 13。
高二下数学第一章导数及其应用单元检测(含答案)
阶段质量检测:导数及其应用(时间: 120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.以正弦曲线y =sin x 上一点P 为切点的切线为直线l ,则直线l 的倾斜角的范围是( ) A.⎣⎡⎦⎤0,π4∪⎣⎡⎭⎫3π4,π B .[0,π) C.⎣⎡⎦⎤π4,3π4 D.⎣⎡⎦⎤0,π4∪⎝⎛⎦⎤π2,3π4 2.函数f (x )=x +2cos x 在⎣⎡⎦⎤0, π2上的极大值点为( ) A .0 B.π6 C.π3 D.π23.函数f (x )的定义域为开区间(a ,b ),导函数f ′(x )在(a ,b )内的图象如图所示,则函数f (x )在开区间(a ,b )内有极小值点( )A .1个B .2个C .3个D .4个 4.若函数()ln f x x a x=+不是单调函数,则实数a 的取值范围是( ).A .[)0,+∞B .(],0-∞C .(),0-∞D .()0,+∞5.若e x ≥k +x 在R 上恒成立,则实数k 的取值范围为( ) A .(-∞,1] B .[1,+∞) C .(-∞,-1] D .[-1,+∞)6.若函数f (x )=x 33-a 2x 2+x +1在区间⎝⎛⎭⎫13,4上有极值点,则实数a 的取值范围是( ) A.⎝⎛⎭⎫2,103 B.⎣⎡⎭⎫2,103 C.⎝⎛⎭⎫103,174 D.⎝⎛⎭⎫2,174 7.函数f (x )=13ax 3+12ax 2-2ax +1的图象经过四个象限,则实数a 的取值范围是( )A.⎝⎛⎭⎫-310,67B.⎝⎛⎭⎫-85,-316C.⎝⎛⎭⎫-83,-116D.⎝⎛⎭⎫-∞,-310∪⎝⎛⎭⎫67,+∞ 8.已知函数f (x )的导函数f ′(x )=a (x -b )2+c 的图象如图所示,则函数f (x )的图象可能是( )9.某产品的销售收入y 1(万元)是产量x (千台)的函数:y 1=17x 2,生产成本y 2(万元)是产量x (千台)的函数:y 2=2x 3-x 2(x >0),为使利润最大,应生产( ) A .6千台 B .7千台 C .8千台D .9千台10..已知f (x )是定义在区间(0,+∞)内的函数,其导函数为f ′(x ),且不等式xf ′(x )<2f (x )恒成立,则( )A.4f (1)<f (2)B.4f (1)>f (2)C.f (1)<4f (2)D.f (1)>4f ′(2)11.已知y =f (x )是定义在R 上的奇函数,且当x <0时不等式f (x )+xf ′(x )<0成立,若a =30.3 ·f (30.3),b =log π3·f (log π3),c =log 319·f ⎝ ⎛⎭⎪⎫log 319,则a ,b ,c 的大小关系是( )A.a >b >cB.c >b >aC.a >c >bD.c >a >b12.若函数f (x )=sin xx ,且0<x 1<x 2<1,设a =21sin x x ,12sin b x x =,则a ,b 的大小关系是( )A .a >bB .a <bC .a =bD .a ,b 的大小不能确定二、填空题(本大题共4小题,每小题5分,满分20分.把答案填在题中的横线上) 13.若f (x )=13x 3-f ′(1)x 2+x +5,则f ′(1)=________.14.若函数f (x )=12x 2+(a -1)x -a ln x 存在唯一的极值,且此极值不小于1,则实数a 的取值范围为________.15.若函数f (x )=4xx 2+1在区间(m,2m +1)上单调递增,则实数m 的取值范围是__________.16.已知函数f (x )满足f (x )=f (π-x ),且当x ∈⎝⎛⎭⎫-π2,π2时,f (x )=x +sin x ,设a =f (1),b =f (2),c =f (3),则a ,b ,c 的大小关系是________.三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17. (本小题满分12分)若函数y =f (x )在x =x 0处取得极大值或极小值,则称x 0为函数y =f (x )的极值点.已知a ,b 是实数,1和-1是函数f (x )=x 3+ax 2+bx 的两个极值点. (1)求a 和b 的值;(2)设函数g (x )的导函数g ′(x )=f (x )+2,求g (x )的极值点.18. (2021·百师联盟考试)设函数f (x )=ln x +ax(a 为常数).(2)不等式f(x)≥1在x∈(0,1]上恒成立,求实数a的取值范围.19.(本小题满分12分)某个体户计划经销A,B两种商品,据调查统计,当投资额为x(x≥0)万元时,在经销A,B商品中所获得的收益分别为f(x)万元与g(x)万元,其中f(x)=a(x-1)+2,g(x)=6ln(x+b)(a>0,b>0).已知投资额为零时收益为零.(1)求a,b的值;(2)如果该个体户准备投入5万元经销这两种商品,请你帮他制定一个资金投入方案,使他能获得最大利润.20.(本小题满分12分) (2020·全国Ⅰ卷)已知函数f(x)=e x+ax2-x.(1)当a=1时,讨论f(x)的单调性;(2)当x≥0时,f(x)≥12x3+1,求a的取值范围.21.(本小题满分12分)已知函数f(x)=ln x+ax+1(a∈R).(2)若函数f (x )的图象与x 轴相切,求证:对于任意互不相等的正实数x 1,x 2,都有f (x 2)-f (x 1)x 2-x 1<1x 1+1x 2.22. (本小题满分12分) 已知函数f (x )=x 2-m ln x ,h (x )=x 2-x +a . (1)当a =0时,f (x )≥h (x )在(1,+∞)上恒成立,求实数m 的取值范围;(2)当m =2时,若函数k (x )=f (x )-h (x )在区间(1,3)上恰有两个不同零点,求实数a 的取值范围.参考答案1.【解析】选A y ′=cos x ,∵cos x ∈[-1,1],∴切线的斜率范围是[-1,1],∴倾斜角的范围是⎣⎡⎦⎤0,π4∪⎣⎡⎭⎫3π4,π. 2.答案:B3.【解析】选A 设极值点依次为x 1,x 2,x 3且a <x 1<x 2<x 3<b ,则f (x )在(a ,x 1),(x 2,x 3)上递增,在(x 1,x 2),(x 3,b )上递减,因此,x 1,x 3是极大值点,只有x 2是极小值点.4.【答案】C【解析】由题意知0x >,()1af x x'=+,要使函数()ln f x x a x =+不是单调函数,则需方程10ax+=在0x >上有解,即x a =-,所以0a <,故选C . 5.解析:选A 由e x ≥k +x ,得k ≤e x -x . 令f (x )=e x -x ,∴f ′(x )=e x -1. 当f ′(x )<0时,解得x <0,当f ′(x )>0时,解得x >0.∴f (x )在(-∞,0)上是减函数,在(0,+∞)上是增函数.∴f (x )min =f (0)=1. ∴实数k 的取值范围为(-∞,1].故选A.6.解析:选D 因为f (x )=x 33-a 2x 2+x +1,所以f ′(x )=x 2-ax +1.函数f (x )=x 33-a 2x 2+x +1在区间⎝⎛⎭⎫13,4上有极值点可化为f ′(x )=x 2-ax +1=0在区间⎝⎛⎭⎫13,4上有解, 即a =x +1x 在区间⎝⎛⎭⎫13,4上有解,设t (x )=x +1x ,则t ′(x )=1-1x 2, 令t ′(x )>0,得1<x <4,令t ′(x )<0,得13<x <1.所以t (x )在(1,4)上单调递增,在⎝⎛⎭⎫13,1上单调递减.所以t (x )min =t (1)=2,又t ⎝⎛⎭⎫13=103,t (4)=174,所以a ∈⎝⎛⎭⎫2,174. 7.【解析】选D f ′(x )=ax 2+ax -2a =a (x +2)(x -1),要使函数f (x )的图象经过四个象限,则f (-2)f (1)<0,即⎝⎛⎭⎫103a +1⎝⎛⎭⎫-76a +1<0,解得a <-310或a >67. 故选D. 8.【解析】选D 由导函数图象可知,当x <0时,函数f (x )递减,排除A 、B ;当0<x <x 1时,f ′(x )>0,函数f (x )递增.因此,当x =0时,f (x )取得极小值,故选D.9.【解析】选A 设利润为y ,则y =y 1-y 2=17x 2-(2x 3-x 2)=18x 2-2x 3,y ′=36x -6x 2,令y ′=0得x =6或x =0(舍),f (x )在(0,6)上是增函数,在(6,+∞)上是减函数,∴x =6时y 取得最大值.10.答案 B【解析】设函数g (x )=f (x )x 2(x >0),则g ′(x )=x 2f ′(x )-2xf (x )x 4=xf ′(x )-2f (x )x 3<0,所以函数g (x )在(0,+∞)上为减函数,因此g (1)>g (2), 即f (1)12>f (2)22,所以4f (1)>f (2). 11.答案 D【解析】 设g (x )=xf (x ),则g ′(x )=f (x )+xf ′(x ),又当x <0时,f (x )+xf ′(x )<0,∴x <0时,g ′(x )<0,g (x )在(-∞,0)上单调递减.由y =f (x )在R 上为奇函数, 知g (x )在R 上为偶函数,∴g (x )在(0,+∞)上是增函数, ∴c =g ⎝ ⎛⎭⎪⎫log 319=g (-2)=g (2),又0<log π3<1<30.3<3<2, ∴g (log π3)<g (30.3)<g (2),即b <a <c .12.【解析】选A f ′(x )=x cos x -sin xx 2,令g (x )=x cos x -sin x ,则g ′(x )=-x sin x +cos x-cos x =-x sin x .∵0<x <1,∴g ′(x )<0,即函数g (x )在(0,1)上是减函数,得g (x )<g (0)=0,故f ′(x )<0,函数f (x )在(0,1)上是减函数,由0<x 1<x 2<1得12211212sin sin ,sin sin x x x x x x x x >∴>,a >b ,故选A. 13.【解析】f ′(x )=x 2-2f ′(1)x +1,令x =1,得f ′(1)=23. 答案:2314.【解析】 对函数求导得f ′(x )=x -1+a ⎝⎛⎭⎫1-1x =(x +a )(x -1)x ,x >0,因为函数存在唯一的极值,所以导函数存在唯一的零点,且零点大于0,故x =1是唯一的极值点,此时-a ≤0,且f (1)=-12+a ≥1,所以a ≥32.答案 ⎣⎡⎭⎫32,+∞ 15.【解析】f ′(x )=4-4x 2(x 2+1)2,令f ′(x )>0,得-1<x <1,即函数f (x )的增区间为(-1,1).又f (x )在(m,2m +1)上单调递增,所以⎩⎪⎨⎪⎧m ≥-1,m <2m +1,2m +1≤1.解得-1<m ≤0.答案:(-1,0]16.【解析】f (2)=f (π-2),f (3)=f (π-3),因为f ′(x )=1+cos x≥0,故f (x )在⎝⎛⎭⎫-π2,π2上是增函数,∵π2>π-2>1>π-3>0,∴f (π-2)>f (1)>f (π-3),即c <a <b .答案:c <a <b17.【解析】(1)由题设知f ′(x )=3x 2+2ax +b ,且f ′(-1)=3-2a +b =0,f ′(1)=3+2a +b =0,解得a =0,b =-3.(2)由(1)知f (x )=x 3-3x .因为f (x )+2=(x -1)2(x +2),所以g ′(x )=0的根为x 1=x 2=1,x 3=-2,于是函数g (x )的极值点只可能是1或-2.当x <-2时,g ′(x )<0;当-2<x <1时, g ′(x )>0,故-2是g (x )的极值点.当-2<x <1或x >1时,g ′(x )>0, 故1不是g (x )的极值点.所以g (x )的极值点为-2. 18.【解析】 (1)函数f (x )的定义域为(0,+∞),f ′(x )=-a x 2+1x =x -ax 2,当a ≤0时,又x >0,∴x -a >0,∴f ′(x )>0, ∴f (x )在定义域(0,+∞)上单调递增;当a >0时,若x >a ,则f ′(x )>0,∴f (x )单调递增; 若0<x <a ,则f ′(x )<0,∴f (x )单调递减.综上可知:当a ≤0时,f (x )在(0,+∞)上是增函数;当a >0时,f (x )在区间(0,a )上是减函数,在区间(a ,+∞)上是增函数. (2)f (x )≥1⇔a x +ln x ≥1⇔ax ≥-ln x +1⇔a ≥ -x ln x +x 对任意x ∈(0,1]恒成立. 令g (x )=-x ln x +x ,x ∈(0,1].则g ′(x )=-ln x -x ·1x +1=-ln x ≥0,x ∈(0,1], ∴g (x )在(0,1]上单调递增,∴g (x )max =g (1)=1, ∴a ≥1,故a 的取值范围为[1,+∞).19.【解析】(1)由投资额为零时收益为零,可知f (0)=-a +2=0,g (0)=6ln b =0, 解得a =2,b =1.(2)由(1)可得f (x )=2x ,g (x )=6ln(x +1).设投入经销B 商品的资金为x 万元(0<x ≤5), 则投入经销A 商品的资金为(5-x )万元,设所获得的收益为S (x )万元, 则S (x )=2(5-x )+6ln(x +1)=6ln(x +1)-2x +10(0<x ≤5).S ′(x )=6x +1-2,令S ′(x )=0,得x =2.当0<x <2时,S ′(x )>0,函数S (x )单调递增;当2<x ≤5时,S ′(x )<0,函数S (x )单调递减.所以当x =2时,函数S (x )取得最大值, S (x )max =S (2)=6ln 3+6≈12.6万元.所以,当投入经销A 商品3万元,B 商品2万元时, 他可获得最大收益,收益的最大值约为12.6万元.20.解 (1)当a =1时,f (x )=e x +x 2-x ,x ∈R ,f ′(x )=e x +2x -1.故当x ∈(-∞,0)时,f ′(x )<0; 当x ∈(0,+∞)时,f ′(x )>0.所以f (x )在(-∞,0)单调递减,在(0,+∞)单调递增. (2)由f (x )≥12x 3+1得,e x +ax 2-x ≥12x 3+1,其中x ≥0, ①当x =0时,不等式为1≥1,显然成立,此时a ∈R .②当x >0时,分离参数a ,得a ≥-e x -12x 3-x -1x 2,记g (x )=-e x -12x 3-x -1x 2,g ′(x )=-(x -2)⎝ ⎛⎭⎪⎫e x -12x 2-x -1x 3.令h (x )=e x-12x 2-x -1(x >0), 则h ′(x )=e x -x -1,令H (x )=e x -x -1,H ′(x )=e x -1>0,故h ′(x )在(0,+∞)上是增函数,因此h ′(x )>h ′(0)=0,故函数h (x )在(0,+∞)上递增,∴h (x )>h (0)=0,即e x -12x 2-x -1>0恒成立,故当x ∈(0,2)时,g ′(x )>0,g (x )单调递增;当x ∈(2,+∞)时,g ′(x )<0,g (x )单调递减.因此,g (x )max =g (2)=7-e 24,综上可得,实数a 的取值范围是⎣⎢⎡⎭⎪⎫7-e 24,+∞. 21.【解析】(1) 函数f (x )的定义域为(0,+∞),f ′(x )=1x +a =ax +1x .当a ≥0时,f ′(x )>0,f (x )在(0,+∞)上单调递增; 当a <0时,由f ′(x )=0,得x =-1a .若x ∈⎝ ⎛⎭⎪⎫0,-1a ,f ′(x )>0,f (x )单调递增;若x ∈⎝ ⎛⎭⎪⎫-1a ,+∞,f ′(x )<0,f (x )单调递减.综上所述:当a ≥0时,f (x )在(0,+∞)上单调递增;当a <0时,f (x )在⎝ ⎛⎭⎪⎫0,-1a 单调递增,在⎝ ⎛⎭⎪⎫-1a ,+∞上单调递减.(2)证明 由(1)知,当a ≥0时,f (x )在(0,+∞)上单调递增,不满足条件. 所以a <0,此时f (x )的极大值为f ⎝ ⎛⎭⎪⎫-1a =-ln(-a ),由已知得-ln(-a )=0,故a =-1,此时f (x )=ln x -x +1.不妨设0<x 1<x 2,则f (x 2)-f (x 1)x 2-x 1<1x 1+1x 2等价于ln x 2x 1<x 2x 1-x 1x 2+x 2-x 1,即证:ln x 2x 1-x 2x 1+x 1x 2<x 2-x 1.令g (x )=ln x -x +1x (x >1),则g ′(x )=1x -1-1x 2=-⎝ ⎛⎭⎪⎫x -122+34x 2<0,故g (x )在(1,+∞)单调递减,所以g (x )<g (1)=0<x 2-x 1.所以对于任意互不相等的正实数x 1,x 2, 都有f (x 2)-f (x 1)x 2-x 1<1x 1+1x 2成立.22.【解析】(1)由f (x )≥h (x ),得m ≤xln x 在(1,+∞)上恒成立.令g (x )=xln x ,则g ′(x )=ln x -1(ln x )2,当x ∈(1,e)时,g ′(x )<0;当x ∈(e ,+∞)时,g ′(x )>0,所以g (x )在(1,e)上递减,在(e ,+∞)上递增. 故当x =e 时,g (x )的最小值为g (e)=e.所以m ≤e.即m 的取值范围是(-∞,e]. (2)由已知可得k (x )=x -2ln x -a .函数k (x )在(1,3)上恰有两个不同零点,相当于函数φ(x )=x -2ln x 与直线y =a 有两个不同的交点.φ′(x )=1-2x =x -2x ,当x ∈(1,2)时,φ′(x )<0,φ(x )递减,当x ∈(2,3)时,φ′(x )>0,φ(x )递增.又φ(1)=1,φ(2)=2-2ln 2,φ(3)=3-2ln 3,要使直线y =a 与函数φ(x )=x -2ln x 有两个交点,则2-2ln 2<a <3-2ln 3.即实数a 的取值范围是(2-2ln 2,3-2ln 3).。
第三章.导数及其应用测试卷(含详细答案)
单元综合测试三(第三章)时间:90分钟 分值:150分第Ⅰ卷(选择题,共60分)一、选择题(每小题5分,共60分)1.已知f (x )=(x +a )2,且f ′(12)=-3,则a 的值为( ) A .-1 B .-2 C .1D .2解析:f (x )=(x +a )2,∴f ′(x )=2(x +a ). 又f ′(12)=-3,∴1+2a =-3,解得a =-2. 答案:B2.函数y =sin x (cos x +1)的导数是( ) A .y ′=cos2x -cos x B .y ′=cos2x +sin x C .y ′=cos2x +cos xD .y ′=cos 2x +cos x解析:y ′=(sin x )′(cos x +1)+sin x (cos x +1)′=cos 2x +cos x -sin 2x =cos2x +cos x .答案:C3.函数y =3x -x 3的单调递增区间是( ) A .(0,+∞) B .(-∞,-1) C .(-1,1)D .(1,+∞)解析:f ′(x )=3-3x 2>0⇒x ∈(-1,1).答案:C4.某汽车启动阶段的路程函数为s (t )=2t 3-5t 2+2,则t =2秒时,汽车的加速度是( )A .14B .4C .10D .6解析:依题意v (t )=s ′(t )=6t 2-10t ,所以a (t )=v ′(t )=12t -10,故汽车在t =2秒时的加速度为a (2)=24-10=14.答案:A5.若曲线f (x )=x sin x +1在x =π2处的切线与直线ax +2y +1=0互相垂直,则实数a 的值为( )A .-2B .-1C .1D .2解析:f ′(x )=x cos x +sin x ,f ′(π2)=1, ∴k =-a2=-1,a =2. 答案:D6.已知P ,Q 为抛物线x 2=2y 上两点,点P ,Q 的横坐标分别为4,-2,过P ,Q 分别作抛物线的切线,两切线交于点A ,则点A 的纵坐标为( )A .1B .3C .-4D .-8解析:如图所示,由已知可设P (4,y 1),Q (-2,y 2), ∵点P ,Q 在抛物线x 2=2y 上,∴⎩⎨⎧42=2y 1, ①(-2)2=2y 2, ②∴⎩⎨⎧y 1=8,y 2=2,∴P (4,8),Q (-2,2).又∵抛物线可化为y =12x 2,∴y ′=x . ∴过点P 的切线斜率为y ′|x =4=4,∴过点P 的切线为y -8=4(x -4),即y =4x -8. 又∵过点Q 的切线斜率为y ′|x =-2=-2.∴过点Q 的切线为y -2=-2(x +2),即y =-2x -2.联立⎩⎨⎧y =4x -8,y =-2x -2,解得x =1,y =-4.∴点A的纵坐标为-4. 答案:C7.若函数y=a(x3-x)的递增区间是(-∞,-33),(33,+∞),则a的取值范围是()A.a>0 B.-1<a<0 C.a>1 D.0<a<1解析:依题意y′=a(3x2-1)>0的解集为(-∞,-33),(33,+∞),故a>0.答案:A8.对任意的x∈R,函数f(x)=x3+ax2+7ax不存在极值点的充要条件是()A.0≤a≤21 B.a=0或a=7C.a<0或a>21 D.a=0或a=21解析:f′(x)=3x2+2ax+7a,当Δ=4a2-84a≤0,即0≤a≤21时,f′(x)≥0恒成立,函数f(x)不存在极值点.故选A.答案:A9.已知函数f(x)=x3-3x,若对于区间[-3,2]上任意的x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是()A.0 B.10C.18 D.20解析:f′(x)=3x2-3,令f′(x)=0,解得x=±1,所以1,-1为函数f(x)的极值点,因为f(-3)=-18,f(-1)=2,f(1)=-2,f(2)=2,所以在区间[-3,2]上,f(x)max=2,f(x)min=-18,所以对于区间[-3,2]上任意的x1,x2,|f(x1)-f(x2)|≤20,所以t≥20,从而t的最小值为20.答案:D10.设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是()A.∀x∈R,f(x)≤f(x0)B.-x0是f(-x)的极小值点C.-x0是-f(x)的极小值点D.-x0是-f(-x)的极小值点解析:取函数f(x)=x3-x,则x=-33为f(x)的极大值点,但f(3)>f(-33),∴排除A.取函数f(x)=-(x-1)2,则x=1是f(x)的极大值点,f(-x)=-(x+1)2,-1不是f(-x)的极小值点,∴排除B;-f(x)=(x-1)2,-1不是-f(x)的极小值点,∴排除C.故选D.答案:D11.若函数y=f(x)满足xf′(x)>-f(x)在R上恒成立,且a>b,则()A.af(b)>bf(a) B.af(a)>bf(b)C.af(a)<bf(b) D.af(b)<bf(a)解析:设g(x)=xf(x),则g′(x)=xf′(x)+f(x)>0,∴g(x)在R上是增函数,又a>b,∴g(a)>g(b)即af(a)>bf(b).答案:B12.设函数f (x )满足x 2f ′(x )+2xf (x )=e x x ,f (2)=e 28,则x >0时,f (x )( )A .有极大值,无极小值B .有极小值,无极大值C .既有极大值又有极小值D .既无极大值也无极小值解析:由题意知f ′(x )=e x x 3-2f (x )x =e x -2x 2f (x )x3.令g (x )=e x-2x 2f (x ),则g ′(x )=e x -2x 2f ′(x )-4xf (x )=e x -2(x 2f ′(x )+2xf (x ))=e x -2e xx =e x ⎝ ⎛⎭⎪⎫1-2x .由g ′(x )=0得x =2,当x =2时,g (x )min =e 2-2×22×e 28=0,即g (x )≥0,则当x >0时,f ′(x )=g (x )x 3≥0,故f (x )在(0,+∞)上单调递增,既无极大值也无极小值.答案:D第Ⅱ卷(非选择题,共90分)二、填空题(每小题5分,共20分)13.若抛物线y =x 2-x +c 上一点P 的横坐标为-2,抛物线过点P 的切线恰好过坐标原点,则c 的值为________.解析:∵y ′=2x -1,∴y ′|x =-2=-5. 又P (-2,6+c ),∴6+c-2=-5.∴c =4. 答案:414.如果函数f (x )=x 3-6bx +3b 在区间(0,1)内存在与x 轴平行的切线,则实数b 的取值范围是________.解析:存在与x 轴平行的切线,即f ′(x )=3x 2-6b =0有解,∵x ∈(0,1),∴b =x 22∈(0,12).答案:{b |0<b <12}15.已知a ≤4x 3+4x 2+1对任意x ∈[-1,1]都成立,则实数a 的取值范围是________.解析:设f (x )=4x 3+4x 2+1,则f ′(x )=12x 2+8x =4x (3x +2),令f ′(x )=0,解得x 1=0,x 2=-23.又f (-1)=1, f (-23)=4327,f (0)=1,f (1)=9,故f (x )在[-1,1]上的最小值为1,故a ≤1.答案:(-∞,1]16.设二次函数f (x )=ax 2+bx +c (a ≠0)的导数为f ′(x ),f ′(0)>0,若∀x ∈R ,恒有f (x )≥0,则f (1)f ′(0)的最小值是________.解析:二次函数f (x )=ax 2+bx +c (a ≠0)的导数为f ′(x )=2ax +b ,由f ′(0)>0,得b >0,又对∀x ∈R ,恒有f (x )≥0,则a >0, 且Δ=b 2-4ac ≤0,故c >0,所以f (1)f ′(0)=a +b +c b =a b +c b +1≥2acb 2+1≥2ac4ac +1=2,所以f (1)f ′(0)的最小值为2.答案:2三、解答题(写出必要的计算步骤,只写最后结果不得分,共70分)17.(10分)已知函数f (x )=ln(2x +a )+x 2,且f ′(0)=23.(1)求f (x )的解析式;(2)求曲线f (x )在x =-1处的切线方程. 解:(1)∵f (x )=ln(2x +a )+x 2,∴f ′(x )=12x +a ·(2x +a )′+2x =22x +a +2x .又∵f ′(0)=23,∴2a =23,解得a =3. 故f (x )=ln(2x +3)+x 2.(2)由(1)知f ′(x )=22x +3+2x =4x 2+6x +22x +3,且f (-1)=ln(-2+3)+(-1)2=1, f ′(-1)=4×(-1)2+6×(-1)+22(-1)+3=0,因此曲线f (x )在(-1,1)处的切线方程是y -1=0(x +1),即y =1.18.(12分)已知函数f (x )=13x 3+ax +b (a ,b ∈R )在x =2处取得极小值-43.(1)求函数f (x )的增区间;(2)若f (x )≤m 2+m +103对x ∈[-4,3]恒成立,求实数m 的取值范围.解:(1)由已知得f (2)=-43,f ′(2)=0,又f ′(x )=x 2+a ,所以83+2a +b =-43,4+a =0,所以a =-4,b =4,则f (x )=13x 3-4x +4,令f ′(x )=x 2-4>0,得x <-2或x >2,所以增区间为(-∞,-2),(2,+∞).(2)f (-4)=-43,f (-2)=283,f (2)=-43,f (3)=1,则当x ∈[-4,3]时,f (x )的最大值为283,故要使f (x )≤m 2+m +103对∈[-4,3]恒成立,只要283≤m 2+m +103,所以实数m 的取值范围是m ≥2或m ≤-3.19.(12分)已知函数f (x )=e x (ax +b )-x 2-4x ,曲线y =f (x )在点(0,f (0))处的切线方程为y =4x +4.(1)求a ,b 的值;(2)讨论f (x )的单调性,并求f (x )的极大值. 解:(1)f ′(x )=e x (ax +a +b )-2x -4.由已知得f (0)=4,f ′(0)=4,故b =4,a +b -4=4,所以a =4,b =4.(2)由(1)知,f (x )=4e x (x +1)-x 2-4x , f ′(x )=4e x(x +2)-2x -4=4(x +2)(e x-12).令f ′(x )=0,得x =-ln2或x =-2.从而当x ∈(-∞,-2)∪(-ln2,+∞)时,f ′(x )>0;当x ∈(-2,-ln2)时,f ′(x )<0.故f (x )在(-∞,-2),(-ln2,+∞)上单调递增,在(-2,-ln2)上单调递减.当x =-2时,函数f (x )取得极大值, 极大值为f (-2)=4(1-e -2).20.(12分)已知函数f (x )=x -a ln x (a ∈R ).(1)当a =2时,求曲线y =f (x )在点A (1,f (1))处的切线方程. (2)求函数f (x )的极值.解:函数f (x )的定义域为(0,+∞),f ′(x )=1-ax . (1)当a =2时,f (x )=x -2ln x ,f ′(x )=1-2x (x >0),所以f (1)=1,f ′(1)=-1,所以y =f (x )在点A (1,f (1))处的切线方程为y -1=-(x -1),即x +y -2=0.(2)由f ′(x )=1-a x =x -ax ,x >0可知:①当a ≤0时,f ′(x )>0,函数f (x )为(0,+∞)上的增函数,函数f(x)无极值;②当a>0时,由f′(x)=0,解得x=a;因为x∈(0,a)时,f′(x)<0,x∈(a,+∞)时,f′(x)>0,所以f(x)在x=a处取得极小值,且极小值为f(a)=a-a ln a,无极大值.综上:当a≤0时,函数f(x)无极值,当a>0时,函数f(x)在x=a处取得极小值a-a ln a,无极大值.21.(12分)某地政府鉴于某种日常食品价格增长过快,欲将这种食品价格控制在适当范围内,决定给这种食品生产厂家提供政府补贴,设这种食品的市场价格为x 元/千克,政府补贴为t 元/千克,根据市场调查,当16≤x ≤24时,这种食品日供应量p 万千克,日需量q 万千克近似地满足关系:p =2(x +4t -14)(t >0),q =24+8ln 20x .当p =q 时的市场价格称为市场平衡价格.(1)将政府补贴表示为市场平衡价格的函数,并求出函数的值域;(2)为使市场平衡价格不高于20元/千克,政府补贴至少为多少元/千克?解:(1)由p =q 得2(x +4t -14) =24+8ln 20x (16≤x ≤24,t >0), 即t =132-14x +ln 20x (16≤x ≤24). ∵t ′=-14-1x <0,∴t 是x 的减函数. ∴t min =132-14×24+ln 2024=12+ln 2024=12+ln 56; t max =132-14×16+ln 2016=52+ln 54, ∴值域为⎣⎢⎡⎦⎥⎤12+ln 56,52+ln 54.(2)由(1)知t =132-14x +ln 20x (16≤x ≤24).而当x =20时,t =132-14×20+ln 2020=1.5(元/千克),∵t 是x 的减函数,∴欲使x ≤20,必须t ≥1.5(元/千克). 要使市场平衡价格不高于20元/千克,政府补贴至少为1.5元/千克.22.(12分)已知函数f (x )=ln x -12ax 2-2x .(1)若函数f (x )在x =2处取得极值,求实数a 的值. (2)若函数f (x )在定义域内单调递增,求实数a 的取值范围. (3)当a =-12时,关于x 的方程f (x )=-12x +b 在[1,4]上恰有两个不相等的实数根,求实数b 的取值范围.解:(1)由题意,得f ′(x )=-ax 2+2x -1x(x >0), 因为x =2时,函数f (x )取得极值,所以f ′(2)=0,解得a =-34,经检验,符合题意.(2)函数f (x )的定义域为(0,+∞),依题意,f ′(x )≥0在x >0时恒成立,即ax 2+2x -1≤0在x >0时恒成立,则a ≤1-2x x 2=⎝ ⎛⎭⎪⎫1x -12-1在x >0时恒成立,即a ≤⎝ ⎛⎭⎪⎫⎝⎛⎭⎪⎫1x -12-1min (x >0),当x =1时,⎝⎛⎭⎪⎫1x -12-1取最小值-1,所以a 的取值范围是(-∞,-1].(3)当a =-12时,f (x )=-12x +b , 即14x 2-32x +ln x -b =0.设g (x )=14x 2-32x +ln x -b (x >0), 则g ′(x )=(x -2)(x -1)2x, 当x 变化时,g ′(x ),g (x )的变化情况如下表:x (0,1) 1 (1,2) 2 (2,4) g ′(x ) + 0 - 0 + g (x )极大极小所以g (x )极小值=g (2)=ln2-b -2, g (x )极大值=g (1)=-b -54, 又g (4)=2ln2-b -2,因为方程g (x )=0在[1,4]上恰有两个不相等的实数根, 则⎩⎪⎨⎪⎧g (1)≥0,g (2)<0,g (4)≥0,解得ln2-2<b ≤-54,所以实数b 的取值范围是(ln2-2,-54).。
2024年高考数学总复习第三章《导数及其应用》测试卷及答案解析
2024年高考数学总复习第三章《导数及其应用》测试卷及答案解析(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.已知曲线y=f(x)在x=5处的切线方程是y=-x+5,则f(5)与f′(5)分别为() A.5,-1B.-1,5C.-1,0D.0,-1答案D解析由题意可得f(5)=-5+5=0,f′(5)=-1,故选D.2.已知函数f(x)=x sin x+ax,且f1,则a等于()A.0B.1C.2D.4答案A解析∵f′(x)=sin x+x cos x+a,且f1,∴sin π2+π2cosπ2+a=1,即a=0.3.若曲线y=mx+ln x在点(1,m)处的切线垂直于y轴,则实数m等于() A.-1B.0C.1D.2答案A解析f(x)的导数为f′(x)=m+1x,曲线y=f(x)在点(1,m)处的切线斜率为k=m+1=0,可得m=-1.故选A.4.已知f1(x)=sin x+cos x,f n+1(x)是f n(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,f n+1(x)=f n′(x),n∈N*,则f2020(x)等于()A.-sin x-cos x B.sin x-cos xC.-sin x+cos x D.sin x+cos x答案B解析∵f1(x)=sin x+cos x,∴f2(x)=f1′(x)=cos x-sin x,∴f3(x)=f2′(x)=-sin x-cos x,∴f4(x)=f3′(x)=-cos x+sin x,∴f5(x)=f4′(x)=sin x+cos x=f1(x),∴f n(x)是以4为周期的函数,∴f2020(x)=f4(x)=sin x-cos x,故选B.5.已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(e)+ln x(其中e为自然对数的底数),则f′(e)等于()A .1B .-1C .-eD .-e -1答案D解析已知f (x )=2xf ′(e)+ln x ,其导数f ′(x )=2f ′(e)+1x,令x =e ,可得f ′(e)=2f ′(e)+1e ,变形可得f ′(e)=-1e ,故选D.6.函数y =12x 2-ln x 的单调递减区间为()A .(-1,1]B .(0,1]C .[1,+∞)D .(0,+∞)答案B解析由题意知,函数的定义域为(0,+∞),又由y ′=x -1x≤0,解得0<x ≤1,所以函数的单调递减区间为(0,1].7.(2019·沈阳东北育才学校模拟)已知定义在(0,+∞)上的函数f (x )=x 2+m ,g (x )=6ln x -4x ,设两曲线y =f (x )与y =g (x )在公共点处的切线相同,则m 值等于()A .5B .3C .-3D .-5答案D解析f ′(x )=2x ,g ′(x )=6x -4,令2x =6x-4,解得x =1,这就是切点的横坐标,代入g (x )求得切点的纵坐标为-4,将(1,-4)代入f (x )得1+m =-4,m =-5.故选D.8.(2019·新乡模拟)若函数f (x )=a e x +sin x 在-π2,0上单调递增,则a 的取值范围为()B .[-1,1]C .[-1,+∞)D .[0,+∞)答案D解析依题意得,f ′(x )=a e x +cos x ≥0,即a ≥-cos xe x 对x ∈-π2,0恒成立,设g (x )=-cos xe x ,x ∈-π2,0,g ′(x )g ′(x )=0,则x =-π4,当x ∈-π2,-g ′(x )<0;当x -π4,0时,g ′(x )>0,故g (x )max =g (0,则a ≥0.故选D.9.(2019·河北衡水中学调研)如图所示,某几何体由底面半径和高均为5的圆柱与半径为5的半球面对接而成,该封闭几何体内部放入一个小圆柱体,且小圆柱体的上下底面均与外层圆柱的底面平行,则小圆柱体积的最大值为()A.2000π9B.4000π27C .81πD .128π答案B解析小圆柱的高分为上下两部分,上部分同大圆柱一样为5,下部分深入底部半球内设为h (0<h <5),小圆柱的底面半径设为r (0<r <5),由于r ,h 和球的半径5满足勾股定理,即r 2+h 2=52,所以小圆柱体积V =πr 2(h +5)=π(25-h 2)(h +5)(0<h <5),求导V ′=-π(3h -5)·(h +5),当0<h ≤53时,体积V 单调递增,当53<h <5时,体积V 单调递减.所以当h =53时,小圆柱体积取得最大值,V max ==4000π27,故选B.10.(2019·凉山诊断)若对任意的0<x 1<x 2<a 都有x 2ln x 1-x 1ln x 2<x 1-x 2成立,则a 的最大值为()A.12B .1C .eD .2e答案B解析原不等式可转化为1+ln x 1x 1<1+ln x 2x 2,构造函数f (x )=1+ln x x ,f ′(x )=-ln xx2,故函数在(0,1)上导数大于零,单调递增,在(1,+∞)上导数小于零,单调递减.由于x 1<x 2且f (x 1)<f (x 2),故x 1,x 2在区间(0,1)上,故a 的最大值为1,故选B.11.(2019·洛阳、许昌质检)设函数y =f (x ),x ∈R 的导函数为f ′(x ),且f (x )=f (-x ),f ′(x )<f (x ),则下列不等式成立的是(注:e 为自然对数的底数)()A .f (0)<e -1f (1)<e 2f (2)B .e -1f (1)<f (0)<e 2f (2)C .e 2f (2)<e -1f (1)<f (0)D .e 2f (2)<f (0)<e -1f (1)答案B解析设g (x )=e -x f (x ),∴g ′(x )=-e -x f (x )+e -x f ′(x )=e -x (f ′(x )-f (x )),∵f ′(x )<f (x ),∴g ′(x )<0,∴g (x )为减函数.∵g (0)=e 0f (0)=f (0),g (1)=e -1f (1),g (-2)=e 2f (-2)=e 2f (2),且g (-2)>g (0)>g (1),∴e -1f (1)<f (0)<e 2f (2),故选B.12.(2019·廊坊省级示范高中联考)已知函数f (x )=-13x 3-12x 2+ax -b 的图象在x =0处的切线方程为2x -y -a =0,若关于x 的方程f (x 2)=m 有四个不同的实数解,则m 的取值范围为()A.-323,-B.-2-323,-2答案D解析由函数f (x )=-13x 3-12x 2+ax -b ,可得f ′(x )=-x 2-x +a ,则f (0)=-b =-a ,f ′(0)=a =2,则b =2,即f (x )=-13x 3-12x 2+2x -2,f ′(x )=-x 2-x +2=-(x -1)(x +2),所以函数f (x )在(-2,1)上单调递增,在(-∞,-2),(1,+∞)上单调递减,又由关于x 的方程f (x 2)=m 有四个不同的实数解,等价于函数f (x )的图象与直线y =m 在x ∈(0,+∞),上有两个交点,又f (0)=-2,f (1)=-56,所以-2<m <-56,故选D.二、填空题(本大题共4小题,每小题5分,共20分)13.(2019·陕西四校联考)已知函数f (x )=ln x +2x 2-4x ,则函数f (x )的图象在x =1处的切线方程为________________.答案x -y -3=0解析∵f (x )=ln x +2x 2-4x ,∴f ′(x )=1x +4x -4,∴f ′(1)=1,又f (1)=-2,∴所求切线方程为y -(-2)=x -1,即x -y -3=0.14.已知函数f (x )=(x -a )ln x (a ∈R ),若函数f (x )存在三个单调区间,则实数a 的取值范围是________.答案-1e2,解析f ′(x )=ln x +1x (x -a )=ln x +1-ax,函数f (x )=(x -a )ln x (a ∈R ),若函数f (x )存在三个单调区间,则f ′(x )有两个变号零点,即f ′(x )=0有两个不等实根,即a =x (ln x +1)有两个不等实根,转化为y =a 与y =x (ln x +1)的图象有两个不同的交点.令g (x )=x (ln x +1),则g ′(x )=ln x +2,令ln x +2=0,则x =1e 2,即g (x )=x (ln x +1)[g (x )]min =-1e 2,当x →0时,g (x )→0,当x →+∞时,f (x )→+∞,所以结合f (x )的图象(图略)可知a -1e 2,15.(2019·山师大附中模拟)已知函数f (x )=x 3-2x +e x -1e x ,其中e 是自然对数的底数,f (a -1)+f (2a 2)≤0,则实数a 的取值范围是________.答案-1,12解析由函数f (x )=x 3-2x +e x -1e x f ′(x )=3x 2-2+e x +1e x ≥-2+e x +1ex ≥-2+2e x ·1e x=0,当且仅当x =0时等号成立,可得f (x )在R 上递增,又f (-x )+f (x )=(-x )3+2x +e -x -e x +x 3-2x +e x -1e x 0,可得f (x )为奇函数,则f (a -1)+f (2a 2)≤0,即有f (2a 2)≤0-f (a -1)=f (1-a ),即有2a 2≤1-a ,解得-1≤a ≤12.16.(2019·湖北黄冈中学、华师附中等八校联考)定义在R 上的函数f (x )满足f (-x )=f (x ),且对任意的不相等的实数x 1,x 2∈[0,+∞)有f (x 1)-f (x 2)x 1-x 2<0成立,若关于x 的不等式f (2mx -ln x-3)≥2f (3)-f (-2mx +ln x +3)在x ∈[1,3]上恒成立,则实数m 的取值范围是______________.答案12e ,1+ln 36解析∵函数f (x )满足f (-x )=f (x ),∴函数f (x )为偶函数.又f (2mx -ln x -3)≥2f (3)-f (-2mx +ln x +3)=2f (3)-f (2mx -ln x -3),∴f (2mx -ln x -3)≥f (3).由题意可得函数f (x )在(-∞,0)上单调递增,在[0,+∞)上单调递减.∴|2mx -ln x -3|≤3对x ∈[1,3]恒成立,∴-3≤2mx -ln x -3≤3对x ∈[1,3]恒成立,即ln x2x ≤m ≤ln x +62x对x ∈[1,3]恒成立.令g (x )=ln x2x ,x ∈[1,3],则g ′(x )=1-ln x 2x 2∴g (x )在[1,e ]上单调递增,在(e,3]上单调递减,∴g (x )max =g (e)=12e .令h (x )=ln x +62x ,x ∈[1,3],则h ′(x )=-5-ln x2x 2<0,∴h (x )在[1,3]上单调递减,∴h (x )min =h (3)=6+ln 36=1+ln 36.综上可得实数m 的取值范围为12e ,1+ln 36.三、解答题(本大题共70分)17.(10分)(2019·辽宁重点高中联考)已知函数f (x )=x 3+mx 2-m 2x +1(m 为常数,且m >0)有极大值9.(1)求m 的值;(2)若斜率为-5的直线是曲线y =f (x )的切线,求此直线方程.解(1)f ′(x )=3x 2+2mx -m 2=(x +m )(3x -m )=0,令f ′(x )=0,则x =-m 或x =13m ,当x 变化时,f ′(x )与f (x )的变化情况如下表:f ′(x )+0-0+f (x )增极大值减极小值增从而可知,当x =-m 时,函数f (x )取得极大值9,即f (-m )=-m 3+m 3+m 3+1=9,∴m =2.(2)由(1)知,f (x )=x 3+2x 2-4x +1,依题意知f ′(x )=3x 2+4x -4=-5,∴x =-1或x =-13,又f (-1)=6,=6827,所以切线方程为y -6=-5(x +1)或y -6827=-即5x +y -1=0或135x +27y -23=0.18.(12分)(2019·成都七中诊断)已知函数f (x )=x sin x +2cos x +ax +2,其中a 为常数.(1)若曲线y =f (x )在x =π2处的切线斜率为-2,求该切线的方程;(2)求函数f (x )在x ∈[0,π]上的最小值.解(1)求导得f ′(x )=x cos x -sin x +a ,由f a -1=-2,解得a =-1.此时2,所以该切线的方程为y -2=-2x +y -2-π=0.(2)对任意x ∈[0,π],f ″(x )=-x sin x ≤0,所以f ′(x )在[0,π]内单调递减.当a ≤0时,f ′(x )≤f ′(0)=a ≤0,∴f (x )在区间[0,π]上单调递减,故f (x )min =f (π)=a π.当a ≥π时,f ′(x )≥f ′(π)=a -π≥0,∴f (x )在区间[0,π]上单调递增,故f (x )min =f (0)=4.当0<a <π时,因为f ′(0)=a >0,f ′(π)=a -π<0,且f ′(x )在区间[0,π]上单调递减,结合零点存在定理可知,存在唯一x 0∈(0,π),使得f ′(x 0)=0,且f (x )在[0,x 0]上单调递增,在[x 0,π]上单调递减.故f (x )的最小值等于f (0)=4和f (π)=a π中较小的一个值.①当4π≤a <π时,f (0)≤f (π),故f (x )的最小值为f (0)=4.②当0<a <4π时,f (π)≤f (0),故f (x )的最小值为f (π)=a π.综上所述,函数f (x )的最小值f (x )min,a ≥4π,π,a <4π.19.(12分)(2019·武汉示范高中联考)已知函数f (x )=4ln x -mx 2+1(m ∈R ).(1)若函数f (x )在点(1,f (1))处的切线与直线2x -y -1=0平行,求实数m 的值;(2)若对于任意x ∈[1,e ],f (x )≤0恒成立,求实数m 的取值范围.解(1)∵f (x )=4ln x -mx 2+1,∴f ′(x )=4x -2mx ,∴f ′(1)=4-2m ,∵函数f (x )在(1,f (1))处的切线与直线2x -y -1=0平行,∴f ′(1)=4-2m =2,∴m =1.(2)∵对于任意x ∈[1,e ],f (x )≤0恒成立,∴4ln x -mx 2+1≤0,在x ∈[1,e ]上恒成立,即对于任意x ∈[1,e ],m ≥4ln x +1x 2恒成立,令g (x )=4ln x +1x 2,x ∈[1,e ],g ′(x )=2(1-4ln x )x 3,令g ′(x )>0,得1<x <14e ,令g ′(x )<0,得14e <x <e ,当x 变化时,g ′(x ),g (x )的变化如下表:x 14(1,e )14e14(e ,e)g ′(x )+0-g (x )极大值∴函数g (x )在区间[1,e ]上的最大值g (x )max =g (14e )=141244ln e 1(e )+=2e e ,∴m ≥2ee,即实数m 的取值范围是2ee ,+20.(12分)已知函数f (x )=ln x -ax (ax +1),其中a ∈R .(1)讨论函数f (x )的单调性;(2)若函数f (x )在(0,1]内至少有1个零点,求实数a 的取值范围.解(1)依题意知,函数f (x )的定义域为(0,+∞),且f ′(x )=1x -2a 2x -a =2a 2x 2+ax -1-x =(2ax -1)(ax +1)-x,当a =0时,f (x )=ln x ,函数f (x )在(0,+∞)上单调递增;当a >0时,由f ′(x )>0,得0<x <12a,由f ′(x )<0,得x >12a,函数f (x )当a <0时,由f ′(x )>0,得0<x <-1a ,由f ′(x )<0,得x >-1a ,函数f (x )-1a,+.(2)①当a =0时,函数f (x )在(0,1]内有1个零点x 0=1;②当a >0时,由(1)知函数f (x )若12a ≥1,即0<a ≤12时,f (x )在(0,1]上单调递增,由于当x →0时,f (x )→-∞且f (1)=-a 2-a <0知,函数f (x )在(0,1]内无零点;若0<12a <1,即当a >12时,f (x )1上单调递减,要使函数f (x )在(0,1]内至少有1个零点,只需满足0,即ln 12a ≥34,又∵a >12,∴ln 12a <0,∴不等式不成立.∴f (x )在(0,1]内无零点;③当a <0时,由(1)知函数f (x )-1a,+若-1a ≥1,即-1≤a <0时,f (x )在(0,1]上单调递增,由于当x →0时,f (x )→-∞,且f (1)=-a 2-a >0,知函数f (x )在(0,1]内有1个零点;若0<-1a <1,即a <-1时,函数f (x )-1a,1上单调递减,由于当x →0时,f (x )→-∞,且当a <-1时,,知函数f (x )在(0,1]内无零点.综上可得a 的取值范围是[-1,0].21.(12分)(2019·湖北黄冈中学、华师附中等八校联考)在工业生产中,对一正三角形薄钢板(厚度不计)进行裁剪可以得到一种梯形钢板零件,现有一边长为3(单位:米)的正三角形钢板(如图),沿平行于边BC 的直线DE 将△ADE 剪去,得到所需的梯形钢板BCED ,记这个梯形钢板的周长为x (单位:米),面积为S (单位:平方米).(1)求梯形BCED 的面积S 关于它的周长x 的函数关系式;(2)若在生产中,梯形BCED 试确定这个梯形的周长x 为多少时,该零件才可以在生产中使用?解(1)∵DE ∥BC ,△ABC 是正三角形,∴△ADE 是正三角形,AD =DE =AE ,BD =CE =3-AD ,则DE +2(3-AD )+3=9-AD =x ,S =(3+AD )·(3-AD )·sin 60°2=3(12-x )(x -6)4(6<x <9),化简得S =34(-x 2+18x -72)(6<x <9).故梯形BCED 的面积S 关于它的周长x 的函数关系式为S =34(-x 2+18x -72)(6<x <9).(2)∵由(1)得S =34(-x 2+18x -72)(6<x <9),令f (x )=S x =x -72x +x <9),∴f ′(x )1令f ′(x )=0,得x =62或x =-62(舍去),f (x ),f ′(x )随x 的变化如下表:x(6,62)62(62,9)f ′(x )+0-f (x )单调递增极大值单调递减∴当x =62时,函数f (x )=S x有最大值,为f (62)=923-36.∴当x =62米时,该零件才可以在生产中使用.22.(12分)(2019·衡水中学调研)已知函数f (x )=k e x -x 2(其中k ∈R ,e 是自然对数的底数).(1)若k =2,当x ∈(0,+∞)时,试比较f (x )与2的大小;(2)若函数f (x )有两个极值点x 1,x 2(x 1<x 2),求k 的取值范围,并证明:0<f (x 1)<1.解(1)当k =2时,f (x )=2e x -x 2,则f ′(x )=2e x -2x ,令h (x )=2e x -2x ,h ′(x )=2e x -2,由于x ∈(0,+∞),故h ′(x )=2e x -2>0,于是h (x )=2e x -2x 在(0,+∞)上为增函数,所以h (x )=2e x -2x >h (0)=2>0,即f ′(x )=2e x -2x >0在(0,+∞)上恒成立,从而f (x )=2e x -x 2在(0,+∞)上为增函数,故f (x )=2e x -x 2>f (0)=2.(2)函数f (x )有两个极值点x 1,x 2,则x 1,x 2是f ′(x )=k e x -2x =0的两个根,即方程k =2x ex 有两个根,设φ(x )=2x e x ,则φ′(x )=2-2x ex ,当x <0时,φ′(x )>0,函数φ(x )单调递增且φ(x )<0;当0<x <1时,φ′(x )>0,函数φ(x )单调递增且φ(x )>0;当x >1时,φ′(x )<0,函数φ(x )单调递减且φ(x )>0.作出函数φ(x )的图象如图所示,要使方程k =2x e x 有两个根,只需0<k <φ(1)=2e,故实数k f (x )的两个极值点x 1,x 2满足0<x 1<1<x 2,由f ′(x 1)=1e x k -2x 1=0得k =112e x x ,所以f (x 1)=1e x k -x 21=112e x x 1e x -x 21=-x 21+2x 1=-(x 1-1)2+1,由于x 1∈(0,1),所以0<-(x 1-1)2+1<1,所以0<f (x 1)<1.。
导数及其应用测试题(有详细答案)
《导数与其应用》一、选择题 1.0()0f x '=是函数()f x 在点0x 处取极值的: A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件 2、设曲线21y x =+在点))(,(x f x 处的切线的斜率为()g x ,则函数()cos y g x x =的部分图象可以为 A. C.D.3.设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个直角坐标系中,不可能正确的是( )4.若曲线y =x 2++b 在点(0,b )处的切线方程是x -y +1=0,则( )A .a =1,b =1B .a =-1,b =1C .a =1,b =-1D .a =-1,b =-15.函数f (x )=x 3+2+3x -9,已知f (x )在x =-3时取得极值,则a 等于( )A .2B .3C .4D .56. 设函数()f x 的导函数为()f x ',且()()221f x x x f '=+⋅,则()0f '等于( )A 、0B 、4-C 、2-D 、2 7. 直线y x =是曲线ln y a x =+的一条切线,则实数a 的值为( )A .1-B .eC .ln 2D .1 8. 若函数)1,1(12)(3+--=k k x x x f 在区间上不是单调函数,则实数k 的取值范围( ) A .3113≥≤≤--≤k k k 或或 B .3113<<-<<-k k 或C .22<<-kD .不存在这样的实数k 9.函数()f x 的定义域为(),a b ,导函数()f x '在(),a b 内的图像如图所示,则函数()f x 在(),a b 内有极小值点 ( )A .1个B .2个C .3个D .4个10.已知二次函数2()f x ax bx c =++的导数为'()f x ,'(0)0f >,对于任意实数x 都有()0f x ≥,则(1)'(0)f f 的最小值为( )A .3B .52C .2D .32二、填空题(本大题共4个小题,每小题5分,共20分) 11.函数sin xy x=的导数为 12、已知函数223)(a bx ax x x f +++=在1处有极值为10,则f (2)等于. 13.函数2cos y x x =+在区间[0,]2π上的最大值是14.已知函数3()f x x ax =+在R 上有两个极值点,则实数a 的取值范围是15. 已知函数)(x f 是定义在R 上的奇函数,0)1(=f ,)()(2>-'x x f x f x )(0>x ,则不等式0)(2>x f x 的解集是三、解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)Ox xx xy y y yOO O16. 设函数32()2338f x x ax bx c=+++在1x=与2x=时取得极值.(1)求a、b的值;(2)若对于任意的[03]x∈,,都有2()f x c<成立,求c的取值范围.17. 已知函数32()23 3.f x x x=-+(1)求曲线()y f x=在点2x=处的切线方程;(2)若关于x的方程()0f x m+=有三个不同的实根,求实数m的取值范围.18. 设函数Rxxxxf∈+-=,56)(3.(1)求)(x f的单调区间和极值;(2)若关于x的方程axf=)(有3个不同实根,求实数a的取值范围.(3)已知当)1()(,),1(-≥+∞∈xkxfx时恒成立,求实数k的取值范围.19. (本题满分12分)已知函数()ln f x x x =. (Ⅰ)求()f x 的最小值;(Ⅱ)若对所有1x ≥都有()1f x ax ≥-,求实数a 的取值范围. 20. 已知()R a x x a ax x f ∈+++-=14)1(3)(23(1)当1-=a 时,求函数的单调区间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导数单元测试题 11.29
一、填空题
1.函数()2
2)(x x f π=的导数是_______
2.函数x
e
x x f -⋅=)(的一个单调递增区间是________
3.若函数b bx x x f 33)(3
+-=在()1,0内有极小值,则实数b 的范围是_______
4.若曲线4
y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为______ 5.曲线x
y e =在点2
(2)e ,处的切线与坐标轴所围三角形的面积为_________
6.设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个直角坐标系中,不可能正确的是_______
7.已知二次函数2
()f x ax bx c =++的导数为'()f x ,'(0)0f >,对于任意实数x 都有
()0f x ≥,则
(1)
'(0)
f f 的最小值为________ 8.设2
:()e ln 21x
p f x x x mx =++++在(0)+∞,内单调递增,:5q m -≥,则p 是q 的______________条件
9. 函数)(x f 的图像如图所示,下列数值排序正确的是( ) (A ))2()3()3()2(0/
/
f f f f -<<< y (B ) )2()2()3()3(0/
/
f f f f <-<< (C ))2()3()2()3(0/
/
f f f f -<<<
(D ))3()2()2()3(0/
/
f f f f <<-< O 1 2 3 4 x 10.函数()ln f x x x =的单调递增区间是____.
11.已知函数3
()128f x x x =-+在区间[3,3]-上的最大值与最小值分别为,M m ,则
M m -=__.
12.点P 在曲线3
2
3
+
-=x x y 上移动,设在点P 处的切线的倾斜角为为α,则α的取值范围是
13.设函数()f x 的导函数为()f x ',且()()2
21f x x x f '=+⋅,则()0f '=_____
14.已知32
()(6)1f x x ax a x =++++有极大值和极小值,则a 的取值范围为_______
二.解答题
15.已知()132
3
+-+=x x ax x f 在R 上是减函数,求a 的取值范围。
16.设函数3
2
()2338f x x ax bx c =+++在1x =及2x =时取得极值.
(1)求a 、b 的值;
(2)若对于任意的[03]x ∈,,都有2
()f x c <成立,求c 的取值范围.
17. 已知函数32
()23 3.f x x x =-+ (1)求曲线()y f x =在点2x =处的切线方程;
(2)若关于x 的方程()0f x m +=有三个不同的实根,求实数m 的取值范围.
18.已知()R a x x a ax x f ∈+++-=14)1(3
)(23
(1)当1-=a 时,求函数的单调区间。
(2)当R a ∈时,讨论函数的单调增区间。
(3)是否存在负实数a ,使[]0,1-∈x ,函数有最小值-3?
一、选择题
1.()∴==,42)(222
x x x f ππ=⋅='x x f 242)(πx x f 28)(π=';
2.∴=⋅=-.)(x x
e x e
x x f []
=⋅-⋅='21)(x x x e e x e x f , ()[]
1,012<∴>⋅-x e e x x x
选(A) 3.()
b x b x x f -=-='2
2333)(,依题意,首先要求b>0, 所以()()
b x b x x f -+='3)(
由单调性分析,b x =
有极小值,由()1,0∈=b x 得.
4.解:与直线480x y +-=垂直的直线l 为40x y m -+=,即4
y x =在某一点的导数为4,而3
4y x '=,所以4
y x =在(1,1)处导数为4,此点的切线为430x y --=,
5.2
2
e 6.(D ) 7.2 8.必要不充分条件
9.B 设x=2,x=3时曲线上的点为AB,点A 处的切线为AT 点B 处的切线为BQ ,
T
=
-)2()3(f f AB k f f =--2
3)
2()3( ,)3(BQ k f =' ,)2(AT k f =' 如图所示,切线BQ 的倾斜角小于
直线AB 的倾斜角小于 切线AT 的倾斜角 <∴BQ k <AB k AT k
10.1,e ⎡⎫+∞⎪⎢⎣⎭ 11.32 12.⎪⎭
⎫⎢⎣⎡⋃⎪⎭⎫⎢⎣⎡πππ,432,0 13,4- 14,a<-3或a>6
三、解答题
(1) 当3-=a 时,()983131333
23+⎪⎭⎫ ⎝
⎛
--=+-+-=x x x x x f 。
由函数3
x y =在R 上的单调性,可知当3-=a 是,函数()x f 对R x ∈为减函数。
(2) 当3->a 时,函数()x f 在R 上存在增区间。
所以,当3->a 时,函数()x f 在
R 上不是单调递减函数。
综合(1)(2)(3)可知3-≤a 。
16.解:(1)2
()663f x x ax b '=++,
因为函数()f x 在1x =及2x =取得极值,则有(1)0f '=,(2)0f '=.
即6630241230a b a b ++=⎧⎨
++=⎩
,
.
解得3a =-,4b =.
(2)由(Ⅰ)可知,3
2
()29128f x x x x c =-++,
2()618126(1)(2)f x x x x x '=-+=--.
当(01)x ∈,时,()0f x '>; 当(12)x ∈,时,()0f x '<; 当(23)x ∈,时,()0f x '>.
所以,当1x =时,()f x 取得极大值(1)58f c =+,又(0)8f c =,(3)98f c =+. 则当[]03x ∈,时,()f x 的最大值为(3)98f c =+. 因为对于任意的[]03x ∈,,有2
()f x c <恒成立,
所以 2
98c c +<, 解得 1c <-或9c >, 因此c 的取值范围为(1)
(9)-∞-+∞,,.
17.解(1)2
()66,(2)12,(2)7,f x x x f f ''=-== ………………………2分
∴曲线()y f x =在2x =处的切线方程为712(2)y x -=-,即12170x y --=;……4分 (2)记3
2
2
()233,()666(1)g x x x m g x x x x x '=-++=-=-
令()0,0g x x '==或1. …………………………………………………………6分 则,(),()x g x g x '的变化情况如下表
………………………10分 由()g x 的简图知,当且仅当(0)0
,(1)0
g g >⎧⎨
<⎩
即30
,3220
m m m +>⎧-<<-⎨+<⎩时,
函数()g x 有三个不同零点,过点A 可作三条不同切线.
所以若过点A 可作曲线()y f x =的三条不同切线,m 的范围是(3,2)--.…………14分
18.(1)(),2,-∞-∈x 或(),,2+∞∈x )(x f 递减; (),2,2-∈x )(x f 递增; (2)1、当,0=a
(),
2,-∞-∈x )(x f 递增;2、当,0<a ,2,2⎪⎭
⎫ ⎝⎛∈a
x )(x f 递增;3、当,10<<a (),2,∞-∈x 或
,,2⎪⎭
⎫
⎝⎛+∞∈a x )(x f 递增; 当,1=a (),,+∞∞-∈x )(x f 递增;当,1>a ,2,⎪⎭
⎫ ⎝
⎛∞-∈a x 或(),,2+∞∈x )
(x f 递增;(3)因,0<a 由②分两类(依据:单调性,极小值点是否在区间[-1,0]上是分类“契机”:
1、当,2,12-≥⇔-≤a a [],2,20,1⎪⎭⎫ ⎝⎛⊆-∈a x )(x f 递增,3)1()(min -=-=f x f ,解得,243->-=a
2、当,2,12-≤⇔->a a
由单调性知:3)2
()(min -==a f x f ,化简得:01332=-+a a ,解得
,2621
3->±-=
a 不合要求;综上,4
3-=a 为所求。
